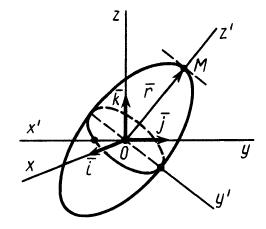
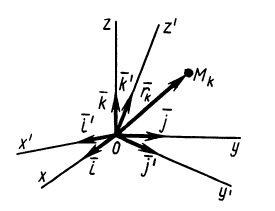
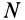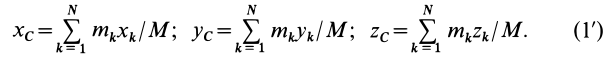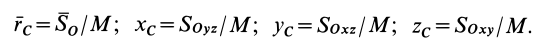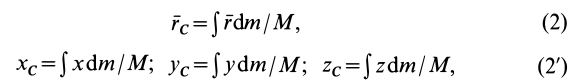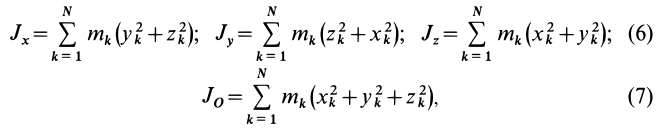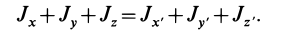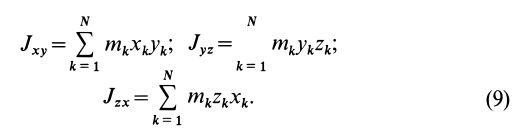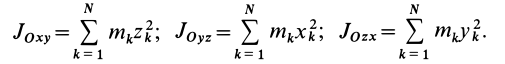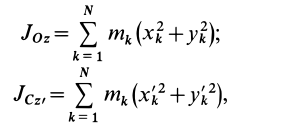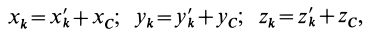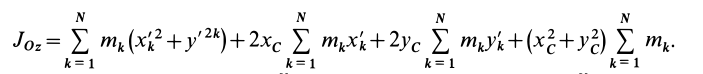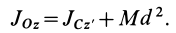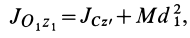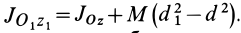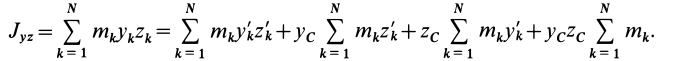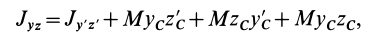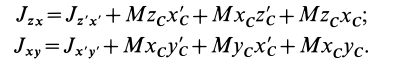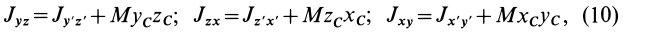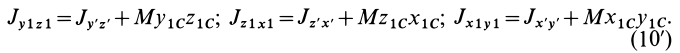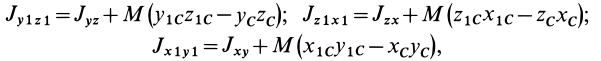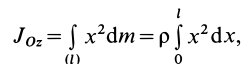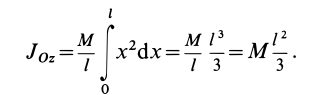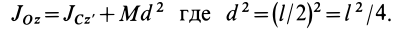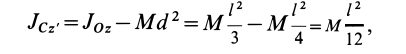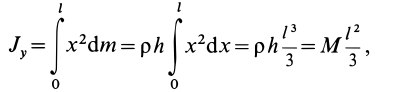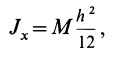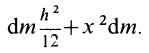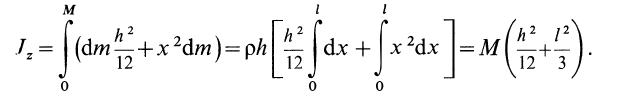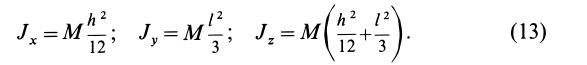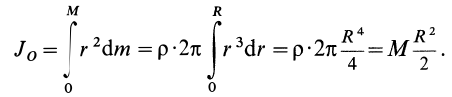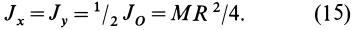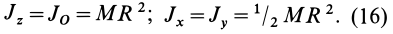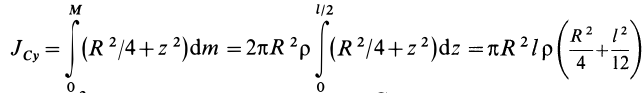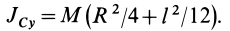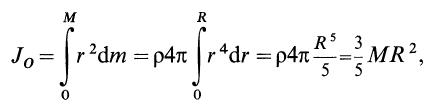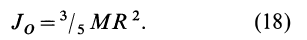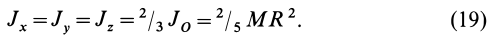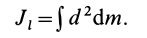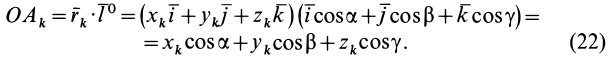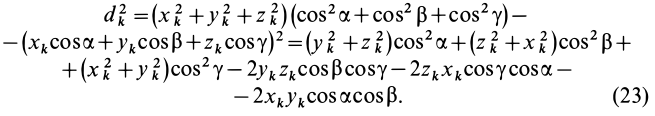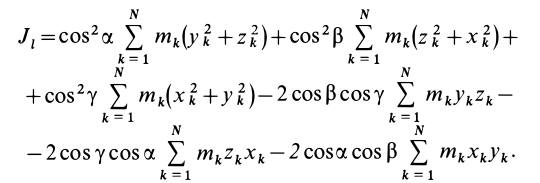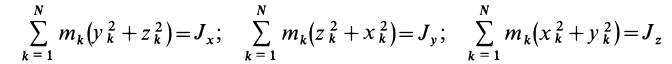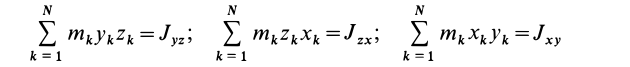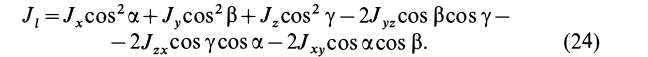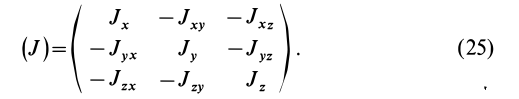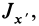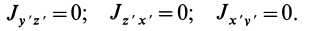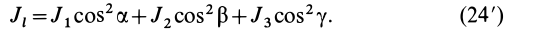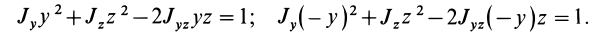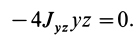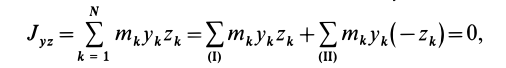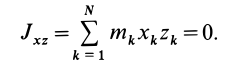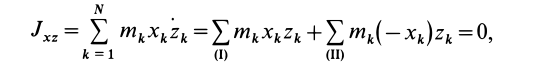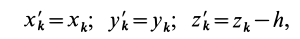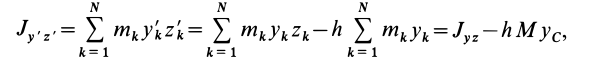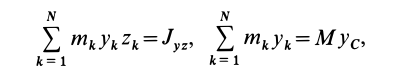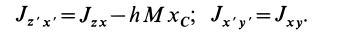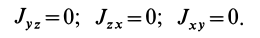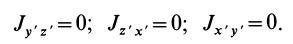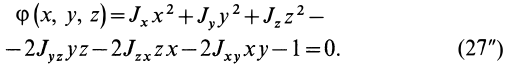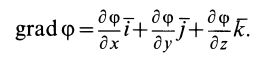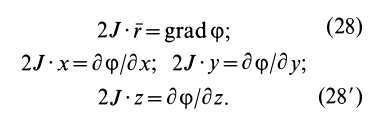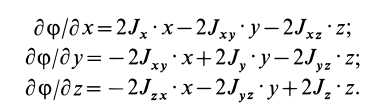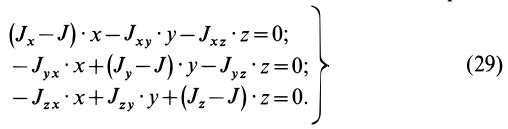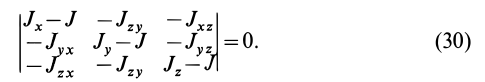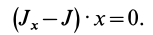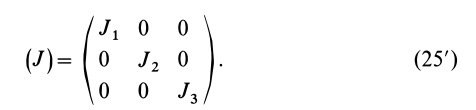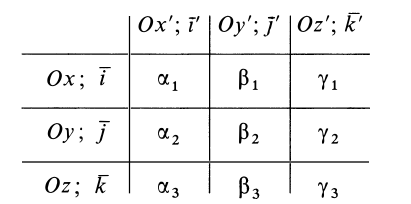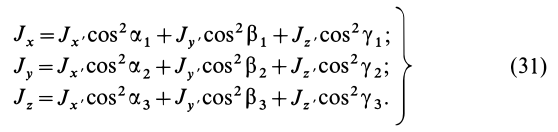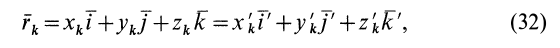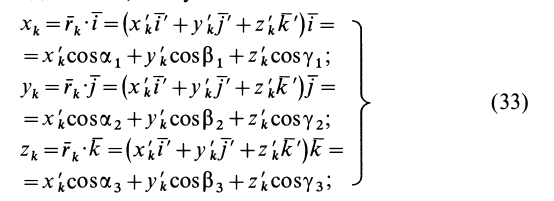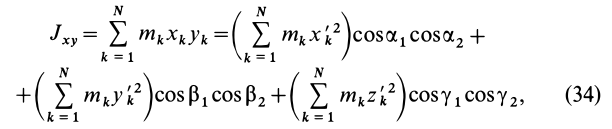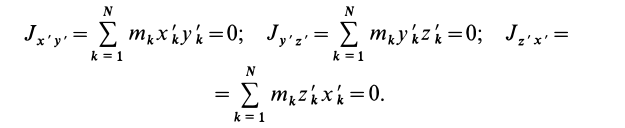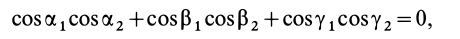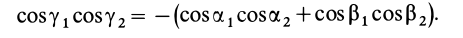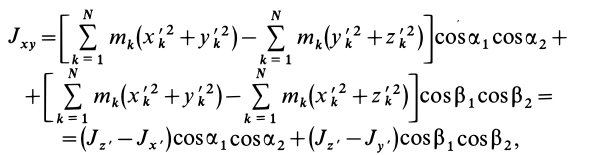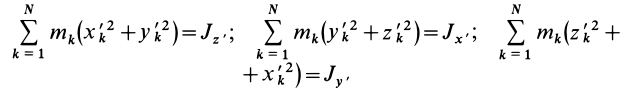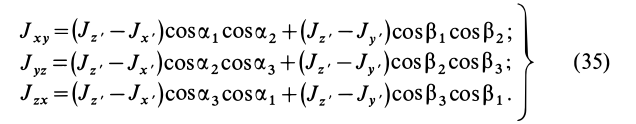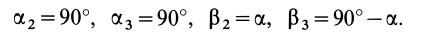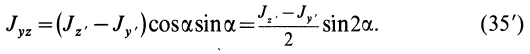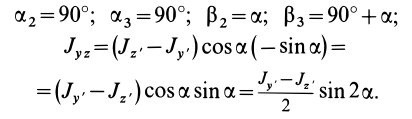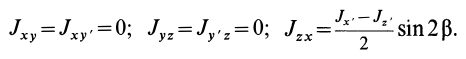Часто мы слышим выражения: «он инертный», «двигаться по инерции», «момент инерции». В переносном значении слово «инерция» может трактоваться как отсутствие инициативы и действий. Нас же интересует прямое значение.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Что такое инерция
Согласно определению инерция в физике – это способность тел сохранять состояние покоя или движения в отсутствие действия внешних сил.
Если с самим понятием инерции все понятно на интуитивном уровне, то момент инерции – отдельный вопрос. Согласитесь, сложно представить в уме, что это такое. В этой статье Вы научитесь решать базовые задачи на тему «Момент инерции».
Определение момента инерции
Из школьного курса известно, что масса – мера инертности тела. Если мы толкнем две тележки разной массы, то остановить сложнее будет ту, которая тяжелее. То есть чем больше масса, тем большее внешнее воздействие необходимо, чтобы изменить движение тела. Рассмотренное относится к поступательному движению, когда тележка из примера движется по прямой.
По аналогии с массой и поступательным движением момент инерции – это мера инертности тела при вращательном движении вокруг оси.
Момент инерции – скалярная физическая величина, мера инертности тела при вращении вокруг оси. Обозначается буквой J и в системе СИ измеряется в килограммах, умноженных на квадратный метр.
Как посчитать момент инерции? Есть общая формула, по которой в физике вычисляется момент инерции любого тела. Если тело разбить на бесконечно малые кусочки массой dm, то момент инерции будет равен сумме произведений этих элементарных масс на квадрат расстояния до оси вращения.
Это общая формула для момента инерции в физике. Для материальной точки массы m, вращающейся вокруг оси на расстоянии r от нее, данная формула принимает вид:
Теорема Штейнера
От чего зависит момент инерции? От массы, положения оси вращения, формы и размеров тела.
Теорема Гюйгенса-Штейнера – очень важная теорема, которую часто используют при решении задач.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Теорема Гюйгенса-Штейнера гласит:
Момент инерции тела относительно произвольной оси равняется сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.
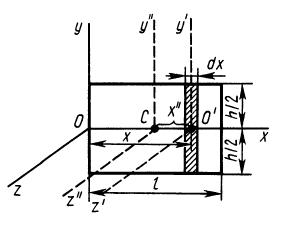
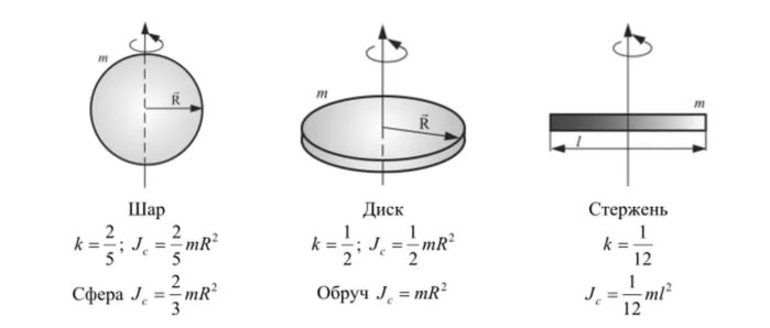
Для тех, кто не хочет постоянно интегрировать при решении задач на нахождение момента инерции, приведем рисунок с указанием моментов инерции некоторых однородных тел, которые часто встречаются в задачах:
Пример решения задачи на нахождение момента инерции
Рассмотрим два примера. Первая задача – на нахождение момента инерции. Вторая задача – на использование теоремы Гюйгенса-Штейнера.
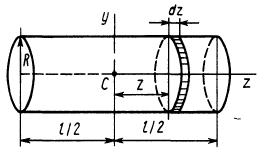
Задача 1. Найти момент инерции однородного диска массы m и радиуса R. Ось вращения проходит через центр диска.
Решение:
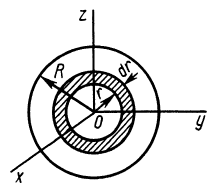
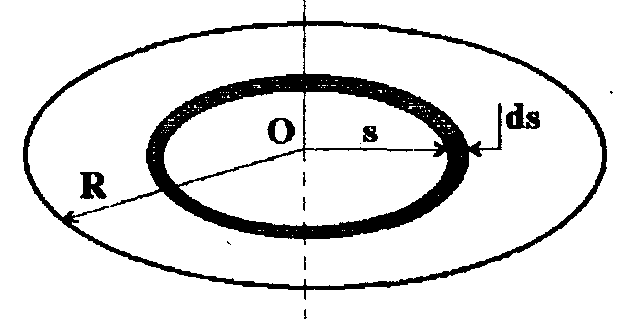
Разобьем диск на бесконечно тонкие кольца, радиус которых меняется от 0 до R и рассмотрим одно такое кольцо. Пусть его радиус – r, а масса – dm. Тогда момент инерции кольца:
Массу кольца можно представить в виде:
Здесь dz – высота кольца. Подставим массу в формулу для момента инерции и проинтегрируем:
В итоге получилась формула для момента инерции абсолютного тонкого диска или цилиндра.
Задача 2. Пусть опять есть диск массы m и радиуса R. Теперь нужно найти момент инерции диска относительно оси, проходящей через середину одного из его радиусов.
Решение:
Момент инерции диска относительно оси, проходящей через центр масс, известен из предыдущей задачи. Применим теорему Штейнера и найдем:
Кстати, в нашем блоге Вы можете найти и другие полезные материалы по физике и решению задач.
Надеемся, что Вы найдете в статье что-то полезное для себя. Если в процессе расчета тензора инерции возникают трудности, не забывайте о студенческом сервисе. Наши специалисты проконсультируют по любому вопросу и помогут решить задачу в считанные минуты.
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
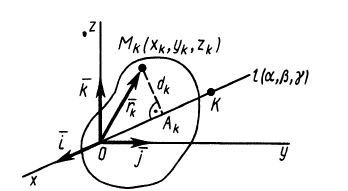
Определение:
Моментом
инерции материальной точки относительно
неподвижной оси называется скалярная
физическая величина, являющаяся мерой
инертности этой точки при вращательном
движении и, равная произведению её массы
на квадрат расстояния до оси,
т.е.
,
а также,
где—
угловая скорость тела относительно
данной оси.
Определение:
Моментом
инерции системы материальных точек
относительно неподвижной оси называется
скалярная физическая величина, являющаяся
мерой инертности этой системы при
вращательном движении и, равная
алгебраической сумме произведений масс
всех материальных точек системы на
квадрат их расстояний до оси,
т.е.
.
Момент
инерции определен только относительно
оси.
В случае непрерывного распределения
масс с плотностью сумма заменится
на интеграл по всему объему тела:
(Интегрирование производится по всему
объёму; пределы интегрирования
устанавливаются исходя из конфигурации
тела и его размеров). Если тело однородно,
то его плотность во всех точках постоянна
и
можно вынести из-под знака интеграла.
Найдем моменты инерции для простейших
(геометрически правильных) форм твердого
тела, масса которого равномерно
распределена по объему, т.е.
.
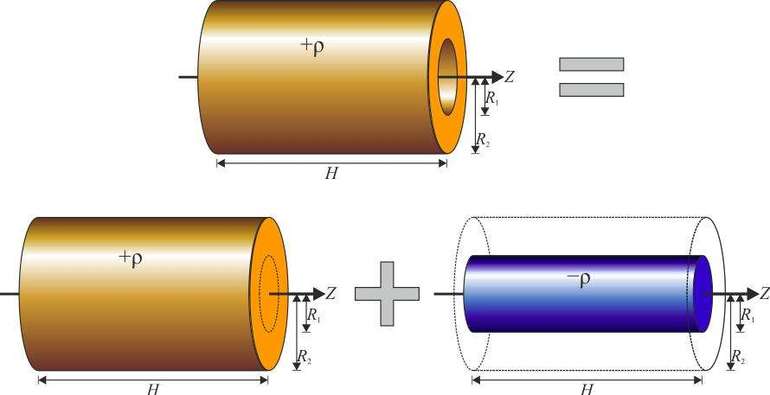
1. Момент инерции
обручаотносительно оси, перпендикулярной
к его плоскости и проходящей через его
центр.
Обруч считается бесконечно тонким, т.е.
толщиной обода можно пренебречь по
сравнению с радиусом R..
Поскольку в этой системе все массы
находятся на одинаковом расстоянии от
оси вращения, R2можно вынести из-под знака интеграла:,
гдеm— полная масса обруча.
2. Момент инерции
дискаотносительно оси, перпендикулярной
его плоскости и проходящей через центр.
Диск считается бесконечно тонким, т.е.
его толщина много меньше радиуса
R.Момент инерции,
согласно определению, величина аддитивная:
момент инерции целого тела равен сумме
моментов инерции его частей. Разобьем
диск на бесконечно тонкие обручи радиусомsи толщинойds
(См.рис.).
Момент инерции диска относительно
перпендикулярной оси, проходящей через
центр.
Площадь поверхности обруча равна
произведению его длины на толщину: 2
s
ds.Поскольку массатдиска распределена равномерна, масса
обручаdmпропорциональна площади его поверхности:
.
Момент инерции обруча мы уже знаем:
. Осталось просуммировать моменты
инерции всех таких обручей:.
Такой же результат получится и для
момента инерции цилиндра конечной
длины относительно его продольной оси.
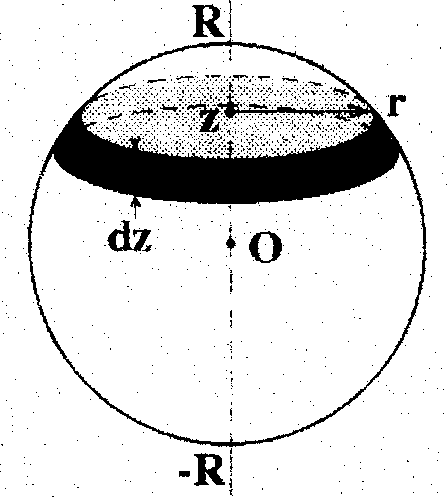
3. Момент инерции
шараотносительно его диаметра.
Поступим аналогичным образом: «нарежем»
шар на бесконечно тонкие диски
толщинойdz.находящиеся на расстоянииzот центра (См.рис.).
Момент инерции шара относительно
диаметра.
Радиус такого диска равен
. Объем дискаdVz
равен произведению его площади
на толщину:
. Массу дискаdmнаходим, разделив массу шаратна его объем
, умножив на объем диска:
.
Момент инерции диска был найден выше.
В применении к данному случаю, он
равен:
.
Момент инерции шара находится
интегрированием по всем таким дискам:
4.Момент инерции
тонкого стержняотносительно оси,
проходящей через его середину
перпендикулярно стержню.
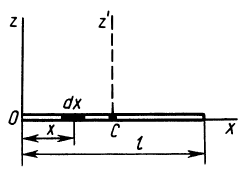
Пусть стержень имеет длину
ℓ.Направим осьxвдоль стержня. Начало координат по
условию находится в центре стрежня.
Возьмем элемент стержня длинойdx.находящийся на расстоянииxот оси вращения. Его масса равна
dm
= (m/ℓ)
dx,а момент инерцииdJ=(m/ℓ)
x2
dx.
Отсюда находим момент инерции стрежня:
(*).
Момент инерции величина аддитивная,
т.е. суммарный момент инерции системы
тел относительно какой-либо оси, равен
сумме моментов инерции каждого из тел
данной системы относительно той же оси:
Физический смысл момента инерции:Инерционные свойства при поступательном
движении характеризуются только массой
тела, т.е. зависит только от массы.
Инерционные свойства при вращательном
движении характеризуются моментом
инерции, т.е. зависят от его массы,
расстояния до оси вращения и расположению
теда по отношению к этой оси. Последнее
означает, что относительно двух разных
осей инерционные свойства вращательного
движения одного и того же движения тела
будут разными. Пример.
Основные понятия и суть
Инерция — это способность тела сохранять приданную ей скорость движения при отсутствии какого-либо внешнего воздействия. Например, во время езды на общественном транспорте всем приходится держаться за поручни. Если этого не сделать, то при изменении скорости движения транспортного средства существует большая вероятность упасть вперёд или назад. Другими словами, возникает какая-то сила, влияющая на пассажира. Когда её действие заканчивается, движение человека всё равно продолжается.
Это свойство и описывается понятием инертность. Раньше изучали это явление известные учёные Галилей, Ньютон, Мах. В соответствии с их исследованиями было установлено классическое правило момента вращения, физический смысл которого заключается в распределении массы в теле, определяемой суммой произведения простейшей массы на расстояние до начального множества в квадрате. Классическая формула, описывающая характеристику, выглядит следующим образом: Ja = Σmi*r2j. В ней:
- mi — масса в точке;
- rj — расстояние от точки до координаты.
То есть момент — это скалярная величина, являющаяся мерой инертности. В качестве единицы измерения по международной системе принято использовать произведение килограмма на квадратный метр (кг*м²). Обозначают параметр латинской буквой I или J. При умножении момента инерции на угловое ускорение можно определить сумму моментов всех сил, приложенных к телу: M = I * E. Фактически это уравнение является аналогом второго закона Ньютона.
М — это момент силы, оказывающий вращательное движение и воздействующий на ускорение тела, а E — угловое ускорение. Мера инертности тела отличается от массы тем, что вторая проявляется, когда его необходимо разогнать, а первая — при его раскручивании.
Вычисление параметра
Характеристика инерции тел зависит от их количественных показателей и формы. Для того чтобы найти характеристику, можно рассмотреть вращение материальной точки, находящейся на невесомой штанге, имеющей длину r и массу m. Для такой ситуации формулу момента инерции можно записать: I = m*r2. Длина r представляет собой радиус кольца, по которому происходит вращение объекта по оси. Таким образом, рассматриваемый момент зависит не только от массы тела, но и геометрических характеристик.
Любое тело можно описать совокупностью материальных точек. Для понятия процесса лучше всего рассмотреть простой пример. Пусть имеется невесомый цилиндр, способный вращаться по радиусу Rc. На него намотана верёвка, к которой приложена сила F. На цилиндр будут насаживаться тела с различной формой. Если известны его радиус и сила, с которой происходит раскручивание, то справедливо будет записать следующее выражение: M = F*Rc.
Допустим, на цилиндр помещены два тела. Одно имеет массу m1 и радиус вращения r1, а другое — m2 и r2. Используя основное уравнение динамики вращательного движения для первого тела с угловым ускорением ƹ1, момент силы можно определить как M1 = I1 * ƹ1. Соответственно, для второго предмета сила будет определяться по формуле: M1 = I2 * ƹ2.
Если эти два тела жёстко скрепить между собой, то они буду представлять собой составные части одного предмета, поэтому их угловые ускорения станут одинаковы (ƹ1 + ƹ2 = ƹ), а требующийся момент M станет равный сумме M1 + M2. Подставив значения, получим равенство M = I1*ƹ + I2*ƹ. Выражение можно упростить до вида M = ƹ (I1+I2). То есть нужный момент для тела, состоящего из совокупности точек, будет равен произведению суммы моментов инерции на угловое ускорение обоих тел.
Из сказанного можно сделать вывод, что момент инерции всего тела равен сумме моментов составных частей. Другим словами, он обладает свойством аддитивности. Используя это, можно составить алгоритм расчёта для любой формы.
Методика решения
Существует универсальный алгоритм, подходящий для расчёта параметра прямоугольника, треугольника, круга или другой фигуры произвольной формы. Допустим, есть сложное тело с заданной осью вращения. Необходимо найти момент его вращения. Для того чтобы решить поставленную задачу, используются два принципа:
- Аддитивность — свойство, обозначающее, что величина целого значения определяется суммой соответствующих ему частей.
- Формула нахождения момента для материальной точки I = m*r2.
Всё тело можно разделить на мельчайшие частички, которые представляют собой материальные точки. Номера этих кусков обозначают в виде i. Масса произвольной части будет определяться как дельта mi. Пусть этот кусок находится на расстоянии ri от оси вращения O. Для этой части момент вращения находится с помощью выражения Ii = Δ mi*ri2. Учитывая аддитивность, общий момент будет равен I = Σ Δ mi*ri2, где i принимает значение от 1 до n.
Эта формула является приближённой, так как точность зависит от массы частей и размера. Если кусочки, на которые разбивается тело, большие, считать их материальными точками нельзя. Чем мельче части, тем точнее будет результат. В соответствии с математическим анализом такие задачи решаются с помощью интегрирования. Понимая физический смысл момента инерции, можно отметить следующие зависимости:
- прямая пропорциональность массе;
- соответствие квадрату размера;
- изменение с учетом оси вращения.
Роль последнего пункта огромна. Например, если рассмотреть два момента вращения велосипедной спицы диаметром 2 мм и длиной 30 сантиметров, то можно увидеть зависимость от выбранной оси поворота.
Относительно вертикальной оси вращение обозначим I1, горизонтальной — I2. Подставив в формулы выражения, используемые для расчётов, можно получить отношение I1/I2 = (m*l2/12) / ((m*d2/8). После его упрощения будет верна запись I1/ I2 = (2/3)*(l/d)2. В итоге получится ответ 15000. Получается, если спицу будут закручивать с одинаковым моментом вокруг вертикальной оси и горизонтальной, то в первом случае она станет крутиться в 15 тыс. раз быстрее.
Моменты простейших объектов
Проведение интегрирования — довольно трудная операция, предполагающая хорошее знание высшей математики. Существует таблица, в которой собраны вычисления инерции для простейших геометрических фигур. При взятии сведений из неё важно обращать внимание на то, относительно какой оси приводится момент вращения объекта. Характеристика инерции для наиболее используемых объектов в физике имеет следующий вид:
- Кольцо. Предположив, что точка имеет симметричное значение с противоположной стороны оси, можно утверждать, что формула не изменится. Если же точку распределить по плоскости перпендикулярной оси, то получится кольцо. Оно будет иметь такую же массу с кусками, находящимися на одинаковом расстоянии от центра r. Вычисление момента относительно оси вращения выполняют по той же формуле, что и для материальной точки: I = m * r2.
- Тонкостенный цилиндр. Нарисовав такую фигуру и указав на ней ось вращения, массу и радиус, несложно будет увидеть, что формула для нахождения момента будет аналогична кольцу.
- Диск. Вращение его происходит относительно оси, проходящей через его центр. Учитывая, что масса однородного диска распределена по всей его площади, то момент его будет меньше, чем у кольца. Проведённые расчёты показали, что момент диска будет меньше в два раза. Таким образом, формула выглядит как I = m*r2 / 2.
- Сплошной цилиндр. Получают такую фигуру простым распределением массы сплошного диска вдоль оси. По аналогии с кольцом расчёт его характеристики инерции будет совпадать с однородным диском.
- Шар. Момент проходящей оси через центр тяжести равен удвоенному произведению m*r2, разделенному на 5: I = (m*r2) * 2/5.
- Сфера. Такой объект отличается от шара лишь тем, что внутри он полый. Направление вращения оси происходит через центр. Значение параметра для неё будет больше, чем шара, так как масса собрана не статически в одном месте, а размещена по всей поверхности. Расчёты показывают, что найти момент можно по формуле I =2*m*r2 /3.
- Стержень. Момент вращения проходит через центр вдоль оси, перпендикулярной стержню: I = (1/12) * m*L2. L — длина стержня.
При использовании этих формул необходимо учитывать, что единицей измерения момента инерции является кг* м², поэтому при расчёте величины следует приводить значения к этим единицам.
Теорема Гюйгенса — Штейнера
Теорема была названа в честь двух математиков, давших формулировку определению характеристики параллельных осей. Например, пусть имеется объект произвольной формы, центробежная сила которого известна. Используя формулу Штейнера, можно вычислить момент тела относительно любой оси параллельной линии, проходящей через середину фигуры. В своём выводе учёные опирались на две формулы:
- Вычисления координаты центра масс: X = (m1*x1 + m2*x2+…+Mi*Xi) / (m1+m2+…+Mi) = (Σ Δ mi*ri 2)/ m.
- Универсального расчёта инерции любого тела: I = Σ Δ mi*ri 2.
Обозначив центр произвольной оси буквой O, а один из множества кусков — Δm, можно воспользоваться универсальной формулой. Сначала необходимо определить квадрат расстояния до оси вращения ri. Для этого через центр проведём ось Oц, а расстояние между O и Oц обозначим как d.
Указанные значения нужно выразить через координаты кусочка. Для этого строится ось абсциссы, проходящая через Oц, и ординаты — O. При таком выборе направления начала координат x центр масс равняется d, а у — нулю. Фактически получится прямоугольный треугольник. Воспользовавшись теоремой Пифагора, можно записать: I = Σ Δ mi* (xi2 + yi2).
В результате можно отметить, что момент в точке O будет прямо пропорционален расстоянию между Δ m и центром. Это и есть главный вектор на чертеже. Для его обозначения вводится длина r’.
Находится ri’2 по формулам для прямоугольного треугольника, в котором один катет равняется yi, а другой — xi — Oц. Значение ri’ совпадает с длиной гипотенузы. Таким образом, ri’2 = (xi — Oц)2 + yi2. Подставив полученное равенство в формулу нахождения параметра момента в центре, можно получить следующую формулу: Io = Σ Δ mi* ((xi — Oц)2 + yi2). После ряда подстановок и упрощения выражения в итоге получится равенство Io = I + m*x i2 — 2*m*xi2 = I — m*xi2.
Так как x центра масс совпадает с d, расстоянием между осями, одну из которых можно направить через центр, то формулу можно переписать как Io = I — m*d2. Выразив из выражения произвольный момент, формула Штейнера примет вид I = Io + m*d2.
Другими словами, теорема определяет, что характеристика инерции тела относительно любой оси находится как сумма моментов относительно параллельной оси, пересекающей центр масс, и произведению массы тела на квадрат расстояния между осями. Сопротивлением вращению пренебрегают.
Пример задачи
Допустим, есть монета с массой m и радиусом r. Вращение происходит вокруг оси, распложенной по касательной. Необходимо найти момент вращения.
Для этого нужно знать характеристику прямой, пересекающей центр монеты Io. Решение будет определяться суммой Io и расстоянием от центра до касательной, которая равняется диаметру монеты: I = Io + md2. Фактически задача состоит в нахождении Io. Определяется этот параметр согласно теореме о взаимно перпендикулярных осях.
Момент вращения относительно диска определяется с помощью выражения I1 = m* d2 / 2. Для решения задачи она будет выглядеть Io = m* d2 / 4. Подставив все данные, получим: I = (1m*d2 / 4) + (md)2 = 5*m*d2 /4.
For the quantity also known as the «area moment of inertia», see Second moment of area.
| Moment of inertia | |
|---|---|

Flywheels have large moments of inertia to smooth out changes in rates of rotational motion. |
|
|
Common symbols |
I |
| SI unit | kg⋅m2 |
|
Other units |
lbf·ft·s2 |
|
Derivations from |
 |
| Dimension | M L2 |
To improve their maneuverability, war planes are designed to have smaller moments of inertia compared to commercial planes.
The moment of inertia, otherwise known as the mass moment of inertia, angular mass, second moment of mass, or most accurately, rotational inertia, of a rigid body is a quantity that determines the torque needed for a desired angular acceleration about a rotational axis, akin to how mass determines the force needed for a desired acceleration. It depends on the body’s mass distribution and the axis chosen, with larger moments requiring more torque to change the body’s rate of rotation.
It is an extensive (additive) property: for a point mass the moment of inertia is simply the mass times the square of the perpendicular distance to the axis of rotation. The moment of inertia of a rigid composite system is the sum of the moments of inertia of its component subsystems (all taken about the same axis). Its simplest definition is the second moment of mass with respect to distance from an axis.
For bodies constrained to rotate in a plane, only their moment of inertia about an axis perpendicular to the plane, a scalar value, matters. For bodies free to rotate in three dimensions, their moments can be described by a symmetric 3-by-3 matrix, with a set of mutually perpendicular principal axes for which this matrix is diagonal and torques around the axes act independently of each other.
Introduction[edit]
When a body is free to rotate around an axis, torque must be applied to change its angular momentum. The amount of torque needed to cause any given angular acceleration (the rate of change in angular velocity) is proportional to the moment of inertia of the body. Moments of inertia may be expressed in units of kilogram metre squared (kg·m2) in SI units and pound-foot-second squared (lbf·ft·s2) in imperial or US units.
The moment of inertia plays the role in rotational kinetics that mass (inertia) plays in linear kinetics—both characterize the resistance of a body to changes in its motion. The moment of inertia depends on how mass is distributed around an axis of rotation, and will vary depending on the chosen axis. For a point-like mass, the moment of inertia about some axis is given by 


In 1673 Christiaan Huygens introduced this parameter in his study of the oscillation of a body hanging from a pivot, known as a compound pendulum.[1] The term moment of inertia («momentum inertiae» in Latin) was introduced by Leonhard Euler in his book Theoria motus corporum solidorum seu rigidorum in 1765,[1][2] and it is incorporated into Euler’s second law.
The natural frequency of oscillation of a compound pendulum is obtained from the ratio of the torque imposed by gravity on the mass of the pendulum to the resistance to acceleration defined by the moment of inertia. Comparison of this natural frequency to that of a simple pendulum consisting of a single point of mass provides a mathematical formulation for moment of inertia of an extended body.[3][4]
The moment of inertia also appears in momentum, kinetic energy, and in Newton’s laws of motion for a rigid body as a physical parameter that combines its shape and mass. There is an interesting difference in the way moment of inertia appears in planar and spatial movement. Planar movement has a single scalar that defines the moment of inertia, while for spatial movement the same calculations yield a 3 × 3 matrix of moments of inertia, called the inertia matrix or inertia tensor.[5][6]
The moment of inertia of a rotating flywheel is used in a machine to resist variations in applied torque to smooth its rotational output. The moment of inertia of an airplane about its longitudinal, horizontal and vertical axes determine how steering forces on the control surfaces of its wings, elevators and rudder(s) affect the plane’s motions in roll, pitch and yaw.
Definition[edit]
The moment of inertia is defined as the product of mass of section and the square of the distance between the reference axis and the centroid of the section.
Video of rotating chair experiment, illustrating moment of inertia. When the spinning professor pulls his arms, his moment of inertia decreases; to conserve angular momentum, his angular velocity increases.
The moment of inertia I is also defined as the ratio of the net angular momentum L of a system to its angular velocity ω around a principal axis,[7][8] that is

If the angular momentum of a system is constant, then as the moment of inertia gets smaller, the angular velocity must increase. This occurs when spinning figure skaters pull in their outstretched arms or divers curl their bodies into a tuck position during a dive, to spin faster.[7][8][9][10][11][12][13]
If the shape of the body does not change, then its moment of inertia appears in Newton’s law of motion as the ratio of an applied torque τ on a body to the angular acceleration α around a principal axis, that is

For a simple pendulum, this definition yields a formula for the moment of inertia I in terms of the mass m of the pendulum and its distance r from the pivot point as,
Thus, the moment of inertia of the pendulum depends on both the mass m of a body and its geometry, or shape, as defined by the distance r to the axis of rotation.
This simple formula generalizes to define moment of inertia for an arbitrarily shaped body as the sum of all the elemental point masses dm each multiplied by the square of its perpendicular distance r to an axis k. An arbitrary object’s moment of inertia thus depends on the spatial distribution of its mass.
In general, given an object of mass m, an effective radius k can be defined, dependent on a particular axis of rotation, with such a value that its moment of inertia around the axis is
where k is known as the radius of gyration around the axis.
Examples[edit]
Simple pendulum[edit]
Mathematically, the moment of inertia of a simple pendulum is the ratio of the torque due to gravity about the pivot of a pendulum to its angular acceleration about that pivot point. For a simple pendulum this is found to be the product of the mass of the particle 

This can be shown as follows: The force of gravity on the mass of a simple pendulum generates a torque 





where 



The quantity 


using a similar derivation to the previous equation.
Similarly, the kinetic energy of the pendulum mass is defined by the velocity of the pendulum around the pivot to yield
This shows that the quantity 

Compound pendulums[edit]
Pendulums used in Mendenhall gravimeter apparatus, from 1897 scientific journal. The portable gravimeter developed in 1890 by Thomas C. Mendenhall provided the most accurate relative measurements of the local gravitational field of the Earth.
A compound pendulum is a body formed from an assembly of particles of continuous shape that rotates rigidly around a pivot. Its moment of inertia is the sum of the moments of inertia of each of the particles that it is composed of.[14][15]: 395–396 [16]: 51–53 The natural frequency (

where 


Thus, to determine the moment of inertia of the body, simply suspend it from a convenient pivot point 

where 
Center of oscillation[edit]
A simple pendulum that has the same natural frequency as a compound pendulum defines the length 

or
The seconds pendulum, which provides the «tick» and «tock» of a grandfather clock, takes one second to swing from side-to-side. This is a period of two seconds, or a natural frequency of 

Notice that the distance to the center of oscillation of the seconds pendulum must be adjusted to accommodate different values for the local acceleration of gravity. Kater’s pendulum is a compound pendulum that uses this property to measure the local acceleration of gravity, and is called a gravimeter.
Measuring moment of inertia[edit]
The moment of inertia of a complex system such as a vehicle or airplane around its vertical axis can be measured by suspending the system from three points to form a trifilar pendulum. A trifilar pendulum is a platform supported by three wires designed to oscillate in torsion around its vertical centroidal axis.[18] The period of oscillation of the trifilar pendulum yields the moment of inertia of the system.[19]
Moment of inertia of area[edit]
Moment of inertia of area is also known as the second moment of area.
These calculations are commonly used in civil engineering for structural design of beams and columns. Cross-sectional areas calculated for vertical moment of the x-axis 

Height (h) and breadth (b) are the linear measures, except for circles, which are effectively half-breadth derived, 
Sectional areas moment calculated thus[20][edit]
- Square:
- Rectangular:
and;
- Triangular:
- Circular:
Motion in a fixed plane[edit]
Point mass[edit]
Four objects with identical masses and radii racing down a plane while rolling without slipping.
From back to front:
- spherical shell,
- solid sphere,
- cylindrical ring, and
- solid cylinder.
The time for each object to reach the finishing line depends on their moment of inertia. (OGV version)
The moment of inertia about an axis of a body is calculated by summing 

Consider the kinetic energy of an assembly of 



This shows that the moment of inertia of the body is the sum of each of the 
Thus, moment of inertia is a physical property that combines the mass and distribution of the particles around the rotation axis. Notice that rotation about different axes of the same body yield different moments of inertia.
The moment of inertia of a continuous body rotating about a specified axis is calculated in the same way, except with infinitely many point particles. Thus the limits of summation are removed, and the sum is written as follows:
Another expression replaces the summation with an integral,
Here, the function 





Note on second moment of area: The moment of inertia of a body moving in a plane and the second moment of area of a beam’s cross-section are often confused. The moment of inertia of a body with the shape of the cross-section is the second moment of this area about the 




Examples[edit]
The moment of inertia of a compound pendulum constructed from a thin disc mounted at the end of a thin rod that oscillates around a pivot at the other end of the rod, begins with the calculation of the moment of inertia of the thin rod and thin disc about their respective centers of mass.[22]
A list of moments of inertia formulas for standard body shapes provides a way to obtain the moment of inertia of a complex body as an assembly of simpler shaped bodies. The parallel axis theorem is used to shift the reference point of the individual bodies to the reference point of the assembly.
As one more example, consider the moment of inertia of a solid sphere of constant density about an axis through its center of mass. This is determined by summing the moments of inertia of the thin discs that can form the sphere whose centers are along the axis chosen for consideration. If the surface of the ball is defined by the equation[22]: 1301
then the square of the radius 


Therefore, the moment of inertia of the ball is the sum of the moments of inertia of the discs along the 
where 
Rigid body[edit]
The cylinders with higher moment of inertia roll down a slope with a smaller acceleration, as more of their potential energy needs to be converted into the rotational kinetic energy.
If a mechanical system is constrained to move parallel to a fixed plane, then the rotation of a body in the system occurs around an axis 
If a system of 



where 


For planar movement the angular velocity vector is directed along the unit vector 




This defines the relative position vector and the velocity vector for the rigid system of the particles moving in a plane.
Note on the cross product: When a body moves parallel to a ground plane, the trajectories of all the points in the body lie in planes parallel to this ground plane. This means that any rotation that the body undergoes must be around an axis perpendicular to this plane. Planar movement is often presented as projected onto this ground plane so that the axis of rotation appears as a point. In this case, the angular velocity and angular acceleration of the body are scalars and the fact that they are vectors along the rotation axis is ignored. This is usually preferred for introductions to the topic. But in the case of moment of inertia, the combination of mass and geometry benefits from the geometric properties of the cross product. For this reason, in this section on planar movement the angular velocity and accelerations of the body are vectors perpendicular to the ground plane, and the cross product operations are the same as used for the study of spatial rigid body movement.
Angular momentum[edit]
The angular momentum vector for the planar movement of a rigid system of particles is given by[14][17]
Use the center of mass 
and define the moment of inertia relative to the center of mass 
then the equation for angular momentum simplifies to[22]: 1028
The moment of inertia 
For a given amount of angular momentum, a decrease in the moment of inertia results in an increase in the angular velocity. Figure skaters can change their moment of inertia by pulling in their arms. Thus, the angular velocity achieved by a skater with outstretched arms results in a greater angular velocity when the arms are pulled in, because of the reduced moment of inertia. A figure skater is not, however, a rigid body.
Kinetic energy[edit]
This 1906 rotary shear uses the moment of inertia of two flywheels to store kinetic energy which when released is used to cut metal stock (International Library of Technology, 1906).
The kinetic energy of a rigid system of particles moving in the plane is given by[14][17]
Let the reference point be the center of mass 

The moment of inertia 
Newton’s laws[edit]
A 1920s John Deere tractor with the spoked flywheel on the engine. The large moment of inertia of the flywheel smooths the operation of the tractor.
Newton’s laws for a rigid system of 


where 
The kinematics of a rigid body yields the formula for the acceleration of the particle 




For systems that are constrained to planar movement, the angular velocity and angular acceleration vectors are directed along 




This yields the resultant torque on the system as
where 


Use the center of mass 

Motion in space of a rigid body, and the inertia matrix[edit]
The scalar moments of inertia appear as elements in a matrix when a system of particles is assembled into a rigid body that moves in three-dimensional space. This inertia matrix appears in the calculation of the angular momentum, kinetic energy and resultant torque of the rigid system of particles.[3][4][5][6][26]
Let the system of 




and the (absolute) velocities are
where 


Angular momentum[edit]
Note that the cross product can be equivalently written as matrix multiplication by combining the first operand and the operator into a skew-symmetric matrix, ![{displaystyle left[mathbf {b} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ce9643510bd433e0ed612edd5d3a9ed7faecfec)

The inertia matrix is constructed by considering the angular momentum, with the reference point 

where the terms containing 

Then, the skew-symmetric matrix ![{displaystyle [Delta mathbf {r} _{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ee5960e77611f673ab2f2050f356dbf0e403132)

where 
is the symmetric inertia matrix of the rigid system of particles measured relative to the center of mass 
Kinetic energy[edit]
The kinetic energy of a rigid system of particles can be formulated in terms of the center of mass and a matrix of mass moments of inertia of the system. Let the system of 



where 
This equation expands to yield three terms
Since the center of mass is defined by
, the second term in this equation is zero. Introduce the skew-symmetric matrix ![{displaystyle [Delta mathbf {r} _{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ee5960e77611f673ab2f2050f356dbf0e403132)
Thus, the kinetic energy of the rigid system of particles is given by
where 

Resultant torque[edit]
The inertia matrix appears in the application of Newton’s second law to a rigid assembly of particles. The resultant torque on this system is,[3][6]
where 






Use the center of mass 
![{displaystyle left[Delta mathbf {r} _{i}right]=left[mathbf {r} _{i}-mathbf {C} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b83ab9af0efe0f59204a493b10b5eb453594c19)

The calculation uses the identity
obtained from the Jacobi identity for the triple cross product as shown in the proof below:
Proof
Then, the following Jacobi identity is used on the last term:
The result of applying Jacobi identity can then be continued as follows:
The final result can then be substituted to the main proof as follows:
Notice that for any vector 
Finally, the result is used to complete the main proof as follows:
Thus, the resultant torque on the rigid system of particles is given by
where 
Parallel axis theorem[edit]
The inertia matrix of a body depends on the choice of the reference point. There is a useful relationship between the inertia matrix relative to the center of mass 

Consider the inertia matrix 

Let 
where 


Distribute over the cross product to obtain
The first term is the inertia matrix 

![{displaystyle [mathbf {d} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5785dcf9605fb6ace7c1a8c8b4d6b365af48366)

The result is the parallel axis theorem,
where 


Note on the minus sign: By using the skew symmetric matrix of position vectors relative to the reference point, the inertia matrix of each particle has the form ![{displaystyle -mleft[mathbf {r} right]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b3ed54432828b43d6ae23e9a2e9c009c7336024)

![{displaystyle mleft[mathbf {r} right]^{mathsf {T}}left[mathbf {r} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/27fed5e06e85cd3d74847c333b7a32cbd6a31fe7)
![{displaystyle [mathbf {r} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba4c4e0b7a62e35392117d1331b60c9e3276b5c9)
Scalar moment of inertia in a plane[edit]
The scalar moment of inertia, 


where 

![{displaystyle [Delta mathbf {r} _{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ee5960e77611f673ab2f2050f356dbf0e403132)

This is derived as follows. Let a rigid assembly of 









where 



To relate this scalar moment of inertia to the inertia matrix of the body, introduce the skew-symmetric matrix ![{displaystyle left[mathbf {hat {k}} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a515c7495954477be07dee4f29d4c4c4ec50cf98)
![{displaystyle left[mathbf {hat {k}} right]mathbf {y} =mathbf {hat {k}} times mathbf {y} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/10d1281a399f50084c4d71e516f5d56b1cf5426f)
noting that 
The magnitude squared of the perpendicular vector is
The simplification of this equation uses the triple scalar product identity
where the dot and the cross products have been interchanged. Exchanging products, and simplifying by noting that 

Thus, the moment of inertia around the line 


where 

This shows that the inertia matrix can be used to calculate the moment of inertia of a body around any specified rotation axis in the body.
Inertia tensor[edit]
For the same object, different axes of rotation will have different moments of inertia about those axes. In general, the moments of inertia are not equal unless the object is symmetric about all axes. The moment of inertia tensor is a convenient way to summarize all moments of inertia of an object with one quantity. It may be calculated with respect to any point in space, although for practical purposes the center of mass is most commonly used.
Definition[edit]
For a rigid object of 

Its components are defined as
where
Note that, by the definition, 
The diagonal elements are more succinctly written as
while the off-diagonal elements, also called the products of inertia, are
Here 




These quantities can be generalized to an object with distributed mass, described by a mass density function, in a similar fashion to the scalar moment of inertia. One then has
where 
Alternatively it can also be written in terms of the angular momentum operator ![{displaystyle [mathbf {r} ]mathbf {x} =mathbf {r} times mathbf {x} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f32ba1c18fa5966e4dcd2275a7f7e3bc21f6dc0)
The inertia tensor can be used in the same way as the inertia matrix to compute the scalar moment of inertia about an arbitrary axis in the direction 
where the dot product is taken with the corresponding elements in the component tensors. A product of inertia term such as 
and can be interpreted as the moment of inertia around the 

The components of tensors of degree two can be assembled into a matrix. For the inertia tensor this matrix is given by,
It is common in rigid body mechanics to use notation that explicitly identifies the 




Alternate inertia convention[edit]
There are some CAD and CAE applications such as SolidWorks, Unigraphics NX/Siemens NX and MSC Adams that use an alternate convention for the products of inertia. According to this convention, the minus sign is removed from the product of inertia formulas and instead inserted in the inertia matrix:
Determine inertia convention (Principal axes method)[edit]
If one has the inertia data 
- The standard inertia convention has been used
.
- The alternate inertia convention has been used
.
Next, one calculates the eigenvectors for the two matrices. The matrix whose eigenvectors are parallel to the principal axes corresponds to the inertia convention that has been used.
Derivation of the tensor components[edit]
The distance 




Rewrite the equation using matrix transpose:
where E3 is the 3×3 identity matrix.
This leads to a tensor formula for the moment of inertia
For multiple particles, we need only recall that the moment of inertia is additive in order to see that this formula is correct.
Inertia tensor of translation[edit]
Let 

where 

Inertia tensor of rotation[edit]
Let 
Inertia matrix in different reference frames[edit]
The use of the inertia matrix in Newton’s second law assumes its components are computed relative to axes parallel to the inertial frame and not relative to a body-fixed reference frame.[6][24] This means that as the body moves the components of the inertia matrix change with time. In contrast, the components of the inertia matrix measured in a body-fixed frame are constant.
Body frame[edit]
Let the body frame inertia matrix relative to the center of mass be denoted 

where vectors 

Notice that 

Principal axes[edit]
Measured in the body frame, the inertia matrix is a constant real symmetric matrix. A real symmetric matrix has the eigendecomposition into the product of a rotation matrix 

where
The columns of the rotation matrix 



A toy top is an example of a rotating rigid body, and the word top is used in names the types of types of rigid bodies. When all principal moments of inertia are distinct, the principal axes through center of mass are uniquely specified and the rigid body is called an asymmetric top. If two principal moments are the same, the rigid body is called a symmetric top and there is no unique choice for the two corresponding principal axes. If all three principal moments are the same, the rigid body is called a spherical top (although it need not be spherical) and any axis can be considered a principal axis, meaning that the moment of inertia is the same about any axis.
The principal axes are often aligned with the object’s symmetry axes. If a rigid body has an axis of symmetry of order 

The motion of vehicles is often described in terms of yaw, pitch, and roll which usually correspond approximately to rotations about the three principal axes. If the vehicle has bilateral symmetry then one of the principal axes will correspond exactly to the transverse (pitch) axis.
A practical example of this mathematical phenomenon is the routine automotive task of balancing a tire, which basically means adjusting the distribution of mass of a car wheel such that its principal axis of inertia is aligned with the axle so the wheel does not wobble.
Rotating molecules are also classified as asymmetric, symmetric, or spherical tops, and the structure of their rotational spectra is different for each type.
Ellipsoid[edit]
An ellipsoid with the semi-principal diameters labelled 


The moment of inertia matrix in body-frame coordinates is a quadratic form that defines a surface in the body called Poinsot’s ellipsoid.[30] Let 
or
defines an ellipsoid in the body frame. Write this equation in the form,
to see that the semi-principal diameters of this ellipsoid are given by
Let a point 




Thus, the magnitude of a point 

See also[edit]
- Central moment
- List of moments of inertia
- Planar lamina
- Rotational energy
- Moment of inertia factor
References[edit]
- ^ a b Mach, Ernst (1919). The Science of Mechanics. pp. 173–187. Retrieved November 21, 2014.
- ^ Euler, Leonhard (1765). Theoria motus corporum solidorum seu rigidorum: Ex primis nostrae cognitionis principiis stabilita et ad omnes motus, qui in huiusmodi corpora cadere possunt, accommodata [The theory of motion of solid or rigid bodies: established from first principles of our knowledge and appropriate for all motions which can occur in such bodies.] (in Latin). Rostock and Greifswald (Germany): A. F. Röse. p. 166. ISBN 978-1-4297-4281-8. From page 166: «Definitio 7. 422. Momentum inertiae corporis respectu eujuspiam axis est summa omnium productorum, quae oriuntur, si singula corporis elementa per quadrata distantiarum suarum ab axe multiplicentur.» (Definition 7. 422. A body’s moment of inertia with respect to any axis is the sum of all of the products, which arise, if the individual elements of the body are multiplied by the square of their distances from the axis.)
- ^ a b c d e f Marion, JB; Thornton, ST (1995). Classical dynamics of particles & systems (4th ed.). Thomson. ISBN 0-03-097302-3.
- ^ a b Symon, KR (1971). Mechanics (3rd ed.). Addison-Wesley. ISBN 0-201-07392-7.
- ^ a b Tenenbaum, RA (2004). Fundamentals of Applied Dynamics. Springer. ISBN 0-387-00887-X.
- ^ a b c d e f g h
Kane, T. R.; Levinson, D. A. (1985). Dynamics, Theory and Applications. New York: McGraw-Hill. - ^ a b Winn, Will (2010). Introduction to Understandable Physics: Volume I — Mechanics. AuthorHouse. p. 10.10. ISBN 978-1449063337.
- ^ a b Fullerton, Dan (2011). Honors Physics Essentials. Silly Beagle Productions. pp. 142–143. ISBN 978-0983563334.
- ^ Wolfram, Stephen (2014). «Spinning Ice Skater». Wolfram Demonstrations Project. Mathematica, Inc. Retrieved September 30, 2014.
- ^ Hokin, Samuel (2014). «Figure Skating Spins». The Physics of Everyday Stuff. Retrieved September 30, 2014.
- ^ Breithaupt, Jim (2000). New Understanding Physics for Advanced Level. Nelson Thomas. p. 64. ISBN 0748743146.
- ^ Crowell, Benjamin (2003). Conservation Laws. Light and Matter. pp. 107. ISBN 0970467028.
ice skater conservation of angular momentum.
- ^ Tipler, Paul A. (1999). Physics for Scientists and Engineers, Vol. 1: Mechanics, Oscillations and Waves, Thermodynamics. Macmillan. p. 304. ISBN 1572594918.
- ^ a b c d e
Paul, Burton (June 1979). Kinematics and Dynamics of Planar Machinery. Prentice Hall. ISBN 978-0135160626. - ^
Halliday, David; Resnick, Robert; Walker, Jearl (2005). Fundamentals of physics (7th ed.). Hoboken, NJ: Wiley. ISBN 9780471216438. - ^
French, A.P. (1971). Vibrations and waves. Boca Raton, FL: CRC Press. ISBN 9780748744473. - ^ a b c d e f
Uicker, John J.; Pennock, Gordon R.; Shigley, Joseph E. (2010). Theory of Machines and Mechanisms (4th ed.). Oxford University Press. ISBN 978-0195371239. - ^ C. Couch and J. Mayes, Trifilar Pendulum for MOI, Happresearch.com, 2016.
- ^ Gracey, William, The experimental determination of the moments of inertia of airplanes by a simplified compound-pendulum method, NACA Technical Note No. 1629, 1948
- ^ Morrow, H. W.; Kokernak, Robert (2011). Statics and Strengths of Materials (7 ed.). New Jersey: Prentice Hall. pp. 192–196. ISBN 978-0135034521.
- ^ In that situation this moment of inertia only describes how a torque applied along that axis causes a rotation about that axis. But, torques not aligned along a principal axis will also cause rotations about other axes.
- ^ a b c d e f g h i Ferdinand P. Beer; E. Russell Johnston; Jr., Phillip J. Cornwell (2010). Vector mechanics for engineers: Dynamics (9th ed.). Boston: McGraw-Hill. ISBN 978-0077295493.
- ^ Walter D. Pilkey, Analysis and Design of Elastic Beams: Computational Methods, John Wiley, 2002.
- ^ a b Goldstein, H. (1980). Classical Mechanics (2nd ed.). Addison-Wesley. ISBN 0-201-02918-9.
- ^ L. D. Landau and E. M. Lifshitz, Mechanics, Vol 1. 2nd Ed., Pergamon Press, 1969.
- ^ L. W. Tsai, Robot Analysis: The mechanics of serial and parallel manipulators, John-Wiley, NY, 1999.
- ^ David, Baraff. «Physically Based Modeling — Rigid Body Simulation» (PDF). Pixar Graphics Technologies.
- ^ Sylvester, J J (1852). «A demonstration of the theorem that every homogeneous quadratic polynomial is reducible by real orthogonal substitutions to the form of a sum of positive and negative squares» (PDF). Philosophical Magazine. 4th Series. 4 (23): 138–142. doi:10.1080/14786445208647087. Retrieved June 27, 2008.
- ^ Norman, C.W. (1986). Undergraduate algebra. Oxford University Press. pp. 360–361. ISBN 0-19-853248-2.
- ^ Mason, Matthew T. (2001). Mechanics of Robotics Manipulation. MIT Press. ISBN 978-0-262-13396-8. Retrieved November 21, 2014.
External links[edit]
- Angular momentum and rigid-body rotation in two and three dimensions
- Lecture notes on rigid-body rotation and moments of inertia
- The moment of inertia tensor
- An introductory lesson on moment of inertia: keeping a vertical pole not falling down (Java simulation)
- Tutorial on finding moments of inertia, with problems and solutions on various basic shapes
- Notes on mechanics of manipulation: the angular inertia tensor
- Easy to use and Free Moment of Inertia Calculator online
Содержание:
Геометрия масс:
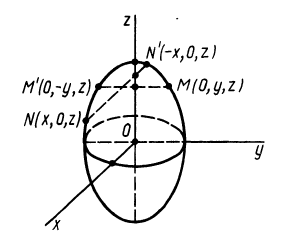
Центр масс
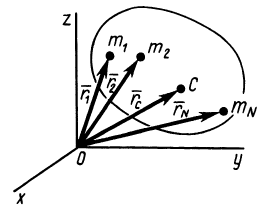
При рассмотрении движения твердых тел и других механических систем важное значение имеет точка, называемая центром масс. Если механическая система состоит из конечного числа материальных точек
где 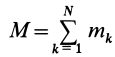
Рис. 21
Центр масс является не материальной точкой, а геометрической. Он может не совпадать ни с одной материальной точкой системы, как, например, в случае кольца. Центр масс системы характеризует распределение масс в системе.
Векторная величина 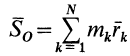
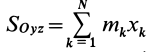
массы относительно координатной плоскости 
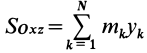
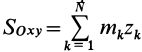
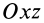
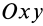
Радиус-вектор и координаты центра масс через статические моменты массы выражаются формулами
Если механическая система представляет собой сплошное тело, то его разбивают на элементарные частицы с бесконечно малыми массами 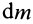
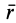
Суммы в пределе переходят в интегралы. Формулы (1) и (Г) принимают форму
где 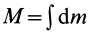
Для однородных сплошных тел 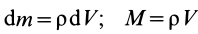
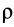
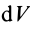
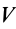
Для тел типа тонкого листа, которые можно принять за однородные материальные поверхности, 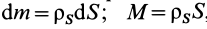
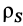
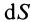
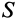
Для тонкой проволоки, которую можно принять за отрезок линии, 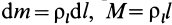
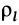
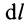
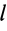
В этих случаях определение центра масс тел сводится к вычислению центра масс объемов, площадей и длин линий соответственно.
Моменты инерции
Для характеристики распределения масс в телах при рассмотрении вращательных движений требуется ввести понятия моментов инерции.
Моменты инерции относительно точки и оси
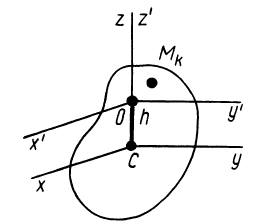
Моментом инерции механической системы, состоящей из 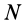
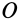
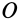
Момент инерции относительно точки часто называют полярным моментом инерции. В случае сплошного тела сумма переходит в интеграл и для полярного момента инерции имеем
где 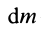
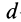
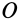
Моментом инерции 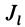
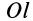
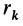
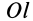
Рис. 22
В частном случае сплошного тела сумму следует заменить интегралом:
Моменты инерции одинаковых по форме однородных тел, изготовленных из разных материалов, отличаются друг от друга. Характеристикой, не зависящей от массы материала, является радиус инерции. Радиус инерции 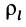
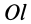
где 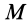
Момент инерции относительно оси через радиус инерции относительно этой оси определяется выражением
В справочниках по моментам инерции приводят таблицы значений радиусов инерции различных тел.
Формула (5′) позволяет считать радиус инерции тела относительно оси расстоянием от этой оси до такой точки, в которой следует поместить массу тела, чтобы ее момент инерции оказался равным моменту инерции тела относительно рассматриваемой оси.
Моменты инерции относительно оси и точки имеют одинаковую размерность — произведение массы на квадрат длины 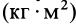
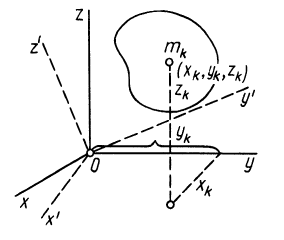
Кроме моментов инерции относительно точки и оси используются также моменты инерции относительно плоскостей и центробежные моменты инерции. Эти моменты инерции удобно рассмотреть относительно координатных плоскостей и осей декартовой системы координат.
Моменты инерции относительно осей координат
Моменты инерции относительно декартовых осей координат 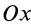
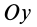
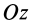
где 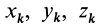
Из приведенных формул следует зависимость
Если через точку 
Из сравнения (8) и (8′) следует, что
Рис. 23
Сумма моментов инерции относительно декартовых осей координат не зависит от ориентации этих осей в рассматриваемой точке, т. е. является величиной, инвариантной по отношению к направлению осей координат.
Для осей координат 
Центробежные моменты инерции часто называют произведениями инерции.
Моменты инерции относительно осей и точек — величины положительные, так как в них входят квадраты координат. Центробежные моменты инерции содержат произведения координат и могут быть как положительными, так и отрицательными.
Центробежные моменты инерции имеют важное значение при рассмотрении давлений на подшипники при вращении твердого тела вокруг неподвижной оси и в других случаях.
Кроме рассмотренных моментов инерции иногда используются моменты инерции относительно координатных плоскостей 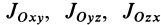
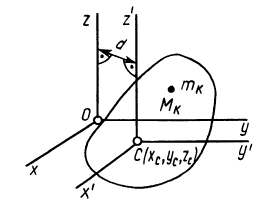
Теорема о моментах инерции относительно параллельных осей (теорема Штейнера)
Установим зависимость между моментами инерции системы относительно параллельных осей, одна из которых проходит через центр масс. Пусть имеем две системы прямоугольных, взаимно параллельных осей координат 
Рис. 24
По определению момента инерции относительно оси имеем
где 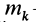
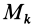
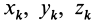
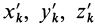
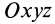
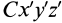
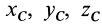
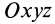
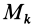
Подставим эти значения координат в выражение момента инерции 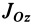
В этом соотношении 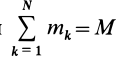
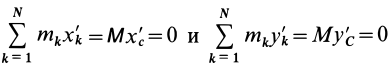
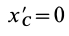
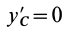
того, что по условию центр масс находится в начале координат этой системы координат.
Величина 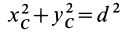
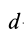
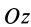
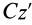
Связь моментов инерции относительно двух параллельных осей, одна из которых проходит через центр масс, составляет содержание так называемой теоремы Штейнера или Гюйгенса— Штейнера: момент инерции системы относительно какой-либо оси равен моменту инерции относительно параллельной оси, проходящей через центр масс, плюс произведение массы системы на квадрат расстояния между этими осями.
Из теоремы Штейнера следует, что для совокупности параллельных осей момент инерции является наименьшим относительно оси, проходящей через центр масс.
Если взять ось 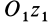
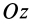
где 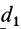
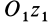
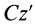
Исключая момент инерции 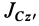
Установим изменение центробежных моментов инерции при параллельном переносе осей координат. Имеем
Учитывая, что 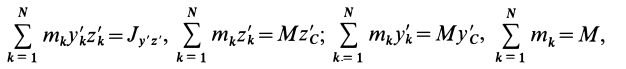
где 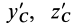
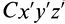
Так как начало системы координат 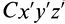
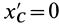
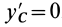
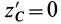
т. е. центробежные моменты инерции при параллельном переносе осей координат из любой точки в центре масс изменяются в соответствии с (10).
Если производится параллельный перенос осей 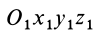
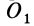
Исключая из (10) и (10′) центробежные моменты инерции Л’з» Лу, получим формулы для изменения центробежных моментов инерции при параллельном переносе осей координат из точки 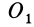
где 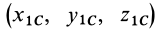
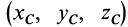
Моменты инерции простейших однородных тел
Моменты инерции тел сложной формы часто удается вычислить, если их предварительно разбить на тела простой формы. Моменты инерции сложных тел получают суммируя моменты инерции частей этих тел. Получим формулы для вычисления моментов инерции некоторых однородных простейших тел.
Однородный стержень
Имеем однородный стержень длиной 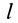
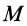
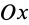
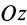
так как 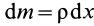
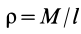
Вычисляя интеграл, получаем
Рис. 25
Таким образом,
Момент инерции стержня относительно оси 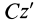
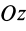
Следовательно,
т. е.
Прямоугольная пластина
Прямоугольная тонкая пластина имеет размеры 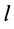
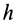
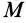
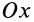
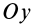
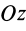
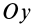
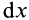
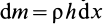
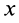
так как 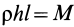
Аналогичные вычисления для оси 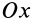
так как эта ось 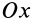
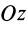
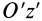
Рис. 26
Интегрируя это выражение в пределах от 0 до 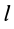
Итак, для моментов инерции пластины относительно осей координат получены следующие формулы:
Круглый диск
Имеем тонкий однородный диск радиусом 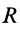
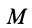
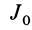
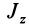
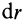
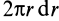
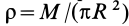
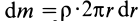
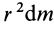
Таким образом,
Рис. 27
Для осей координат 
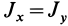
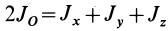
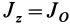
В случае тонкого проволочного кольца или круглого колеса, у которых масса распределена не по площади, а по его ободу, имеем
Круглый цилиндр
Рис. 28
Для круглого однородного цилиндра, масса которого 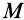
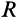
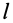
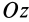
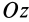
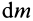
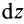
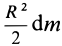
т.е.
Вычислим момент инерции цилиндра относительно его поперечной оси симметрии 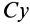
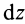
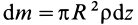
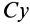
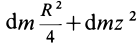
Чтобы получить момент инерции всего цилиндра относительно оси 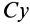
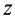
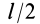
Но 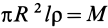
Таким образом, момент инерции цилиндра относительно его поперечной оси симметрии получается как сумма моментов инерции относительно этой оси диска и стержня, массы которых равны по отдельности массе цилиндра. Диск получается из цилиндра симметричным сжатием его с торцов до срединной плоскости при сохранении радиуса, а стержень — сжатием цилиндра в однородный стержень, расположенный по оси цилиндра, при сохранении длины.
Шар
Пусть масса шара 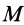
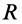
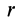
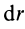
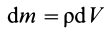
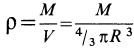
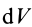
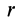
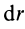
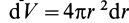
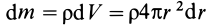
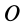
т.е.
Рис. 29
Для осей координат, проходящих через центр шара, в силу симметрии 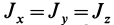
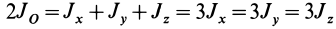
Моменты инерции относительно осей, проходящих через заданную точку
В заданной точке 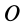
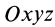
или для сплошных тел
В дальнейшем используется определение (20). Сплошные тела считаются разбитыми на 
Из прямоугольного треугольника 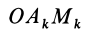
где 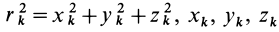
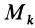
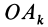
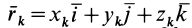
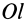
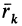
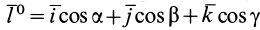
Умножая в (21) 
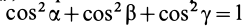
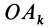
Подставляя (23) в (20) и вынося косинусы углов за знаки сумм, имеем
Учитывая, что
— моменты инерции относительно осей координат, а
— центробежные моменты инерции относительно тех же осей, получим
Для определения момента инерции 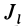
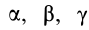
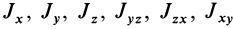
Матрица, или таблица (25), составленная из осевых и центробежных моментов инерции относительно декартовых осей координат, называется тензором инерции в точке 
Для определения момента инерции относительно какой-либо оси, проходящей через заданную точку, для рассматриваемого тела необходимо иметь тензор инерции в этой точке и углы, определяющие направление оси с осями координат.
Рис. 30
Эллипсоид инерции
Для характеристики распределения моментов инерции тела относительно различных осей, проходящих через заданную точку, используется поверхность второго порядка — эллипсоид инерции. Для построения этой поверхности на каждой оси 
Геометрическое место концов отрезков 
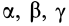
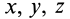
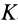
Подставляя эти значения косинусов углов в (24) и сокращая на 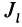
Это действительно уравнение эллипсоида, так как отрезок 
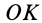
Для каждой точки 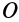
В случае эллипсоида вращения все прямые, расположенные в экваториальной плоскости эллипсоида, перпендикулярной оси вращения, будут главными осями инерции. Для шара любая прямая, проходящая через его центр, есть главная ось инерции.
Моменты инерции относительно главных осей инерции называются главными моментами инерции, а относительно главных центральных осей инерции — главными центральными моментами инерции.
Если уравнение эллипсоида инерции отнести к его главным осям 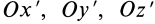
где 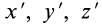
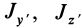
Справедливо и обратное утверждение: если центробежные моменты инерции относительно трех взаимно перпендикулярных осей равны нулю, то эти оси являются главными осями инерции. Обращение в нуль трех центробежных моментов инерции является необходимым и достаточным условием того, что соответствующие прямоугольные оси координат есть главные оси инерции.
Главные моменты инерции часто обозначают 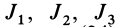
- Заказать решение задач по теоретической механике
Свойства главных осей инерции
Теорема 1. Если одна из декартовых осей координат, например 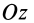
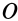
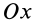
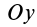
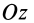
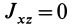
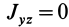
Главная ось инерции 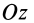
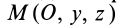
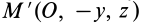
Вычитая из первого уравнения второе, имеем
Так как всегда можно выбрать точки, для которых 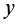
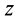
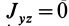
Рис. 31
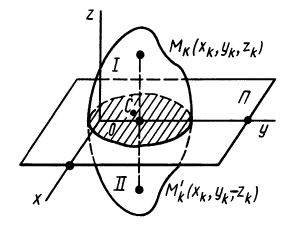
Аналогичные рассуждения для двух симметричных относительно оси 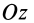
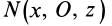
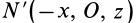
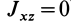
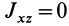
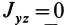
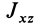
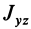
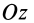
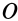
Теорема 2. Если однородное тело имеет плоскость симметрии, то для любой точки, лежащей в этой плоскости, одна из главных осей инерции перпендикулярна плоскости симметрии, а две другие главные оси инерции расположены в этой плоскости.
Рис. 32
Для доказательства теоремы выберем в плоскости симметрии 
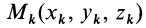
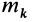
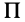
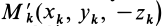
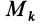
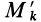
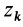
Для центробежного момента инерции 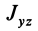
так как часть тела (I), соответствующая точкам с положительными координатами 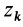
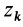
Так как центробежные моменты инерции 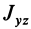
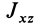
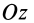
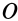
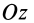
Центр масс однородного симметричного тела находится в плоскости симметрии. Поэтому одна из главных центральных осей инерции перпендикулярна плоскости симметрии, а две другие расположены в этой плоскости.
Доказанная теорема справедлива и для неоднородного тела, имеющего плоскость материальной симметрии.
Теорема 3. Если однородное тело имеет ось симметрии или неоднородное тело имеет ось материальной симметрии, то эта ось является главной центральной осью инерции.
Теорема доказывается аналогично предыдущей. Для каждой точки тела 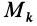
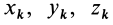
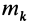
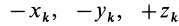
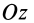
так как суммы по симметричным относительно оси частям тела (I) и (II) отличаются друг от друга только знаком у координаты 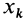
Аналогично доказывается, что 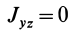
Таким образом, ось 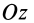
Теорема 4. Главные оси инерции для точки 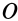
Выберем в точке 
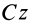
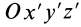
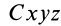
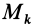
где 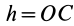
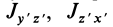
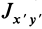
так как
где 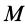
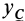
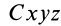
Если 
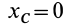
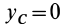
Используя полученные формулы при этих условиях, имеем:
Рис. 33
Следовательно, оси 
Из доказанной теоремы в качестве следствия получаем: главная центральная ось инерции является главной осью инерции для всех своих точек. Действительно, главная ось инерции 
Определение главных моментов инерции и направления главных осей
Пусть известны компоненты тензора инерции в точке 
Если оси координат 

Параллельные векторы отличаются друг от друга скалярным множителем, который обозначим 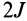
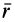

Рис. 34
В этих уравнениях 
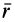
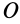
Для частных производных из (27′) получаем:
Подставляя их значения в (28′) и перенося все слагаемые в левую часть, после объединения и сокращения на общий множитель получим следующую систему уравнений для определения координат 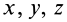
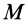
Так как (29) является однородной системой линейных уравнений, то отличные от нуля решения для координат 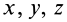
Это кубическое уравнение для определения 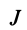
В общем случае имеется три различных действительных корня кубического уравнения 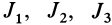
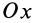
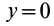
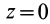
Так как 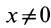
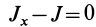
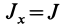
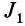
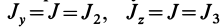
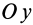
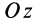
Подставляя в (29) 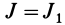
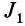
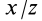
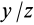
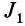
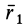
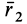
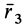
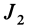
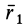

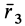
Таким образом, если известен тензор инерции для осей 
Выражение компонентов тензора инерции через главные моменты инерции
Определим компоненты тензора инерции в точке 
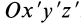
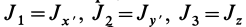
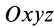
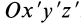
Осевые моменты инерции относительно осей 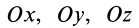
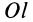
Для выражения центробежных моментов инерции через главные моменты инерции используем формулы преобразования координат точек тела при повороте осей координат вокруг точки 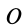
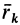
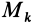
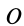
где 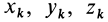
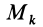
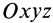
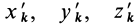
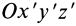
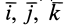
Рис. 35
Используя (33) для центробежного момента инерции 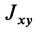
так как центробежные моменты инерции относительно главных осей инерции равны нулю, т. е.
Оси координат 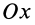
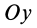
или
Используя это соотношение для исключения величины 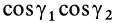
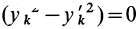
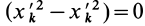
где
— главные моменты инерции. Аналогично получаются выражения для 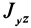
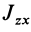
Формулы (31) и (35) дают выражения всех компонентов тензора инерции для осей координат 
Если ось 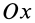
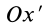
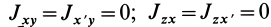
Из (35) имеем
В формуле (35′) с полюсом следует брать главный момент инерции с индексом той оси, на положительное направление которой указывает дуговая стрелка поворота осей 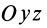
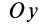
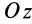
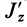
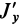
Рис. 36
Если оси расположены, как показано на рис. 37, то дуговая стрелка поворота осей 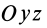
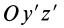
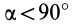
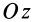
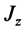
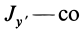
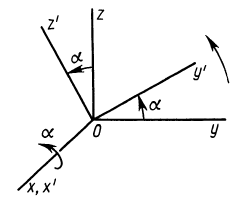
= 90°; р2 = а; Р3 = 90° + а;
Рис. 37
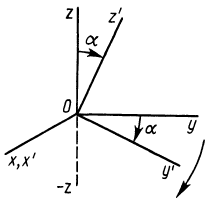
Аналогично при совпадении осей 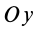
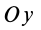
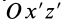
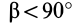
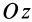
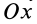
При совпадении осей 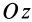
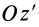
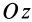
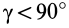
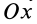
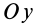
- Свойства внутренних сил системы
- Дифференциальное уравнение движения системы
- Теоремы об изменении количества движения и о движении центра масс
- Теорема об изменении кинетического момента
- Прямолинейное движение точки
- Криволинейное движение материальной точки
- Движение несвободной материальной точки
- Относительное движение материальной точки



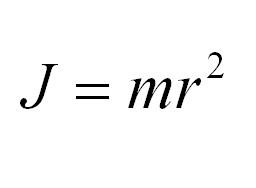
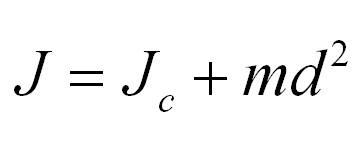

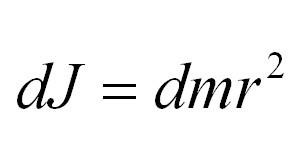


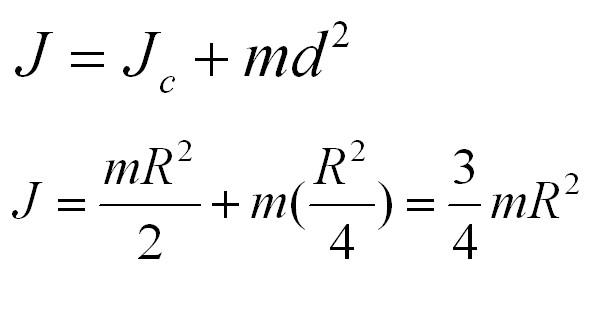
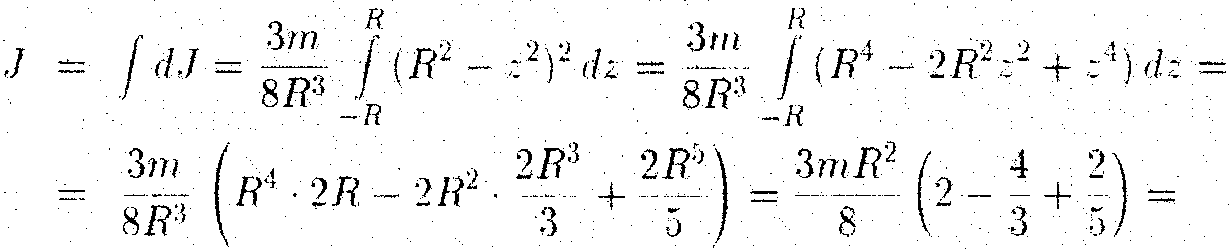

































![{displaystyle {begin{aligned}I_{C,{text{ball}}}&=int _{-R}^{R}{frac {pi rho }{2}}r(z)^{4},dz=int _{-R}^{R}{frac {pi rho }{2}}left(R^{2}-z^{2}right)^{2},dz\&={frac {pi rho }{2}}left[R^{4}z-{frac {2}{3}}R^{2}z^{3}+{frac {1}{5}}z^{5}right]_{-R}^{R}\&=pi rho left(1-{frac {2}{3}}+{frac {1}{5}}right)R^{5}\&={frac {2}{5}}mR^{2},end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/42e610139e74980c31f979cff68d8cdd3684dd05)

















![{displaystyle {begin{aligned}mathbf {b} times mathbf {y} &equiv left[mathbf {b} right]mathbf {y} \left[mathbf {b} right]&equiv {begin{bmatrix}0&-b_{z}&b_{y}\b_{z}&0&-b_{x}\-b_{y}&b_{x}&0end{bmatrix}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4782eb664e98a6d680dd96b77601ff9bc12ab4a)

![{displaystyle mathbf {L} =left(-sum _{i=1}^{n}m_{i}left[Delta mathbf {r} _{i}right]^{2}right){boldsymbol {omega }}=mathbf {I} _{mathbf {C} }{boldsymbol {omega }},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26ff4f4ab9aa3fff11085b8828fc71a4af7de700)
![{displaystyle mathbf {I} _{mathbf {C} }=-sum _{i=1}^{n}m_{i}left[Delta mathbf {r} _{i}right]^{2},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6766e8a9ce07ff8f32ec86aaa929f1e5a3ce1a21)



![{displaystyle {begin{aligned}E_{text{K}}&={frac {1}{2}}left(sum _{i=1}^{n}m_{i}left(left[Delta mathbf {r} _{i}right]{boldsymbol {omega }}right)cdot left(left[Delta mathbf {r} _{i}right]{boldsymbol {omega }}right)right)+{frac {1}{2}}left(sum _{i=1}^{n}m_{i}right)mathbf {V} _{mathbf {C} }cdot mathbf {V} _{mathbf {C} }\&={frac {1}{2}}left(sum _{i=1}^{n}m_{i}left({boldsymbol {omega }}^{mathsf {T}}left[Delta mathbf {r} _{i}right]^{mathsf {T}}left[Delta mathbf {r} _{i}right]{boldsymbol {omega }}right)right)+{frac {1}{2}}left(sum _{i=1}^{n}m_{i}right)mathbf {V} _{mathbf {C} }cdot mathbf {V} _{mathbf {C} }\&={frac {1}{2}}{boldsymbol {omega }}cdot left(-sum _{i=1}^{n}m_{i}left[Delta mathbf {r} _{i}right]^{2}right){boldsymbol {omega }}+{frac {1}{2}}left(sum _{i=1}^{n}m_{i}right)mathbf {V} _{mathbf {C} }cdot mathbf {V} _{mathbf {C} }.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c246c5646e149b67a600084c164f154ec7dda89)



![{displaystyle {boldsymbol {tau }}=left(-sum _{i=1}^{n}m_{i}left[Delta mathbf {r} _{i}right]^{2}right){boldsymbol {alpha }}+{boldsymbol {omega }}times left(-sum _{i=1}^{n}m_{i}left[Delta mathbf {r} _{i}right]^{2}right){boldsymbol {omega }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b93d7ec560fb15fbaaba36a2fd0869da807fd92e)

![{displaystyle {begin{aligned}{boldsymbol {tau }}&=sum _{i=1}^{n}(mathbf {r_{i}} -mathbf {R} )times (m_{i}mathbf {a} _{i})\&=sum _{i=1}^{n}{boldsymbol {Delta }}mathbf {r} _{i}times (m_{i}mathbf {a} _{i})\&=sum _{i=1}^{n}m_{i}[{boldsymbol {Delta }}mathbf {r} _{i}times mathbf {a} _{i}];ldots {text{ cross-product scalar multiplication}}\&=sum _{i=1}^{n}m_{i}[{boldsymbol {Delta }}mathbf {r} _{i}times (mathbf {a} _{{text{tangential}},i}+mathbf {a} _{{text{centripetal}},i}+mathbf {A} _{mathbf {R} })]\&=sum _{i=1}^{n}m_{i}[{boldsymbol {Delta }}mathbf {r} _{i}times (mathbf {a} _{{text{tangential}},i}+mathbf {a} _{{text{centripetal}},i}+0)]\&;;;;;ldots ;mathbf {R} {text{ is either at rest or moving at a constant velocity but not accelerated, or }}\&;;;;;;;;;;;{text{the origin of the fixed (world) coordinate reference system is placed at the center of mass }}mathbf {C} \&=sum _{i=1}^{n}m_{i}[{boldsymbol {Delta }}mathbf {r} _{i}times mathbf {a} _{{text{tangential}},i}+{boldsymbol {Delta }}mathbf {r} _{i}times mathbf {a} _{{text{centripetal}},i}];ldots {text{ cross-product distributivity over addition}}\&=sum _{i=1}^{n}m_{i}[{boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {alpha }}times {boldsymbol {Delta }}mathbf {r} _{i})+{boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {omega }}times mathbf {v} _{{text{tangential}},i})]\{boldsymbol {tau }}&=sum _{i=1}^{n}m_{i}[{boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {alpha }}times {boldsymbol {Delta }}mathbf {r} _{i})+{boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {omega }}times ({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r} _{i}))]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a1a1b0804a6cf8a550a81732385fca1083051df)
![{displaystyle {begin{aligned}0&={boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {omega }}times ({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r} _{i}))+{boldsymbol {omega }}times (({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r} _{i})times {boldsymbol {Delta }}mathbf {r} _{i})+({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r} _{i})times ({boldsymbol {Delta }}mathbf {r} _{i}times {boldsymbol {omega }})\&={boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {omega }}times ({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r} _{i}))+{boldsymbol {omega }}times (({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r} _{i})times {boldsymbol {Delta }}mathbf {r} _{i})+({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r} _{i})times -({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r} _{i});ldots {text{ cross-product anticommutativity}}\&={boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {omega }}times ({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r} _{i}))+{boldsymbol {omega }}times (({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r} _{i})times {boldsymbol {Delta }}mathbf {r} _{i})+-[({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r} _{i})times ({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r} _{i})];ldots {text{ cross-product scalar multiplication}}\&={boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {omega }}times ({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r} _{i}))+{boldsymbol {omega }}times (({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r} _{i})times {boldsymbol {Delta }}mathbf {r} _{i})+-[0];ldots {text{ self cross-product}}\0&={boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {omega }}times ({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r} _{i}))+{boldsymbol {omega }}times (({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r} _{i})times {boldsymbol {Delta }}mathbf {r} _{i})end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88ab33d54b34674092a14d55c8ccefb765a2e7ae)
![{displaystyle {begin{aligned}{boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {omega }}times ({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r} _{i}))&=-[{boldsymbol {omega }}times (({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r} _{i})times {boldsymbol {Delta }}mathbf {r} _{i})]\&=-[({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r} _{i})({boldsymbol {omega }}cdot {boldsymbol {Delta }}mathbf {r} _{i})-{boldsymbol {Delta }}mathbf {r} _{i}({boldsymbol {omega }}cdot ({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r} _{i}))];ldots {text{ vector triple product}}\&=-[({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r} _{i})({boldsymbol {omega }}cdot {boldsymbol {Delta }}mathbf {r} _{i})-{boldsymbol {Delta }}mathbf {r} _{i}({boldsymbol {Delta }}mathbf {r} _{i}cdot ({boldsymbol {omega }}times {boldsymbol {omega }}))];ldots {text{ scalar triple product}}\&=-[({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r} _{i})({boldsymbol {omega }}cdot {boldsymbol {Delta }}mathbf {r} _{i})-{boldsymbol {Delta }}mathbf {r} _{i}({boldsymbol {Delta }}mathbf {r} _{i}cdot (0))];ldots {text{ self cross-product}}\&=-[({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r} _{i})({boldsymbol {omega }}cdot {boldsymbol {Delta }}mathbf {r} _{i})]\&=-[{boldsymbol {omega }}times ({boldsymbol {Delta }}mathbf {r} _{i}({boldsymbol {omega }}cdot {boldsymbol {Delta }}mathbf {r} _{i}))];ldots {text{ cross-product scalar multiplication}}\&={boldsymbol {omega }}times -({boldsymbol {Delta }}mathbf {r} _{i}({boldsymbol {omega }}cdot {boldsymbol {Delta }}mathbf {r} _{i}));ldots {text{ cross-product scalar multiplication}}\{boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {omega }}times ({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r} _{i}))&={boldsymbol {omega }}times -({boldsymbol {Delta }}mathbf {r} _{i}({boldsymbol {Delta }}mathbf {r} _{i}cdot {boldsymbol {omega }}));ldots {text{ dot-product commutativity}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb1ab7d45bf04c0df3101e84282bc6695ddecf68)
![{displaystyle {begin{aligned}{boldsymbol {tau }}&=sum _{i=1}^{n}m_{i}[{boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {alpha }}times {boldsymbol {Delta }}mathbf {r} _{i})+{boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {omega }}times ({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r} _{i}))]\&=sum _{i=1}^{n}m_{i}[{boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {alpha }}times {boldsymbol {Delta }}mathbf {r} _{i})+{boldsymbol {omega }}times -({boldsymbol {Delta }}mathbf {r} _{i}({boldsymbol {Delta }}mathbf {r} _{i}cdot {boldsymbol {omega }}))]\&=sum _{i=1}^{n}m_{i}[{boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {alpha }}times {boldsymbol {Delta }}mathbf {r} _{i})+{boldsymbol {omega }}times {0-{boldsymbol {Delta }}mathbf {r} _{i}({boldsymbol {Delta }}mathbf {r} _{i}cdot {boldsymbol {omega }})}]\&=sum _{i=1}^{n}m_{i}[{boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {alpha }}times {boldsymbol {Delta }}mathbf {r} _{i})+{boldsymbol {omega }}times {[{boldsymbol {omega }}({boldsymbol {Delta }}mathbf {r} _{i}cdot {boldsymbol {Delta }}mathbf {r} _{i})-{boldsymbol {omega }}({boldsymbol {Delta }}mathbf {r} _{i}cdot {boldsymbol {Delta }}mathbf {r} _{i})]-{boldsymbol {Delta }}mathbf {r} _{i}({boldsymbol {Delta }}mathbf {r} _{i}cdot {boldsymbol {omega }})}];ldots ;{boldsymbol {omega }}({boldsymbol {Delta }}mathbf {r} _{i}cdot {boldsymbol {Delta }}mathbf {r} _{i})-{boldsymbol {omega }}({boldsymbol {Delta }}mathbf {r} _{i}cdot {boldsymbol {Delta }}mathbf {r} _{i})=0\&=sum _{i=1}^{n}m_{i}[{boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {alpha }}times {boldsymbol {Delta }}mathbf {r} _{i})+{boldsymbol {omega }}times {[{boldsymbol {omega }}({boldsymbol {Delta }}mathbf {r} _{i}cdot {boldsymbol {Delta }}mathbf {r} _{i})-{boldsymbol {Delta }}mathbf {r} _{i}({boldsymbol {Delta }}mathbf {r} _{i}cdot {boldsymbol {omega }})]-{boldsymbol {omega }}({boldsymbol {Delta }}mathbf {r} _{i}cdot {boldsymbol {Delta }}mathbf {r} _{i})}];ldots {text{ addition associativity}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/66f6f583aacfd008f43218fc24e97547511a6a91)
![{displaystyle {begin{aligned}&=sum _{i=1}^{n}m_{i}[{boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {alpha }}times {boldsymbol {Delta }}mathbf {r} _{i})+{boldsymbol {omega }}times {{boldsymbol {omega }}({boldsymbol {Delta }}mathbf {r} _{i}cdot {boldsymbol {Delta }}mathbf {r} _{i})-{boldsymbol {Delta }}mathbf {r} _{i}({boldsymbol {Delta }}mathbf {r} _{i}cdot {boldsymbol {omega }})}-{boldsymbol {omega }}times {boldsymbol {omega }}({boldsymbol {Delta }}mathbf {r} _{i}cdot {boldsymbol {Delta }}mathbf {r} _{i})];ldots {text{ cross-product distributivity over addition}}\&=sum _{i=1}^{n}m_{i}[{boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {alpha }}times {boldsymbol {Delta }}mathbf {r} _{i})+{boldsymbol {omega }}times {{boldsymbol {omega }}({boldsymbol {Delta }}mathbf {r} _{i}cdot {boldsymbol {Delta }}mathbf {r} _{i})-{boldsymbol {Delta }}mathbf {r} _{i}({boldsymbol {Delta }}mathbf {r} _{i}cdot {boldsymbol {omega }})}-({boldsymbol {Delta }}mathbf {r} _{i}cdot {boldsymbol {Delta }}mathbf {r} _{i})({boldsymbol {omega }}times {boldsymbol {omega }})];ldots {text{ cross-product scalar multiplication}}\&=sum _{i=1}^{n}m_{i}[{boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {alpha }}times {boldsymbol {Delta }}mathbf {r} _{i})+{boldsymbol {omega }}times {{boldsymbol {omega }}({boldsymbol {Delta }}mathbf {r} _{i}cdot {boldsymbol {Delta }}mathbf {r} _{i})-{boldsymbol {Delta }}mathbf {r} _{i}({boldsymbol {Delta }}mathbf {r} _{i}cdot {boldsymbol {omega }})}-({boldsymbol {Delta }}mathbf {r} _{i}cdot {boldsymbol {Delta }}mathbf {r} _{i})(0)];ldots {text{ self cross-product}}\&=sum _{i=1}^{n}m_{i}[{boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {alpha }}times {boldsymbol {Delta }}mathbf {r} _{i})+{boldsymbol {omega }}times {{boldsymbol {omega }}({boldsymbol {Delta }}mathbf {r} _{i}cdot {boldsymbol {Delta }}mathbf {r} _{i})-{boldsymbol {Delta }}mathbf {r} _{i}({boldsymbol {Delta }}mathbf {r} _{i}cdot {boldsymbol {omega }})}]\&=sum _{i=1}^{n}m_{i}[{boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {alpha }}times {boldsymbol {Delta }}mathbf {r} _{i})+{boldsymbol {omega }}times {{boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r} _{i})}];ldots {text{ vector triple product}}\&=sum _{i=1}^{n}m_{i}[{boldsymbol {Delta }}mathbf {r} _{i}times -({boldsymbol {Delta }}mathbf {r} _{i}times {boldsymbol {alpha }})+{boldsymbol {omega }}times {{boldsymbol {Delta }}mathbf {r} _{i}times -({boldsymbol {Delta }}mathbf {r} _{i}times {boldsymbol {omega }})}];ldots {text{ cross-product anticommutativity}}\&=-sum _{i=1}^{n}m_{i}[{boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {Delta }}mathbf {r} _{i}times {boldsymbol {alpha }})+{boldsymbol {omega }}times {{boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {Delta }}mathbf {r} _{i}times {boldsymbol {omega }})}];ldots {text{ cross-product scalar multiplication}}\&=-sum _{i=1}^{n}m_{i}[{boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {Delta }}mathbf {r} _{i}times {boldsymbol {alpha }})]+-sum _{i=1}^{n}m_{i}[{boldsymbol {omega }}times {{boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {Delta }}mathbf {r} _{i}times {boldsymbol {omega }})}];ldots {text{ summation distributivity}}\{boldsymbol {tau }}&=-sum _{i=1}^{n}m_{i}[{boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {Delta }}mathbf {r} _{i}times {boldsymbol {alpha }})]+{boldsymbol {omega }}times -sum _{i=1}^{n}m_{i}[{boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {Delta }}mathbf {r} _{i}times {boldsymbol {omega }})];ldots ;{boldsymbol {omega }}{text{ is not characteristic of particle }}P_{i}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/adeb5bbad0d607e038f18398c83a2761c4af3102)
![{displaystyle {begin{aligned}-sum _{i=1}^{n}m_{i}[{boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {Delta }}mathbf {r} _{i}times mathbf {u} )]&=-sum _{i=1}^{n}m_{i}left({begin{bmatrix}0&-Delta r_{3,i}&Delta r_{2,i}\Delta r_{3,i}&0&-Delta r_{1,i}\-Delta r_{2,i}&Delta r_{1,i}&0end{bmatrix}}left({begin{bmatrix}0&-Delta r_{3,i}&Delta r_{2,i}\Delta r_{3,i}&0&-Delta r_{1,i}\-Delta r_{2,i}&Delta r_{1,i}&0end{bmatrix}}{begin{bmatrix}u_{1}\u_{2}\u_{3}end{bmatrix}}right)right);ldots {text{ cross-product as matrix multiplication}}\[6pt]&=-sum _{i=1}^{n}m_{i}left({begin{bmatrix}0&-Delta r_{3,i}&Delta r_{2,i}\Delta r_{3,i}&0&-Delta r_{1,i}\-Delta r_{2,i}&Delta r_{1,i}&0end{bmatrix}}{begin{bmatrix}-Delta r_{3,i},u_{2}+Delta r_{2,i},u_{3}\+Delta r_{3,i},u_{1}-Delta r_{1,i},u_{3}\-Delta r_{2,i},u_{1}+Delta r_{1,i},u_{2}end{bmatrix}}right)\[6pt]&=-sum _{i=1}^{n}m_{i}{begin{bmatrix}-Delta r_{3,i}(+Delta r_{3,i},u_{1}-Delta r_{1,i},u_{3})+Delta r_{2,i}(-Delta r_{2,i},u_{1}+Delta r_{1,i},u_{2})\+Delta r_{3,i}(-Delta r_{3,i},u_{2}+Delta r_{2,i},u_{3})-Delta r_{1,i}(-Delta r_{2,i},u_{1}+Delta r_{1,i},u_{2})\-Delta r_{2,i}(-Delta r_{3,i},u_{2}+Delta r_{2,i},u_{3})+Delta r_{1,i}(+Delta r_{3,i},u_{1}-Delta r_{1,i},u_{3})end{bmatrix}}\[6pt]&=-sum _{i=1}^{n}m_{i}{begin{bmatrix}-Delta r_{3,i}^{2},u_{1}+Delta r_{1,i}Delta r_{3,i},u_{3}-Delta r_{2,i}^{2},u_{1}+Delta r_{1,i}Delta r_{2,i},u_{2}\-Delta r_{3,i}^{2},u_{2}+Delta r_{2,i}Delta r_{3,i},u_{3}+Delta r_{2,i}Delta r_{1,i},u_{1}-Delta r_{1,i}^{2},u_{2}\+Delta r_{3,i}Delta r_{2,i},u_{2}-Delta r_{2,i}^{2},u_{3}+Delta r_{3,i}Delta r_{1,i},u_{1}-Delta r_{1,i}^{2},u_{3}end{bmatrix}}\[6pt]&=-sum _{i=1}^{n}m_{i}{begin{bmatrix}-(Delta r_{2,i}^{2}+Delta r_{3,i}^{2}),u_{1}+Delta r_{1,i}Delta r_{2,i},u_{2}+Delta r_{1,i}Delta r_{3,i},u_{3}\+Delta r_{2,i}Delta r_{1,i},u_{1}-(Delta r_{1,i}^{2}+Delta r_{3,i}^{2}),u_{2}+Delta r_{2,i}Delta r_{3,i},u_{3}\+Delta r_{3,i}Delta r_{1,i},u_{1}+Delta r_{3,i}Delta r_{2,i},u_{2}-(Delta r_{1,i}^{2}+Delta r_{2,i}^{2}),u_{3}end{bmatrix}}\[6pt]&=-sum _{i=1}^{n}m_{i}{begin{bmatrix}-(Delta r_{2,i}^{2}+Delta r_{3,i}^{2})&Delta r_{1,i}Delta r_{2,i}&Delta r_{1,i}Delta r_{3,i}\Delta r_{2,i}Delta r_{1,i}&-(Delta r_{1,i}^{2}+Delta r_{3,i}^{2})&Delta r_{2,i}Delta r_{3,i}\Delta r_{3,i}Delta r_{1,i}&Delta r_{3,i}Delta r_{2,i}&-(Delta r_{1,i}^{2}+Delta r_{2,i}^{2})end{bmatrix}}{begin{bmatrix}u_{1}\u_{2}\u_{3}end{bmatrix}}\&=-sum _{i=1}^{n}m_{i}[Delta r_{i}]^{2}mathbf {u} \[6pt]-sum _{i=1}^{n}m_{i}[{boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {Delta }}mathbf {r} _{i}times mathbf {u} )]&=left(-sum _{i=1}^{n}m_{i}[Delta r_{i}]^{2}right)mathbf {u} ;ldots ;mathbf {u} {text{ is not characteristic of }}P_{i}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/059812b4501e0672712b5b7adff834e79c3b4bff)
![{displaystyle {begin{aligned}{boldsymbol {tau }}&=-sum _{i=1}^{n}m_{i}[{boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {Delta }}mathbf {r} _{i}times {boldsymbol {alpha }})]+{boldsymbol {omega }}times -sum _{i=1}^{n}m_{i}{boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {Delta }}mathbf {r} _{i}times {boldsymbol {omega }})]\&=left(-sum _{i=1}^{n}m_{i}[Delta r_{i}]^{2}right){boldsymbol {alpha }}+{boldsymbol {omega }}times left(-sum _{i=1}^{n}m_{i}[Delta r_{i}]^{2}right){boldsymbol {omega }}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0971bbc71e7ceb3c810afa1043b08aca54608486)

![{displaystyle mathbf {I} _{mathbf {R} }=-sum _{i=1}^{n}m_{i}left[mathbf {r} _{i}-mathbf {R} right]^{2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93e62233b3acff4fc919fc24e8d6241551543087)

![{displaystyle mathbf {I} _{mathbf {R} }=-sum _{i=1}^{n}m_{i}[mathbf {r} _{i}-left(mathbf {C} +mathbf {d} right)]^{2}=-sum _{i=1}^{n}m_{i}[left(mathbf {r} _{i}-mathbf {C} right)-mathbf {d} ]^{2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0063409d605348215928372e62f294287f06fb98)
![{displaystyle mathbf {I} _{mathbf {R} }=-left(sum _{i=1}^{n}m_{i}[mathbf {r} _{i}-mathbf {C} ]^{2}right)+left(sum _{i=1}^{n}m_{i}[mathbf {r} _{i}-mathbf {C} ]right)[mathbf {d} ]+[mathbf {d} ]left(sum _{i=1}^{n}m_{i}[mathbf {r} _{i}-mathbf {C} ]right)-left(sum _{i=1}^{n}m_{i}right)[mathbf {d} ]^{2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68eee7fefe0e716823fd5d80384303b8aef58b99)
![{displaystyle mathbf {I} _{mathbf {R} }=mathbf {I} _{mathbf {C} }-M[mathbf {d} ]^{2},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c59b0848c4b1d69fff75c4257005225cd42c74d)
![{displaystyle I_{L}=mathbf {hat {k}} cdot left(-sum _{i=1}^{N}m_{i}left[Delta mathbf {r} _{i}right]^{2}right)mathbf {hat {k}} =mathbf {hat {k}} cdot mathbf {I} _{mathbf {R} }mathbf {hat {k}} =mathbf {hat {k}} ^{mathsf {T}}mathbf {I} _{mathbf {R} }mathbf {hat {k}} ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78bb7c062959fd615347939341b32bf66de221c6)

![{displaystyle -left[mathbf {hat {k}} right]^{2}equiv left|mathbf {hat {k}} right|^{2}left(mathbf {E} -mathbf {hat {k}} mathbf {hat {k}} ^{mathsf {T}}right)=mathbf {E} -mathbf {hat {k}} mathbf {hat {k}} ^{mathsf {T}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d92be0b3adbb50fbe61b31dc0237f0fc102476a0)
![{displaystyle {begin{aligned}left|Delta mathbf {r} _{i}^{perp }right|^{2}&=left(-left[mathbf {hat {k}} right]^{2}Delta mathbf {r} _{i}right)cdot left(-left[mathbf {hat {k}} right]^{2}Delta mathbf {r} _{i}right)\&=left(mathbf {hat {k}} times left(mathbf {hat {k}} times Delta mathbf {r} _{i}right)right)cdot left(mathbf {hat {k}} times left(mathbf {hat {k}} times Delta mathbf {r} _{i}right)right)end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d205a6da935ecfa8f5e13feb1a930f1d032022a)

![{displaystyle {begin{aligned}&left(mathbf {hat {k}} times left(mathbf {hat {k}} times Delta mathbf {r} _{i}right)right)cdot left(mathbf {hat {k}} times left(mathbf {hat {k}} times Delta mathbf {r} _{i}right)right)\={}&left(left(mathbf {hat {k}} times left(mathbf {hat {k}} times Delta mathbf {r} _{i}right)right)times mathbf {hat {k}} right)cdot left(mathbf {hat {k}} times Delta mathbf {r} _{i}right)\={}&left(mathbf {hat {k}} times Delta mathbf {r} _{i}right)cdot left(-Delta mathbf {r} _{i}times mathbf {hat {k}} right)\={}&-mathbf {hat {k}} cdot left(Delta mathbf {r} _{i}times Delta mathbf {r} _{i}times mathbf {hat {k}} right)\={}&-mathbf {hat {k}} cdot left[Delta mathbf {r} _{i}right]^{2}mathbf {hat {k}} .end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62111ff66a6922e2705a7eb60478088077b7d9bf)
![{displaystyle {begin{aligned}I_{L}&=sum _{i=1}^{N}m_{i}left|Delta mathbf {r} _{i}^{perp }right|^{2}\&=-sum _{i=1}^{N}m_{i}mathbf {hat {k}} cdot left[Delta mathbf {r} _{i}right]^{2}mathbf {hat {k}} =mathbf {hat {k}} cdot left(-sum _{i=1}^{N}m_{i}left[Delta mathbf {r} _{i}right]^{2}right)mathbf {hat {k}} \&=mathbf {hat {k}} cdot mathbf {I} _{mathbf {R} }mathbf {hat {k}} =mathbf {hat {k}} ^{mathsf {T}}mathbf {I} _{mathbf {R} }mathbf {hat {k}} ,end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f4a4a61db87467a4b76294e68bba221a2810cdf)





![{displaystyle mathbf {I} =iiint _{V}rho (mathbf {r} )[mathbf {r} ]^{textsf {T}}[mathbf {r} ],dV=-iiint _{Q}rho (mathbf {r} )[mathbf {r} ]^{2},dV}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f468dc8f2e4246bf78b1916390083f90998be5c)



![{displaystyle {begin{aligned}I_{xy}=I_{yx} &{stackrel {mathrm {def} }{=}} sum _{k=1}^{N}m_{k}x_{k}y_{k},\I_{xz}=I_{zx} &{stackrel {mathrm {def} }{=}} sum _{k=1}^{N}m_{k}x_{k}z_{k},\I_{yz}=I_{zy} &{stackrel {mathrm {def} }{=}} sum _{k=1}^{N}m_{k}y_{k}z_{k},\[3pt]mathbf {I} ={begin{bmatrix}I_{11}&I_{12}&I_{13}\I_{21}&I_{22}&I_{23}\I_{31}&I_{32}&I_{33}end{bmatrix}}&={begin{bmatrix}I_{xx}&-I_{xy}&-I_{xz}\-I_{yx}&I_{yy}&-I_{yz}\-I_{zx}&-I_{zy}&I_{zz}end{bmatrix}}={begin{bmatrix}sum _{k=1}^{N}m_{k}left(y_{k}^{2}+z_{k}^{2}right)&-sum _{k=1}^{N}m_{k}x_{k}y_{k}&-sum _{k=1}^{N}m_{k}x_{k}z_{k}\-sum _{k=1}^{N}m_{k}x_{k}y_{k}&sum _{k=1}^{N}m_{k}left(x_{k}^{2}+z_{k}^{2}right)&-sum _{k=1}^{N}m_{k}y_{k}z_{k}\-sum _{k=1}^{N}m_{k}x_{k}z_{k}&-sum _{k=1}^{N}m_{k}y_{k}z_{k}&sum _{k=1}^{N}m_{k}left(x_{k}^{2}+y_{k}^{2}right)end{bmatrix}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a01acaa1d453d5d3f4c7faf8a74da5b2637bb01)





![{displaystyle mathbf {I} =mathbf {I} _{0}+m[(mathbf {R} cdot mathbf {R} )mathbf {E} _{3}-mathbf {R} otimes mathbf {R} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22568fa28674e243955b8fdddced7496b8e6487d)