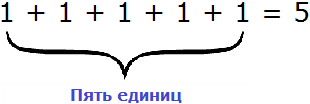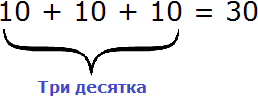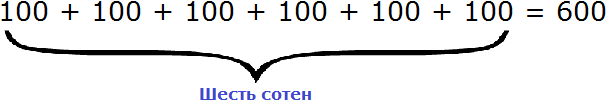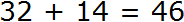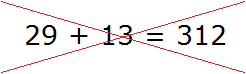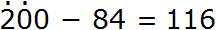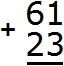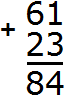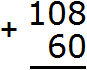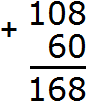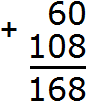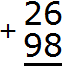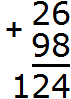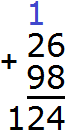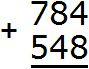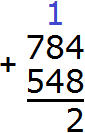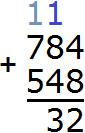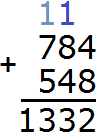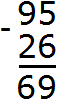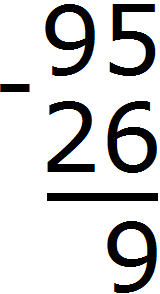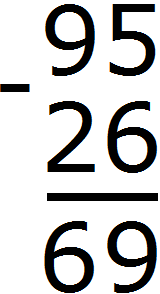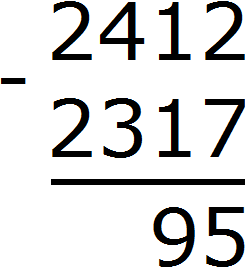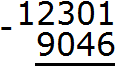Как найти десятки количество десятков в числе

Один десяток — это сколько? 7 сотен — это сколько десятков? Сколько десятков в числе 496, в числе 620, в числе 23564, в числе 700380, в числе 813290? Как считать десятки, если число с десятичной дробью? Чтобы узнать, сколько десятков в каком-то числе нужно это число разделить на 10. Всё просто. Соответственно, в сотне: 100/10 = 10 десятков; в тысяче: 1000/10 = 100 десятков; в семи сотнях: 700/10 = 7 десятков. Ну, а разделить-то на десять, думаю, Вы знаете как: просто передвиньте запятую на одну цифру влево или отделите одну цифру запятой. 496/10 = 49,6; 620/10 = 62; 23564/10 = 2356,4; 700380/10 = 70038; 813290/10 = 81329; 382/10 = 38,2; 38,2/10 = 3,82. И так далее. автор вопроса выбрал этот ответ лучшим Чтобы определить, сколько десятков в числе, нужно просто закрыть последнюю цифру и прочитать число В одной сотне — 10 десятков, в одной тысяче — 100 десятков. десять единиц вместе будет один десяток В числах 496, 620, 23564 и т.д закрываем последнюю цифру и получаем 49 десятков, 62 десятка, 2356 десятка и т.д. Вовсе не нужно боятся чисел, которые записаны десятичной дробью — в этом случае чтобы определить количество десятков в числе, на цифры после запятой не обращаем внимания (будто их и не было вовсе) и делаем как раньше, ниже несколько примеров: число 2783,07 содержит в себе 278 десятков число 1501,99 содержит в себе 150 десятков Что такое десяток? Прежде всего это десять единиц, которые объединившись образовали более крупную формацию — десяток. Поэтому определяя в большом числе количество десятков, надо упускать единицы, последнюю цифру числа, ведь там единицы не набрались до десятка. В круглых числах все очень просто — отбрасываем последний ноль и получаем число десятков — для 100 — это 10 десятков, для 13450 — это 1345 десятка. Ничуть не сложнее посчитать число десятков не в круглых числах — так же отбрасываем последнюю цифру показывающую единицы и получаем что в 756 — 75 десятков и можно уточнить еще 6 единиц. Если же число имеет и дробную часть, то про нее вовсе забываем, она даже меньше единицы и на количество десятков никакого влияния не оказывает. Например 276.5 содержит 27 десятков, 6 единиц и 5 десятых от единицы. Adgjm­p [140K] 7 лет назад  Десяток сам и говорит за сбя. Если челое число единица, то десяток- это десять единиц. Но далее нам надо узнавать сколько десятков в числах. Поэтому надо делить число на десять, отбрасывать единицы еслиони есть и мы получим количество десятков. Либо просто переносить с зади на перёд на одну цифру запятую и всё тоже самое с отбрасыванием единиц, если таковые имеются. 90- девять десятков. 99- девять десятков. 99,9- девять десятков. 900- девяносто десятков и т.д. Zolot­ynka [551K] 7 лет назад  Чтобы узнать, количество десятков в любом числе, нужно это число разделить на 100. Так, в сотне — 10 десятков, в тысяче — 100 и т.д. Если число не круглое, соответственно, количество десятков тоже будет не круглым: 496 разделим на 10, получим 49,6 десятков. Если разделим на 10 число 813290, количество десятков будет 81329 (просто убираем нолик) ну, и так далее. Галин­а Васил­ьна [163K] 7 лет назад  В одном десятке десять единиц, то есть 10. Семь сотен, это семь раз по сто 7х100=700. Чтобы узнать, сколько тут десятков, нужно убрать у 700 один ноль, получится 70 — столько десятков в семистах. Чтобы узнать, сколько десятков в числе, нужно убрать последний знак, или поставить запятую перед последним знаком в числе. У 469 будет 46 десятков или 46,9 десятка. Округлять в таких случаях не нужно. Проще просто убрать последнюю цифру. MaiAs­im [43K] 7 лет назад  Все предельно просто. Вам нужно то число, в котором вы хотите определить количество десятков разделить на 10. Делить числа на 10 очень просто, нужно всего лишь запятую переносить на одну единицу влево. Так, в сотне — 10 десятков (100,0 — переносим запятую и получаем — 10,00) в тысяче — 100 десятков и так далее С остальными числами то же самое 496,0 — переносим и получаем 49,60 десятков Про10­0 й [76.8K] 7 лет назад  В одном десятке всего десять единиц будет. В сотне десятков будет ровно десять. В тысяче десятков будет 100, находим методом деления этого числа на 10 и получаем ответ ( 100 : 10 = 10, 1000 : 10 = 100) 700 : 10 = 70 десятков. в числе 496 будет 46 десятков, остальное это единицы. в числе 620 будет 62 десятка. в числе 23564 десятков будет 2356 в числе 700380 — 70038 Краси­вая полян­а [36.6K] 7 лет назад  Один десяток это число десять. В ста единицах содержится десять десятков: 100:10=10. А в тысяче единиц будет содержаться сто десятков: 1000:10=100. Как видно из примеров, чтобы определиться сколько в числе содержится десятков нужно разделить это число на десять, например: 10:10=1. Семь сотен это: 700:10=70 итого семьдесят десятков. Vasqu­ez [5.8K] 8 лет назад  В одной сотне десять десятков. Это знают все, кто учил таблицу умножения, 10 х 10 = 100. Тысяча в десять раз больше сотни, и в числе 1000 получается 100 десятков. Это просто проверить так как каждый ноль прибавляемый справа дает умножение на 10. Значит, в сотне 10 десятков, а в тысяче их 100. Знаете ответ?

                                           I.НУМЕРАЦИЯ
ЧИСЕЛ

Для записи чисел люди придумали десять знаков, которые
называются цифрами. Это: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

С помощью десяти цифр можно записать любое натуральное число.

Число, состоящее из одного знака (цифры), называется
однозначным. Наименьшее однозначное число — 1, наибольшее — 9.

Число, состоящее из двух знаков (цифр), называется двузначным. Наименьшее
двузначное число — 10, наибольшее — 99.

Числа, записанные с помощью двух, трёх, четырёх и более цифр,
называются двузначными, трёхзначными, четырёхзначными или многозначными.
Наименьшее трёхзначное число — 100, наибольшее — 999.

Разряд — это место (позиция), на
котором в записи числа стоит цифра.

Разряды отсчитываются с конца числа.

Разряд единиц — это самый младший разряд, которым заканчивается
любое число.

Разряд  десятков — это разряд, который стоит перед разрядом
единиц.

Разряд   сотен — это разряд, который стоит перед разрядом
десятков.

Если в числе отсутствует какой-либо разряд, то в записи числа на
его месте будет стоять цифра 0.

Пример. В числе 807 содержится 8 сотен, 0 десятков и 7 единиц —
такая запись называется разрядным составом числа.

Каждые 10 единиц любого разряда образуют новую единицу более
высокого разряда. Например, 10 единиц образуют 1 десяток, а 10 десятков
образуют 1 сотню.

Таким образом, значение цифры от разряда к разряду (от единиц к
десяткам, от десятков к сотням) увеличивается в 10 раз. Поэтому система счёта
(счисления), которую мы используем, называется десятичной системой счисления.

Классы и разряды

В записи числа разряды, начиная справа, группируются в классы по
три разряда в каждом.

III  КЛАСС  —  КЛАСС  МИЛЛИОНОВ	II  КЛАСС   — КЛАСС ТЫСЯЧ	I КЛАСС  — КЛАСС   ЕДИНИЦ
сотни миллионов	десятки миллионов	единицы миллионов	сотни тысяч	десятки тысяч	единицы тысяч	сотни	десятки	единицы

    9             8            7             6           
5             4            3              2           1

Класс единиц или первый класс — это
класс, который образуют первые три разряда (справа от конца числа): разряд
единиц, разряд десятков и разряд сотен.

 Класс тысяч или второй класс — это
класс, который образуют следующие три разряда: единицы тысяч, десятки тысяч и
сотни тысяч.

Класс миллионов или третий класс — это
класс, который образуют следующие три разряда: единицы миллионов, десятки миллионов
и сотни миллионов.

Чтобы прочитать многозначное число, надо назвать по очереди
слева направо число единиц каждого класса и добавить название класса.

Не произносят название класса единиц, а также название класса,
все три цифры которого нули.

Например, число 134 590 720 читаем: сто тридцать четыре миллиона
пятьсот девяносто тысяч семьсот двадцать.

Число 418 000 547 читаем: четыреста восемнадцать миллионов
пятьсот сорок семь.

Как определить, сколько в числе:                                         

всего единиц

всего десятков

всего сотен

всего единиц тысяч

всего десятков тысяч

всего сотен тысяч

Чтобы определить, сколько всего единиц в числе, нужно
прочитать всё число.

Чтобы определить, сколько всего десятков в числе, надо
закрыть одну цифру справа и  прочитать получившееся число десятков.

Чтобы определить, сколько всего сотен в
числе, надо закрыть две цифры справа и прочитать получившееся число сотен.

Чтобы определить, сколько всего единиц тысяч
в числе, надо закрыть три цифры справа и
прочитать получившееся число

Чтобы определить, сколько всего десятков тысяч
в числе, надо закрыть четыре цифры справа и прочитать получившееся число
десятков тысяч.

Чтобы определить, сколько всего сотен тысяч в
числе, надо закрыть пять цифр справа, и прочитать получившееся число сотен
тысяч.

1.      Запиши
числа.

Девятьсот тысяч семьсот пятнадцать

шестьсот шестьдесят тысяч пятьсот семь

один миллион восемьсот два

девять тысяч два

три тысячи шестьдесят

семьсот восемьдесят тысяч девятьсот тридцать

четыреста тысяч два

восемьсот пятьдесят пять тысяч пятьсот восемь

восемьсот тысяч шесть

шестьсот девять тысяч семьсот тридцать семь

восемьсот двадцать тысяч девятьсот шесть

пять тысяч восемьсот семьдесят

сто миллионов девятьсот десять тысяч тридцать

пятьсот двадцать тысяч семь

двенадцать тысяч шестьсот пять

семьсот тридцать девять тысяч пятьсот семь

шестьсот пятьдесят миллионов пять тысяч два

девятьсот тысяч шестнадцать

пятьсот восемьдесят тысяч девять

шестьсот восемь тысяч восемьсот тридцать пять

восемьдесят тысяч двадцать шесть

девять тысяч десять

два миллиона триста две тысячи семьдесят три

 сто восемьдесят пять миллионов тридцать два три тысячи
девятьсот шестьдесят четыре

пятьсот девять миллионов тридцать две тысячи

семьсот миллионов четыреста шестнадцать тысяч

тридцать два тысячи шестьсот восемнадцать

четыре миллиона пятьдесят пять тысяч один

2 Запиши числа, которые
расположены между числами.

100 297 и 100 305 —           

678 501 и 678 490-

802 000 и 801 988
—

799 998 и 800 002-

599 999 и 600 010
—

399 997 и 400 003-

478 999 и 479 010
—

40 997 и 41 003-

246 668 и 246 675 —

200 995 и 201 000 –

307 602 и 307 596 –

567 401 и 567 390 –

701 000 и 700 988 –

699 998 и 700 002 –

499 999 и 500 010 –

299 997 и 300 003 –

896 999 и 897 003 –

199 997 и 200 001-

200 398 и 200 406-

3. Сравни
числа.

504009… 507080               970100 … 900 700           
70090… 7009

4789785 … 589348              7000009 … 700019             847090
… 3905000

100065… 100660               50 024 … 435 000               509020…
70308

4000… 400000                   433000… 32500                  7000…
700000

4.Запиши число, в котором:

тридцать одна единица III
класса, шестнад­цать единиц I класса

восемьсот единиц III
класса, пять единиц II класса

девять единиц II
класса, восемь единиц I класса

шестьдесят единиц III
класса, шестьсот пять

единиц II класса

девять единиц II
класса, шестьдесят единиц I класса

одна единица II
класса, четыреста единиц I класса

пятьсот единиц III
класса, двадцать семь единиц II класса, одна единица I
класса

двадцать семь единиц II
класса, одна едини­ца I класса

шесть единиц III
класса, девятьсот единиц I класса

семьдесят единиц II
класса, девятьсот единиц I класса

шесть единиц III
класса, десять един пи I класса

5.  Напиши предыдущие числа
для чисел:

700000                              40670000      

 300001000                       2050000

38000010                          7600000      

501000000                        30101000  

700000                             900000    

60680000                          900030000

6. Напиши последующие числа
для чисел:

500999000                         401010010                        

7900                                 15999010                                         

800990900                         5040000

5600                                  65000200    

5970010                                 804000     

683000                             200500

7.Запиши число, в котором:

9 единиц 6 разряда, 9 единиц 4 разряда  8
единиц 2 разряда

5 единиц 6 разряда, 5 единиц 3 разряда

3 единицы 5 разряда, 6 единиц 2 разряда 4 единицы
1 разряда

1 единица 6 разряда, 6 единиц 4 разряда

8  единиц 6 разряда, 5 единиц 5 разряда,1
единица 3 разряда

5 единиц 6 разряда, 8 единиц 1 разряда

9 единиц 6 разряда, 1 единица 4 разряда, 18 единиц 2 разряда

2 единицы 5 разряда, 8 единиц 1 разряда

1 единица 6 разряда, 7 единиц 5 разряда,3
единицы 4 разряда

3 единицы 6 разряда, 2 единицы 5 разряда, 7 единиц 3 разряда, 8
единиц 2 разряда

3 единицы 6 разряда, 2 единицы 5 разряда, 7 единиц 3 разряда, 8
единиц 2 разряда

6 единиц 7 разряда, 5 единиц 2 разряда

2 единицы 7 разряда, 6 единиц 3 разряда, 4
единицы 2 разряда

1 единица б разряда, 6 единиц 4 разряда

9  единиц 5 разряда, 5 единиц 4 разряда, 1
единица 2 разряда

8 единиц 6 разряда, 8 единиц 4 разряда

5  единиц 6 разряда, 7 единиц 5 разряда, 4
единицы 1 разряда

3 единицы 6 разряда, 5 единиц 3 разряда

9 единиц 6 разряда, 4 единицы 4 разряда

6 единиц 3 разряда, 3 единицы 1 разряда

8.  Запиши число, в котором:
                                

7 сот. тыс. 3 дес. тыс. 3 сот. 4 дес.

4 сот. тыс. 5 дес. тыс. 1 ед. тыс. 4 ед.

5 сот. тыс. 4 дес. тыс. 3 сот. 7 ед.

3 дес. млн 4 дес. тыс. 9 ед. тыс. 6 сот. 5 дес. 2 ед.

5 сот. млн 2 дес. млн 4 сот. 7 дес.

1 сот. тыс. 7 ед. тыс. 6 дес. 3 ед.

3 сот. тыс. 8 ед. тыс. 1 ед. 2 сот. 4 ед.

8 сот. тыс. 1 дес. 3 ед.

6 сот. тыс. 4 дес. тыс. 5 ед. тыс. 9 сот. 2 ед.

3 сот. млн 9 ед. тыс. 4 сот. 8дес.

8 сот. тыс. 3 дес. тыс. 8 дес. 6 ед.

3 сот. тыс. 4 дес. тыс. 1 сот. 4 ед.

2 сот. млн 1 сот. тыс. 1 сот. 1 дес. 6 ед.

2 сот. тыс. 7 дес. тыс. 7 сот. 6 дес.

3 сот. тыс. 5 дес. тыс. 4 ед. тыс. 8 сот. 6 дес.

8 сот. млн 4 сот. тыс. 7 дес. тыс. 6 сот. 5 ед.

3 дес. млн 5 дес.
тыс. 1 сот. 9 дес.

7 сот. млн 2 ед.
млн 4 сот. тыс.
5 дес. тыс. 6
сот.

3 сот. млн 8 дес.
млн 5 ед. тыс.
4 сот. 8 дес.

6 сот. тыс. 3 ед.
тыс. 6 сот. 9 дес.7
ед.

4 сот. тыс. 5 дес.
тыс. 7 сот. 6 дес.
3 ед.

 6 ед. млн
2 сот. тыс. 4 дес.
тыс. 6 дес.

9. Запиши число.
Представь его в виде суммы разрядных слагаемых.

14352 = 10000 + 4000 + 300 + 50 + 2

701090                                              904150

 900046                                            800203

107008                                             258090

300520                                             200084

 600031                                            800305

806000                                             602000

6710214                                           98700   

260030                                             800200                             

17613000                                          6710214  

 300060                                            702000    

402006                                             100280

10.Напиши,
сколько в числах

	Всего единиц	Всего десятков	Всего сотен	Всего единиц тысяч	Всего десятков тысяч	Всего сотен тысяч
153 456
690 900
208 083
730 798
600 952
627 980
204 398
730 798
208 083
108 309
659 349
236 981
306 545
701 247
447 912

                                                  
II.СЛОЖЕНИЕ

11.737246 + 54337=          392476 + 1346=        
       28238 + 5468=         

358219 + 12275=               516739 + 175152=             485754
+ 334674=

175216 + 419335=             427753 + 16824=               23862+31637=

867517 + 275352=             636376 + 231157=             125528
+ 212345 =

III.ВЫЧИТАНИЕ

12.500000 — 290737
=        800000 – 605409=             900000
– 465074=

300100 — 103212 =             200000
– 1956=                 700100-4345=

700001 — 369024 =             6009000
– 564532=            500000-290067=

800200 — 87923  =              400000
– 290078=             801200-329004=

801300 — 239005 =            1000000 — 783865 =           901000-455987=

500000 – 35906=               800000-6759=                   500000-44905=

600010 – 25086 =              701000-99405=                  800000-6648=

IV.УМНОЖЕНИЕ

 Если любое число умножить на 0, получится 0

 Чтобы умножить
число на 10, достаточно
справа приписать к
нему 1 нуль.

 6 · 10 = 60

 Чтобы умножить
число на 100, достаточ­но
справа приписать
к нему 2 нуля.

 6 ·100 = 600

 Чтобы умножить
число на 1000, достаточ­но
справа приписать
к нему 3 нуля.

 6 · 1000 = 6000

 Вычисли.

13.400 · 100=                    1000
· 200=                       200 ·
10=

300 · 100=                        10000
· 50=                        80 ·
100=                 

200 · 10=                          30 ·1000=                          
2000 · 10=               

500 · 1000=                       
10О · 100=                        1000
· 30=

10О · 10000=                    
 400 · 100=                          100
· 400=                       

400 · 1000 =                      
200 · 1000=                       
150 · 100=

14.507х7          
708х5             2350х5                  8900х9          23073х7

    104х8            809х6            
8970х5                  5600х5          69005х6

         406х3          
203х9             8900х8                   6600х7          38902х3

    707х2           793х3             3970х3               
   8800х9          32001х3

15.77
∙ 55         53 ∙ 69         44 ∙19      46 ∙ 39         25 ∙25          52 ∙ 43

    44 ∙ 66         
52 ∙ 99         58 ∙ 75     32 ∙ 23         64 ∙ 46         37 ∙ 88

16.3468 ∙ 67      5864 ∙ 72     4159 ∙ 64       763
∙ 34     1289 ∙ 52     2657 ∙ 65  

      3456х45                
1235х74              3782х23            5612х37           7109х21             8905х46

17.105·370         174·49           37·129       210·350      2103·721       
 605·307                5400·308           209·560          829·703      506·908      397·160     
      704·306      426·580       
     908 ·270          336·775      409·628      860·374    
       612·823    
579·956             480·245         817·241     532·384    
315·627            456·191

V.ДЕЛЕНИЕ

Если 0 разделить на любое число, получится 0.

На 0 делить нельзя!

Чтобы разделить
число на 10, достаточно
справа убрать
1 нуль.

6000:10 = 600

Чтобы разделить
число на 100, достаточ­но
справа убрать
2 нуля.

6000:100 = 60

Чтобы разделить
число на 1000, достаточно
справа убрать
3 нуля.

 6000:1000 = 6

При делении одного круглого числа на другое можно убрать
одинаковое число нулей.

600:20= 60:2=30             600:200=
6:2=3                 1720:20=172:2=86

Вычисли.

18. 800000: 1000=                  
700000: 100=                      800000
: 1000=

900000 : 100=                         600000:10=
                        1300000 : 10000=

800000 : 10=                         10ОООО
: 10000=                  280000 : 1000=  

400000 : 100=                         600000
: 1000=                     45000 : 100=

19. 332:4            603 :3             
3672:9                    3216:4          37112:2

     840:6             508 :2             
4798:2                    2204:4          42336:6

     170:5             903 :3             
2896:8                    6315:5          49693:7

     290:2             909 :9             
1525:5                    8376:4          45378:6

     304:2             804 :4             
2342:2                    7146:2          95004:2

     498:2             670 :5             
7308:2                    9448:8          93054:3

     168:8             905 :5             
6708:2                    3568:2          45720:9

     171:9             700 :5             
3603:3                    8056:2          45003:3

20. 69 802 : 34         2 744 : 56         123 968
: 64             69 384 :28                     79 736
: 44              

        5 372 : 68          1428:42            2376:33                  4316:52                       1242:54

    2924:68        
3456:54        9761:43              6968:52                 7626:62

    9900:44         6890:13 
      10560:15            3060:15                 18240:32

21. 681 : 227 =           654
: 218 =              957:319 =                 896:112=

525:175 =                   492:123=                  992 : 124
=               835 :167=

536 : 134=                  784 :112=                858:286
=                596:169=

654 : 218 =                 784 : 112=                472:118 = 
               876:219=

692 : 173 =                 348 :116=                954:159
=                784:112=

492 : 123 =                 856 : 214 =               575:115
=                 744:186=

549:183  =                  648:216=                 575 : 115
=               585 :117=

678:113  =                  807:269 =                875:175
=                738:246=

22.27434 : 638                                  36271
: 83

16728 : 204                                      32128 : 502

18411 : 323                                      27434: 638

36271 : 437                                      40338 : 747

22275:297                                                56144 :
638

52731 : 567                                        42583
: 439

VI.СЛОЖНЫЕ
ВЫРАЖЕНИЯ

23.465-57х4           405+72:4-131           210+(198+147х2)     
   196+104:4х6         

302+4х5-24            398-306:3-23             (79х4-96)+137            
677-145:5+124х3         

90-86:2+462          143-5х3+50              
345+72:3+138              501-34х5+78         

455+3х8-161          391-(139+145)         
459+17х6-186               157х5-178+245:5

24.   (90-42:3·2):2                  15·(54:3-84:7)              168:8·6:2·5                         (136 + 164):6·9 -250          (140:14
+ 650): 6·3 (156:3 + 48) ·8:4

45·10:9 + 90 — 36                480:4·5 -50 + 300          (186 + 24):3·8:10       

440·2:8 -100                       (1237+108-126) ·61         245+315-28·15

25.836:4·17-1 892 + 546   

    8000-1 725 + 11 088:132·50

    462-208:154
+ 2382 — 1 371

    10000 — 210656:232·10 + 1 180

VII.ВЕЛИЧИНЫ

 Единицы длины.

1 см = 10 мм

1 дм = 10 см = 100 мм

1 м = 10 дм = 100 см = 1000 мм

I км = 1000м = 10000дм = 100000см = 1000000мм

26.Вырази в сантиметрах.

9 м 93 см =                1 м
7 см =            8 м
5 дм =                    93000 мм
= 

9дм 10 мм =             3 дм
1 см =          8 м 82 см =                   7 м
4 дм =

6 дм 7 см =               8 м
6 см =            2 км 62м =                   З
м 6 см =

320 мм =                   4м 9 см =            
4 м 6 дм 9 см =             7дм 90 мм =      

2м 5 см 210мм =         710дм
=               82000 мм
=                   4 дм 2 см =

90 м =                       5
м 9 дм 1 см =     7м 95 см =                   
1 м 80 см =          

З м 4 см =                  6
м 5 дм =            З км =            
              5 м 20 см =

27.Вырази в миллиметрах.

5 см 2 мм =                8 дм 3
см 4 мм =        7 см 6мм=                 2 м 58
мм=

9 дм 4 мм =                52
см =                     9 дм =                     4 см 5 мм =

39 см =                     5 м
45 см =                3 м 5 дм 7 мм =         63см =

 9 м 3 дм =                2 м
92 см =                1 м 5 см
=                 25 дм 6 см =

7 дм 2 мм =                4
м 6 дм 8мм =           6 дм 9 мм
=               7 см 4 мм =                   

8 м 2 дм 4 мм =          2 дм 5 см 6 мм =        8
дм 3 мм =               9
см 6 мм =                                    2
м 4 дм 6 мм =          10 дм 28 см =            6
м 56 см =               1 дм
6 мм =

4 дм 7 см =               41см=                      3
м 23 см =               4
м 34 см =

28.Вырази в метрах.

80 дм =                  670дм =              
700 дм =                  9 км 100м
=

11 км =                  9 км
=                   7 км 10 м =               100
дм =

890 дм =               900дм =               11
км 200м =             13
км 87м =

21 км 40 дм =         87км 200 м =         2700 дм =               
54 км 80 м =     

2 км 10 м 50 дм =   4100см =              8 км
=                      79000 см =       

29.Переведи:  

7см = … мм                               2 дм
5 см = … мм               960 мм = … см … мм

5дм 8 см = … дм                        69 дм = … см … мм            306
см = … дм … см

730 см = … дм … см                   7269 м
= … км … м            1090 м = … км … м

5 м 47 см = … мм                       5 км 43 м
= … м                  3 дм = …
мм

5001 м = … км … м                    20
см = … дм                    19600
мм = … м… мм

1006 м = … км … м                    7269
мм = … м … мм          9 м
= … см

1090 мм = … м …мм                   96
мм = … см … мм            9483 м = … км … м

Единицы измерения площади

1 см ²= 100 мм²

1 дм² = 100 см²=
10000 мм²

1м² = 100 дм² = 10000 см²
= 1000000 мм²

1км² = 1000000м ² 

30.Переведи.

602 дм² = … м²… см²
               5089004 м² = … км²… м²            205
дм² = … м²… см²

983 мм² = … см² … мм²
               86905 см² = … м²… см²         5
м 42 см² = … см²

9008060 м² = … км²… м²     
     5730 дм² = …м²… см²                 753
дм² = …м²… см²

927 мм² = …см²… мм²                   24986
см² = … м²… см²              5401 мм²
= … см²…мм²

Единицы массы

1кг =1000 г

1 ц = 100 кг = 100000 г

1 т = 10 ц = 1000 кг = 1000000 г

31. Вырази в килограммах.

6ц =                           5 ц 43
кг =                 29 ц 8 кг =        40000
ц = … .т

4 т 250 кг =                36000 г 
=                 60 ц =              7 т 580
кг = …… кг

7ц =                          6 ц 54
кг=                 30 ц =              704
ц = …т… ц

5 т 360 кг =               47000 г 
=                 70 ц 30кг =       62 ц 700
кг =…т

8ц =                          7 ц
65 кг =                 41 ц
=              71 ц = … т … кг

6 т 470 кг =               58000г 
=                  80ц =               32
т = … ц

9ц =                           8 ц 76
кг =                52 ц =               82000
кг = … т 

7 т 580 кг =                69000г =                  
90 ц =               14 т = …
ц

Единицы времени

1 век = 100 лет

1 год = 12 мес

1 год = 365 или 366 сут

1 мес. = 30 или 31 сут

1 сут. = 24 ч = 1440 мин

1 ч =  60 мин = 3600 с

1 мин = 60 с

32.Переведи:

2 г 50 сут. = … сут.            7200 с = … ч             1
мес. 6 сут. = … сут

2 мин 30 с = … с               2 в. 5 лет =… лет       1
в. 96 лет = … лет

46 мес =… лет… месс.        72
мес = … лет          180 мин -= … ч

600 с = … мин … с             1 сут 10 ч = …ч          1 мин
16 с = …с

2 сут. 3 ч = …ч                  2 ч 10 мин = …мин     2 мин 4 с
= …. с

300 мин = …ч                    240 ч = …..сут           3 сут.
7 час = ….ч

6 мин 32 с = …с                 3в. 56 л = …лет          1 мес 8
сут. = ….сут

8000 лет = ….в.                 4 в. 7 л. = …..лет       657 лет
= …в …лет

186 лет = …в. ….лет           1 в 96 лет = ….лет      3 ч 40 с =
….с

2 ч. 5 мин. = ….мин.           6 мес. = ….сут.          1 год 50
сут. = …сут

609 лет = …в ….лет            96 мес = …лет            2 в. 17
лет = ….лет

380 лет = …в …лет             2 мес 11 сут.= … сут   3 в. 28 лет
= …..лет

3 в. 78 лет = …..лет            56 в = ….лет              540 мин
= …. ч

6000 лет = ….в.                 178 лет = …в….лет     9 ч 15 мин =
…..мин

33.Реши задачи.

1.  Динара
вышла из дому в 8 ч 10 мин и шла в школу в 8 ч 25 мин. Сколько

минут  Динара потратила на
дорогу?

2.  На
дорогу до рынка и обратно мама за 1 ч 30 мин. До рынка она доехала за

15 мин в магазине она пробыла
45 мин. Сколько минут потратила мама на обратный путь?

3.  Бабушка
поехала в больницу к дедушке в 10 часов. Дорога до больницы и обратно заняла 2
ч 15 мин. В больнице у дедушки она пробыла 5 ч.

Во сколько часов вернулась бабушка?

4.  Булочная
открывается в 8 часов утра, а закрывается в 10 часов вечера. Перерыв с 13 до
14  часов дня. Сколько часов в сутки работает булочная.

5.  На
дорогу до поликлиники и обратно дедушка потратил 1 ч 20 мин. До
поликлиники он дошел за 25 мин, в поликлинике он пробыл 48 мин. Сколько минут
потратил дедушка на и путь?

6.  Мама
пошла в магазин в 12 часов. Дорога до магазина и обратно заняла 40 мин. В
магазине мама пробыла 2 ч 10 мин. Когда мама вернулась из магазина?

7.  Путь от
дома до газетного киоска у дедушки занял 15 мин, а от газетного киоска до
поликлиники 18 мин. Сколько минут затратил дедушка на весь путь от дома до поликлиники?

Умножение величин на число.

1. Запиши выражение.

2. Первый множитель переведи в более мелкую величину.

3. Реши выражение.

Образец:

2 км 425 м · 8 =

Первый множитель выражаем в метрах:

2 км 425 м = 2425 м

Полученные числа перемножаем.

х2425

       
8

19400

Результат выражаем в кило­метрах и метрах.

19400 м = 19 км 400 м

34.Выполни умножение.

7кг275г  ·  6=                       43кг175г
· 2=

8 т 327 кг · 3=                      3
км 236 м ·8=

8 км 367 м · 4=                     8
т 456 кг · 4=

8 км 124 м · 3=                     3
км 536 м ·
8=

65 кг 784 г
· 7=                    2 ц 92 кг · 8=

8 кг 386 г ·
7=                      54 кг 286 г
· 3=

Сложение и вычитание величин.

1. Запиши выражение.

2. Приведи величины к одинаковым
единицам.

3. Реши выражение.

 Образец:

8 км 645 м +
4 км 654 м =

Оба слагаемых выражаем в метрах:

8 км 645 м = 8645 м

4 км 654 м = 4654 м

Полученные числа складываем.

+8645

   4654

 13299

Результат выражаем в километрах и метрах:  13299 м = 13 км 299 м

35.Выполни действия.

2 сут 15 ч + 3 сут 17 ч = … сут … ч             11 лет — 11
мес = … лет … мес

8 км 936 м + 195 м = … км … м                   7
кг 300 г — 3 кг 967 г = … кг … г

8 м — 5 м 47 см = … м … мм                        79654
кг + 18 т 786 кг = … т … кг

7 т 817 кг + 3 т 658 кг = … т … кг               43
м — 6 м 8 мм = … м … дм … см … мм

36 кг 850 г + 73 кг 950 г = … кг … г            15 км 24 м —
7 км 639 м = … км … м

36.Сравни.

26 м … 260 дм                                          185 мин … 3 ч                             520 ц  … 52 т            

7 км 650 м ….7650 м                            2 ч 5 мин … 130 мин                  20 м ² …2000 дм ²

9 т 516 кг
…9156 кг                               3 400 см² …43 дм ²                                
7 м 3 дм…730 дм                                                                                              135 км 090 м…13 590 м          8
т 5 ц…8500 кг                24т780кг…24780кг 85ц…9т                               
5с…5 мин                         
7 т 5 ц … 7 т 500 кг 60  с …  6  мин                                 13  км … 13010 м             
1  ч … 100 с

37. Выбери правильный ответ.

1.Сколько метров
содержится в 7 км 7 м?      7700 м      7070 м         7007 м

2. Сколько центнеров
содержится в 6000 кг? 600 ц         60 ц            6000 ц

3. Сколько всего лет
содержится в 3 веках и 4 годах?    34 г.    340 лет     304 г.

4. Сколько лет
составляют 72 месяца?   7 лет и 2 мес.      6 лет           4 года

5. Какая
единица времени самая крупная?   час    секунда       век     год

6. Какое
утверждение верное? век = 365 суток   1 час =60 сек.    1 год = 12 мес.

7. Найди
ошибку. 1 ч. 15 мин = 105 мин.       2 сут. = 28 ч.          2 в. = 200 л

8. В каком ряду
единицы измерения расположены в порядке возрастания?

А) тонна, центнер,
килограмм, грамм;

Б) центнер, грамм,
тонна , килограмм;

В) грамм, килограмм,
центнер, тонна.

VIII.ПЕРИМЕТР
И ПЛОЩАДЬ

Прямоугольник
– это четырёхугольник, у которого все углы прямые. Противоположные стороны
прямоугольника  равны.

Квадрат
– это прямоугольник, у которого все стороны равны.

Периметр(
Ρ) – это сумма длин сторон какой-нибудь геометрической
фигуры.

Площадь(S)
– это внутренняя часть какой-нибудь геометрической  фигуры.

Чтобы найти периметр
прямоугольника, нужно сложить все 4 стороны   прямоугольника

 или

сложить длину и
ширину прямоугольника и умножить на 2.

        Ρ=a+b+a+b       
 или       Ρ=(a+b)·2     
 или      Ρ=a·2
+ b·2

У квадрата 4 стороны,
равные между собой. Чтобы найти сторону квадрата, нужно Ρ□
разделить на 4.

a=Ρ:4

     Как
найти сторону прямоугольника, если известен периметр и другая  сторона?

Чтобы найти
сторону прямоугольника, нужно Ρ разделить
на 2  и  вычесть другую сторону.

a=Ρ:2
– b

b=Ρ:2
– a

     Чтобы найти площадь прямоугольника,
надо длину прямоугольника умножить  на его ширину.

S=  a
· b

    Площадь квадрата
равна произведению двух его сторон.

S□ = 
a · a

     Как найти сторону прямоугольника, если
известна площадь и другая его   сторона?

Чтобы найти одну из сторон прямоугольника, 
нужно площадь прямоугольника разделить на известную сторону.

а =
S: 
b

b =
S  :
a

Образцы
записи задач.

 Сторона квадрата 9 см. Чему равны его периметр и площадь?

  а
= 9 см

  Р — ?

  S
— ?

  Р = а · 4

  S
= а · а

  Р = 9 · 4 = 36 (см)

  S = 9 · 9 = 81 (см²)

  Ответ: 36 см, 81 см²

 Длина   участка  
прямоугольной    формы —   82 м.
Ширина в 2 раза меньше. Найти пло­щадь
и периметр участка.

а =  82
м 

в —41?,
в 2 р. м. 

Р — ?

S — ?

1) 82 : 2
=41(м)- в

Р = (а +
в) · 2

S = а · в

Р = ( 82 + 41) · 2 = 246 ( м)

S = 82 · 41 = 3362 ( м² )

Ответ: 246 м, 3362 м²

Длина стола 3 м, а его ширина 12 дм. Найти площадь и периметр стола.

а =  3 м
= 30 дм

в = 12 дм

Р — ?

S — ?

Р = (а +
в) · 2

S = а · в

Р = ( 30 + 12) · 2 = 84 (дм)

S = 30 · 12 = 360 (дм² )

Ответ: 84 дм, 360 дм²

Периметр квадрата 12 см.  Чему равна его сторона?

Р = 12 см

а — ?

а = Р : 4

а = 12 : 4 = 3 (см)

Ответ: 3 см

Реши задачи.

38.Длина
прямоугольника 4 см, .а ширина на 3 см короче.
Чему равен его периметр?

39.Ширина
прямоугольника 2   см, а длина на 4   см
больше. Чему равен его периметр?

40.Длина
прямоугольника 40 дм, а ширина на 2 см меньше. Чему равна его площадь?

41.Ширина
прямоугольника 30   дм, а дли­на на 2  м больше.
. Чему равна его площадь?

42.Длина
прямоугольника 4 см, а ширина 2
мм. Чему равен периметр прямоугольника?

43.Длина
прямоугольника 90 м, а ширина на 200 см
короче. Чему равен его периметр?

44.Периметр
квадрата 32 см.  Чему равна его сторона?

45.Периметр
квадрата 48 см.  Чему равна его площадь?

46.Ширина  
прямоугольника   3   см.   Чему равна длина,
если периметр 16 см?

47.Длина  
прямоугольника   9   м,   ширина 8  дм. Найдите его площадь и периметр.

48.Ширина  
прямоугольника   2   дм,   а   его    длина 42 см. Найти площадь и периметр.

49.Площадь
участка 80  м². Его ширина составляет 50 дм. Каков его периметр?

50.Длина  
участка   прямоугольной    формы —   82 м.
Ширина в 2 раза меньше. Найти пло­щадь и
периметр участка.

                                                              
IX.ЗАДАЧИ

Цена	Кол-во	Стоимость
:	:	·

Цена- это сколько
стоит 1 вещь (рубли, копейки)

Количество- сколько
вещей купили (штуки)

Стоимость- сколько
стоят все вещи( рубли, копейки)

Образцы записи задач.

В двух пакетах 5 кг картофеля.  Сколько пакетов потребуется для
30 кг картофеля?

2 п.  
—   5 кг

  ?      — 30 кг

30·2:5=12(п.)

Ответ : 12 пакетов.

В магазине было 250 кг лимонов и мандари­нов. Лимоны лежали в 5 ящиках по 20 кг, а ман­дарины в нескольких ящиках по 50 кг. Сколько ящиков мандаринов было в магазине?

1	Кол-во	Всего
Л.-      20 кг М.-      50 кг	5 ящ.           ?	100           250 кг 150

1) 20 · 5 = 100 (кг.) –лимоны

2) 250 – 100 = 150 (кг)
–мандарины

3) 150 : 50 = 3 (ящ.)
–мандаринов

Ответ: 3 ящика

 Две
девочки купили 5 м ленты по одинаковой 
цене.   Одна  уплатила  15  рублей,   а другая  —  10 рублей.  Сколько  метров  ленты купила каждая девочка?

Цена	Кол-во	Стоимость
I—                      5       одинак.   II—                     5	?             5 м  ?	15 руб.                    25       10 руб.

1) 15 + 10 = 25 (руб.) – всего

2) 25 : 5 = 5 (руб.) –цена

3) 15 : 5 = 3 (руб.) — 1 девочка

4) 10 : 5 = 2 (руб.) – 2 девочка

Ответ: 3 рубля, 2 рубля

Реши задачи.

51.15 кг сена выдали двум лошадям.
Сколько лошадей получат 60 кг сена?

52.25 кг чёрной смородины
собр.али с трёх кус­тов. Со скольких кустов соберут 100 кг чёр­ной смородины?

53.Марина за 5 дней прочитала 60 страниц.
Сколько страниц она прочитает за 10 дней?

54.В 4 чайных ложках умещаемся 21 г сахара.
Сколько потребуется чайных ложек для  126 г сахара?

55.18м драпа идёт на 4
пальто. Сколько пальто сошьют из 90 м драпа?

56.В трёх одинаковых коробках умещатся17 кг
крупы. Нужно разложить 68 кг крупы.     Сколько потребуется коробок?

57.На изготовление пяти цепочек пошло 14 г
серебра. Сколько цепочек можно изготовить из 112 г серебра?

58.Для кружка
купили 4 набора цветной бу­маги по 10
листов в каждом и несколько набо­ров картона
по 5 листов в каждом. Всего купи­ли 100 листов
бумаги и картона. Сколько набо­ров картона
купили?

59.Дети клеили
игрушки. Всего они склеили 94 
игрушки.   10  мальчиков  склеили  по  3  иг­рушки. По скольку игрушек склеила каждая из 8 девочек?

60.Для детского
сада купили 68 кг конфет. Кара­мель лежала в 6 коробках по 4 кг
в каждой, а шо­коладные конфеты в 4
коробках. Сколько кг шоко­ладных
конфет в каждой коробке?

61.В магазине
было 200 кг лимонов и мандари­нов. Лимоны
лежали в 5 ящиках по 20 кг, а ман­дарины в
нескольких ящиках по 50 кг. Сколько ящиков
мандаринов было в магазине?

62.В зоопарке
92 попугая. В 8 клетках было по 7 попугаев и в нескольких клетках по 9 по­пугаев.
Сколько клеток с 9 попугаями?

63.Дети
собрали из 150 деталей конструктора 5 машин и 2
трактора. На каждую машину шло по 20 деталей. Сколько деталей
шло на каждый трактор?

64.Купили 
95  груш.   В  4  больших  пакетах лежало по 20
груш. В каждом маленьком паке­те лежало по 5 груш. Сколько было маленьких пакетов?

65.Школьники помогли колхозу собрать 2 т свеклы. С первого участка школьники собрали 1208 кг свеклы,  со второго участка в  2 раза меньше, чем с первого, а остальную свеклу со­брали с третьего участка. Сколько килограммов свеклы
собрали дети с третьего участка?

66.Школьники
помогли колхозу собрать 3  т моркови. С
первого участка они собрали 1408 кг  моркови, со второго участка в 2 раза меньше, чем   с первого, а остальную морковь собрали с третье­го участка. Сколько килограммов моркови собра­ли школьники с третьего участка?

67.С  
одного   участка   школьники   собрали 161 кг
свеклы, а с другого 289 кг. Всю свеклу они разложили в ящики по 15 кг в каждый ящик. Сколько потребовалось ящиков  для свеклы?

68.После   
того    как    школьники    собрали 12 ящиков
лука по 8 кг в каждом ящике, им осталось
собрать еще 396 кг. Сколько всего килограммов
лука надо было собрать школь­никам?

69.Со  школьного 
огорода  собрали   116  кг моркови,
свеклы на 32 кг меньше, чем мор­кови, а
картофеля в 2 раза больше, чем мор­кови и свеклы
вместе. Сколько килограммов картофеля
собрали со школьного огорода?

Задачи
на движение.

v—
скорость (км/ч,  м/мин,  м/с)      v
= s : t

t— 
время     (ч, мин, с)                   t
= s : v

s—
расстояние ( км, м, см)              s
= v ∙ t

Образцы записи задач.

 Два
самолета вылетели из 2-х городов одновременно навстречу
друг другу и встре­тились через 3 часа.
Скорость первого 320 км/ч, второго —
450 км/ч. Каково рас­стояние между
городами?

v	t	s
I —      320 км/ч II—      450 км/ч	3 ч	?

1) 320 +450 = 770 (км/ч) – v сближения

2)  770 х 3 = 2310 (км) – s

Ответ: 2310 км

Расстояние 360 км товарный поезд про­шел  за 9  ч,  а пассажирский  —  за  6  ч.  На сколько километров в час скорость пассажир­ского поезда больше скорости товарного?

v	t	s
Т.- 40     ?                             на ?    П.- 60    ?	9 ч            6 ч	360 км       360 км

1) 360 : 9 = 40 (км/ч) –v товарного поезда

2) 360 : 6 =  60 (км/ч) –v пассажирского поезда

3)  60 – 40 – 20 (км/ч)

Ответ: на 20 км/ч

70.Запиши решение задачи.

v	t	s		v	t	s
5 км/ч      ?	4 ч      3 ч	32 км	7  км/ч     6 км/ч	?	21 км    24 км

v	t	s		v	t	s
	5 ч    8 ч	30 км      ?	?	3 ч	18 км    15 км

v	t	s		v	t	s
12 км/ч  10 км/ч	3 ч	?	10 км/ч    15 км/ч	3 ч               ?

Реши задачи.

71.Моторная
лодка, двигаясь со скоростью 17 км в час,
прошла путь между пристанями за 5 часов.
Сколько потребуется времени, что­бы пройти этот же путь на байдарке, если она движется со скоростью 5 км/час?

72.Турист прошёл 45 км. Первые 3 часа он шёл со скоростью 5 км/час. Остальную часть пути он прошёл за 5 часов. С какой скоростью шёл турист после остановки?

73.Лыжник
шёл со скоростью 18 км/час и был в пути 3
часа. Сколько времени потребу­ется пешеходу,
чтобы пройти такое же рас­стояние,
если его скорость 9 км/час?

74.Отряд
прошел 39 км. Первые 3 ч он шел со  
скоростью 5 км/час. Остальную часть   пу­ти
отряд прошел за 6 ч. С    какой скоростью отряд прошел остальную часть пути?

75.Ворона
летела 3 ч со скоростью 50 км/час. Скворец  
такое   же расстояние   пролетит за 2 ч. С
какой скоростью летит скворец?

76.Туристы
в 1-й день были в пути 7 ч, а во 2-й день
— 4   ч,   двигаясь   с   одинаковой скоростью.  
В   1-й  день  туристы  прошли  на15 км больше,
чем во 2-й день. Сколько ки­лометров
прошли туристы в каждый день?

77.Лыжник
шёл со скоростью. 12 км/час и был в пути   3 ч. Сколько времени
понадобится, чтобы пройти    такое же
расстояние пешеходу, скорость которого  6 км/час?

78.Теплоход
в течение 2 дней   был в пути15 часов. В
первый день он прошёл 200 км, а во  второй  
175  км.  Сколько часов  теплоход был в пути
каждый  день, если он всё время шёл с
одинаковой скоростью?

79.От
двух пристаней отошли одновременно навстречу  
друг   другу   катер   и   лодка.   Они встретились 
через   5   часов.   Скорость   лодки  12
км/час, а скорость катера в 5 раз больше. Найдите расстояние между пристанями.

80.От двух пристаней навстречу друг другу одновременно вышли теплоход и катер. Теп­лоход шёл со скоростью 33 км/час, а катер —25 км/час. Через 3 часа они встретились. Че­му равно расстояние между пристанями?

81.Из
двух деревень одновременно навстре­чу друг другу
вышли девочка, которая двига­лась со
скоростью 3 км/час, и мальчик, который двигался
в 2 раза быстрее, чем девочка. Встреча
произошла через 4 часа. Каково рас­стояние между
деревнями?

82.Часть пути
до школы школьник шел со скоростью 50
м/мин в течение 4 минут. Ос­тальную  
часть   пути   он   шел   со   скоростью 80
м/мин. На весь путь до школы он затратил 10 минут. Чему равно расстояние до школы?

83.От дома до леса лыжник шел 2 часа со скоростью 8 км/час. По лесу он шел со скоро­стью 7 км/час. Сколько времени он шел по лесу, если всего прошел 37 км?

84.Автобус проехал  180 км за 4 часа. За какое время проедет  это  расстояние автомо­биль, скорость которого в 2 раза больше?

85.Велосипедист
за 3 часа проехал 24 км, а пешеход за 4
часа прошел 16 км. Во сколько раз скорость
велосипедиста больше скорости пешехода?

86.В
первый день автомобилист ехал пять ча­сов со
скоростью 72 км/час, во второй день он проехал
такое же расстояние за 4 часа. С какой скоростью
ехал автомобилист во второй день?

87.Самолет
за три часа пролетел 960 км, а ав­томобиль за 5 часов проехал 400 км. Во
сколько скорость самолета больше скорости
автомобиля?

88.Мотоциклист
ехал 2 часа со скоростью 80 км/час и
три часа со скоростью 70 км/час. Какой путь
проехал автомобилист?

89.Мотоциклист
проехал до места назначе­ния 420 км,
сделав в пути одну остановку. До остановки он
был в пути 4 часа и ехал со ско­ростью 80 км/час. Остальной путь он проехал за
два часа. С какой скоростью ехал мотоцик­лист
после остановки?

90.Автотуристы
в 1 день проехали 600 км, во   2-й день
200 км. На весь этот путь они за­тратили 8
часов. Сколько часов были в пути туристы
каждый день, если они ехали с оди­наковой
скоростью?

91.Расстояние   между   поселками   30    км лыжник прошел за 3 часа. На обратном  пути он уменьшил скорость на 4 км/час. Сколько  времени он потратил на путь туда и обратно?

92.От одной  станции одновременно в проти­воположных направлениях вышли два поезда, один из которых шел со скоростью 62 км/час. Через   5  часов  расстояние  между  ними  было 630
км. Чему равна скорость второго поезда?

93.С
одного аэродрома одновременно в про­тивоположных направлениях вылетели 2 само­лета.
Один летел со скоростью 420 км/час, ско­рость
другого на 80 км/час меньше. Какое рас­стояние будет между ними
через 3 часа?

94.Автомобиль
и мотоцикл  выехали  одно­временно  в  противополож-ных  
направлениях из     одного     города.    
Скорость     автомобиля 60 км/час,
мотоцикл — 70 км/час. Какое рас­стояние
будет между ними через 3 часа?

95.Машина
шла до  остановки   5  часов   со скоростью 72
км/час. После этого ей осталось проехать 
вдвое  меньший   путь,  на  который она  
потратила   3   часа.   С   какой    скоростью ехала машина после остановки?

96.Велосипедист
проехал 24 км   со скоростью   8   км/час.   Пешеход  
потратил   на   этот путь на 1 час больше. С
какой скоростью шел пешеход?

97.Мальчик проплыл 100 метров со скоро­стью 25 м/мин.
Девочка потратила на эту дистанцию на
1 минуту больше. С какой ско­ростью плыла
девочка?

98.Один  мотоциклист был  в  пути  3  часа, другой   —  5 часов.  Они ехали с одинаковой скоростью. Второй проехал на 80 км  больше первого.
Сколько км проехал каждый?

99.Две
машины шли с одинаковой скоростью. Одна прошла
400 км, а другая 480 км. Вторая машина была в
пути на 2 часа меньше первой. Сколько
часов была в пути каждая машина?

100.Из
двух городов, расстояние между которыми 484
км,  вышли одновременно навстречу друг другу
два поезда. Скорость одного поезда 45 км/час.
Определите скорость другого поезда, если поезда
встретились через 4 часа.

101.Из
двух городов одновременно навстречу друг  другу 
отправились пассажирский  и  товарный
поезда. Они встретились через 12 часов. Каково
расстояние между городами, если известно, 
что  скорость пассажирского  поезда 75 км/час,
товарного 35 км/час?

102.Из двух городов одновременно навстречу друг другу вышли два поезда.  Один шёл со скоростью
42 км/час, а другой — 52км/час. Через  
б   часов   поезда   встретились.   Найдите расстояние между городами.

103.Расстояние по реке между двумя городами 275 км. Из этих городов одновременно навстре­чу друг
другу вышли пароход и баржа. Пароход шёл
со скоростью 28 км/час. Найдите скорость баржи,
если известно, что её встреча с парохо­дом
произошла через 5 часов после выхода.

104.Из
двух городов, расстояние между ко­торыми  
1380   км,   вышли   одновременно   на­встречу
друг другу два поезда и встретились через   
10   часов.    Скорость   одного   из    них 75 км/час. Найдите скорость другого поезда.

105.Расстояние   между  сёлами   48   км.   Через сколько часов встретятся два пешехода, которые вышли одновременно навстречу друг другу, если скорость одного 3 км/час, а другого 5 км/час?

106.Баржа
проплыла против течения расстоя­ние в 100 км
за 10 часов, а на обратном пути её скорость
увеличилась на 10 км/час За сколько часов
проплыла баржа обратный путь по течению?

107.Машина
прошла расстояние между города­ми за 5
часов, идя со скоростью 48 км/час. Об­ратный
путь она прошла за 6 часов. На сколько км/час 
скорость  машины  на  обратном  пути была
меньше?

108.От  пристани  одновременно  в  противопо­ложных направлениях отошли два теплохода. Через   6   часов   расстояние  между   ними   было 360 км. Один из них шёл со скоростью 28 км/час. С какой скоростью шёл другой теплоход?

109. Со
станции в одно и то же время в противоположных
направ-лениях вышли два поезда. Скорость
одного из них 74 км/час,  а другого 61 км/час.
Через сколько часов поезда будут на­ходиться на
расстоянии 540 км друг от друга?

110.Расстояние    
между     двумя     пристанями  864 км. Теплоход прошёл это расстояние по тече­нию со
скоростью 27 км/час, а обратный путь про­тив
течения со скоростью 24 км/час. За сколько ча­сов прошёл весь путь теплоход туда и обратно?

111.Расстояние
между городами 432 км. Сколь­ко времени
потребуется машине на проезд туда и обратно,
если скорость машины в одном направ­лении 54 км/час, а в другом на 6 км/час
меньше?

112.Мальчики   прошли  до  деревни   20   км, двигаясь  со  скоростью   5   км/час,   а  обратно они ехали на велосипеде в 2 раза быстрее. За сколько часов они проедут это расстояние?

113.Одновременно   в   противоположных   направлениях отправи-лись катер со  скоростью 60 км/час и байдарка, скорость которой в 4 раза меньше. Через сколько часов расстоя­ние между ними будет 375 км?

114.От двух пристаней одновременно отправились 2 теплохода навстречу друг другу. Они встрети­лись
через 6 часов. Какой путь прошел каждый теплоход,
если скорость первого 42 км/ч, а рас­стояние
между пристанями 474 км?

115.Два самолета вылетели из 2-х городов одновременно
навстречу друг другу и встре­тились через 3
часа. Скорость первого 320 км/ч,
второго — 450 км/ч. Каково рас­стояние
между городами?

116.Две   девочки   вышли   одновременно   из своих домов навстречу друг другу. Первая де­вочка шла со скоростью 60 м/мин и прошла до встречи 420 м. Вторая девочка шла со ско­ростью 70 м/мин. Какое расстояние до встре­чи прошла вторая девочка?

117.Два   автомобиля   выехали   одновременно навстречу друг
другу из 2-х городов, расстояние между
которыми 450 км. Скорость первого ав­томобиля
70 км/час. Какова скорость второго 
автомобиля, если они встретились через 3 часа?

 118.Два мальчика поплыли
одновременно  навстречу друг другу с 2-х концов бассейна,
длина которого   100   м.   Первый   плыл   со  
скоростью 20 м/мин, второй — со скоростью 30 м/мин. Ка­кое расстояние до встречи проплыл каждый?

 119.От  двух  пристаней,  
расстояние   между которыми  90 км, 
одновременно    вышли на­встречу  
друг   другу два   теплохода. Первый теплоход   шел со  
скоростью 20   км/час,   вто­рой- со  
скоростью 25    км/час. Через сколько часов
они встретились?

120.Две    
ласточки      летят      со      скоростью 23 м/сек.
Через сколько секунд они встретятся, если
расстояние между ними 920 м?

121.Два
поезда вышли из двух городов одновременно
навстречу друг другу. Один поезд шёл со
скоростью 63 км/ч. С какой скоростью шёл второй поезд, если
расстояние между городами 564 км?
Встретились поезда через 4 часа.

122.От 
двух причалов,   расстояние   между   которыми
90    км, одновременно вышли навстречу друг
другу две лодки.  Первая шла со скоростью 8 км/час, вторая — со скоростью 10 км/час.   Через сколько часов лодки встретились?

123.Из посёлка и города выехали одновременно навстречу друг другу велосипедист и мотоциклист. Велосипедист ехал со скоростью 16 км/ч, а мотоциклист со скоростью 54 км/час. Велосипедист проехал до встречи  48 км. Какое  расстояние до встречи проехал мотоциклист?

124.Два  
мальчика   одновременно   побежали навстречу
друг другу по спортивной дорожке, длина которой
200 м. Они встретились через 20 с. Первый
бежал со скоростью 5 м/сек.С какой
скоростью бежал второй мальчик?

125.Мотоциклист   ехал   2   ч   со   скоростью 60 км/час, а велосипедист 3 ч со скоростью 14   км/час.   На   сколько   больше   километров
проехал мотоциклист?

126.За 6 часов в теплоход прошёл 300 км, а поезд за   6 часов прошёл 450 км. На сколько скорость поезда больше скорости теплохода?

127.Туристы
сделали 3 перехода по 4км,а потом  прошли
ещё 9 км. Сколько километров им  осталось
пройти, если весь путь составляет 32 км?

128.За 3
минуты самолёт пролетел 30  км.Какое
расстояние он  пролетит за 40   минут,если
его скорость увеличится на 5 км/мин?

129.За
два дня самолёт пролетел с одинако­вой скоростью
10240 км. В 1й день в полёте он был   10
часов, а во 2-й — 6 часов. Сколько  километров
пролетел самолёт в каждый день?

130.Автомобиль
за 4 часа прошёл  240   км. Сколько км   он пройдёт за 7  часов,если его скорость увеличится на 6 км/час?

131.Самолёт
пролетает 960   км   за 2 часа.  За сколько
часов пролетит то же расстояние другой самолёт,
скорость которого в два раза больше?

132.Поезд,
скорость которого 30 км/час, прохо­дит путь от
одного города до другого за 6 часов. За
сколько часов пройдёт автомобиль половину этого пути, если будет проходить по 45 км/час?

133.Машина в 1-й   день прошла за 9 часов 522  км.  Во  2-й   день  машина  была  в  пути 7 часов и шла с прежней  скоростью. Сколько
всего километров прошла машина за эти 2 дня?

134.Туристы за
два дня похода прошли 84 км, двигаясь с
одинаковой скоростью.В 1-й день они были в пути
7 часов, а во 2-й — 5 часов. Какое

расстояние прошли туристы в каждый из этих
дней?

135.Какое время
туристы затратили на весь путь, если
90  км   они проехали на катере со скоростью 30
км/час и 12 км прошли пешком
со скоростью 4 км/час?

136.Пешеход шёл
со скоростью 9 км/час в течение  
2   часов.   После   этого   ему   осталось пройти в 3 раза больше того, что он прошёл.
Сколько всего км должен пройти пешеход?

Олимпиадные
задачи.

137.Один
брат старше второго на 5 лет. Суммарный возраст обоих братьев равен 17 годам. Сколько
лет братьям?

138.В книге 60 страниц.
Прочитали в 2 раза больше страниц, чем осталось прочитать. Сколько страниц
осталось прочитать?

139.На автостоянке стоит
24 автомобиля, причем легковых автомобилей в 3 раза больше, чем грузовых.
Сколько грузовых автомобилей стоит на автостоянке?

140.Кусок полотна в 124
м надо разрезать на две части так, чтобы длина одной части была на 12 м больше
другой. По сколько метров полотна будет в каждой части?

141.В школу привезли 690
столов и стульев. Стульев было на 230 больше, чем столов. Сколько столов и
стульев в отдельности привезти в школу?

 142.В соревнованиях по лыжам
участвовали 53 человека. Девочек было на 17 меньше, чем мальчиков. Сколько
мальчиков и сколько девочек участвовало в соревнованиях?

143.За конфеты заплатили
в 3 раза больше или на 6 р. больше, чем за печенье. Сколько заплатили за
печенье?

 144.За тетради заплатили в 4 раза
больше или на 7 р. 20 к. больше, чем за линейки. Сколько заплатили за линейки?

145.Папа в 8 раз старше
дочери, а дочь на 28 лет моложе папы. Сколько лет папе?

146.
Мама в 6 раз старше сына, а сын на 25 лет моложе мамы. Сколько лет маме?

 147.Десяти собакам и кошкам скормили
56 галет. Каждой собаке досталось 6 галет, а каждой кошке — 5. Сколько было
собак и сколько кошек?

148.В хозяйстве имеются
куры и овцы. Сколько тех и других, если у них вместе 19 голов и 46
ног?          

149. У пятнадцати
треугольников и четырехугольников 53 угла. Сколько треугольников? Сколько
четырехугольников?

150.Сумму в 74 р.
заплатили девятнадцатью монетами по 2 и 5 р. Сколько было монет по 2 р.?

151.На
100 р. куплено 5 м ткани двух сортов. Известно, что 1 м ткани первого сорта
стоил 17 р., а 1 м ткани второго сорта стоил 22 р. Сколько метров каждого сорта
купили?

152.Куплено 2 м одной и
3 м другой ткани на 180 р. Известно, что 1 м первой ткани в 3 раза дороже 1 м
второй ткани. Сколько стоит 1 м каждой ткани?

153.8 телят и 5 овец
съели 835 кг корма. За все время каждому теленку дали на 28 кг корма больше,
чем овце. Сколько корма съел каждый теленок, сколько каждая овца?

154.В первой вазе стояло
в 3 раза больше роз, чем во второй, а в третьей — на 5 роз больше, чем во
второй. Сколько роз стояло в первой вазе, если всего было 45 роз?

 155.В
первой вазе лежало в 2 раза больше конфет, чем в третьей, а во второй вазе — на
4 конфеты больше, чем в третьей. Сколько конфет лежало в первой вазе, если
всего было 164 конфеты?

156.С трех участков
собрали 237 т картофеля. С первого и второго — поровну, а с третьего участка
собрали на 12 т больше, чем с каждого из первых двух. Сколько тонн картофеля
собрали с каждого из трех участков?

157.Разделите
число 480 на 3 части так, чтобы первая была на 40, а вторая на 80 больше
третьей.

158.Веревку длиной 28 м
разрезали на 3 части так, что вторая часть была в 3,5 раза, а третья в 2,5 раза
больше первой. Найти длину каждой части.

 159.На двух полках 72 книги. Когда с
первой полки переставили на вторую 14 книг, то книг на полках стало поровну.
Сколько книг стояло на каждой полке первоначально?

 160.В
двух бумажниках было 250 р. Если из одного переложить в другой 25 р., то в
обоих бумажниках денег станет поровну. Сколько рублей было в каждом?

 161.На первом складе в два раза
больше муки, чем на втором. Когда из первого склада вывезли 48 т, а из второго
11 т, то муки на складах стало поровну. Сколько тонн муки было на первом складе
первоначально?

162.Написали число,
приписали к нему справа нуль. Число увеличилось на  405. Найдите первое число.

163.Старинная задача.
Некто, желая раздать деньги нищим, рассчитал, что если каждому дать по 15 к.,
то у него не хватит 10 к., а если каждому дать по 12 к., то останется 14 к.
Сколько было нищих и сколько у него было денег?

 164.Куплены тетради для учеников первого
класса. Если каждому дать по 9 тетрадей, то не хватило бы семи ученикам по
тетради, а потому каждый получил по 8 тетрадей, и тогда еще осталось 16
тетрадей. Сколько куплено тетрадей и сколько было учеников в классе?

165. В
обществе желали собрать некоторую сумму денег в пользу бедного семейства. Если
каждый из присутствующих пожертвует по 1 р., то соберется на 3 р. больше
предполагаемой суммы; если же каждый внесет по 50 к., то не хватит 11 р.
Сколько особ было в обществе, и как велика была предположенная к сбору сумма?

 166.Старинная
задача (Китай, I в.). Сообща покупают вещь. Если каждый человек внесет по 8, то
избыток равен 3. Если каждый человек внесет по 7, то недостаток равен 4.
Спрашивается количество людей и стоимость вещи.

167.Старинная задача
(Китай, II в.). Сообща покупают курицу. Если каждый человек внесет по 9
(денежных единиц), то останется 11, если же каждый внесет по 6, то не хватит
16. Найти количество людей и стоимость курицы.

 168.Работники получили за некоторую
работу по 120 р. Если бы их было на 2 меньше, то каждый из них получил бы по
150 р. Сколько было работников?

 169.Токарь
ежедневно перевыполняет норму на 20 деталей. Сколько деталей ежедневно
обтачивает токарь, если пятидневную норму он выполняет за 3 дня?

X.УРАВНЕНИЯ

    
   +               =                                                   —       
     =    

          
·              =                                               :              =

170.Вставь нужный знак:

х + 67 = 490		х – 35 = 502		451 – х =349		45 + у = 240		х – 31 = 32
х : 5 = 432		148 : у = 8		х + 17 = 564		20 ∙ х = 89		х ∙ 2 = 490
х – 137 = 678		368 – х =21		х : 56 = 33		140 : х = 2		х : 76 = 2
у + 21 = 564		2000 – х =74		у : 2 = 123		х – 13 = 890		t + 33 = 90
х : 5 = 532		х : 5 = 533		х : 5 = 532		х + 66 = 464		х – 2532 = 502
24 ∙ х = 86		45 + х = 430		х – 232 = 702		900 – х =532		b : 7 = 532
t : 5 = 533		х – 232 = 502		456 – х =52		45 + х = 430		х – 7732 = 40
х – 272 = 502		t ∙ 3 = 490		t – 532 = 502		х : 5 = 532		у : 5 = 532
b ∙ 2 = 490		х – 232 = 503		х : 7 = 532		t – 2530 = 52		918 – х =532
451 – c =532		b – 243 = 502		450 – х =303		х – 2732 = 50		24 ∙ х = 86
618 – х =532		х : 5 = 432		45 + х = 430		459 – х =21		х : 7 = 532
z : 5 = 532		618 – z =532		998 – у =532		у : 7 = 532		х – 47 = 50
х ∙ 2 = 490		43 ∙ у = 86		43 ∙ t = 89		b ∙ 2 = 490		z : 5 = 532
618 – х =532		451 – х =100		z ∙ 2 = 490		х – 72 = 502		b ∙ 2 = 490
z : 7 = 532		х – 18 = 53		х – 2532 = 5		459 – х =72		х : 5 = 532
148 : у = 8		618 – b =532		у : 5 = 532		148 : у = 8		у : 5 = 532
236 : х = 5		х – 252 = 123		51 – c =32		х – 32 = 502		х – 27 = 50
44 + х = 430		24 ∙ х = 89		х + 67 = 969		у ∙ 2 = 490		236 : b = 8
х : 7 = 433		х : 4 = 532		z : 7 = 532		c : 5 = 532		х ∙ 2 = 490
451 – t =533		у : 7 = 533		216 : у = 8		х : 4 = 16		148 : у = 8
х – 252 = 345		х + 97 = 764		х – 253= 147		43 ∙ у = 86		876 – z =542
451 – х =53		918 – z =732		236 : х = 8		765 – у =432		608 – у =432
236 : c = 8		148 : у = 8		у : 5 = 532		b ∙ 2 = 494		41 ∙ х = 86
43 ∙ z = 89		х – 232 = 702		236 : у = 8		х : 5 = 532		148 : у = 8
у : 7 = 532		451 – у =432		24 ∙ х = 86		618 – х =532		618 – c =532
45 + х = 430		43 ∙ z = 86		b + 32 = 579		451 – х =54		х – 14 = 502
х – 82 = 502		236 : c = 8		х ∙ 2 = 490		148 : z = 8		1000 – z =538
у ∙ 2 = 490		у : 7 = 532		618 – c =512		t – 252 = 502		х : 5 = 532
918 – t =732		х – 532 = 502		898 – х =732		х – 112 = 641		618 – b =533
х : 5 = 531		451 – c =234		у – 252 = 502		z + 97 = 564		30 ∙ х = 86

    171.Реши уравнения.

    216 : у = 8                х : 5 =
530                     324 – c =54                у
∙ 2 = 648

     у : 7 = 532               у – 145 =
897                b : 9 = 165                 у
: 8 = 531                 

    b –
243 = 502            х ∙ 3 = 963                    х ∙ 5 = 790                 979
– х =862

    2 ∙ х = 894               896 – х
=253                 29 + у = 270               х + 168 = 953

    895 – х =326             х – 147 =
389                906 : у = 3                  b
∙ 6 = 720

    450 : у = 9              146 : у =
2                    х – 160 = 87                b
– 128 = 415

    у ∙ 2 = 490               х + 66 =
895                 398 + х = 542              у : 9 = 127           

    х + 67 = 460           21 + у =
125                 х + 43 = 760               125 + у = 280

Устный
счет

54х0    45х0  
0х72    0:21    567х0      0х290      0: 389       678х0     0х23

37х0    16х0   0х13   
0:36    132х0      0х692      0: 391        0: 56    0х77

89х0    53х0  
0х90    0:87    817х0       0х0          0: 0         214х0    0:231

450:10    140:10  
20х10   1000:10   500:10   2380х10   250:10   6850х10

230х10    300:10  
400:10   1230х10   790:10   2630х10   560х10   780:10

 6400:100   
2300х100     45600:100     346х100    100х100    12300:100

900:100       
864х100     89900:100     23700х100    82500:100    215х100

6460:10    
2320х100     45000:1000      26х1000    500х100    45600:10

500:100   
864х10      89000:100      700х100    825000:1000     15х10

20х3   20х5  20х2   
20х4     200х3   200х5  200х2    200х4    1000:4

25х2    25х3   
25х4   250х4    250х3    250х2    100:4    100:5   1000:5

60:20     100:20   
100:25    1000:25    500:2   75:3    750:3    125х8

12х2   12х4   12х6  
12х3   12х5    60:12   72:12    24:12    60:5   60:12

11х3   11х6   11х9  
11х2   33:3   44:11   99:11  77:11  11х5   11х7   11х8

15х2   15х6    
15х3    15х5    15х4     60:15     30:15     45:15  75:15

 6460:10    
2320х100     45000:1000      26х1000    500х100    45600:10

500:100   
864х10      89000:100      700х100    825000:1000     15х10

905х4    506х4   
807х4     108х4    205х4    708х4    809х4    204х4

500-15      400-67   
200-34     800-75     900-29     100-31    700-54

300-56     
700-83     100-25     400-76    1000-32      1000-43

 54х0   
45х0   0х72    0:21    567х0      0х290      389: 389       678х1      

37х0    16х1  
0х13    36:36    132х0      1х692      0: 391        0: 56    1х77

89х0    53х0  
0х90    87:87    817х0       0х0          0: 0         214х0    

30х20   60х30  
80х90    20х50    40х70     17х300   12х200     36х200

320: 8   320:80   
640:8     640: 80   350: 70   120:6    540:9   720:90

630:70    
24000:3     2500:50     160:20    400:80    18000:900    400:20

450:9   300х7    
640:8     4000х2       7000х4       2400:6       63000:7

320: 8   320:80   
640:8     640: 80   350: 70   120:6    540:9   720:90

630:70    
24000:3     2500:50     160:20    400:80    18000:900    400:20

45-у=45      
х-18=18        х+20=37        а-37=20         60-х=45

12+12   13+13  
14+14    15+15   16+16   17+17   18+18   19+19

90-71   100-25  
80-43    50-13   80-42    100-75   100-34   90-21

72:12     
60:15       42:14      72:18     72:24       45:15      32:16     48:12

24х2  15х3   17х3 
18х4  19х3  14х5    48:4     36:2    54:2    36:3   64:2

12х2   12х4   12х6  
12х3   12х5    60:12   72:12    24:12    60:5   60:12

24х2  15х3   17х3 
18х4  19х3  14х5    48:4     36:2    54:2    36:3   28:2

72:3   48:4   
84:7     72:6     36:3      72:4      56:4     82:2     75:5

84:28    72:36   
48:12    96:16     80:15    72:12    84:42    75:15   75:25

125х2     134х2    
230х3    450х2     112х3    236х2     710х2    112х4

84:28    72:36   
48:12    96:16     80:15    72:12    84:42    75:15   75:25

Онлайн калькулятор поможет определить сколько десятков в числе.

Число десятков в числе

Разделитель групп разрядов Округлить до Число прописью

Содержание

• — Сколько десятков и сколько единиц в числе 17?
• — Сколько десятков и единиц в числе 9?
• — Сколько десятков и сколько единиц в числе 18?
• — Сколько десятков в числе 20013?
• — Сколько единиц в числе 16?
• — Сколько в 20 десятков и единиц?
• — Что такое десяток в математике?
• — Какие бывают разряды чисел?
• — Сколько единиц в числе 80?
• — Сколько единиц в цифре 10?
• — Что такое десятки единицы?
• — Чему равны 10 десятков?
• — Как найти число десятков в числе?
• — Что такое три десятка?
• — Сколько единиц в числе 63?

Например: В числе 16 — 1 десяток и 6 единиц.

Сколько десятков и сколько единиц в числе 17?

В числе 17 1 десяток. Ответ: 1 десяток.

Сколько десятков и единиц в числе 9?

К примеру, число 9 содержит 9 единиц. Число 12 содержит две единицы и один десяток. Число 123 содержит три единицы, два десятка и одну сотню.

Сколько десятков и сколько единиц в числе 18?

18- 1 десяток, 8 единиц; 34- 3 дес.

Сколько десятков в числе 20013?

Общее число десятков – 27. 3.

Например: В числе 16 — 1 десяток и 6 единиц.

Сколько в 20 десятков и единиц?

Двузначное число – это число, которое состоит из двух знаков (цифр): 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20 Десяток – это 10 единиц. 2 – две единицы; 7 – семь единиц; 15 — один десяток и пять единиц; 13 – один десяток и три единицы; 19 – один десяток и девять единиц; 20 – два десятка.

Что такое десяток в математике?

Десяток – счётная единица, равная десяти, а также десять одинаковых предметов. Круглое число – число, которое оканчивается одним или несколькими нулями. Возьмем счётные палочки. … Оказывается десятки можно считать как обычные числа.

Какие бывают разряды чисел?

Классы чисел

• первый — класс единиц,
• второй — класс тысяч,
• третий — класс миллионов,
• четвёртый — класс миллиардов,
• пятый — класс триллионов,
• шестой — класс квадриллионов,
• седьмой — класс квинтиллионов,
• восьмой — класс секстиллионов.

24 дек. 2020 г.

Сколько единиц в числе 80?

80? 28 — 2 дес. 8 ед.

Сколько единиц в цифре 10?

Ответ: Число 10 содержит 1 десяток 0 единиц.

Что такое десятки единицы?

Десятки, единицы – это разрядные единицы. Единицы – это наименьший разряд в записи любого числа. Десяток – это второй разряд в записи числа. Один десяток содержит 10 единиц.

Чему равны 10 десятков?

Это число состоит из 10 десятков и называется “сто”, или “сотня”. – Записывается это число так: 100. 1 сот. = 10 дес.

Как найти число десятков в числе?

Чтобы определить общее число десятков в числе, достаточно, число разделить на 10, то есть отбросить в записи числа одну цифру справа.

Что такое три десятка?

Правильный ответ: 3 десятка — это число 30.

Сколько единиц в числе 63?

3. 6 десятков и 3 единицы (это число 63).

Интересные материалы:

Как называется большой коллектив музыкантов играющих на различных музыкальных инструментах?
Как называется большой шар на котором летают?
Как называется брат от другого отца?
Как называется брат родной по отцу?
Как называется бросок мяча вдоль сетки в волейболе?
Как называется бумага из которой делают поделки?
Как называется бумага которую кладут в подарок?
Как называется бумага на которой рисуют художник?
Как называется бычки сигарет?
Как называется бывший город Орджоникидзе?

Сколько тысяч, сотен, десятков, единиц в числе

Онлайн калькулятор для определения общего числа единиц, десятков, сотен, тысяч.
Например число: 1497 = 1 тысяча, 4 сотни, 9 десятков, 7 единиц.

Для вычисления количества миллионов в числе — используйте этот калькулятор
Для определения количества сотен в числе — используйте этот калькулятор
Что бы узнать сколько десятков в числе — используйте этот калькулятор

как определить сколько в числе всего тысяч, десятков и тд.

Действительно, как узнать, сколько в числе всего единиц, всего десятков, всего сотен, всего тысяч
и т. д. ? Давай учиться этому на примере.
В числе 781 593 (семьсот восемьдесят одна тысяча пятьсот девяносто три) содержится 7 ст. 8 д. т. 1т. 5с. 9 д. 3 ед. (ст. — сотни тысяч, д. т. — десятки тысяч) . Откуда мы это знаем?
— Всё число покажет тебе, сколько в нём единиц: 781 593 единицы в числе 781 593.
— Отбрось первую цифру справа — цифру разряда единиц, оставшиеся цифры покажут число десятков: 78159 десятков в числе 781 593.
— Отбрось две цифры справа — цифры разряда единиц и разряда десятков, и оставшиеся цифры покажут число сотен: 7 815 сотен в числе 781 593.
— Отбрось три цифры справа — цифры разрядов единиц, десятков, сотен, и те цифры, которые останутся, покажут число тысяч: 781 тысяча в числе 781 593.
— Отбрось четыре цифры справа — цифры разрядов единиц, десятков, сотен, тысяч, и ты узнаешь, сколько в этом числе десятков тысяч: 78 десятков тысяч в числе 781 593.
— Отбрось пять цифр справа — цифры разрядов единиц, десятков, сотен, тысяч, десятков тысяч. Осталось число сотен тысяч: 7 сотен тысяч в числе 781 593.

Десяток — это 10, сотня — это 100, тысяча — это 1 000. Чтобы узнать сколько в числе всего единиц,

то прочитай все число. Чтобы узнать сколько в числе всего десятков, всего сотен и всего тысяч, закрой с конца в числе столько нулей, сколько их в 10, 100 и 1 000 и получишь ответы

Разряды для начинающих

Наш первый урок назывался числа. Мы рассмотрели лишь малую часть этой темы. На самом деле тема чисел достаточно обширна. В ней много тонкостей и нюансов, много хитростей и интересных фишек.

Сегодня мы продолжим тему чисел, но опять же не будем рассматривать её всю, чтобы не затруднять обучение лишней информацией, которая на первых порах не особо то и нужна. Мы поговорим о разрядах.

Что такое разряд?

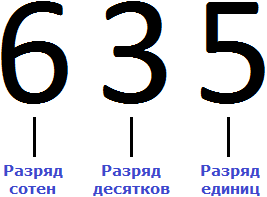
Если говорить простым языком, то разряд это позиция цифры в числе или место, где располагается цифра. Возьмём для примера число 635. Это число состоит из трёх цифр: 6, 3 и 5.

Разряды надо читать справа налево. В числе 635 на первой позиции располагается цифра 5, на второй позиции – цифра 3, на третьей позиции – цифра 6.

Позиция, где располагается цифра 5, называется разрядом единиц

Позиция, где располагается цифра 3, называется разрядом десятков

Позиция, где располагается цифра 6, называется разрядом сотен

Каждый из нас слышал со школы такие вещи как «единицы», «десятки», «сотни». Разряды помимо того, что играют роль позиции цифры в числе, сообщают нам некоторую информацию о самом числе. В частности, разряды сообщают нам вес числа. Они сообщают сколько в числе единиц, сколько десятков и сколько сотен.

Вернёмся к нашему числу 635. В разряде единиц располагается пятёрка. О чём это говорит? А говорит это о том, что разряд единиц содержит пять единичек. Выглядит это так:

В разряде десятков располагается тройка. Это говорит о том, что разряд десятков содержит три десятка. Выглядит это так:

В разряде сотен располагается шестёрка. Это говорит о том, что в разряде сотен располагаются шесть сотен. Выглядит это так:

Если сложить число получившихся единиц, число десятков и число сотен, то получим наше изначальное число 635

Существуют и более старшие разряды такие как разряд тысяч, разряд десятков тысяч, разряд сотен тысяч, разряд миллионов и так далее. Такие большие числа мы будем рассматривать редко, но тем не менее о них тоже желательно знать.

Например, в числе 1 645 832 разряд единиц содержит 2 единицы, разряд десятков — 3 десятка, разряд сотен — 8 сотен, разряд тысяч — 5 тысяч, разряд десятков тысяч — 4 десятка тысяч, разряд сотен тысяч — 6 сотен тысяч, разряд миллионов — 1 миллион.

На первых этапах изучения разрядов желательно разбираться сколько единиц, десятков, сотен содержит то или иное число. К примеру, число 9 содержит 9 единиц. Число 12 содержит две единицы и один десяток. Число 123 содержит три единицы, два десятка и одну сотню.

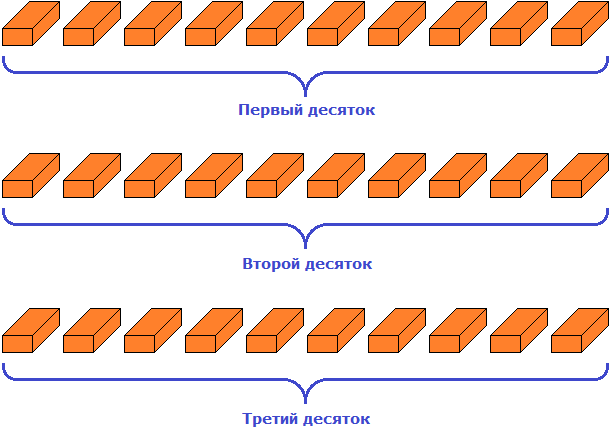
Группировка предметов

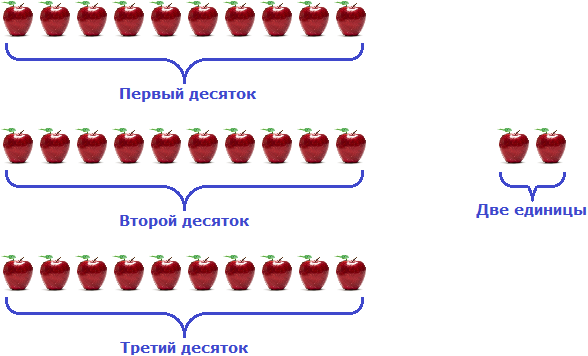
После подсчета каких-нибудь предметов, разряды можно использовать для группировки этих предметов. К примеру, если мы насчитали во дворе 35 кирпичей, то можно использовать разряды для группировки этих кирпичей. В случае группировки предметов, разряды можно читать слева направо. Так, цифра 3 в числе 35 будет говорить о том, что в числе 35 содержатся три десятка. А это значит, что 35 кирпичей можно сгруппировать три раза по десять штук.

Итак, сгруппируем кирпичи три раза по десять штук:

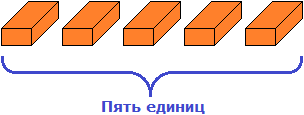
Получилось тридцать кирпичей. Но осталось еще пять единиц кирпичей. Их мы назовем как «пять единиц»

Получилось три десятка и пять единиц кирпичей.

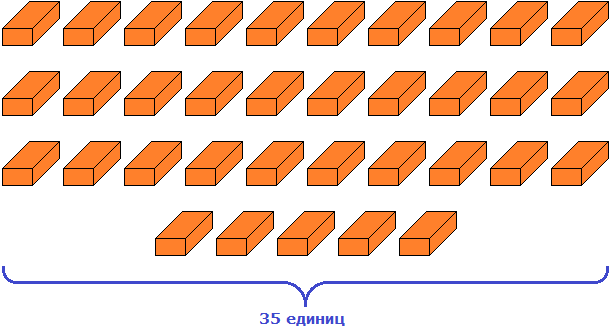
А если бы мы не стали группировать кирпичи на десятки и единицы, то можно было бы сказать, что число 35 содержит тридцать пять единиц. Такая группировка тоже была бы допустимой:

Аналогично можно рассуждать и про другие числа. К примеру, о числе 123. Ранее мы сказали, что это число содержит три единицы, два десятка и одну сотню. Но можно ещё сказать, что это число содержит 123 единицы. Более того, можно сгруппировать это число и другим образом, сказав что оно содержит 12 десятков и 3 единицы.

Слова единицы, десятки, сотни, заменяют собой множимые 1, 10 и 100. К примеру, в разряде единиц числа 123 располагается цифра 3. С помощью множимого 1 можно записать, что эта единица содержится в разряде единиц три раза:

Далее в разряде десятков числа 123 располагается цифра 2. С помощью множимого 10 можно записать, что эта десятка содержится в разряде десятков два раза:

Далее в разряде сотен числа 123 располагается цифра 1. С помощью множимого 100 можно записать, что эта сотня содержится в разряде сотен один раз:

Если сложить полученные результаты 3, 20 и 100, то получим число 123

3 + 20 + 100 = 123

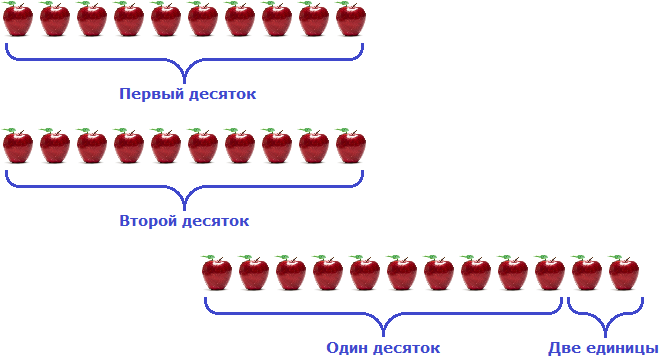
То же самое будет происходить если мы скажем, что число 123 содержит 12 десятков и 3 единицы. Другими словами, десятки будут сгруппированы 12 раз:

А единицы три раза:

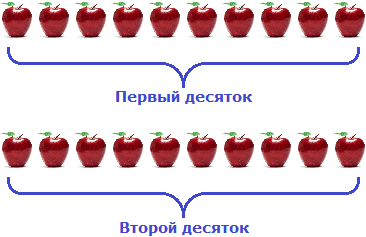
Это можно понять на следующем примере. Если имеется 123 яблока, то можно сгруппировать первые 120 яблок 12 раз по 10 штук:

Получилось сто двадцать яблок. Но осталось еще три яблока. Их мы назовем как «три единицы»

Если сложить полученные результаты 120 и 3, снова получим число 123

Ещё можно сгруппировать 123 яблока на одну сотню, два десятка и три единицы.

Сгруппируем два десятка:

Сгруппируем три единицы:

Если сложить полученные результаты 100, 20 и 3, снова получим число 123

100 + 20 + 3 = 123

Ну и наконец, рассмотрим последнюю возможную группировку, где яблоки не будут распределяться на десятки и сотни, а будут собраны вместе. В таком случае число 123 будет читаться как «сто двадцать три единицы» . Такая группировка тоже будет допустимой:

Пример 3. Прочитать число 523 всеми возможными способами.

Число 523 можно прочесть, как 3 единицы, 2 десятка и 5 сотен:

1 × 3 = 3 (три единицы)

10 × 2 = 20 (два десятка)

100 × 5 = 500 (пять сотен)

3 + 20 + 500 = 523

Ещё можно прочесть, как 3 единицы 52 десятка:

1 × 3 = 3 (три единицы)

10 × 52 = 520 (пятьдесят два десятка)

Ещё число 523 можно прочесть, как 523 единицы:

1 × 523 = 523 (пятьсот двадцать три единицы)

Где применить разряды?

Разряды существенно облегчают некоторые вычисления. Представьте, что вы у доски и решаете задачу. Вы почти закончили задачу, осталось только вычислить последнее выражение и получить ответ. Выражение, которое надо вычислить, выглядит следующим образом:

Калькулятора под рукой нет, а хочется быстро записать ответ и удивить всех скоростью своих вычислений. Всё просто, если отдельно сложить единицы, отдельно десятки и отдельно сотни. Начинать нужно с разряда единиц. В первую очередь после знака равно (=) необходимо мысленно поставить три точки. Вместо этих точек будет располагаться новое число (наш ответ):

Теперь начинаем складывать. В разряде единиц числа 632 располагается цифра 2, а в разряде единиц числа 264 — цифра 4. Это означает, разряд единиц числа 632 содержит две единицы, а разряд единиц числа 264 содержит четыре единицы. Складываем 2 и 4 единицы — получаем 6 единиц. Записываем цифру 6 в разряде единиц нового числа (нашего ответа):

Далее складываем десятки. В разряде десятков числа 632 располагается цифра 3, а в разряде десятков числа 264 — цифра 6. Это означает, что разряд десятков числа 632 содержит три десятка, а разряд десятков числа 264 содержит шесть десятков. Складываем 3 и 6 десятков — получаем 9 десятков. Записываем цифру 9 в разряде десятков нового числа (нашего ответа):

Ну и в завершении складываем отдельно сотни. В разряде сотен числа 632 располагается цифра 6, а в разряде сотен числа 264 — цифра 2. Это означает, что разряд сотен числа 632 содержит шесть сотен, а разряд сотен числа 264 содержит две сотни. Складываем 6 и 2 сотни, получаем 8 сотен. Записываем цифру 8 в разряде сотен нового числа (нашего ответа):

Таким образом, если к числу 632 прибавить 264, получается 896. Конечно, вы вычислите подобное выражение быстрее и окружающие начнут удивляться вашим способностям. Они будут думать, что вы быстро вычисляете большие числа, а на самом деле вы вычисляли маленькие. Согласитесь, что маленькие числа вычислять легче, чем большие.

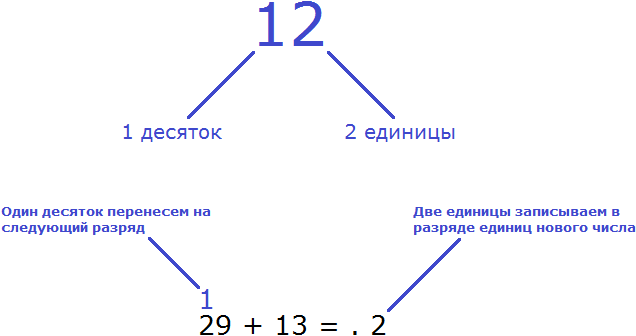
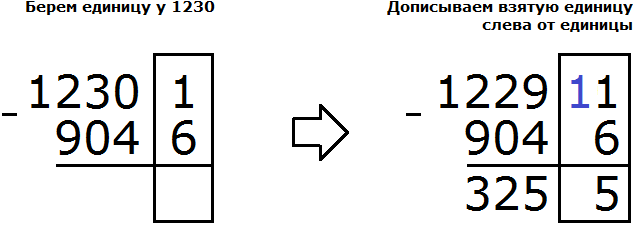
Переполнение разряда

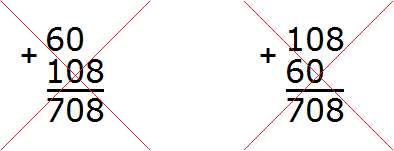
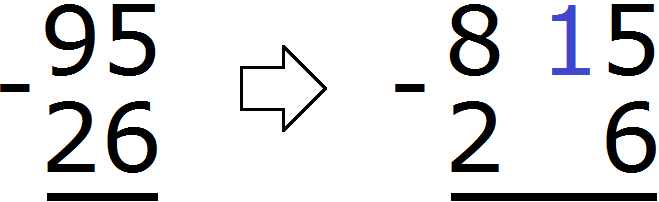
Разряд характеризуется одной цифрой от 0 до 9. Но иногда при вычислении числового выражения в середине решения может произойти переполнение разряда.

Например, при сложении чисел 32 и 14 переполнения не происходит. Сложение единиц этих чисел даст 6 единиц в новом числе. А сложение десятков этих чисел даст 4 десятка в новом числе. Получится ответ 46 или шесть единиц и четыре десятка .

А вот при сложении чисел 29 и 13 произойдёт переполнение. Сложение единиц этих чисел даёт 12 единиц, а сложение десятков 3 десятка. Если в новом числе в разряде единиц записать полученные 12 единиц, а в разряде десятков записать полученные 3 десятка, то получится ошибка:

Значение выражения 29 + 13 равно 42 , а не 312 . Как же следует поступать при переполнении? В нашем случае переполнение случилось в разряде единиц нового числа. При сложении девяти и трёх единиц у нас получилось 12 единиц. А в разряд единиц можно записывать только цифры в диапазоне от 0 до 9.

Дело в том, что 12 единиц это не просто «двенадцать единиц» . По другому это число можно прочитать как «две единицы и один десяток» . Разряд единиц предназначен только для единиц. Десяткам там не место. Здесь и заключается наша ошибка. Сложив 9 единиц и 3 единицы мы получили 12 единиц, которые по-другому можно назвать двумя единицами и одним десятком. Записав две единицы и один десяток в одном разряде, мы допустили ошибку, которая в итоге привела к неправильному ответу.

Чтобы исправить ситуацию, две единицы нужно записать в разряде единиц нового числа, а оставшийся десяток перенести на следующий разряд десятков. После сложения десятков в примере 29 + 13 , мы прибавим к полученному результату тот десяток, который остался при сложении единиц.

Итак, из 12 единиц две единицы запишем в разряде единиц нового числа, а один десяток перенесем на следующий разряд

Как видно на рисунке, 12 единиц мы представили как 1 десяток и 2 единицы. Две единицы мы записали в разряде единиц нового числа. А один десяток перенесли к разрядам десятков. Этот десяток мы прибавим к результату сложения десятков чисел 29 и 13. Чтобы не забыть о нем, мы надписали его над десятками числа 29.

Теперь складываем десятки. Два десятка плюс один десяток будет три десятка, плюс один десяток, который остался от предыдущего сложения. В результате в разряде десятков получаем четыре десятка:

Пример 2. Сложить по разрядам числа 862 и 372.

Начинаем с разряда единиц. В разряде единиц числа 862 располагается цифра 2, в разряде единиц числа 372 — также цифра 2. Это означает, что разряд единиц числа 862 содержит две единицы, и разряд единиц числа 372 также содержит две единицы. Складываем 2 единицы плюс 2 единицы — получаем 4 единицы. Записываем цифру 4 в разряде единиц нового числа:

Далее складываем десятки. В разряде десятков числа 862 располагается цифра 6, а в разряде десятков числа 372 — число 7. Это означает, что разряд десятков числа 862 содержит шесть десятков, а разряд десятков числа 372 содержит семь десятков. Складываем 6 десятков и 7 десятков — получаем 13 десятков. Произошло переполнение разряда. 13 десятков это десятка повторенная 13 раз. А если повторить десятку 13 раз, то получится число 130

Число 130 состоит из трех десятков и одной сотни. Три десятка мы запишем в разряде десятков нового числа, а одну сотню отправим на следующий разряд:

Как видно на рисунке, 13 десятков (число 130) мы представили как 1 сотню и 3 десятка. Три десятка мы записали в разряде десятков нового числа. А одну сотню перенесли к разрядам сотен. Эту сотню мы прибавим к результату сложения сотен чисел 862 и 372. Чтобы не забыть о ней, мы надписали её над сотнями числа 862.

Теперь складываем сотни. Восемь сотен плюс три сотни будет одиннадцать сотен плюс одна сотня, которая осталась от предыдущего сложения. В результате в разряде сотен получаем двенадцать сотен:

Здесь также происходит переполнение разряда сотен, но это не приводит к ошибке, поскольку решение завершено. При желании с 12 сотнями можно провести те же действия, что мы провели с 13 десятками.

12 сотен это сотня, повторенная 12 раз. А если повторить сотню 12 раз, то получится 1200

В числе 1200 две сотни и одна тысяча. Две сотни записываются в разряд сотен нового числа, а одна тысяча перенеслась к разряду тысяч.

Теперь рассмотрим примеры на вычитание. Для начала вспомним, что такое вычитание. Это операция, которая позволяет от одного числа вычесть другое. Вычитание состоит из трёх параметров: уменьшаемого, вычитаемого и разности. Вычитать тоже нужно по разрядам.

Пример 3. Вычесть из числа 65 число 12.

Начинаем с разряда единиц. В разряде единиц числа 65 располагается цифра 5, а в разряде единиц числа 12 — цифра 2. Это означает, что разряд единиц числа 65 содержит пять единиц, а разряд единиц числа 12 содержит две единицы. Вычтем из пяти единиц две единицы, получим три единицы. Записываем цифру 3 в разряде единиц нового числа:

Теперь вычитаем десятки. В разряде десятков числа 65 располагается цифра 6, а в разряде десятков числа 12 — цифра 1. Это означает, что разряд десятков числа 65 содержит шесть десятков, а разряд десятков числа 12 содержит один десяток. Вычтем из шести десятков один десяток, получим пять десятков. Записываем цифру 5 в разряде десятков нового числа:

Пример 4 . Вычесть из числа 32 число 15

В разряде единиц числа 32 содержится две единицы, а в разряде единиц числа 15 — пять единиц. От двух единиц не вычесть пять единиц, поскольку две единицы меньше, чем пять единиц.

Сгруппируем 32 яблока так, чтобы в первой группе было три десятка яблок, а во второй — оставшиеся две единицы яблок:

Итак, нам нужно из этих 32 яблок вычесть 15 яблок, то есть вычесть пять единиц и один десяток яблок. Причем вычесть по разрядам.

От двух единиц яблок нельзя вычесть пять единиц яблок. Чтобы выполнить вычитание, две единицы должны взять несколько яблок у соседней группы (разряда десятков). Но нельзя брать сколько хочется, поскольку десятки строго упорядочены по десять штук. Разряд десятков может дать двум единицам только один целый десяток.

Итак, берём один десяток из разряда десятков и отдаём его двум единицам:

К двум единицам яблок теперь присоединился один десяток яблок. Получается 12 единиц яблок. А от двенадцати можно вычесть пять, получится семь. Записываем цифру 7 в разряде единиц нового числа:

Теперь вычитаем десятки. Поскольку разряд десятков отдал единицам один десяток, сейчас он имеет не три, а два десятка. Поэтому вычитаем из двух десятков один десяток. Останется один десяток. Записываем цифру 1 в разряде десятков нового числа:

Чтобы не забывать, что в каком-то разряде был взят один десяток (либо сотня либо тысяча), над этим разрядом принято ставить точку.

Пример 5. Вычесть из числа 653 число 286

В разряде единиц числа 653 содержится три единицы, а в разряде единиц числа 286 — шесть единиц. От трёх единиц не вычесть шесть единиц, поэтому берем один десяток у разряда десятков. Ставим точку над разрядом десятков, чтобы помнить о том, что мы взяли оттуда один десяток:

Взятый один десяток и три единицы вместе образуют тринадцать единиц. От тринадцати единиц можно вычесть шесть единиц, получится семь единиц. Записываем цифру 7 в разряде единиц нового числа:

Теперь вычитаем десятки. Раньше разряд десятков числа 653 содержал пять десятков, но мы взяли с него один десяток, и теперь в разряде десятков содержатся четыре десятка. Из четырех десятков не вычесть восемь десятков, поэтому берем одну сотню у разряда сотен. Ставим точку над разрядом сотен, чтобы помнить о том, что мы взяли оттуда одну сотню:

Взятая одна сотня и четыре десятка вместе образуют четырнадцать десятков. От четырнадцати десятков можно вычесть восемь десятков, получится шесть десятков. Записываем цифру 6 в разряде десятков нового числа:

Теперь вычитаем сотни. Раньше разряд сотен числа 653 содержал шесть сотен, но мы взяли с него одну сотню, и теперь в разряде сотен содержатся пять сотен. Из пяти сотен можно вычесть две сотни, получается три сотни. Записываем цифру 3 в разряде сотен нового числа:

Намного сложнее вычитать из чисел вида 100, 200, 300, 1000, 10000. То есть числа, у которых на конце нули. Чтобы выполнить вычитание, каждому разряду приходится занимать десятки/сотни/ тысячи у следующего разряда. Давайте посмотрим, как это происходит.

Пример 6. Вычесть из числа 200 число 84

В разряде единиц числа 200 содержится ноль единиц, а в разряде единиц числа 84 — четыре единицы. От нуля не вычесть четыре единицы, поэтому берем один десяток у разряда десятков. Ставим точку над разрядом десятков, чтобы помнить о том, что мы взяли оттуда один десяток:

Но в разряде десятков нет десятков, которые мы могли бы взять, поскольку там тоже ноль. Чтобы разряд десятков смог дать нам один десяток, мы должны взять для него одну сотню у разряда сотен. Ставим точку над разрядом сотен, чтобы помнить о том, что мы взяли оттуда одну сотню для разряда десятков:

Взятая одна сотня это десять десятков. От этих десяти десятков мы берём один десяток и отдаём его единицам. Этот взятый один десяток и прежние ноль единиц вместе образуют десять единиц. От десяти единиц можно вычесть четыре единицы, получится шесть единиц. Записываем цифру 6 в разряде единиц нового числа:

Теперь вычитаем десятки. Чтобы вычесть единицы мы обратились к разряду десятков за одним десятком, но на тот момент этот разряд был пуст. Чтобы разряд десятков смог дать нам один десяток, мы взяли одну сотню у разряда сотен. Эту одну сотню мы назвали «десять десятков» . Один десяток мы отдали единицам. Значит на данный момент в разряде десятков содержатся не десять, а девять десятков. От девяти десятков можно вычесть восемь десятков, получится один десяток. Записываем цифру 1 в разряде десятков нового числа:

Теперь вычитаем сотни. Для разряда десятков мы брали у разряда сотен одну сотню. Значит сейчас в разряде сотен содержатся не две сотни, а одна. Поскольку в вычитаемом разряд сотен отсутствует, мы переносим эту одну сотню в разряд сотен нового числа:

Получили окончательный ответ 116.

Естественно, выполнять вычитание таким традиционным методом довольно сложно, особенно на первых порах. Поняв сам принцип вычитания, можно воспользоваться нестандартными способами.

Первый способ заключается в том, чтобы уменьшить число, у которого на конце нули на одну единицу. Далее из полученного результата вычесть вычитаемое и к полученной разности прибавить единицу, которую изначально вычли из уменьшаемого. Давайте решим предыдущий пример этим способом:

Уменьшаемое здесь это число 200. Уменьшим это число на единицу. Если от 200 вычесть 1 получится 199. Теперь в примере 200 − 84 вместо числа 200 записываем число 199 и решаем пример 199 − 84 . А решение этого примера не составляет особого труда. Единицы вычтем из единиц, десятки из десятков, а сотню просто перенесем к новому числу, поскольку в числе 84 нет сотен:

Получили ответ 115. Теперь к этому ответу прибавляем единицу, которую мы изначально вычли из числа 200

Получили окончательный ответ 116.

Пример 7. Вычесть из числа 100000 число 91899

Вычтем из 100000 единицу, получим 99999

Теперь из 99999 вычитаем 91899

К полученному результату 8100 прибавим единицу, которую мы вычли из 100000

Получили окончательный ответ 8101.

Второй способ вычитания заключается в том, чтобы рассматривать цифру, находящуюся в разряде, как самостоятельное число. Решим несколько примеров этим способом.

Пример 8. Вычесть из числа 75 число 36

Будем считать, что каждая цифра в разряде это самостоятельное число.

Итак, в разряде единиц числа 75 располагается число 5, а в разряде единиц числа 36 располагается число 6. Из пяти не вычесть шести, поэтому берем одну единицу у следующего числа, находящегося в разряде десятков.

В разряде десятков располагается число 7. Берем от этого числа одну единицу и мысленно дописываем её слева от числа 5

А поскольку от числа 7 взята одна единица, это число уменьшится на одну единицу и обратится в число 6

Теперь в разряде единиц числа 75 располагается число 15, а в разряде единиц числа 36 число 6. Из 15 можно вычесть 6, получится 9. Записываем число 9 в разряде единиц нового числа:

Переходим к следующему числу, находящемуся в разряде десятков. Раньше там располагалось число 7, но мы взяли с этого числа одну единицу, поэтому сейчас там располагается число 6. А в разряде десятков числа 36 располагается число 3. Из 6 можно вычесть 3, получится 3. Записываем число 3 в разряде десятков нового числа:

Пример 9. Вычесть из числа 200 число 84

Будем считать, что каждая цифра в разряде это самостоятельно число.

Итак, в разряде единиц числа 200 располагается ноль, а в разряде единиц числа 84 — располагается четыре. От нуля не вычесть четыре, поэтому берем одну единицу у следующего числа, находящегося в разряде десятков. Но в разряде десятков тоже ноль. Ноль не сможет дать нам единицу. В таком случае за следующее принимаем число 20.

Берём одну единицу от числа 20 и мысленно дописываем её слева от нуля, располагающегося в разряде единиц. А поскольку от числа 20 взята одна единица, это число обратится в число 19

Теперь в разряде единиц располагается число 10. Десять минус четыре равно шесть. Записываем число 6 в разряде единиц нового числа:

Переходим к следующему числу, находящемуся в разряде десятков. Раньше там располагался ноль, но этот ноль вместе со следующей цифрой 2 образовал число 20, от которого мы брали одну единицу. В результате число 20 обратилось в число 19. Получается, что теперь в разряде десятков числа 200 располагается число 9, а в разряде десятков числа 84 располагается число 8. Девять минус восемь равно одному. Записываем число 1 в разряде десятков нашего ответа:

Переходим к следующему числу, находящемуся к разряду сотен. Раньше там располагалось число 2, но это число вместе с цифрой 0 мы приняли за число 20, от которого взяли одну единицу. В результате число 20 обратилось в число 19. Получается, что теперь в разряде сотен числа 200 располагается число 1, а в числе 84 разряд сотен пустой, поэтому мы переносим эту единицу к новому числу:

Этот метод поначалу кажется сложным и лишенным всякого смысла, но на деле он самый лёгкий. В основном мы будем им пользоваться при сложении и вычитании чисел в столбик.

Сложение в столбик

Сложение в столбик это школьная операция, которую помнят многие, но не мешает вспомнить её ещё раз. Сложение в столбик происходит по разрядам — единицы складываются с единицами, десятки с десятками, сотни с сотнями, тысячи с тысячами.

Рассмотрим несколько примеров.

Пример 1. Сложить 61 и 23.

Сначала записываем первое число, а под ним второе число так, чтобы единицы и десятки второго числа оказались под единицами и десятками первого числа. Всё это соединяем знаком сложения (+) по вертикали:

Теперь единицы первого числа складываем с единицами второго числа, а десятки первого числа складываем с десятками второго числа:

Получили 61 + 23 = 84.

Пример 2. Сложить 108 и 60

Записываем числа в столбик. Единицы под единицами, десятки под десятками:

Теперь складываем единицы первого числа с единицами второго числа, десятки первого числа с десятками второго числа, сотни первого числа с сотнями второго числа. Но сотня есть только у первого числа 108. В этом случае цифра 1 из разряда сотен добавляется к новому числу (нашему ответу). Как говорили в школе «сносится»:

Видно, что мы снесли цифру 1 к нашему ответу.

Когда речь идёт о сложении, нет разницы в каком порядке записывать числа. Наш пример вполне можно было записать и так:

Первая запись, где число 108 было наверху, более удобнее для вычисления. Человек вправе выбирать любую запись, но обязательно нужно помнить, что единицы надо записывать строго под единицами, десятки под десятками, сотни под сотнями. Другими словами, следующие записи будут неправильными:

Если вдруг при сложении соответствующих разрядов получится число, которое не помещается в разряд нового числа, то необходимо записать одну цифру из младшего разряда, а оставшуюся перенести на следующий разряд.

Речь в данном случае идет о переполнении разряда, о котором мы говорили ранее. Например, при сложении 26 и 98 получается 124. Давайте посмотрим, как это получилось.

Записываем числа в столбик. Единицы под единицами, десятки под десятками:

Складываем единицы первого числа с единицами второго числа: 6+8=14. Получили число 14, которое не вместится в разряд единиц нашего ответа. В таких случаях мы сначала вытаскиваем из 14 цифру, находящуюся в разряде единиц и записываем её в разряде единиц нашего ответа. В разряде единиц числа 14 располагается цифра 4. Записываем эту цифру в разряде единиц нашего ответа:

А куда девать цифру 1 из числа 14? Здесь начинается самое интересное. Эту единицу мы переносим на следующий разряд. Она будет добавлена к разряду десятков нашего ответа.

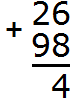
Складываем десятки с десятками. 2 плюс 9 равно 11, плюс добавляем единицу, которая досталась нам от числа 14. Добавив к 11 нашу единицу, мы получим число 12, которое и запишем в разряде десятков нашего ответа. Поскольку это конец решения, здесь уже не стоит вопрос о том, вместится ли полученный ответ в разряд десятков. 12 мы записываем целиком, образуя окончательный ответ.

Получили ответ 124.

Говоря традиционным методом сложения, при сложении 6 и 8 единиц получилось 14 единиц. 14 единиц это 4 единицы и 1 десяток. Четыре единицы мы записали в разряде единиц, а один десяток отправили на следующий разряд (к разрядам десятков). Затем сложив 2 десятка и 9 десятков, мы получили 11 десятков, плюс добавили 1 десяток, который остался при сложении единиц. В результате получили 12 десятков. Эти двенадцать десятков мы записали целиком, образуя окончательный ответ 124.

Этот простенький пример демонстрирует школьную ситуацию, в которой говорят «четыре пишем, один в уме» . Если вы будете решать примеры и у вас после сложения разрядов останется цифра, которую надо держать в уме, запишите её над тем разрядом, куда она будет потом добавлена. Это позволит вам не забыть о ней:

Пример 2. Сложить числа 784 и 548

Записываем числа в столбик. Единицы под единицами, десятки под десятками, сотни под сотнями:

Складываем единицы первого числа с единицами второго числа: 4+8=12. Число 12 не вмещается в разряд единиц нашего ответа, поэтому мы из 12 вынимаем цифру 2 из разряда единиц и записываем её в разряд единиц нашего ответа. А цифру 1 переносим на следующий разряд:

Теперь складываем десятки. Складываем 8 и 4 плюс единица, которая осталась от предыдущей операции (единица осталась от 12, на рисунке она выделена синим цветом). Складываем 8+4+1=13. Число 13 не вместится в разряд десятков нашего ответа, поэтому мы запишем цифру 3 в разряде десятков, а единицу перенесём на следующий разряд:

Теперь складываем сотни. Складываем 7 и 5 плюс единица, которая осталась от предыдущей операции: 7+5+1=13. Записываем число 13 в разряд сотен:

Вычитание в столбик

Пример 1. Вычтем из числа 69 число 53.

Запишем числа в столбик. Единицы под единицами, десятки под десятками. Затем вычитаем по разрядам. Из единиц первого числа вычитаем единицы второго числа. Из десятков первого числа вычитаем десятки второго числа:

Получили ответ 16.

Пример 2. Найти значение выражения 95 − 26

Записываем в столбик данное выражение:

Разряд единиц числа 95 содержит 5 единиц, а разряд единиц числа 26 содержит 6 единиц. От пяти единиц нельзя вычесть шесть единиц, поэтому берем один десяток у разряда десятков. Этот десяток и имеющиеся пять единиц вместе составляют 15 единиц. Из 15 единиц можно вычесть 6 единиц, получится 9 единиц. Записываем цифру 9 в разряде единиц нашего ответа:

Теперь вычитаем десятки. Разряд десятков числа 95 раньше содержал 9 десятков, но мы взяли с этого разряда один десяток, и сейчас он содержит 8 десятков. А разряд десятков числа 26 содержит 2 десятка. Из восьми десятков можно вычесть два десятка, получится шесть десятков. Записываем цифру 6 в разряде десятков нашего ответа:

Воспользуемся нестандартным способом вычитания при котором каждая цифра, входящая в число, рассматривается как отдельное число. При вычитании больших чисел в столбик этот способ очень удобен.

В разряде единиц уменьшаемого располагается число 5. А в разряде единиц вычитаемого число 6. Из пятёрки не вычесть шестёрку. Поэтому берем одну единицу у числа 9. Взятая единица мысленно дописывается слева от пятёрки. А поскольку у числа 9 мы взяли одну единицу, это число уменьшится на одну единицу:

В результате пятёрка обращается в число 15. Теперь можно из 15 вычесть 6. Получается 9. Записываем число 9 в разряде единиц нашего ответа:

Переходим к разряду десятков. Раньше там располагалось число 9, но поскольку мы взяли у него одну единицу оно обратилось в число 8. В разряде десятков второго числа располагается число 2. Восемь минус два будет шесть. Записываем число 6 в разряде десятков нашего ответа:

Пример 3. Найдем значение выражения 2412 − 2317

Записываем в столбик данное выражение:

В разряде единиц числа 2412 располагается число 2, а в разряде единиц числа 2317 располагается число 7. Из двойки не вычесть семёрку, поэтому берем единицу у следующего числа 1. Взятую единицу мысленно дописываем слева от двойки:

В результате двойка обращается в число 12. Теперь можно из 12 вычесть 7. Получается 5. Записываем цифру 5 в разряде единиц нашего ответа:

Переходим к десяткам. В разряде десятков числа 2412 раньше располагалось число 1, но поскольку мы взяли у него одну единицу, оно обратилось в 0. А в разряде десятков числа 2317 располагается число 1. Из нуля не вычесть единицу. Поэтому берем одну единицу у следующего числа 4. Взятую единицу мысленно дописываем слева от нуля. А поскольку у числа 4 мы взяли одну единицу, это число уменьшится на одну единицу:

В результате ноль обращается в число 10. Теперь можно из 10 вычесть 1. Получается 9. Записываем цифру 9 в разряде десятков нашего ответа:

В разряде сотен числа 2412 раньше располагалось число 4, но сейчас там располагается число 3. В разряде сотен числа 2317 также располагается число 3. Три минус три равно нулю. То же самое и с разрядами тысяч в обоих числах. Два минус два равно нулю. А если разность старших разрядов равна нулю, то этот ноль не записывают. Поэтому окончательным ответом будет число 95.

Пример 4. Найти значение выражения 600 − 8

Запишем в столбик данное выражение:

В разряде единиц числа 600 располагается ноль, а в разряде единиц числа 8 само это число. Из нуля не вычесть восьмерку, поэтому берем единицу у следующего числа. Но следующее число это тоже ноль. Тогда за следующее число принимаем число 60. Берем одну единицу у этого числа и мысленно дописываем её слева от нуля. А поскольку у числа 60 мы взяли одну единицу, это число уменьшится на одну единицу:

Теперь в разряде единиц располагается число 10. Из 10 можно вычесть 8, получится 2. Записываем число 2 в разряде единиц нового числа:

Переходим к следующему числу, находящемуся в разряде десятков. В разряде десятков раньше располагался ноль, но сейчас там располагается число 9, а во втором числе разряд десятков отсутствует. Поэтому число 9 переносится к новому числу:

Переходим к следующему числу, находящемуся в разряде сотен. В разряде сотен раньше располагалось число 6, но сейчас там располагается число 5, а во втором числе разряд сотен отсутствует. Поэтому число 5 переносится к новому числу:

Пример 5. Найти значение выражения 10000 − 999

Запишем в столбик данное выражение:

В разряде единиц числа 10000 располагается 0, а в разряде единиц числа 999 располагается число 9. Из нуля не вычесть девятку, поэтому берем одну единицу у следующего числа, находящегося в разряде десятков. Но в следующем разряде тоже ноль. Тогда за следующее число принимаем 1000 и берем от этого числа единицу:

Следующее число в данном случае было 1000. Взяв у него единицу, мы обратили его в число 999. А взятую единицу дописали слева от нуля.

Дальнейшее вычисление не составило особого труда. Десять минус девять равно одному. Вычитание чисел, находящихся в разряде десятков обоих чисел дало ноль. Вычитание чисел, находящихся в разряде сотен обоих чисел тоже дало ноль. А девятка из разряда тысяч была перенесена к новому числу:

Пример 6. Найти значение выражения 12301­ − 9046

Запишем в столбик данное выражение:

В разряде единиц числа 12301 располагается число 1, а в разряде единиц числа 9046 располагается число 6. Из единицы не вычесть шесть, поэтому берем одну единицу у следующего числа, находящегося в разряде десятков. Но в следующем разряде располагается ноль. Ноль ничего нам дать не сможет. Тогда за следующее число принимаем 1230 и берем от этого числа единицу:

Следующее число в данном случае было 1230. Взяв у него единицу, мы обратили его в число 1229. А взятую единицу мысленно дописали слева от единицы, находящейся в разряде единиц.

Дальнейшее вычисление не составило особого труда. Одиннадцать минус шесть равно пять. Вычитание чисел, находящихся в разряде десятков обоих чисел дало число 5. Вычитание чисел, находящихся в разряде сотен обоих чисел дало число 2. Вычитание чисел, находящихся в разряде тысяч обоих чисел дало число 3.