План урока:
Понятие перпендикуляра
Расстояния между плоскостями и прямыми
Теорема о трех перпендикулярах
Угол между прямой и плоскостью
Задачи на перпендикуляры, наклонные, расстояния
Понятие перпендикуляра
Пусть есть некоторая плоскость α и точка М в пространстве, не лежащая на α. Проведем через М прямую, перпендикулярную α. Она пересечет α в какой-нибудь точке К. Отрезок МК именуют перпендикуляром к плоскости α.
Если через М мы проведем ещё одну прямую, пересекающую α, то она пересечет α в какой-нибудь точке Н. В результате мы получим прямоугольный ∆МНК:
Запомним некоторые геометрические термины. В таком построении:
- отрезок МН – это наклонная;
- отрезок НК – это проекция наклонной, или просто проекция;
- К – основание перпендикуляра;
- Н – основание наклонной.
Заметим, что в ∆МНК отрезок МН – это гипотенуза, а МК – это катет. Напомним, что катет всегда меньше гипотенузы. Отсюда вытекает вывод – длина перпендикуляра всегда меньше длины наклонной (конечно, если они проведены из одной точки).
Это значит, что из всех отрезков, которыми можно соединить точку и плоскость, именно перпендикуляр будет кратчайшим. Поэтому его называют расстоянием между точкой и плоскостью.
Расстояния между плоскостями и прямыми
Докажем довольно очевидный факт:
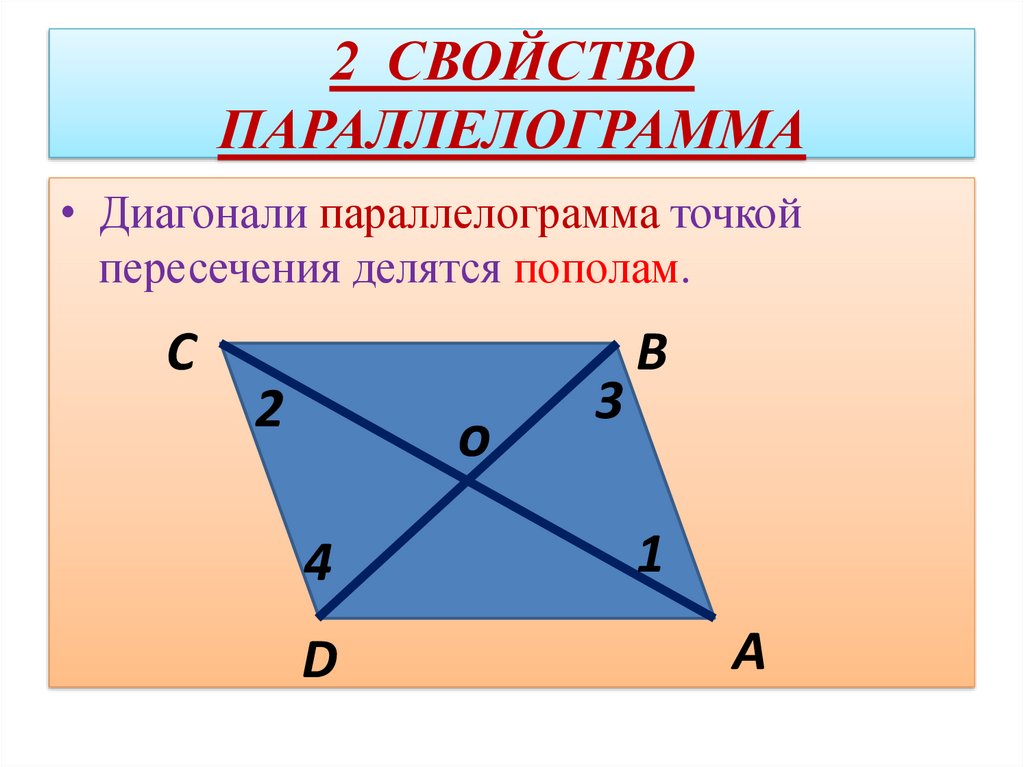
Действительно, пусть α и β – параллельные плоскости. Выберем на α произвольные точки М и Р, а далее опустим перпендикуляры из точек М и Р на β, которые пересекут β в точках Н и К соответственно:
Так как МН и РК перпендикулярны плоскости α, то они параллельны. Но также и α||β. Тогда, по теореме 12 из этого урока, отрезки МН и РК одинаковы, ч. т. д.
Этот факт позволяет ввести понятия расстояния между параллельными плоскостями.
Уточним, что если плоскости пересекаются, то расстояние между ними не может быть определено.
Далее рассмотрим случай с плоскостью α и параллельной ей прямой m. Оказывается, и в этом случае точки прямой равноудалены от плоскости.
Действительно, отметим на m произвольную точку К. Далее через K проведем такую плоскость β, что α||β. Так как точки β равноудалены от α, то нам достаточно показать, что m будет полностью принадлежать β:
Так как m и β уже имеют общую точку K, то они m либо пересекает β, либо лежит в ней. Будем рассуждать от противного и предположим, что m и β пересекаются. Так как m||α, то в α можно построить прямую n, параллельную m. Если m пересекает β, то и nтакже должна ее пересекать (по теореме 3 из этого урока). Но если n пересекает β, то точка их пересечения будет одновременно принадлежать и β, и α. То есть у этих плоскостей будет общая точка. Но α и β параллельны и потому не могут иметь общих точек. Значит, на самом деле m и β НЕ пересекаются. Остается один вариант – m принадлежит β, ч. т. д.
Из этой теоремы вытекает понятие расстояния между прямой и плоскостью.
Уточним, что если плоскость и прямая не параллельны, то расстояние между ними определить нельзя.
Осталось понять, как определять расстояние между прямыми в пространстве. Для параллельных прямых определение расстояния известно ещё из курса планиметрии. Естественно, что для пересекающихся прямых расстояние определить невозможно. Остается только случай скрещивающихся прямых.
Пусть прямые m и n скрещиваются. Тогда через n можно построить плоскость α, параллельную m. И наоборот, через m возможно провести плоскость β, параллельную n:
Далее опустим из какой-нибудь точки m перпендикуляр на α. Обозначим этот перпендикуляр как р. Тогда через пересекающиеся прямые m и р можно провести единственную плоскость γ:
Заметим, что плоскости α и γ обязательно пересекутся по некоторой прямой m’, причем m’||m. Действительно, m’ и m не могут скрещиваться, ведь они находятся в одной плоскости γ. Не могут они и пересекаться, ведь в противном случае точка их пересечения была бы общей для m и α, а они параллельны и общих точек не имеют.
Также заметим, что прямые n и m’ пересекаются, ведь они располагаются в одной плоскости α. Параллельными они быть не могут, ведь тогда по свойству транзитивности параллельности получилось бы, что и n||m, а это не так. Обозначим точку пересечения n и m’ буквой K.
Далее через K в плоскости γ проведем прямую р’, параллельную р:
Теперь начнем рассуждения. Если р⊥α, то также р⊥m’. Так как р’||р, то и р’⊥m’, ведь прямая, перпендикулярная одной из параллельных прямых, будет перпендикулярна и второй прямой. По этому же правилу из того факта, что m’||m и р’⊥m’ вытекает, что и m⊥р’. Наконец, если р⊥α, то р⊥n. Для ясности отметим все найденные нами прямые углы на рисунке:
В итоге получилось, что отрезок HK перпендикулярен и n, и m. По этой причине его называют общим перпендикуляром к прямым n и m. Именно он и считается расстоянием между скрещивающимися прямыми m и n.
Отдельно отметим, что HK – это ещё и общий перпендикуляр к α и β. Понятно, что так как р⊥α и р’||р, то и р’⊥α, то есть HK – перпендикуляр к α.
Теперь через точку H проведем прямую n’, параллельную n. Так как β||n, то n’ будет находиться в β (по теор. 6 в этом уроке).
Раз n||n’ и р’⊥n, то и р’⊥n’. Тогда получается, что в β есть сразу две пересекающихся прямых (это m и n’), которые перпендикулярны р’. Поэтому можно утверждать, что р’⊥β, то есть HK– перпендикуляр к β.
Отсюда сразу вытекает ещё один важный вывод – плоскости α и β параллельны, так как имеют общий перпендикуляр.
Итак, мы показали, что общий перпендикуляр можно построить для любых двух скрещивающихся прямых. Но можно построить ещё один такой перпендикуляр? Нельзя, и это можно показать.
Сначала заметим, что второй перпендикуляр нельзя провести через точку К, ведь в таком случае получалось бы, что к m проведены два различных перпендикуляра из одной и той же точки, что невозможно. Аналогично перпендикуляр не может проходить и через Н.
Предположим тогда, что второй перпендикуляр проходит через точки С и D, причем С находится на m, а D находится на n. То есть CD⊥m и СD⊥n:
Проведем через С прямую n’’, параллельную n. Раз СD⊥n и n||n’’, то и СD⊥n’’. При этом n’’ находится в β (это доказывается также, как и в случае с n’). Тогда получается, что в β есть две прямые, n’’ и m, каждая из которых перпендикулярна СD, и при этом n’’ и m пересекаются. Тогда CD⊥β. Из этого вытекает, что СD и HK параллельны, а потому через них можно провести плоскость δ. Этой плоскости будут принадлежать точки С, H, К и D. Но тогда в этой плоскости должны находиться прямые m и n, ведь они имеют с ней по две общих точки. Но m и n – скрещивающиеся прямые, то есть они никак не могут находиться в одной плоскости. Это противоречие означает, что второй общий перпендикуляр CD не существует.
Итак, из всех наших рассуждений мы можем сделать следующие выводы:
Теорема о трех перпендикулярах
Сформулируем важное утверждение, которое называют теоремой о трех перпендикулярах.
Проиллюстрируем теорему с помощью картинки:
Доказательство этой теоремы очень простое. Так как МК⊥α, то также МК⊥m. Теперь рассмотрим расположение плоскости МНК и прямой m. МК⊥m и HK⊥m. Тогда по признаку перпендикулярности можно утверждать, что m перпендикулярна всей плоскости HM, то есть каждой находящейся в ней прямой. В частности, m⊥HK, ч. т. д.
Оказывается, верно и обратное утверждение (так называемая обратная теорема о трех перпендикулярах):
Доказательство аналогично предыдущему. Так как m⊥MH и m⊥MK, то m⊥HMK. Отсюда вытекает, что и m⊥HK.
Угол между прямой и плоскостью
Проекция наклонной позволяет ввести такое понятие, как угол между прямой и плоскостью.
Пусть надо определить угол между прямой HM и плоскостью α:
Здесь надо просто построить перпендикуляр МК. В результате появится отрезок HK– проекция HM на α. Тогда угол между HM и HK, то есть ∠MHK, как раз и будет углом между HM и α.
Однако не всегда таким образом можно построить проекцию прямой. Проблемы возникнут, если прямая либо параллельна, либо перпендикулярна плоскости. В таких случаях используются такие правила:
Задачи на перпендикуляры, наклонные, расстояния
Рассмотрим несколько задач, в каждой из которых рассматривается куб АВСDEFGH. При этом предполагается, что ребро такого куба имеет длину, равную единице.
Задание. В кубе АВСDEFGH найдите расстояние между точкой А и гранью CDHG:
Решение. Ребро AD перпендикулярно грани DH (так как AD⊥DH и AD⊥CD). Поэтому как раз АD и является расстоянием между А и СDHG. Значит, оно равно единице.
Ответ: 1.
Примечание. Для решения следующих задач запомним, что ребро DH перпендикулярно грани АВСD. Вообще в кубе все ребра, пересекающиеся с гранями, перпендикулярны таким граням.
Задание. Найдите в кубе расстояние между вершиной А и плоскостью BDH:
Решение. Проведем на грани АВСD перпендикуляр АК из А к прямой BD:
Докажем, что АК – перпендикуляр в BDH. Для этого надо найти две прямые в BDH, перпендикулярные АК. Первая такая прямая – это BD (мы специально провели АК⊥BD). Вторая такая прямая – это DH. Действительно, DH перпендикулярна всей грани АВСD, а значит, и прямой АК.
Теперь найдем длину АК. Ее можно вычислить из прямоугольного ∆АКD. В нём ∠ADB =45°, ведь это угол между стороной квадрата АВСD и его диагональю.
Найти АК можно с помощью тригонометрии в ∆АКD:
Задание. Найдите расстояние от H до плоскости EDG:
Решение. Обозначим середину отрезка ЕD буквой М.Далее в ∆МНG опустим высоту из НК на сторону MG:
Попытаемся доказать, что HK – это перпендикуляр к EDG. Заметим, что ∆HDG и ∆EHG равны, ведь у них одинаковую длину имеют ребра DH, EH, ребро GH – общее, а ∠DHG и ∠EHG прямые. Тогда одинаковы отрезки EG и DG. Это означает, что ∆EGD – равнобедренный.
В ∆EGDMG– это медиана. Так как ∆EGD – равнобедренный, то MG одновременно ещё и высота, поэтому MD⊥MG.
Аналогично ∆EHD– равнобедренный (EH = HD), а потому MH в нем – и медиана, и высота. Поэтому MD⊥MH.
Получили, что MD перпендикулярен и MH, и MG, то есть двум прямым в плоскости MHG. Тогда MD перпендикулярен всей плоскости MHG, и, в частности, отрезку HK: HK⊥MD.
Но также MD⊥MG. Получается, KH перпендикулярен двум прямым в плоскости EDG, и потому он является перпендикуляром к плоскости EDG. Значит, именно его длину нам и надо найти.
Рассмотрим ∆MDH. Он прямоугольный, а ∠MDH = 45° (угол между стороной и диагональю квадрата). Тогда длину MH можно найти так:
Так как ребро GH перпендикулярно грани АЕНD, то ∆MHG – прямоугольный. Тогда по теореме Пифагора можно найти MG:
Далее можно найти HK разными способами, но проще воспользоваться подобием ∆MHG и ∆MKH. Они оба – прямоугольные, и у них есть общий угол ∠KMH, этого достаточно для подобия треугольников. Записываем пропорцию:
Здесь слева записано отношение сторон, лежащих против ∠KMH, а справа – отношение сторон, лежащих против прямых углов (то есть отношение гипотенуз). Используем пропорцию дальше:
Задание. Найдите расстояние между прямыми ВС и DH:
Решение. ВС и DH – скрещивающиеся. Надо найти общий перпендикуляр к ним. В данном случае он очевиден – это отрезок CD. Действительно, CD⊥ВС как стороны квадрата АВСD, но и DH⊥CD как стороны в другом квадрате, СDHG.. Длина же ребра CD равна единице, ведь у куба все ребра одинаковы.
Ответ: 1.
Задание. Каково расстояние между прямыми ВС и DG:
Решение.На грани СDHG опустим из С перпендикуляр СК на диагональ GD:
Будет ли СК являться расстоянием между ВС и DG? Ясно, что СК⊥DG. При этом ребро ВС перпендикулярно грани СGHD, так как ВС⊥СG и ВС⊥СD. Значит, также ВС⊥СК. То есть СК – общий перпендикуляр к ВС и DG, и по определению как раз и является искомым расстоянием.
Длину СК найдем из прямоугольного ∆СKG. ∠СGK составляет 45°, ведь это угол между диагональю DG и стороной квадрата СG. Тогда можно записать:
Задание. Найдите расстояние между ребрами АВ и HG:
Решение. Здесь ребра АВ и HG параллельны, так как каждая их них параллельна ребру CD. Проведем отрезок АН. Так как и АВ, и HG перпендикулярны грани АЕНD, то эти ребра одновременно перпендикулярны и АН. То есть АН – общий перпендикуляр к АВ и HG, и поэтому именно его длину и надо найти.
Сделать это можно из прямоугольного ∆АНD, в котором ∠НАD составляет 45°:
Задание. Чему равно расстояние между ребром AB и диагональю FD:
Решение. Пусть А1, D1, H1 и Е1 – середины ребер АВ, DC, HG, и EF соответственно. Проведем через А1, D1, H1 плоскость. Диагональ FD пересечет ее в какой-нибудь точке К:
Сначала покажем, что плоскости α и ADH (то есть нижняя грань) параллельны.
Заметим, что в четырехугольнике АА1D1D стороны АА1 и DD1 параллельны (ведь они лежат на сторонах квадрата АВСD) и одинаковы (ведь они составляют половину от длины ребер АВ и CD, то есть имеют длину 0,5). Тогда АА1D1D – параллелограмм. Более того, раз у него есть прямые углы ∠А1АDи ∠АDD1, то можно утверждать, что АА1D1D – прямоугольник. Тогда АD||A1D1. Аналогично можно показать, что DHH1D1 – прямоугольник, и DH||D1H1.
Далее можно действовать разными способами. Первый способ – это использование признака параллельности плоскостей (теорема 9 из этого урока). Так как в α есть пересекающиеся прямые А1D1и D1H1, а в плоскости ADH находятся прямые AD и DH, и АD||A1D1, и DH||D1H1, то по этому признаку α||ADH.
Однако, если этот признак вдруг оказался «забыт», то можно использовать отрезок DD1. Он перпендикулярен и грани ADHE, и плоскости α, ведь в каждой из них есть по две прямых, перпендикулярных ему. Это AD и DH на грани ADHE и A1D1и D1H1 в α. Тогда α и ADH перпендикулярны одной и той же прямой, а потому они параллельны. Так или иначе, мы выяснили, что α||ADH.
Отсюда вытекает, что α должна проходить через середину Е1. Действительно, расстояние между параллельными плоскостями не зависит от выбора точек измерения. В данном случае оно равно отрезку АА1, то есть 0,5. Но FE– это также общий перпендикуляр к α и ADH. Значит, α пересекает FE в точке, находящейся на расстоянии 0,5 от Е. А это как раз и есть середина FE, то есть точка Е1.
Далее докажем, что точка К, в которой прямая FD пересекает α – это середина отрезка Е1D1. Для этого удобно отдельно показать плоскость, проходящую через параллельные ребра FE и CD, то есть четырехугольник FEDC:
Заметим, так как ребра FE и CD перпендикулярны верхней и нижней грани, то они перпендикулярны и отрезкам FC и ED, то есть FEDC прямоугольник. Тогда FC||ED, и ∠Е1FD = ∠D1DF (накрест лежащие углы при секущей FD). ∠FKE1 и ∠DKD1 одинаковы уже как вертикальные углы. Тогда ∆FKE1 и ∆DKD1 подобны по 2 углам. Но отрезки FE1 и DD1 одинаковы как половины равных ребер FE и CD. Получается, что ∆FKE1 и ∆DKD1 равны, и поэтому Е1К = KD1. Это и значит, что К – середина Е1D1.
Также отметим, что Е1D1 – диагональ в четырехугольнике А1Е1Н1D1. Докажем, что А1Е1Н1D – это квадрат. Ранее мы уже показали, что АА1D1D и DHH1D1 – прямоугольники. Аналогично можно продемонстрировать, что прямоугольниками являются также АА1Е1Е и ЕЕ1Н1Н. Из этого вытекает равенство сторон:
То есть в А1Е1Н1D1 все стороны одинаковы, и эта фигура – ромб. Теперь надо показать, что и углы в этом четырехугольнике составляют 90°. Продемонстрируем это на примере ∠А1D1H1. AD⊥CDHG и AD||A1D1, поэтому А1D1⊥CDHG. Значит, также А1D перпендикулярна любой прямой на грани CDHG, в том числе и D1H1. То есть ∠А1D1H1 = 90°. Но если в ромбе хотя бы один угол прямой, то он является квадратом.
Итак, мы выяснили, что А1Е1Н1D1 – квадрат, а К – середина его диагонали Е1D1. Получается, что К – точка пересечения диагоналей квадрата А1Е1Н1D1, ведь эта точка пересечения как раз делит диагонали пополам.
Теперь мы можем наконец доказать, что А1К – это и есть искомое расстояние. Действительно, так как АВ – перпендикуляр к α, та А1К принадлежит α, то А1К⊥АВ. Но как же доказать, что А1К⊥FD. Здесь поможет теорема о трех перпендикулярах. Е1К – это проекция FK на α, и Е1К⊥А1К, ведь диагонали квадрата пересекаются под прямым углом. Раз отрезок А1К перпендикулярен проекции, то он перпендикулярен и самой наклонной, то есть А1К⊥FK.
Осталось лишь вычислить длину А1К. Для этого по аналогии с предыдущими задачами используем прямоугольный∆А1Е1К, в котором ∠А1Е1К = 45°:
Отвлечемся от куба и рассмотрим другую задачу.
Задание. В ∆АВС вписана окружность. Через центр этой окружности (точку О) проведена прямая ОН, причем она перпендикулярна плоскости АВС. Верно ли, что точка Н находится на одинаковом расстоянии от прямых АВ, АС и ВС?
Решение. Пусть N, K и M – точки касания окружности и сторон АВ, АС и ВС соответственно. Тогда ОN, OK и OM– радиусы, а они должны быть перпендикулярны касательным, то есть
Заметим, что ОN, OK и OM – это также проекции прямых HN, HK и HM соответственно. Раз отрезки АВ, АС и ВС перпендикулярны этим проекциям, то они должны быть перпендикулярны и наклонным:
Это значит, что HN, HK и HM– это расстояния от H до сторон ∆АВС. Осталось показать, что они одинаковы. Это можно сделать с помощью ∆HON, ∆HOK и ∆HOM. Они все прямоугольные, причем катет OH– общий, а катеты ON, OM и OK одинаковы как радиусы одной окружности. Отсюда вытекает вывод, что эти треугольники равны, то есть одинаковы и их гипотенузы HN, HKи HM, ч. т. д.
Теперь снова вернемся к кубу, чтобы на практике научиться определять угол между прямой и плоскостью.
Задание. Найдите угол между ребром куба BD и гранью СDHG:
Решение. ВС – это перпендикуляр к грани СDHG, поэтому CD– проекция BD на грань СDHG. Тогда нам надо найти ∠BDC. Он составляет 45°, так как это угол между стороной и диагональю квадрата АВСD:
Ответ: 45°.
Задание. Вычислите угол между ребром CD и плоскостью BDHF:
Решение. Нам надо из С опустить перпендикуляр на BDHF. Несложно догадаться, что для этого надо на грани ABCD опустить перпендикуляр СК на диагональ BD:
Действительно, СK⊥BD. Надо найти ещё одну прямую в BDHF, перпендикулярную СК. И такой прямой может быть BF. Так как BF перпендикулярна всей грани АВСD, то она обязательно перпендикулярна и СК. Получаем, что СК⊥BF и CK⊥BD, и тогда СK⊥BDHF.
Если СK– перпендикуляр, то KD – это проекция СD. Тогда искомый нами угол – это ∠СDK. Он равен 45°, ведь BD – диагональ квадрата АВСD, а CD – его сторона.
Ответ: 45°
Задание. Чему равен угол между прямой BD и плоскостью ABGH:
Решение. На нижней грани АЕНD опустим на АН перпендикуляр DK:
Заметим, что ребро АВ перпендикулярно грани АЕНD, поэтому KD⊥АВ. Но также KD⊥AH (мы специально построили так KD). Тогда можно утверждать, что KD – это перпендикуляр ко всей плоскости АВGH.
В таком случае BK – это проекция BD на AB. Значит, нам необходимо вычислить ∠DBK. Его можно найти из прямоугольного ∆DBK, но сперва надо вычислить длины сторон KD и BD.
ВD найдем из прямоугольного ∆ABD:
Теперь мы можем найти ∠DBK, а точнее его синус, из ∆DBK:
По таблице синусов легко определить, что ∠DBK = 30°.
Ответ: 30°.
В ходе сегодняшнего урока мы узнали о перпендикуляре к плоскости. Перпендикуляры используются для определения расстояний в стереометрии, а также угла между прямой и плоскостью.
Общие сведения
Серединным перпендикуляром отрезка называют прямую, которая проходит под прямым углом через среднюю точку, т. е. середину отрезка. Для полного понимания материала следует остановиться на базовых элементах геометрии.
Точка — единица, при помощи которой строятся прямые, отрезки, лучи и фигуры. Прямая — простая фигура в форме бесконечной линии, состоящей из множества точек, лежащих в одной плоскости. Луч — базовая геометрическая фигура в виде бесконечной линии с одной стороны и точки-ограничителя — с другой. Иными словами, луч имеет начало, но не имеет конца. Отрезок — некоторая часть прямой (луча или другого отрезка), ограниченная двумя точками.
Кроме того, в геометрии серединный перпендикуляр встречается в треугольниках. Из определения можно сделать вывод, что им может быть прямая, отрезок и даже луч.
Аксиомы геометрии Евклида
Евклидовой геометрией называется наука о фигурах на плоскости, основанная на аксиомах и теоремах. Аксиома — базовое утверждение, не требующее доказательства. Оно используется для доказательства каких-либо теорем. Математики выделяют пять аксиом:
- Принадлежности.
- Порядка.
- Конгруэнтности.
- Параллельности прямых.
- Непрерывности.
Формулировка первой имеет такой вид: если существует в геометрическом пространстве плоскость, состоящая из множества точек, то через любые из них можно провести только одну прямую. Иными словами, можно взять произвольные две точки и провести через них одну прямую. Чтобы начертить еще одну прямую, следует взять две другие точки.
Следующее утверждение называется аксиомой порядка. Она гласит, что существует точка, которая лежит между двумя другими на прямой. Значение слова «конгруэнтность» не совсем понятно для новичка, однако нужно постепенно привыкать к терминологии. Оно обозначает «равенство». Третий геометрический факт формулируется таким образом: когда два отрезка или угла конгруэнтны третьему, тогда они равны между собой. Аксиома касается только отрезков и углов.
Чтобы убедиться в ее правильности, нужно разобрать следующий пример: длина первого отрезка составляет 10 см, второго — тоже, а третий равен первому. Необходимо доказать, что они равны между собой. Это делается очень просто:
- Вводятся обозначения: первый — MN, второй — OP и третий — RS.
- Устанавливаются значения по условию: MN = 10 см, ОР = 10 см, а RS = MN.
- Доказательство строится таким образом: MN = RS = 10 (см). Следовательно, отрезки равны, поскольку MN = ОР = RS = 10 (см).
Следует отметить, что данные действия оказались лишними — было потрачено время на понимание простой «истины». Параллельность прямых является также аксиомой и формулируется таким образом: если существует некоторая прямая на плоскости и точка, не лежащая на ней, то через последнюю можно провести только одну параллельную ей прямую.
И последняя аксиома называется Архимедовой. Ее формулировка имеет такой вид: для произвольных отрезков, лежащих на одной прямой, существует некоторая последовательность базовых элементов (точек), лежащих на одном и другом отрезках, таких, что заданные их части равны между собой. Иными словами, на одной прямой могут быть расположены равные между собой отрезки.
Информация о треугольниках
Треугольником является любая фигура, состоящая из трех вершин (точек) соединенных отрезками (сторонами), причем точки не лежат на одной прямой в одной плоскости. Они классифицируются по такому типу:
- Углам.
- Сторонам.
- Подобию.
В первом случае фигуры делятся на остроугольные, тупоугольные и прямоугольные. Остроугольным называется треугольник, у которого все углы острые (меньше 90 градусов). У тупоугольного — один угол тупой (> 90), а в прямоугольном — один из углов равен 90 градусам. Следует отметить, что сумма градусных мер углов любого треугольника эквивалентна 180.
Когда стороны у треугольника неравны между собой, тогда его называют разносторонним. При равенстве двух боковых сторон он считается равнобедренным, у которого третья сторона — основание. Если все стороны равны, то значит, фигура является равносторонней или правильной.
У треугольника есть еще и другие параметры. Их называют медианой, биссектрисой и высотой. Первый параметр является отрезком, который проводится из любой вершины на среднюю точку стороны. Высота — часть прямой, которая проводится из произвольной вершины и перпендикулярна противоположной стороне. Биссектрисой называется прямая, делящая угол на две равные части.
Медиана, высота и биссектриса, проведенные из вершины к основанию, совпадают и эквивалентны серединному перпендикуляру в треугольниках равнобедренного и равностороннего типов. Это очень важно при решении задач. Еще одним признаком, по которому выполняется классификация — подобность треугольников. У них могут быть равными только углы и некоторые стороны. Они отличаются между собой по определенному параметру, который называется коэффициентом подобия. Последний влияет только на размерность сторон. Говорят, что фигуры подобны по определенному признаку (их всего три).
Основные теоремы
Теорема — гипотеза (предположение), которую нужно доказать. Они применяются для оптимизации расчетов и вычисления отдельных параметров заданной фигуры. Кроме того, существуют следствия, полученные при доказательстве таких научных предположений. Эти аспекты упрощают и автоматизируют вычисления. Например, при вычислении площади треугольника нет необходимости выводить формулу, достаточно воспользоваться уже готовой.
Математики выделяют всего три теоремы о СП, которые могут значительно упростить расчеты. К ним можно отнести следующие:
- Прямая.
- Обратная.
- Пересечение в треугольнике.
Первая теорема называется прямой о СП. Она показывает, каким свойством обладают точки серединного перпендикуляра. Ее формулировка следующая: произвольная точка, которая взятая на перпендикуляре, удалена на равные расстояния от конечных точек отрезка, ограничивающих его на плоскости.
Для доказательства следует рассмотреть два прямоугольных треугольника с общей вершиной (искомая точка), общей стороной — катетом и равными катетами (по определению). Фигуры равны по одному из признаков равенства треугольников. Следовательно, их гипотенузы (стороны, равенство которых нужно доказать), равны между собой. Первая теорема доказана.
Следующая теорема — обратная: если точка удалена на равные расстояния от концов отрезка, то значит, она лежит на СП. В этом случае следует рассматривать равнобедренный треугольник, вершиной которого она является. Удалена точка на одинаковые расстояния от вершин основания по условию. Следовательно, этот факт доказывает, что полученный треугольник является равнобедренным, а в нем медиана, проведенная к основанию, является биссектрисой и высотой. Значит, она лежит на серединном перпендикуляре. Утверждение доказано.
Следующую теорему нет необходимости доказывать, поскольку известно, что в равнобедренном и равностороннем треугольниках высоты (медианы и биссектрисы) имеют общую точку пересечения. Они являются также и СП. Следовательно, это утверждение справедливо для них.
Важные свойства
Иногда трех теорем недостаточно для решения какой-либо сложной задачи. В этом случае необходимо знать еще и некоторые свойства СП:
- Центр описанной окружности вокруг треугольника соответствует точке их пересечения.
- Точка, взятая на СП, равноудалена от конечных точек отрезка и образует равнобедренный или равносторонний треугольник.
- В треугольниках равнобедренного и равностороннего типов им является высота, медиана и биссектриса.
В первом случае все зависит от типа треугольника. Если он является остроугольным, то центр лежит внутри него. Для тупоугольного — во внешнем пространстве, а в прямоугольном — на середине гипотенузы.
Следует отметить, что есть формулы для его расчета. Если предположить, что существует некоторый произвольный треугольник со сторонами а, b и с. Кроме того, для них выполняется условие a >= b >= c. Исходя из полученных данных, можно записать формулы перпендикуляров (Р), проведенных к определенной стороне:
- а: Pa = (2 * а * S) / (a^2 + b^2 — c^2).
- b: Pb = (2 * b * S) / (a^2 + b^2 — c^2).
- c: Pc = (2 * c * S) / (a^2 — b^2 + c^2).
Иными словами, Р является отношением удвоенного произведения стороны на площадь треугольника к сумме квадратов смежных сторон без квадрата противоположной. Кроме того, справедливы неравенства: Pa >= Pb и Pс >= Pb. Стороны — известные параметры, а вот площадь находится по некоторым соотношениям, которые выглядят следующим образом:
- Основание и высоту, проведенную к нему: S = (1/2) * a * Ha = (1/2) * b * Hb = (1/2) * c * Hc.
- Через радиус вписанной окружности: S = (1/2) * r * (a + b + c).
- Формулу Герона через полупериметр (р) и без него: S = [p * (p — a) * (p — b) * (p — c)]^(1/2) и S = 1/4 * [(a + b + c) * (b + c — a) * (а + c — b) * (a + b — c)]^(1/2).
В основном по таким соотношениям и нужно определить площадь. Полупериметр вычисляется таким образом: р = (а + b + с) / 2.
Бывают задачи, в которых необходимо просто подставить значения в формулу. Они называются простейшими. Однако встречаются и сложные. К ним относятся все виды без некоторых промежуточных параметров фигуры.
Пример решения задачи
В интернете попадаются примеры решения простых задач, а сложные приходится решать самостоятельно, просить помощи у кого-нибудь или покупать на сайтах готовое решение. Для примера нужно решить задание с такими данными:
- Прямоугольник, изображенный на рисунке 1 с диагональю равной d.
- Серединный перпендикуляр, проведенный к диагонали прямоугольника.
- Точка Е делит сторону на отрезки а и 2а.
Нужно найти: углы, указанные на рисунке, стороны и ОЕ. Кроме того, дополнительные данные можно узнать из чертежа, который используется для решения задачи (рис. 1). К любому заданию нужно делать графическое представление, поскольку оно позволяет избежать ошибок при вычислении
Рисунок 1. Чертеж для решения задачи.
Числовых значений нет, тогда необходимо решать в общем виде. Углы можно найти по такому алгоритму:
- Нужно рассмотреть треугольник ВДЕ. Он является равнобедренным, поскольку ОЕ — СП, а диагональ — отрезок. Следовательно, ВЕ = ДЕ = 2а.
- Необходимо найти угол ЕВО. Сделать это проблемно. Рекомендуется обратить внимание на треугольник АВЕ.
- При помощи тригонометрической функции синуса можно вычислить значение угла АBE: sin(АBE) = a/2а = 0,5. Следовательно, arcsin(0,5) = 30 (градусов).
- Угол СВЕ вычисляется следующим образом: 90 — 30 = 60 (градусов).
- Следовательно, искомый угол равен 30, поскольку 90 — 30 — 30 = 30.
- В равнобедренном треугольнике углы при основании равны между собой: ЕДО = ЕВО = 30 (градусов).
Для нахождения сторон нужно составить уравнение в общем виде, обозначив неизвестную величину АВ литерой «х». Рассмотрев прямоугольный треугольник АВЕ, по теореме Пифагора можно вычислить АВ: x = [4a^2 + a^2]^(1/2) = a * [5]^(1/2). Следовательно, АВ = a * [5]^(1/2) и ВС = 3а. ОЕ находится по формуле: ОЕ = (2 * 2 * а * S) / (8 * a^2 — d^2). Можно править соотношение таким образом через прямоугольный треугольник ДОЕ: ОЕ = [4 * a^2 — (d^2) / 4]^(1/2).
Таким образом, нахождение серединного перпендикуляра позволяет значительно уменьшить объемы вычислений. Однако для этого нужно знать не только основные теоремы, но и его свойства.
Свойства и признаки прямоугольника.
|
Заглавная страница КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
⇐ ПредыдущаяСтр 3 из 4Следующая ⇒ 1) Диагонали прямоугольника равны. 2) Если диагонали параллелограмма равны, то этот параллелограмм — прямоугольник. 21. Ромб. Ромбом называется четырехугольник, все стороны которого равны. Свойства и признаки ромба. 1) Диагонали ромба перпендикулярны. 2) Диагонали ромба делят его углы пополам. 3) Если диагонали параллелограмма перпендикулярны, то этот параллелограмм — ромб. 4) Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм — ромб. 22. Квадрат. Квадратом называется прямоугольник, все стороны которого равны. 23. Геометрическое место точек, равноудаленных от данной прямой — две параллельные прямые. 24. Теорема Фалеса. Обобщенная теорема Фалеса. Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки. 25. Средняя линия треугольника. Отрезок, соединяющий середины двух сторон треугольника называется средней линией треугольника. Теорема о средней линии треугольника. Средняя линия треугольника параллельна стороне треугольника и равна ее половине. 26. Свойство середин сторон четырехугольника. Середины сторон любого четырехугольника являются вершинами параллелограмма. 27. Теорема о медианах треугольника. Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2 : 1, считая от вершины. 28. а) Если медиана треугольника равна половине стороны, к которой она проведена, то треугольник прямоугольный. б) Медиана прямоугольного треугольника, проведенная из вершины прямого угла, равна половине гипотенузы. 29. Трапеция. Трапецией называется четырехугольник, у которого только две противоположные стороны (основания) параллельны. Средней линией трапеции называется отрезок, соединяющий середины непараллельных сторон (боковых сторон). Теорема о средней линии трапеции. Средняя линия трапеции параллельна основаниям и равна их полусумме. 30. Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований. 31. Трапеция называется равнобедренной, если ее боковые стороны равны. Свойства и признаки равнобедренной трапеции. 1) Углы при основании равнобедренной трапеции равны. 2) Диагонали равнобедренной трапеции равны. 3) Если углы при основании трапеции равны, то она равнобедренная. 4) Если диагонали трапеции равны, то она равнобедренная. 5) Проекция боковой стороны равнобедренной трапеции на основание равна полуразности оснований, а проекция диагонали — полусумме оснований. 32. Окружность. Окружностью называется геометрическое место точек плоскости, удаленных от данной точки, называемой центром окружности, на одно и то же положительное расстояние. Свойства окружности. 1) Диаметр, перпендикулярный хорде, делит ее пополам. 2) Диаметр, проходящий через середину хорды, не являющейся диаметром, перпендикулярен этой хорде. 3) Серединный перпендикуляр к хорде проходит через центр окружности. 4) Равные хорды удалены от центра окружности на равные расстояния. 5) Хорды окружности, удаленные от центра на равные расстояния, равны. 6) Окружность симметрична относительно любого своего диаметра. 7) Дуги окружности, заключенные между параллельными хордами, равны. 9) Диаметр есть наибольшая хорда окружности. 33. Замечательное свойство окружности. Геометрическое место точек M, из которых отрезок AB виден под прямым углом (∠AMB = 90º), есть окружность с диаметром AB без точек A и B. 34. Свойство серединных перпендикуляров к сторонам треугольника. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке, которая является центром окружности, описанной около треугольника. 35. Линия центров двух пересекающихся окружностей перпендикулярна их общей хорде. 36. Центр окружности, описанной около прямоугольного треугольника — середина гипотенузы. 37. Теорема о высотах треугольника. Прямые, содержащие высоты треугольника, пересекаются в одной точке. 38. Касательная к окружности. Прямая, имеющая с окружностью единственную общую точку, называется касательной к окружности. 1) Касательная перпендикулярна радиусу, проведенному в точку касания. 2) Если прямая l, проходящая через точку на окружности, перпендикулярна радиусу, проведенному в эту точку, то прямая l — касательная к окружности. 3) Если прямые, проходящие через точку M, касаются окружности в точках A и B, то MA = MB. 4) Центр окружности, вписанной в угол, лежит на биссектрисе этого угла. 5) Теорема о биссектрисах треугольника. Биссектрисы треугольника пересекаются в одной точке, которая является центром окружности, вписанной в треугольник. 39. Радиус окружности, вписанной в прямоугольный треугольник с катетами a, b и гипотенузой c, равен (a+b −c)/2. 40. Если M — точка касания со стороной AC окружности, вписанной в треугольник ABC, то AM = p −BC, где p — полупериметр треугольника. 41. Окружность касается стороны BC треугольника ABC и продолжений сторон AB и AC. Тогда расстояние от вершины A до точки касания окружности с прямой AB равно полупериметру треугольника ABC. 42. Окружность, вписанная в треугольник ABC, касается сторон AB, BC и AC соответственно в точках K, L и M. Если ∠BAC =, то ∠KLM =90º − /2. 43. Если в четырехугольник можно вписать окружность, то суммы его противоположных сторон равны. 44. Касающиеся окружности. Говорят, что две окружности касаются, если они имеют единственную общую точку (точка касания). 1) Точка касания двух окружностей лежит на их линии центров. 2) Окружности радиусов r и R с центрами O1 и O2 касаются внешним образом тогда и только тогда, когда R + r =O1O2. 3) Окружности радиусов r и R (r < R) с центрами O1 и O2 касаются внутренним образом тогда и только тогда, когда R −r =O1O2. 4) Окружности с центрами O1 и O2 касаются внешним образом в точке K. Некоторая прямая касается этих окружностей в различных точках A и B и пересекается с общей касательной, проходящей через точку K, в точке C. Тогда ∠AKB =90º и ∠O1CO2 =90º. ⇐ Предыдущая1234Следующая ⇒ Читайте также: Где возникла философия и почему? Относительная высота сжатой зоны бетона Сущность проекции Гаусса-Крюгера и использование ее в геодезии Тарифы на перевозку пассажиров |
|
Последнее изменение этой страницы: 2019-05-20; просмотров: 126; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Планиметрия. Страница 4
|
1.Параллелограмм. 3.Ромб. |
|||||||||||||||||||||||
|
1 2 3 4 5 6 7 8 9 10 11 12 |
|||||||||||||||||||||||
1.
|
|||||||||||||||||||||||
|
Параллелограмм — это геометрическая фигура, у которой диагонали пересекаются в точке, делящей их пополам, а противолежащие стороны параллельны. Теорема: если диагонали четырехугольника пересекаются и делятся этой точкой пересечения пополам, то такой четырехугольник называется параллелограммом. Доказательство. Пусть АВСD данный четырехугольник. Точка О — точка пересечения его диагоналей (рис.1). Тогда треугольники Δ АОD и Δ ВOC равны по двум сторонам и углу между ними. А следовательно, угол ODA равен углу CBO и угол OAD равен углу BCO. Таким образом, эти углы являются внутренними накрест лежащими для прямых AD и BC и секущей AC. А по признаку параллельности прямых, прямые AD и BC параллельны. |
Рис.1 Теорема. Параллелограмм. |
||||||||||||||||||||||
| 2.Свойство диагоналей параллелограмма | |||||||||||||||||||||||
|
Теорема. если четырехугольник является параллелограммом, то его диагонали делятся точкой пересечения пополам. Доказательство. Пусть дан параллелограмм АВСD. (Рис. 2) Тогда его стороны AD и BC равны и лежат на параллельных прямых а и b. Если мы проведем секущие с и d так, чтобы прямая с проходила через точку А и С, а прямая d проходила через точку B и D, то угол ОАD будет равен углу ОСВ, а угол ОDА будет равен углу ОВС, как внутренние накрест лежащие. |
Рис.2 Теорема. Свойство диагоналей параллелограмма. |
||||||||||||||||||||||
3.Ромб |
|||||||||||||||||||||||
|
Ромб — это геометрическая фигура, у которой все стороны равны. Теорема. диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов. Доказательство. |
Рис.3 Теорема. Свойство диагоналей ромба. |
||||||||||||||||||||||
Задача |
|||||||||||||||||||||||
|
В параллелограмме АВСD проведена биссектриса угла А, которая пересекает сторону ВС в точке Е. Необходимо найти отрезки ВЕ и ЕС, если АВ = 9 см, АD = 14 см (рис.4) Решение. |
Рис.4 Задача. |
||||||||||||||||||||||
4.Теорема Фалеса |
|||||||||||||||||||||||
|
Теорема: параллельные прямые, пересекающие стороны угла и отсекающие на одной его стороне равные отрезки, отсекают равные отрезки и на другой его стороне. Доказательство. Пусть дан угол и пересекающие его параллельные прямые (рис.5). Точки А1А2А3А4 и В1В2В3В4 — точки пересечения. Проведем прямую ОЕ. Тогда А1ЕОА3 — параллелограмм. И ОЕ = А1А3 Треугольники В1В2Е и ОВ2В3 равны по стороне (ОВ2 = ЕВ2) и прилегающим к ней углам. Из равенства треугольников следует, что В1В2 = В2В3. |
Рис.5 Теорема Фалеса. |
||||||||||||||||||||||
5.Средняя линия треугольника |
|||||||||||||||||||||||
|
Теорема. средняя линия треугольника, которая соединяет середины двух данных сторон, параллельна третьей его стороне и равна ее половине. Доказательство. |
Рис.5 Теорема. Средняя линия треугольника. |
||||||||||||||||||||||
6.Трапеция |
|||||||||||||||||||||||
|
Трапеция — это геометрическая фигура, у которой только две противолежащие стороны параллельны. Теорема. средняя линия трапеции параллельна двум своим основаниям и равна их полусумме. Доказательство. Пусть АВСD — трапеция.(Рис. 6). Проведем прямую от вершины В через середину стороны СD точку Н к основанию, т.е. достроим треугольник АВО. Тогда треугольники ВСН и DHO равны по сторонам СН и НD и прилегающим к ним углам. Следовательно отрезок АО равен сумме оснований АD и ВС. Рассмотрим треугольник АВО. ЕН это средняя линия треугольника, которая равна половине основания АО, т.е. полусумме оснований трапеции АD и ВС. |
Рис.6 Теорема. Средняя линия трапеции. |
||||||||||||||||||||||
7.
|
|||||||||||||||||||||||
|
Теорема. параллельные прямые, которые пересекают стороны угла, отсекают от его сторон пропорциональные отрезки. Доказательство. Пусть дан угол и пересекающие его параллельные прямые. Разобьем угол ВAС параллельными прямыми на n частей. Тогда АВ = ns, a AB1 = ms. Где s — отрезок некоторой длины. По теореме Фалеса эти прямые разбивают сторону AС также на равные части. Тогда: |
Рис.7 Теорема о пропорциональных отрезках. |
||||||||||||||||||||||
|
Допустим, что Отложим на луче АС отрезок АС2 Т.е. мы пришли к противоречию, так как изначально мы взяли отрезок АС2 = АС*АВ1/АВ. |
Рис.8 Теорема о пропорциональных отрезках. |
||||||||||||||||||||||
|
|||||||||||||||||||||||
Пример 1 |
|||||||||||||||||||||||
|
Через точку пересечения диагоналей параллелограмма проведена прямая. Докажите, что ее отрезок, заключенный между параллельными сторонами, делится этой точкой пополам. |
|||||||||||||||||||||||
|
Доказательство: Пусть ABCD данный параллелограмм. EF данный отрезок, проходящий через точку О пересечения диагоналей. Рассмотрим треугольники COF и AOE. Сторона АО треугольника АОЕ равна стороне ОС треугольника COF по свойству параллелограмма. Угол при вершине А треугольника АОЕ равен углу при вершине С треугольника COF, как внутренние накрест лежащие углы. Углы при вершине О у обоих треугольников равны как вертикальные. Отсюда можно сделать вывод, что треугольники АОЕ и COF равны по второму признаку равенства треугольников (по стороне и прилегающим к ней углам). Следовательно, отрезки OF и ОЕ равны. |
Рис. |
||||||||||||||||||||||
Пример 2 |
|||||||||||||||||||||||
|
Две стороны параллелограмма относятся как 3:4, а его периметр равен 2,8 м. Найдите стороны параллелограмма. (Рис.10) |
|||||||||||||||||||||||
|
Решение: Пусть ABCD данный параллелограмм. Обозначим сторону АВ как 3х, а сторону ВС как 4х. Тогда составим следующее соотношение: 14х = 2,8 Отсюда: х = 0,2 м. Следовательно, АВ = 3х = 0,6 м. ВС = 4х = 0,8 м. |
Рис.10 Задача. Две стороны параллелограмма… |
||||||||||||||||||||||
Пример 3 |
|||||||||||||||||||||||
|
В параллелограмме ABCD перпендикуляр, опущенный из вершины В на сторону AD, делит ее пополам. Найдите диагональ BD и стороны параллелограмма, если периметр параллелограмма равен 4 м, а периметр треугольника ABD равен 3 м. (Рис.11) |
|||||||||||||||||||||||
|
Решение: Так как перпендикуляр BE, опущенный на сторону AD, делит ее пополам, то треугольники ABE и BED равны по первому признаку равенства треугольников (по двум сторонам и углу между ними). Обозначим сторону АВ как х, а сторону AD — как 2y. Тогда можно составить следующие соотношения: PABCD = 2*(х + 2y) = 4, PABD = 2x +2y = 3 Следовательно, PABCD = 2х + 4y = 4, а 2х = 4 — 4y. Тогда подставим 4 — 4y во второе уравнение: АВ = BD = 1 м. AD = 1 м. |
Рис.11 Задача. В параллелограмме ABCD перпендикуляр… |
||||||||||||||||||||||
Пример 4 |
|||||||||||||||||||||||
|
В прямоугольный треугольник, каждый катет которого равен 8 см, вписан прямоугольник, имеющий с треугольником общий угол. |
|||||||||||||||||||||||
|
Решение: Пусть АВС данный треугольник. АВ = АС = 8 см. Тогда углы при вершинах В и С равны 45°. А следовательно, углы при вершине Е в треугольниках FEC и BDE также равны 45°. Если обозначить часть катета АF как х, то FC будет равно 8 — х. Отсюда следует, что FE = AD = 8-х, а BD = х. Теперь можно составить следующее соотношение: РADEF = 2*(х + 8 — х) = 16 см. Периметр прямоугольника ADEF равен 16 см. |
Рис.12 Задача. В прямоугольный треугольник… |
||||||||||||||||||||||
Пример 5 |
|||||||||||||||||||||||
|
Докажите, что если у параллелограмма диагонали перпендикулярны, то он является ромбом. |
|||||||||||||||||||||||
|
Доказательство: Пусть АВСD данный параллелограмм. По свойству параллелограмма, у него противоположные стороны параллельны и равны. Следовательно, стороны АВ и CD можно рассматривать как параллельные прямые, а диагональ BD — как секущую. Тогда в треугольниках АВО и DOC углы при вершинах B и D равны как внутренние накрест лежащие. Так же как и углы при вершинах А и С. Отсюда следует, что эти треугольники равны по второму признаку равенства треугольников (по стороне и прилегающим к ней углам). Сторона АВ = DC и внутренние накрест лежащие углы при них равны. Следовательно, АО = ОС, а ВО = OD. Теперь рассмотрим треугольники AOD и DOC. Они также равны, но по первому признаку равенства треугольников. Сторона АО = ОС, а сторона OD у них общая. Следовательно, можно сделать вывод, что сторона AD = DC = AB = BC, т.е. данный параллелограмм является ромбом. |
Рис.13 Задача. Докажите, что если у параллелограмма… |
||||||||||||||||||||||
|
1 2 3 4 5 6 7 8 9 10 11 12 |
|||||||||||||||||||||||
Содержание |
|||||||||||||||||||||||
| Страница 1 | Страница 7 | ||||||||||||||||||||||
1. Основные фигуры планиметрии. Основные фигуры планиметрии.2.Аксиомы планиметрии. 3.Смежные углы. 4.Вертикальные углы. 5.Перпендикулярные прямые. 6.Признаки равенства треугольников. |
1.Движение и его свойства. 2.Симметрия относительно точки. 3.Симметрия относительно прямой. 4.Параллельный перенос и его свойства. |
||||||||||||||||||||||
| Страница 2 | Страница 8 | ||||||||||||||||||||||
|
1.Параллельность прямых. 2.Признаки параллельности прямых. 3.Свойство углов при пересечении параллельных прямых. 4.Сумма углов треугольника. 5.  Единственность перпендикуляра к прямой. Единственность перпендикуляра к прямой.6.Высота, биссектриса и медиана треугольника. 7.Свойство медианы равнобедренного треугольника. |
1.Вектор и его абсолютная величина. 2.Сложение векторов. 3.Умножение вектора на число. 4.Разложение вектора по двум неколлинеарным векторам. 5.Скалярное произведение векторов. |
||||||||||||||||||||||
| Страница 3 | Страница 9 | ||||||||||||||||||||||
|
1.Окружность. 2.Окружность описанная около треугольника. 3.Окружность вписанная в треугольник. 4.Геометрическое место точек. |
1. Преобразование подобия и его свойства. Преобразование подобия и его свойства.2.Подобие фигур. Подобие треугольников по двум углам. 3.Подобие треугольников по двум пропорциональным сторонам и углу между ними. 4.Подобие треугольников по трем пропорциональным сторонам. 5.Подобие прямоугольных треугольников. |
||||||||||||||||||||||
| Страница 4 | Страница 10 | ||||||||||||||||||||||
|
1.Параллелограмм. 2.Свойства диагоналей параллелограмма. 3.Ромб. 4.Теорема Фалеса. 5.Средняя линия треугольника. 6.Трапеция. 7.Теорема о пропорциональных отрезках. |
1.Углы, вписанные в окружность. 2.Пропорциональность хорд и секущих окружности. 3.Теорема косинусов. 4.Теорема синусов. 5.Соотношение между углами и сторонами в треугольнике. |
||||||||||||||||||||||
| Страница 5 | Страница 11 | ||||||||||||||||||||||
|
1.Теорема Пифагора. 2.Египетский треугольник. 3.Соотношение между углами и сторонами в прямоугольном треугольнике. 4.Основные тригонометрические тождества. |
1.Многоугольники. Правильные многоугольники. 2.Радиус вписанной и описанной окружностей правильных многоугольников. 3.Подобие многоугольников. 4.Длина окружности. |
||||||||||||||||||||||
| Страница 6 | Страница 12 | ||||||||||||||||||||||
1. Декартова система координат. Декартова система координат.2.Расстояние между точками. 3.Уравнение окружности. 4.Уравнение прямой. 5.Координаты точки пересечения. |
1.Площадь прямоугольника. 2.Площадь параллелограмма. 3.Площадь треугольника. 4.Площадь круга. 5.Площадь подобных фигур. 6.Площадь трапеции. |
||||||||||||||||||||||
Доказать теорему если диагонали параллелограмма перпендик… -reshimne.ru
Новые вопросы
Ответы
ПустьABCD – данный параллелограмм, AC и BD – его диагонали и (AC) (BD). Пусть O – точка пересечения диагоналей параллелограмма. Треугольник ABC – равнобедренный с основанием AC. Действительно, так как диагонали параллелограмма в точке пересечения делятся пополам, то AO = OC, и тогда BO – медиана треугольника ABC, проведенная к стороне AC.
Похожие вопросы
Помогите решить эту работу. Очень срочно пожалуйста…
Один из углов, образовавшихся при пересечение двух прямых на 70 градуса больше другого….
Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите BC, если AB = 34…
Как будет: лучшая подруга.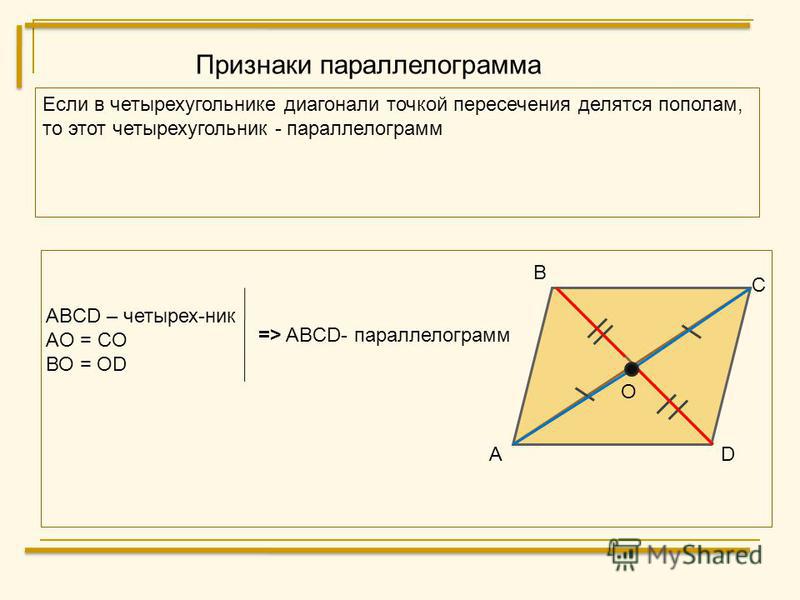
Улитка ползёт 5 см за 10 минут. За сколько минут она с такой скоростью проползёт всю длину вашего стола?…
Найти углы параллелограмма ABCD
Угол А 40 ,Угол С 25…
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Химия
Физика
Биология
Другие предметы
История
Обществознание
Окружающий мир
География
Українська мова
Українська література
Қазақ тiлi
Беларуская мова
Информатика
Экономика
Музыка
Право
Французский язык
Немецкий язык
МХК
ОБЖ
Психология
Анализ геометрических высказываний.
| 1 | Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части. | Смотреть видеоразбор >> |
| 2 | Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, перпендикулярна основанию. | Смотреть видеоразбор >> |
| 3 | Биссектриса треугольника делит пополам сторону, к которой проведена. | Смотреть видеоразбор >> |
| 4 | Биссектрисы треугольника пересекаются в центре его вписанной окружности. | Смотреть видеоразбор >> |
| 5 | В любой прямоугольник можно вписать окружность. | Смотреть видеоразбор >> |
| 6 | В любой ромб можно вписать окружность. | Смотреть видеоразбор >> |
| 7 | В любой треугольник можно вписать окружность. | Смотреть видеоразбор >> |
| 8 | В любой четырёхугольник можно вписать окружность. |
Смотреть видеоразбор >> |
| 9 | В любом параллелограмме диагонали точкой пересечения делятся пополам. | Смотреть видеоразбор >> |
| 10 | В любом прямоугольнике диагонали взаимно перпендикулярны. | Смотреть видеоразбор >> |
| 11 | В любом тупоугольном треугольнике есть острый угол. | Смотреть видеоразбор >> |
| 12 | В остроугольном треугольнике все углы острые. | Смотреть видеоразбор >> |
| 13 | В параллелограмме есть два равных угла. | Смотреть видеоразбор >> |
| 14 | В плоскости все точки, равноудалённые от заданной точки, лежат на одной окружности. | Смотреть видеоразбор >> |
| 15 | В плоскости для точки, лежащей вне круга, расстояние до центра круга больше его радиуса. | Смотреть видеоразбор >> |
| 16 | В прямоугольном треугольнике гипотенуза равна сумме катетов. |
Смотреть видеоразбор >> |
| 17 | В прямоугольном треугольнике квадрат гипотенузы равен разности квадратов катетов. | Смотреть видеоразбор >> |
| 18 | В треугольнике против большего угла лежит большая сторона. | Смотреть видеоразбор >> |
| 19 | В треугольнике против большей стороны лежит больший угол. | Смотреть видеоразбор >> |
| 20 | В тупоугольном треугольнике все углы тупые. | Смотреть видеоразбор >> |
| 21 | Вертикальные углы равны. | Смотреть видеоразбор >> |
| 22 | Внешний угол треугольника больше не смежного с ним внутреннего угла. | Смотреть видеоразбор >> |
| 23 | Внешний угол треугольника равен сумме его внутренних углов. | Смотреть видеоразбор >> |
| 24 | Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.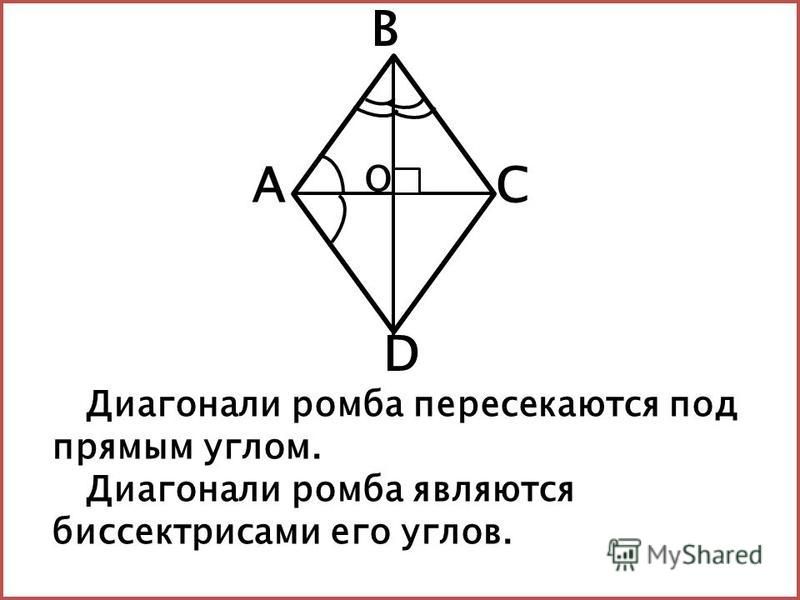 |
Смотреть видеоразбор >> |
| 25 | Вокруг любого параллелограмма можно описать окружность. | Смотреть видеоразбор >> |
| 26 | Вокруг любого треугольника можно описать окружность. | Смотреть видеоразбор >> |
| 27 | Вписанный угол, опирающийся на диаметр окружности, прямой. | Смотреть видеоразбор >> |
| 28 | Вписанный угол, опирающийся на диаметр окружности, прямой. | Смотреть видеоразбор >> |
| 29 | Все высоты равностороннего треугольника равны. | Смотреть видеоразбор >> |
| 30 | Все диаметры окружности равны между собой. | Смотреть видеоразбор >> |
| 31 | Все квадраты имеют равные площади. | Смотреть видеоразбор >> |
| 32 | Все прямоугольные треугольники подобны. | Смотреть видеоразбор >> |
| 33 | Все равнобедренные треугольники подобны. |
Смотреть видеоразбор >> |
| 34 | Все равносторонние треугольники подобны. | Смотреть видеоразбор >> |
| 35 | Все углы прямоугольника равны. | Смотреть видеоразбор >> |
| 36 | Все углы ромба равны. | Смотреть видеоразбор >> |
| 37 | Все хорды одной окружности равны между собой. | Смотреть видеоразбор >> |
| 38 | Все хорды одной окружности равны между собой. | Смотреть видеоразбор >> |
| 39 | Всякий равнобедренный треугольник является остроугольным. | Смотреть видеоразбор >> |
| 40 | Всякий равносторонний треугольник является остроугольным. | Смотреть видеоразбор >> |
| 41 | Всякий равносторонний треугольник является равнобедренным. | Смотреть видеоразбор >> |
| 42 | Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности.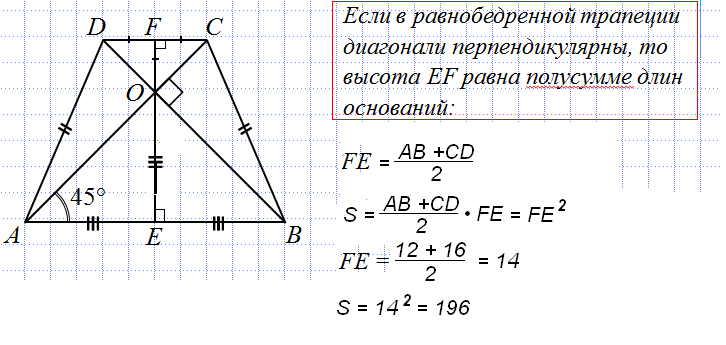 |
Смотреть видеоразбор >> |
| 43 | Две прямые, параллельные третьей прямой, перпендикулярны друг другу. | Смотреть видеоразбор >> |
| 44 | Две прямые, перпендикулярные третьей прямой, параллельны друг другу. | Смотреть видеоразбор >> |
| 45 | Две прямые, перпендикулярные третьей прямой, перпендикулярны друг другу. | Смотреть видеоразбор >> |
| 46 | Диагонали квадрата взаимно перпендикулярны. | Смотреть видеоразбор >> |
| 47 | Диагонали квадрата точкой пересечения делятся пополам. | Смотреть видеоразбор >> |
| 48 | Диагонали любого прямоугольника делят его на 4 равных треугольника. | Смотреть видеоразбор >> |
| 49 | Диагонали любого прямоугольника равны. | Смотреть видеоразбор >> |
| 50 | Диагонали параллелограмма равны. |
Смотреть видеоразбор >> |
| 51 | Диагонали прямоугольника равны. | Смотреть видеоразбор >> |
| 52 | Диагонали прямоугольной трапеции равны. | Смотреть видеоразбор >> |
| 53 | Диагонали равнобедренной трапеции равны. | Смотреть видеоразбор >> |
| 54 | Диагонали ромба перпендикулярны. | Смотреть видеоразбор >> |
| 55 | Диагонали ромба равны. | Смотреть видеоразбор >> |
| 56 | Диагонали ромба точкой пересечения делятся пополам. | Смотреть видеоразбор >> |
| 57 | Диагонали трапеции пересекаются и делятся точкой пересечения пополам. | Смотреть видеоразбор >> |
| 58 | Диагональ параллелограмма делит его на два равных треугольника. | Смотреть видеоразбор >> |
| 59 | Диагональ равнобедренной трапеции делит её на два равных треугольника. |
Смотреть видеоразбор >> |
| 60 | Диагональ трапеции делит её на два равных треугольника. | Смотреть видеоразбор >> |
| 61 | Для точки, лежащей внутри круга, расстояние до центра круга меньше его радиуса. | Смотреть видеоразбор >> |
| 62 | Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу. | Смотреть видеоразбор >> |
| 63 | Если в параллелограмме две смежные стороны равны, то такой параллелограмм является ромбом. | Смотреть видеоразбор >> |
| 64 | Если в параллелограмме две смежные стороны равны, то такой параллелограмм является ромбом. | Смотреть видеоразбор >> |
| 65 | Если в параллелограмме две соседние стороны равны, то такой параллелограмм является ромбом. | Смотреть видеоразбор >> |
| 66 | Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм – квадрат. |
Смотреть видеоразбор >> |
| 67 | Если в ромбе один из углов равен 90°, то такой ромб – квадрат. | Смотреть видеоразбор >> |
| 68 | Если в треугольнике есть один острый угол, то этот треугольник остроугольный. | Смотреть видеоразбор >> |
| 69 | Если в четырёхугольнике диагонали перпендикулярны, то этот четырёхугольник – ромб. | Смотреть видеоразбор >> |
| 70 | Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и углу другого прямоугольного треугольника, то такие треугольники равны. | Смотреть видеоразбор >> |
| 71 | Если два угла треугольника равны, то равны и противолежащие им стороны. | Смотреть видеоразбор >> |
| 72 | Если две различные прямые на плоскости перпендикулярны третьей прямой, то эти две прямые параллельны. | Смотреть видеоразбор >> |
| 73 | Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны. |
Смотреть видеоразбор >> |
| 74 | Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники подобны. | Смотреть видеоразбор >> |
| 75 | Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны. | Смотреть видеоразбор >> |
| 76 | Если две стороны треугольника равны, то равны и противолежащие им углы. | Смотреть видеоразбор >> |
| 77 | Если диагонали выпуклого четырёхугольника равны и перпендикулярны, то это квадрат. | Смотреть видеоразбор >> |
| 78 | Если диагонали параллелограмма перпендикулярны, то это ромб. | Смотреть видеоразбор >> |
| 79 | Если диагонали параллелограмма равны, то он является ромбом. | Смотреть видеоразбор >> |
| 80 | Если диагонали параллелограмма равны, то это квадрат. |
Смотреть видеоразбор >> |
| 81 | Если диагонали параллелограмма равны, то это прямоугольник. | Смотреть видеоразбор >> |
| 82 | Если диагонали параллелограмма равны, то это ромб. | Смотреть видеоразбор >> |
| 83 | Если один из углов треугольника прямой, то треугольник прямоугольный. | Смотреть видеоразбор >> |
| 84 | Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90°, то эти две прямые параллельны. | Смотреть видеоразбор >> |
| 85 | Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны, то эти прямые параллельны. | Смотреть видеоразбор >> |
| 86 | Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны. | Смотреть видеоразбор >> |
| 87 | Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны. |
Смотреть видеоразбор >> |
| 88 | Если точка лежит на биссектрисе угла, то она равноудалена от сторон этого угла. | Смотреть видеоразбор >> |
| 89 | Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то треугольники подобны. | Смотреть видеоразбор >> |
| 90 | Если три угла одного треугольника равны соответственно трём углам другого треугольника, то такие треугольники равны. | Смотреть видеоразбор >> |
| 91 | Если три угла одного треугольника равны трём углам другого треугольника, то такие треугольники подобны. | Смотреть видеоразбор >> |
| 92 | Если три угла одного треугольника соответственно равны трём углам другого треугольника, то такие треугольники подобны. | Смотреть видеоразбор >> |
| 93 | Если угол острый, то смежный с ним угол также является острым. |
Смотреть видеоразбор >> |
| 94 | Из двух хорд окружности больше та, середина которой находится дальше от центра окружности. | Смотреть видеоразбор >> |
| 95 | Каждая из биссектрис равнобедренного треугольника является его высотой. | Смотреть видеоразбор >> |
| 96 | Каждая из биссектрис равнобедренного треугольника является его медианой. | Смотреть видеоразбор >> |
| 97 | Касательная к окружности перпендикулярна радиусу, проведённому в точку касания. | Смотреть видеоразбор >> |
| 98 | Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон. | Смотреть видеоразбор >> |
| 99 | Квадрат является прямоугольником. | Смотреть видеоразбор >> |
| 100 | Косинус острого угла прямоугольного треугольника равен отношению гипотенузы к прилежащему к этому углу катету. |
Смотреть видеоразбор >> |
| 101 | Любая биссектриса равнобедренного треугольника является его медианой. | Смотреть видеоразбор >> |
| 102 | Любая высота равнобедренного треугольника является его биссектрисой. | Смотреть видеоразбор >> |
| 103 | Любая медиана равнобедренного треугольника является его биссектрисой. | Смотреть видеоразбор >> |
| 104 | Любой квадрат можно вписать в окружность. | Смотреть видеоразбор >> |
| 105 | Любой квадрат является прямоугольником. | Смотреть видеоразбор >> |
| 106 | Любой квадрат является ромбом. | Смотреть видеоразбор >> |
| 107 | Любой параллелограмм можно вписать в окружность. | Смотреть видеоразбор >> |
| 108 | Любой прямоугольник можно вписать в окружность. | Смотреть видеоразбор >> |
| 109 | Любые два диаметра окружности пересекаются. |
Смотреть видеоразбор >> |
| 110 | Любые два равносторонних треугольника подобны. | Смотреть видеоразбор >> |
| 111 | Медиана равнобедренного треугольника, проведённая из вершины угла, противолежащего основанию, делит этот угол пополам. | Смотреть видеоразбор >> |
| 112 | Медиана равнобедренного треугольника, проведённая к его основанию, является его высотой. | Смотреть видеоразбор >> |
| 113 | Медиана треугольника делит пополам угол, из которого проведена. | Смотреть видеоразбор >> |
| 114 | На плоскости существует единственная точка, равноудалённая от концов отрезка. | Смотреть видеоразбор >> |
| 115 | Не существует прямоугольника, диагонали которого взаимно перпендикулярны. | Смотреть видеоразбор >> |
| 116 | Один из двух смежных углов острый, а другой тупой. |
Смотреть видеоразбор >> |
| 117 | Один из углов треугольника всегда не превышает 60°. | Смотреть видеоразбор >> |
| 118 | Основания равнобедренной трапеции равны. | Смотреть видеоразбор >> |
| 119 | Отношение площадей подобных треугольников равно коэффициенту подобия. | Смотреть видеоразбор >> |
| 120 | Площадь квадрата равна произведению двух его смежных сторон. | Смотреть видеоразбор >> |
| 121 | Площадь квадрата равна произведению его диагоналей. | Смотреть видеоразбор >> |
| 122 | Площадь круга меньше квадрата длины его диаметра. | Смотреть видеоразбор >> |
| 123 | Площадь любого параллелограмма равна произведению длин его сторон. | Смотреть видеоразбор >> |
| 124 | Площадь параллелограмма равна половине произведения его диагоналей. |
Смотреть видеоразбор >> |
| 125 | Площадь прямоугольника равна произведению длин всех его сторон. | Смотреть видеоразбор >> |
| 126 | Площадь прямоугольника равна произведению длин его смежных сторон. | Смотреть видеоразбор >> |
| 127 | Площадь прямоугольного треугольника равна произведению длин его катетов. | Смотреть видеоразбор >> |
| 128 | Площадь ромба равна произведению двух его смежных сторон на синус угла между ними. | Смотреть видеоразбор >> |
| 129 | Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне. | Смотреть видеоразбор >> |
| 130 | Площадь трапеции равна произведению основания трапеции на высоту. | Смотреть видеоразбор >> |
| 131 | Площадь трапеции равна произведению средней линии на высоту. |
Смотреть видеоразбор >> |
| 132 | Площадь треугольника не превышает произведения двух его сторон. | Смотреть видеоразбор >> |
| 133 | Против большей стороны треугольника лежит больший угол. | Смотреть видеоразбор >> |
| 134 | Против большей стороны треугольника лежит меньший угол. | Смотреть видеоразбор >> |
| 135 | Против равных сторон треугольника лежат равные углы. | Смотреть видеоразбор >> |
| 136 | Ромб не является параллелограммом. | Смотреть видеоразбор >> |
| 137 | Серединные перпендикуляры к сторонам треугольника пересекаются в центре его описанной окружности. | Смотреть видеоразбор >> |
| 138 | Смежные углы равны. | Смотреть видеоразбор >> |
| 139 | Средняя линия трапеции параллельна её основаниям.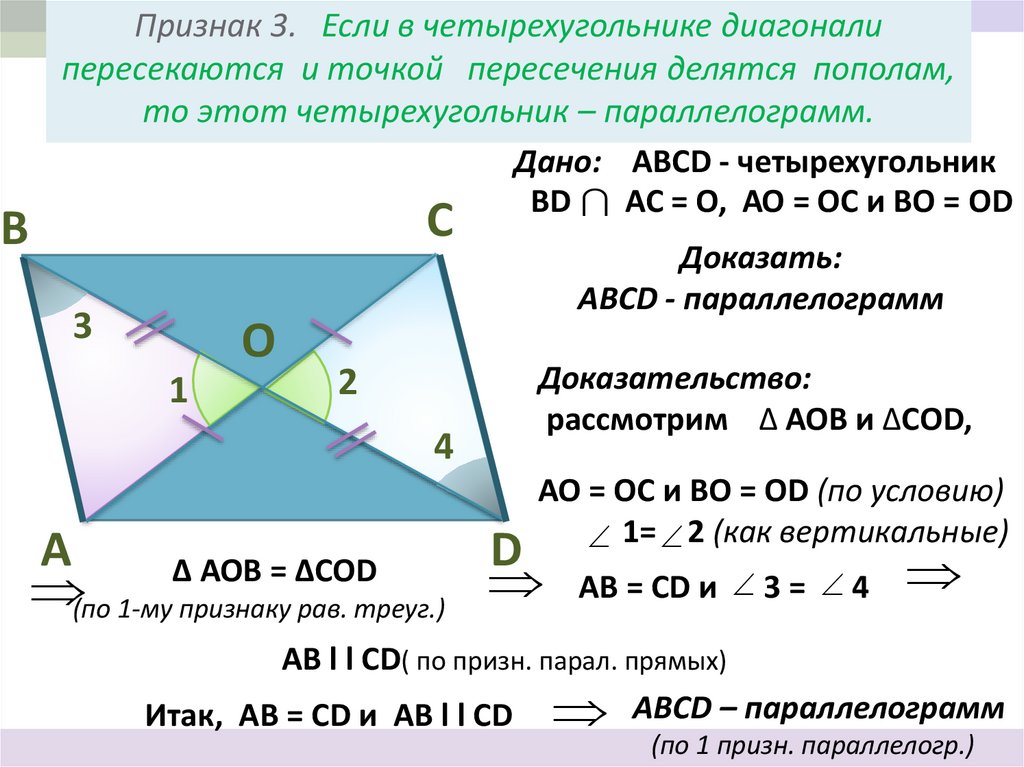 |
Смотреть видеоразбор >> |
| 140 | Средняя линия трапеции равна полусумме её оснований. | Смотреть видеоразбор >> |
| 141 | Средняя линия трапеции равна сумме её оснований. | Смотреть видеоразбор >> |
| 142 | Сумма квадратов диагоналей прямоугольника равна сумме квадратов всех его сторон. | Смотреть видеоразбор >> |
| 143 | Сумма острых углов прямоугольного треугольника равна 90°. | Смотреть видеоразбор >> |
| 144 | Сумма смежных углов равна 180°. | Смотреть видеоразбор >> |
| 145 | Сумма углов выпуклого четырёхугольника равна 360°. | Смотреть видеоразбор >> |
| 146 | Сумма углов любого треугольника равна 180°. | Смотреть видеоразбор >> |
| 147 | Сумма углов любого треугольника равна 360°. | Смотреть видеоразбор >> |
| 148 | Сумма углов остроугольного треугольника равна 180°. |
Смотреть видеоразбор >> |
| 149 | Сумма углов прямоугольного треугольника равна 90°. | Смотреть видеоразбор >> |
| 150 | Сумма углов равнобедренного треугольника равна 180°. | Смотреть видеоразбор >> |
| 151 | Сумма углов тупоугольного треугольника равна 180°. | Смотреть видеоразбор >> |
| 152 | Существует квадрат, который не является прямоугольником. | Смотреть видеоразбор >> |
| 153 | Существует квадрат, который не является ромбом. | Смотреть видеоразбор >> |
| 154 | Существует параллелограмм, который не является прямоугольником. | Смотреть видеоразбор >> |
| 155 | Существует прямоугольник, диагонали которого взаимно перпендикулярны. | Смотреть видеоразбор >> |
| 156 | Существует прямоугольник, который не является параллелограммом. |
Смотреть видеоразбор >> |
| 157 | Существует ромб, который не является квадратом. | Смотреть видеоразбор >> |
| 158 | Существуют три прямые, которые проходят через одну точку. | Смотреть видеоразбор >> |
| 159 | Тангенс любого острого угла меньше единицы. | Смотреть видеоразбор >> |
| 160 | Точка пересечения двух окружностей равноудалена от центров этих окружностей. | Смотреть видеоразбор >> |
| 161 | Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка. | Смотреть видеоразбор >> |
| 162 | Точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к этому отрезку. | Смотреть видеоразбор >> |
| 163 | Треугольник с углами 40°, 70°, 70° – равнобедренный. | Смотреть видеоразбор >> |
| 164 | Треугольник со сторонами 1, 2 и 4 существует. |
Смотреть видеоразбор >> |
| 165 | Треугольника со сторонами 1, 2 и 4 не существует. | Смотреть видеоразбор >> |
| 166 | У любой прямоугольной трапеции есть два равных угла. | Смотреть видеоразбор >> |
| 167 | У любой трапеции боковые стороны равны. | Смотреть видеоразбор >> |
| 168 | У любой трапеции боковые стороны равны. | Смотреть видеоразбор >> |
| 169 | У любой трапеции основания параллельны. | Смотреть видеоразбор >> |
| 170 | У равнобедренного треугольника есть ось симметрии. | Смотреть видеоразбор >> |
| 171 | У равнобедренного треугольника есть центр симметрии. | Смотреть видеоразбор >> |
| 172 | У равностороннего треугольника есть центр симметрии. | Смотреть видеоразбор >> |
| 173 | У равностороннего треугольника три оси симметрии. |
Смотреть видеоразбор >> |
| 174 | Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу. | Смотреть видеоразбор >> |
| 175 | Угол, опирающийся на диаметр окружности, прямой. | Смотреть видеоразбор >> |
| 176 | Центр вписанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника. | Смотреть видеоразбор >> |
| 177 | Центр описанной около треугольника окружности всегда лежит внутри этого треугольника. | Смотреть видеоразбор >> |
| 178 | Центр описанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника. | Смотреть видеоразбор >> |
| 179 | Центром вписанной в треугольник окружности является точка пересечения его биссектрис. | Смотреть видеоразбор >> |
| 180 | Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к сторонам треугольника. |
Смотреть видеоразбор >> |
| 181 | Центром описанной окружности треугольника является точка пересечения серединных перпендикуляров к его сторонам. | Смотреть видеоразбор >> |
| 182 | Центры вписанной и описанной окружностей равнобедренного треугольника совпадают. | Смотреть видеоразбор >> |
| 183 | Центры вписанной и описанной окружностей равностороннего треугольника совпадают. | Смотреть видеоразбор >> |
| 184 | Через две различные точки на плоскости проходит единственная прямая. | Смотреть видеоразбор >> |
| 185 | Через заданную точку плоскости можно провести единственную прямую. | Смотреть видеоразбор >> |
| 186 | Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой. | Смотреть видеоразбор >> |
| 187 | Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой.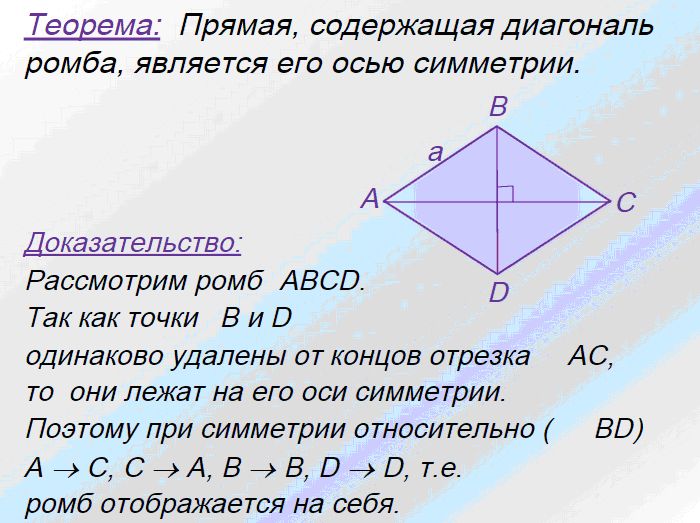 |
Смотреть видеоразбор >> |
Задания 19 ОГЭ по математике
Математика по полочкам: 26. Четырехугольники
МАТЕРИАЛ ДЛЯ ПОВТОРЕНИЯ
Параллелограмм
Четырехугольник, противоположные стороны которого попарно параллельны, называется параллелограммом.
Свойства параллелограмма
1. Противоположные стороны параллелограмма равны: AB=CD, AD=BC.
2. Противоположные углы параллелограмма равны: A=C, B=D.
3. Диагонали параллелограмма делятся точкой пересечения пополам AO=OC, BO=OD.
4. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон: d12+d22=2(a2+b2).
5. Каждая диагональ параллелограмма делит его на два равных треугольника.
6. Сумма внутренних углов параллелограмма 360°.
7. Сумма углов при двух соседних вершинах равна 180°.
Признаки параллелограмма
1. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
2. Если в четырехугольнике две противолежащие стороны равны и параллельны, то этот четырехугольник — параллелограмм.
3. Если у четырехугольника диагонали точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Площадь параллелограмма
1. Площадь параллелограмма равна произведению его основания на высоту: S=BH*AD.
2. Площадь параллелограмма равна произведению его смежных сторон на синус угла между ними: S=AB*AD*sin A.
Ромб
Параллелограмм у которого все стороны равны называется ромбом.
Свойства ромба
Так ромб является параллелограммом, то он имеет все свойства параллелограмма.
1.
2. Диагонали ромба являются биссектрисами его углов.
Признаки ромба
1. Если у параллелограмма диагонали взаимно перпендикулярны, то этот параллелограмм — ромб.
2. Если у параллелограмма одна из диагоналей лежит на биссектрисе, то этот параллелограмм — ромб.
Площадь ромба
1. Площадь ромба равна произведению его основания на высоту: S=СH*AВ.
2. Площадь ромба равна произведению квадрата его стороны на синус угла между сторонами: S=AB2*sin A.
3. Площадь ромба равна половине произведения его диагоналей: S=(d1*d2):2.
Прямоугольник
Параллелограмм, у которого все углы прямые называется прямоугольником.
Свойства прямоугольника
Так прямоугольник является параллелограммом, то он имеет все свойства параллелограмма.
1. Диагонали прямоугольника равны.
Признак прямоугольника
Если у параллелограмма диагонали равны, то этот параллелограмм — прямоугольник.
Площадь прямоугольника
Площадь прямоугольника равна произведению его смежных сторон: S = a*b.
Квадрат
Прямоугольник, у которого все стороны равны называется квадратом.
Свойства квадрата
Квадрату имеет все свойства параллелограмма, ромба и прямоугольника.
Площадь квадрата
Площадь квадрата равна квадрату его стороны: S=а2
Трапеция
Четырехугольник, две стороны которого параллельны, а две другие не параллельны называется трапецией.
Параллельные стороны трапеции называются ее основаниями (AD и ВС), а две другие — боковыми сторонами (АВ и СD).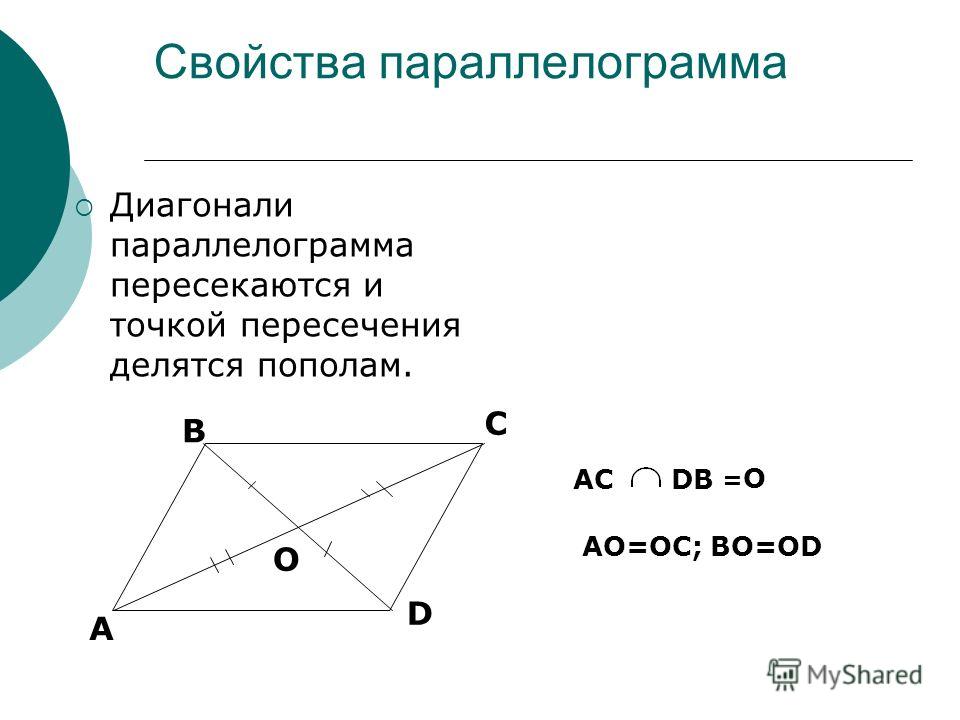
Трапеция, боковые стороны которой равны (АВ=СD), называется равнобедренной.
У равнобедренной трапеции углы при основании равны: A=D, B=C.
Диагонали равнобедренной трапеции равны: АС=BD.
Трапеция, у которой есть прямой угол называется прямоугольной.
Отрезок, соединяющий середины боковых сторон трапеции, называется средней линией трапеции.
Средняя линия трапеции параллельна основаниям трапеции равна их полусумме: MN=(a+b):2.
Средняя линия трапеции делит высоту трапеции на два равных отрезка.
Площадь трапеции
Площадь трапеции равна произведению полусуммы оснований на высоту: S =(a+b):2*h.
УПРАЖНЕНИЯ
1. а) Любой ли параллелограмм является ромбом:
1) Да; 2) Нет; 3) зависит от длин его сторон; 4) зависит от величин его углов.
б) Любой ли параллелограмм является прямоугольником:
1) Да; 2) Нет; 3) зависит от длин его сторон; 4) зависит от величин его углов.
Решение:
а)зависит от длин его сторон.
Ответ: 3.
2. Является ли четырехугольник параллелограммом:
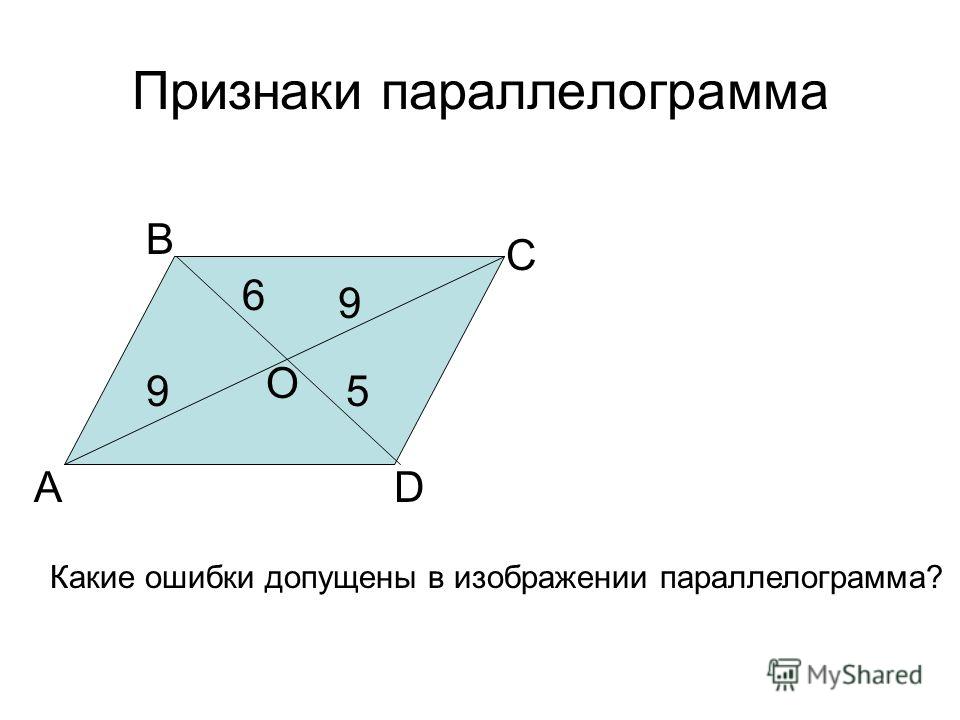
Решение:
а) В параллелограмме диагонали точкой пересечения делятся пополам, т.е. должно быть АО=ОС и ВО=OD, но ВО не равно OD ( 3 не равно 4).
Ответ: не является.
3. Найдите площадь закрашенной голубым цветом фигуры:
Решение:
а) Площадь прямоугольника ABCD равна 12*16=192.
Площадь квадрата KLMN равна 4*4=16.
Площадь фигуры, закрашенной голубым цветом равна 192-16=176.
Ответ: 176 кв.ед.
4. а) Сумма противоположных углов параллелограмма равна 160°. Найдите все углы параллелограмма.
б) Сумма противоположных углов параллелограмма равна 20°. Найдите все углы параллелограмма.
Решение:
а)
∠A+∠C=160°, т.к. противоположные углы параллелограмма равны, то ∠A=∠C=80°.
∠A+∠В =180° — по свойствам параллелограмма, тогда ∠В=180°-80°=100°.
Т.к. противоположные углы параллелограмма равны, то ∠В=∠D=100°.
Ответ: 80°, 100°, 80°, 100°.
5. а) Периметр ромба равен 24 см, а один из углов равен 120°. Найдите большую диагональ ромба.
б) Один из углов ромба равен 60°. Найдите периметр ромба, если его меньшая диагональ равна 4 см.
Решение:
а)
1) У ромба все стороны равны, тогда АВ=Р:4=24:4=6 см.
2) Пусть ∠A=120°, тогда большая диагональ ромба BD.
BD=BO+OD, т.к. диагонали ромба точкой пересечения делятся пополам.
3) ∠ВAО=120°: 2=60°, т.к. диагонали ромба являются биссектрисами его углов.
4) Рассмотри треугольник АВО, он прямоугольный, т.к. диагонали ромба пересекаются под прямым углом.
5) Найдем ВО:
ВО=АВ*sin ∠ВAО;
6. а) Докажите, что биссектрисы углов А и В параллелограмма ABCD взаимно перпендикулярны.
б) Докажите, что биссектрисы углов А и С параллелограмма ABCD параллельны.
Решение:
а)
Доказательство:
1) ∠DAК=∠ВКA как внутренние накрест лежащие при параллельных прямых ВС и AD и секущей АК.
2) ∠ВAК=∠КAD, т.к. АК — биссектриса угла BAD.
3) Следовательно, ∠ВAК=∠ВКA, тогда треугольник АВК — равнобедренный.
4) Биссектриса ВО в равнобедренном треугольнике АВК является и высотой, т.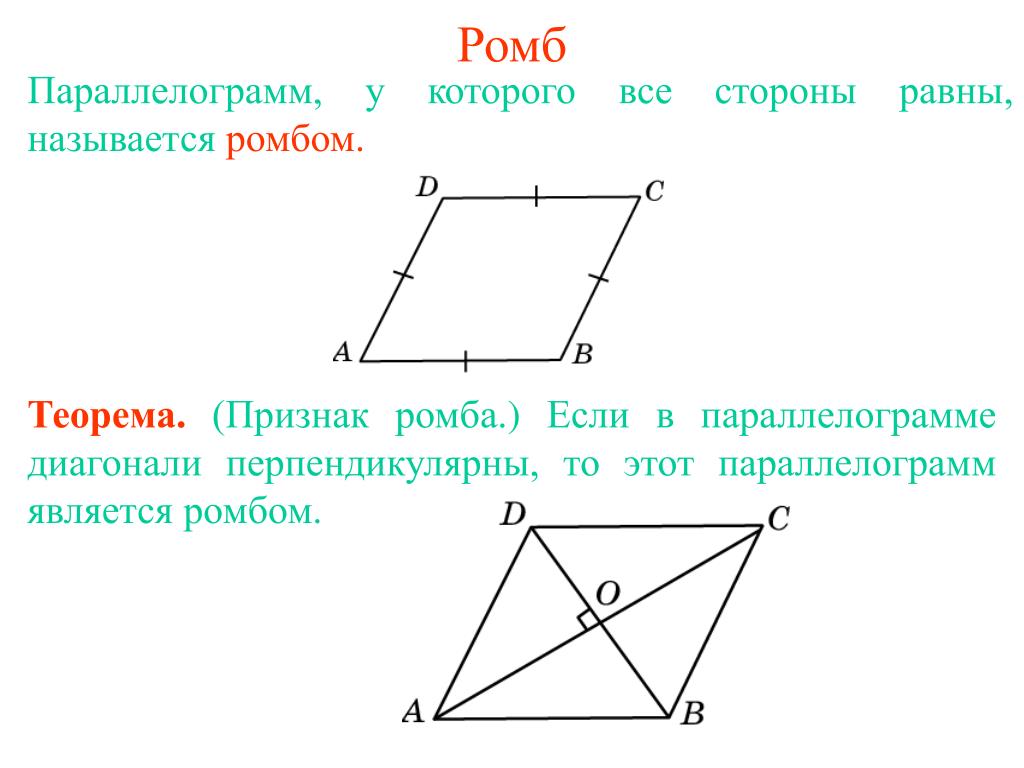
Что и требовалось доказать.
7. а) Диагональ DB параллелограмма ABCD перпендикулярна стороне АВ. сosA=3/5. Сторона AD=20 см. Найдите площадь параллелограмма.
б) Диагональ АС параллелограмма ABCD перпендикулярна стороне СD. sin CAD=2/3. Сторона AD=15 см. Найдите площадь параллелограмма.
Решение:
а)
Площадь параллелограмма может быть вычислена по формуле S=BD*AB.
1) Найдем АВ:
cos A=AB:AD, AB=AD*cos A=20*3/5=12 см.
2) Найдем BD:
По теореме Пифагора: BD2=AD2-AB2=400-144=256, BD=16 см.
3) Найдем площадь:
S=16*12=192 см2
Ответ: 192 см2
8.
б) Площадь равнобедренной трапеции равна 54 см2. Средняя линия трапеции равна 9 см. Диагонали перпендикулярны боковым сторонам. Найдите основания трапеции.
Решение:
а)
1) Треугольник ACD прямоугольный. Проведем к гипотенузе этого треугольника высоту СН.
HD=(AD-BC):2=(10-6):2=2 см, т.к. ABCD — равнобедренная трапеция.
2)CH2=АН*HD=10*2=20,
2)
9. а) АМ и DM — биссектрисы параллелограмма ABCD. М лежит на стороне ВС параллелограмма. Найти площадь параллелограмма, если АМ=4 см, DM=3 см.
б) BМ и CM — биссектрисы параллелограмма ABCD. М лежит на стороне AD параллелограмма.
Решение:
а)
1) Найдем угол AMD:
∠А+∠D=180° как углы при соседних вершинах. ∠МАD+∠ADM=(∠А+∠D):2=90°, т.к. АМ и DM — биссектрисы углов А и D.
Тогда ∠AMD=180-(∠МАD+∠ADM)=180-90=90°.
2) Треугольник AMD — прямоугольный, тогда по теореме Пифагора найдем AD:
AD2=AM2+MD2=16+9=25, AD=5 см.
3) Найдем высоту параллелограмма.
МН — высота в прямоугольном треугольнике, а также и высота параллелограмма.
SAMD = AM*MD:2=4*3:2=6 см.
SAMD = MH*AD:2; 6=MH*5:2; MH=2,4 см
4) Найдем площадь параллелограмма:
S=MH*AD=2,4*5=12 см2.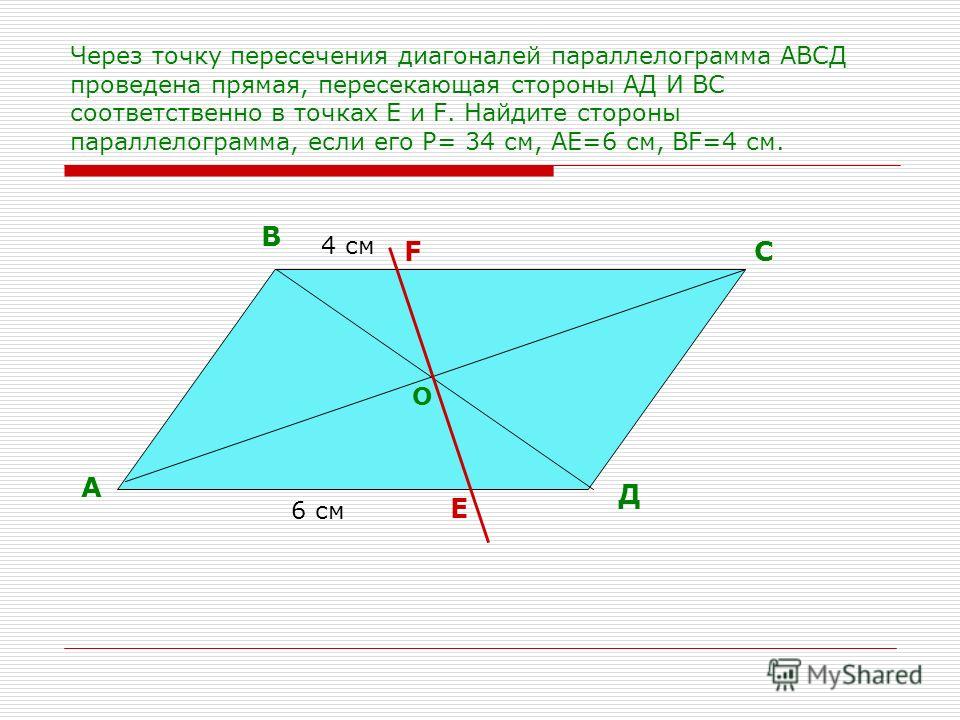
Ответ: 12 см2.
10. а) В трапеции ABCD проведена прямая, параллельная основаниям, которая пересекает боковые стороны трапеции в точках E и F. Найти площадь трапеции AEFD, если площадь трапеции EBCF равна 20 см2 и ВС=4 см, EF=8 см, AD=16 см.
б) В трапеции ABCD проведена прямая, параллельная основаниям, которая пересекает боковые стороны трапеции в точках M и N. Найти площадь трапеции MBCN, если площадь трапеции AMND равна 48 см2 и ВС=4 см, MN=6 см, AD=9 см.
Решение:
а)
1) Трапеции AEFD и EBCF подобны:
1. ∠1=∠2, ∠3=∠4 как соответственные углы при параллельных прямых EF и AD.
2. ∠5=∠6, ∠7=∠8 как соответственные углы при параллельных прямых EF и ВС.
2) Найдем коэффициент подобия:
k=EF:BC=8:4=2.
3) Площади подобных фигур относятся как коэффициент подобия в квадрате.
SAEFD = SEDCF *k2= 20*4=80
см2.
Ответ: 80 см2.
11. а) В параллелограмме ABCD отрезок CF пересекает диагональ BD в точке О (F лежит на стороне АD). Найдите площадь параллелограмма, если площади треугольников ODF и CDO раны 12 см2 и 20 см2 соответственно.
б) В параллелограмме ABCD отрезок ВF пересекает диагональ АС в точке О (F лежит на стороне АD). Найдите площадь параллелограмма, если площади треугольников OFA и OBA раны 12 см2 и 8 см2 соответственно.
Решение:
а)
1) Проведем к CF высоту DH.
Рассмотрим площади треугольников FOD и OCD:
SODF = DH*OE:2; 12= DH*OE:2; DH*OF=24. (1)
SCDO = DH*OC:2; 20 = DH*OC:2; DH*OC=40. (2)
Разделим выражение (2) на (1): OC:OF=40:24, OC:OF=5:3.
2) Треугольники BOC и FOD подобны по двум углам:
1. ∠FOD=∠BOC как вертикальные углы;
2. ∠СFD=∠FCB как внутренние накрест лежащие при параллельных прямых ВС и AD и секущей FC.
3) Площади подобных фигур относятся как коэффициент подобия в квадрате.
SBOC = SFOD*k2=12*(5/3)2=100/3 см2.
4) Найдем площадь треугольника BCD:
SBCD= SBCO + SOCD=100/3+20=53 1/3 см2.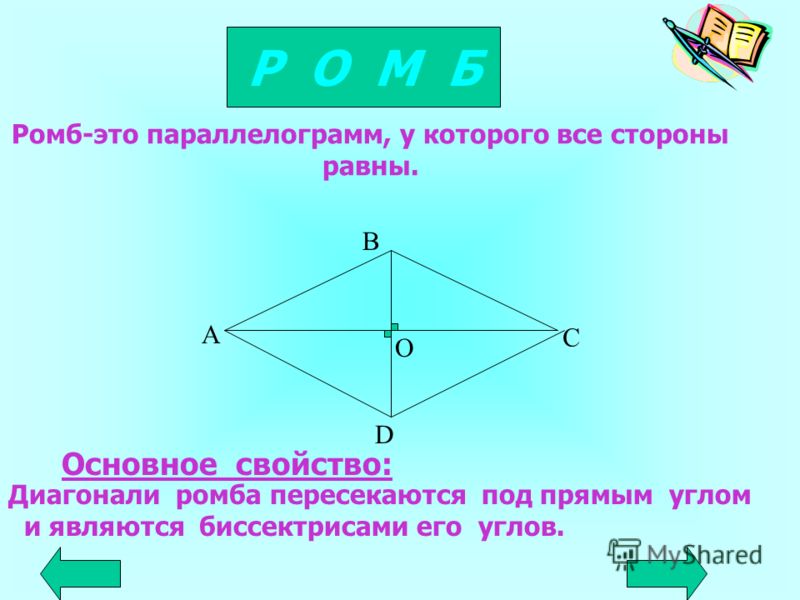
5) Найдем площадь параллелограмма:
SABCD=2*SBCD=106 2/3 см2.
Ответ: 106 2/3 см2.
12. а) Средняя линия трапеции равна 5 см, диагонали трапеции равны 14 см и 8 см. Найдите площадь трапеции.
б) Средняя линия трапеции равна 10 см, диагонали трапеции равны 14 см и 10 см. Найдите площадь трапеции.
Решение:
а)
Дано: ABCD — трапеция;
АС=14 см;
BD=8 см;
MN — средняя линия; MN=5 см.
Найти: S трапеции.
1) AD+BC=2*MN=2*5=10 см.
2) AB+CD=BC+AD=10 cм.
3) Проведем прямую СЕ параллельно прямой BD. E — точка пересечения прямых AD и CE.
DBCE — параллелограмм, т.к. две пары противолежащих сторон параллельны.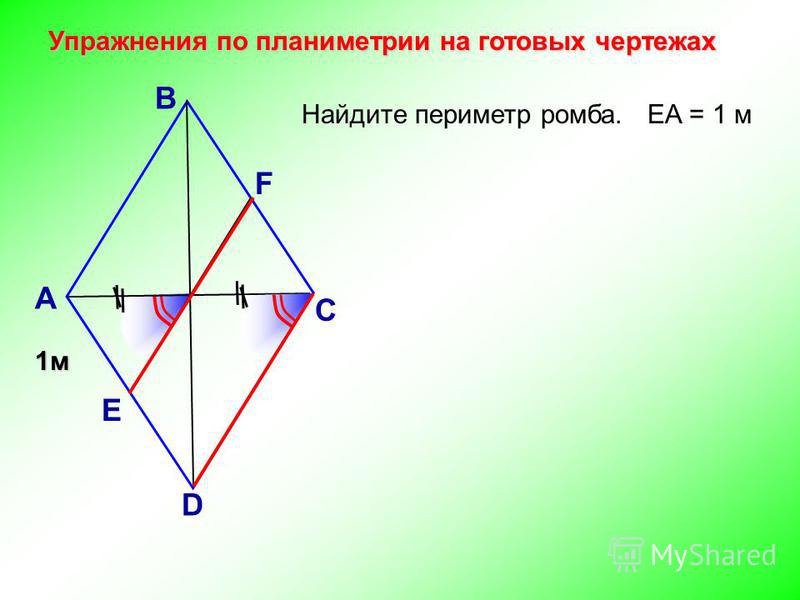
DE=BC и BD=CE=8 см, т.к. противолежащие стороны параллелограмма равны.
АЕ=AD+DE=AD+BC=10 см.
4) Найдем площадь треугольника АСЕ по формуле Герона:
р=(АС+СЕ+АЕ):2=(14+8+10):2=16 см.
5) Найдем площадь трапеции:
Треугольники ABC и CED имеют одинаковую площадь, т.к. их площади равны половине произведения высоты трапеции на равные стороны ВС и DE.
Тогда площадь трапеции равна площади треугольника АСЕ:
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Если в четырехугольнике противоположные стороны попарно равны, то это:
а) квадрат; б) ромб; в) трапеция; г) прямоугольник; д) параллелограмм.
2. Является ли четырехугольник параллелограммом, если одна пара его противоположных сторон равна, а другая параллельна?
3. В равнобедренной трапеции ABCD с основаниями AB и CD сумма углов А, В, С равна 340°.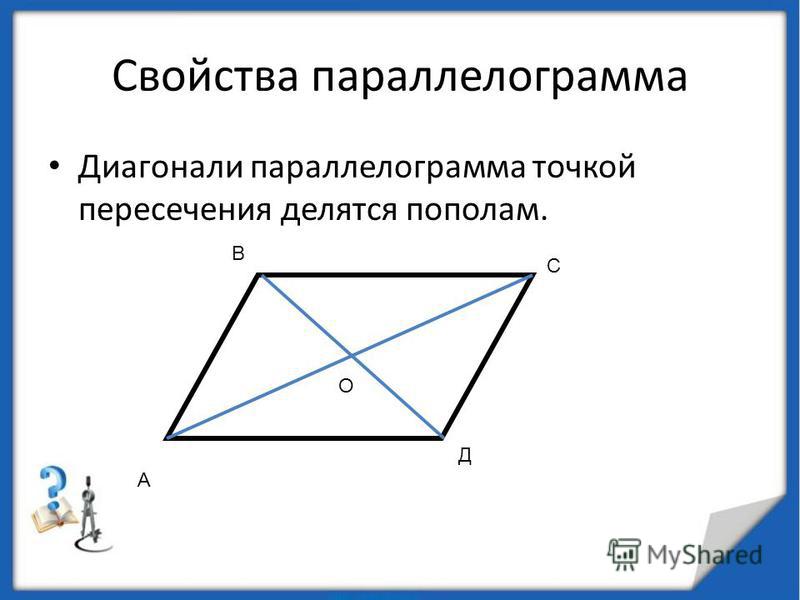
4. В параллелограмме ABCD угол А равен 60°, сторона ВС равна 10 см, высота СН проведена из вершины С к стороне AD и АН=14 см. Найдите периметр параллелограмма.
5. Диагонали ромба относятся как 2:5. Найдите площадь ромба, если его периметр равен 10 см.
6. Площадь прямоугольника равна 54 см2. Найдите площадь четырехугольника вершинами которого являются середины сторон данного прямоугольника.
7. В параллелограмме ABCD к сторонам BC и DC проведены высоты из точки А, угол между высотами равен 45° и одна из высот делит сторону DC на отрезки 3 см и 4 см, считая от вершины С. Найдите площадь параллелограмма.
8. Найдите среднюю линию трапеции, если ее диагонали взаимно перпендикулярны и равны 12 см и 16 см.
9. Может ли четырехугольник с противоположными наборами сторон a и b, c и d являться трапецией, если да, то найти ее площадь:
а) a=5 см, b=4 см, c=6 см, d=3 см; б) a= 3 см, b=4 см, c=5 см, d=3 см.
10.
ПРОВЕРЬТЕ СЕБЯ
ЕГЭ — математика (база): Трапеция
Четырёхугольник
Параллелограмм.
Параллелограммом называется четырёхугольник, противоположные стороны которого попарно параллельны.
Свойства и признаки параллелограмма
1. Диагональ разбивает параллелограмм на два равных треугольника.
2. Противоположные стороны параллелограмма попарно равны.
3. Противоположные углы параллелограмма попарно равны.
4. Диагонали параллелограмма пересекаются и делятся точкой пересечения пополам.
5. Если противоположные стороны четырёхугольника попарно равны, то этот четырёхугольник — параллелограмм.
6. Если две противоположные стороны четырёхугольника равны и параллельны, то этот четырёхугольник — параллелограмм.
7. Если диагонали четырёхугольника делятся точкой пересечения пополам, то этот четырёхугольник — параллелограмм.
Свойство середин сторон четырёхугольника. Середины сторон любого четырёхугольника являются вершинами параллелограмма, площадь которого равна половине площади четырёхугольника.
Прямоугольник. Прямоугольником называется параллелограмм с прямым углом.
Свойства и признаки прямоугольника
1. Диагонали прямоугольника равны.
2. Если диагонали параллелограмма равны, то этот параллелограмм — прямоугольник
Квадрат. Квадратом называется прямоугольник, все стороны которого равны.
Формулы площади четырёхугольника
1. Площадь параллелограмма равна произведению основания на высоту
2. Площадь параллелограмма равна произведению его соседних сторон на синус угла между ними.
3. Площадь прямоугольника равна произведению двух его соседних сторон.
Основные формулы
Далее S — площадь фигуры, P — периметр, p — полупериметр.
| Чертежи | Обозначения | Формулы |
| a, b, c, d — стороны; D1, D2 — диагонали; γ — угол между диагоналями; h2, h3 — длины перпендикуляров, опущенных на диагональ D1; α, β — два противолежащих угла четырёхугольника. |
||
| a, b — стороны; h — расстояние между сторонами b; α — угол параллелограмма; D1, D2 — диагонали; γ — угол между диагоналями |
Площадь четырёхугольника
Площадь прямоугольника равна произведению его смежных сторон:
S = ab.
На рисунке 156 приведены чертежи некоторых прямоугольников, у которых показаны смежные стороны a и b
Ромб
Квадрат. Квадратом называется прямоугольник, все стороны которого равны.
Свойства и признаки ромба
1. Диагонали ромба перпендикулярны.
2. Диагонали ромба делят его углы пополам
3.
4. Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм — ромб.
Площадь ромба равна половине произведения его диагоналей
Основные формулы
Далее S — площадь фигуры, P — периметр, p — полупериметр.
| Чертежи | Обозначения | Формулы |
| a, b, c, d — стороны; D1, D2 — диагонали; γ — угол между диагоналями; h2, h3 — длины перпендикуляров, опущенных на диагональ D1; α, β — два противолежащих угла четырёхугольника. |
||
| a — сторона; α — угол ромба; D1, D2 — диагонали. |
Трапеция
Трапецией называется четырёхугольник, у которого только две противоположные стороны (основания) параллельны. Средней линией трапеции называется отрезок, соединяющий середины непараллельных сторон (боковых сторон).
1. Теорема о средней линии трапеции. Средняя линия трапеции параллельна основаниям и равна их полусумме.
2. Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований.
Замечательное свойство трапеции. Точка пересечения диагоналей трапеции, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой.
Равнобедренная трапеция. Трапеция называется равнобедренной, если её боковые стороны равны.
Свойства и признаки равнобедренной трапеции
1. Углы при основании равнобедренной трапеции равны.
2. Диагонали равнобедренной трапеции равны
3. Если углы при основании трапеции равны, то она равнобедренная.
4. Если диагонали трапеции равны, то она равнобедренная
5. Проекция боковой стороны равнобедренной трапеции на основание равна полуразности оснований, а проекция диагонали — полусумме оснований.
Основные формулы
Далее S — площадь фигуры, P — периметр, p — полупериметр.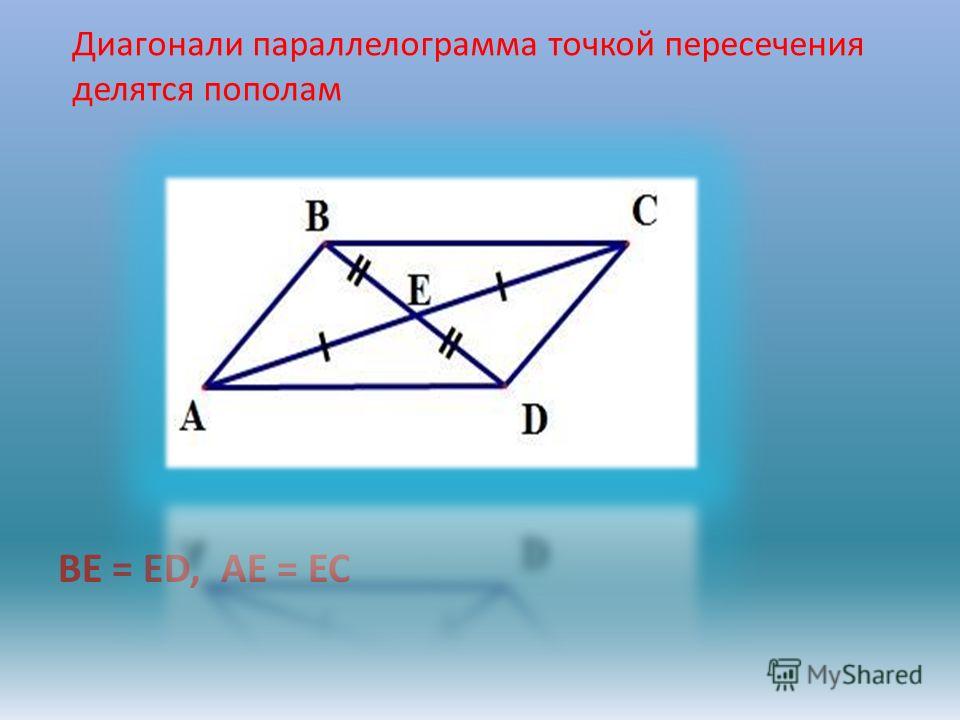
| Чертежи | Обозначения | Формулы |
| a, b, c, d — стороны; D1, D2 — диагонали; γ — угол между диагоналями; h2, h3 — длины перпендикуляров, опущенных на диагональ D1; α, β — два противолежащих угла четырёхугольника. |
||
| a, b — основания; c, d — боковые стороны; D1, D2 — диагонали; α — угол между диагоналями; m — средняя линия; h — высота |
Площадь трапеции равна половине произведения суммы оснований (a + b) на высоту (h):
На рисунке 168 приведены чертежи некоторых трапеций, у каждой из которых показаны основания a и b и высота h.
Площадь четырёхугольника равна половине произведения его диагоналей на синус угла между ними.
Основные формулы
Далее S — площадь фигуры, P — периметр, p — полупериметр.
| Чертежи | Обозначения | Формулы |
| a, b, c, d — стороны; D1, D2 — диагонали; γ — угол между диагоналями; h2, h3 — длины перпендикуляров, опущенных на диагональ D1; α, β — два противолежащих угла четырёхугольника.  |
||
| n — число сторон; a — сторона; R — радиус описанной окружности; r — радиус вписанной окружности; α = 180° − 2γ — угол многоугольника |
Когда параллелограмм является ромбом?
Я думаю о параллелограмме, диагонали которого перпендикулярны. Назовите этот параллелограмм.
Если вы догадались, что это квадрат, то вы плохо читали заголовок этого раздела. Это ромб! Хорошая вещь в работе с параллелограммами заключается в том, что диагонали создают множество треугольников, просто умоляющих, чтобы их конгруэнтность была доказана. На рис. 16.6 диагонали параллелограмма ABCD перпендикулярны. Конгруэнтные треугольники пытаются общаться с вами. Слушайте внимательно.
Рисунок 16.6 Параллелограмм ABCD с ¯AC ¯BD.
- Теорема 16.6 : Если диагонали параллелограмма перпендикулярны, то параллелограмм является ромбом.
Давайте сразу перейдем к плану игры.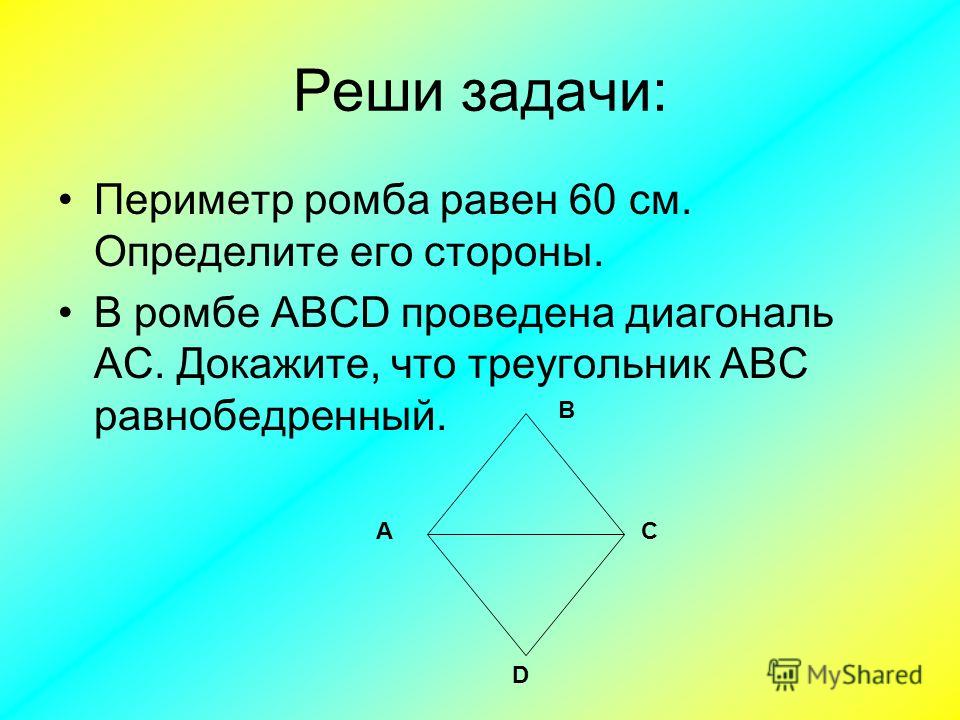
5 0029
| Statements | Reasons | |||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1. | Parallelogram ABCD has ¯AC ¯BD | Given | ||||||||||||||||||||||||||||||||||||||||||||
| 2. | AMB and CMB are right | Definition of | ||||||||||||||||||||||||||||||||||||||||||||
| 3 | mAMB = 90° и mCMB = 90° | Определение прямого угла | ||||||||||||||||||||||||||||||||||||||||||||
| 4. | AMB ~= CMB | Определение ~= | ¯AM ~= ¯MC | Theorem 15.6 | ||||||||||||||||||||||||||||||||||||||||||
| 6. | ¯BM ~= ¯BM | Reflexive property of ~= | ||||||||||||||||||||||||||||||||||||||||||||
7. |
AMB ~= CMB | SAS Postulate | ||||||||||||||||||||||||||||||||||||||||||||
| 8. | ¯ab ~ = ¯BC | CPOCTAC | ||||||||||||||||||||||||||||||||||||||||||||
| 9. | Parallelogram ABCD — Rhombus | . Предположим, у вас есть прямоугольник ABCD. Найдите середины каждой стороны прямоугольника и последовательно соедините их, чтобы получился четырехугольник MNOP, как показано на рис. 16.7. Какой четырехугольник получился?
Рисунок 16.7 Прямоугольник ABCD, середины каждой стороны которого последовательно соединены вместе, образуя четырехугольник MNOP. Судя по картинке, это похоже на параллелограмм. Вы должны быть осторожны, потому что ooks может быть обманчивым. Также похоже, что диагонали вновь созданного четырехугольника перпендикулярны. Если рисунок точен, у вас может возникнуть соблазн заключить, что четырехугольник является ромбом. Давайте докажем это.
Для этого нужен серьезный план игры. Поскольку M, N, O и P являются серединами ¯AB, ¯BC, ¯CD и ¯AD, вы знаете, что ¯BN ~= ¯NC ~= ¯AP ~= ¯PD и ¯AM ~= ¯MB ~= ¯OD ~= ¯CO. Поскольку вы имеете дело с прямоугольником, вы знаете, что mA = 90°, mB = 90°, mC = 90° и mD = 90°. Итак, согласно постулату SAS, PAM ~= NBM ~= PDO ~= NCO. Применяя принцип CPOCTAC ¯MN ~= ¯MP ~= ¯PO ~= ¯NO. Значит противоположные стороны равны и четырехугольник MNOP является параллелограммом. Кроме того, смежные стороны равны, поэтому параллелограмм MNOP является ромбом.
Выдержки из Полное руководство идиота по геометрии © 2004 Дениз Сечеи, доктор философии. Чтобы заказать эту книгу непосредственно у издателя, посетите веб-сайт Penguin USA или позвоните по телефону 1-800-253-6476. Вы также можете приобрести эту книгу на Amazon.com и в Barnes & Noble.
РомбГорячая математика
А
Формула для
А
куда
Область
|
| 1. | Каковы свойства параллелограмма? |
| 2. | Свойства диагоналей параллелограмма |
| 3. | Теоремы о свойствах параллелограмма |
| 4. | Часто задаваемые вопросы о свойствах параллелограмма |
Каковы свойства параллелограмма?
Параллелограмм — это тип четырехугольника, в котором противоположные стороны параллельны и равны. В параллелограмме при вершинах четыре угла. Понимание свойств параллелограмма помогает легко связать его углы и стороны. Кроме того, свойства полезны для вычислений в задачах, касающихся сторон и углов параллелограмма.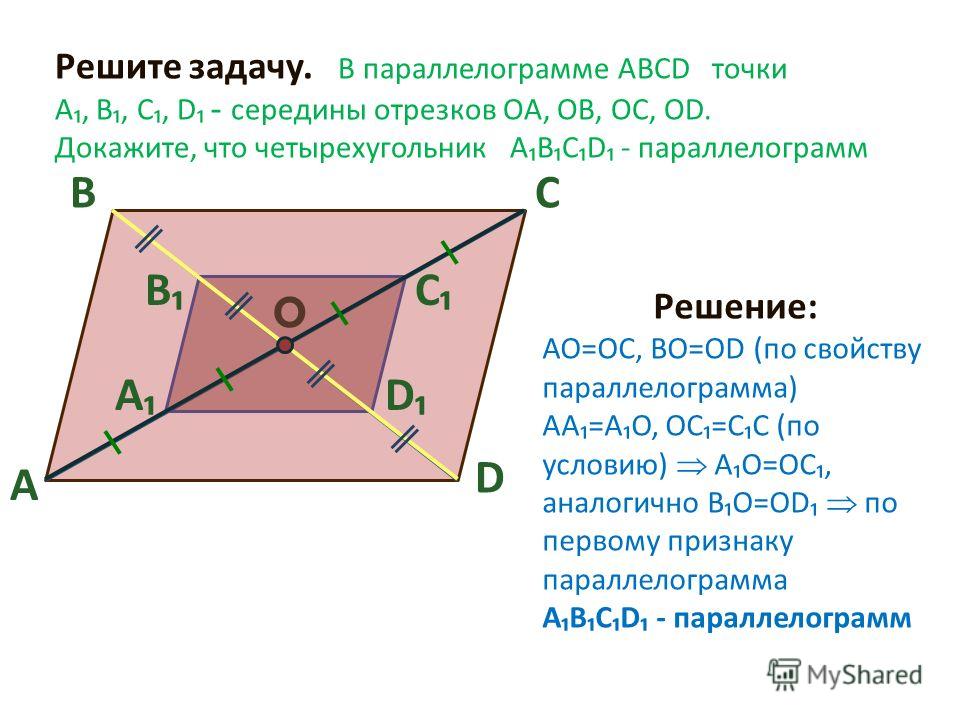
Четыре важных свойства углов и сторон параллелограмма таковы:
- Противоположные стороны параллелограмма равны и параллельны друг другу.
- Противолежащие углы равны, т. е. ∠A = ∠C и ∠B = ∠D.
- Все углы параллелограмма в сумме дают 360°, то есть ∠A + ∠B + ∠C + ∠D = 360°.
- Последовательные углы параллелограмма являются дополнительными, т. е.
∠А + ∠В = 180°
∠В + ∠С = 180°
∠С + ∠D = 180°
∠D + ∠А = 180°
Все вышеперечисленные свойства справедливы для всех типов параллелограммов, но теперь давайте также узнаем об индивидуальных свойствах некоторых специальных параллелограммов. Три разных параллелограмма — квадрат, прямоугольник и ромб, которые отличаются друг от друга из-за своих свойств, но все они подпадают под категорию параллелограммов.
Свойства квадрата:
- Все четыре стороны квадрата равны.
- Все четыре угла равны и по 90 градусов каждый.
- Диагонали квадрата делят его углы пополам.
- Обе диагонали имеют одинаковую длину.
- Противоположные стороны равны и параллельны друг другу.
Свойства прямоугольника:
- Противоположные стороны прямоугольника равны и параллельны.
- Все четыре угла равны и равны 90 градусов каждый.
- Обе диагонали имеют одинаковую длину.
Свойства ромба:
- Все стороны равны по длине.
- Диагонали делят друг друга пополам под углом 90 градусов.
- Сумма любых двух смежных внутренних углов равна 180 градусов.
- Противоположные стороны равны и параллельны друг другу.
Теперь давайте расширим наши знания, изучив свойства диагоналей параллелограммов в следующем разделе.
Свойства диагоналей параллелограмма
Сначала вспомним значение диагонали. Диагонали – это отрезки, соединяющие противоположные вершины.
- Диагонали параллелограмма делят друг друга пополам, т. е. OB = OD и OA = OC.
- Каждая диагональ делит параллелограмм на два конгруэнтных треугольника, т. е. ΔCDA ≅ ΔABC и ΔBAD ≅ ΔDCB.
- Закон параллелограмма: Сумма квадратов сторон равна сумме квадратов диагоналей, т. е. AB 2 + BC 2 + CD 2 + DA 2 = AC 2 + БД 2 .
Теоремы о свойствах параллелограмма
Теоремы о свойствах параллелограмма помогают определить правила решения задач на параллелограммы. Свойства, относящиеся к сторонам и углам параллелограмма, легко понять и применить для решения различных задач. Кроме того, эти теоремы также поддерживают понимание концепций других четырехугольников. Ниже приведены четыре важные теоремы, относящиеся к свойствам параллелограмма:
- Противоположные стороны параллелограмма равны
- Противоположные углы параллелограмма равны
- Диагонали параллелограмма делят друг друга пополам
- Если одна пара противоположных сторон равна и параллельна в четырехугольнике, то это параллелограмм
Теорема 1.
Доказательство:
Дано: ABCD — параллелограмм.
Доказать: Противоположные стороны равны, AB = CD и BC = AD.
В параллелограмме ABCD сравните треугольники ABC и CDA. В этих треугольниках:
- AC = CA (общая сторона)
- ∠BAC = ∠DCA (альтернативные внутренние углы)
- ∠BCA = ∠DAC (альтернативные внутренние углы)
Следовательно, по критерию ASA оба треугольника конгруэнтны и соответствующие стороны равны. Следовательно, мы имеем AB = CD и BC = AD.
Обратное к теореме 1: если в четырехугольнике противоположные стороны равны, то это параллелограмм.
Доказательство:
Дано: В четырехугольнике ABCD противоположные стороны равны, AB = CD и BC = AD.
Доказать: ABCD — параллелограмм.
В четырехугольнике ABCD дано, что AB = CD и AD = BC.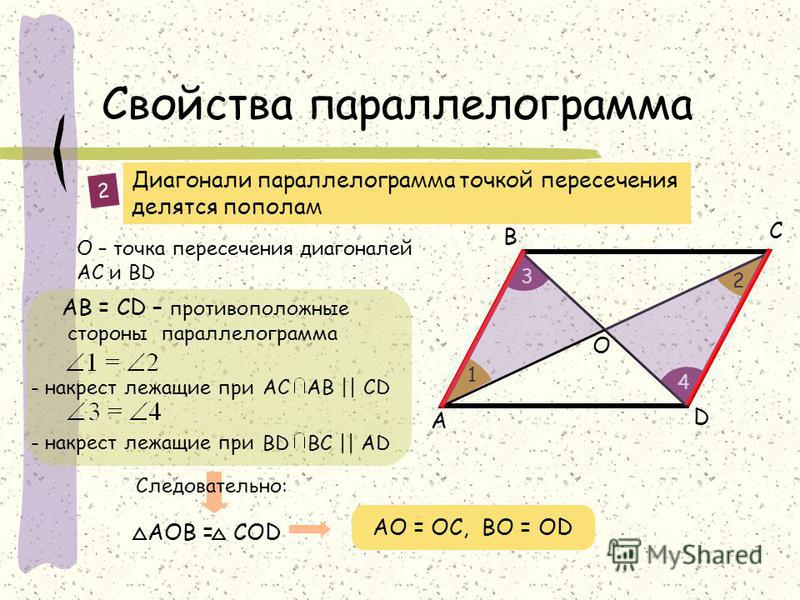
- AC = AC (общие стороны)
- AB = CD (поскольку внутренние углы равны)
- г. н.э. = до н.э. (дано).
Таким образом, по критерию SSS оба треугольника равны и соответствующие углы равны. Отсюда можно сделать вывод, что ∠BAC = ∠DCA, а ∠BCA = ∠DAC.
Поэтому AB || CD, Британская Колумбия || AD, ABCD — параллелограмм.
Теорема 2. В параллелограмме противоположные углы равны.
Проба:
Дано: ABCD — параллелограмм, а ∠A, ∠B, ∠C, ∠D — четыре угла.
Доказать: ∠A = ∠C и ∠B = ∠D
Предположим, что ABCD — параллелограмм. Теперь сравните треугольники ABC и CDA. Здесь у нас есть,
- AC = CA (общая сторона)
- ∠1 = ∠4 (чередующиеся внутренние углы)
- ∠2 = ∠3 (чередующиеся внутренние углы)
Таким образом, согласно ASA, два треугольника конгруэнтны, а это означает, что ∠B = ∠D.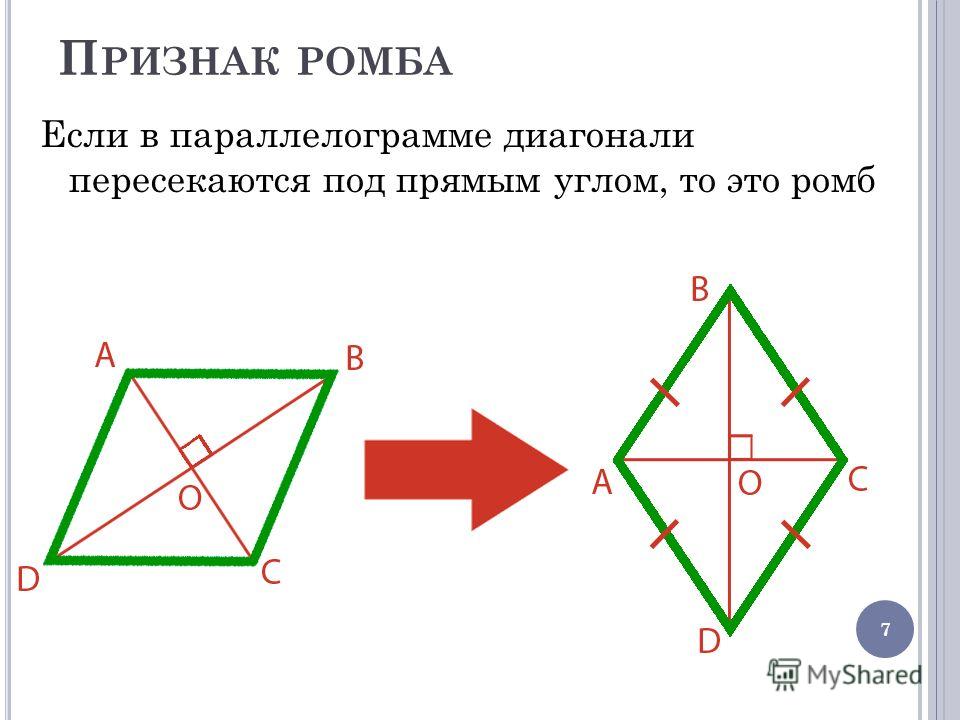
Обратное к теореме 2: Если в четырехугольнике противоположные углы равны, то это параллелограмм.
Доказательство:
Дано: ∠A = ∠C и ∠B = ∠D в четырехугольнике ABCD.
Доказать: ABCD — параллелограмм.
Предположим, что ∠A = ∠C и ∠B = ∠D в приведенном выше параллелограмме ABCD. Нам нужно доказать, что ABCD — параллелограмм. Имеем:
∠A + ∠B + ∠C + ∠D = 360º
2(∠A + ∠B) =360º
∠А + ∠В = 180º.
Это должно означать, что AD || ДО Н.Э. Аналогично можно показать, что AB || CD. Следовательно, АД || до н.э. и АВ || CD. Следовательно, ABCD — параллелограмм.
Теорема 3. Диагонали параллелограмма делят друг друга пополам.
Доказательство:
Дано: PQTR — параллелограмм.
Доказать: Диагонали PT и RQ делят друг друга пополам, т. е. PE = ET и ER = EQ.
Сначала предположим, что PQTR — параллелограмм. Сравните треугольники TER и треугольник PEQ. Имеем,
- PQ = RT (противоположные стороны параллелограмма PQTR)
- ∠QRT = ∠PQR (альтернативные внутренние углы)
- ∠PTR = ∠QPT (альтернативные внутренние углы).
По критерию ASA два треугольника конгруэнтны, что означает по CPCTC, PE = ET и RE = EQ. Таким образом, две диагонали PT и RQ делят друг друга пополам, а PE = ET и ER = EQ.
Обратное к теореме 3: Если диагонали в четырехугольнике делят друг друга пополам, то это параллелограмм. В четырехугольнике PQTR, если PE=ET и ER=EQ, то это параллелограмм.
Дано: Диагонали PT и QR делят друг друга пополам.
Доказать: PQRT — параллелограмм.
Доказательство: Предположим, что диагонали PT и QR делят друг друга пополам.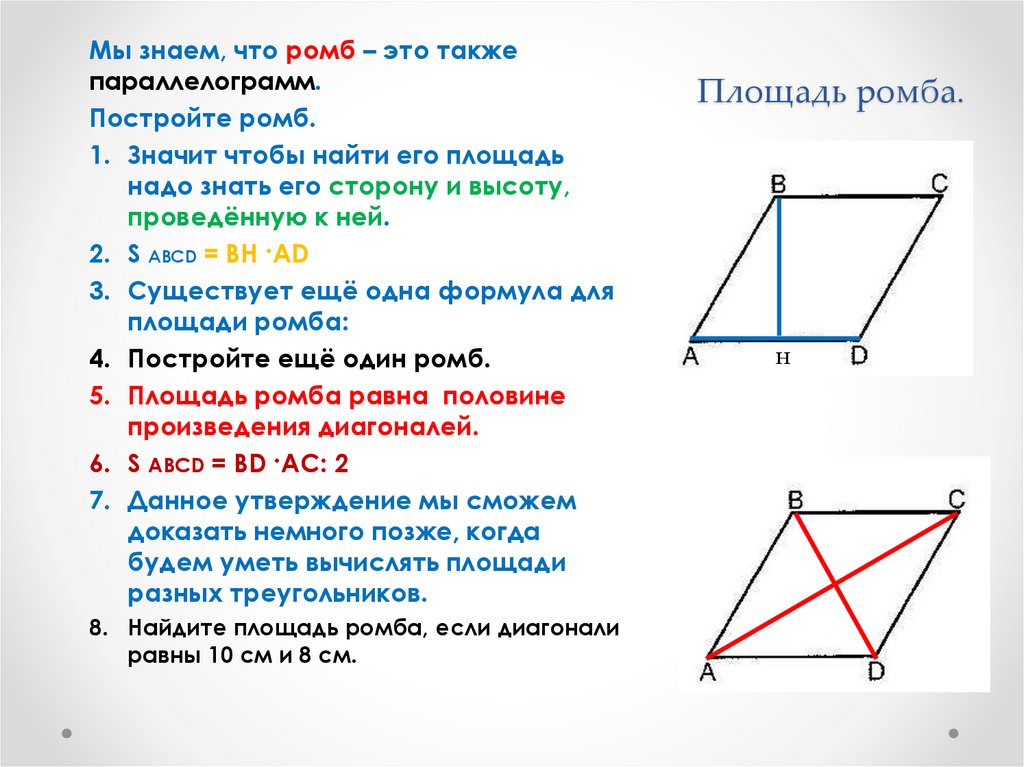
- RE = EQ
- ET = PE (диагонали делят друг друга пополам)
- ∠RET =∠PEQ (вертикально противоположные углы).
Следовательно, по критерию SAS два треугольника конгруэнтны. Это означает, что ∠QRT = ∠PQR и ∠PRT = ∠QPT. Следовательно, PQ || РТ и РТ || КТ. Таким образом, PQRT является параллелограммом.
Теорема 4: Если одна пара противоположных сторон равна и параллельна в четырехугольнике, то это параллелограмм.
Доказательство:
Дано: Дано, что AB = CD и AB || CD.
Доказать: ABCD — параллелограмм.
Сравним треугольник AEB и треугольник CED. Имеем,
- AB = CD (дано)
- ∠1 = ∠3 (чередующиеся внутренние углы)
- ∠2 = ∠4 (чередующиеся внутренние углы)
Таким образом, по критерию ASA два треугольника конгруэнтны. Отсюда можно сделать вывод, что по CPCTC AE = EC, а BE = ED.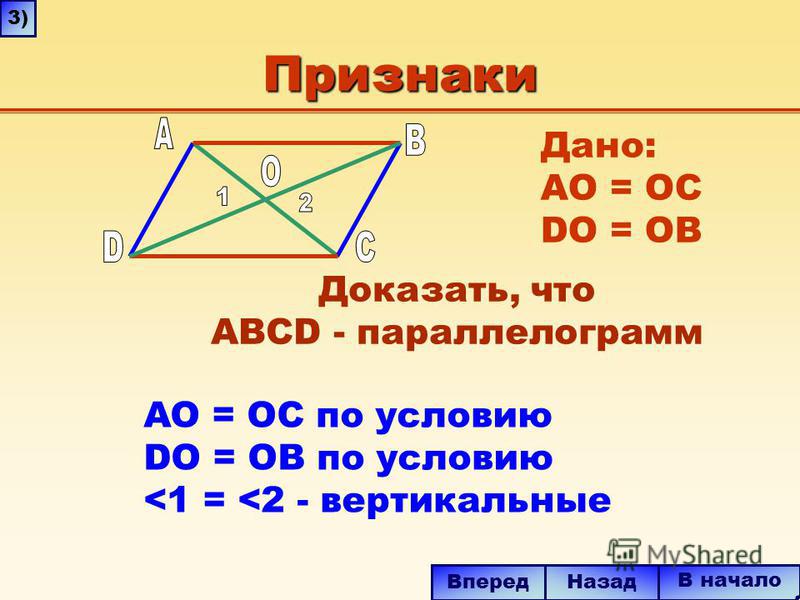
Важные примечания:
Четырехугольник является параллелограммом, если:
- противоположные стороны четырехугольника равны и параллельны.
- противоположные углы четырехугольника равны.
- диагонали делят друг друга пополам.
- одна пара противоположных сторон равна и параллельна.
Вы знаете?
- Почему воздушный змей не является параллелограммом?
- Является ли равнобедренная трапеция параллелограммом?
Также проверьте:
- Формула параллелограмма
- Площадь параллелограмма
- Свойства прямоугольника
- Разница между прямоугольником и параллелограммом
Часто задаваемые вопросы о свойствах параллелограмма
Каковы 7 свойств параллелограмма?
Семь свойств параллелограмма таковы:
- Противоположные стороны равны.
- Противоположные углы параллелограмма равны.
- Последовательные углы являются дополнительными.
- Если один угол параллелограмма прямой, то все углы прямые.
- Диагонали параллелограмма делятся пополам.
- Каждая диагональ параллелограмма делит его пополам на два равных треугольника.
- Если одна пара противоположных сторон четырехугольника равна и параллельна, то четырехугольник является параллелограммом.
Каковы свойства параллелограмма относительно диагоналей?
Диагонали параллелограмма обладают двумя важными свойствами. Диагональ параллелограмма делит параллелограмм на два равных треугольника. А диагонали параллелограмма делят друг друга пополам.
Диагонали параллелограмма равны?
Диагонали параллелограмма НЕ равны. Противоположные стороны и противоположные углы параллелограмма равны. Диагонали квадрата и прямоугольника равны, что является особым видом параллелограмма.
Каковы четыре важных свойства параллелограмма?
Параллелограмм – это четырехугольник, у которого противоположные стороны равны и параллельны.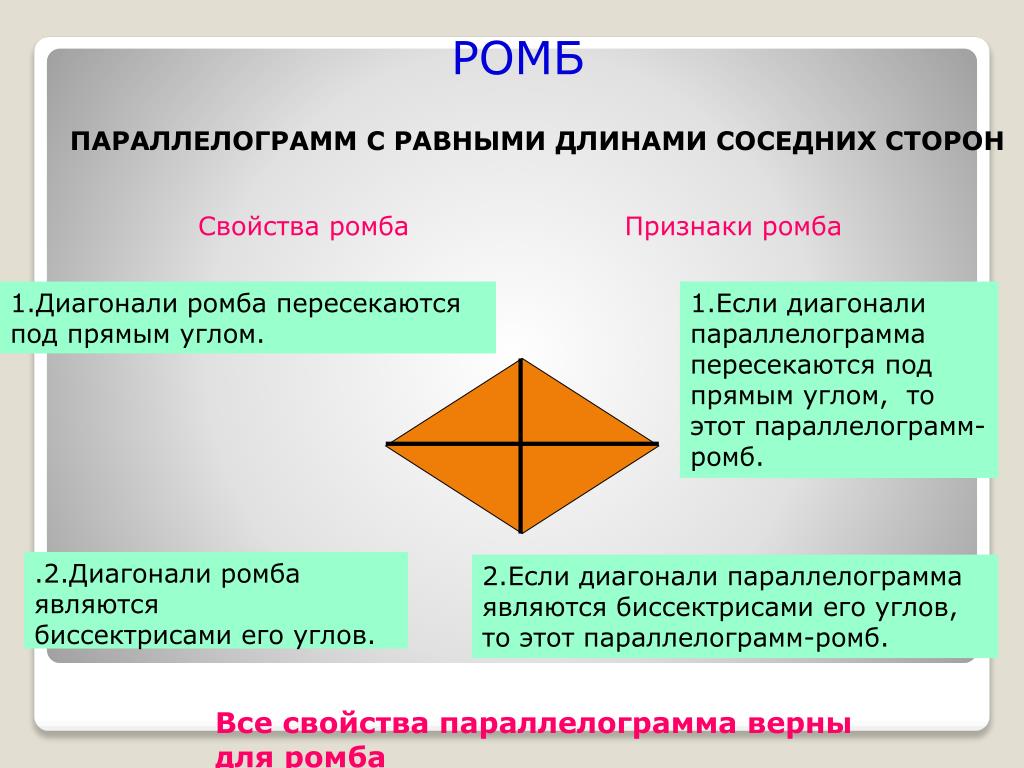
- Противоположные стороны равны
- Противоположные углы равны
- Смежные углы дополнительные
- Диагонали параллелограмма делят друг друга пополам
Можно ли прямоугольник назвать параллелограммом?
Противоположные стороны прямоугольника равны и параллельны. Таким образом, прямоугольник удовлетворяет всем свойствам параллелограмма, поэтому его можно назвать параллелограммом.
Каковы уникальные свойства параллелограммов?
Уникальные свойства параллелограмма, отличающие его от других четырехугольников, приведены ниже:
- Противоположные стороны каждого параллелограмма равны и параллельны.
- Противоположные углы всегда равны.
- Сумма смежных углов всегда равна 180°.
Каковы различные свойства каждого специального параллелограмма?
Существует три особых типа параллелограммов — квадрат, прямоугольник и ромб. Квадрат – это четырехугольник, у которого все стороны и углы равны. У прямоугольника противоположные стороны равны и параллельны. Все углы квадрата и прямоугольника равны и равны 9по 0 градусов каждый. Ромб — это параллелограмм с четырьмя равными сторонами, но его углы не обязательно должны быть прямыми.
Как отличить параллелограмм от четырехугольника по свойствам параллелограмма?
Каждый параллелограмм можно назвать четырехугольником, но не каждый четырехугольник можно назвать параллелограммом. Трапецию и воздушного змея можно назвать четырехугольниками, но они не полностью удовлетворяют свойствам параллелограмма и, следовательно, не могут быть названы параллелограммом.
CA Диагонали параллелограмма
CA Диагонали параллелограмма
Деятельность в классе и самооценка в классе
16 октября 2000 г.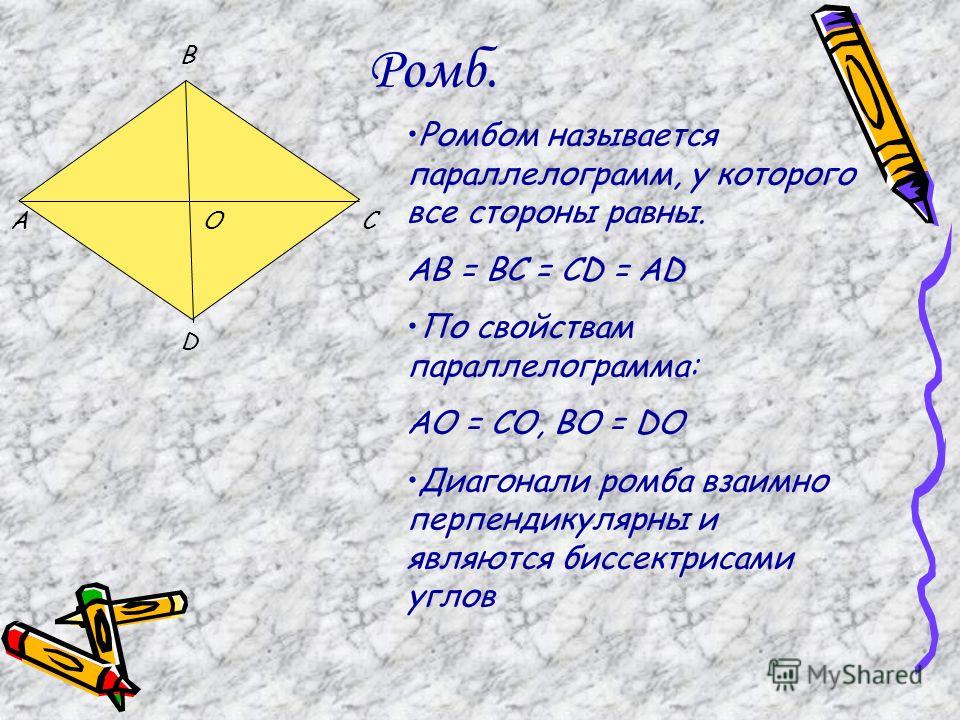
Задача 1
была задана как групповое задание в классе. Время отведено 25 минут. Эта теорема является «если и только если», поэтому решение состоит из двух частей.
Задача 2 была быстро продемонстрирована на слайде и не выполнялась в групповом режиме.
Задача 1. Диагонали параллелограмма
Укажите определение параллелограмма (тот, что в B&B). Докажите, что четырехугольник является параллелограммом тогда и только тогда, когда его диагонали делят друг друга пополам. (Другими словами, диагонали пересекаются в точке M, которая является серединой каждой диагонали.)
Определение. Четырехугольник ABCD является параллелограммом, если AB параллелен CD, а BC параллелен DA.
Утверждение 1. Если ABCD — параллелограмм, то диагонали ABCD делят друг друга пополам.
Доказательство утверждения 1.
Пусть O пересечение диагоналей AC и BD. Утверждение можно переформулировать так: О — середина АС, а также середина BD.
Поскольку O находится на отрезке AC, O является серединой AC, если AO = CO. Точно так же O является серединой BD, если BO = DO. Это то, что мы докажем, используя конгруэнтные треугольники.
Сначала мы покажем, что треугольник ABO подобен треугольнику CDO, используя угол-угол. Так как прямая AC является секущей параллельных прямых AB и CD, то угол OAB = угол CAB = угол ACD = угол OCD. Кроме того, по вертикальным углам угол AOB = угол COD. Таким образом, треугольник ABO подобен треугольнику CDO.
Далее мы покажем, что эти два треугольника конгруэнтны, показав, что отношение подобия равно 1. Мы знаем из домашнего задания (*), что противоположные стороны ABCD, AB = CD. Это две соответствующие стороны подобных треугольников, поэтому треугольники ABO и CDO равны.
Из сравнения заключаем, что АО = СО и ВО = DO.
QED
Утверждение 2. Если ABCD — четырехугольник, у которого диагонали AC и BD делят друг друга пополам, то ABCD — параллелограмм.
Доказательство утверждения 2.
Пусть M — пересечение AC и BD. Нам дано, что M является серединой AC, а также BD, поэтому MA = MC и MB = MD.
Мы также знаем, что угол AMB равен углу CMD по вертикальным углам. Таким образом, мы заключаем, что треугольник AMB конгруэнтен треугольнику CMD по SAS.
Соответственные углы равны. Таким образом, угол MAB (равный углу CAB) и угол MCD (равный углу ACD) равны. Поскольку AC является секущей прямых AB и CD, из этих равных внутренних углов следует, что прямые AB и CD параллельны.
Таким образом, мы видим, что две противоположные стороны ABCD параллельны. Поскольку в этих двух сторонах не было ничего особенного, используя тот же аргумент, мы также можем заключить, что BC и DA параллельны, поэтому по определению ABCD является параллелограммом.
Задача 2. Ромб
- Ромбом называется четырехугольник с четырьмя равными сторонами. Докажите, что ромб является параллелограммом.
Доказательство: В домашнем задании было доказано, что если четырехугольник ABCD имеет равные противоположные стороны, то это параллелограмм. Это следует из этого результата.
(b) Докажите, что параллелограмм с перпендикулярными диагоналями является ромбом.
Доказательство. Из задачи 1 мы знаем, что диагонали параллелограмма ABCD делят друг друга пополам. Пусть М — пересечение диагоналей. Отсюда мы знаем, что MA = MC и MB = MD.
Если мы также предположим, что AC перпендикулярен BC, то каждый из углов AMB, AMD, CMB и CMD будет прямым. Таким образом, треугольники AMB, AMD, CMB и CMD конгруэнтны по SAS. Отсюда следует, что все гипотенузы конгруэнтны: AB = AD = CB = CD. Это говорит о том, что ABCD по определению является ромбом.
QED
(*) Доказательство домашней задачи. (Противоположные стороны параллелограмма равны.)
Утверждение: если ABCD — параллелограмм, то его противоположные стороны равны.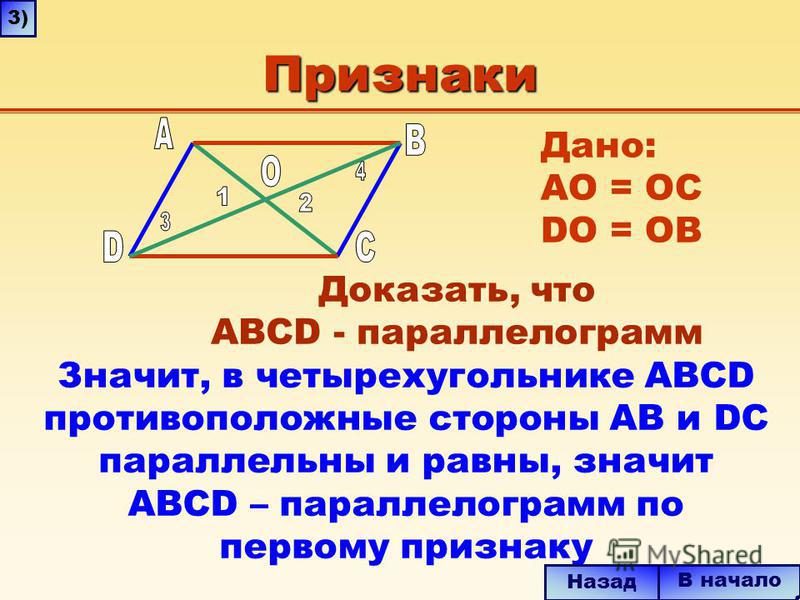
Доказательство. По определению прямая AB параллельна прямой CD, а прямая BC параллельна прямой DA. Мы должны доказать, что AB = CD и BC = DA.
Докажем, что треугольник ABC равен треугольнику CDA по ASA. Два треугольника имеют общую сторону АС = СА.
Чтобы доказать равенство углов, мы используем секущую. Прямая AC является секущей параллельных прямых AB и CD, поэтому угол CAB равен углу ACD. Также прямая AC является секущей параллельных прямых BC и DA, поэтому угол ACB равен углу CAD.
Таким образом, по ASA треугольники ABC и CDA равны. Соответствующие стороны равны, поэтому AB = CD и BC = DA.
QED
[Дополнительная кредитная возможность. Первый человек, отправивший электронное письмо на адрес электронной почты Math 444-487 и сообщивший, какие слова обозначают инициалы Q.E.D и что они означают, получает дополнительный балл.]
Диагонали параллелограмма перпендикулярны?
Вопрос задан: Судьей Николаем III
Оценка: 4,9/5
(53 голоса)
Если четырехугольник ромб, то он параллелограмм.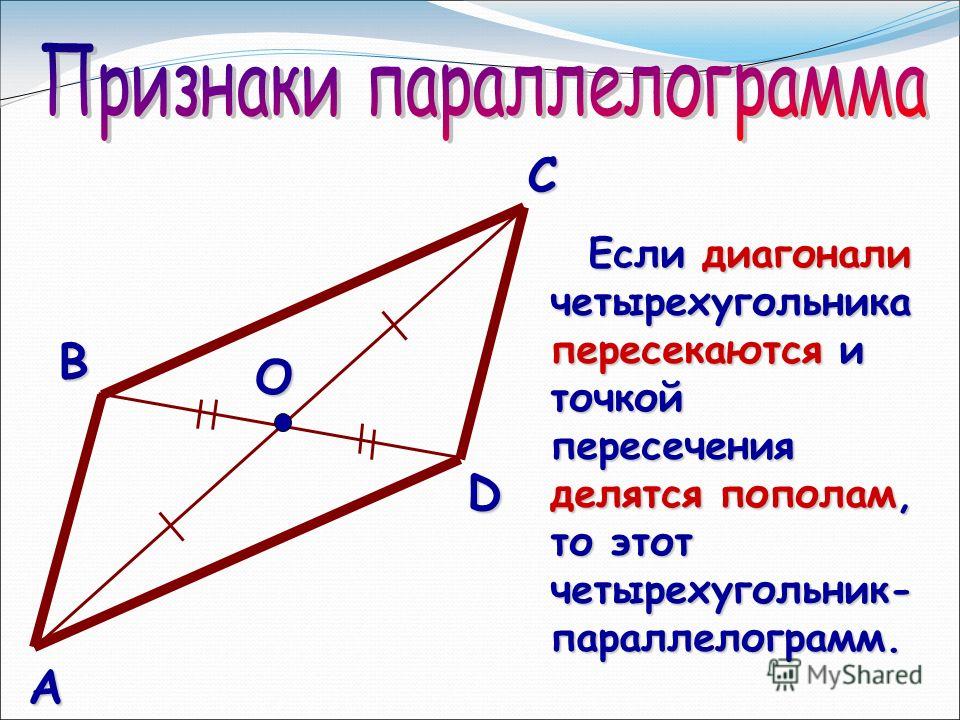
Всегда ли диагонали в параллелограмме перпендикулярны?
Диагонали параллелограмма иногда совпадают. диагоналей ромба всегда перпендикулярны . Последовательные углы параллелограмма никогда не дополняют друг друга. Квадрат всегда ромб.
Как называется параллелограмм с перпендикулярными диагоналями?
‘Если диагонали параллелограмма перпендикулярны, то это ромб . ‘
Содержит ли параллелограмм перпендикуляр?
Параллелограмм – это четырехугольник, у которого противоположные стороны параллельны, но смежные стороны не перпендикулярны .
Как доказать, что диагонали параллелограмма перпендикулярны?
Доказательство того, что диагонали ромба перпендикулярны
Соответствующие части равных треугольников равны , поэтому все 4 угла (те, что в середине) равны.
Докажите, что диагонали этого параллелограмма перпендикулярны
Найдено 27 связанных вопросов
Что такое перпендикуляр в параллелограмме?
Высотой (или высотой) параллелограмма является перпендикулярное расстояние от основания до противоположной стороны (которую, возможно, придется продлить). … Противоположные стороны конгруэнтны (равны по длине) и параллельны. Изменяя форму параллелограмма в верхней части страницы, обратите внимание на то, что противоположные стороны всегда имеют одинаковую длину.
Какой параллелограмм имеет перпендикулярные стороны?
Параллелограмм с перпендикулярными диагоналями — это ромб
Ромб — особый вид параллелограмма, у которого все стороны равны. Мы видели, что одним из свойств ромба является то, что его диагонали перпендикулярны друг другу.
Диагонали квадрата перпендикулярны?
Диагонали квадрата делят друг друга пополам и перпендикулярны (показаны красным на рисунке выше). Кроме того, они делят пополам каждую пару противоположных углов (показаны синим цветом).
Диагонали какого четырехугольника не перпендикулярны?
Прямоугольник — это четырехугольник, диагонали которого равны и делятся пополам, но не перпендикулярны.
Делят ли диагонали углы пополам в параллелограмме?
Параллелограмм – это четырехугольник, у которого противоположные стороны параллельны. Противоположные углы параллелограмма равны. … Диагонали параллелограмма делят друг друга пополам .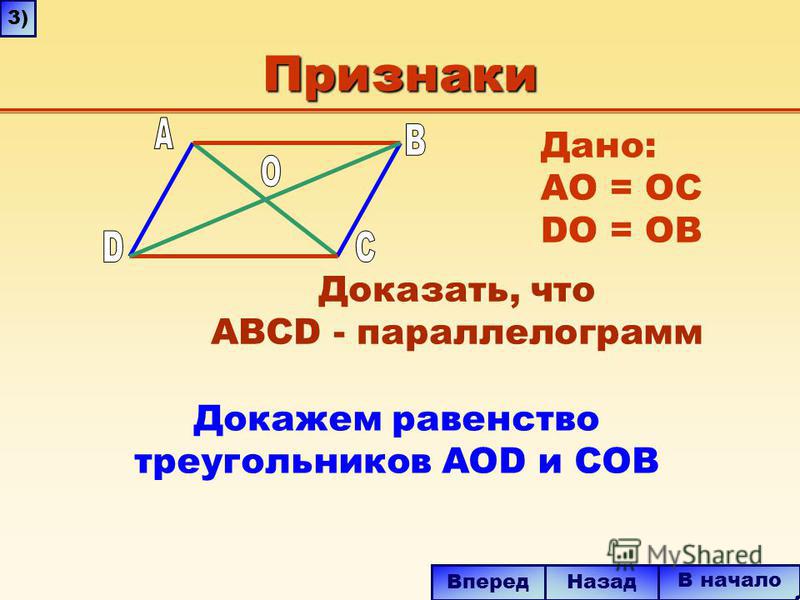
Что верно в отношении диагоналей параллелограмма?
Диагонали параллелограмма делят друг друга пополам . … В любом параллелограмме диагонали (линии, соединяющие противоположные углы) делят друг друга пополам. То есть каждая диагональ разрезает другую на две равные части.
Все ли диагонали параллелограмма равны?
Применяются все свойства параллелограмма (здесь важны параллельность сторон, конгруэнтность противоположных сторон и делимость диагоналей пополам). … Диагонали равны .
Почему диагонали параллелограмма не равны?
Диагонали в параллелограммах
Диагонали параллелограмма проводятся от одной противоположной стороны параллелограмма к другой. … Это происходит потому, что противоположные углы параллелограмма равны . Сами диагонали не будут конгруэнтны друг другу, если параллелограмм также не является квадратом или ромбом.
Диагонали параллелограмма равны?
Диагонали параллелограмма равны? диагоналей параллелограмма НЕ равны .
Какие четырехугольники обладают всеми свойствами параллелограмма?
Прямоугольник обладает всеми свойствами параллелограмма, а также следующими: Диагонали равны.
Что из следующего не верно в отношении параллелограмма?
Если провести диагонали, соединив противоположные вершины в параллелограмм, то нельзя сказать, что диагоналей делят пополам противоположные углы . Диагонали делят друг друга пополам, но не делят углы пополам. Следовательно, это утверждение неверно.
Диагонали ромба перпендикулярны?
Сал доказывает, что диагонали ромба перпендикулярны и пересекаются в их серединах.
Как найти диагонали параллелограмма?
Часто задаваемые вопросы о формуле диагонали параллелограмма
Для любого параллелограмма abcd формула для длин диагоналей имеет вид: p=√x2+y2−2xycosA=√x2+y2+2xycosB p = x 2 + y 2 − 2 x y cos A = x 2 + y 2 + 2 x y cos B и q = √x2 + y2 + 2xycosA = √x2 + y2−2xycosB q = x 2 + y 2 + 2 x y cos A = x 2 + y 2 − 2 х у, потому что
У каких из них диагонали перпендикулярны друг другу?
Ответ: Ромб ; площадь.
Делят ли диагонали противоположные углы пополам?
Противоположные углы равны . … Диагонали делят друг друга пополам, и каждая диагональ делит параллелограмм на два конгруэнтных треугольника. Если один из углов параллелограмма прямой, то все остальные углы прямые и параллелограмм становится прямоугольником.
Если все углы прямые, то параллелограмм A?
Параллелограмм, у которого все углы прямые это прямоугольник !
Диагонали какого из следующих параллелограммов не равны, но перпендикулярны друг другу?
Если параллелограмм является ромбом , то его диагонали перпендикулярны. Если параллелограмм является ромбом, то каждая диагональ делит пополам пару противоположных углов. Если диагонали параллелограмма перпендикулярны, то параллелограмм является ромбом.
Как узнать, перпендикулярна ли диагональ?
Чтобы доказать, что две прямые перпендикулярны, когда все, что у нас есть, это эти две прямые, мы можем использовать Теорему о парных перпендикулярах — Если две прямые пересекаются в точке и образуют линейную пару равных углов , они перпендикулярны .
Загрузить PDF
Загрузить PDF
Диагональ — это отрезок, который соединяет две противолежащие вершины прямоугольника.[1]
В прямоугольнике две равные диагонали.[2]
Если известны стороны прямоугольника, диагональ можно найти по теореме Пифагора, потому что диагональ делит прямоугольник на два прямоугольных треугольника. Если стороны не даны, но известны другие величины, например, площадь и периметр или отношение сторон, можно найти стороны прямоугольника, а затем по теореме Пифагора вычислить диагональ.
-
1
-
2
-
3
Длину и ширину возведите в квадрат, а затем сложите полученные результаты. Помните, что при возведении числа в квадрат оно умножается на себя.
-
4
Извлеките квадратный корень из обеих сторон уравнения. Воспользуйтесь калькулятором, чтобы быстро извлечь квадратный корень. Также можно воспользоваться онлайн-калькулятором.[5]
Вы найдете, то есть гипотенузу треугольника, а значит и диагональ прямоугольника.
Реклама
-
1
Запишите формулу для вычисления площади прямоугольника. Формула:
, где
— площадь прямоугольника,
— длина прямоугольника,
— ширина прямоугольника.[6]
(На рисунке вместо S использовано обозначение А.) -
2
В формулу подставьте значение площади прямоугольника. Это значение подставляется вместо
.
- Например, если площадь прямоугольника равна 35 квадратных сантиметров, формула запишется так:
.
- Например, если площадь прямоугольника равна 35 квадратных сантиметров, формула запишется так:
-
3
Перепишите формулу так, чтобы обособить
. Для этого разделите обе стороны уравнения на
. Затем полученное выражение нужно подставить в формулу для вычисления периметра.
-
4
Запишите формулу для вычисления периметра прямоугольника. Формула:
, где
— длина прямоугольника,
— ширина прямоугольника.[7]
-
5
В формулу подставьте значение периметра прямоугольника. Это значение подставляется вместо
.
- Например, если периметр прямоугольника равен 24 сантиметра, формула запишется так:
.
- Например, если периметр прямоугольника равен 24 сантиметра, формула запишется так:
-
6
Разделите обе стороны уравнения на 2. Вы получите сумму сторон прямоугольника, а именно
.
-
7
В формулу подставьте выражение для вычисления
. Это выражение, полученное при обособлении
.
-
8
Избавьтесь от дроби. Для этого обе части уравнения умножьте на
.
-
9
Приравняйте уравнение к 0. Для этого из обеих сторон уравнения вычтите член с переменной первого порядка.
-
10
Упорядочьте члены уравнения. Первым членом будет член с переменной второго порядка, затем член с переменной первого порядка, а затем свободный член. При этом не забудьте про знаки («плюс» и «минус»), которые стоят перед членами. Обратите внимание, что уравнение запишется в виде квадратного уравнения.
-
11
Разложите квадратное уравнение на множители. Чтобы получить подробные инструкции, прочитайте эту статью.
-
12
Найдите
. Для этого приравняйте каждый множитель к нулю и вычислите
. Вы получите два значения (это корни уравнения), которые в случае прямоугольника являются его длиной и шириной.
-
13
-
14
-
15
Длину и ширину возведите в квадрат, а затем сложите полученные результаты. Помните, что при возведении числа в квадрат оно умножается на себя.
-
16
Извлеките квадратный корень из обеих сторон уравнения. Воспользуйтесь калькулятором, чтобы быстро извлечь квадратный корень. Также можно воспользоваться онлайн-калькулятором.[10]
Вы найдете, то есть гипотенузу треугольника, а значит, и диагональ прямоугольника.
Реклама
-
1
-
2
-
3
В формулу подставьте значение площади прямоугольника. Это значение подставляется вместо
.
- Например, если площадь прямоугольника равна 35 квадратных сантиметров, формула примет вид:
.
- Например, если площадь прямоугольника равна 35 квадратных сантиметров, формула примет вид:
-
4
В формулу подставьте выражение, характеризующее отношение сторон. В случае прямоугольника можно подставить выражение для вычисления
или
.
-
5
Запишите квадратное уравнение. Для этого раскройте скобки и приравняйте уравнение к нулю.
-
6
Разложите квадратное уравнение на множители. Чтобы получить подробные инструкции, прочитайте эту статью.
-
7
Найдите
. Для этого приравняйте каждый множитель к нулю и вычислите
. Вы получите два значения (так называемые корни уравнения).
-
8
Подставьте найденное значение ширины (или длины) в уравнение, характеризующее отношение сторон. Так можно найти другую сторону прямоугольника.
-
9
-
10
-
11
Длину и ширину возведите в квадрат, а затем сложите полученные результаты. Помните, что при возведении числа в квадрат оно умножается на себя.
-
12
Извлеките квадратный корень из обеих сторон уравнения. Воспользуйтесь калькулятором, чтобы быстро извлечь квадратный корень. Также можно воспользоваться онлайн-калькулятором.[16]
Вы найдете, то есть гипотенузу треугольника, а значит и диагональ прямоугольника.
Реклама
Об этой статье
Эту страницу просматривали 557 104 раза.
Была ли эта статья полезной?
3. Геометрия на плоскости (планиметрия). Часть I
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Параллелограмм и его свойства
Сумма внутренних углов любого четырехугольника равна (360^circ).
Свойства параллелограмма:
(blacktriangleright) Противоположные стороны попарно равны;
(blacktriangleright) Диагонали точкой пересечения делятся пополам;
(blacktriangleright) Противоположные углы попарно равны, а сумма соседних равна (180^circ).
Признаки параллелограмма.
Если для выпуклого четырехугольника выполнено одно из следующих условий, то это – параллелограмм:
(blacktriangleright) если противоположные стороны попарно равны;
(blacktriangleright) если две стороны равны и параллельны;
(blacktriangleright) если диагонали точкой пересечения делятся пополам;
(blacktriangleright) если противоположные углы попарно равны.
Площадь параллелограмма
Площадь параллелограмма равна произведению высоты на основание, к которому проведена эта высота.
Задание
1
#1783
Уровень задания: Легче ЕГЭ
Периметр параллелограмма равен (100), его большая сторона равна (32). Найдите меньшую сторону параллелограмма.
Так как у параллелограмма противоположные стороны равны, то его периметр равен удвоенной сумме его непараллельных сторон, тогда сумма большей и меньшей сторон равна (100 : 2 = 50), значит, меньшая сторона параллелограмма равна (50 — 32 = 18).
Ответ: 18
Задание
2
#1784
Уровень задания: Равен ЕГЭ
Периметр параллелограмма равен (15). При этом одна сторона этого параллелограмма на (5) больше другой. Найдите меньшую сторону параллелограмма.
У параллелограмма противоположные стороны равны. Пусть (BC = AB +
5), тогда периметр параллелограмма (ABCD) равен (AB + BC + CD + AD =
AB + AB + 5 + AB + AB + 5 = 4cdot AB + 10 = 15), откуда находим (AB
= 1,25). Тогда меньшая сторона параллелограмма равна (1,25).
Ответ: 1,25
Задание
3
#273
Уровень задания: Равен ЕГЭ
В параллелограмме (ABCD): (BE) – высота, (BE = ED = 5). Площадь параллелограмма (ABCD) равна 35. Найдите длину (AE).
Площадь параллелограмма равна произведению основания на высоту, проведённую к этому основанию, тогда (35 = BE cdot AD = 5cdot(5 + AE)), откуда находим (AE = 2).
Ответ: 2
Задание
4
#1785
Уровень задания: Равен ЕГЭ
Из точки (C) параллелограмма (ABCD) опустили перпендикуляр на продолжение стороны (AD) за точку (D). Этот перпендикуляр пересёк прямую (AD) в точке (E), причём (CE = DE). Найдите (angle B) параллелограмма (ABCD). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда (angle EDC = angle DCE). Так как (angle DEC = 90^{circ}), а сумма углов треугольника равна (180^{circ}), то (angle EDC =
45^{circ}), тогда (angle ADC = 180^{circ} — 45^{circ} =
135^{circ}). Так как в параллелограмме противоположные углы равны, то (angle B = angle ADC = 135^{circ}).
Ответ: 135
Задание
5
#1686
Уровень задания: Равен ЕГЭ
Диагональ (BD) параллелограмма (ABCD) перпендикулярна стороне (DC) и равна (4). Найдите площадь параллелограмма (ABCD), если (AD=5).
По теореме Пифагора находим: (AB^2=AD^2 — BD^2 = 25 — 16 = 9) (Rightarrow) (AB = 3). (S_{ABCD} = 4cdot3 = 12).
Ответ: 12
Задание
6
#1685
Уровень задания: Равен ЕГЭ
В параллелограмме (ABCD): (P_{triangle AOB} = 
(P_{triangle AOB} = AO + OB + AB), (P_{triangle AOD} = AO + OD + AD), (BO = OD) (Rightarrow) (P_{triangle AOD} — P_{triangle AOB} = AD — AB = 1), но (AD + AB = 7) (Rightarrow) (AD = 4), (AB = 3) (Rightarrow) (ADcdot AB = 12).
Ответ: 12
Задание
7
#3617
Уровень задания: Равен ЕГЭ
Стороны параллелограмма равны (9) и (15). Высота, опущенная на первую сторону, равна (10). Найдите высоту, опущенную на вторую сторону параллелограмма.
Площадь параллелограмма равна произведению высоты на сторону, к которой высота проведена. Следовательно, с одной стороны, площадь (S=9cdot 10), с другой стороны, (S=15cdot h), где (h) – высота, которую нужно найти.
Следовательно, [9cdot 10=15cdot hquadLeftrightarrowquad h=6]
Ответ: 6
Задачи из раздела «Геометрия на плоскости» являются обязательной частью аттестационного экзамена у выпускников средней школы. Теме «Параллелограмм и его свойства» в ЕГЭ традиционно отводится сразу несколько заданий. Они могут требовать от школьника как краткого, так и развернутого ответа с построением чертежа. Поэтому если одним из ваших слабых мест являются именно задачи на вычисление площадей параллелограмма или его сторон и углов, то вам непременно стоит повторить или вновь разобраться в материале.
Сделать это легко и эффективно вам поможет образовательный портал «Школково». Наши опытные специалисты подготовили необходимый теоретический материал, изложив его таким образом, чтобы школьники с любым уровнем подготовки смогли восполнить пробелы в знаниях и легко решить задачи ЕГЭ на вычисление площадей, сторон, углов или свойства биссектрисы параллелограмма. Найти базовую информацию вы можете в разделе «Теоретическая справка».
Чтобы успешно решить задачи ЕГЭ по теме «Параллелограмм и его свойства», предлагаем попрактиковаться в выполнении соответствующих упражнений. Большая подборка заданий представлена в блоке «Каталог». Специалисты портала «Школково» регулярно дополняют и обновляют данный раздел.
Последовательно выполнять упражнения учащиеся из Москвы и других городов могут в режиме онлайн. При необходимости любое задание можно сохранить в разделе «Избранное» и в дальнейшем вернуться к нему, чтобы обсудить с преподавателем.

УСТАЛ? Просто отдохни























































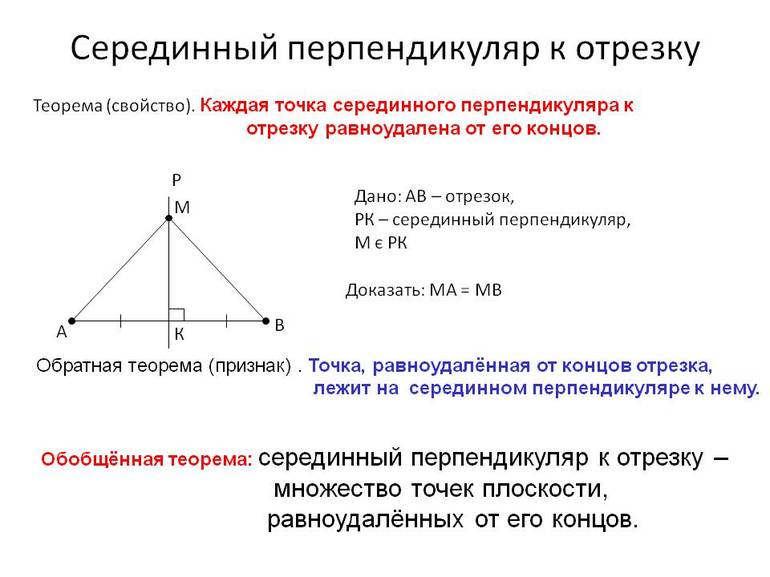
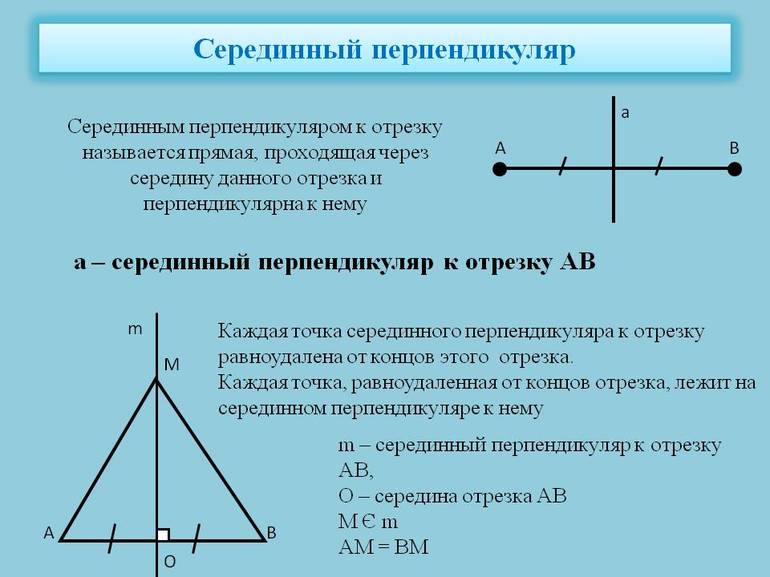
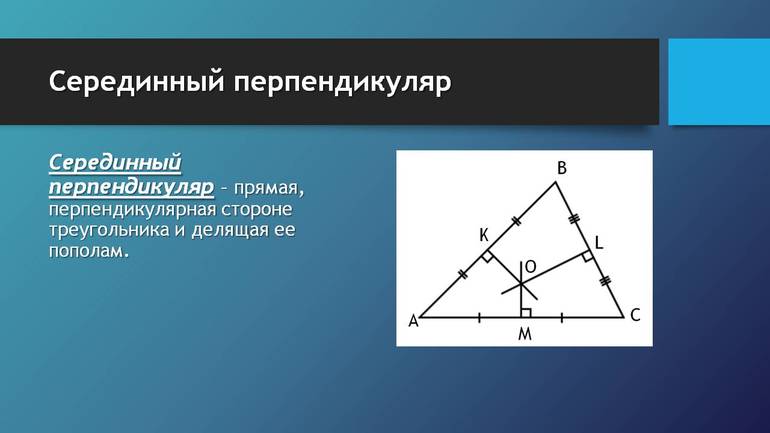
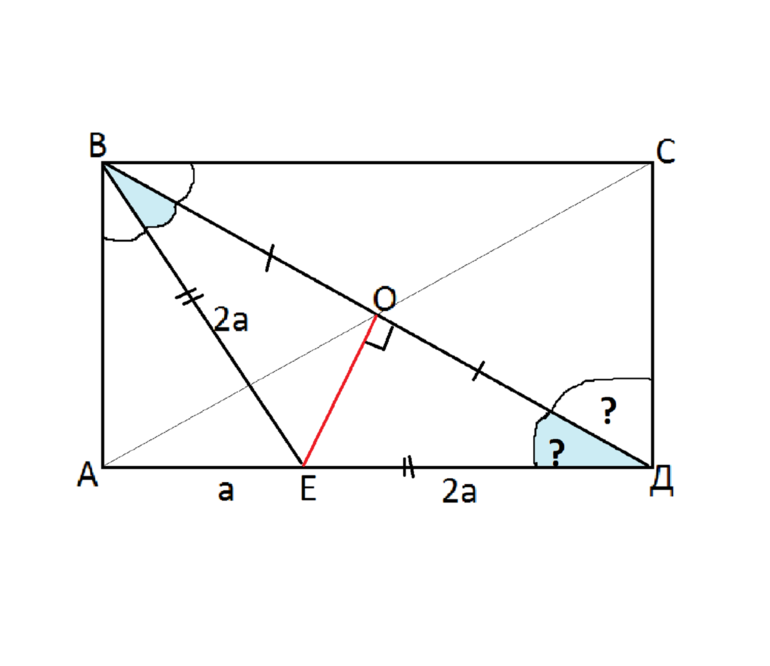
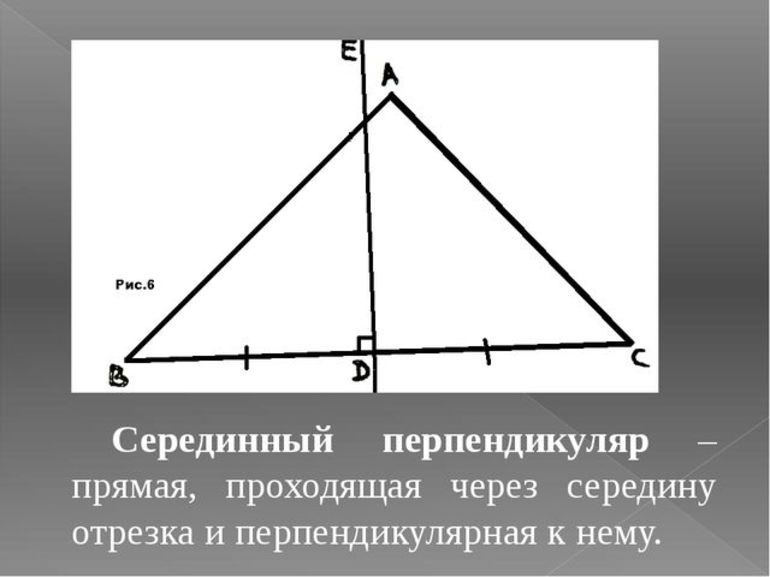
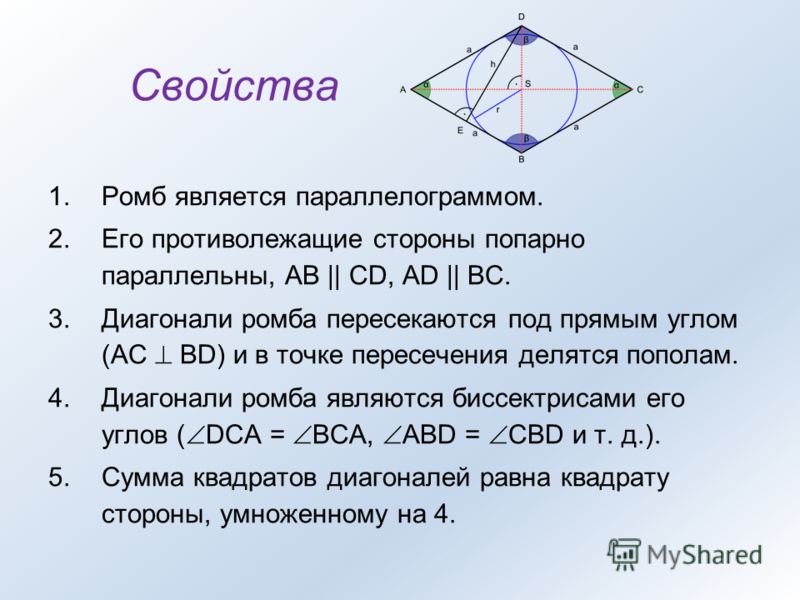 Если на одной стороне угла отложить равные отрезки и через их концы провести параллельные прямые, пересекающие второю сторону угла, то на второй стороне угла отложатся также равные отрезки.
Если на одной стороне угла отложить равные отрезки и через их концы провести параллельные прямые, пересекающие второю сторону угла, то на второй стороне угла отложатся также равные отрезки.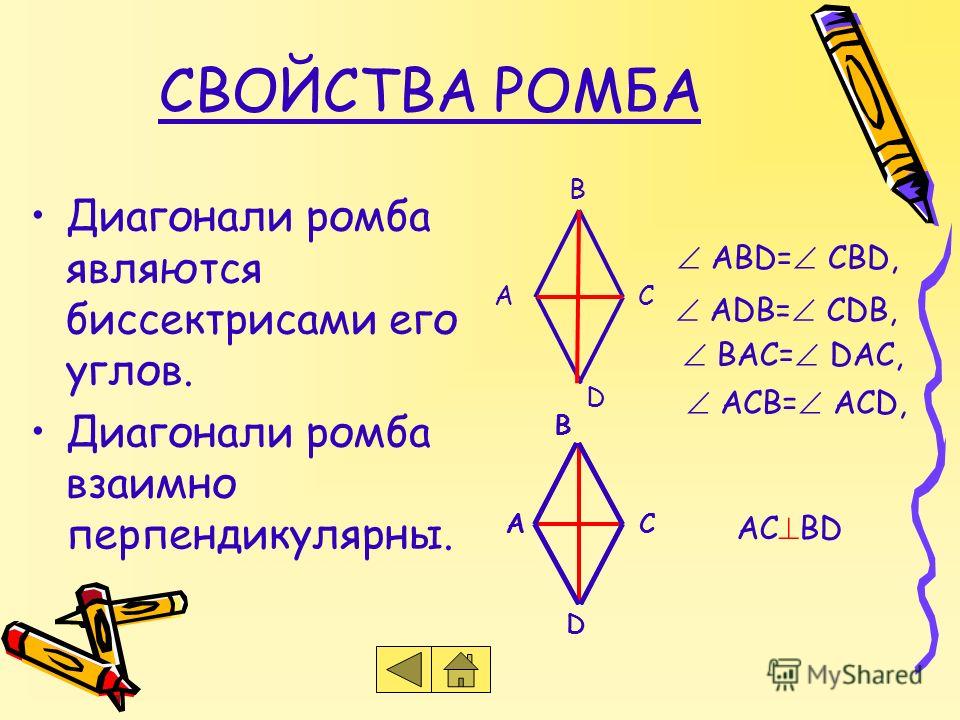

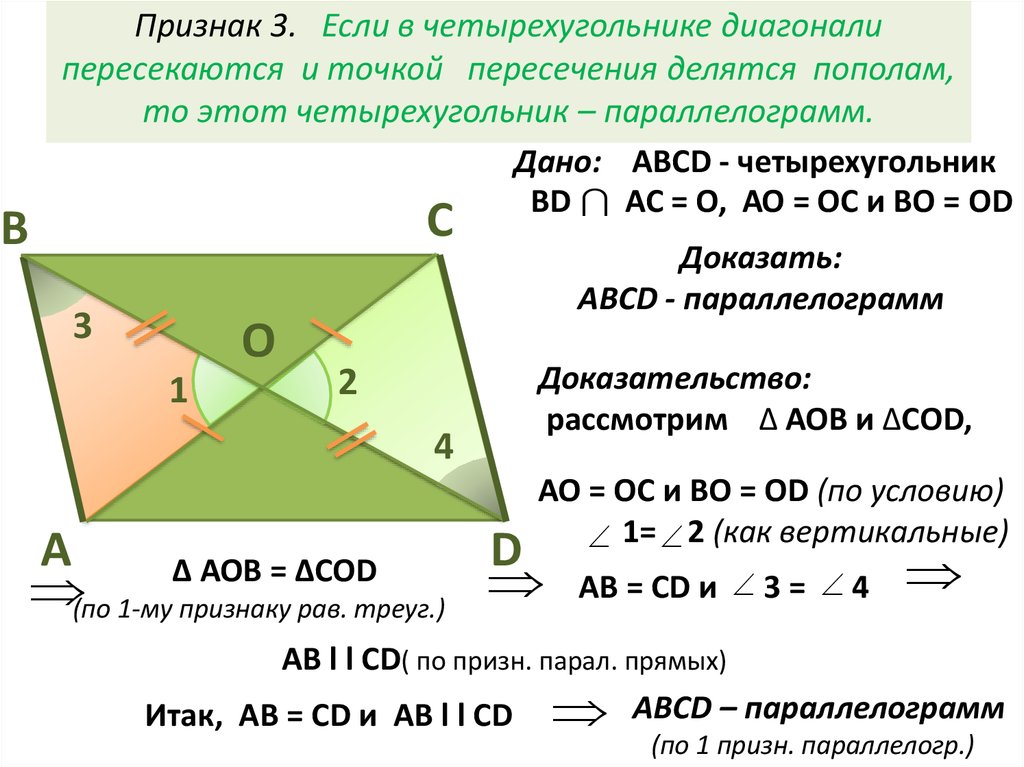


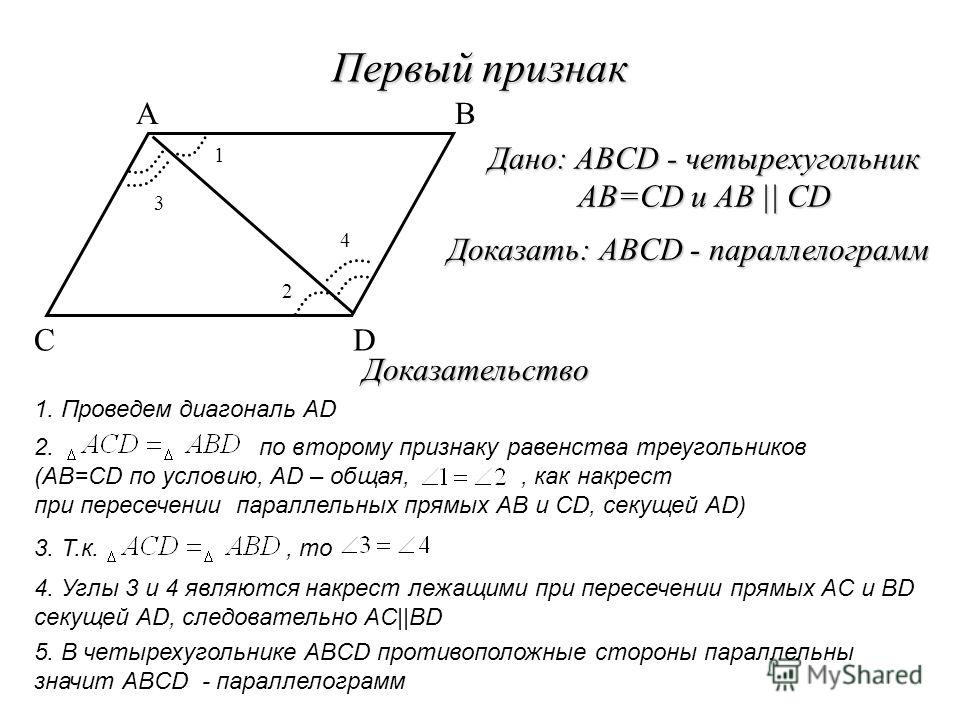 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.01 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.01 с.)  Параллелограмм
Параллелограмм
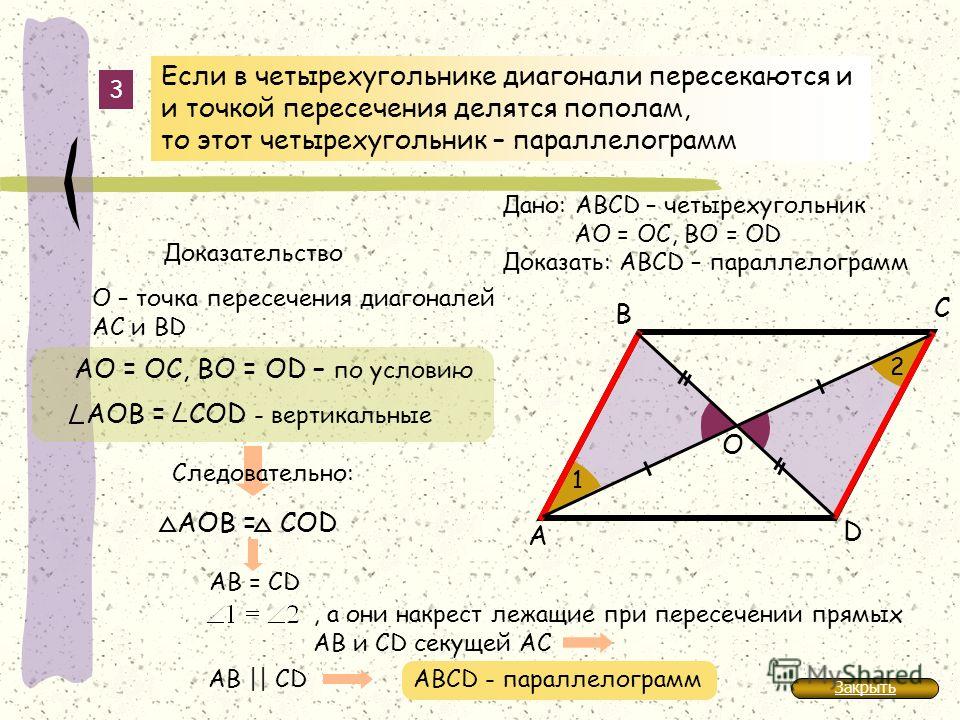 Аналогично можно доказать, что прямая АВ параллельна ВС. Теорема доказана.
Аналогично можно доказать, что прямая АВ параллельна ВС. Теорема доказана. Следовательно, треугольники АОD и ВОС равны по стороне и прилегающим к ней углам. А отсюда следует и равенство сторон этих треугольников. Т.е. АО = ОС, а ВО = ОD. Сумма этих сторон и есть диагонали параллелограмма.
Следовательно, треугольники АОD и ВОС равны по стороне и прилегающим к ней углам. А отсюда следует и равенство сторон этих треугольников. Т.е. АО = ОС, а ВО = ОD. Сумма этих сторон и есть диагонали параллелограмма.  Пусть АВСD — ромб.(Рис. 3). Тогда треугольник АВС — равнобедренный. А это значит, что отрезок ВО, который является половиной диагонали, является биссектрисой медианой и высотой. Следовательно диагонали ромба АС и ВD пересекаются под прямым углом.
Пусть АВСD — ромб.(Рис. 3). Тогда треугольник АВС — равнобедренный. А это значит, что отрезок ВО, который является половиной диагонали, является биссектрисой медианой и высотой. Следовательно диагонали ромба АС и ВD пересекаются под прямым углом. Так как прямая АЕ биссектриса, то это значит, что треугольники АВЕ и АЕР равны. Так как угол ВАЕ равен углу АЕР, а угол ЕАР равен углу ВЕА как внутренние накрест лежащие. Следовательно АВЕР — ромб, так как угол ВАЕ равен углу ЕАР ( по условию). Отсюда следует, что АВ = ВЕ = 9 см, а ЕС = 5 см.
Так как прямая АЕ биссектриса, то это значит, что треугольники АВЕ и АЕР равны. Так как угол ВАЕ равен углу АЕР, а угол ЕАР равен углу ВЕА как внутренние накрест лежащие. Следовательно АВЕР — ромб, так как угол ВАЕ равен углу ЕАР ( по условию). Отсюда следует, что АВ = ВЕ = 9 см, а ЕС = 5 см.
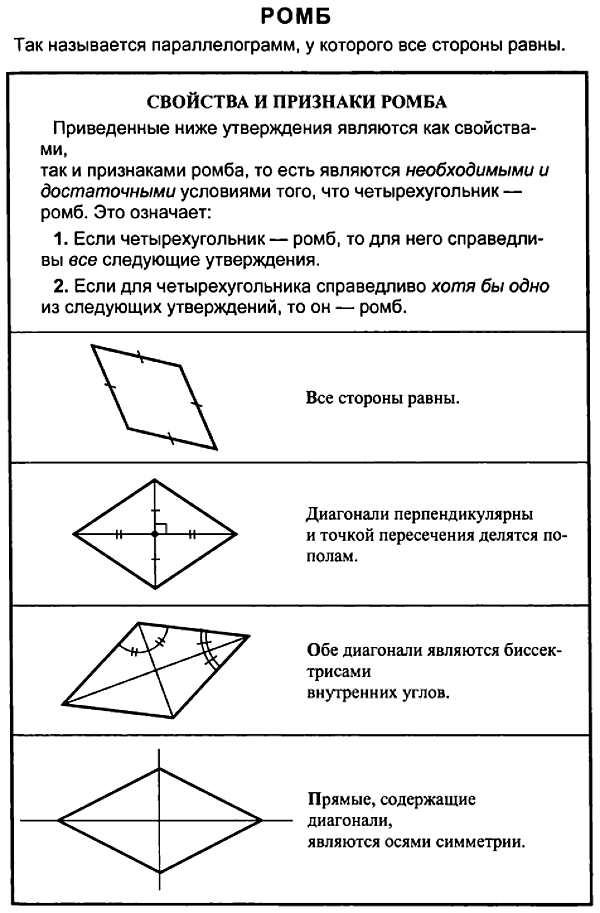 Пусть АВС — треугольник. Отрезок ЕР соединяет середины сторон АВ и ВС (Рис. 5). Тогда по теореме Фалеса отрезок ЕР параллелен основанию АС, так как он делит стороны АВ и ВС на равные части.
Пусть АВС — треугольник. Отрезок ЕР соединяет середины сторон АВ и ВС (Рис. 5). Тогда по теореме Фалеса отрезок ЕР параллелен основанию АС, так как он делит стороны АВ и ВС на равные части.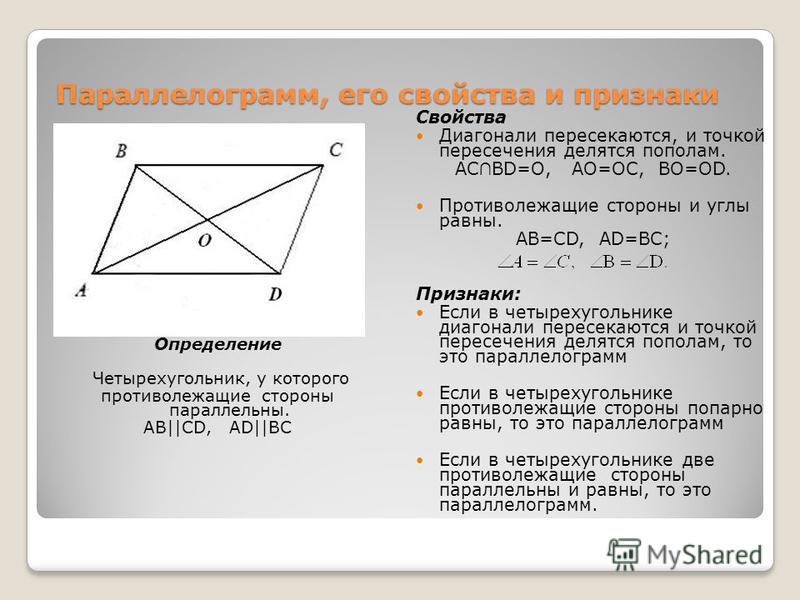
 Теорема о пропорциональных отрезках
Теорема о пропорциональных отрезках 

 (Рис.9)
(Рис.9) 9 Задача. Через точку пересечения диагоналей…
9 Задача. Через точку пересечения диагоналей…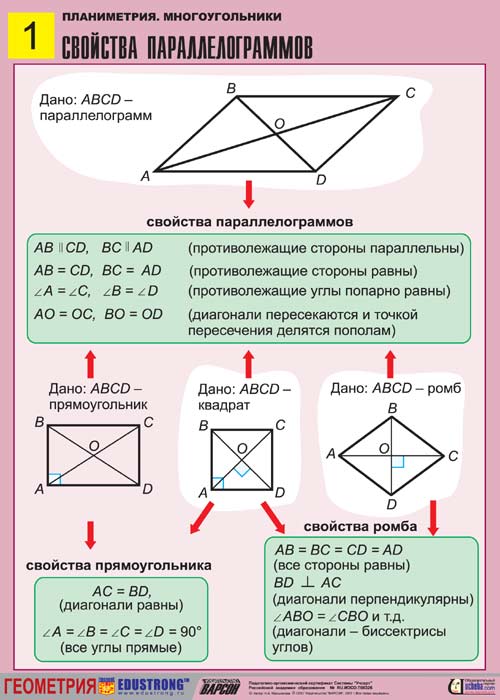
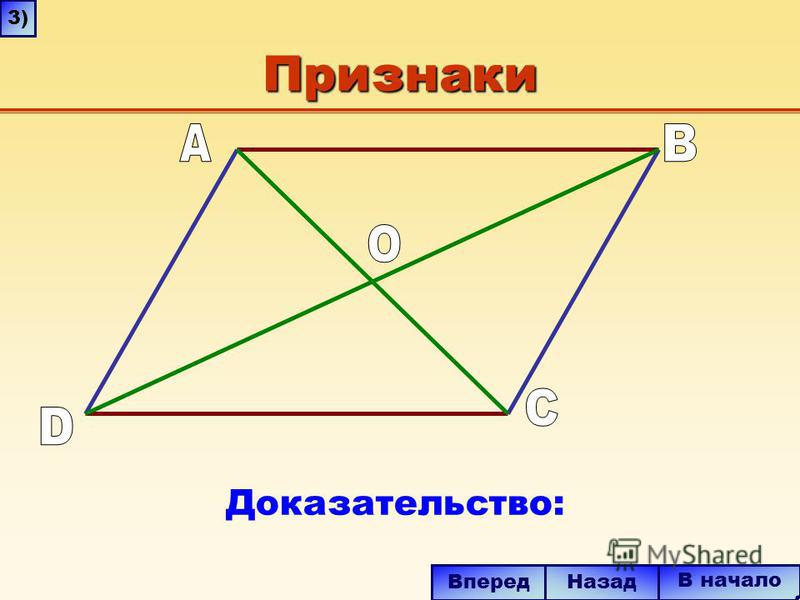 У них сторона АЕ равна стороне ED, сторона BE — общая, а углы при вершине Е равны 90°.Отсюда следует, что диагональ BD равна стороне АВ.
У них сторона АЕ равна стороне ED, сторона BE — общая, а углы при вершине Е равны 90°.Отсюда следует, что диагональ BD равна стороне АВ.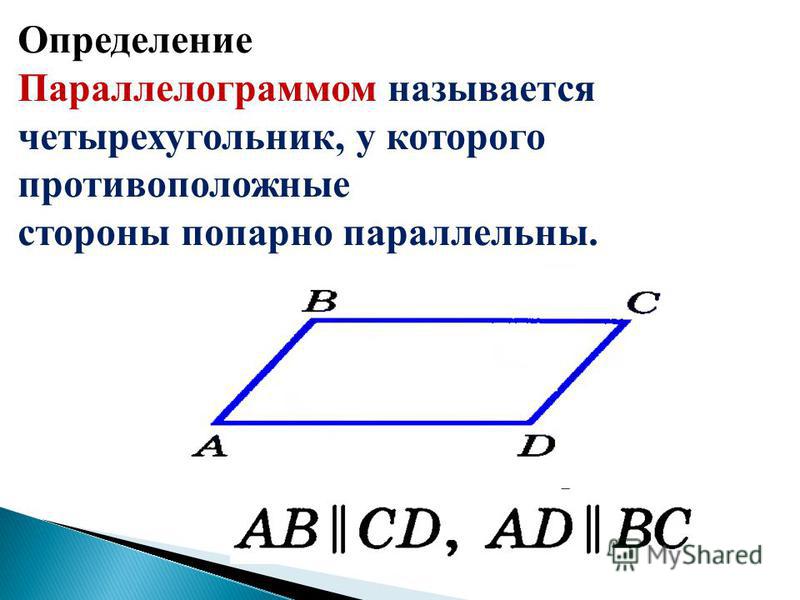 Найдите периметр прямоугольника.(Рис.12)
Найдите периметр прямоугольника.(Рис.12) (Рис.13)
(Рис.13) Углы при вершине О равны 90°. Т.е. по двум сторонам и углу между ними.
Углы при вершине О равны 90°. Т.е. по двум сторонам и углу между ними.

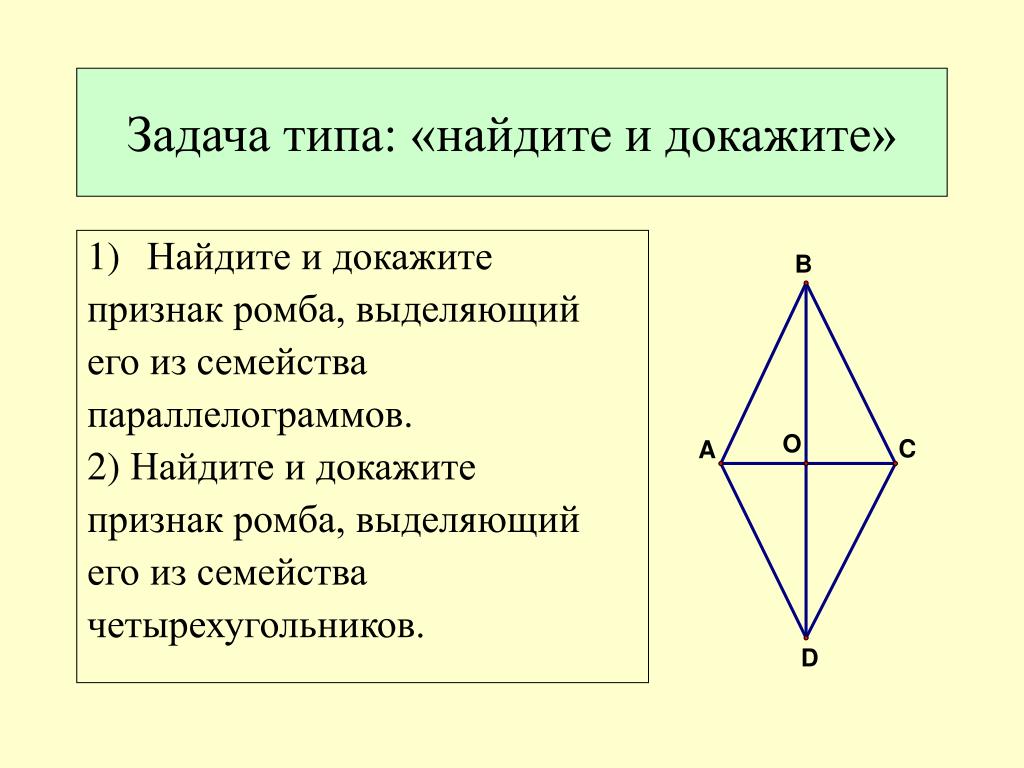 4
4 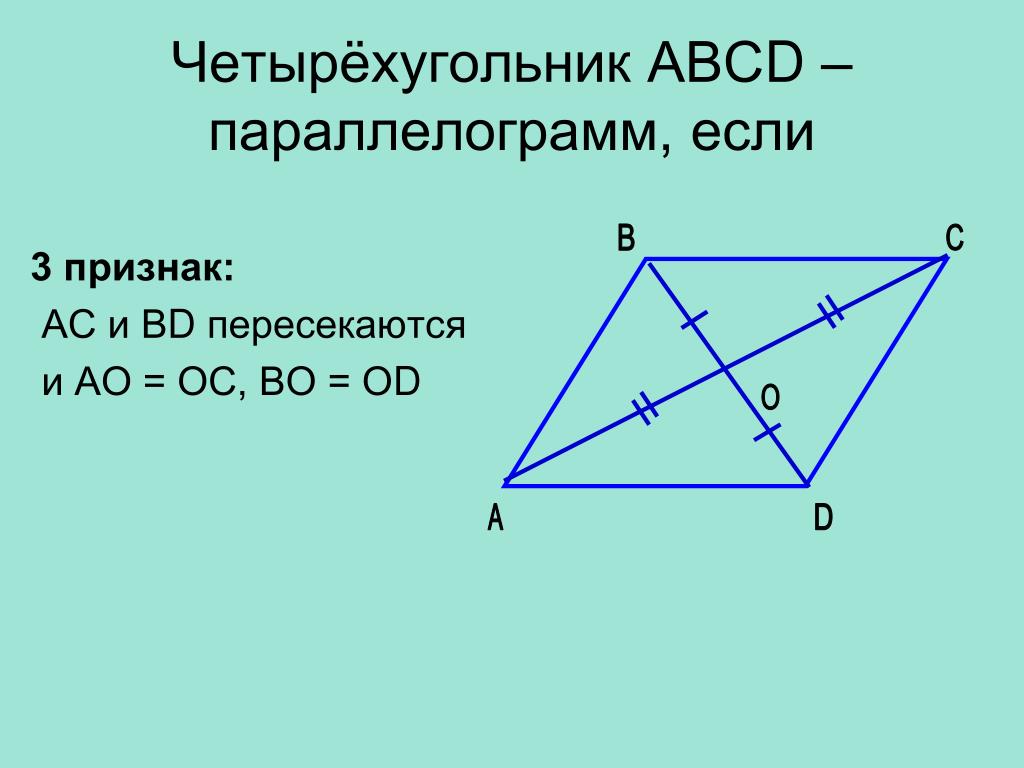 Все права защищены, включая право на полное или частичное воспроизведение в любой форме. Используется по договоренности с Alpha Books , членом Penguin Group (USA) Inc.
Все права защищены, включая право на полное или частичное воспроизведение в любой форме. Используется по договоренности с Alpha Books , членом Penguin Group (USA) Inc. 
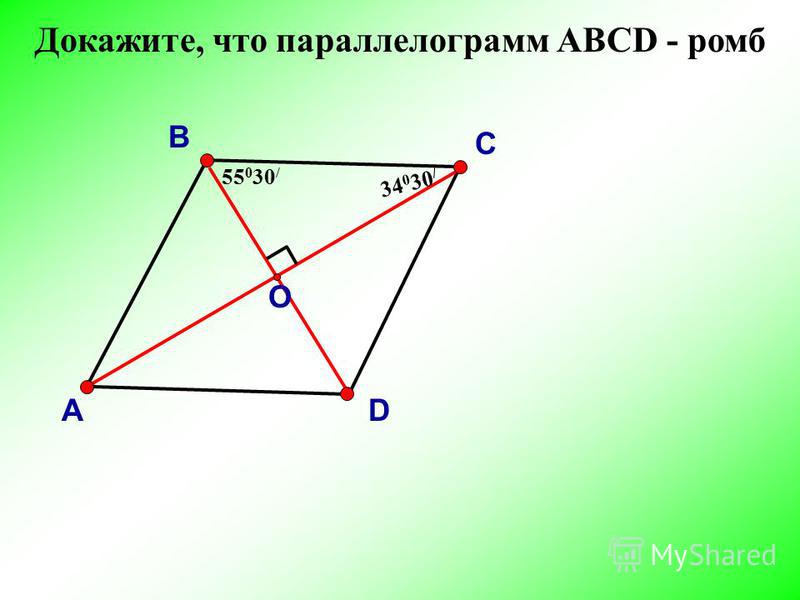

 Находить
Находить В геометрии этот ромб называется ромбом: геометрическая фигура с четырьмя равными сторонами. Ромб является одновременно и параллелограммом, и четырехугольником. В частности, ромб представляет собой четырехстороннюю плоскую фигуру (четырехугольник), противоположные стороны которой параллельны друг другу (параллелограмм). Однако его особая характеристика наличия четырех равных сторон — это то, что отличает ромбы от других четырехугольников.
В геометрии этот ромб называется ромбом: геометрическая фигура с четырьмя равными сторонами. Ромб является одновременно и параллелограммом, и четырехугольником. В частности, ромб представляет собой четырехстороннюю плоскую фигуру (четырехугольник), противоположные стороны которой параллельны друг другу (параллелограмм). Однако его особая характеристика наличия четырех равных сторон — это то, что отличает ромбы от других четырехугольников. 

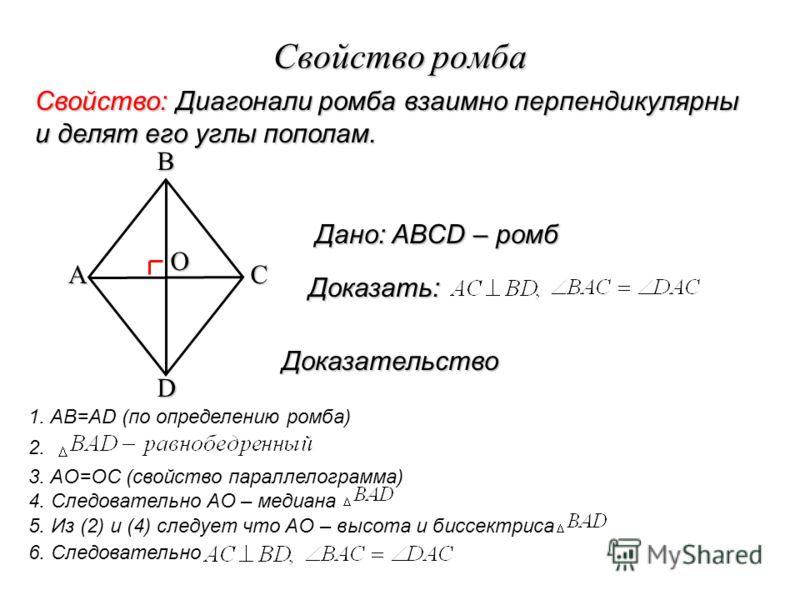 Кроме того, все 4 угла квадрата прямые.
Кроме того, все 4 угла квадрата прямые. 
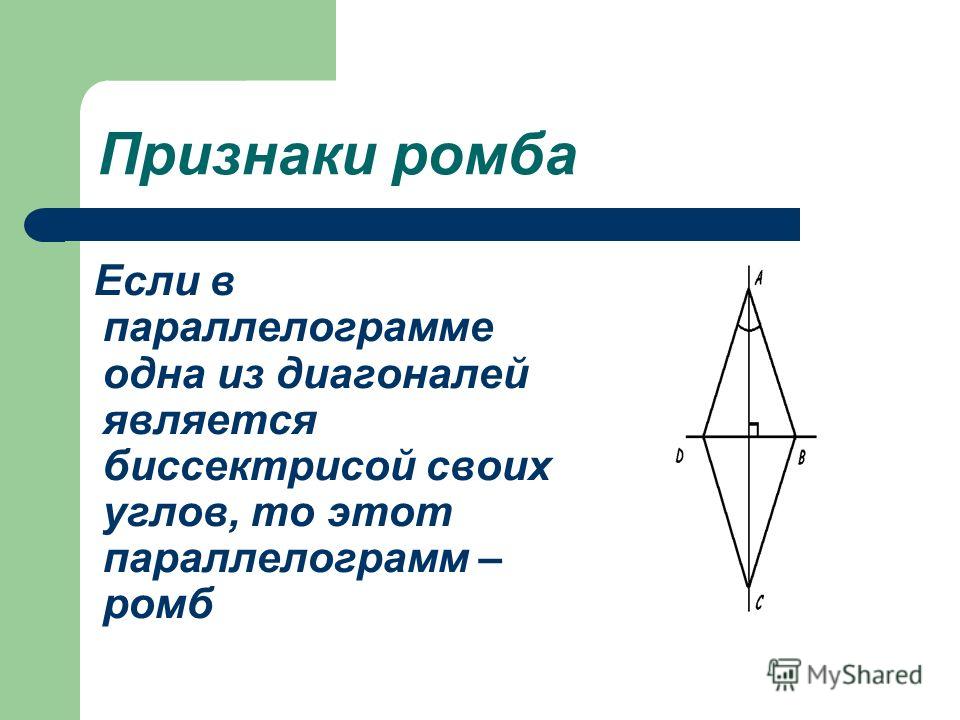 Прежде чем мы узнаем о свойствах, давайте сначала узнаем о параллелограммах. Это четырехсторонняя замкнутая фигура с равными и параллельными противоположными сторонами и равными противоположными углами. Давайте узнаем больше о свойствах параллелограмма подробно в этой статье.
Прежде чем мы узнаем о свойствах, давайте сначала узнаем о параллелограммах. Это четырехсторонняя замкнутая фигура с равными и параллельными противоположными сторонами и равными противоположными углами. Давайте узнаем больше о свойствах параллелограмма подробно в этой статье.