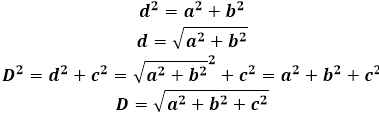Геометрический калькулятор для прямоугольного параллелепипеда можно запустить также, зная два из трех ребер тела и его диагональ. Поскольку диагональ параллелепипеда равна по теореме Пифагора квадратному корню из суммы квадратов всех трех его ребер, то из этого выражения алгебраически можно вывести формулу для третьего неизвестного ребра. (рис.22.4)
d_4=√(a^2+b^2+c^2 )
b=√(a^2+c^2-〖d_4〗^2 )
Имея возможность вычислить неизвестное ребро параллелепипеда, можно следом найти все остальные диагонали его боковых граней. (рис.22.1, 22.2, 22.3)
d_1=√(a^2+c^2 )
d_2=√(a^2+b^2 )=√(a^2+a^2+c^2-〖d_4〗^2 )=√(2a^2+c^2-〖d_4〗^2 )
d_3=√(b^2+c^2 )=√(a^2+c^2-〖d_4〗^2+c^2 )=√(a^2+2c^2-〖d_4〗^2 )
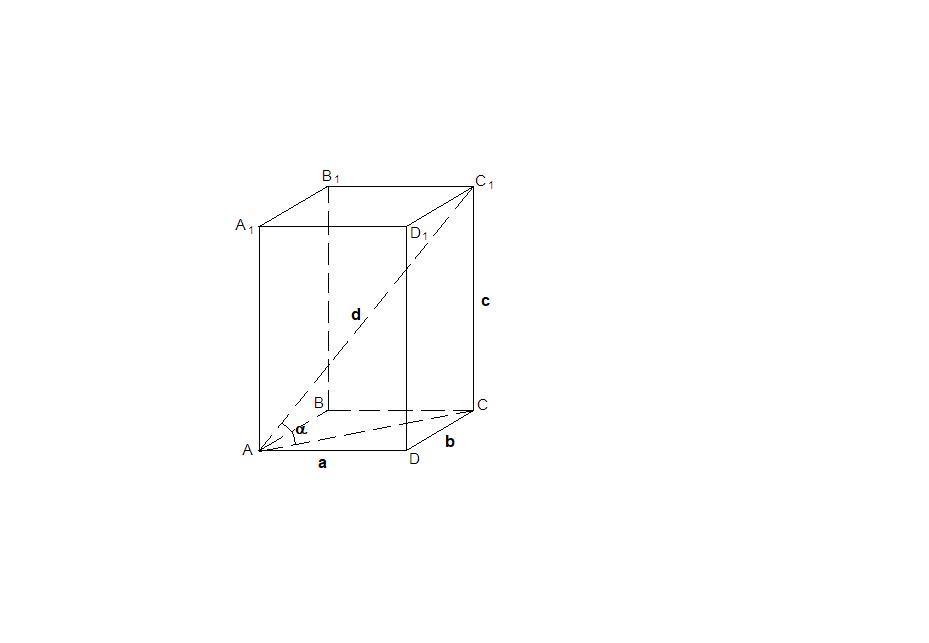
Чтобы найти угол α между диагональю прямоугольного параллелепипеда и диагональю его основания, необходимо воспользоваться отношением синуса — известного бокового ребра а к диагонали параллелепипеда. (рис.22.5)
sinα=a/d_4
Периметр прямоугольного параллелепипеда равен учетверенной сумме ребер, составляющих параллелепипед. Для неизвестного ребра в формулу подставляется полученное из теоремы Пифагора выражение через диагональ параллелепипеда.
P=4(a+b+c)
Площадь полной поверхности прямоугольного параллелепипеда через диагональ также можно вычислить посредством замены неизвестной переменной на соответствующее выражение. Изначально площадь параллелепипеда равна удвоенной сумме попарных произведений его ребер.
S=2(ab+bc+ac)=2((a+c) √(a^2+c^2-〖d_4〗^2 )+ac)
Чтобы найти объем прямоугольного параллелепипеда, зная диагональ, нужно умножить два известных ребра параллелепипеда на квадратный корень из разности квадрата диагонали от суммы квадратов этих ребер.
V=abc=ac√(a^2+c^2-〖d_4〗^2 )
Прямоугольный параллелепипед показан на рисунке.
Имеем b = 6 м, а = 8 м и с = 10м. Найти угол между диагональю параллелепипеда d =AG и плоскостью его основания ABCD, то есть угол между диагоналями AG и АС. (На рисунке диагональ АС не нарисована). Вначале найдем длину диагонали АС = sqrt(a^2 + b^2) = sqrt(8^2 + 6^2) = sqrt(64 + 36) = sqrt(100) = 10 м. (На рисунке диагональ АС не прочерчена, на своем рисунке прочертите ее для наглядности). Значок sqrt означает квадратный корень (от английских слов square root). Математический знак корня БВ не понимает, поэтому ставит вместо него знак вопроса ?). БВ не понимает ни греческие буквы, ни математические знаки, которых нет на клавиатуре. Итак, АС = 10 м. Имеем прямоугольный треугольник АСG. Теперь легко найти угол CAG в этом треугольнике CAG. Угол GCA будет прямоугольным (90°), так как ребро GC в параллелепипеде перпендикулярно основанию ADCB. Из прямоугольного треугольника AGC находим тангенс угла GAC. При этом заметим, GC = с = 10 м, так как оба эти катета – высота параллелепипеда. Имеем tg(GAC) = GC/AC = 10/10 = 1. А если тангенс равен 1, то это угол в 45°. Ответ 45°.
Как найти диагонали параллелепипеда
Параллелепипед — частный случай призмы, у которой все шесть граней являются параллелограммами или прямоугольниками. Параллелепипед с прямоугольными гранями называют также прямоугольным. У параллелепипеда имеется четыре пересекающиеся диагонали. Если даны три ребра а, b, с, найти все диагонали прямоугольного параллелепипеда можно, выполняя дополнительные построения.
Инструкция
Нарисуйте прямоугольный параллелепипед. Запишите известные данные: три ребра а, b, с. Вначале постройте одну диагональ m. Для ее определения используем свойство прямоугольного параллелепипеда, согласно которому все его углы являются прямыми.
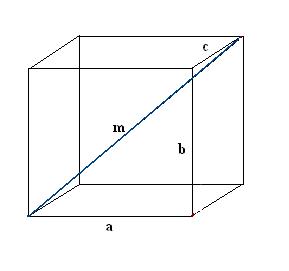
Постройте диагональ n одной из граней параллелепипеда. Построение проведите так, чтобы известное ребро, искомая диагональ параллелепипеда и диагональ грани вместе образовывали прямоугольный треугольник а, n, m.
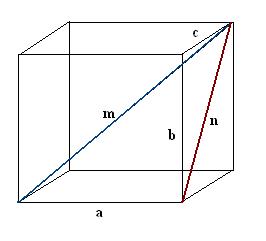
Найдите построенную диагональ грани. Она является гипотенузой другого прямоугольного треугольника b, с, n. Согласно теореме Пифагора n² = с² + b². Вычислите данное выражение и возьмите корень квадратный из полученного значения – это будет диагональ грани n.
Найдите диагональ параллелепипеда m. Для этого в прямоугольном треугольнике а, n, m найдите неизвестную гипотенузу: m² = n² + a². Подставьте известные значения, затем вычислите корень квадратный. Полученный результат и будет первой диагональю параллелепипеда m.
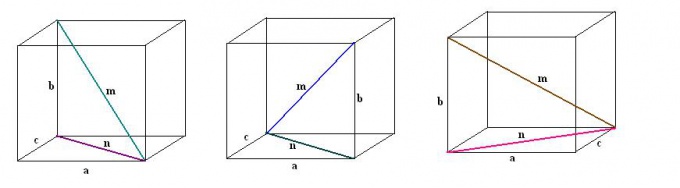
Аналогичным образом проведите последовательно все остальные три диагонали параллелепипеда. Также для каждой из них выполните дополнительные построения диагоналей прилегающих граней. Рассматривая образуемые прямоугольные треугольники и применяя теорему Пифагора, найдите значения остальных диагоналей прямоугольного параллелепипеда.
Видео по теме
Источники:
- нахождение параллелепипеда
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Ответ: 10√2, 45°
Объяснение:
a = 6, b = 8, c = 10.
Диагональ прямоугольного параллелепипеда находится по формуле:
d = √(6² + 8² + 10²) = √(36 + 64 + 100) = √200 = 10√2
AC — проекция диагонали АС₁ на плоскость основания, значит ∠С₁АС — угол наклона диагонали к плоскости основания.
ΔС₁АС: ∠С₁СА = 90°,
sinα = c / d = 10 / (10√2) = 1/√2 = √2/2, ⇒
α = 45°
Параллелепипед — это частный случай призмы, в основании которой лежит прямоугольник с длиной a и шириной b. Двигаясь по вертикальной или наклонной оси на определенную высоту c, данный прямоугольник создает объемное тело, именуемое параллелепипедом.
Параллелепипед по определению может быть наклонным или прямым, то есть угол между высотой и прямоугольником в основании варьируется от 0 до 90 градусов. Прямой параллелепипед имеет в качестве граней исключительно прямоугольники, и даже иногда квадрат (в основании), поэтому решение задач с его участием значительно облегчено. В случае с наклонным параллелепипедом в формулах необходимо учитывать, что боковой гранью является параллелограмм, строение которого зависит также от угла его наклона.
Помимо трех вышеуказанных параметров параллелепипеда — длины, ширины высоты, являющихся его ребрами, в данном теле можно также провести еще несколько отрезков, соединяющих его вершины. Как и в геометрических фигурах на плоскости, линии, проходящие внутри основного каркаса через вершины, называются диагоналями. Диагонали боковых граней прямоугольного параллелепипеда идентичны диагоналям прямоугольников, которыми представлены грани — их, соответственно, можно вычислить, используя подходящий онлайн калькулятор для прямоугольников.
Другое дело — диагональ, проходящая не по внешней поверхности прямоугольного параллелепипеда, а сквозь него, соединяя противоположные вершины верхнего и нижнего оснований. При этом, какая именно пара противоположных вершин соединена, не имеет значения для расчетов, так как если рассмотреть сечения, можно увидеть, что обе диагонали параллелепипеда идентичны и найти их можно одним и тем же способом.
Итак, для того чтобы вывести формулу диагонали через длину, ширину и высоту, необходимо заключить диагональ в плоскую геометрическую фигуру, свойства которой можно будет использовать. Для этого в любом основании — верхнем или нижнем, проводится диагональ, которая образует с диагональю параллелепипеда и боковым ребром (высотой) прямоугольный треугольник. Применив одну лишь теорему Пифагора, можно найти диагональ основания через ширину и длину,а затем диагональ прямоугольного параллелепипеда, добавив в расчеты высоту.
Используя последнюю и предпоследнюю формулу, можно также успешно найти длину, ширину или высоту прямоугольного параллелепипеда, имея в заданных условиях три параметра из четырех, включая диагональ параллелепипеда.
Например: 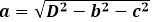
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»