Как найти диагональ треугольника по клеткам - Исправление недочетов и поиск решений вместе с Examum.ru

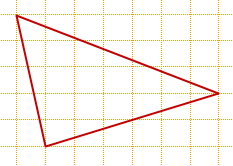
Рассмотрим задачи,в которых требуется найти площадь треугольника изображённого на клетчатой бумаге.

Начнем с прямоугольных треугольников.

Задача 1

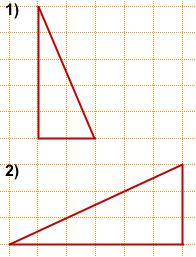
На клетчатой бумаге с размером клетки 1×1 изображен прямоугольный треугольник.

Найти его площадь.

Решение:

Площадь прямоугольного треугольника будем искать с помощью формулы

$[S = frac{1}{2}ab,]$

где a и b — катеты.

Длину катетов считаем по клеточкам.

1) a=2, b=5,

$[ S = frac{1}{2} cdot 2 cdot 5 = 5. ]$

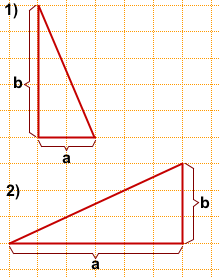
2) a=6, b=3,

$[ S = frac{1}{2} cdot 6 cdot 3 = 9. ]$

Задача 2

На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найти его площадь.

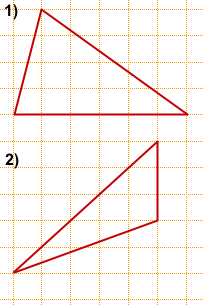
Решение:

Чаще всего площадь произвольного треугольника, изображённого на клетчатой бумаге, ищут по формуле

$[S = frac{1}{2}ah_a ,]$

где a — сторона треугольника, h_a — высота, проведённая к этой стороне.

a и h_a вычисляем по клеточкам (одна из этих величин должна лежать на горизонтальной линии, другая — на вертикальной).

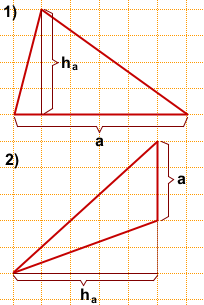
1) a=6, h_a=4,

$[ S = frac{1}{2}ah_a = frac{1}{2} cdot 6 cdot 4 = 12. ]$

2) a=3, h_a=5,

$[ S = frac{1}{2}ah_a = frac{1}{2} cdot 3 cdot 5 = 7,5. ]$

А как найти площадь, если ни одна из сторон треугольника не лежит на горизонтальной или вертикальной линии клеток?

Иногда площадь треугольника можно найти как разность площадей других фигур.

Задача 3

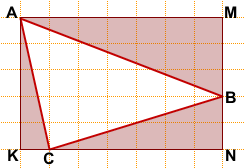
На клетчатой бумаге с размером клетки 1×1 изображён треугольник.

Найдите его площадь.

Решение:

Обозначим вершины треугольника, площадь которого мы ищем, через A, B и C.

Площадь треугольника ABC можно найти как разность площадей прямоугольника AMNK и треугольников AKC, AMB и CBN:

$[S_{Delta ABC} = S_{AMNK} - S_{Delta AKC} - S_{Delta AMB} - S_{Delta CBN} .]$

Площадь прямоугольника найдём по формуле S=ab.

$[ S_{AMNK} = AM cdot AK = 7 cdot 5 = 35. ]$

Площади прямоугольных треугольников найдём по формуле

$[ S = frac{1}{2}ab, ]$

где a и b — катеты.

$[S_{Delta AKC} = frac{1}{2}AK cdot KC = frac{1}{2} cdot 5 cdot 1 = 2,5;]$

$[S_{Delta AMB} = frac{1}{2}AM cdot MB = frac{1}{2} cdot 7 cdot 3 = 10,5;]$

$[S_{Delta CBN} = frac{1}{2}CN cdot BN = frac{1}{2} cdot 6 cdot 2 = 6.]$

Отсюда

$[S_{Delta ABC} = 35 - 2,5 - 10,5 - 6 = 16.]$

Источник

Скольки равна диагональ одной клетки тетради? Ответ дайте корнем пжст. И объясните как вычислит…

Скольки равна диагональ одной клетки тетради? Ответ дайте корнем пжст. И объясните как вычислить… (Да, я тупой)

Комментариев (0)

Проводишь диагональ. У тебя получается в клетке два маленьких прямоугольных треугольника. Длина двух катетов 0,5 см каждый дальше по теореме Пифагора 0,5^2+0,5^2=диагональ клетки тетради^2
0,25+0,25=0,5
Диагональ клетки тетради = корень квадратный из 0,5 (вычисли на калькуляторе, мне лень)

Комментариев (0)

Ваш ответ

Источник

1)На клетчатой бумаге с размером клеток 1 х 1 см изображен треугольник АВС. Найдите высоту, проведенную из вершины А.
2) На клетчатой бумаге с размером клеток 1 х 1 см изображен четырехугольник ABCD. Найдите диагональ BD.

HCN

HCN
8 лет назад

Светило науки — 49 ответов — 0 раз оказано помощи

1. Проведем две высоты. ВН1 к АС и АН2 к ВС.
2. Найдем ВС. ВС² = 3² + 4² = 9+16 =25.
ВС = 5.
3. Найдем площадь треугольника по формуле: S = (а*h)/2, где а — сторона, h — проведенная к ней высота.
4. S = (АС * ВН1)/2 = 5*4/2 = 10
5. С другой стороны площадь этого же треугольника равна S = (BC*AH2)/2.
т.е. 10 = (5*АН2)/2.
6. Отсюда искомая высота равна 4.

1. Проведем диагональ BD. Достроим прямоугольный треугольник.
2. По т.Пифагора ВD² = 3²+4²=25. Т.е. BD = 5.

Светило науки — 2 ответа — 0 раз оказано помощи

Держи дорогая:

1) Площадь треугольника равна 1/2 произведения основания не высоту. То есть 3 х 6 и разделить пополам. получится 9 см квадратных .
2) Диагональ со сторонами квадрата образуют прямоугольный треугольник, где диагональ будет гипотенузой , а катеты по 1 см( по условию). По тереме Пифагора получаем, что диагональ = гипотенузе =

корень квадратный из 2.

Источник

СДАМ ГИА: РЕШУ ОГЭ

Образовательный портал для подготовки к экзаменам

Математика

сайты — меню — вход — новости

СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ

Зарегистрироваться

Восстановить пароль

Войти через ВКонтакте

НАШИ БОТЫ

На сайте что-то не так? Отключите адблок

Новости

30 марта

Подготовься к ЕГЭ или ОГЭ за 1,5 месяца на курсе Флеш

21 марта

Новый сервис: рисование

9 февраля

Об ошибках в математике: проверьте браузер

31 января

Внедрили тёмную тему!

17 января

Разместили утвержденное расписание ОГЭ 2022

9 октября

Как восстановить доступ к Решу ЕГЭ, если у вас Windows XP

ЧУЖОЕ НЕ БРАТЬ!

Зайчиков и Поваляев стащили наши тесты

Задания

Версия для печати и копирования в MS Word

Задание 18 № 348446

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

Спрятать решение

Решение.

По рисунку видно, что длина большей диагонали равна 10.

Ответ: 10.

Аналоги к заданию № 348446: 348586 349027 349478 350071 352059 352113 352152 352709 352791 353130 … Все

Раздел кодификатора ФИПИ: 5.1 Планиметрия. Нахождение геометрических величин.

Спрятать решение

Сообщить об ошибке · Помощь

О проекте · Редакция · Правовая информация · О рекламе

Характеристика задания

Задание 12 ОГЭ по математике представляет собой задачу по планиметрии на вычисление по готовому чертежу, изображённому на клетчатой бумаге. В таких задачах данные представлены в виде чертежа на бумаге в клетку, причём размеры клеток одинаковы и заданы условием. Это задачи на вычисление углов, расстояний, площадей, связанные со всеми изучаемыми в школьном курсе фигурами. Клетки в таких задачах по су- ти выполняют роль линейки: посчитав «по клеточкам» необходимые длины и используя известные геометрические факты и свойства, можно довольно быстро получить ответ на вопрос задачи. К этим задачам вплотную примыкают задания на вычисление элементов плоских фигур по готовому чертежу, на котором указаны координаты некоторых точек фигуры (например, вершин треугольника или четырёх- угольника), позволяющие после выполнения несложных вычислений ответить на вопрос задачи. При этом, как правило, не требуется применения дополнительных формул метода координат

Фигуры на квадратной решетке

В 12 задании необходимо найти какую-либо часть фигуры, нарисованной на клетчатой бумаге. Именно клетчатая бумага 1×1 является особенностью данного задания. Задание не сложное, необходимо внимательно посчитать количество клеток и при необходимости выполнить действие. Опять же нам понадобятся элементарные знания геометрии для успешного решения данного задания. Ниже я разобрал типичные задания. Давайте на них посмотрим.

На клетчатой бумаге размером 1×1 изображён ромб. Найдите длину его большей диагонали.

Внимательно смотрим на рисунок и видим, что длина одной диагонали ромба равна 2, а второй 4.

Так как нас спрашивают длину большей диагонали, то в ответе нужно указать 4.

Ответ: 4.

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линии

Мы знаем, что средняя линия равна полусумме оснований. Нижнее основание данной трапеции равно 8 клеткам, а верхнее — 4 клеткам. Полусумма оснований:

( 8 + 4 ) / 2 = 6

Ответ: 6

На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.

Проведем необходимые отрезки:

Из рисунка можно вычислить длину — это 3.

Ответ: 3.

Четвертый вариант задания (демонстрационный вариант 2017)

Найдите тангенс угла AOB треугольника, изображённого на рисунке.

Для успешного решения все что нам нужно — это определение тангенса: отношение противолежащего катета к прилежащему.

В нашем случае, это означает:

AB / AO

Длины возьмем, посчитав число клеток:

AB = 4

AO = 2

AB / AO = 4 / 2 = 2

Ответ: 2

Найдите площадь территории, которая не занята постройками и полями. Ответ дайте в квадратных метрах.

Владимир купил участок, чтобы заняться фермерством. План его фермы изображен на рисунке, сторона каждой клетки равна 2 м. Ферму планируется обнести забором. Вход будет осуществляться через единственные ворота. Прямо перед воротами предполагается построить жилой дом. За ним будет построен гараж с отдельным въездом. Наибольшее поле будет отведено под посев картофеля. На поле рядом с ним планируется посадить кукурузу. Поле, обозначенное на плане цифрой 3, планируется засеять морковью. Поле, ближайшее к гаражу, планируется отвести под капусту. Оставшееся поле будет засеяно репой. Пустое пространство между полями планируется засыпать гравием. Чтобы засыпать 4 м² гравием, требуется 0,2 м³ материала. Также Владимир планирует купить трактор для хозяйственных нужд.

Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.

Объекты	Жилой дом	Репа	Капуста	Кукуруза
Цифры

Гравий продаётся в больших мешках по 2 м³. Сколько мешков с гравием понадобится для того, чтобы засыпать пространство между полями?

Найдите расстояние между противоположными углами (диагональ) участка в метрах.

Владимир планирует купить трактор для обслуживания полей. Он рассматривает два варианта: трактор с бензиновым двигателем и трактор с дизельным двигателем. Цены за покупку трактора и стоимость топлива, данные о расходе топлива даны в таблице.

	Цена трактора	Средний расход топлива	Стоимость топлива руб. за л
Дизельный двигатель	990 000	5,5 л/ч	47
Бензиновый двигатель	900 000	7 л/ч	53

Обдумав оба варианта, Владимир решил купить трактор с дизельным двигателем. Через сколько часов непрерывной работы экономия от использования трактора с дизельным двигателем вместо трактора с бензиновым двигателем компенсирует разность в стоимости этих тракторов?

Спрятать решение

Решение.

Площадь всего участка равна

м².

Площадь гаража равна

м².

Площадь жилого дома равна

м².

Площадь полей, засеянных капустой, морковью и репой, равна

м².

Площадь полей, засеянных кукурузой и картофелем, равна

м².

Таким образом, площадь территории, которая не занята постройками или полями, равна

м².

Ответ: 248.

Квадрат — это прямоугольник, у которого все стороны равны.
Можно дать и другое определение квадрата:
квадрат — это ромб, у которого все углы прямые.

Получается, что квадрат обладает всеми свойствами параллелограмма, прямоугольника и ромба.

Перечислим свойства квадрата:

Все углы квадрата — прямые, все стороны квадрата — равны.
Диагонали квадрата равны и пересекаются под прямым углом.
Диагонали квадрата делят его углы пополам.

Площадь квадрата, очевидно, равна квадрату его стороны: S=a^2 .
Диагональ квадрата равна произведению его стороны на sqrt{2} , то есть
.

Разберем несколько простых задач на тему «Квадрат». Все они взяты из Банка заданий ФИПИ.

1. Найдите сторону квадрата, диагональ которого равна sqrt{8} .

Мы знаем, что . Тогда $a=genfrac{}{}{}{0}{displaystyle d}{displaystyle sqrt{2}}= 2$ .

2. Найдите радиус окружности, описанной около квадрата со стороной, равной sqrt{8} .

Очевидно, радиус окружности равен половине диагонали квадрата.

Ответ: .

3. Найдите сторону квадрата, описанного около окружности радиуса .

Диаметр окружности равен стороне квадрата.

Ответ: .

4. Найдите радиус окружности, вписанной в квадрат , считая стороны квадратных клеток равными sqrt{2} .

Чуть более сложная задача. Нарисуйте окружность, вписанную в данный квадрат, то есть касающуюся всех его сторон. Вы увидите, что диаметр этой окружности равен стороне квадрата.

Ответ: .

5. Найдите радиус окружности, вписанной в четырехугольник . В ответе укажите
.

Считаем стороны клеток равными единице. Четырехугольник — квадрат. Все его стороны равны, все углы — прямые. Как и в предыдущей задаче, радиус окружности, вписанной в квадрат, равен половине его стороны.

Найдем на чертеже прямоугольный треугольник. По теореме Пифагора найдем сторону, например, . Она равна . Тогда радиус вписанной окружности равен $genfrac{}{}{}{0}{displaystyle sqrt{10}}{displaystyle 2}$ . В ответ запишем .

Ответ: .

Источник

Скольки равна диагональ одной клетки тетради?

Ответ дайте корнем пжст.

И объясните как вычислить.

(Да, я тупой).

На этой странице находится вопрос Скольки равна диагональ одной клетки тетради?, относящийся к категории
Математика. По уровню сложности данный вопрос соответствует знаниям
учащихся 10 — 11 классов. Здесь вы найдете правильный ответ, сможете
обсудить и сверить свой вариант ответа с мнениями пользователями сайта. С
помощью автоматического поиска на этой же странице можно найти похожие
вопросы и ответы на них в категории Математика. Если ответы вызывают
сомнение, сформулируйте вопрос иначе. Для этого нажмите кнопку вверху.

Источник

Скольки равна диагональ одной клетки тетради? Ответ дайте корнем пжст. И объясните​ как вычислит…

Ваш ответ

Фигуры на квадратной решетке

Четвертый вариант задания (демонстрационный вариант 2017)

Скольки равна диагональ одной клетки тетради? Ответ дайте корнем пжст. И объясните как вычислит…