Свойства параллелограмма:
1. Противоположные стороны равны и параллельны
2. Противоположные углы равны
3. Точка пересечения диагоналей, делит их пополам
1. Длина диагонали параллелограмма через стороны, известную диагональ и угол.
a, b — стороны параллелограмма
D — большая диагональ
d — меньшая диагональ
α, β — углы параллелограмма
Формулы диагонали через стороны и углы параллелограмма (по теореме косинусов), (D, d):
Формулы диагонали через стороны и известную диагональ (по формуле- сумма квадратов диагоналей), (D, d):
2. Длина диагонали параллелограмма через площадь, известную диагональ и угол.
D — большая диагональ
d — меньшая диагональ
α, β — углы между диагоналями
S — площадь параллелограмма
Формулы диагонали через площадь, известную диагональ и угол между диагоналями, (D, d):
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
- Подробности
-
Опубликовано: 03 ноября 2011
-
Обновлено: 13 августа 2021
Параллелограмм представляет собой геометрическую фигуру, где лежащие напротив друг друга ребра
взаимно параллельны.
В задачах по геометрии иногда нужно найти длину его диагонали. В некоторых из них это прямой вопрос,
а в некоторых диагональ нужно вычислить, чтобы потом через нее вычислять другие геометрические
объекты. Например, используя значения длины отрезков, соединяющих вершины, ребер этой геометрической
фигуры, ее углов, вычисляется значение ее площади, другая диагональ. Если в параллелограмме
неизвестны его углы, но известны стороны и угол между диагоналями, то из этих значений узнаются
через расчет углы параллелограмма.
- Длинная диагональ параллелограмма через две стороны и тупой
угол - Короткая диагональ параллелограмма через две стороны и
тупой угол - Длинная диагональ параллелограмма через две стороны и
острый угол - Короткая диагональ параллелограмма через две стороны и
острый угол - Диагональ параллелограмма через две стороны и другую
известную диагональ - Диагональ параллелограмма через площадь, другую известную
диагональ и угол между диагоналями
Длинная диагональ через две стороны и тупой угол
В параллелограмме для вычисления длины наибольшей диагонали при имеющихся данных о его ребрах и тупом
угле между ними следует рассчитать квадрат ребер, суммировать эти значения. После этого умножить
значение одного ребра на другое, на косинус тупого угла между ними, на два. Затем от первой суммы
отнять это произведение и найти из этой разности квадратный корень.
D = √(a² + b² – 2 * a * b * cosβ
где D – диагональ этой геометрической фигуры, a, b – ее ребра, cos β – косинус тупого угла между
ребрами этой фигуры
Цифр после
запятой:
Результат в:
Пример. Значения ребер этого четырехугольника 2 и 4, а косинус тупого угла (120
градусов) между ними -0,5. Диагональ равна: D = √(2²+ 4² – 2 * 2 * 4 * (-0,5)) = √(4+16 – 16 *( -0,5)) = √(20 + 
(ответ округлен)
Диагональ через две стороны и другую известную диагональ
В параллелограмме для вычисления длины проведенной в нем диагонали через его стороны и другую
диагональ следует возвести в квадрат каждую его сторону и умножить на 2 оба результата, затем
сложить полученные значения (это первый результат). Потом следует возвести в квадрат значение длины
другой диагонали (это второй результат). Затем из первого результата вычесть второй и найти из
полученного значения квадратный корень.
D = √(2 * a² + 2 * b² – d²)
где D – диагональ параллелограмма, a, b – его стороны, d – другая диагональ параллелограмма
Цифр после
запятой:
Результат в:
Пример. Пусть стороны параллелограмма 2 и 4, а одна из диагоналей 4. Тогда вторая
диагональ равна: D = √(2 * 2²+ 2 * 4² – 4²) = √(8 + 32 – 16) = √24 = 4,9 (ответ
округленный)
Короткая диагональ через две стороны и тупой угол
Для нахождения наименьшего отрезка соединяющего противоположные вершины в этой геометрической фигуре
через его ребра и тупой угол между ними возводятся в квадрат длины его ребер, складываются
полученные числа (один результат). Далее перемножаются значения длины ребер, косинус тупого угла,
удваивается полученное число (это другой результат). К одному результату прибавляется другой и
находится из полученного значения квадратный корень.
D = √(a² + b² + 2 * a * b * cosβ)
где D – диагональ параллелограмма, a, b – его стороны, cos β – косинус тупого угла между ребрами.
Цифр после
запятой:
Результат в:
Пример. Если ребра этой геометрической фигуры 1 и 3, а косинус тупого угла (120)
между ними -0,5. Тогда диагональ равна: D = √(1²+ 3² + 2 * 1 * 3 * (-0,5)) = √(1 + 9 + 6 * (-0,5)) = √(10 – 3) = 2,6
(ответ округлен)
Длинная диагональ через две стороны и острый угол
В этом четырехугольнике для расчета значения протяженности большего отрезка, соединяющего в нем
расположенные друг напротив друга вершины, через два его ребра и острый угол нужно сначала возвести
в квадрат значение длины его ребер, потом складываются результаты этого вычисления (это первое
слагаемое для последующего сложения). Затем умножаются длины ребер друг на друга, на косинус острого
угла, найденное произведение еще на 2 (это второе слагаемое). Затем оба слагаемых складываются и из
суммы вычисляется квадратный корень.
D = √(a² + b² + 2 * a * b * cos α)
где D – диагональ этой геометрической фигуры, a, b – его ребра, cos α – косинус острого угла
Цифр после
запятой:
Результат в:
Пример. Если ребра этого четырехугольника 2 и 5, а косинус острого угла (60
градусов) 0,5. Тогда диагональ рассчитывается: D = √(2²+ 5² + 2 * 2 * 5 * 0,5) = √(4 + 25 + 20 * 0,5 = √(29 + 10) = 6,2
(округленно)
Короткая диагональ через две стороны и острый угол
В параллелограмме для вычисления длины наименьшей проведенной в нем диагонали через его стороны и
острый угол между ними следует возвести в квадрат каждую его сторону, затем сложить полученные
значения (это первый результат). Потом следует перемножить между собой стороны, косинус тупого угла
между ними, удвоить полученное значение (это второй результат). Затем из первого результата вычесть
второй и найти из полученного значения квадратный корень.
D = √(a² + b²– 2 * a * b * cosα)
где D – диагональ параллелограмма, a, b – его стороны, cos α – косинус острого угла между сторонами
параллелограмма
Цифр после
запятой:
Результат в:
Пример. Пусть стороны параллелограмма 2 и 4, а косинус острого угла (60) между ними
0,5. Тогда диагональ равна: D = √(2²+ 4² – 2 * 2 * 4 * 0,5) = √(4 + 16 – 16 * 0,5) = √(20 — 
(ответ округлен)
Диагональ через площадь, другую известную диагональ и угол между диагоналями
В параллелограмме для вычисления длины проведенного в нем отрезка, соединяющего противоположные
вершины, используя значение его площади, другой диагонали и угол между диагоналями, следует удвоить
значение его площади (это первый результат). Потом следует умножить значение длины другого отрезка,
соединяющего противоположные вершины, на синус угла между диагоналями (это второй результат). Затем
следует разделить первый результат на второй.
D = (2 * S) / (d * sin α)
где D – диагональ параллелограмма, S – площадь параллелограмма, d – вторая диагональ этой
геометрической фигуры, sinα – синус угла между диагоналями параллелограмма
Цифр после
запятой:
Результат в:
Пример. Значение площади составляет 30, одна из диагоналей 4, синус угла (30
градусов) между диагоналями 0,5. Тогда другая диагональ равна: D = 2 * 30 / 4 * 0,5 = 60 / 2 = 30
Параллелограмм — это четырехугольник, у которого по определению противоположные стороны параллельны и равны. Как следствие, противоположные углы параллелограмма также будут между собой равны, а так как сумма всех углов в четырехугольнике равна 360 градусам, то можно сделать вывод, что сумма двух последовательных углов будет равна 180 градусам. Данное свойство будет играть существенную роль для нахождения диагоналей параллелограмма, с учетом того, что они разной длины.
Так как каждая диагональ параллелограмма делит его на два равновеликих треугольника, именно их свойства и будут использованы для выведения формулы диагонали параллелограмма.
В любом треугольнике угол и сторона, лежащие напротив, пропорциональны друг другу. Для параллелограмма это будет значить, что более длинная диагональ будет лежать напротив тупого угла, а более короткая диагональ — напротив острого.С учетом того, что стороны треугольников, полученных в результате проведения диагоналей, одинаковы — это стороны параллелограмма, значение градусной меры угла между данными сторонами определяет чему будет равна длина диагонали,вычисленной по формуле. Другими словами, если в формулудиагонали подставить значение острого угла параллелограмма, то калькулятор вычислит длину короткой диагонали, а если подставить значение тупого угла — то длинной.
Для того чтобы перейти от одного угла к другому, используется разность 180 градусов и заданного угла, таким образом калькулятор одновременно может вычислить обе диагонали.
α=180°-β
Чтобы вывести формулу диагонали параллелограмма, используется теорема косинусов в треугольнике, который диагональ образует со сторонами. В любом из подобных треугольников, диагональ является стороной, противолежащей углу параллелограмма и, соответственно, ее квадрат равен сумме квадратов двух других сторон треугольника (сторон параллелограмма, в данном случае) за вычетом удвоенного произведения тех же сторон на косинус приведенного угла. Чтобы найти длину диагонали параллелограмма, калькулятор вычисляет квадратный корень из данного выражения.
Параллелограмм – свойства, признаки, определение
Определение параллелограмма
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны и равны. Как выглядит параллелограмм:
Частные случаи параллелограмма: ромб, прямоугольник, квадрат.
Диагонали — отрезки, которые соединяют противоположные вершины.
Свойства диагоналей параллелограмма:
- В параллелограмме точка пересечения диагоналей делит их пополам.
- Любая диагональ параллелограмма делит его на два равных треугольника.
- Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон.
Биссектриса угла параллелограмма — это отрезок, который соединяет вершину с точкой на одной из двух противоположных сторон и делит угол при вершине пополам.
Свойства биссектрисы параллелограмма:
- Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
- Биссектрисы углов, прилежащих к одной стороне параллелограмма пересекаются под прямым углом.
- Отрезки биссектрис противоположных углов равны и параллельны.
Как найти площадь параллелограмма:
- S = a × h, где a — сторона, h — высота.
- S = a × b × sinα, где a и b — две стороны, sinα — синус угла между ними. Для ромба формула примет вид S = a2 × sinα.
- Для ромба: S = 0,5 × (d1 × d2), где d1 и d2 — две диагонали.
Для параллелограмма: S = 0,5 × (d1 × d2) × sinβ, где β — угол между диагоналями.
Периметр параллелограмма — сумма длины и ширины, умноженная на два.
P = 2 × (a + b), где a — ширина, b — высота.
У нас есть отличные дополнительные курсы по математике для учеников с 1 по 11 классы!
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой.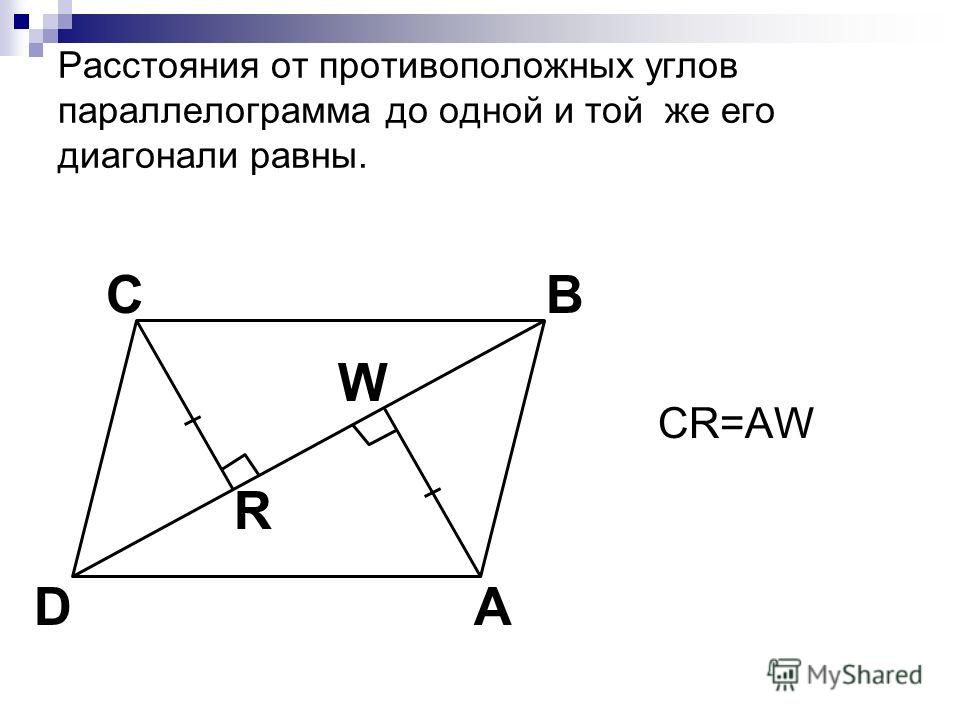
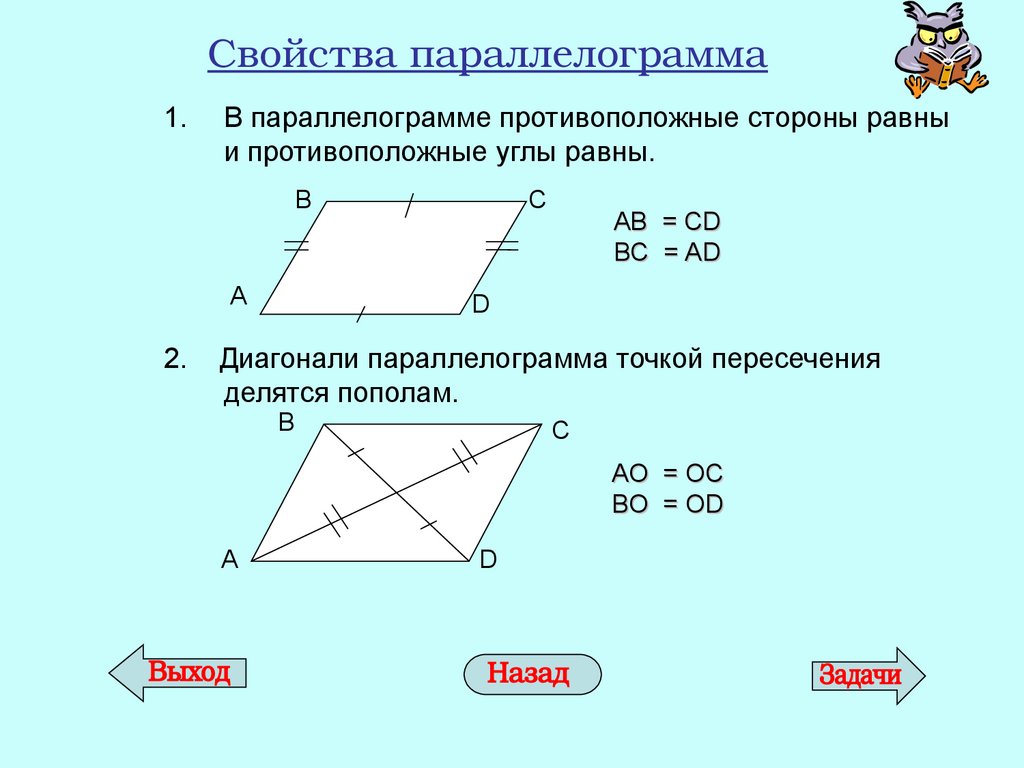
Свойства параллелограмма
Геометрическая фигура — это любое множество точек. У каждой фигуры есть свои свойства, которые отличают их между собой и помогают решать задачи по геометрии в 8 классе.
Рассмотрим основные свойства диагоналей и углов параллелограмма, узнаем чему равна сумма углов параллелограмма и другие особенности этой фигуры. Вот они:
- Противоположные стороны параллелограмма равны.
ABCD — параллелограмм, значит, AB = DC, BC = AD. - Противоположные углы параллелограмма равны.
ABCD — параллелограмм, значит, ∠A = ∠C, ∠B = ∠D. - Диагонали параллелограмма точкой пересечения делятся пополам.
ABCD — параллелограмм, AC и BD — диагонали, AC∩BD=O, значит, BO = OD, AO = OC. - Диагональ делит параллелограмм на два равных треугольника.
ABCD — параллелограмм, AC — диагональ, значит, △ABC = △CDA. - Сумма углов в параллелограмме, прилежащих к одной стороне, равна 180 градусам.
ABCD — параллелограмм, значит, ∠A + ∠D = 180°. - В параллелограмме диагонали d1, d2 и стороны a, b связаны следующим соотношением: d12 + d22 = 2 × (a2 + b2 ).
А сейчас докажем теорему, которая основана на первых двух свойствах.
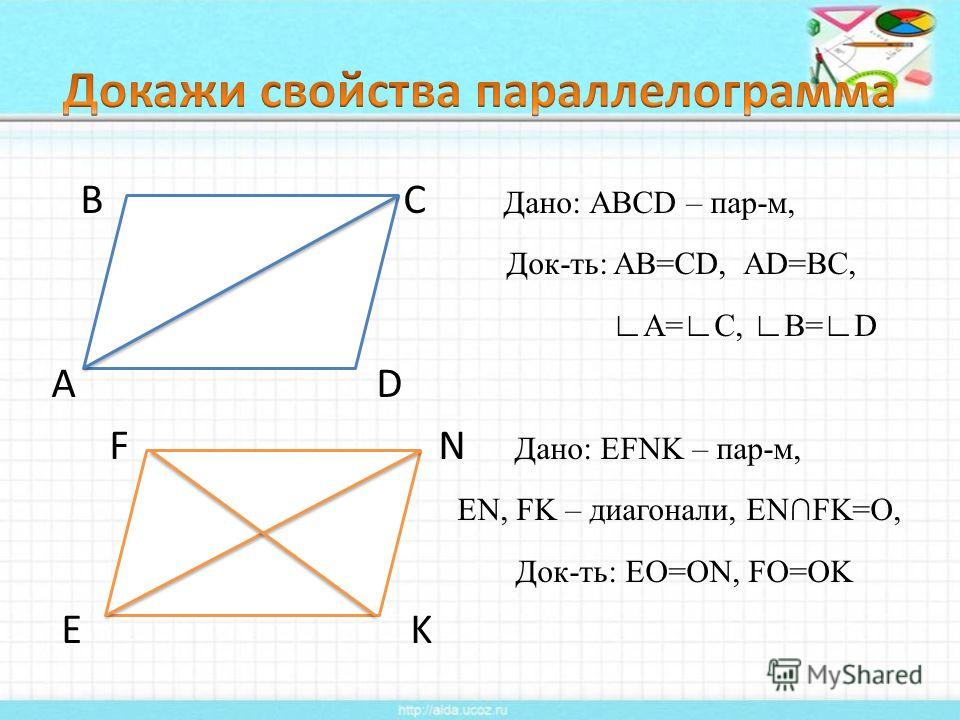
Теорема 1. В параллелограмме противоположные стороны и противоположные углы равны.
В любом выпуклом четырехугольнике диагонали пересекаются. Все, что мы знаем о точке их пересечения — это то, что она лежит внутри четырехугольника.
Если мы проведем обе диагонали в параллелограмме, точка пересечения разделит их пополам. Убедимся, так ли это:
- AB = CD как противоположные стороны параллелограмма.
- ∠1 = ∠2 как накрест лежащие углы при пересечении секущей AC параллельных прямых AB и CD; ∠3 = ∠4 как накрест лежащие углы при пересечении секущей BD параллельных прямых AB и CD.
- Следовательно, треугольник AOB равен треугольнику COD по второму признаку равенства треугольников, то есть по стороне и прилежащим к ней углам, из чего следует:
- CO = AO
- BO = DO
Теорема доказана.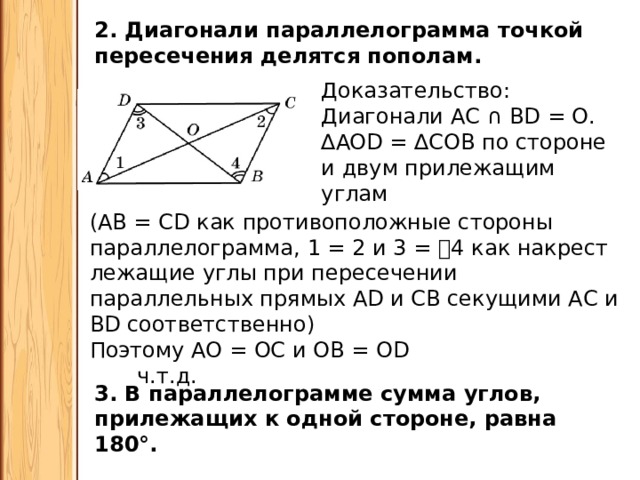
Признаки параллелограмма
Признаки параллелограмма помогают распознать эту фигуру среди других четырехугольников. Сформулируем три основных признака.
Первый признак параллелограмма. Если в четырехугольнике две противолежащие стороны равны и параллельны, то этот четырехугольник — параллелограмм.
Докажем 1 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
- AB || CD
- AB = CD
Чтобы назвать этот четырехугольник параллелограммом, нужно внимательно рассмотреть его стороны.
Сейчас мы видим одну пару параллельных сторон. Нужно доказать, что вторая пара сторон тоже параллельна.
Шаг 2. Проведем диагональ. Получились два треугольника ABC и CDA, которые равны по первому признаку равенства, то есть по по двум сторонам и углу между ними:
- AC — общая сторона;
- По условию AB = CD;
- ∠1 = ∠2 как внутренние накрест лежащие углы при пересечении параллельных прямых AB и CD секущей АС.
Шаг 3. Из равенства треугольников также следует:
- ∠3 = ∠4
Эти углы тоже являются внутренними накрест лежащими для прямых CB и AD. А это как раз и есть признак параллельности прямых. Значит, CB || AD и ABCD — параллелограмм.
Вот так быстро мы доказали первый признак.
Второй признак параллелограмма. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
Докажем 2 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
- AB = CD
- BC = AD
Шаг 2. Проведем диагональ AC и рассмотрим треугольники ABC и CDA:
- AC — общая сторона;
- AB = CD по условию;
- BC = AD по условию.
Из этого следует, что треугольники ABC и CDA равны по третьему признаку, а именно по трем сторонам.
Шаг 3. Из равенства треугольников следует:
- ∠ DCA = ∠BAC
А так как эти углы — накрест лежащие при сторонах BC и AD и диагонали AC, значит, стороны BC и AD параллельны.
- ∠DAC = ∠BCA
Эти углы — накрест лежащие при сторонах AB и CD и секущей AC. Поэтому стороны AB и CD тоже параллельны. Значит, четырехугольник ABCD — параллелограмм, ЧТД.
Доказали второй признак.
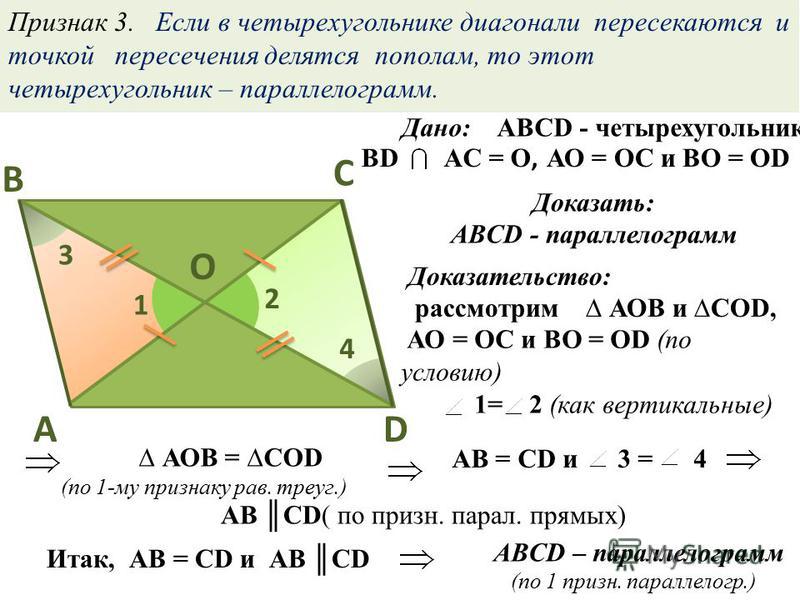
Третий признак параллелограмма. Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Докажем 3 признак параллелограмма:
Шаг 1. Если диагонали четырехугольника ABCD делятся пополам точкой O, то треугольник AOB равен треугольнику COD по двум сторонам и углу между ними:
- CO = OA;
- DO = BO;
- углы между ними равны, как вертикальные, то есть угол AOB равен углу COD.
Шаг 2. Из равенства треугольников следует, что CD = AB.
Эти стороны параллельны CD || AB, по равенству накрест лежащих углов: ∠1 = ∠2 (следует из равенства треугольников AOB и COD).
Значит, ABCD является параллелограммом по первому признаку, который мы доказали ранее.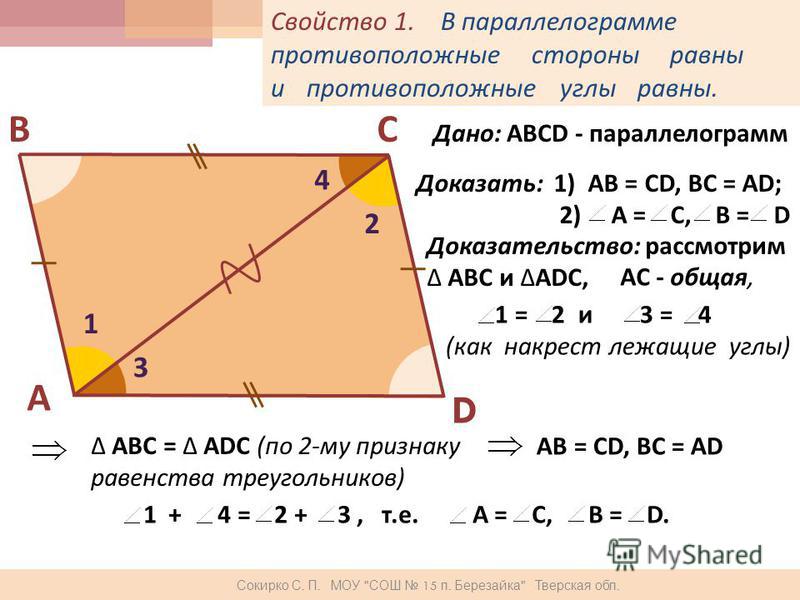
Теперь мы знаем свойства параллелограмма и то, что выделяет его среди других четырехугольников — признаки. Так как они совпадают, эти формулировки можно использовать для определения параллелограмма. Но самое распространенное определение все-таки связано с параллельностью противоположных сторон.
Как найти диагональ параллелограмма? – Обзоры Вики
Часто задаваемые вопросы о диагонали формулы параллелограмма
Для любого параллелограмма abcd формула длин диагоналей имеет вид p=u221ax2+y2u22122xycosA=u221ax2+y2+2xycosB p = x 2 + y 2 u2212 2 xy cos u2061 A = x 2 + y 2 + 2 xy cos u2061 B и q=u221ax2+y2+2xycosA=u221ax2+y2u22122xycosB q = x 2 + y 2 + 2 ху, потому что u2061 А = х 2 + у 2 u2212 2 ху, потому что u2061
Следовательно, равны ли диагонали параллелограмма 180°? Диагонали Bisect друг друга под углом 90 градусов. Сумма любых двух смежных внутренних углов равна 180 градусов. Противоположные стороны равны и параллельны друг другу.
Как найти диагональ квадратного примера?
Диагональ формула квадрата = a√2; где «а» — длина стороны. Данную длину стороны подставляют в эту формулу, чтобы получить длину диагонали. Например, если длина стороны квадрата равна 10 см, мы подставим в формулу значение d = a√2.
По какой формуле найти площадь параллелограмма? Площадь параллелограмма – это пространство, заключенное между его четырьмя сторонами. Площадь равна произведению длины и высоты параллелограмма .
…
Площадь = ½ × d 1 × д 2
грех (у)
| Все формулы для вычисления площади параллелограмма | |
|---|---|
| Использование базы и высоты | А = б × ч |
| Использование тригонометрии | А = ab sin (х) |
• 17 июня 2020 г.
Как найти диагональ восьмиугольника? Диагональ восьмиугольника — это отрезок, соединяющий любые две несмежные вершины.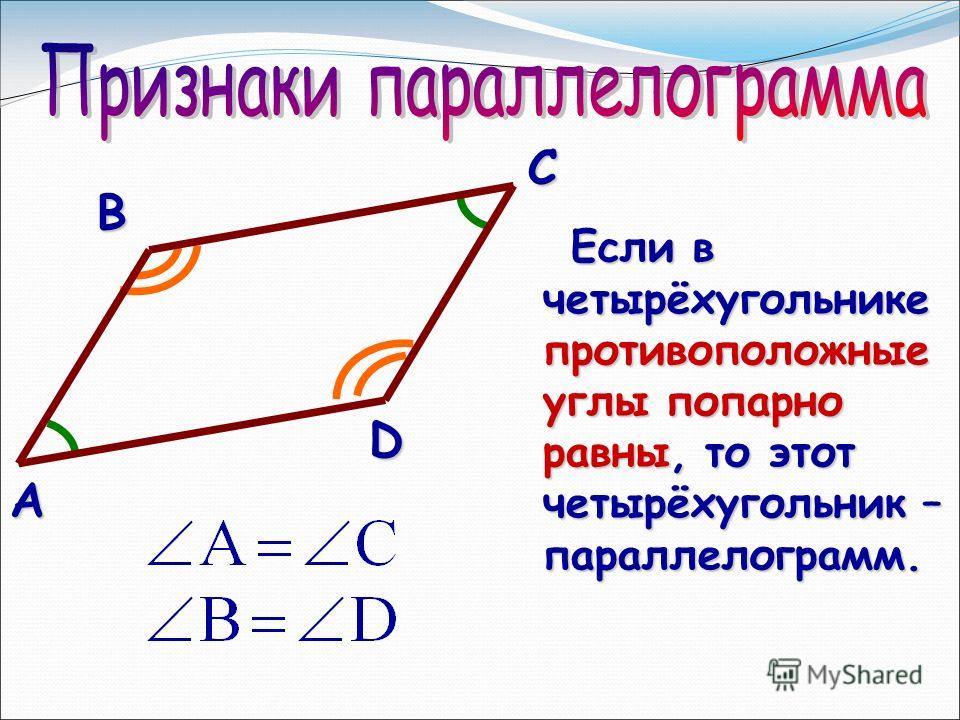
Что такое диагональ в математике?
В геометрии диагональ отрезок, соединяющий две вершины многоугольника или многогранника, когда эти вершины не находятся на одном ребре. … В матричной алгебре диагональ квадратной матрицы — это набор элементов, простирающихся от одного угла до самого дальнего угла. Есть и другие, не математические применения.
Какая диагональ у квадрата 12 × 12?
Нахождение диагонали квадрата
| Квадратный размер | Диагональ |
|---|---|
| 12 « | 17 » |
| 12 1 / 2 ″ | 17 5 / 8 ″ |
| 13 « | 18 3 / 8 ″ |
| 13 1 / 2 ″ | 19 1 / 8 ″ |
Какова диагональ квадрата 48? Каждая сторона будет 48/44 = 12 дюймов.
Диагонали квадрата равны?
Диагонали квадрата делят его углы пополам. Противоположные стороны квадрата параллельны и равны по длине. Все четыре угла квадрата равны (каждый равен 360°/4 = 90°, прямой угол). … Диагонали квадрата равны равный.
Как найти площадь параллелограмма со сторонами и диагоналями?
Площадь параллелограмма можно вычислить, если известны диагонали и угол их пересечения. Формула дается как, площадь = ½ × d1 × d2 sin(x), где «d1» и «d2» — длины диагоналей параллелограмма, а «x» — угол между ними.
Каково полное расстояние вокруг параллелограмма? Периметр параллелограмма – это сумма длин его четырех сторон.
Что такое диагональный многоугольник?
Применительно к многоугольнику диагональ отрезок, соединяющий любые две непоследовательные вершины.
Сколько диагоналей в восьмиугольнике? ∴ Восьмиугольник имеет 20 диагонали. Следовательно, вариант С является правильным ответом. Примечание: Восьмиугольник — это многоугольник в геометрии, который имеет 8 сторон и 8 углов.
Сколько диагоналей у додекагона?
Следовательно, есть 54 диагонали в двенадцатиугольнике.
…
Треугольники в додекагоне.
| Свойства | Ценности |
|---|---|
| Внутренний угол | 150° |
| Внешний угол | 30° |
| Количество диагоналей | 54 |
| Количество треугольников | 10 |
Какая диагональ выглядит? Диагональ состоит из прямая линия, расположенная под углом, а не прямо вверх или поперек.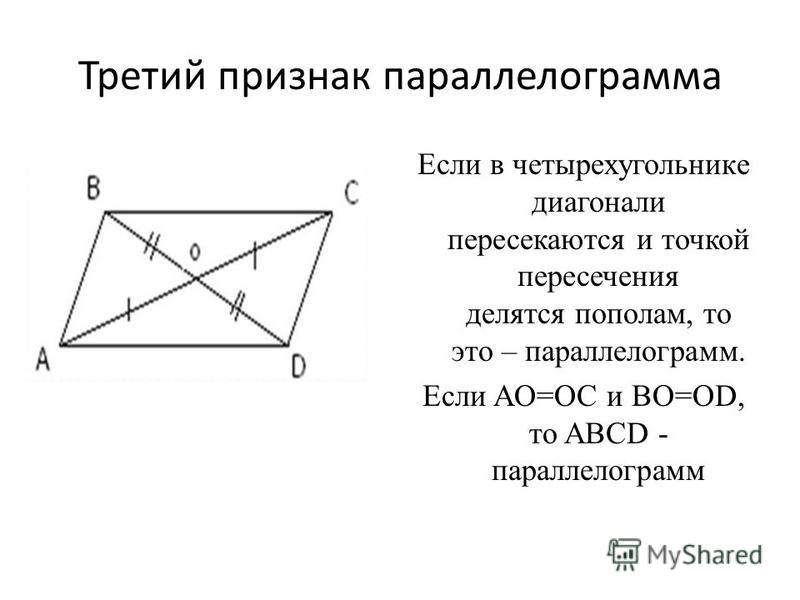
Что такое диагональный ответ?
Диагональ отрезок, соединяющий один угол (вершину) многоугольника с другим, но не являющийся ребром (стороной). Другими словами, он соединяет любые две несмежные вершины многоугольника. Итак, мы образуем диагональ в многоугольнике, когда мы напрямую соединяем любые две вершины, которые не соединены ни одной стороной.
Что такое диагональ и пример? Определение диагонали — это что-то с наклонными линиями или линией, которая соединяет один угол с самым дальним углом. Пример диагонали линия, идущая от нижнего левого угла квадрата к верхнему правому углу. … (геометрия) Диагональная линия или плоскость.
Как найти количество сторон диагонали?
Количество диагоналей в многоугольнике находится по формуле п (п-3) / 2 где n — количество сторон многоугольника.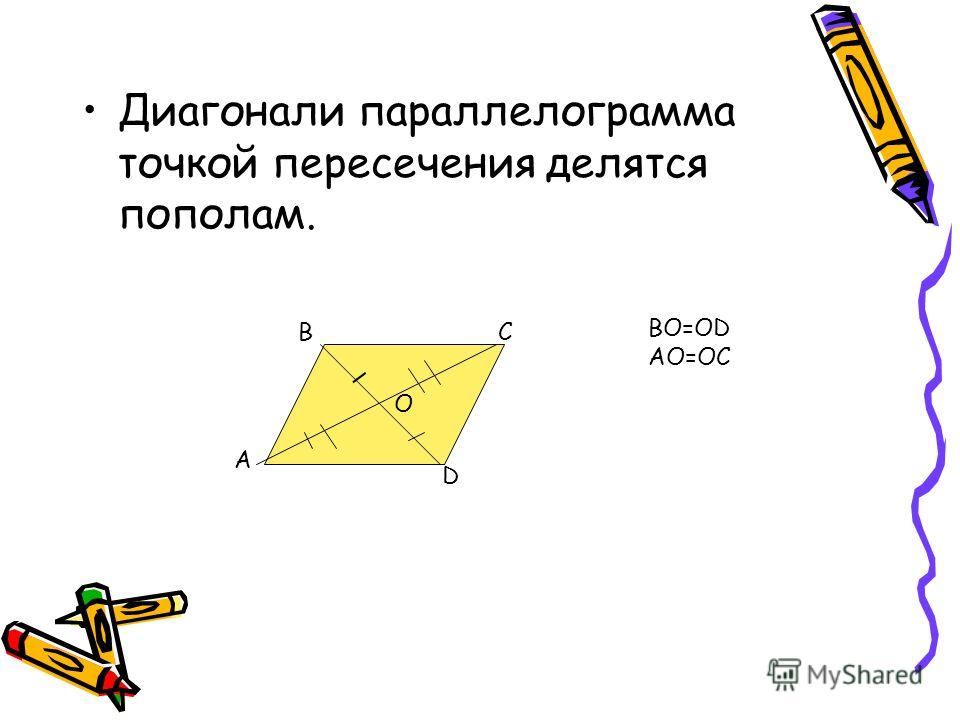
Что такое диагональная форма? Диагональ прямая линия, соединяющая две несмежные вершины фигуры, то есть два угла фигуры, которые не находятся рядом друг с другом. … Например, у воздушного змея два угла одинакового размера, и эти углы диагонально противоположны друг другу.
Чему равна диагональ квадратной тарелки, длина которой 28 см?
сторона = 28 см. = 28√2. значит диагональ квадрата 28√2 см.
Как найти длину стороны квадрата, если известна диагональ?
Определение диагонали параллелограмма. Параллелограмм
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны. На следующем рисунке представлен параллелограмм ABCD. У него сторона AB параллельна стороне CD, а сторона BC параллельна стороне AD.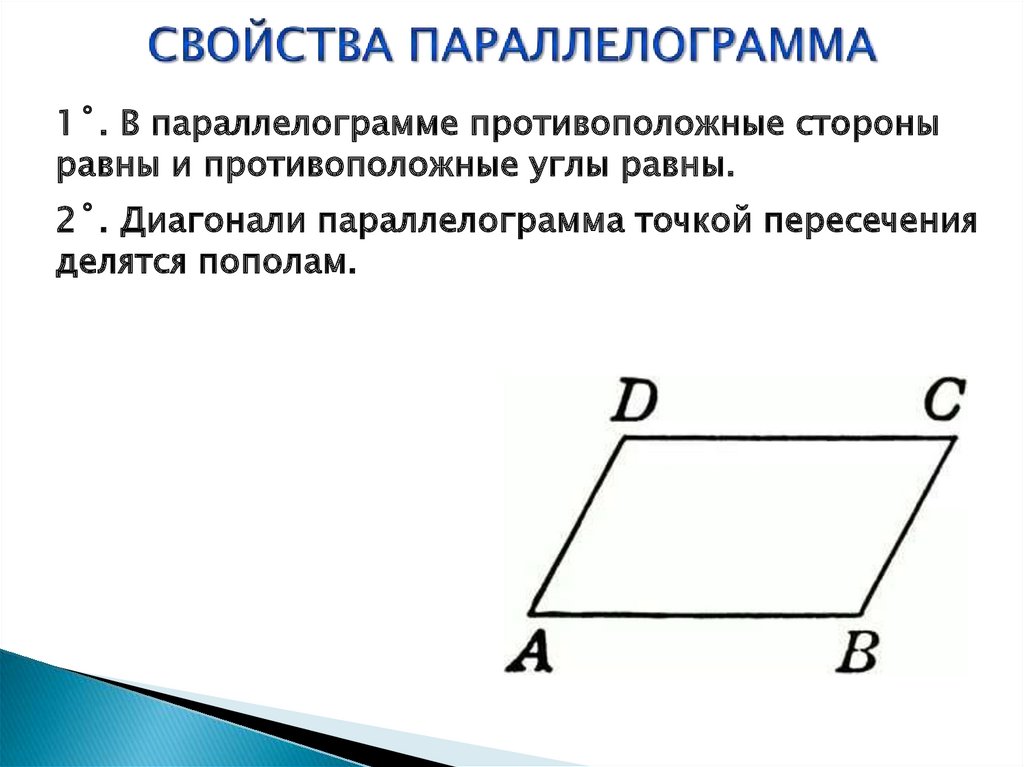
Как вы уже успели догадаться, параллелограмм является выпуклым четырехугольником. Рассмотрим основные свойства параллелограмма.
Свойства параллелограмма
1. В параллелограмме противоположные углы и противоположные стороны равны. Докажем это свойство — рассмотрим параллелограмм, представленный на следующем рисунке.
Диагональ BD разделяет его на два равных треугольника: ABD и CBD. Они равны по стороне BD и двум прилежащим к ней углам, так как углы накрест лежащие при секущей BD параллельных прямых BC и AD и AB и CD соответственно. Следовательно, AB = CD и
BC = AD. А из равенства углов 1, 2 ,3 и 4 следует, что угол A = угол1 +угол3 = угол2 + угол4 = угол С.
2. Диагонали параллелограмма точкой пересечения делятся пополам. Пусть точка О есть точка пересечения диагоналей AC и BD параллелограмма ABCD.
Тогда треугольник AOB и треугольник COD равны между собой, по стороне и двум прилежащим к ней углам. (AB=CD так как это противоположные стороны параллелограмма.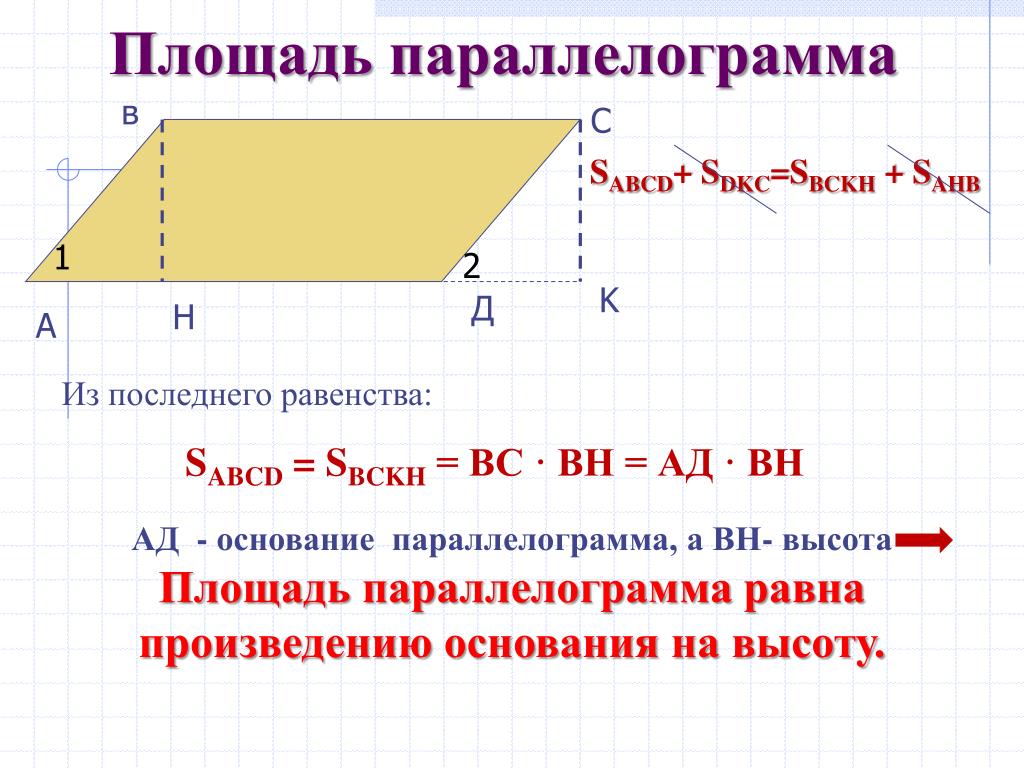
Все основные свойства проиллюстрированы на следующих трех рисунках.
1. Определение параллелограмма.
Если пару параллельных прямых пересечём другой парой параллельных прямых, то получим четырёхугольник, у которого противоположные стороны попарно параллельны.
В четырёхугольниках ABDС и ЕFNМ (рис. 224) ВD || АС и AB || СD;
ЕF || МN и ЕМ || FN.
Четырёхугольник, у которого противоположные стороны попарно параллельны, называется параллелограммом.
2. Свойства параллелограмма.
Теорема
. Диагональ параллелограмма делит его на два равных треугольника.
Пусть имеется параллелограмм ABDС (рис. 225), в котором AB || СD и АС || ВD.
Требуется доказать, что диагональ делит его на два равных треугольника.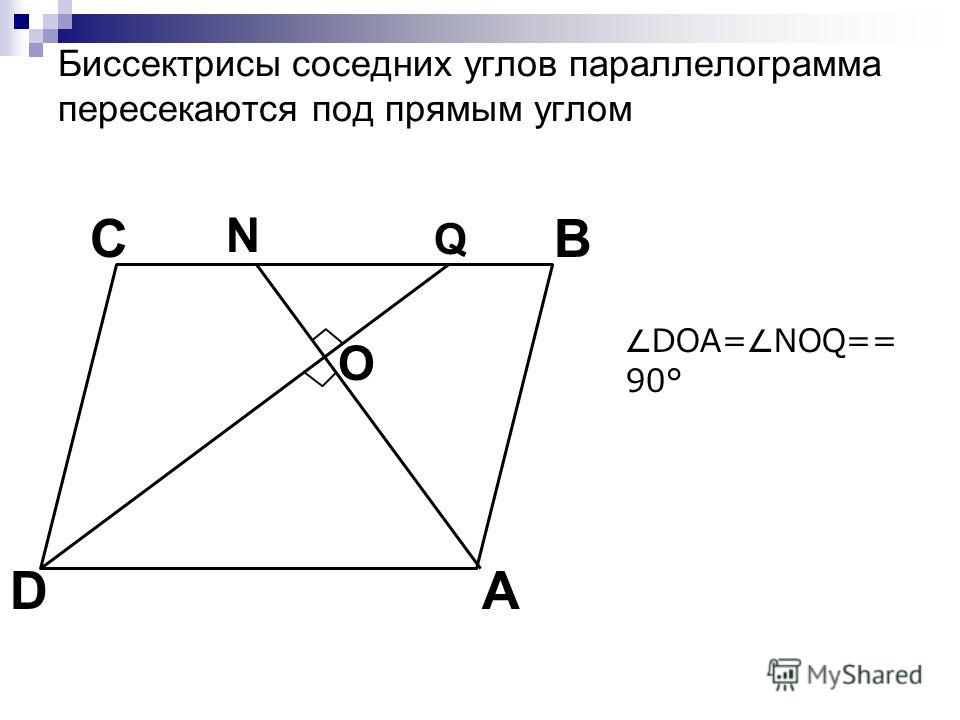
Проведём в параллелограмме ABDС диагональ СВ. Докажем, что (Delta)CAB = (Delta)СDВ.
Сторона СВ общая для этих треугольников; ∠ABC = ∠BCD, как внутренние накрест лежащие углы при параллельных AB и СD и секущей СВ; ∠ACB = ∠СВD, тоже как внутренние накрест лежащие углы при параллельных АС и ВD и секущей CB.
Отсюда (Delta)CAB = (Delta)СDВ.
Таким же путём можно доказать, что диагональ AD разделит параллелограмм на два равных треугольника АСD и ABD.
Следствия:
1
. Противоположные углы параллелограмма равны между собой.
∠А = ∠D, это следует из равенства треугольников CAB и СDВ.
Аналогично и ∠С = ∠В.
2. Противоположные стороны параллелограмма равны между собой.
AB = СD и АС = ВD, так как это стороны равных треугольников и лежат против равных углов.
Теорема 2.
Диагонали параллелограмма в точке их пересечения делятся пополам.
Пусть BC и AD — диагонали параллелограмма AВDС (рис.
Для этого сравним какую-нибудь пару противоположно расположенных треугольников, например (Delta)AOB и (Delta)СОD.
В этих треугольниках AB = СD, как противоположные стороны параллелограмма;
∠1 = ∠2, как углы внутренние накрест лежащие при параллельных AB и СD и секущей AD;
∠3 = ∠4 по той же причине, так как AB || СD и СВ — их секущая.
Отсюда следует, что (Delta)AOB = (Delta)СОD. А в равных треугольниках против равных углов лежат равные стороны. Следовательно, АО = OD и СО = OB.
Теорема 3.
Сумма углов, прилежащих к одной стороне параллелограмма, равна
180°
.
В параллелограмме ABCD проведем диагональ АС и получим два треугольника ABC и ADC.
Треугольники равны, так как ∠1 = ∠4, ∠2 = ∠3 (накрест лежащие углы при параллельных прямых), а сторона АС общая.
Из равенства (Delta)ABC = (Delta)ADC следует, что AB = CD, BC = AD, ∠B = ∠D.
Сумма углов, прилежащих к одной стороне, например углов А и D, равна 180° как односторонних при параллельных прямых.
Это четырёхугольник, противоположные стороны которого попарно параллельны.
Свойство 1
. Любая диагональ параллелограмма делит его на два равных треугольника.
Доказательство
. По II признаку (накрест лежащие углы и общая сторона).
Теорема доказана
.
Свойство 2
. В параллелограмме противолежащие стороны равны, противолежащие углы равны.
Доказательство
.
Аналогично,
Теорема доказана
.
Свойство 3.
В параллелограмме диагонали точкой пересечения делятся пополам.
Доказательство
.
Теорема доказана
.
Свойство 4
. Биссектриса угла параллелограмма, пересекая противоположную сторону, делит его на равнобедренный треугольник и трапецию. (Ч. сл. — вершину — два равнобедренных?-ка).
Доказательство
.
Теорема доказана
.
Свойство 5
. В параллелограмме отрезок с концами на противоположных сторонах, проходящий через точку пересечения диагоналей, делится этой точкой пополам.
Доказательство
.
Теорема доказана
.
Свойство 6
. Угол между высотами, опущенными из вершины тупого угла параллелограмма, равен острому углу параллелограмма.
Доказательство
.
Теорема доказана
.
Свойство 7
. Сумма углов параллелограмма, прилежащих к одной стороне, равна 180°.
Доказательство
.
Теорема доказана
.
Построение биссектрисы угла. Свойства биссектрисы угла треугольника.
1) Построить произвольный луч DE.
2) На данном луче построить произвольную окружность с центром в вершине и такую же
с центром в начале построенного луча.
3) F и G — точки пересечения окружности со сторонами данного угла, H — точка пересечения окружности с построенным лучом
Построить окружность с центром в точке H и радиусом, равным FG.
5) I — точка пересечения окружностей построенного луча.
6) Провести прямую через вершину и I.
IDH — требуемый угол.
)
Свойство 1
. Биссектриса угла треугольника разбивает противоположную сторону пропорционально прилежащим сторонам.
Доказательство
. Пусть x, y-отрезки стороны c. Продолжим луч BC. На луче BC отложим от C отрезок CK, равный AC.
Понятие параллелограмма
Определение 1
Параллелограмм
— это четырехугольник, в котором противоположные стороны параллельны между собой (рис. 1).
Рисунок 1.
Параллелограмм имеет два основных свойства. Рассмотрим их без доказательства.
Свойство 1:
Противоположные стороны и углы параллелограмма равны, соответственно, между собой.
Свойство 2:
Диагонали, проведенные в параллелограмме, делятся пополам их точкой пересечения.
Признаки параллелограмма
Рассмотрим три признака параллелограмма и представим их в виде теорем.
Теорема 1
Если две стороны четырехугольника равны между собой, а также параллельны, то этот четырехугольник будет параллелограммом.
Доказательство.
Пусть нам дан четырехугольник $ABCD$. В котором $AB||CD$ и $AB=CD$ Проведем в нем диагональ $AC$ (рис.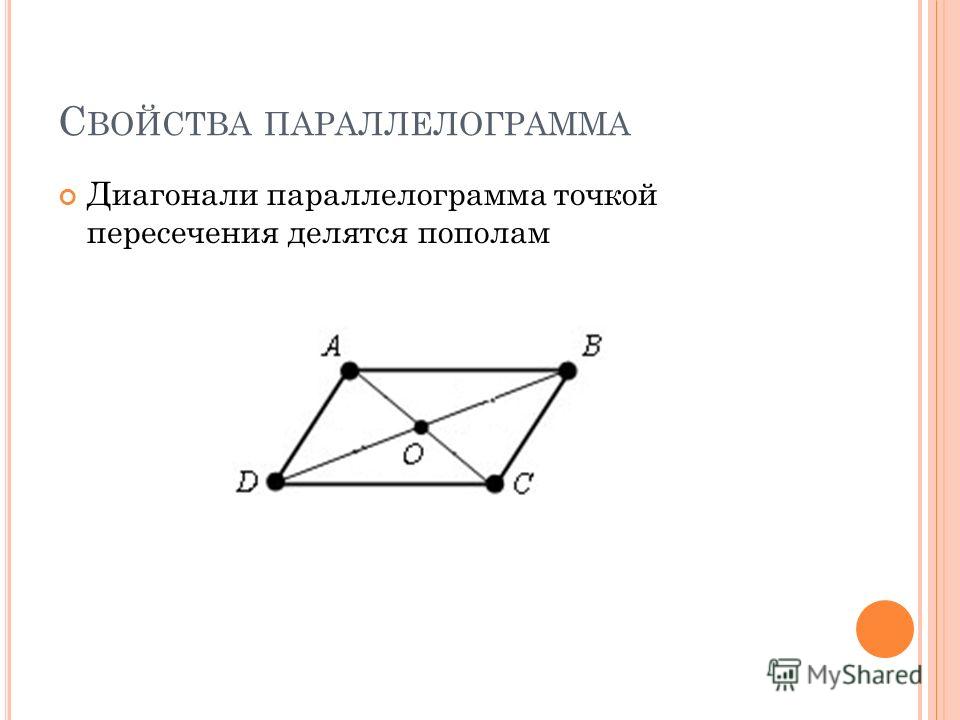
Рисунок 2.
Рассмотрим параллельные прямые $AB$ и $CD$ и их секущую $AC$. Тогда
[angle CAB=angle DCA]
как накрест лежащие углы.
По $I$ признаку равенства треугольников,
так как $AC$ — их общая сторона, а $AB=CD$ по условию. Значит
[angle DAC=angle ACB]
Рассмотрим прямые $AD$ и $CB$ и их секущую $AC$, по последнему равенству накрест лежащих углов получим, что $AD||CB$.}Следовательно, по определению $1$, данный четырехугольник является параллелограммом.
Теорема доказана.
Теорема 2
Если противоположные стороны четырехугольника равны между собой, то он является параллелограммом.
Доказательство.
Пусть нам дан четырехугольник $ABCD$. В котором $AD=BC$ и $AB=CD$. Проведем в нем диагональ $AC$ (рис. 3).
Рисунок 3.
Так как $AD=BC$, $AB=CD$, а $AC$ — общая сторона, то по $III$ признаку равенства треугольников,
[triangle DAC=triangle ACB]
[angle DAC=angle ACB]
Рассмотрим прямые $AD$ и $CB$ и их секущую $AC$, по последнему равенству накрест лежащих углов получим, что $AD||CB$.
Следовательно, по определению $1$, данный четырехугольник является параллелограммом.
[angle DCA=angle CAB]
Рассмотрим прямые $AB$ и $CD$ и их секущую $AC$, по последнему равенству накрест лежащих углов получим, что $AB||CD$.
Следовательно, по определению 1, данный четырехугольник является параллелограммом.
Теорема доказана.
Теорема 3
Если диагонали, проведенные в четырехугольнике, своей точкой пересечения делятся на две равные части, то этот четырехугольник является параллелограммом.
Доказательство.
Пусть нам дан четырехугольник $ABCD$. Проведем в нем диагонали $AC$ и $BD$. Пусть они пересекаются в точке $O$ (рис. 4).
Рисунок 4.
Так как, по условию $BO=OD, AO=OC$, а углы $angle COB=angle DOA$ как вертикальные, то, по $I$ признаку равенства треугольников,
[triangle BOC=triangle AOD]
[angle DBC=angle BDA]
Рассмотрим прямые $BC$ и $AD$ и их секущую $BD$, по последнему равенству накрест лежащих углов получим, что $BC||AD$.
Как в евклидовой геометрии точка и прямая — главные элементы теории плоскостей, так и параллелограмм является одной из ключевых фигур выпуклых четырехугольников. Из него, как нитки из клубка, втекают понятия «прямоугольника», «квадрата», «ромба» и других геометрических величин.
Вконтакте
Определение параллелограмма
Выпуклый четырехугольник,
состоящий из отрезков, каждая пара из которых параллельна, известен в геометрии как параллелограмм.
Как выглядит классический параллелограмм изображает четырехугольник ABCD. Стороны называются основаниями (AB, BC, CD и AD), перпендикуляр, проведенный из любой вершины на противоположную этой вершине сторону, — высотой (BE и BF), линии AC и BD — диагоналями.
Внимание!
Квадрат, ромб и прямоугольник — это частные случаи параллелограмма.
Стороны и углы: особенности соотношения
Ключевые свойства, по большому счету, предопределены самим обозначением
, их доказывает теорема.
- Стороны, которые являются противоположными, — попарно одинаковые.
- Углы, расположенные противоположно друг другу — попарно равны.
Доказательство: рассмотрим ∆ABC и ∆ADC, которые получаются вследствие разделения четырехугольника ABCD прямой AC. ∠BCA=∠CAD и ∠BAC=∠ACD, поскольку AC для них общая (вертикальные углы для BC||AD и AB||CD, соответственно). Из этого следует: ∆ABC = ∆ADC (второй признак равенства треугольников).
Отрезки AB и BC в ∆ABC попарно соответствуют линиям CD и AD в ∆ADC, что означает их тождество: AB = CD, BC = AD. Таким образом, ∠B соответствует ∠D и они равны. Так как ∠A=∠BAC+∠CAD, ∠C=∠BCA+∠ACD, которые так же попарно одинаковые, то ∠A = ∠C. Свойство доказано.
Характеристики диагоналей фигуры
Основной признак
этих линий параллелограмма: точка пересечения разделяет их пополам.
Доказательство: пусть т. Е — это точка пересечения диагоналей AC и BD фигуры ABCD. Они образуют два соизмеримых треугольника — ∆ABE и ∆CDE.
AB=CD, так как они противоположные. Согласно прямых и секущей, ∠ABE = ∠CDE и ∠BAE = ∠DCE.
По второму признаку равенства ∆ABE = ∆CDE. Это означает, что элементы ∆ABE и ∆CDE: AE = CE, BE = DE и при этом они соразмерные части AC и BD. Свойство доказано.
Особенности смежных углов
У смежных сторон сумма углов равна 180°
, поскольку они лежат по одну сторону параллельных линий и секущей. Для четырехугольника ABCD:
∠A+∠B=∠C+∠D=∠A+∠D=∠B+∠C=180º
Свойства биссектрисы:
- , опущенные на одну сторону, являются перпендикулярными;
- противолежащие вершины имеют параллельные биссектрисы;
- треугольник, полученный проведением биссектрисы, будет равнобедренным.
Определение характерных черт параллелограмма по теореме
Признаки этой фигуры вытекают из ее основной теоремы, которая гласит следующее: четырехугольник считается параллелограммом
в том случае, если его диагонали пересекаются, а эта точка разделяет их на равные отрезки.
Доказательство: пусть в т. Е прямые AC и BD четырехугольника ABCD пересекаются. Так как ∠AED = ∠BEC, а AE+CE=AC BE+DE=BD, то ∆AED = ∆BEC (по первому признаку равенства треугольников). То есть ∠EAD = ∠ECB. Они также являются внутренними перекрестными углами секущей AC для прямых AD и BC. Таким образом, по определению параллельности — AD || BC. Аналогичное свойство линий BC и CD выводится также. Теорема доказана.
Вычисление площади фигуры
Площадь этой фигуры находится несколькими методами,
одним из самых простых: умножения высоты и основания, к которому она проведена.
Доказательство: проведем перпендикуляры BE и CF из вершин B и C. ∆ABE и ∆DCF — равные, поскольку AB = CD и BE = CF. ABCD — равновеликий с прямоугольником EBCF, так как они состоят и соразмерных фигур: S ABE и S EBCD , а также S DCF и S EBCD . Из этого следует, что площадь этой геометрической фигуры находится так же как и прямоугольника:
S ABCD = S EBCF = BE×BC=BE×AD.
Для определения общей формулы площади параллелограмма обозначим высоту как hb
, а сторону — b
.
Другие способы нахождения площади
Вычисления площади через стороны параллелограмма и угол
, который они образуют, — второй известный метод.
,
Sпр-ма — площадь;
a и b — его стороны
α — угол между отрезками a и b.
Этот способ практически основывается на первом, но в случае, если неизвестна. всегда отрезает прямоугольный треугольник, параметры которого находятся тригонометрическими тождествами, то есть . Преобразуя соотношение, получаем . В уравнении первого способа заменяем высоту этим произведением и получаем доказательство справедливости этой формулы.
Через диагонали параллелограмма и угол,
который они создают при пересечении, также можно найти площадь.
Доказательство: AC и BD пересекаясь, образуют четыре треугольника: ABE, BEC, CDE и AED. Их сумма равна площади этого четырехугольника.
Площадь каждого из этих ∆ можно найти за выражением , где a=BE, b=AE, ∠γ =∠AEB. Поскольку , то в расчетах используется единое значение синуса.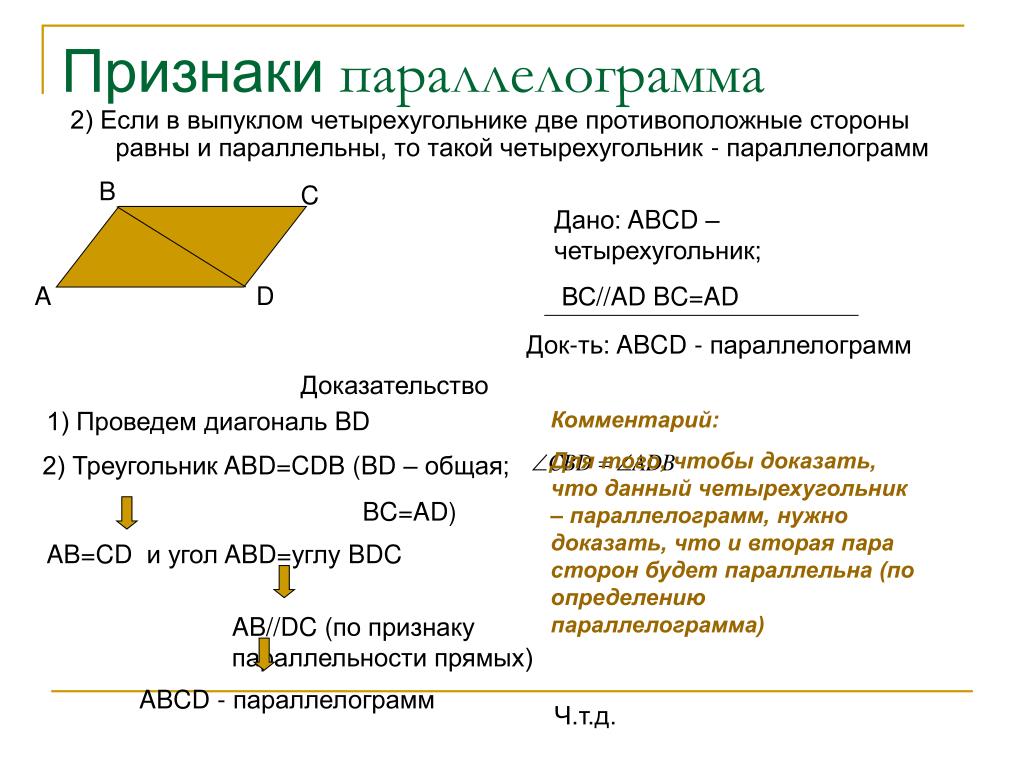
.
Применение в векторной алгебре
Особенности составляющих частей этого четырехугольника нашли применение в векторной алгебре, а именно: сложении двух векторов. Правило параллелограмма утверждает, что если заданные векторы
и
не
коллинеарны, то их сумма будет равна диагонали этой фигуры, основания которой соответствуют этим векторам.
Доказательство: из произвольно выбранного начала — т. о. — строим векторы и . Далее строим параллелограмм ОАСВ, где отрезки OA и OB — стороны. Таким образом, ОС лежит на векторе или сумме .
Формулы для вычисления параметров параллелограмма
Тождества приведены при следующих условиях:
- a и b, α — стороны и угол между ними;
- d 1 и d 2 , γ — диагонали и в точке их пересечения;
- h a и h b — высоты, опущенные на стороны a и b;
| Параметр |
Формула |
| Нахождение сторон |
|
| по диагоналям и косинусу угла между ними | |
| по диагоналям и стороне | |
| через высоту и противоположную вершину | |
| Нахождение длины диагоналей |
|
| по сторонам и величине вершины между ними |
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
Поиск по сайту:
| Справочник по математике | Геометрия (Планиметрия) | Четырехугольники |
| Свойства и признаки параллелограмма |
| Свойства и признаки прямоугольника |
| Свойства и признаки ромба |
| Свойства и признаки квадрата |
Замечание.
Свойства и признаки параллелограмма
| Тип утверждения | Фигура | Рисунок | Формулировка |
| Определение | Параллелограмм | Параллелограммом называют четырёхугольник, у которого противолежащие стороны параллельны | |
| Определение | Диагонали параллелограмма | Диагональю параллелограмма называют отрезок, соединяющий противоположные вершины | |
| Определение | Высота параллелограмма | Высотой параллелограмма называют перпендикуляр, опущенный из любой точки на стороне параллелограмма на противоположную сторону параллелограмма или ее продолжение | |
| Свойство | Равенство противолежащих сторон | Если четырёхугольник является параллелограммом, то его противолежащие стороны равны | |
| Признак | Если у четырёхугольника противолежащие стороны равны, то он является параллелограммом | ||
| Признак | Равенство и параллельность двух противолежащих сторон | Если у четырёхугольника две противолежащие стороны равны и параллельны, то он является параллелограммом | |
| Свойство | Диагонали точкой пересечения делятся пополам | Если четырёхугольник является параллелограммом, то его диагонали точкой пересечения делятся пополам | |
| Признак | Если у четырёхугольника диагонали точкой пересечения делятся пополам, то он является параллелограммом | ||
| Свойство | Суммы углов, прилежащих к сторонам | Если четырёхугольник является параллелограммом, то сумма углов, прилежащих к любой его стороне равна 180° | |
| Признак | Если у четырёхугольника сумма углов, прилежащих к любой его стороне равна 180°, то четырёхугольник является параллелограммом | ||
| Свойство | Равенство противолежащих углов | Если четырёхугольник является параллелограммом, то его противолежащие углы равны | |
| Признак | Если у четырёхугольника противолежащие углы равны, то четырёхугольник является параллелограммом | ||
| Свойство | Два треугольника, на которые каждая диагональ делит четырёхугольник | Если четырёхугольник является параллелограммом, то каждая диагональ делит его на два равных треугольника | |
| Признак | Если каждая диагональ четырёхугольника делит его на два равных треугольника, то четырёхугольник является параллелограммом | ||
| Свойство | Четыре треугольника, на которые диагонали делят четырёхугольник | Если четырёхугольник является параллелограммом, то диагонали делит его на четыре треугольника равной площади (равновеликих треугольника) | |
| Признак | Если диагонали четырёхугольника делят его на четыре треугольника равной площади (равновеликих треугольника), то четырёхугольник является параллелограммом |
| Определение: параллелограмм | |
| Параллелограммом называют четырёхугольник, у которого противолежащие стороны параллельны | |
| Определение: диагонали параллелограмма | |
| Диагональю параллелограмма называют отрезок, соединяющий противоположные вершины | |
| Определение: высота параллелограмма | |
| Высотой параллелограмма называютперпендикуляр, опущенный из любой точки на стороне параллелограмма на противоположную сторону параллелограмма или ее продолжение | |
| Свойство: равенство противолежащих сторон | |
| Если четырёхугольник является параллелограммом, то его противолежащие стороны равны | |
| Признак: равенство противолежащих сторон | |
| Если у четырёхугольника противолежащие стороны равны, то он является параллелограммом | |
| Признак: равенство и параллельность двух противолежащих сторон | |
| Если у четырёхугольника две противолежащие стороны равны и параллельны, то он является параллелограммом | |
| Свойство: диагонали точкой пересечения делятся пополам | |
| Если четырёхугольник является параллелограммом, то его диагонали точкой пересечения делятся пополам | |
| Признак: диагонали точкой пересечения делятся пополам | |
| Если у четырёхугольника диагонали точкой пересечения делятся пополам, то он является параллелограммом | |
| Свойство: суммы углов, прилежащих к сторонам | |
| Если четырёхугольник является параллелограммом, то сумма углов, прилежащих к любой его стороне равна 180° | |
| Признак: суммы углов, прилежащих к сторонам | |
| Если у четырёхугольника сумма углов, прилежащих к любой его стороне равна 180°, то четырёхугольник является параллелограммом | |
| Свойство: равенство противолежащих углов | |
| Если четырёхугольник является параллелограммом, то его противолежащие углы равны | |
| Признак: равенство противолежащих углов | |
| Если у четырёхугольника противолежащие углы равны, то четырёхугольник является параллелограммом | |
| Свойство: два треугольника, на которые каждая диагональ делит четырёхугольник | |
| Если четырёхугольник является параллелограммом, то каждая диагональ делит его на два равных треугольника | |
| Признак: два треугольника, на которые каждая диагональ делит четырёхугольник | |
| Если каждая диагональ четырёхугольника делит его на два равных треугольника, то четырёхугольник является параллелограммом | |
| Свойство: четыре треугольника, на которые диагонали делят четырёхугольник | |
| Если четырёхугольник является параллелограммом, то диагонали делит его на четыре треугольника равной площади (равновеликих треугольника) | |
| Признак: четыре треугольника, на которые диагонали делят четырёхугольник | |
| Если диагонали четырёхугольника делят его на четыре треугольника равной площади (равновеликих треугольника), то четырёхугольник является параллелограммом |
| Параллелограмм |
|
Определение: Параллелограммом называют четырёхугольник, у которого противолежащие стороны параллельны |
| Диагонали параллелограмма |
|
Определение: Диагональю параллелограмма называют отрезок, соединяющий противоположные вершины |
| Высота параллелограмма |
|
Определение: Высотой параллелограмма называют перпендикуляр, опущенный из любой точки на стороне параллелограмма на противоположную сторону параллелограмма или ее продолжение |
| Равенство противолежащих сторон |
|
Свойство: Если четырёхугольник является параллелограммом, то его противолежащие стороны равны. Признак: Если у четырёхугольника противолежащие стороны равны, то он является параллелограммом. |
| Равенство и параллельность двух противолежащих сторон |
|
Признак: Если у четырёхугольника две противолежащие стороны равны и параллельны, то он является параллелограммом. |
| Диагонали точкой пересечения делятся пополам |
|
Свойство: Если четырёхугольник является параллелограммом, то его диагонали точкой пересечения делятся пополам. Признак: Если у четырёхугольника диагонали точкой пересечения делятся пополам, то он является параллелограммом. |
| Суммы углов, прилежащих к сторонам |
|
Свойство: Если четырёхугольник является параллелограммом, то сумма углов, прилежащих к любой его стороне равна 180°. Признак: Если у четырёхугольника сумма углов, прилежащих к любой его стороне равна 180°, то четырёхугольник является параллелограммом. |
| Равенство противолежащих углов |
|
Свойство: Если четырёхугольник является параллелограммом, то его противолежащие углы равны. Признак: Если у четырёхугольника противолежащие углы равны, то четырёхугольник является параллелограммом. |
| Два треугольника, на которые каждая диагональ делит четырёхугольник |
|
Свойство: Если четырёхугольник является параллелограммом, то каждая диагональ делит его на два равных треугольника. Признак: Если каждая диагональ четырёхугольника делит его на два равных треугольника, то четырёхугольник является параллелограммом. |
| Четыре треугольника, на которые диагонали делят четырёхугольник |
|
Свойство: Если четырёхугольник является параллелограммом, то диагонали делит его на четыре треугольника равной площади (равновеликих треугольника) Признак: Если диагонали четырёхугольника делят его на четыре треугольника равной площади (равновеликих треугольника), то четырёхугольник является параллелограммом. |
Свойства и признаки прямоугольника
| Тип утверждения | Фигура | Рисунок | Формулировка |
| Определение | Прямоугольник | Прямоугольником называют параллелограмм, у которого все углы прямые | |
| Свойство | Равенство диагоналей | Если параллелограмм является прямоугольником, то его диагонали равны | |
| Признак | Если у параллелограмма диагонали равны, то он является прямоугольником |
| Определение: прямоугольник | |
| Прямоугольником называют параллелограмм, у которого все углы прямые | |
| Свойство: равенство диагоналей | |
| Если параллелограмм является прямоугольником, то его диагонали равны | |
| Признак: равенство диагоналей | |
| Если у параллелограмма диагонали равны, то он является прямоугольником |
| Прямоугольник |
|
Определение: Прямоугольником называют параллелограмм, у которого все углы прямые. |
| Равенство диагоналей |
|
Свойство: Если параллелограмм является прямоугольником, то его диагонали равны. Признак: Если у параллелограмма диагонали равны, то он является прямоугольником. |
Свойства и признаки ромба
| Тип утверждения | Фигура | Рисунок | Формулировка |
| Определение | Ромб | Ромбом называют параллелограмм, у которого все стороны равны | |
| Свойство | Биссектрисы углов диагонали |
Если параллелограмм является ромбом, то его диагонали является биссектрисами углов | |
| Признак | Если у параллелограмма диагонали являются биссектрисами углов, то параллелограмм является ромбом | ||
| Свойство | Перпендикулярность диагоналей | Если параллелограмм является ромбом, то его диагонали перпендикулярны | |
| Признак | Если у параллелограмма диагонали перпендикулярны, то он является ромбом |
| Определение: ромб | |
| Ромбом называют параллелограмм, у которого все стороны равны | |
| Свойство: биссектрисы углов и диагонали | |
| Если параллелограмм является ромбом, то его диагонали являются биссектрисами углов | |
| Признак: биссектрисы углов и диагонали | |
| Если у параллелограмма диагонали являются биссектрисами углов, то параллелограмм является ромбом | |
| Свойство: перпендикулярность диагоналей | |
| Если параллелограмм является ромбом, то его диагонали перпендикулярны | |
| Признак: перпендикулярность диагоналей | |
| Если у параллелограмма диагонали перпендикулярны, то он является ромбом |
| Ромб |
|
Определение: Ромбом называют параллелограмм, у которого все стороны равны |
| Биссектрисы углов и диагонали |
|
Свойство: Если параллелограмм является ромбом, то его диагонали являются биссектрисами углов Признак: Если у параллелограмма диагонали являются биссектрисами углов, то параллелограмм является ромбом |
| Перпендикулярность диагоналей |
|
Свойство: Если параллелограмм является ромбом, то его диагонали перпендикулярны Признак: Если у параллелограмма диагонали перпендикулярны, то он является ромбом |
Свойства и признаки квадрата
| Тип утверждения | Фигура | Рисунок | Формулировка |
| Определение | Квадрат | Квадратом называют параллелограмм, у которого все стороны равны и все углы равны | |
| Свойство | Перпендикулярность и равенство диагоналей |
Если параллелограмм является квадратом, то его диагонали перпендикулярны и равны | |
| Признак | Если у параллелограмма диагонали перпендикулярны и равны, то он является квадратом | ||
| Свойство | Перпендикулярность диагоналей | Если прямоугольник является квадратом, то его диагонали перпендикулярны | |
| Признак | Если у прямоугольника диагонали перпендикулярны, то он является квадратом | ||
| Свойство | Равенство диагоналей | Если ромб является квадратом, то его диагонали равны | |
| Признак | Если у ромба диагонали равны, то он является квадратом |
| Определение: квадрат | |
| Квадратом называют параллелограмм, у которого все стороны равны и все углы равны | |
| Свойство: перпендикулярность и равенство диагоналей | |
| Если параллелограмм является квадратом, то его диагонали перпендикулярны и равны | |
| Признак: перпендикулярность и равенство диагоналей | |
| Если у параллелограмма диагонали перпендикулярны и равны, то он является квадратом | |
| Свойство: перпендикулярность диагоналей | |
| Если прямоугольник является квадратом, то его диагонали перпендикулярны | |
| Признак: перпендикулярность диагоналей | |
| Если у прямоугольника диагонали перпендикулярны, то он является квадратом | |
| Свойство: равенство диагоналей | |
| Если ромб является квадратом, то его диагонали равны | |
| Признак: равенство диагоналей | |
| Если у ромба диагонали равны, то он является квадратом |
| Квадрат |
|
Определение: Квадратом называют параллелограмм, у которого все стороны равны и все углы равны |
| Перпендикулярность и равенство диагоналей |
|
Свойство: Если параллелограмм является квадратом, то его диагонали перпендикулярны и равны Признак: Если у параллелограмма диагонали перпендикулярны и равны, то он является квадратом |
| Перпендикулярность диагоналей |
|
Свойство: Если прямоугольник является квадратом, то его диагонали перпендикулярны Признак: Если у прямоугольника диагонали перпендикулярны, то он является квадратом |
| Равенство диагоналей |
|
Свойство: Если ромб является квадратом, то его диагонали равны Признак: Если у ромба диагонали равны, то он является квадратом |
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Диагонали параллелограмма : Геометрия
Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
| Limit79 |
Диагонали параллелограмма 19. |
|
29/08/11 |
Параллелограмм построен на векторах и . , , Требуется найти длины диагоналей этого параллелограмма. Векторы и сонаправлены, и имеют одинаковую длину, следовательно . , то есть . Никак не могу понять, если и — противоположные стороны параллелограмма, то каким образом могут полностью совпадать координаты векторов и ? |
| _Ivana |
Re: Диагонали параллелограмма 19. |
|
05/09/12 |
А что такое координаты вектора? |
| Limit79 |
Re: Диагонали параллелограмма 19.10.2013, 17:11 |
|
29/08/11 |
_Ivana Цитата: Координатами вектора называются коэффициенты его разложения по базисным векторам. — 19.10.2013, 18:13 — Или, иначе говоря, проекции на координатные оси. |
| _Ivana |
Re: Диагонали параллелограмма 19.10.2013, 17:18 |
|
05/09/12 |
И понимание еще не пришло? Рисуйте на плоскости систему координат, задавайте любой параллелограмм и считайте координаты векторов его сторон. |
| Limit79 |
Re: Диагонали параллелограмма 19.10.2013, 17:28 |
|
29/08/11 |
_Ivana А, я просто думал, что от нуля координаты вектора откладываются То есть могут быть два вектора с одинаковыми координатами, но при этом они не будут полностью совпадать? |
| mihailm |
Re: Диагонали параллелограмма 19. |
|
19/05/10 |
Вот две нарисованные на бумаге шестерки, они равны? они обязаны совпадать? |
| Limit79 |
Re: Диагонали параллелограмма 19. |
|
29/08/11 |
mihailm |
| VAL |
Re: Диагонали параллелограмма 19.10.2013, 17:45 |
|
27/06/08 |
Проблема в том, что когда Вам в школе определяли вектор, как направленный отрезок, Вас, мягко говоря, обманывали. |
| Limit79 |
Re: Диагонали параллелограмма 19.10.2013, 17:48 |
|
29/08/11 |
VAL в сообщении #777233 писал(а): разные направленные отрезки могут определять один и тот же вектор. Как так? Ведь: Цитата: Векторы называются равными, если они сонаправлены и их длины равны. — 19.10.2013, 18:57 — То есть все-таки равные векторы могут и не совпадать? — 19.10.2013, 19:07 — И еще вопрос: по координатам вектора нельзя однозначно определить его положение на плоскости/в пространстве? |
| VAL |
Re: Диагонали параллелограмма 19.10.2013, 18:15 |
|
27/06/08 |
Limit79 в сообщении #777235 писал(а): VAL в сообщении #777233 писал(а): разные направленные отрезки могут определять один и тот же вектор. Как так? Ведь: Цитата: Векторы называются равными, если они сонаправлены и их длины равны. Это как-то противоречит, тому что написано выше? Цитата: То есть все-таки равные векторы могут и не совпадать? Равные векторы (числа, матрицы…) не могут не совпадать. Еще раз. Чтобы разобраться с возникшими у Вас трудностями, надо первым делом отказаться от мысли, что «вектор» и «направленный отрезок» это одно и то же. Чтобы геометрический образ вектора в Вашем сознании не отличался от того, что понимают под вектором в математике, нужно представлять себе нечто имеющее величину и направление, но уж точно не имеющее ни начала, ни конца. Почувствуйте разницу: |
| Limit79 |
Re: Диагонали параллелограмма 20.10.2013, 15:25 |
|
29/08/11 |
VAL в сообщении #777255 писал(а): Это как-то противоречит, тому что написано выше? Извините, прочитал «разнонаправленные». Спасибо, более-менее понял. |
Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию
| Страница 1 из 1 | [ Сообщений: 11 ] |
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Параллелограмм.

Навигация по странице:
Определение параллелограмма
Признаки параллелограмма
Основные свойства параллелограмма
Стороны параллелограмма
Диагонали параллелограмма
Периметр параллелограмма
Площадь параллелограмма
Определение.
Параллелограмм — это четырехугольник у которого противоположные стороны попарно параллельны (лежат на параллельных прямых).
Параллелограммы отличаются между собой как размером прилегающих сторон, так и углами, однако противоположные углы одинаковые.
Признаки параллелограмма
Четырехугольник ABCD будет параллелограммом, если выполняется хотя бы одно из следующих условий:
1. Четырехугольник имеет две пары параллельных сторон:
AB||CD, BC||AD
2.
AB||CD, AB = CD (или BC||AD, BC = AD)
3. В четырехугольнике противоположные стороны попарно равны:
AB = CD, BC = AD
4. В четырехугольнике противоположные углы попарно равны:
∠DAB = ∠BCD, ∠ABC = ∠CDA
5. В четырехугольнике диагонали точкой пересечения делятся пополам:
AO = OC, BO = OD
6. Сумма углов четырехугольника прилегающих к любой стороне равна 180°:
∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180°
7. В четырехугольнике сумма квадратов диагоналей равна сумме квадратов его сторон:
AC2 + BD2 = AB2 + BC2 + CD2 + AD2
Основные свойства параллелограмма
Квадрат, прямоугольник и ромб — есть параллелограммом.
1.
AB = CD, BC = AD
2. Противоположные стороны параллелограмма параллельны:
AB||CD, BC||AD
3. Противоположные углы параллелограмма одинаковые:
∠ABC = ∠CDA, ∠BCD = ∠DAB
4. Сумма углов параллелограмма равна 360°:
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
5. Сумма углов параллелограмма прилегающих к любой стороне равна 180°:
∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180°
6. Каждая диагональ делит параллелограмма на два равных треугольника
7. Две диагональ делят параллелограмм на две пары равных треугольников
8. Диагонали параллелограмма пересекаются и точкой пересечения делят друг друга пополам:
| AO = CO = | d1 |
| 2 | |
| BO = DO = | d2 |
| 2 |
9.
10. Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон:
AC2 + BD2 = 2AB2 + 2BC2
11. Биссектрисы противоположных углов параллелограмма всегда параллельны
12. Биссектрисы соседних углов параллелограмма всегда пересекаются под прямым углом (90°)
Стороны параллелограмма
Формулы определения длин сторон параллелограмма:
1. Формула сторон параллелограмма через диагонали и угол между ними:
| a = | √d12 + d22 — 2d1d2·cosγ | = | √d12 + d22 + 2d1d2·cosδ |
| 2 | 2 |
| b = | √d12 + d22 + 2d1d2·cosγ | = | √d12 + d22 — 2d1d2·cosδ |
| 2 | 2 |
2.
3. Формула сторон параллелограмма через высоту и синус угла:
4. Формула сторон параллелограмма через площадь и высоту:
Диагонали параллелограмма
Определение.
Диагональю параллелограмма называется любой отрезок соединяющий две вершины противоположных углов параллелограмма.
Параллелограмм имеет две диагонали — длинную d1, и короткую — d2
Формулы определения длины диагонали параллелограмма:
1. Формулы диагоналей параллелограмма через стороны и косинус угла β (по теореме косинусов)
d1 = √a2 + b2 — 2ab·cosβ
d2 = √a2 + b2 + 2ab·cosβ
2. Формулы диагоналей параллелограмма через стороны и косинус угла α (по теореме косинусов)
d1 = √a2 + b2 + 2ab·cosα
d2 = √a2 + b2 — 2ab·cosα
3. Формула диагонали параллелограмма через две стороны и известную другую диагональ:
d1 = √2a2 + 2b2 — d22
d2 = √2a2 + 2b2 — d12
4.
| d1 = | 2S | = | 2S |
| d2·sinγ | d2·sinδ |
| d2 = | 2S | = | 2S |
| d1·sinγ | d1·sinδ |
Периметр параллелограмма
Определение.
Периметром параллелограмма называется сумма длин всех сторон параллелограмма.
Формулы определения длины периметра параллелограмма:
1. Формула периметра параллелограмма через стороны параллелограмма:
P = 2a + 2b = 2(a + b)
2. Формула периметра параллелограмма через одну сторону и две диагонали:
P = 2a + √2d12 + 2d22 — 4a2
P = 2b + √2d12 + 2d22 — 4b2
3.
Площадь параллелограмма
Определение.
Площадью параллелограмма называется пространство ограниченный сторонами параллелограмма, т.е. в пределах периметра параллелограмма.
Формулы определения площади параллелограмма:
1. Формула площади параллелограмма через сторону и высоту, проведенную к этой стороне:
S = a · ha
S = b · hb
2. Формула площади параллелограмма через две стороны и синус угла между ними:
S = ab sinα
S = ab sinβ
3.
Формулы по геометрии
Квадрат. Формулы и свойства квадрата
Прямоугольник. Формулы и свойства прямоугольника
Параллелограмм. Формулы и свойства параллелограмма
Ромб. Формулы и свойства ромба
Трапеция. Формулы и свойства трапеции
— Равнобедренная трапеция. Формулы и свойства равнобедренной трапеции
— Прямоугольная трапеция. Формулы и свойства прямоугольной трапеции
Формулы площади геометрических фигур
Формулы периметра геометрических фигур
Формулы объема геометрических фигур
Формулы площади поверхности геометрических фигур
Все таблицы и формулы
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Формула диагонали параллелограмма — GeeksforGeeks
Параллелограмм определяется как четырехугольник, который имеет равные пары противоположных сторон и углов.
На приведенном выше рисунке изображен параллелограмм ABCD со сторонами AB, BC, CD и AD и диагоналями AC и BD. Здесь длины противоположных сторон AB и CD равны друг другу. Точно так же длины BC и AD одинаковы. Пары противоположных углов, то есть ∠A и ∠C и ∠B и ∠D, равны между собой.
Формула диагонали параллелограмма
Формула длины диагонали параллелограмма равна величине равнодействующей любых двух смежных сторон.
x = √ (A 2 + B 2 — 2AB COS A) = √ (A 2 + B 2 + 2AB COS B)
Y = √ (A 2AB COS B)
Y = √ (A 2 + b 2 + 2ab cos A) = √(a 2 + b 2 – 2ab cos B)
где
x и y длины диагоналей,
3 a и b 9 длины смежных сторон,
A и B — углы, образованные между сторонами.

Длины диагоналей и сторон параллелограмма связаны друг с другом. Сумма квадратов диагоналей равна удвоенной сумме квадратов двух соседних сторон.
x 2 + Y 2 = 2 (A 2 + B 2 )
, где,
x, и Y — диагональные длины,
A и B -длинные длины.
Примеры задач
Задача 1. Вычислить длину диагоналей параллелограмма с длинами сторон 5 м и 10 м, если один из внутренних углов равен 60°.
Решение:
У нас есть,
a = 5
b = 10
∠A = 60°
∠B = 120°
Нам нужно найти длины диагоналей x и y.
Используя формулу получаем,
x = √(a 2 + b 2 – 2ab cos A)
= √(5 2 + 10 2 ) ( COS 60 °)
= √75
= 8,66 м
y = √ (A 2 + B 2 + 2AB COS A)
= √ (5 2 + 10 2 + 2.
(5) (10) cos 60°)
= √175
= 13,22 м
Задача 2. Вычислить длину диагоналей параллелограмма с длинами сторон 4 м и 7 м, если один из внутренних углов равен 30°.
Решение:
Имеем
a = 4
b = 7
∠A = 30°
Нам нужно найти длины диагоналей x и y.
Используя формулу получаем,
x = √(a 2 + b 2 – 2ab cos A)
= √ (4 2 + 7 2 — 2 (4) (7) COS 30 °)
= √16.48
= 4,06 M
Y = √ (A 2 + B 2
Y = √ (A 2 + B 2 + 2AB COS A)
= √ (4 2 + 7 2 + 2 (4) (7) COS 30 °)
= √73.63
= 8,5 М
Проблема 3. Рассчитайте. длина одной из диагоналей параллелограмма со сторонами 5 м и 9 м, если один из внутренних углов равен 25°.
Решение:
Имеем,
a = 5
b = 9
∠A = 25°
Нам нужно найти длину диагонали.

Используя формулу получаем,
x = √(a 2 + b 2 – 2ab cos A)
= √(5 2 + 9 2
(9 2 –
cos 25°)
= √24,40
= 4,06 м
Задача 4. Вычислить длину одной из диагоналей параллелограмма со сторонами 12 м и 16 м, если один из внутренних углов равен 37° .
Решение:
Имеем
a = 12
b = 16
∠A = 37°
Нам нужно найти длину диагонали.
Используя формулу получаем,
x = √(a 2 + b 2 – 2ab cos A)
= √(12 2 + 16 2 – 9001) (2) cos 37°)
= √93,315
= 9,66 м
Задача 5. Вычислить длину одной из диагоналей параллелограмма со сторонами 4 м и 6 м, если другая диагональ равна 8 м.
Решение:
Мы имеем,
A = 4
B = 6
x = 8
с использованием формулы, которую мы получаем,
x 2 + Y 2 = 2 ( A 2 + B 2 )
=> 8 2 + Y 2 = 2 (4 2 + 6 2 )
=> 64 + Y 2 = 2 (1603
=> 64 + Y 2 = 2 (160003
=> 64 + Y 2 = 2 (160003
=> 64 + Y 2 = 2 (16.
+ 36)
=> 64 + у 2 = 104
=> у 2 = 40
=> y = 6,32 м
Задача 6. Вычислить длину одной из диагоналей параллелограмма с длинами сторон 8 м и 12 м, если другая диагональ равна 14 м.
Решение:
Мы имеем,
A = 8
B = 12
x = 14
с использованием формулы, которую мы получаем,
x 2 + Y 2 = 2 (
x 2 + Y 2 = 2 ( a 2 + b 2 )
=> 14 2 + y 2 = 2 (8 2 + 12 2 )
=> 196 + Y 2 = 2 (16 + 144)
=> 196 + Y 2 = 320
=> Y 2 = 124
. => y = 11,13 м
Задача 7. Вычислить длину одной из диагоналей параллелограмма с длинами сторон 7 м и 9 м, если другая диагональ равна 11 м.
Решение:
Имеем,
a = 7
b = 9
x = 11
Использование формулы, которую мы получаем,
x 2 + Y 2 = 2 (A 2 + B 2 )
=> 11 2 + Y 2 = 2 (7 2 + 9 2 )
=> 121 + Y 2 = 2 (49 + 81)
=> 121 + Y 2 = 260
=> y 2 = 139
=> > y = 11,78 м
Как найти длину диагонали параллелограмма
Как найти длину диагонали параллелограмма — ACT Math
—>
- Войти
- Биографии репетитора
-
Подготовка к тесту
СРЕДНЯЯ ШКОЛА
- ACT Репетиторство
- SAT Репетиторство
- Репетиторство PSAT
- ASPIRE Репетиторство 904:30
- ШСАТ Репетиторство
- Репетиторство STAAR
ВЫСШАЯ ШКОЛА
- Репетиторство MCAT
- Репетиторство GRE
- Репетиторство по LSAT
- Репетиторство по GMAT
К-8
- Репетиторство AIMS
- Репетиторство по HSPT
- Репетиторство ISEE
- Репетиторство по ISAT
- Репетиторство по SSAT
- Репетиторство STAAR
Поиск 50+ тестов
-
Академическое обучение
репетиторство по математике
- алгебра
- Исчисление
- Элементарная математика 904:30
- Геометрия
- Предварительное исчисление
- Статистика
- Тригонометрия
Репетиторство по естественным наукам
- Анатомия
- Биология
- Химия
- Физика
- Физиология
иностранные языки
- французский
- немецкий
- Латинский
- Китайский мандарин
- Испанский
начальное обучение
- Чтение
- Акустика
- Элементарная математика
прочие
- Бухгалтерский учет
- Информатика
- Экономика
- Английский
- Финансы
- История
- Письмо
- Лето
Поиск по 350+ темам
-
О
- Обзор видео
- Процесс выбора наставника
- Онлайн-репетиторство
- Мобильное обучение
- Мгновенное обучение
- Как мы работаем
- Наша гарантия
- Влияние репетиторства
- Обзоры и отзывы
- Освещение в СМИ
- О преподавателях университета
Звоните прямо сейчас, чтобы записаться на обучение:
(888) 888-0446
Все математические ресурсы ACT
14 диагностических тестов
767 практических тестов
Вопрос дня
Карточки
Learn by Concept
ACT Math Help »
Геометрия »
Плоская геометрия »
Четырехугольники »
Параллелограммы »
Как найти длину диагонали параллелограмма
Если прямоугольный участок имеет размеры , какова длина диагонали участка в футах?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы ответить на этот вопрос, мы должны найти диагональ прямоугольника на .
Поскольку прямоугольный треугольник образован диагональю, мы можем использовать теорему Пифагора, а именно:
и каждый из которых представляет собой отдельный катет треугольника и представляет длину гипотенузы, которая в данном случае совпадает с длиной диагонали.
Затем мы можем подставить наши известные значения и найти
Теперь мы должны извлечь квадратный корень из каждой стороны, чтобы найти
Следовательно, диагональ прямоугольника равна .
Сообщить об ошибке
является параллелограммом. Найдите длину диагонали .
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти длину диагонали, мы можем рассмотреть только треугольник и использовать закон косинусов, чтобы найти длину неизвестной стороны.
Закон косинусов:
Где – длина неизвестной стороны, и – длины известных сторон, и – угол между и .
Из задачи:
Сообщить об ошибке
является параллелограммом. Найдите длину диагонали .
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти длину диагонали, мы можем рассмотреть только треугольник и использовать закон косинусов, чтобы найти длину неизвестной стороны.
Закон косинусов:
Где — длина неизвестной стороны, и — длины известных сторон, и — угол между и.
Из задачи:
Сообщить об ошибке
является параллелограммом. Найдите длину диагонали .
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти длину диагонали, мы можем рассмотреть только треугольник и использовать закон косинусов, чтобы найти длину неизвестной стороны.
Закон косинусов:
Где – длина неизвестной стороны, и – длины известных сторон, и – угол между и .
Из задачи:
Сообщить об ошибке
является параллелограммом. Найдите длину диагонали .
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти длину диагонали, мы можем рассмотреть только треугольник и использовать закон косинусов, чтобы найти длину неизвестной стороны.
Закон косинусов:
Где – длина неизвестной стороны, и – длины известных сторон, и – угол между и .
Из задачи:
Сообщить об ошибке
является параллелограммом. Найдите длину диагонали. .
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти длину диагонали, мы можем рассмотреть только треугольник и использовать закон косинусов, чтобы найти длину неизвестной стороны.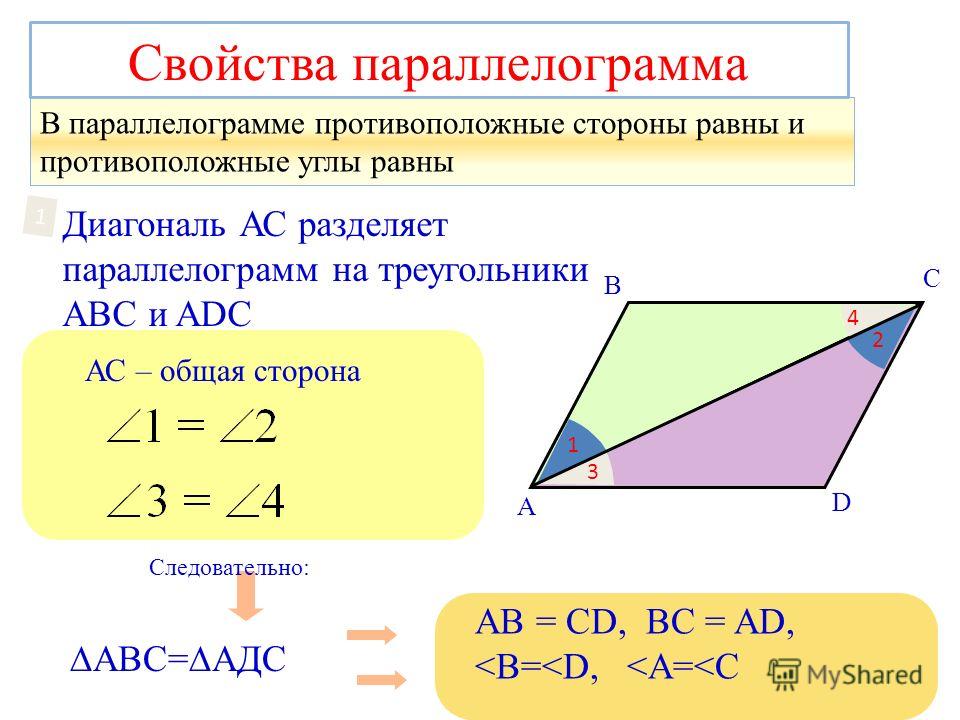
Закон косинусов:
Где – длина неизвестной стороны, и – длины известных сторон, и – угол между и .
Из задачи:
Сообщить об ошибке
является параллелограммом. Найдите длину диагонали .
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти длину диагонали, мы можем рассмотреть только треугольник и использовать закон косинусов, чтобы найти длину неизвестной стороны.
Закон косинусов:
Где — длина неизвестной стороны, и — длины известных сторон, и — угол между и.
Из этой задачи:
Отчет о ошибке
Уведомление об авторском праве
Посмотреть акт математики
Rohan
Сертифицированный Tutor
Университет ST Johns, Bachelor Science, Pharmacy.
Просмотр репетиторов по математике ACT
Charles
Сертифицированный репетитор
Университет Северной Алабамы, бакалавр наук, химия. Университет Вандербильта, доктор философии, органическая химия.
View ACT Репетиторы по математике
Элисон
Сертифицированный репетитор
Технологический институт Джорджии, главный кампус, нынешний студент бакалавриата, машиностроение.
Все математические ресурсы ACT
14 диагностических тестов
767 практических тестов
Вопрос дня
Карточки
Учитесь по концепции
Как найти длину диагонали параллелограмма
Как найти длину диагонали параллелограмма — Промежуточная геометрия
—>
- Войти
- Биографии репетитора
-
Подготовка к тесту
СРЕДНЯЯ ШКОЛА
- ACT Репетиторство
- SAT Репетиторство
- Репетиторство PSAT
- ASPIRE Репетиторство
- ШСАТ Репетиторство
- Репетиторство STAAR
ВЫСШАЯ ШКОЛА
- Репетиторство MCAT
- Репетиторство GRE
- Репетиторство по LSAT
- Репетиторство по GMAT 904:30
К-8
- Репетиторство AIMS
- Репетиторство по HSPT
- Репетиторство ISEE
- Репетиторство по ISAT
- Репетиторство по SSAT
- Репетиторство STAAR
Поиск 50+ тестов
-
Академическое обучение
репетиторство по математике
- алгебра
- Исчисление
- Элементарная математика
- Геометрия
- Предварительное исчисление
- Статистика
- Тригонометрия
Репетиторство по естественным наукам
- Анатомия
- Биология
- Химия
- Физика
- Физиология
иностранные языки
- французский
- немецкий
- Латинский
- Китайский мандарин
- Испанский
начальное обучение
- Чтение
- Акустика
- Элементарная математика
прочее
- Бухгалтерский учет
- Информатика
- Экономика
- Английский
- Финансы
- История
- Письмо
- Лето
Поиск по 350+ темам
-
О
- Обзор видео
- Процесс выбора наставника
- Онлайн-репетиторство
- Мобильное обучение
- Мгновенное обучение
- Как мы работаем
- Наша гарантия 904:30
- Влияние репетиторства
- Обзоры и отзывы
- Освещение в СМИ
- О преподавателях университета
Звоните прямо сейчас, чтобы записаться на обучение:
(888) 888-0446
Все ресурсы по промежуточной геометрии
8 Диагностические тесты
250 практических тестов
Вопрос дня
Карточки
Учитесь по концепции
Справка по промежуточной геометрии »
Плоская геометрия »
Четырехугольники »
Параллелограммы »
Как найти длину диагонали параллелограмма
Длина параллелограмма см, а ширина см.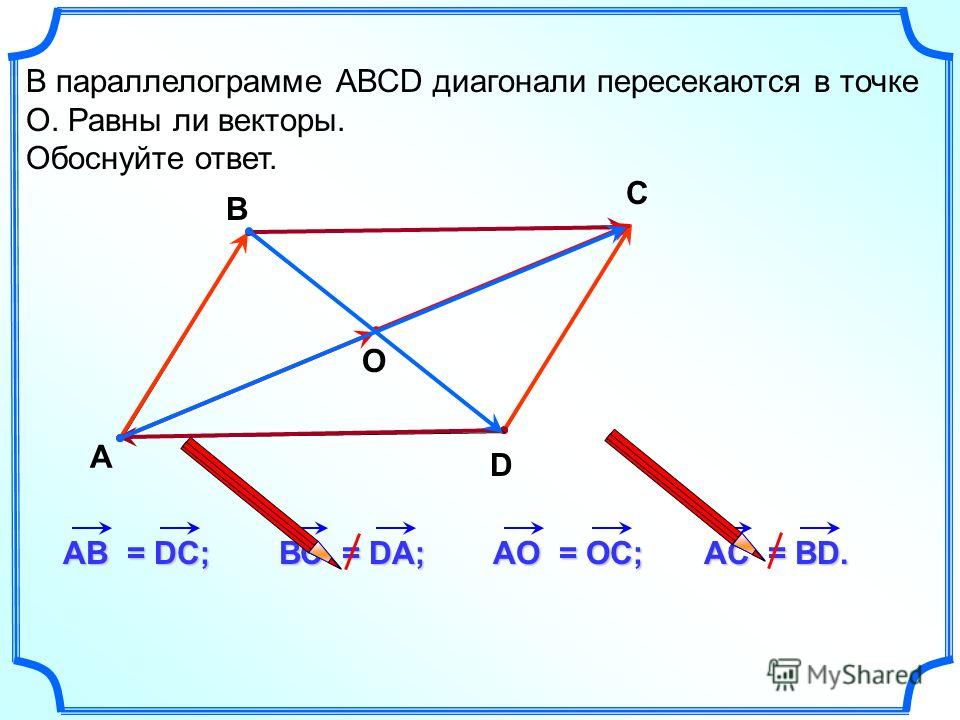
Возможные ответы:
Ни один из других ответов.
Правильный ответ:
Объяснение:
Формула отношения между диагоналями и сторонами параллограмма:
,
, где представляет одну диагональ,
представляет другую диагональ,
представляет собой сторону, а
представляет примыкающую сторону.
Итак, в этой задаче подставьте известные значения и найдите недостающую диагональ.
Итак, недостающая диагональ равна см.
Сообщить об ошибке
В приведенном выше параллограмме найдите длину отмеченной диагонали.
Возможные ответы:
Ни один из других ответов.
Правильный ответ:
Объяснение:
В параллограмме диагонали делят друг друга пополам, поэтому вы можете установить два отрезка, отмеченных на рисунке, равными друг другу, а затем найти .
Итак,
.
Если , то вы можете подставить 14 в каждый помеченный сегмент, чтобы получить в общей сложности 52.
Сообщить об ошибке
В приведенном ниже параллограмме найдите длину помеченной диагонали.
Возможные ответы:
Ни один из других ответов.
Правильный ответ:
Объяснение:
В параллелограмме диагонали делят друг друга пополам, поэтому вы можете установить помеченные сегменты равными друг другу, а затем найти .
.
Если , то подставьте 6 в каждый помеченный сегмент, чтобы получить в сумме 40.
Сообщить об ошибке
В приведенном выше параллелограмме найдите длину отмеченной диагонали.
Возможные ответы:
Ни один из других ответов.
Правильный ответ:
Объяснение:
В параллелограмме диагонали делят друг друга пополам, так что вы можете установить помеченные сегменты равными друг другу, а затем найти .
.
Затем подставьте 4,8 вместо в каждом помеченном сегменте, чтобы получить в сумме 11,2 для длины диагонали.
Сообщить об ошибке
Предположим, площадь квадрата равна 6. Какова диагональ параллелограмма?
Возможные ответы:
Правильный ответ:
Пояснение:
Напишите формулу для нахождения стороны квадрата по площади.
Найти сторону.
Диагональ квадрата можно решить с помощью теоремы Пифагора.
Подставьте и решите диагональ, .
Сообщить об ошибке
Если длина стороны квадрата , какова диагональ квадрата?
Возможные ответы:
Правильный ответ:
Пояснение:
Запишите диагональную формулу квадрата.
Подставьте длину стороны и уменьшите.
Сообщить об ошибке
Параллелограмм содержит диагонали и . а также .
Верно, ложно или не определено: параллелограмм – это прямоугольник. 9
Неверно
Пояснение:
Одной из характеристик прямоугольника является то, что его диагонали равны. Поскольку диагонали параллелограмма разной длины, он не может быть прямоугольником.
Сообщить об ошибке
Параллелограмм имеет диагонали и . а также .
Верно, неверно или не определено: параллелограмм – это ромб.
Возможные ответы:
Верно
Не определено
Неверно
Правильный ответ:
Не определено
3
Пояснение:
Одной из характеристик ромба является то, что его диагонали перпендикулярны; никаких ограничений на их длину не существует. Перпендикулярны ли диагонали, не указано, поэтому фигура может быть ромбом, а может и не быть.
Сообщить об ошибке
Уведомление об авторских правах
Посмотреть репетиторов
Джоанна
Сертифицированный репетитор
Государственный колледж Томаса Эдисона, бакалавр ядерных технологий. Университет Гранд-Каньон, магистр образования, испанский язык…
Просмотр репетиторов
Леонель
Сертифицированный репетитор
Университет Сент-Мэрис, бакалавриат, биология, общие.
Просмотреть репетиторов
Джори
Сертифицированный репетитор
Университет Дилларда, бакалавр изящных искусств, педагогическое образование в области драмы и танцев. Тулейнский университет Луизианы, магистр изящных искусств …
Все ресурсы промежуточной геометрии
8 Диагностические тесты
250 практических тестов
Вопрос дня
Карточки
Учитесь по концепции
Диагональ параллелограмма – формула, свойства, примеры
Диагональ параллелограмма – это отрезок, соединяющий его несмежные вершины. У параллелограмма 2 диагонали и длину диагоналей параллелограмма можно найти по различным формулам в зависимости от заданных параметров и размеров. Давайте узнаем больше о диагоналях параллелограмма в этой статье.
| 1. | Что такое диагональ параллелограмма? |
| 2. | Диагональ параллелограмма Формула |
3. |
Часто задаваемые вопросы о диагонали параллелограмма |
Что такое диагональ параллелограмма?
Диагонали параллелограмма можно провести, соединив две несмежные вершины параллелограмма. Следует отметить, что две диагонали параллелограмма делят друг друга пополам и делят параллелограмм на конгруэнтные треугольники.
Диагональ параллелограмма Формула
Формула диагоналей параллелограмма используется для вычисления длины диагоналей данного параллелограмма. Существуют разные формулы для разных видов параллелограммов. Обратите внимание на приведенный ниже рисунок, на котором показан параллелограмм вместе с его диагоналями. Здесь «p» и «q» — диагонали, а «x» и «y» — две стороны параллелограмма.
Ниже приведена простая формула для нахождения длины диагоналей параллелограмма. Для этой формулы нам понадобится длина сторон и любой из известных углов. Если мы будем следовать рисунку, приведенному выше, мы можем заметить, что: 92 — 2xy cos B} )
Формула 2: Другая формула, которая выражает отношение между длинами диагоналей и сторон параллелограмма:
p 2 + q 2 = 2( x 2 + y 2 )
Где
- p и q — диагонали соответственно.
- x и y — стороны параллелограмма.
Следует отметить, что квадрат, прямоугольник и ромб относятся к категории параллелограммов. А так как свойства у них разные, то и формула для нахождения их диагоналей тоже разная. Например, диагональ квадрата (d) = a√2; где «d» — диагональ, а «а» — сторона квадрата. Диагональ прямоугольника (d) = √( l 2 + w 2 ), где l = длина прямоугольника, а w = ширина прямоугольника. Поэтому формула диагонали параллелограмма различается для разных видов параллелограммов.
Свойства диагоналей параллелограмма
Следующие пункты показывают свойства диагоналей параллелограмма. Так как параллелограмм включает в себя квадрат, прямоугольник, ромб, диагонали этих фигур имеют несколько общих свойств и несколько различных.
- Диагонали параллелограмма всегда делят друг друга пополам.
- В квадрате диагонали равны и делят друг друга пополам под прямым углом.
- В прямоугольнике диагонали равны и делят друг друга пополам, но не под прямым углом.
- В ромбе диагонали могут быть не обязательно равными, но они перпендикулярны друг другу.
☛ Статьи по теме
- Диагональ квадрата 904:30
- Диагональ прямоугольника
- Диагональ куба Формула
- Диагональ ромба
Примеры использования формулы диагонали параллелограмма
-
Пример 1: Найдите длину диагоналей ромба со стороной 4 дюйма, если внутренние углы равны 120° и 60°.
Решение:
Дано, внутренний угол A = 120°, а угол B = 60°.
х = 4, у = 4 92 + (2 times 4 times 4 times cos 60)} \ &= sqrt{32 + 16} \ p &= sqrt {48} \ p &= 6.92 end{align} )Ответ: Длина диагоналей 4 дюйма и 6,92 дюйма.
-
Пример 2: Для параллелограмма ABCD, если длины смежных сторон 35 футов и 82 фута. Если один из внутренних углов равен 37°. Найдите длину любой диагонали.
Решение:
Дано, внутренний угол A = 37° 92 — (2 times 35 times 82 times cos 37)} \ &= sqrt{3365} \ p &= 58 end{align})
Ответ: Длина диагонали 58 футов
-
Пример 3: Вычислите длину диагонали параллелограмма со сторонами 4 звена, 6 звеньями и внутренним углом А, равным 60 градусам.
Решение:
Дано, a = 4 единицы, b = 6 единиц, угол A = 60°
Используя диагональ формулы параллелограмма, 92 — 24})= (sqrt28) = 5,291
Ответ: Диагональ параллелограмма = 5,291 ед.
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами
Запишитесь на бесплатный пробный урок
Практические вопросы по диагонали параллелограмма
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о диагонали параллелограмма
Что такое диагональ параллелограмма?
Диагональ параллелограмма — это отрезок, соединяющий две несмежные вершины параллелограмма.
Какие компоненты формулы диагонали параллелограмма?
Формула диагонали параллелограмма помогает найти длину диагоналей, используя длину сторон и любой из известных углов. Таким образом, его составляющие включают в себя стороны параллелограмма и соответствующие им углы.
Делят ли диагонали параллелограмма пополам?
Да, диагонали параллелограмма делят друг друга пополам. Это означает, что диагонали параллелограмма делят друг друга на 2 равные части.
Равны ли диагонали параллелограмма?
Параллелограмм состоит из квадрата, прямоугольника и ромба. В то время как диагонали квадрата и прямоугольника равны, диагонали ромба не обязательно равны.
Как найти диагонали параллелограмма без углов?
Длину диагоналей параллелограмма можно вычислить, даже если не известны внутренние углы.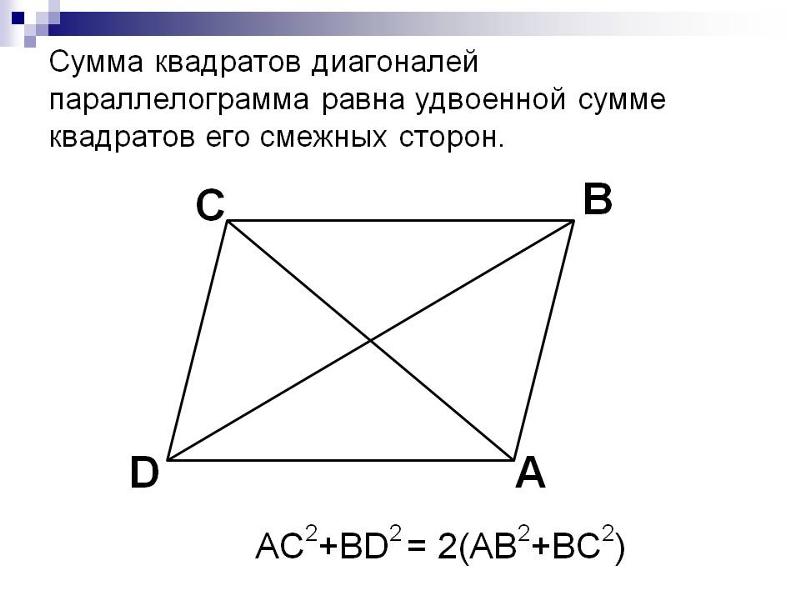
Диагональ формулы параллелограмма – определение и типы
- Автор Priya Wadhwa
- Последнее изменение 20 июля 2022 г.
- Автор
Прия Вадхва - Последнее изменение 20 июля 2022 г.
Диагональ параллелограмма Формула: Название параллелограмма происходит от греческого слова parallelogrammon, что означает ограниченный параллельными линиями. В результате параллелограмм представляет собой четырехугольник с параллельными прямыми на противоположных сторонах. Противоположные стороны параллелограмма будут параллельны и равны.
Диагонали параллелограмма — это отрезки, соединяющие противоположные вершины параллелограмма.
Мы можем вычислить длины диагоналей параллелограмма, если нам известны меры его смежных сторон и смежных углов. В этой статье мы подробно обсудим диагональ формулы параллелограмма.
Что такое параллелограмм?
Параллелограмм представляет собой тип четырехугольника, образованного параллельными прямыми. Противоположные стороны параллелограмма параллельны и равны. Угол параллелограмма между соседними сторонами может быть разным, но противоположные углы равны.
Изучение концепций экзамена на Embibe
Изучите приведенную ниже диаграмму, на которой представлены три вида параллелограммов. Это частные случаи параллелограммов.
Диагональ
Диагональ — это отрезок, соединяющий два угла многоугольника, не являющегося ребром. В результате мы можем сделать диагональ, соединив любые два угла (вершины), которые ранее не были соединены ребром.
Количество диагоналей параллелограмма
Для (n)-стороннего правильного многоугольника количество диагоналей можно получить по следующей формуле:
Количество диагоналей ( = frac{{nleft( {n – 3} right)} }{2})
Для параллелограмма (n = 4)
Следовательно, количество диагоналей в параллелограмме ( = frac{{4left( {4 – 3} right)}}{ 2} = 2.)
Практические экзаменационные вопросы
Диагонали параллелограмма
Диагонали параллелограмма — это отрезки, соединяющие противоположные вершины параллелограмма.
Параллелограмм имеет две пары противоположных вершин и, следовательно, две диагонали.
В параллелограмме (ABCD,,AC) и (BD) — диагонали.
Диагонали параллелограмма Формула
Формула диагоналей параллелограмма используется для определения длины диагоналей параллелограмма. Используя длины сторон и меру углов, мы можем вычислить длины диагоналей.
Попытка пробных тестов
Для любого параллелограмма (ABCD,) пусть (a) и (b) — длины сторон параллелограмма, а (p) и (q) — длины диагоналей, тогда 92}} right))
Где (p) и (q) — длины диагоналей соответственно, а (a) и (b) — стороны параллелограмма.
Типы параллелограмма
Параллелограмм можно разделить на несколько видов в зависимости от его различных свойств. В основном он подразделяется на три отдельные категории:
1. Прямоугольник
2. Квадрат
3. Ромб
1. Прямоугольник
Прямоугольник – это параллелограмм с четырьмя прямыми углами и двумя наборами равных и параллельных противоположных сторон.
Диагонали прямоугольника
Диагональ прямоугольника — это отрезок, соединяющий любые две его несмежные вершины. Диагонали следующего прямоугольника равны (AC) и (BD). Как видите, длины (AC) и (BD) равны. Диагональ делит прямоугольник на два прямоугольных треугольника, каждый из которых имеет стороны, равные сторонам прямоугольника, и гипотенузу, которая является диагональю треугольника.
Длина диагонали (d) прямоугольника, длина которого равна (l) единиц, а ширина — (b) единиц, вычисляется по теореме Пифагора. 92}} .)
2.

Параллелограмм с четырьмя равными сторонами и четырьмя прямыми углами называется квадратом.
Диагонали квадрата
Диагональ квадрата — это отрезок, соединяющий любые две его противоположные вершины.
В данном квадрате длины отрезков (AC) и (BD) равны. Диагональ любого квадрата делит его на два равных прямоугольных треугольника, причем диагональ образует гипотенузу прямоугольного треугольника.
Теорема Пифагора используется для вычисления длины диагонали (d) квадрата со стороной (a) единиц. 92},cos,theta} = asqrt {2 – 2,cos,theta} )
Свойства диагонали параллелограмма
Диагонали параллелограмма (ABCD) равны (AC) и (BD). Свойства диагоналей параллелограмма следующие:
1. Диагонали параллелограмма делят друг друга пополам. (OB = OD) и (OA = OC)
2. Каждая диагональ делит параллелограмм на два равных треугольника.
3. Закон параллелограмма: Сумма квадратов сторон равна сумме квадратов диагоналей.
Решенные примеры – Диагональ формулы параллелограмма
Q.1. Explain how a square is:
(i) a quadrilateral
(ii) a parallelogram
(iii) a rhombus
(iv) a rectangle
Ответ: (i) Квадрат является четырехугольником, так как представляет собой замкнутую двумерную фигуру с четырьмя прямолинейными отрезками. 9{rm{o}}}} )
(q = 4sqrt {2 — 2 times left( { — frac{1}{2}} right)} )
(q = 4sqrt {2 + 1} = 4 times 1,732 = 6,928,{rm{см}})
Следовательно, длина диагоналей равна (4,{rm{см}}) и (6,928,{rm{см}}{rm{.}})
Q.3. Найдите длину диагоналей прямоугольника, длина которого 3 см, а ширина 4 см?
Ответ: Дано, (l = 3,{rm{см}}) и (b= 4,{rm{см}})
Используя формулу диагонали прямоугольника,
( d = sqrt {{l ^ 2} + {b ^ 2}} ) 92}} )
(d = sqrt {9 + 16} = sqrt {25} = 5,{rm{см}})
Следовательно, длина диагонали данного прямоугольника равна (5,{rm{см}}. )
Q.4. Назовите четырехугольщики, чьи диагонали:
(i) Потройте каждую другая
(II) — перпендикулярные бисекторы друг от друга
(III) 9177 2
(III) — это равные 9177
(III). (i) Диагонали делят друг друга пополам в ромбе, параллелограмме, прямоугольнике или квадрате. 9{rm{o}}}} right)} )
(p = sqrt {4 + 36 — 24 times 0,707} )
(p = sqrt {40 — 16,968} )
(p = sqrt {23,032} )
(p = 4,799,{rm{см}})
Следовательно, длина диагонали параллелограмма равна (4,799,{rm{см} }{rm{.}})
Сводка
В этой статье обсуждалось, что параллелограмм — это многоугольник, у которого противоположные стороны равны и параллельны. В этой статье мы также узнали об определении параллелограмма, его диагонали, типах параллелограмма и длине их диагоналей, свойствах параллелограмма, формуле для нахождения длины диагоналей параллелограмма. Мы также решили несколько примеров, касающихся всего этого.
Изучите все концепции геометрии
Часто задаваемые вопросы (FAQ) – Диагональ формулы параллелограмма
Q.1. Диагонали параллелограмма равны?
Ответ: Нет, диагонали параллелограмма не равны. Но диагонали делят параллелограмм на две пары конгруэнтных треугольников. Диагонали будут равны, если параллелограмм является прямоугольником или квадратом.
Q.2 . Чему равна диагональ параллелограмма?
Ответ: Диагонали параллелограмма — это отрезки, соединяющие противоположные вершины параллелограмма. В параллелограмме две диагонали.
Q.3. Какова диагональ квадрата (5) дюймов?
Ans: Мы знаем, что длина диагонали квадрата равна (asqrt 2 ,), где (a) — сторона квадрата.
Следовательно, для квадрата (5,{rm{дюйм}}) длина диагонали равна (5sqrt 2 ,{rm{дюйм}}{rm{. }} ) 92} + 2,ab,cos,left( B right)} )
Q.5. Как использовать формулу диагонали параллелограмма?
Ответ: Для любого параллелограмма пусть (a) и (b) — стороны параллелограмма, а (p,) и (q) — длины диагоналей, тогда
Шаг 1 : Проверьте заданные параметры, стороны параллелограмма и соответствующие углы.
Шаг 2: Подставьте значения в формулу для (a,,b,,A) и (B) и решите, чтобы получить значения (p) и (q), которые длина диагоналей параллелограмма. 92} + 2,ab,cos,left( B right)} )
Теперь у вас есть вся необходимая информация о диагонали формулы параллелограмма, и мы надеемся, что эта подробная статья будет вам полезна. Если у вас есть какие-либо вопросы относительно этой статьи, отправьте нам сообщение через раздел комментариев ниже, и мы свяжемся с вами как можно скорее.
Пройдите бесплатные пробные тесты, связанные с параллелограммами
Диагональ формулы параллелограмма с примерами и практическими вопросами
Параллелограмм – это четырехугольник, у которого обе пары противоположных сторон параллельны. Некоторые из свойств параллелограмма заключаются в том, что его противоположные стороны равны, его противоположные углы равны, а его диагонали делят друг друга пополам.
Рассмотрим следующий параллелограмм, стороны которого известны, скажем, a и a. Чтобы найти длину одной из его диагоналей, мы можем использовать правило косинусов для треугольников.
Что такое диагональ?
Когда учащиеся узнают о четырехугольниках, они узнают об их различных типах и названиях. Четырехугольники или многоугольники — это геометрические фигуры на плоскости с 4 сторонами, 4 вершинами и 4 углами. В зависимости от длины сторон и степени угла, который они образуют при соединении вершин, они классифицируются и называются по-разному. Различают следующие типы четырехугольников:
-
Квадрат: Имея равные стороны и угол 90 градусов, это самый распространенный и простой четырехугольник, с которым мы все знакомы.
-
Прямоугольник: похож на квадрат тем, что имеет равные все 5 углов по 90 градусов, но отличается неравными сторонами. Противоположные стороны равны, а соседние стороны не равны.
-
Неправильный четырехугольник: Это самая неправильная форма с неравными сторонами и углами.
-
Параллелограмм: в параллелограмме смежные стороны и углы не равны, но противоположные стороны и углы равны друг другу.
-
Ромб: Две смежные стороны попарно равны. И равны только два угла, противоположные друг другу.
-
Трапеция или трапеция: это четырехугольник с одной парой сторон, противоположных друг другу, разной длины и параллельных друг другу.
-
Равнобедренная трапеция: Это особый тип трапеции с непараллельными сторонами, имеющими одинаковую длину.
Вот некоторые из простых четырехугольников, которые мы изучали в предыдущем классе.
Каждый четырехугольник имеет две диагонали, которые делят друг друга пополам в центре четырехугольника. Точно так же диагонали параллелограмма делят друг друга пополам, но не равны по длине. Учащиеся могут легко найти диагонали параллелограмма или любого другого четырехугольника, соединив противоположные вершины. У квадрата и ромба они всегда пересекаются перпендикулярно друг другу, а у других не перпендикулярно.
(Изображение скоро будет загружено)
В [Delta] АЦП, используя правило косинуса, мы вычисляем длину переменного тока следующим образом. 92}}]
= [sqrt {104 — 28} = sqrt {76} = 2sqrt {19} ] ,cm
Почему бы вам не попытаться решить следующую задачу, чтобы узнать, вы освоили эти формулы?
Вопрос:
Один из углов параллелограмма равен 135°, а его диагонали равны [$3,см$ и $3sqrt 5 ,см$] соответственно.
Как найти диагональ параллелограмма, если даны стороны
Параллелограмм — это четырехугольник, противоположные стороны которого параллельны. Прямые, соединяющие его противоположные углы, называются диагоналями. Их длина зависит не только от длин сторон фигуры, но и от величин углов в вершинах этого многоугольника, поэтому без знания хотя бы одного из углов вычислить длины диагоналей можно только в исключительных случаях. Таковыми являются частные случаи параллелограмма — квадрат и прямоугольник.
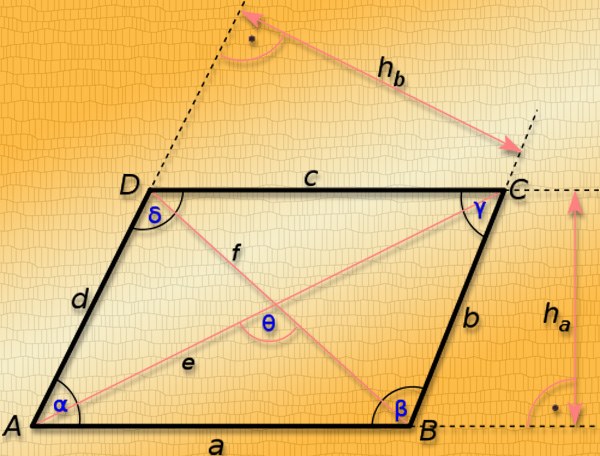
Инструкция
Если длины всех сторон параллелограмма одинаковы (a), то эту фигуру можно назвать еще и квадратом. Величины всех его углов равны 90°, а длины диагоналей (L) одинаковы и могут быть рассчитаны по теореме Пифагора для прямоугольного треугольника. Умножьте длину стороны квадрата на корень из двойки — результат и будет длиной каждой из его диагоналей: L=a*√2.
Если о параллелограмме известно, что он является прямоугольником с указанными в условиях длиной (a) и шириной (b), то и в этом случае длины диагоналей (L) будут равны. И здесь тоже задействуйте теорему Пифагора для треугольника, в котором гипотенузой является диагональ, а катетами — две смежные стороны четырехугольника. Искомую величину рассчитайте извлечением корня из суммы возведенных в квадрат ширины и высоты прямоугольника: L=√(a²+b²).
Для всех остальных случаев знания одних только длин сторон хватит лишь для определения величины, включающей в себя длины сразу обеих диагоналей — сумма их квадратов по определению равна удвоенной сумме квадратов длин сторон. Если же в дополнение к длинам двух смежных сторон параллелограмма (a и b) известен еще и угол между ними (γ), то это позволит рассчитать длины каждого отрезка, соединяющего противоположные углы фигуры. Длину диагонали (L₁), лежащей напротив известного угла, найдите по теореме косинусов — сложите квадраты длин смежных сторон, от результата отнимите произведение этих же длин на косинус угла между ними, а из полученной величины извлеките квадратный корень: L₁ = √(a²+b²-2*a*b*cos(γ)). Для нахождения длины другой диагонали (L₂) можно воспользоваться свойством параллелограмма, приведенным в начале этого шага — удвойте сумму квадратов длин двух сторон, от результата отнимите квадрат уже рассчитанной диагонали, а из полученного значения извлеките корень. В общем виде эту формулу можно записать так: L₂ = √(a²+b²- L₁²) = √(a²+b²-(a²+b²-2*a*b*cos(γ))) = √(a²+b²-a²-b²+2*a*b*cos(γ)) = √(2*a*b*cos(γ)).
Источники:
- как найти длину диагонали параллелограмма
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

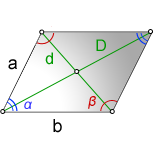
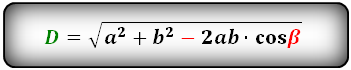
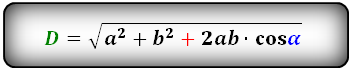
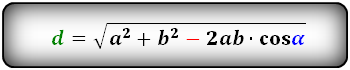

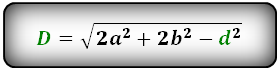
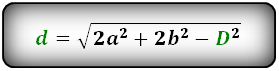

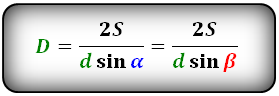
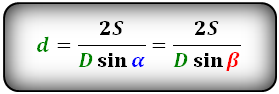
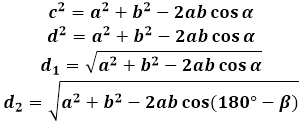

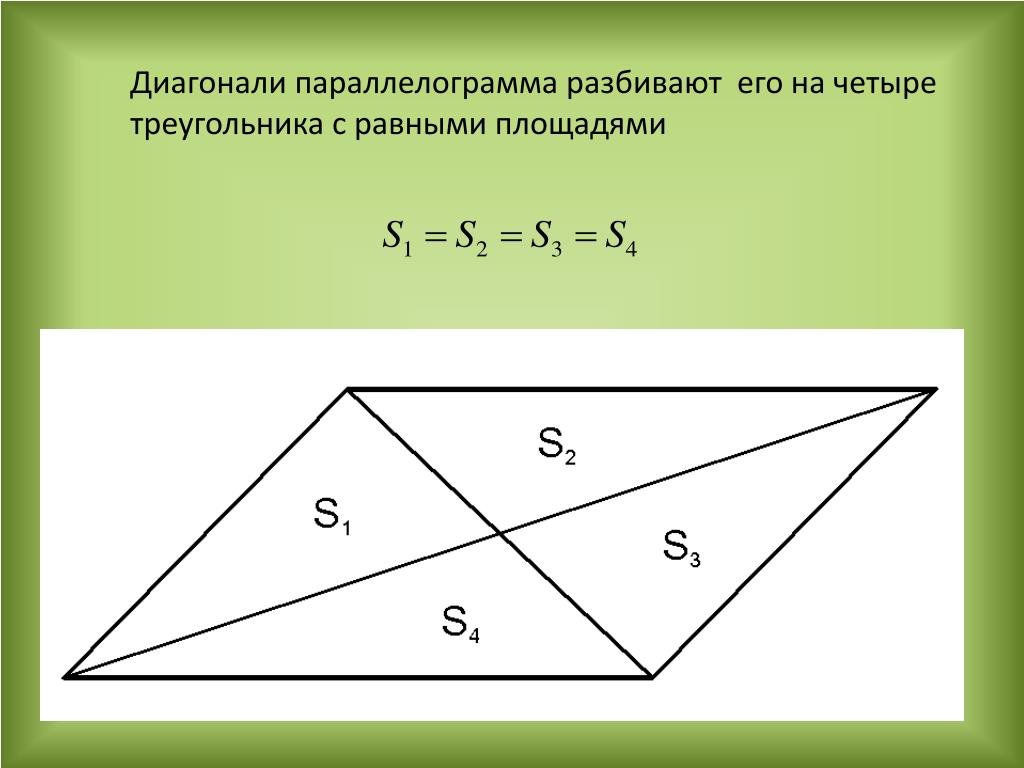
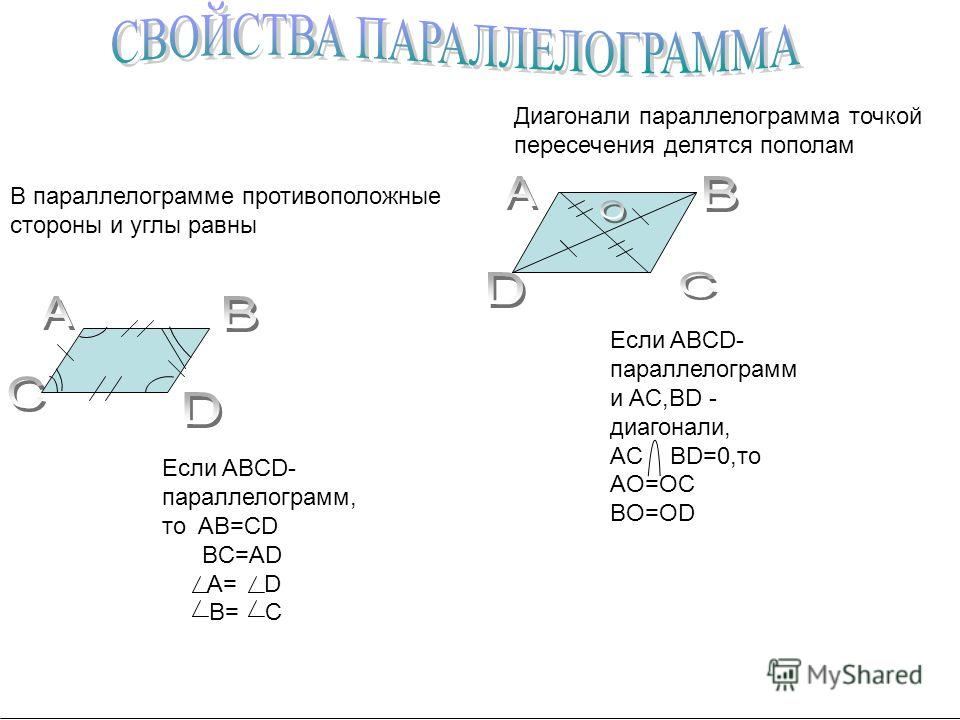
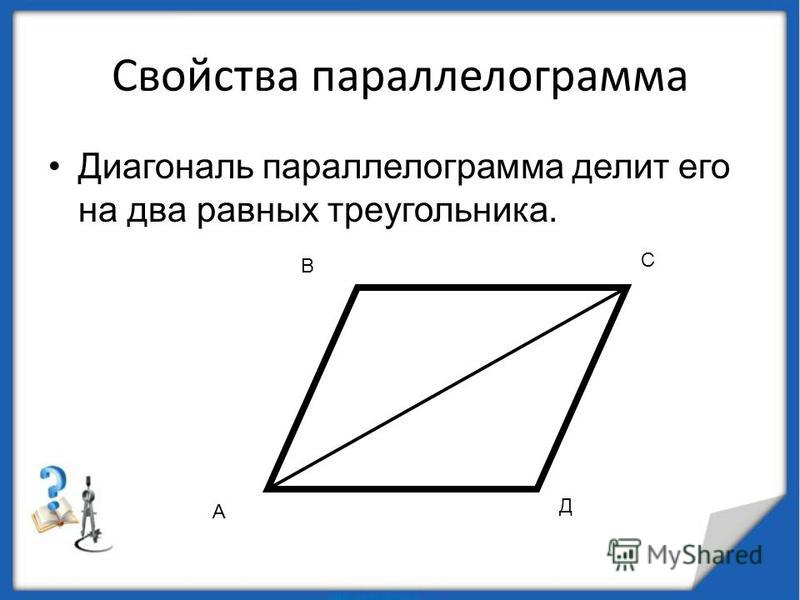
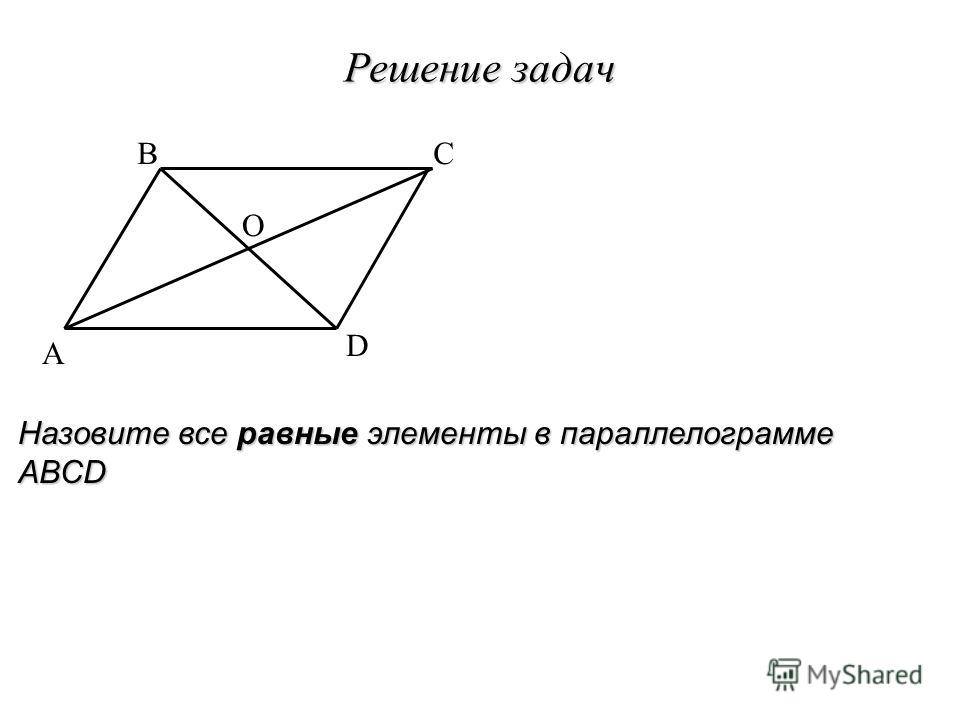
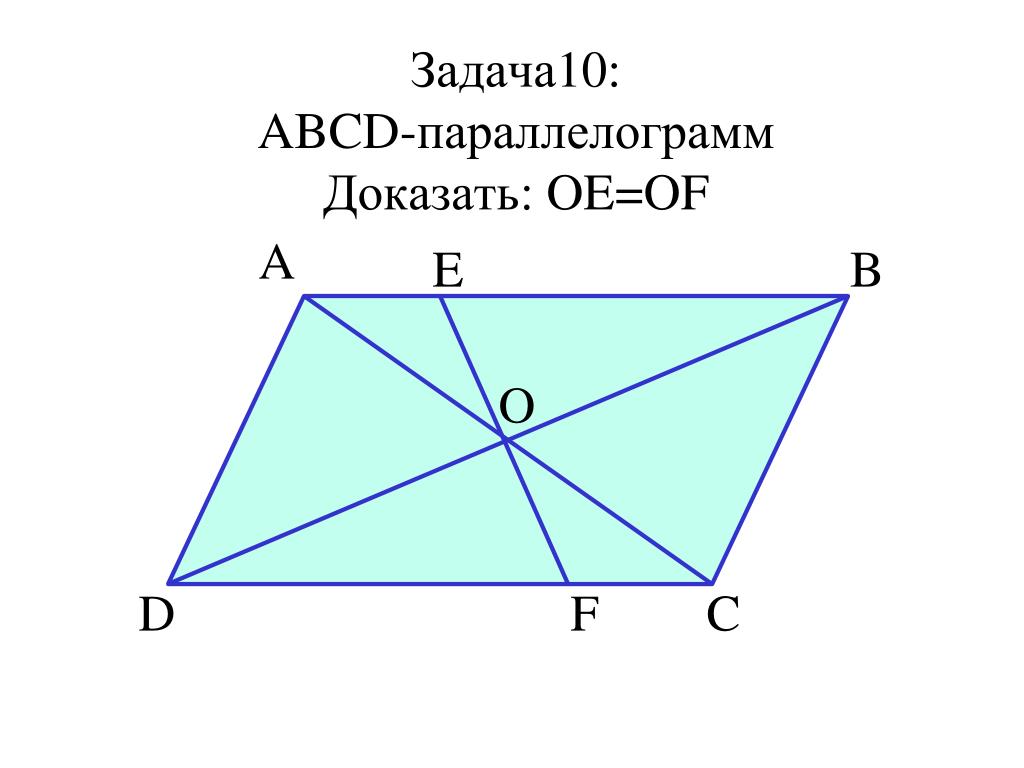
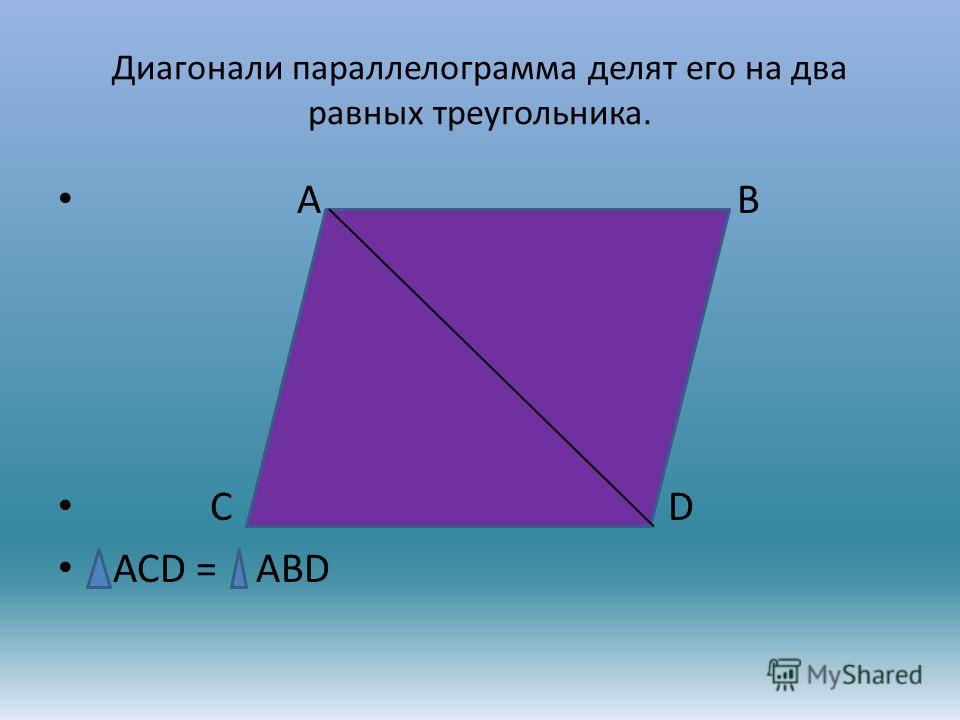 10.2013, 17:02
10.2013, 17:02 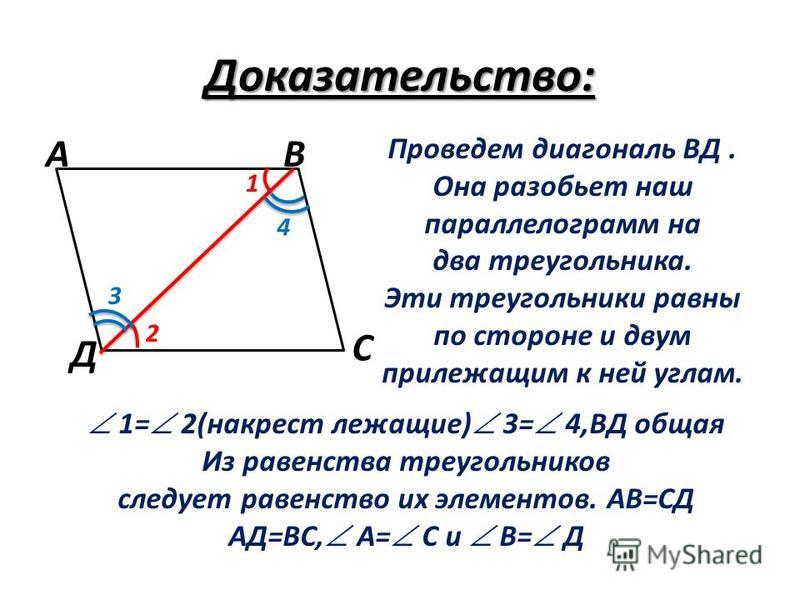 10.2013, 17:06
10.2013, 17:06 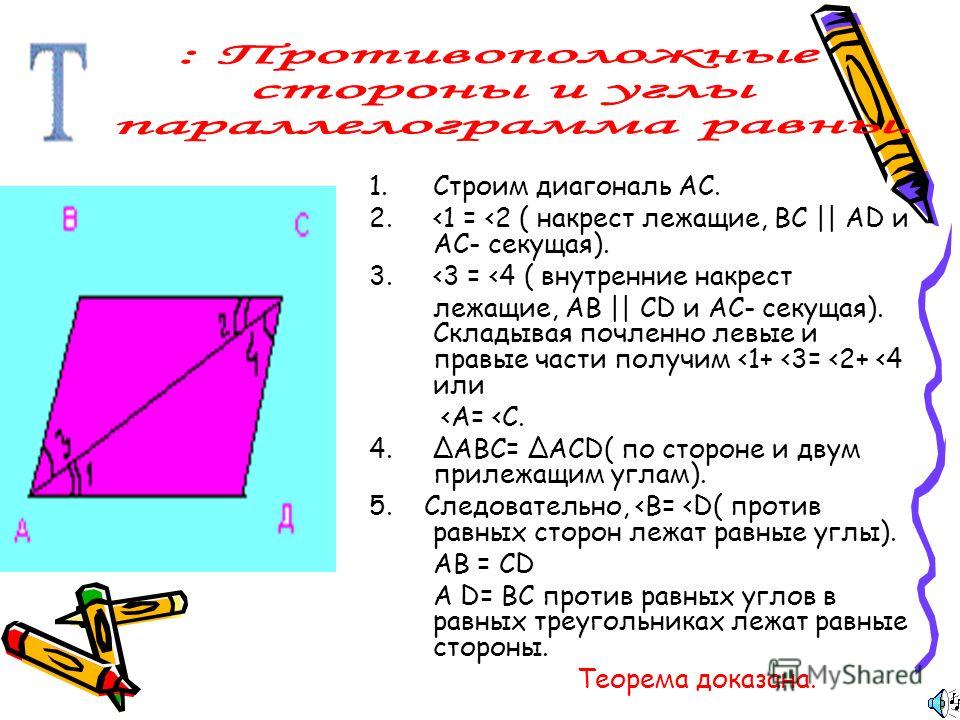

 10.2013, 17:33
10.2013, 17:33 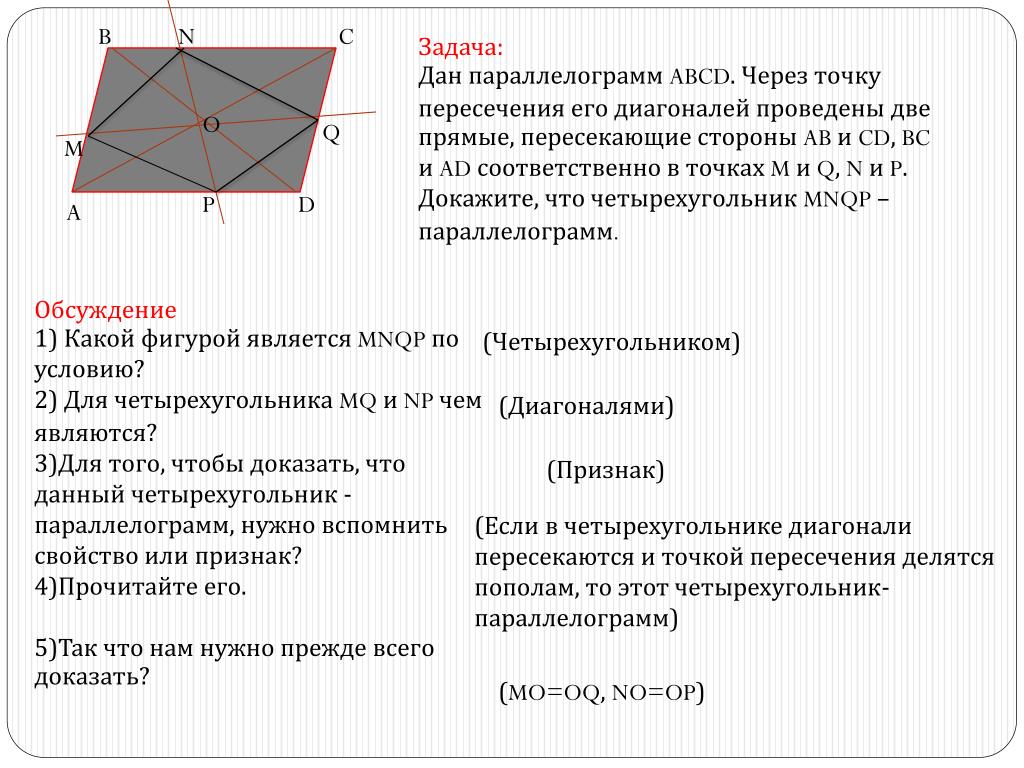 10.2013, 17:42
10.2013, 17:42 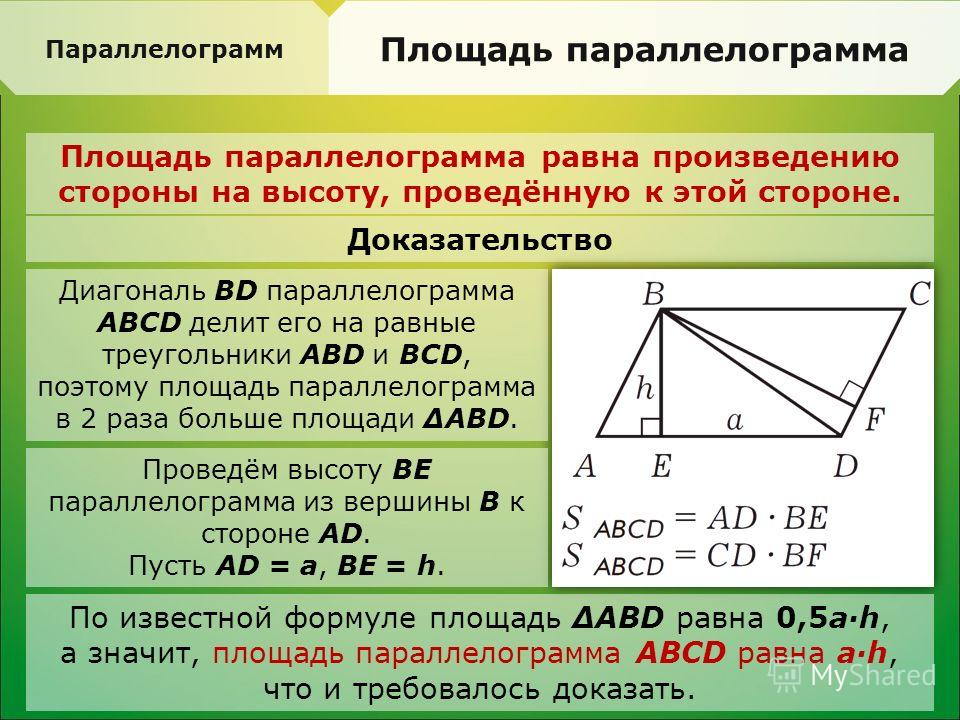

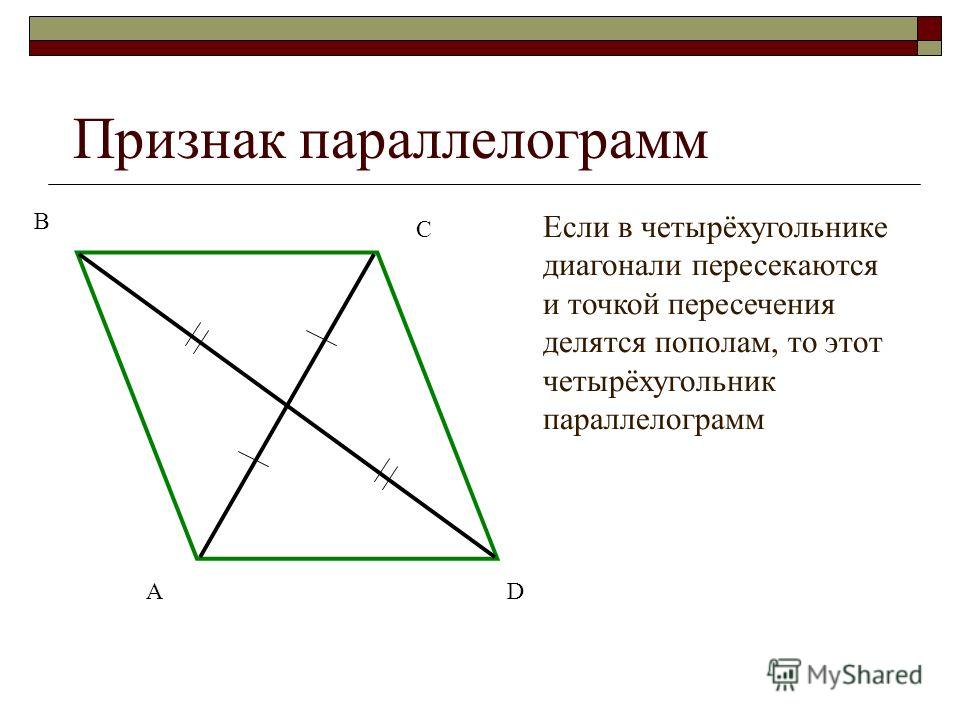
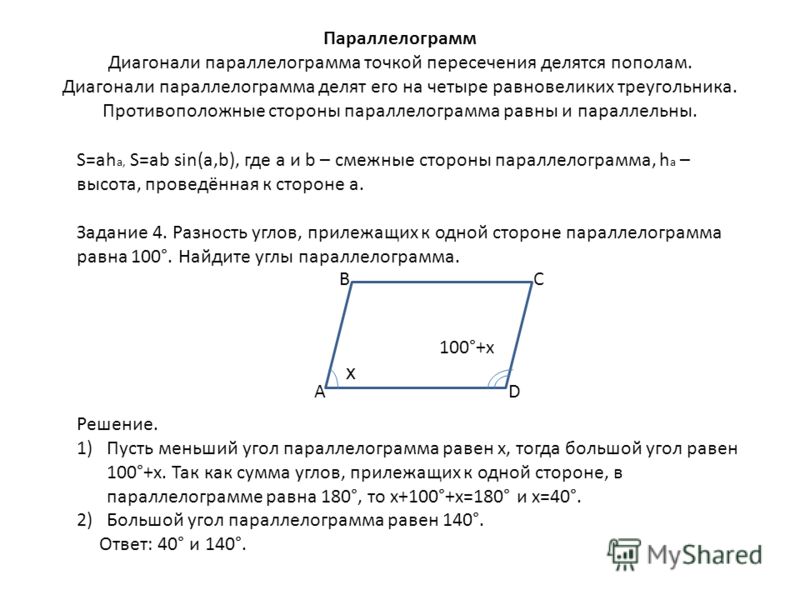
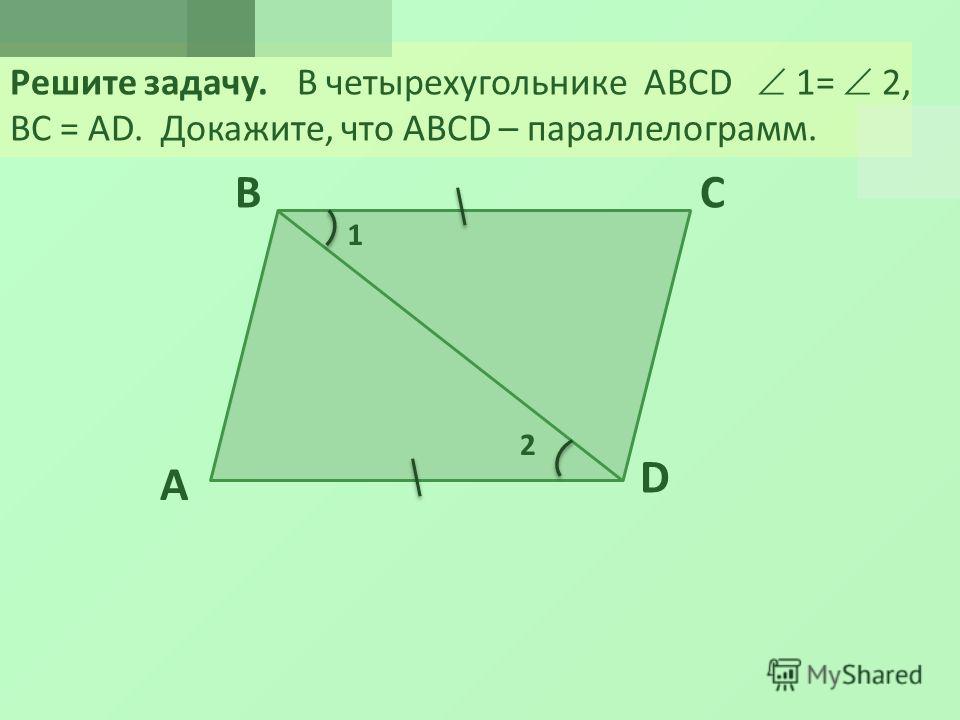

 (5) (10) cos 60°)
(5) (10) cos 60°) 
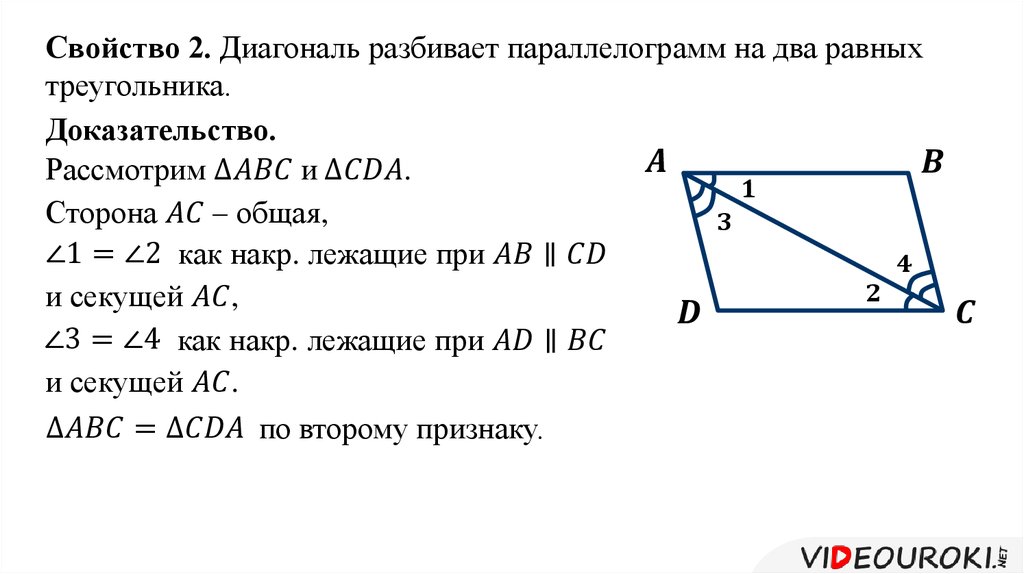 + 36)
+ 36) 

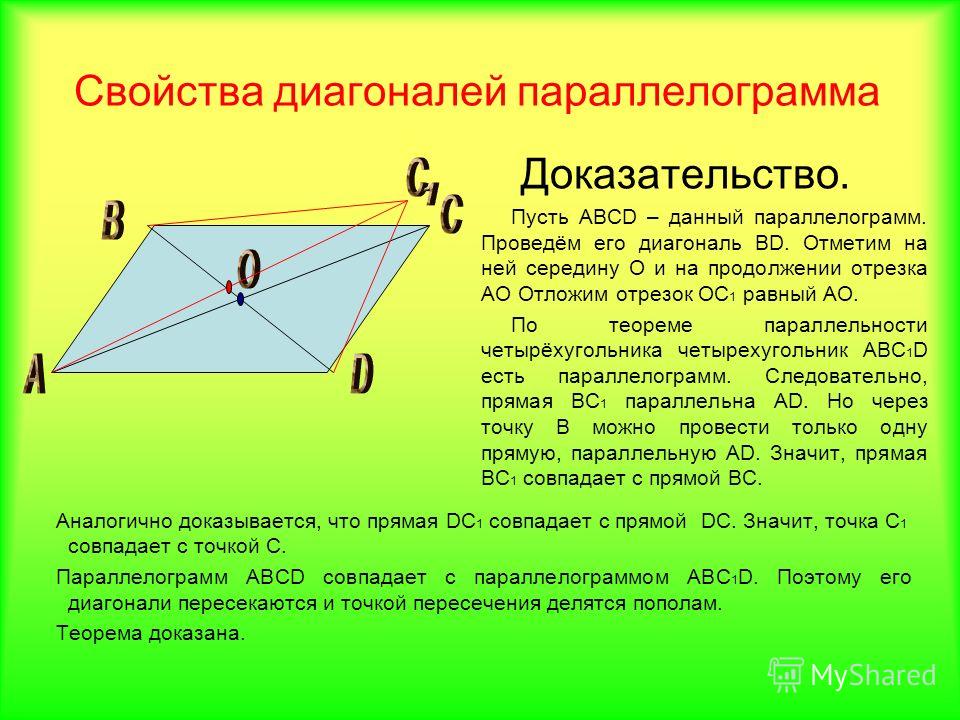
 Диагонали параллелограмма — это отрезки, соединяющие противоположные вершины параллелограмма.
Диагонали параллелограмма — это отрезки, соединяющие противоположные вершины параллелограмма.