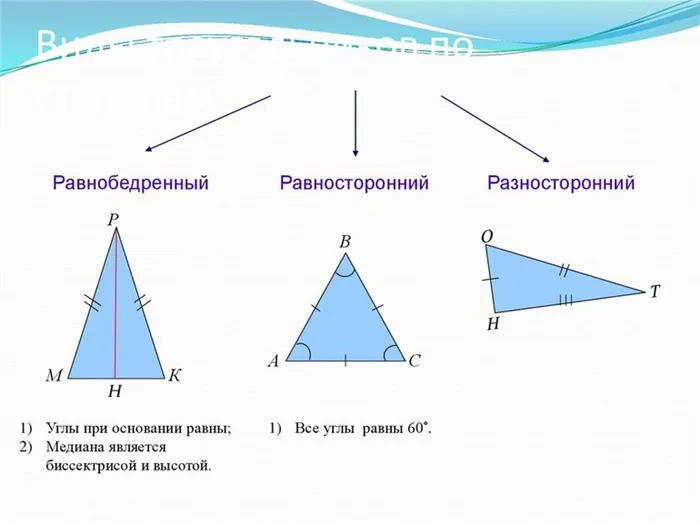
Свойства равностороннего треугольника: теория и пример задачи
В данной статье мы рассмотрим определение и свойства равностороннего (правильного) треугольника. Также разберем пример решения задачи для закрепления теоретического материала.
Определение равностороннего треугольника
Равносторонним (или правильным) называется треугольник, в котором все стороны имеют одинаковую длину. Т.е. AB = BC = AC.
Примечание: правильный многоугольник – это выпуклый многоугольник, имеющий равные стороны и углы между ними.
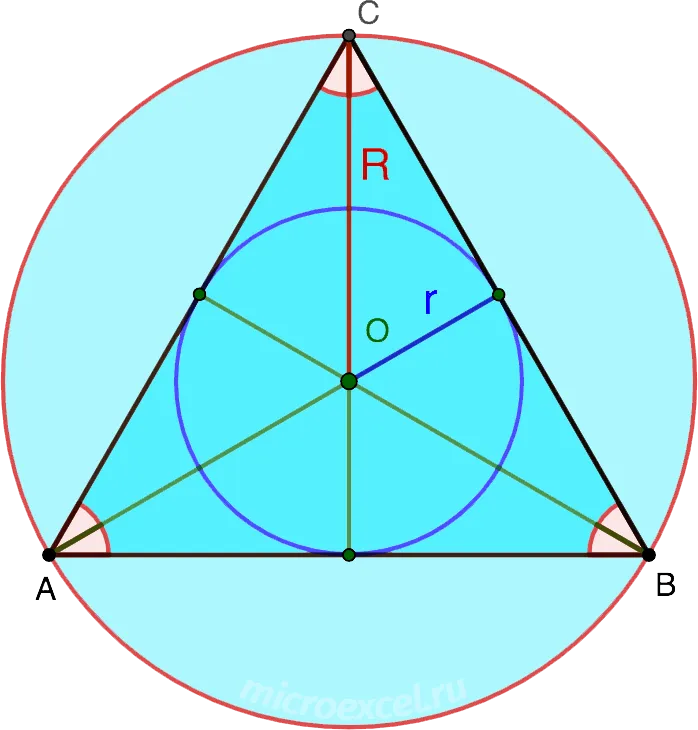
Свойства равностороннего треугольника
Свойство 1
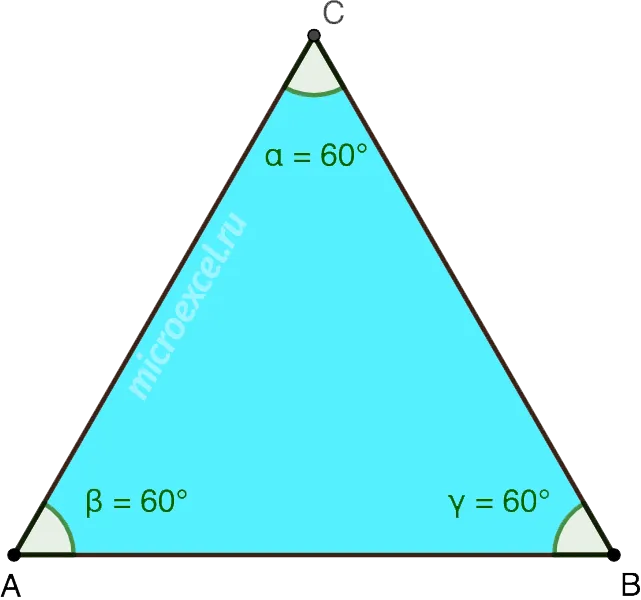
В равностороннем треугольнике все углы равны 60°. Т.е. α = β = γ = 60°.
Свойство 2
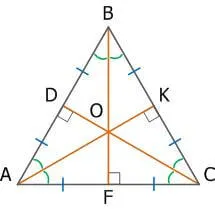
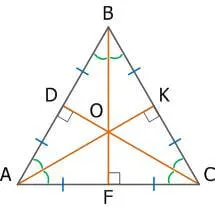
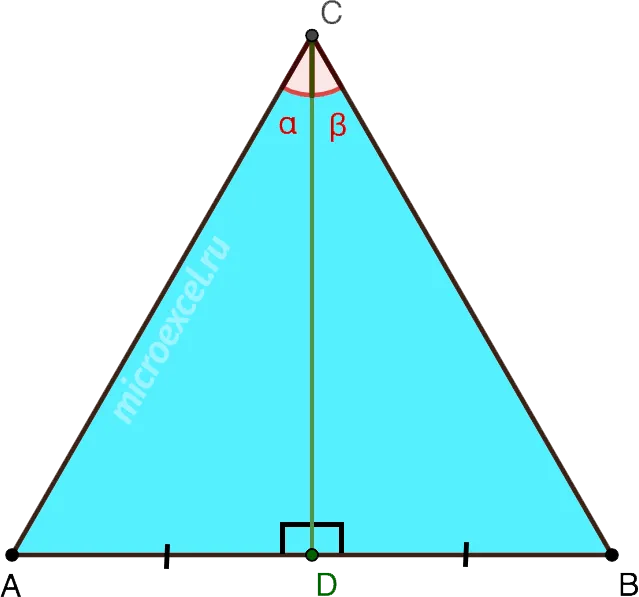
В равностороннем треугольнике высота, проведенная к любой из сторон, одновременно является биссектрисой угла, из которого она проведена, а также медианой и серединным перпендикуляром.
CD – медиана, высота и серединный перпендикуляр к стороне AB, а также биссектриса угла ACB.
Свойство 3
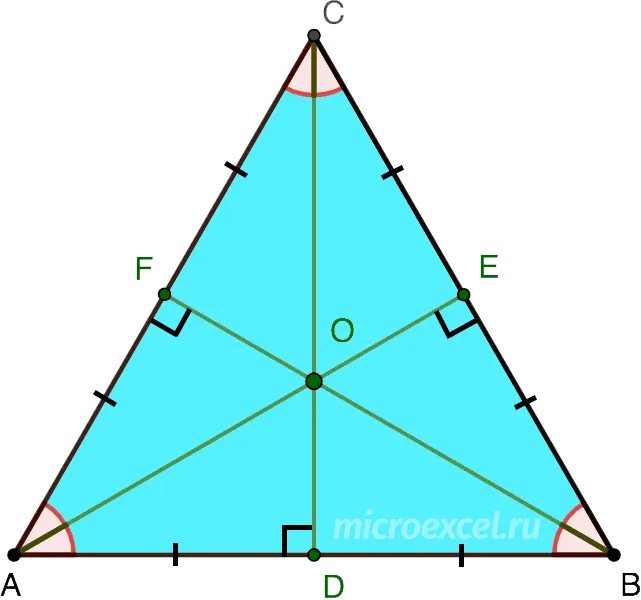
В равностороннем треугольнике биссектрисы, медианы, высоты и серединные перпендикуляры, проведенные ко всем сторонам, пересекаются в одной точке.
Свойство 4
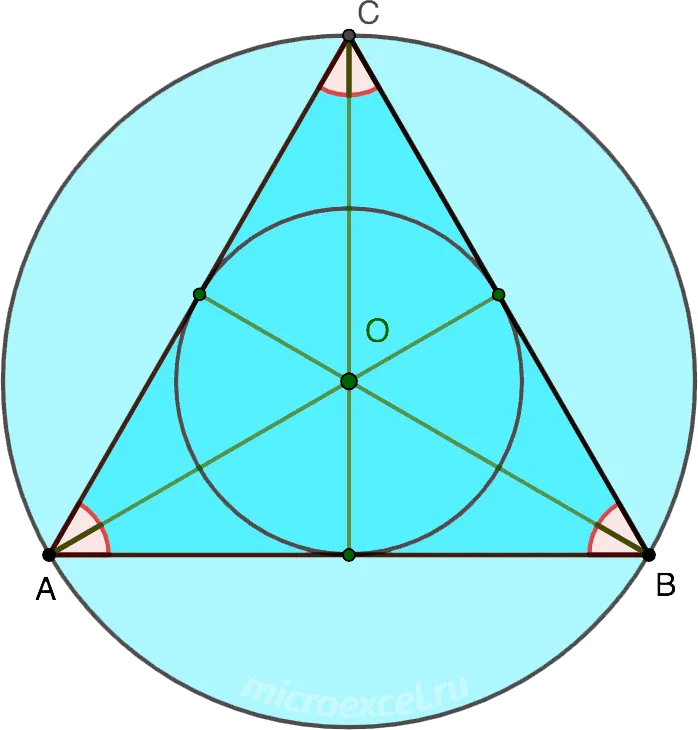
Центры вписанной и описанной вокруг равностороннего треугольника окружностей совпадают и находятся на пересечении медиан, высот, биссектрис и серединных перпендикуляров.
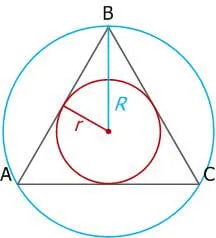
Свойство 5
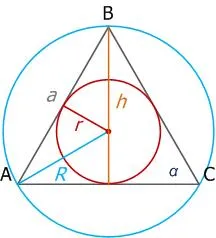
Радиус описанной вокруг равностороннего треугольника окружности в 2 раза больше радиуса вписанной окружности.
- R – радиус описанной окружности;
- r – радиус вписанной окружности;
- R = 2r.
Свойство 6
В равностороннем треугольнике, зная длину стороны (условно примем ее за “a”), можно вычислить:
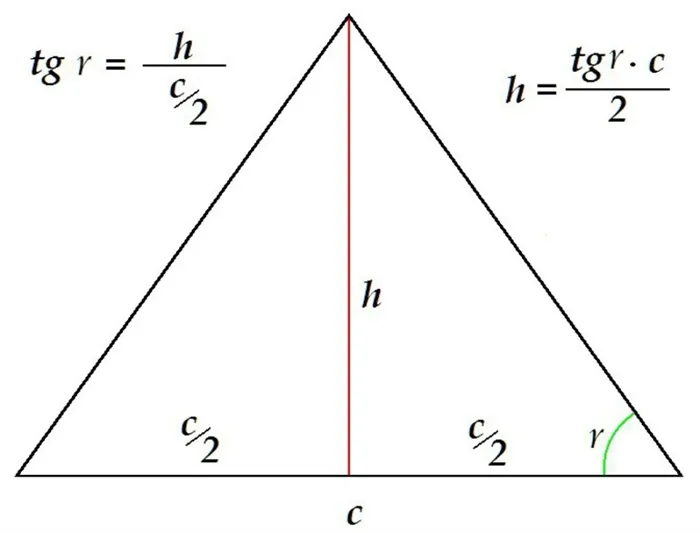
1. Высоту/медиану/биссектрису:
2. Радиус вписанной окружности:
3. Радиус описанной окружности:
4. Периметр:
5. Площадь:
Пример задачи
Дан равносторонний треугольник, сторона которого равна 7 см. Найдите радиус описанной вокруг и вписанной окружности, а также, высоту фигуры.
Решение
Применим формулы, приведеные выше, для нахождения неизвестных величин:
Свойства равностороннего треугольника
Основные свойства равностороннего треугольника непосредственно следуют из свойств равнобедренного треугольника, частным случаем которого он является.
Свойства равностороннего треугольника
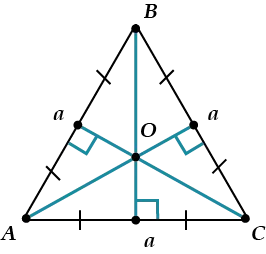
2) Высота, медиана и биссектриса, проведённые к каждой из сторон равностороннего треугольника, совпадают:
AK — высота, медиана и биссектриса, проведённые к стороне BC;
BF — высота, медиана и биссектриса, проведённые к стороне AC;
CD — высота, медиана и биссектриса, проведённые к стороне AB.
Длины всех трёх высот (медиан, биссектрис) равны между собой:
Если a — сторона треугольника, то
3) Точка пересечения высот, биссектрис и медиан называется центром правильного треугольника и является центром вписанной и описанной окружностей (то есть в равностороннем треугольнике центры вписанной и описанной окружностей совпадают).
4) Точка пересечения высот, биссектрис и медиан правильного треугольника делит каждую из них в отношении 2:1, считая от вершин:
5) Расстояние от точки пересечения высот, биссектрис и медиан
до любой вершины треугольника равно радиусу описанной окружности:
6) Расстояние от точки пересечения высот, биссектрис и медиан до любой стороны треугольника равно радиусу вписанной окружности:
7) Сумма радиусов вписанной и описанной окружностей правильного треугольника равна его высоте, медиане и биссектрисе: R+r=BF.

Диагональ треугольника – формула
Очень часто в начале изучения фигуры ученики путают значение диагонали прямоугольника и треугольника. Поэтому, чтобы не путаться в обозначениях, лучше разобраться в тематике раз и навсегда.
Треугольник
Треугольник – это фигура, состоящая из трех сторон и трех углов. Треугольник имеет три характеризующих отрезка:
Треугольник не может иметь диагональ в принципе. Дело в том, что диагонали могут быть проведены только в многоугольниках, количество сторон которых больше 3.
Почему так? Потому что диагональ это отрезок, соединяющий противоположные вершины. В треугольнике противоположных вершин нет и быть не может. Существует сторона, противоположная вершине, но сами по себе вершины всегда смежные, т.е. соединенные одной стороной. Значит, диагонали треугольника не существует
Рис. 1. Три медианы в треугольнике.
Прямоугольник
Прямоугольник – это первая фигура школьного курса математики, которая имеет диагональ. Так же, как диагональ имеет и квадрат.
Диагональ прямоугольника или квадрата всегда:
- Делит фигуру на две равных прямоугольных треугольника.
- В полученных треугольниках диагональ будет являться гипотенузой
- Диагональ будет равняться корню квадратному из суммы квадратов катетов согласно теореме Пифагора
Диагоналей в любом четырехугольнике 2, а в квадрате и прямоугольнике обе диагонали равны между собой.
При этом правило не касается других четырехугольников. Например, диагонали параллелограмма всегда неравны между собой. Запомните, если перед вами произвольный четырехугольник использовать утверждение о равенстве диагоналей без доказательства нельзя. Любое утверждение в геометрии, кроме аксиом должно быть доказано.
Кроме прямоугольника и квадрата равными диагоналями обладает ромб. При этом диагонали ромба перпендикулярны друг другу и, так же, как и диагонали квадрата и прямоугольника, точкой пересечения делятся пополам.
Многоугольник
На самом деле, многоугольником может называться любая фигура с количеством углов, больше 2. По факту, любая фигура может называться многоугольником, поскольку 2 угла у замкнутой фигуры быть не может.
Рассмотрим многоугольники с количеством углов больше 4, поскольку четырехугольники мы уже рассмотрели.
Рис. 2. Диагонали многоугольника.
В многоугольнике, если он не является правильным, не получится решить задачу нахождения диагонали без дополнительных построений. В правильном многоугольнике все диагонали равны между собой и точкой пересечения делятся пополам.
Правильным многоугольником зовется фигура, все стороны и углы которой соответственно равны между собой.
Количество диагоналей можно посчитать, прикинув количество смежных и несмежных вершин. Смежными зовутся вершины, соединенные одним отрезком.
Например, в четырехугольнике у любой вершины есть две смежные вершины. Значит, для каждой вершины есть только одна диагональ. Диагональ соединяет две противоположные вершины, всего вершин 4, значит 4:2=2 – в любом четырехугольнике 2 диагонали.
Но этот способ не подойдет, если в задаче требуется подсчитать количество диагоналей у многоугольника с 5989 сторонами. Такая фигура вполне возможна в теории. На практике начертить ее весьма утомительно, как и подсчитать диагонали на чертеже. Поэтому была выведена формула числа диагоналей многоугольника:
$P=>$ – где n это число сторон многоугольника.
Проверим для квадрата:
Рис. 3. Диагонали квадрата.
Что мы узнали?
Мы узнали, почему не существует формулы диагонали треугольника. Поговорили о том, что диагонали в принципе нет, и не может быть в многоугольниках с количеством сторон, меньше 3. Обсудили различные свойства диагоналей в различных фигурах.
http://sprint-olympic.ru/uroki/matematika-uroki/15430-diagonal-treygolnika-formyla.html
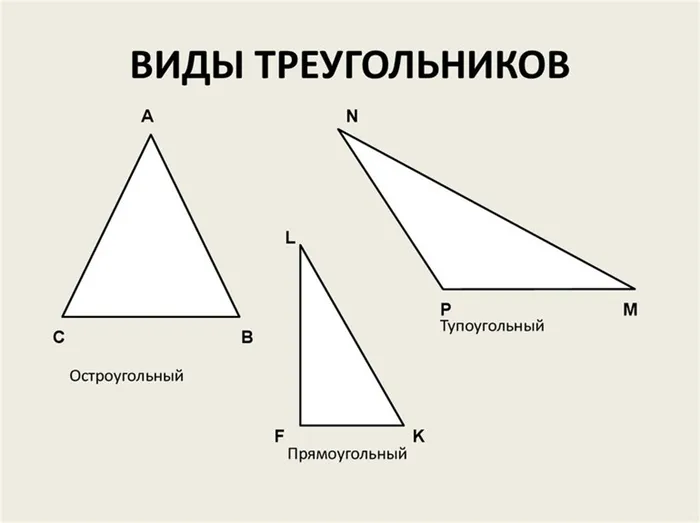
Тупоугольный треугольник содержит тупой угол. То есть угол более 90 градусов. Два других угла в таком треугольнике острые.
Равносторонний треугольник, свойства, признаки и формулы
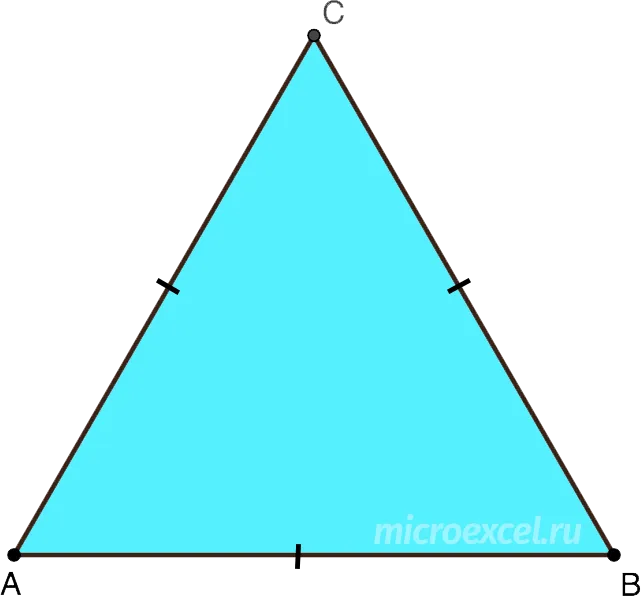
Равносторонний треугольник — это треугольник, у которого все стороны одинаковой длины и все углы одинаковой величины (60°).
Равносторонний треугольник (понятие, определение):
Равносторонний треугольник — это треугольник, у которого все стороны одинаковой длины и все углы одинаковой величины (60°).
Равносторонний треугольник также называют правильным или равносторонним треугольником.
По определению, каждый прямоугольный (равнобедренный) треугольник также является равнобедренным, но не каждый равнобедренный треугольник является прямоугольным (равносторонним). Другими словами, правильный треугольник — это частный случай равнобедренного треугольника.
Рисунок 1: Равнобедренный треугольник
AB = BC = AC — стороны треугольника, ∠ ABC = ∠ BAC = ∠ AC = 60° — углы треугольника.
Свойства равностороннего треугольника:
1. в равностороннем треугольнике все стороны имеют одинаковую длину.
2. в равностороннем треугольнике углы равны и составляют 60°.
3. в равностороннем треугольнике каждая диагональ, проведенная к каждой стороне, является биссектрисой угла, а высота и равны друг другу.
В равностороннем треугольнике биссектриса угла, проведенная к каждой стороне, является средней линией, а высота и равны друг другу.
В равностороннем треугольнике высота, проведенная на каждой стороне, является биссектрисой угла, а средняя линия и равны друг другу.
Рисунок 2. равнобедренный треугольник
4. в равностороннем треугольнике высоты, биссектрисы углов, медианы и медианы пересекаются в точке, называемой центром равностороннего треугольника. Он также является центром эндоцикла и перицикла.
Рисунок 3. равнобедренный треугольник
R — радиус окружности, r — радиус эндо окружности.
5. радиус окружности равнобедренного треугольника в два раза больше радиуса эндокруга.
6. пересечение высот, биссектрис и медиан правильного треугольника делит каждую из них в соотношении 2:1, измеренном от вершин.
Рисунок 4. равнобедренный треугольник
AO : OK = BO : OA = CO : OD = 2 : 1
Определение равностороннего треугольника
Равносторонний (или прямоугольный) треугольник — это треугольник, у которого все стороны равны по длине. То есть, AB = BC = AC .
Примечание: Правильный многоугольник — это выпуклый многоугольник с равными сторонами и углами между ними.
Свойства равностороннего треугольника
Свойство 1
В равностороннем треугольнике все углы равны 60°. То есть, a = b = c = 60° .
Свойство 2
Высота равностороннего треугольника равна биссектрисе угла, из которого он образован, среднему и центру.
CD — медиана, высота и среднее значение AB и биссектриса угла ACB.
- CD перпендикулярна AB =>∠ADC = ∠BDC = 90°
- AD = DB
- ∠ACD = ∠DCB = 30°
Свойство 3
В равностороннем треугольнике биссектрисы, медианы, высоты и средние значения всех сторон пересекаются в одной точке.
Свойство 4
Центры акроокружности и окружности совпадают и пересекаются на пересечении медиан, высот, биссектрис углов и центров.
Свойство 5
Решение Примените формулы, приведенные выше, чтобы найти неизвестные величины:
- R – радиус описанной окружности;
- r – радиус вписанной окружности;
- R = 2r .
Свойство 6
Свойство 2. В равностороннем треугольнике точки пересечения высот, биссектрис, медиан и перпендикуляров совпадают — это одна и та же точка. Эта точка называется центром треугольника.
Почему? Рассмотрим равносторонний треугольник.
Он равнобедренный независимо от того, какая сторона взята за основание — он равнобедренный со всех сторон, так сказать.
Таким образом, каждая высота в равностороннем треугольнике также является биссектрисой угла, медианой и средним перпендикуляром!
В равностороннем треугольнике не (12) отдельных линий, как в обычном треугольнике, а только три!
Центр равностороннего треугольника — это центр конечной окружности и перикруга, а также пересечение высот и медиан.
Пример задачи
Свойство 3. В равностороннем треугольнике радиус перикруга в два раза больше радиуса конечного круга. (R=2cdot r)
Теперь должно быть понятно, почему это так.
Публикации по теме:
- Нахождение площади квадрата: формула и примеры
- Нахождение площади прямоугольника: формула и пример
- Нахождение площади треугольника: формула и примеры
- Нахождение площади круга: формула и примеры
- Нахождение площади ромба: формула и примеры
- Нахождение площади трапеции: формула и примеры
- Нахождение площади параллелограмма: формула и примеры
- Нахождение площади эллипса: формула и пример
- Нахождение площади выпуклого четырехугольника: формула и пример
- Нахождение периметра квадрата: формула и задачи
- Нахождение периметра прямоугольника: формула и задачи
- Нахождение периметра ромба: формула и задачи
- Нахождение периметра трапеции: формула и задачи
- Нахождение периметра параллелограмма: формула и задачи
- Нахождение длины окружности: формула и задачи
- Теорема Пифагора для прямоугольного треугольника: формула и задачи
- Теорема косинусов для треугольника: формула и задачи
- Теорема о сумме углов треугольника: формула и задачи
- Тригонометрические функции острого угла в прямоугольном треугольнике
- Нахождение объема конуса: формула и задачи
- Нахождение объема куба: формула и задачи
- Нахождение объема шара: формула и задачи
- Нахождение объема пирамиды: формула и задачи
- Нахождение площади правильного шестиугольника: формула и примеры
- Нахождение объема тетраэдра: формула и задачи
- Нахождение объема призмы: формула и задачи
- Нахождение площади поверхности куба: формула и задачи
- Нахождение площади поверхности цилиндра: формула и задачи
- Нахождение площади поверхности конуса: формула и задачи
- Нахождение площади поверхности шара (сферы): формула и задачи
- Нахождение площади поверхности вписанного в цилиндр шара
- Нахождение радиуса шара: формула и примеры
- Нахождение радиуса круга: формула и примеры
- Нахождение радиуса цилиндра: формула и примеры
- Нахождение площади правильной призмы: формула и задачи
- Нахождение площади правильной пирамиды: формулы
- Формула Герона для треугольника
- Теорема Менелая: формулировка и пример с решением
- Теорема о внешнем угле треугольника: формулировка и задачи
- Теорема Чевы: формулировка и пример с решением
- Теорема Стюарта: формулировка и пример с решением
- Теорема о трех перпендикулярах
- Теорема Фалеса: формулировка и пример решения задачи
- Геометрическая фигура: треугольник
- Признаки равенства треугольников
- Признаки подобия треугольников
- Признаки равенства прямоугольных треугольников
- Свойства равнобедренного треугольника: теория и задача
- Определение и свойства медианы треугольника
- Определение и свойства медианы прямоугольного треугольника
Свойства равностороннего треугольника
Свойство 1. В равностороннем треугольнике все углы равны между собой и равны (^>)
Естественно, не правда ли? Три одинаковых угла, в сумме (^>), значит, каждый по (^>)
Рассмотрим рисунок: Точка(O) является центром треугольника.
Таким образом, (OB) — это радиус окружности (обозначается (R)), а (OK) — радиус эндоцикла (обозначается (r)).
Но точка (O) также является пересечением пространств! Напомним, что медианы делятся пересечением в соотношении (2:1), считая от вершины.
Поэтому (OB=2cdot OK), т.е. (R=2cdot r).
Свойство 4. В равностороннем треугольнике длины всех элементов «хорошо» выражаются длиной стороны.
Давайте убедимся в этом.
Это уже должно быть понятно:
Мы постоянно работаем над улучшением этого учебника, и вы можете помочь нам. Доступ и неограниченное использование учебника Юклава (более 100 статей по всем темам ЕГЭ и ОГЭ, более 2000 решенных задач, более 20 вебинаров — практических занятий).
Радиус вписанной окружности равностороннего треугольника
Открыть ответы…
Равносторонний треугольник, свойства, признаки и формулы.
Равносторонний треугольник – это треугольник, у которого все стороны равны между собой по длине, все углы также равны и составляют 60°.
Равносторонний треугольник (понятие, определение)
Свойства равностороннего треугольника
Признаки равностороннего треугольника
Формулы равностороннего треугольника
Остроугольный треугольник, прямоугольный треугольник, равнобедренный треугольник, равносторонний треугольник, тупоугольный треугольник
Равносторонний треугольник (понятие, определение):
Равносторонний треугольник – это треугольник, у которого все стороны равны между собой по длине, все углы также равны и составляют 60°.
Равносторонний треугольник называется также правильным или равноугольным треугольником.
По определению, каждый правильный (равносторонний) треугольник также является равнобедренным, но не каждый равнобедренный треугольник – правильным (равносторонним). Иными словами, правильный (равносторонний) треугольник является частным случаем равнобедренного треугольника.
Рис. 1. Равносторонний треугольник
АВ = ВС = АС – стороны треугольника, ∠ АВС = ∠ BАC = ∠ BСA = 60° – углы треугольника
Свойства равностороннего треугольника:
1. В равностороннем треугольнике все стороны равны между собой.
2. В равностороннем треугольнике углы равны и составляют 60°.
3. В равностороннем треугольнике каждая медиана, проведенная к каждой стороне, является биссектрисой и высотой, и они равны между собой.
В равностороннем треугольнике биссектриса, проведенная к каждой стороне, является медианой и высотой, и они равны между собой.
В равностороннем треугольнике высота, проведенная к каждой стороне, является биссектрисой и медианой, и они равны между собой.
Рис. 2. Равносторонний треугольник
АK = BF = CD
4. В равностороннем треугольнике высоты, биссектрисы, медианы и серединные перпендикуляры пересекаются в одной точке, которая называется центром равностороннего треугольника. Она же является центром вписанной и описанной окружностей.
Рис. 3. Равносторонний треугольник
R – радиус описанной окружности, r – радиус вписанной окружности
5. В равностороннем треугольнике радиус описанной окружности в два раза больше радиуса вписанной.
6. Точка пересечения высот, биссектрис и медиан правильного треугольника делит каждую из них в отношении 2:1, если считать от вершин.
Рис. 4. Равносторонний треугольник
AO : OK = BO : OА = CO : OD = 2 : 1
Признаки равностороннего треугольника:
– если в треугольнике три угла равны, то он равносторонний;
– если в треугольнике три стороны равны, то он равносторонний.
Формулы равностороннего треугольника:
Пусть a – длина стороны равностороннего треугольника, h – высота (l – биссектриса, m – медиана) равностороннего треугольника, проведенная к каждой стороне, α – угол равностороннего треугольника, α = 60°, R – радиус описанной окружности, r – радиус вписанной окружности (см. Рис. 6).
Рис. 6. Равносторонний треугольник
Формула радиуса вписанной окружности (r):

Формула радиуса описанной окружности (R):

.
Формулы периметра (Р) равностороннего треугольника:
.
Формулы площади (S) равностороннего треугольника:

Формулы высоты (h), медианы (m) и биссектрисы (l) треугольника:

Прямоугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Примечание: © Фото https://www.pexels.com, https://pixabay.com
Коэффициент востребованности
21 692
| Равносторонний треугольник | |
|---|---|
 |
|
| Тип | Правильный многоугольник |
| Ребра и вершины | 3 |
| Schläfli символ | {3} |
| диаграмма Кокстера | |
| Группа симметрии | D3 |
| Площадь | 3 4 a 2 { displaystyle { tfrac { sqrt {3}} {4}} a ^ {2} } |
| Внутренний угол (градусов ) | 60 ° |
В геометрии, равносторонний треугольник представляет собой треугольник в у которых все три стороны имеют одинаковую длину. В известной евклидовой геометрии равносторонний треугольник также равноугольный ; то есть все три внутренних угла также конгруэнтны друг другу и имеют угол 60 °. Это также правильный многоугольник, поэтому его также называют правильным треугольником .
Содержание
- 1 Принцип свойства
- 2 Характеристики
- 2.1 Стороны
- 2.2 Полупериметр
- 2.3 Углы
- 2.4 Площадь
- 2.5 Окружной радиус, внутренний и внешний радиус
- 2.6 Равные чевианы
- 2.7 Совпадающие центры треугольников
- 2.8 Шесть треугольников, образованных разделением по медианам
- 2.9 Точки на плоскости
- 3 Известные теоремы
- 4 Другие свойства
- 5 Геометрическое построение
- 6 Вывод формулы площади
- 6.1 Использование Теорема Пифагора
- 6.2 Использование тригонометрии
- 7 В культуре и обществе
- 8 См. Также
- 9 Ссылки
- 10 Внешние ссылки
Основные свойства

a = b = c { displaystyle a = b = c}

α = β = γ { displaystyle alpha = beta = gamma}

ha = hb = hc { displaystyle h_ {a} = h_ {b} = h_ {c}}

Обозначение общей длины стороны равностороннего треугольника как a { displaystyle a}
Обозначив радиус описанной окружности R, мы можем определить с помощью тригонометрии, что:
- Площадь треугольника равно A = 3 3 4 R 2 { displaystyle mathrm {A} = { frac {3 { sqrt {3}}} {4}} R ^ {2}}
Многие из этих величин имеют простые отношения к высоте («h») каждой вершины с противоположной стороны:
В равностороннем треугольнике высота, биссектриса угла, серединный перпендикуляр и медиана каждой стороны совпадают.
Характеристики
Треугольник ABC со сторонами a, b, c, полупериметр s, площадь T, exradii ra, r b, r c (касательная к a, b, c соответственно), и где R и r — радиусы описанной окружности и вписанный в круг соответственно, является равносторонним тогда и только тогда, когда истинно любое из утверждений в следующих девяти категориях. Таким образом, эти свойства уникальны для равносторонних треугольников, и знание того, что любое из них истинно, прямо подразумевает, что у нас есть равносторонний треугольник.
Стороны
Полупериметр
Углы
Площадь
Окружной радиус, внутренний и внешний радиус
Равные чевианы
Три вида чевианов совпадают и равны для (и только для) равносторонних треугольников:
- Три вида высоты имеют равную длину.
- Три медианы имеют равную длину.
- Три биссектрисы угла имеют равную длину.
Совпадающие центры треугольников
Каждый центр равностороннего треугольника совпадает с wi th его центроид, что подразумевает, что равносторонний треугольник является единственным треугольником без линии Эйлера, соединяющей некоторые из центров. Для некоторых пар центров треугольников их совпадения достаточно, чтобы треугольник был равносторонним. В частности:
- Треугольник является равносторонним, если любые два из центра описанной окружности, центра, центроида или ортоцентра совпадают.
- Это также является равносторонним, если его центр описанной окружности совпадает с точкой Нагеля или если его центр совпадает с его центром из девяти точек.
Шесть треугольников, образованных разделением медианами
Для В любом треугольнике три медианы делят треугольник на шесть меньших треугольников.
- Треугольник является равносторонним тогда и только тогда, когда любые три из меньших треугольников имеют одинаковый периметр или одинаковый радиус.
- Треугольник является равносторонним тогда и только тогда, когда центры окружности любых трех меньших треугольников имеют одинаковое расстояние от центроида.
Точки на плоскости
- Треугольник является равносторонним тогда и только тогда, когда для каждой точки P на плоскости имеются расстояния p, q и r до сторон треугольника и расстояния x, y и z в его вершины,
-
- 4 (p 2 + q 2 + r 2) ≥ x 2 + y 2 + z 2. { displaystyle 4 (p ^ {2} + q ^ {2} + r ^ {2}) geq x ^ {2} + y ^ {2} + z ^ {2}.}
- 4 (p 2 + q 2 + r 2) ≥ x 2 + y 2 + z 2. { displaystyle 4 (p ^ {2} + q ^ {2} + r ^ {2}) geq x ^ {2} + y ^ {2} + z ^ {2}.}
Известные теоремы

| 1. | Показаны ближайшие расстояния от точки P до сторон равностороннего треугольника ABC. |
| 2. | Линии DE, FG и HI, параллельные AB, BC и CA, соответственно, определяют меньшие треугольники PHE, PFI и PDG. |
| 3. | Поскольку эти треугольники равносторонние, их высоту можно повернуть вертикально. |
| 4. | Поскольку PGCH представляет собой параллелограмм, треугольник PHE можно сдвинуть вверх, чтобы показать, что сумма высот равна высоте треугольника ABC. |
Теорема Морли о трисекторах утверждает, что в любом треугольнике три точки пересечения смежных трисекторов угла образуют равносторонний треугольник.
Теорема Наполеона гласит, что если равносторонние треугольники построены на сторонах любого треугольника, либо все наружу, либо все внутрь, центры этих равносторонних треугольников сами образуют равносторонний треугольник.
Версия изопериметрического неравенства для треугольников гласит, что треугольник с наибольшей площадью среди всех треугольников с заданным периметром является равносторонним.
Теорема Вивиани утверждает, что для любой внутренней точки P в равностороннем треугольнике с расстояниями d, e и f от сторон и высотой h,
- d + e + f = h, { displaystyle d + e + f = h,}
независимо от расположения P.
Теорема Помпейу утверждает, что если P — произвольная точка в плоскости равностороннего треугольника ABC, но не на его описанной окружности, то существует треугольник со сторонами длиной PA, PB и PC. То есть PA, PB и PC удовлетворяют неравенству треугольника , согласно которому сумма любых двух из них больше третьего. Если P находится на описанной окружности, то сумма двух меньших из них равна самому длинному, и треугольник выродился в линию, этот случай известен как теорема Ван Скутена.
Другие свойства
By неравенство Эйлера, равносторонний треугольник имеет наименьшее отношение R / r радиуса описанной окружности к внутреннему радиусу любого треугольника: в частности, R / r = 2.
Треугольник с наибольшей площадью из всех этих вписанная в данный круг — равносторонняя; и треугольник наименьшей площади из всех описанных вокруг данного круга является равносторонним.
Отношение площади вписанной окружности к площади равностороннего треугольника, π 3 3 { displaystyle { frac { pi} {3 { sqrt {3}}}}}
Отношение площади к квадрату периметр равностороннего треугольника, 1 12 3, { displaystyle { frac {1} {12 { sqrt {3}}}},}
Если сегмент разделяет равносторонний треугольник на две области с равным периметром и с областями A 1 и A 2, то
- 7 9 ≤ A 1 А 2 ≤ 9 7. { displaystyle { frac {7} {9}} leq { frac {A_ {1}} {A_ {2}}} leq { frac {9} {7}}.}
Если треугольник помещается в комплексную плоскость с комплексными вершинами z 1, z 2 и z 3, затем для любого нереального кубический корень ω { displaystyle omega}
- z 1 + ω z 2 + ω 2 z 3 = 0. { displaystyle z_ { 1} + omega z_ {2} + omega ^ {2} z_ {3} = 0.}
Для точки P внутри равностороннего треугольника отношение суммы ее расстояний от вершин сумма расстояний от сторон больше или равна 2, равенство сохраняется, когда P является центроидом. Ни в каком другом треугольнике нет точки, для которой это отношение было бы равно 2. Это неравенство Эрдеша – Морделла ; более сильным вариантом этого является неравенство Барроу, которое заменяет перпендикулярные расстояния до сторон на расстояния от P до точек, где биссектрисы угла APB, ∠BPC и ∠ CPA пересекает стороны (A, B и C — вершины).
Для любой точки P на плоскости с расстояниями p, q и t от вершин A, B и C соответственно
- 3 (p 4 + q 4 + t 4 + a 4) = (р 2 + д 2 + т 2 + а 2) 2. { displaystyle displaystyle 3 (p ^ {4} + q ^ {4} + t ^ {4} + a ^ {4}) = (p ^ {2} + q ^ {2} + t ^ {2} + a ^ {2}) ^ {2}.}
Для любой точки P на плоскости с расстояниями p, q и t от вершин
- p 2 + q 2 + t 2 = 3 ( R 2 + L 2) { displaystyle displaystyle p ^ {2} + q ^ {2} + t ^ {2} = 3 (R ^ {2} + L ^ {2})}
и
- п 4 + q 4 + t 4 = 3 [(R 2 + L 2) 2 + 2 R 2 L 2], { displaystyle displaystyle p ^ {4} + q ^ {4} + t ^ {4} = 3 [(R ^ {2} + L ^ {2}) ^ {2} + 2R ^ {2} L ^ {2}],}
где R — описанный радиус, а L — расстояние между точками P и центр тяжести равностороннего треугольника.
Для любой точки P вписанной окружности равностороннего треугольника с расстояниями p, q и t от вершин
- 4 (p 2 + q 2 + t 2) = 5 a 2 { displaystyle displaystyle 4 (p ^ {2} + q ^ {2} + t ^ {2}) = 5a ^ {2}}
и
- 16 (p 4 + q 4 + t 4) = 11 а 4. { displaystyle displaystyle 16 (p ^ {4} + q ^ {4} + t ^ {4}) = 11a ^ {4}.}
Для любой точки P на малой дуге BC описанной окружности с расстояния p, q и t от A, B и C соответственно,
- p = q + t { displaystyle displaystyle p = q + t}
и
- q 2 + qt + t 2 = а 2; { displaystyle displaystyle q ^ {2} + qt + t ^ {2} = a ^ {2};}
кроме того, если точка D на стороне BC делит PA на сегменты PD и DA, причем DA имеет длину z и PD имеет длину y, тогда
- z = t 2 + tq + q 2 t + q, { displaystyle z = { frac {t ^ {2} + tq + q ^ {2}} {t + q} },}
, что также равно t 3 — q 3 t 2 — q 2 { displaystyle { tfrac {t ^ {3} -q ^ {3}} {t ^ {2} -q ^ {2}}}}
- 1 q + 1 t = 1 y, { displaystyle { frac {1} {q}} + { frac {1} {t}} = { frac {1} {y}},}
, которое является оптическим уравнением .
Существует множество неравенств треугольника , которые выполняются с равенством тогда и только тогда, когда треугольник является равносторонним.
Равносторонний треугольник — это наиболее симметричный треугольник, имеющий 3 линии отражения и симметрию вращения порядка 3 относительно его центра. Его группа симметрии — это двугранная группа порядка 6 D3.
Равносторонние треугольники — единственные треугольники, у которых эллипс Штейнера является окружностью (в частности, это вписанная окружность).
Целочисленный равносторонний треугольник — единственный треугольник с целыми сторонами и тремя рациональными углами, измеренными в градусах.
Равносторонний треугольник — единственный остроугольный треугольник, который подобен своему ортогональному треугольнику (с вершинами в основании на высотах ) (семиугольный треугольник является единственным тупым треугольником).

Равносторонние треугольники встречаются во многих других геометрических конструкциях. Пересечение окружностей, центры которых находятся на расстоянии радиуса друг от друга, представляет собой пару равносторонних арок, в каждую из которых можно вписать равносторонний треугольник. Они образуют грани правильных и однородных многогранников. Три из пяти Платоновых тел состоят из равносторонних треугольников. В частности, правильный тетраэдр имеет четыре равносторонних треугольника для граней и может считаться трехмерным аналогом формы. Плоскость может быть выложена плиткой с использованием равносторонних треугольников, что дает треугольную мозаику.
Геометрическая конструкция

Равносторонний треугольник легко построить с помощью линейка и циркуль, потому что 3 — это простое число Ферма. Нарисуйте прямую линию, поместите точку циркуля на один конец линии и проведите дугу от этой точки до другой точки отрезка. Повторите то же самое с другой стороной линии. Наконец, соедините точку, где две дуги пересекаются с каждым концом отрезка линии
Альтернативный метод — нарисовать круг с радиусом r, поместить точку циркуля на круг и нарисовать еще один круг с такой же радиус. Два круга пересекутся в двух точках. Равносторонний треугольник можно построить, взяв два центра окружностей и любую из точек пересечения.
В обоих методах побочным продуктом является образование vesica piscis.
Доказательство того, что полученная фигура представляет собой равносторонний треугольник, является первым предложением Книги I Элементов Евклида.
Вывод формулы площади
Формула площади A = 3 4 a 2 { displaystyle A = { frac { sqrt {3}} {4}} a ^ {2}}
Использование теоремы Пифагора
Площадь треугольника равна половине одной стороны, умноженной на высоту h с этой стороны:
- A = 1 2 a h. { displaystyle A = { frac {1} {2}} ах.}

Катеты любого прямоугольного треугольника, образованного высотой равностороннего треугольника, составляют половину основания a, а гипотенуза — это сторона a равностороннего треугольника. Высоту равностороннего треугольника можно найти с помощью теоремы Пифагора
- (a 2) 2 + h 2 = a 2 { displaystyle left ({ frac {a} {2}} right) ^ {2} + h ^ {2} = a ^ {2}}
, так что
- h = 3 2 a. { displaystyle h = { frac { sqrt {3}} {2}} a.}
Подстановка h в формулу площади (1/2) ah дает формулу площади равностороннего треугольника:
- A = 3 4 а 2. { displaystyle A = { frac { sqrt {3}} {4}} a ^ {2}.}
Используя тригонометрию
Используя тригонометрию, площадь треугольник с любыми двумя сторонами a и b, а угол C между ними равен
- A = 1 2 ab sin C. { displaystyle A = { frac {1} {2}} ab sin C.}
Каждый угол равностороннего треугольника равен 60 °, поэтому
- A = 1 2 a b sin 60 ∘. { displaystyle A = { frac {1} {2}} ab sin 60 ^ { circ}.}
Синус 60 ° равен 3 2 { displaystyle { tfrac { sqrt { 3}} {2}}}
- A = 1 2 ab × 3 2 = 3 4 ab = 3 4 a 2 { displaystyle A = { frac {1} {2}} ab times { frac { sqrt {3}} { 2}} = { frac { sqrt {3}} {4}} ab = { frac { sqrt {3}} {4}} a ^ {2}}
, поскольку все стороны равностороннего треугольника равны.
В культуре и обществе
Равносторонние треугольники часто появлялись в искусственных сооружениях:
- Форма встречается в современной архитектуре, например, в поперечном сечении Арки ворот.
- Его применение во флагах и геральдике включает флаг Никарагуа и флаг Филиппин.
- Это форма различных дорожных знаков, включая знак уступки.
См. Также
Ссылки
Внешние ссылки
Фундаментальный выпуклый правильный и равномерный многогранник в измерениях 2–10 |
||||
|---|---|---|---|---|
| An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn |
| Треугольник | Квадрат | p- гон | Шестиугольник | Пентагон |
| Тетраэдр | Октаэдр • Куб | Демикуб | Додекаэдр • Икосаэдр | |
| 5-элементный | 16 ячеек • Tesseract | Demitesseract | 24-элементный | 120-элементный • 600-элементный |
| 5-симплексный | 5-ортоплексный • 5-куб | 5-полукуб | ||
| 6-симплекс | 6-ортоплекс • 6-куб | 6-полукуб | 122 • 221 | |
| 7-симплекс | 7-ортоплекс • 7-куб | 7-полукуб | 132 • 231 • 321 | |
| 8-симплекс | 8-ортоплекс • 8-куб | 8-полукуб | 142 • 241 • 421 | |
| 9-симплекс | 9-ортоплекс • 9-куб | 9-демикуб | ||
| 10-симплекс | 10-ортоплекс • 10-куб | 10-полукуб | ||
| n-симплекс | n-ортоплекс • n- куб | n-полукуб | 1k2 • 2k1 • k21 | n-пятиугольный многогранник |
| Темы: Семейства многогранников • Обычные многогранник • Список правильных многогранников и соединений |
Если ваш учитель попросил вас вычислить диагональ треугольника, она уже дала вам некоторую ценную информацию. Эта фраза говорит вам, что вы имеете дело с прямоугольным треугольником, где две стороны перпендикулярны друг другу (или, говоря иначе, они образуют прямоугольный треугольник), и только одна сторона остается «диагональной» по отношению к другим, Эта диагональ называется гипотенузой, и вы можете найти ее длину, используя теорему Пифагора.
TL; DR (слишком долго; не читал)
Чтобы найти длину диагонали (или гипотенузы) прямоугольного треугольника, подставьте длины двух перпендикулярных сторон в формулу a 2 + b 2 = c 2 , где a и b — длины перпендикулярных сторон, а c — длина гипотенузы. Тогда решите для ц .
Теорема Пифагора
Теорема Пифагора — иногда называемая также теоремой Пифагора после того, как ее открыли греческий философ и математик, — утверждает, что если a и b — длины перпендикулярных сторон прямоугольного треугольника, а c — длина гипотенузы, то:
-
Заменяющие значения для a и b
-
Упростить уравнение
-
Возьмите квадратный корень обеих сторон
-
Что если вы знаете длину диагонали треугольника и еще одну сторону? Вы можете использовать ту же формулу для определения длины неизвестной стороны. Просто замените длины сторон, которые вы знаете, выделите оставшуюся переменную буквы на одной стороне знака равенства, а затем найдите эту букву, которая представляет длину неизвестной стороны.
Подставим известные значения a и b — две перпендикулярные стороны прямоугольного треугольника — в теорему Пифагора. Так что, если две перпендикулярные стороны треугольника измеряют 3 и 4 единицы соответственно, у вас будет:
3 2 + 4 2 = c 2
Работайте экспоненты (когда это возможно — в этом случае вы можете) и упрощайте подобные термины. Это дает вам:
9 + 16 = с 2
С последующим:
с 2 = 25
Возьмите квадратный корень с обеих сторон, последний шаг в решении для c . Это дает вам:
с = 5
Таким образом, длина диагонали, или гипотенузы, этого треугольника составляет 5 единиц.

















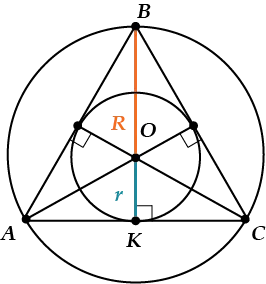
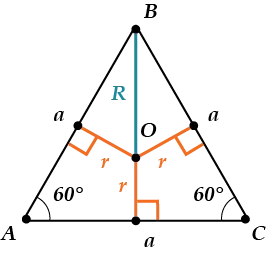











![{ displaystyle displaystyle p ^ {4} + q ^ {4} + t ^ {4} = 3 [(R ^ {2} + L ^ {2}) ^ {2} + 2R ^ {2} L ^ {2}],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff063b69969470976ae19283a567f72c89d68440)













