Свойства ромба:
1. Ромб — частный случай параллелограмма
2. Противоположные стороны — параллельны
3. Все четыре стороны — равны
4. Диагонали пересекаются под прямым углом (90°)
5. Диагонали являются биссектрисами
a — сторона ромба
D — большая диагональ
d — меньшая диагональ
α — острый угол
β — тупой угол
Формулы диагоналей через сторону и угол, ( D d):
Формулы диагоналей через сторону и половинный угол, (D d):
Формулы диагоналей через сторону и другую диагональ, (D d):
Формулы диагоналей через угол и другую диагональ, (D d):
Формулы диагоналей через площадь (D d):
Формулы площади ромба
Формула периметра ромба
Все формулы по геометрии
- Подробности
-
Опубликовано: 23 ноября 2011
-
Обновлено: 13 августа 2021
Каким способом высчитать диагональ:
Способ расчёта
Введите размеры:
Результат:
Решение:
Ссылка на страницу с результатом:
# Теория
Ромб — это параллелограмм у которого все стороны равны.
Свойства ромба:
- Диагонали ромба делят его углы пополам.
- Cумма углов прилежащих к одной стороне равна 180°.
- Диагонали ромба пересекаются под прямым углом (90°).
- Диагонали ромба в точке пересечения делятся попалам.
- Диагонали ромба являются биссектрисами его углов.
Диагональ — это отрезок, соединяющий несмежные вершины многоугольника или многогранника.
Формулы расчёта диагонали ромба
Длину диагоналей ромба можно посчитать несколькими способами. В зависимости от известных данных, для расчёта применяют следующие формулы:
Через сторону и другую диагональ
D
d
a
a
a
a
D = sqrt{4a^2 — d^2}
d = sqrt{4a^2 — D^2}
- D — большая диагональ ромба
- d — меньшая диагональ ромба
- a — сторона ромба
Через сторону и угол
D
d
a
a
a
a
α
β
- D — большая диагональ
- d — меньшая диагональ ромба
- a — сторона ромба
- α — острый угол ромба (от 0° до 90°)
- β — тупой угол ромба (от 90° до 180°)
D = a sqrt{2 + 2 cdot cos alpha}
D = a sqrt{2 — 2 cdot cos beta}
d = a sqrt{2 — 2 cdot cos alpha}
d = a sqrt{2 + 2 cdot cos beta}
Через угол и вторую диагональ
D = d cdot tg ( dfrac{beta}{2} )
d = D cdot tg ( dfrac{alpha}{2} )
- D — большая диагональ ромба
- d — меньшая диагональ ромба
- α — острый угол ромба (от 0° до 90°)
- β — тупой угол ромба (от 90° до 180°)
Через площадь и вторую диагональ
D = dfrac{2 cdot S}{d}
d = dfrac{2 cdot S}{D}
- D — большая диагональ ромба
- d — меньшая диагональ ромба
- S — площадь ромба
Похожие калькуляторы:
Войдите чтобы писать комментарии
|
Начнем с того что у ромба две диагонали. Одна большая D, а другая маленькая d. Рассмотрим способы нахождения большой диагонали D.
Также D находится по площади ромба и малой диагонали: D=(2*S)/d; Рассмотрим способы нахождения меньшей диагонали d.
Малую диагональ d тоже можно найти через площадь ромба и большую диагональ: d=(2*S)/D; автор вопроса выбрал этот ответ лучшим Alexsandr82 6 лет назад У ромба есть две диаганали: большая (d1) и малая (d2), а также углы а — острый угол ромба (в ромбе два острых угла и оба равны между собой), и b — тупой угол (их тоже два и они тоже равны). Если нам известна сторона ромба (x) и один из углов то мы можем найти любую диагональ по формулам: d1 = 2x*cos(a/2) d2 = 2x*sin(a/2) Или d1 = 2x*sin(b/2) d2 = 2x*cos(b/2) Кроме этого если нам извесна площадь ромба и одна из диагоналей мы можем найти вторую диагональ по формулам: d1 = 2S/d2 d2 = 2S/d1 Если нам дан радус вписанной в ромб окружности и любой из углов мы также можем рассчитать диагональ ромба: d1 = 2r/sin(a/2) d2 = 2r/sin(b/2) Где r — радиус вписанной окружности. Знаете ответ? |
Rhombus is also known as a four-sided quadrilateral. It is considered to be a special case of a parallelogram. A rhombus contains parallel opposite sides and equal opposite angles. A rhombus is also known by the name diamond or rhombus diamond. A rhombus contains all the sides of a rhombus as equal in length. Also, the diagonals of a rhombus bisect each other at right angles.
Properties of a Rhombus
A rhombus contains the following properties:
- A rhombus contains all equal sides.
- Diagonals of a rhombus bisect each other at right angles.
- The opposite sides of a rhombus are parallel in nature.
- The sum of two adjacent angles of a rhombus is equal to 180o.
- There is no inscribing circle within a rhombus.
- There is no circumscribing circle around a rhombus.
- The diagonals of a rhombus lead to the formation of four right-angled triangles.
- These triangles are congruent to each other.
- Opposite angles of a rhombus are equal.
- When you connect the midpoint of the sides of a rhombus, a rectangle is formed.
- When the midpoints of half the diagonal are connected, another rhombus is formed.
Diagonal of a Rhombus
A rhombus has four edges joined by vertices. On connecting the opposite vertices of a rhombus, additional edges are formed, which result in the formation of diagonals of a rhombus. Therefore, a rhombus can have two diagonals each of which intersects at an angle of 90°.
Properties of diagonal of a rhombus
The diagonals of a rhombus have the following properties:
- The diagonals bisect each other at right angles.
- The diagonals of a rhombus divide into four congruent right-angled triangles.
- The diagonals of a rhombus may or may not be equal in length.
Computation of diagonal of rhombus
The length of the diagonals of the rhombus can be calculated by using the following methods:
By Pythagoras Theorem
Let us assume d1 to be the diagonal of the rhombus.
Since, we know, all adjacent sides in a rhombus subtend an angle of 90 degrees.
Therefore,
In the triangle, BCD we have,
BC2 + CD2 = BD2
Now, we have,
In the case of a square rhombus with all sides equal,
Square Diagonal: a√2
where a is the length of the side of the square
In the case of a rectangle rhombus, we have,
Rectangle Diagonal: √[l2 + b2]
where,
- l is the length of the rectangle.
- b is the breadth of the rectangle.
By using the area of rhombus
Let us consider, O to be the point of intersection of two diagonals, namely d1 and d2.
Now,
The area of the rhombus is equivalent to,
A = 4 × area of ∆AOB
= 4 × (½) × AO × OB sq. units
= 4 × (½) × (½) d1 × (½) d2 sq. units
= 4 × (1/8) d1 × d2 square units
= ½ × d1 × d2
Therefore, Area of a Rhombus = A = ½ × d1 × d2
Area of rhombus using diagonals
Consider a rhombus ABCD, having two diagonals, i.e. AC & BD.
- Step 1: Compute the length of the line segment AC, by joining the points A and C. Let this be diagonal 1, i.e. d1.
The diagonals of a rhombus are perpendicular to each other subtending right triangles upon intersection with each other at the centre of the rhombus.
- Step 2: Similarly, compute the length of diagonal 2, i.e. d2 which is the distance between points B and D.
- Step 3: Multiply both the calculated diagonals, d1, and d2.
- Step 4: The result is obtained by dividing the product by 2.
The resultant will give the area of a rhombus ABCD.
Sample Questions
Question 1. One of the sides of a rhombus is equivalent to 5 cm. One of the diagonals of the rhombus is 8 cm, compute the length of the other diagonal.
Solution:
Let us consider, ABCD to be a rhombus, where AC and BD are the diagonals.
We have,
Side of the rhombus is 5 cm
BD = 8 cm
Since, we know that the diagonals of rhombus perpendicularly bisect each other.
∴ BO = 4cm
By Pythagoras theorem, we have,
In right angled △AOB,
⇒ (AB)2 = (AO)2 + (BO)2
⇒ (5)2 = (AO)2 + (4)2
⇒ 25 = (AO)2 + 16
⇒ (AO)2 = 9
∴ AO = 3cm
⇒ AC = 2 × 3 = 6 cm
∴ The length of other diagonal of the rhombus is equivalent to 6 cm.
Question 2. Calculate the area of a rhombus with diagonals equivalent to 6 cm and 8 cm respectively.
Solution:
We know,
Diagonal 1, d1 = 6 cm
Diagonal 2, d2 = 8 cm
Area of a rhombus, A = (d1 × d2) / 2
Substituting the values,
= (6 ×
/ 2
= 48 / 2
= 24 cm2
Hence, the area of the rhombus is 24 cm2.
Question 3. A rectangular park has 10m length and breadth is 8m. Compute the diagonal of park.
Solution:
We have,
Length = 100m
Breadth = 8 mComputing diagonals, we obtain,
Rectangle Diagonal = √[l2 + b2]
= √[102 + 82 ]
= √[164]
= 12.80 m
Question 4. A square rhombus has a side of 5 cm. Compute the length of diagonal.
Solution:
We have,
Side of square, a = 5 units
Computing diagonals, we obtain,
Square Diagonal = a√2
= 5√2
= 7.07 cm
Question 5. The area of rhombus is 315 cm² and its perimeter is 180 cm. Find the altitude of the rhombus.
Solution:
We have,
Perimeter of rhombus = 180 cm
Calculating for the side of rhombus,
Side of rhombus,b = P/4 = 180/4 = 45 cm
Now,
Area of rhombus = b × h
Substituting the values,
⇒ 315 = 45 × h
⇒ h = 315/45
⇒ h =7 cm
Therefore, altitude of the rhombus is 7 cm.
Last Updated :
05 Oct, 2021
Like Article
Save Article
Диагональ параллелограмма – это отрезок, соединяющий противоположные вершины фигуры. В зависимости от
вида геометрической фигуры диагональ обладает важными свойствами, на которые основываются базовые
правила и формулы. Рассмотрим подробнее, как найти длину данного отрезка, построенного в
параллелограмме с равными сторонами, т.е. ромбе.
- Диагональ ромба через сторону и другую известную
диагональ - Длинная диагональ ромба через сторону и острый угол
- Длинная диагональ ромба через сторону и тупой угол
- Короткая диагональ ромба через сторону и острый угол
- Короткая диагональ ромба через сторону и тупой угол
- Длинная диагональ ромба через короткую диагональ и тупой
угол - Короткая диагональ ромба через длинную диагональ и острый
угол - Диагональ ромба через площадь ромба и другую известную
диагональ
Диагональ ромба через сторону и другую известную диагональ
В случае, если в ромбе известны значения одной диагонали (d) и стороны (a) фигуры, прийти к
определению длины второго отрезка будет несложно, благодаря тождеству параллелограмма, которое
гласит, что сумма квадратов диагоналей равна квадрату стороны, умноженному на 4:
d = √(4a² — d²)
где a — сторона, d — известная диагональ.
Цифр после
запятой:
Результат в:
Пример. Дан ромб с диагональю равной 6 мм и стороной, длина которой 5 мм. Нужно
найти вторую диагональ ромба. d = √(4 * 5² — 6²) = √(4 * 25 — 36) = √(100 — 36) = √64 = 8 мм
– длина неизвестной диагонали.
Как найти длину большей диагонали через сторону и острый угол
Найти величину длинной диагонали можно по формуле:
d = a * √(2 + 2 * cos α)
где a — сторона, cos α — острый угол.
Цифр после
запятой:
Результат в:
Проведенный отрезок, который соединяет противоположные вершины фигуры, делит ее на равнобедренные
треугольники. По свойствам равнобедренного треугольника косинус углов при основании равен половине
основания (в данном случае диагонали), деленного на боковую сторону (сторону ромба).
Пример. Острый угол между сторонами ромба длиной 6 см равен 45 градусам. Найти
биссектрису острого угла ромба (в данном случае диагональ). d = 6 * √(2 + 2 * cos 45°) = 6 * √(2 + 2 * √2 / 2) = 6 * √(2 + 2 * 0,7) = 11см
– длинна неизвестного отрезка.
Как найти длину большей диагонали через сторону и известное значение тупого угла
Как уже известно, построенная диагональ в ромбе, делит его на 2 равнобедренных треугольника. Если
дополнить картину второй проведенной диагональю, получится прямоугольный треугольник. Косинус
половинки тупого угла (c) это отношение прилежащего катета к гипотенузе (стороне ромба a). На
основании всех этих свойств можно прийти к простой формуле нахождения нужной диагонали через сторону
ромба (в данном случае гипотенузу) и косинус тупого угла:
d = a * √( 2 — 2 * cos β)
где a — сторона, cos β — тупой угол
Цифр после
запятой:
Результат в:
Пример. Дан ромб со стороной 4,65 м, величина тупого угла которого равна 120
градусам. Необходимо найти противолежащую известному углу диагональ. d = 4,65 * √(2 — 2 * cos 120°) = 4,65 * √(2 — 2 * (-0,5) = 8 м
– длина неизвестного отрезка.
Как вычислить длину меньшей диагонали через сторону и острый угол
Так как ситуация аналогична предыдущей (только известный противолежащий угол острый), формула
нахождения короткой диагонали практически ничем не отличается от алгоритма определения длинного
отрезка, соединяющего противолежащие вершины ромба.
d = a * √(2 — 2 * cos α)
где a — сторона, cos α — острый угол
Цифр после
запятой:
Результат в:
Пример. В ромбе со стороной 4,65 м проведена диагональ, которая является основанием
равнобедренного треугольника с углом при вершине равным 52 градусам. Найти основание треугольника
(меньшую диагональ). d = 4,65 * √(2 — 2 * cos 52°) = 4 м.
Короткая диагональ ромба через длинную диагональ и острый угол
Аналогично с предыдущей ситуацией, через тангенс острого угла находим величину неизвестного катета
(половинку искомой диагонали). Упрощенная формула:
d = D * tg (α / 2)
где D — длинная диагональ, α — острый угол
Цифр после
запятой:
Результат в:
Пример. Острый угол ромба, в котором построена диагональ длиной 11 мм, равен 58
градусам. Найти длину второй диагонали. d = 11 * tg 29° = 6 мм – длина
меньшей диагонали ромба.
Короткая диагональ через сторону и тупой угол
Формула для нахождения меньшей диагонали ромба при помощи значения стороны и тупого угла такова:
d = a * √(2 + 2 * cos β)
где a — сторона, cos β — тупой угол
Цифр после
запятой:
Результат в:
Пример. Дан ромб со стороной 4,65 мм, один из углов которого равен 128 градусов, а
меньшая диагональ фигуры – искомая величина. d = a * √(2 + 2 * cos β) = 4,65 * √(2 + 2 * cos 128°) = 4 мм.
Длинная диагональ ромба через короткую диагональ и тупой угол
Длина большей диагонали ромба легко находится по формуле:
D = d * tg (β / 2)
где d — короткая диагональ, β — тупой угол
Цифр после
запятой:
Результат в:
Благодаря теореме Пифагора, зная длину короткой диагонали (половина катета прямоугольного
треугольника) и значение тупого угла ромба (половина которого является углом прямоугольного
треугольника), не составит труда определить значение большей диагонали ромба через тангенс тупого
угла.
Пример. Дан ромб с диагональю 6,5 см, которая является биссектрисой тупого угла
величиной 119 градусов. Нужно найти неизвестную диагональ ромба. D = 6,5 * tg (119 / 2) = 11 см
– искомая величина.
Диагональ ромба через площадь и другую известную диагональ
Найти любую из двух диагоналей ромба можно по формуле:
D = 2 * S / d
где d – длина известного отрезка, а S-площадь фигуры.
Цифр после
запятой:
Результат в:
Пример. Дан ромб с площадью равной 64 см², его диагональ равна 8,5 см. Необходимо
найти длину второго отрезка, соединяющего противолежащие вершины. D = 2 * S / d = 2 * 64 / 8,5 = 15 см.
Ромб относится к плоским выпуклым геометрическим фигурам. Данный вид параллелограмма отличается
равными сторонами, а также тем, что его диагонали при пересечении перпендикулярны друг другу.
Существуют и другие свойства ромба, которые подробно раскрывают смысл указанных выше формул:
- Диагонали, пересекаясь под прямым углом, делятся точкой пересечения пополам. Таким образом, они
всегда разделяют фигуру на 4 прямоугольных треугольника. - Противоположные стороны ромба попарно параллельны.
- Противолежащие углы равны, а смежные – в сумме образуют 180 градусов.
- Диагонали служат биссектрисами всех углов ромба.
- Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4.
- Если соединить середины сторон ромба, получится прямоугольник.
- Точка пересечения диагоналей — центр вписанной окружности.
Определение диагонали ромба часто встречается в задачах школьной программы. Найдя данное значение,
можно прийти к искомому результату задания. Через диагональ можно найти стороны ромба, площадь,
периметр и все внутренние углы ромба.
Геометрия в школьной программе включается в себя немалое количество формул, основанных на теоремах и
правилах. Некоторые из которых помогают значительно сократить время для решения задач на контрольной
или при выполнении домашней работы. Данная статья поможет быстро прийти к логическому решению
задания и правильному результату. Знание и применение выше перечисленных формул способствуют умению
решать задачи по геометрии любой сложности.


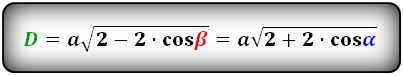
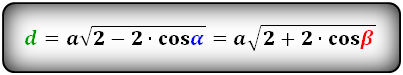
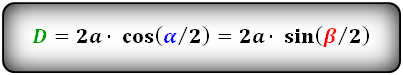
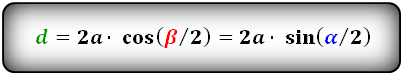


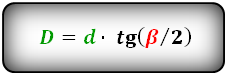
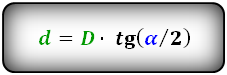
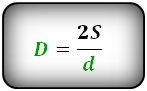
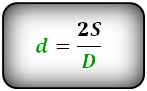


 / 2
/ 2