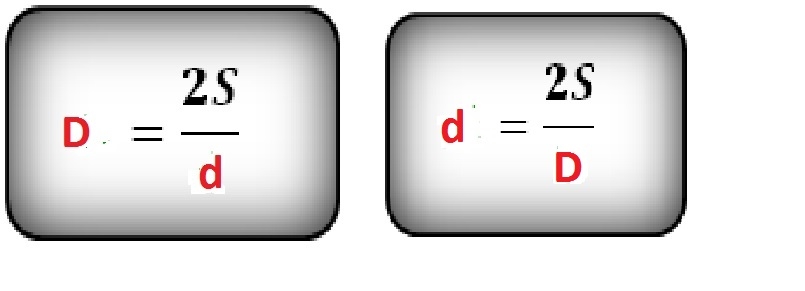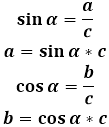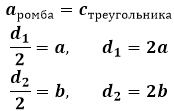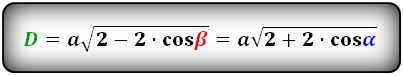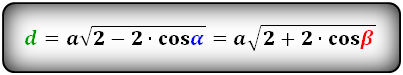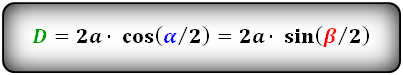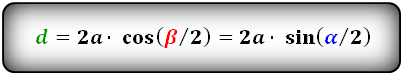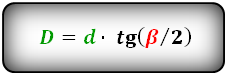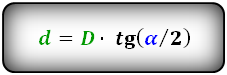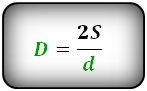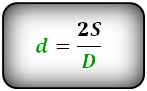Как найти диагонали ромба зная их отношение - Исправление недочетов и поиск решений вместе с Examum.ru

Каким способом высчитать диагональ:

Способ расчёта

Введите размеры:

Результат:

Решение:

Ссылка на страницу с результатом:

# Теория

Ромб — это параллелограмм у которого все стороны равны.

Свойства ромба:

Диагонали ромба делят его углы пополам.
Cумма углов прилежащих к одной стороне равна 180°.
Диагонали ромба пересекаются под прямым углом (90°).
Диагонали ромба в точке пересечения делятся попалам.
Диагонали ромба являются биссектрисами его углов.

Диагональ — это отрезок, соединяющий несмежные вершины многоугольника или многогранника.

Формулы расчёта диагонали ромба

Длину диагоналей ромба можно посчитать несколькими способами. В зависимости от известных данных, для расчёта применяют следующие формулы:

Через сторону и другую диагональ

D
d
a
a
a
a

D = sqrt{4a^2 — d^2}

d = sqrt{4a^2 — D^2}

D — большая диагональ ромба
d — меньшая диагональ ромба
a — сторона ромба

Через сторону и угол

D
d
a
a
a
a

D — большая диагональ
d — меньшая диагональ ромба
a — сторона ромба
α — острый угол ромба (от 0° до 90°)
β — тупой угол ромба (от 90° до 180°)

D = a sqrt{2 + 2 cdot cos alpha}

D = a sqrt{2 — 2 cdot cos beta}

d = a sqrt{2 — 2 cdot cos alpha}

d = a sqrt{2 + 2 cdot cos beta}

Через угол и вторую диагональ

D = d cdot tg ( dfrac{beta}{2} )

d = D cdot tg ( dfrac{alpha}{2} )

D — большая диагональ ромба
d — меньшая диагональ ромба
α — острый угол ромба (от 0° до 90°)
β — тупой угол ромба (от 90° до 180°)

Через площадь и вторую диагональ

D = dfrac{2 cdot S}{d}

d = dfrac{2 cdot S}{D}

D — большая диагональ ромба
d — меньшая диагональ ромба
S — площадь ромба

Ответы

Автор ответа: murysenichka

Ответ:

Площадь ромба можно найти по формуле:

$s = frac{d1 times d2}{2}$

, где d1 и d2 — диагонали ромба.

Пусть меньшая диагональ будет равна n, тогда большая — 3n.(так как их отношение 1:3)

Тогда:

$24 = frac{n times 3n}{2 } = frac{ {3n}^{2} }{2}$

48=3n²

n²=16

n1=-4

n2=4

Но диагональ не может быть меньше нуля, значит n=4, тогда 3n=12(большая диагональ)

Значит, большая диагональ равна 12.

Ответ:

Объяснение:

Площадь ромба равна половине произведения диагоналей

S= $frac{1}{2}$ * d1*d2=24

По условию задачи: d1=х, d2=3х

$frac{1}{2}$ * х * 3х = 24

3х²=48

х²=16

х=4

Тогда большая диагональ: 3х=3*4=12

Интересные вопросы

5 предложений со словами slim ,full lips,moustache,straihtg hair,beard,with,wavy,well-built,speak etalian,yellowish,complexion,skin,flatish nose,swim,slanting eyes,quite fast,sign,very well,very dark skin.поже срочно надо

Источник

Как найти диагональ ромба

Ромб – четырехугольник, стороны которого равны и попарно параллельны. В отличие от квадрата, углы у которого прямые, ромб имеет по два острых и два тупых угла, лежащих на противоположных сторонах. А вот диагонали пересекаются под прямым углом и являются одновременно биссектрисами. Точка пересечения диагоналей делит их на равные части.

Формул для нахождения диагоналей ромба много, необходимо лишь знать исходные данные и подобрать подходящую.

Как найти диагональ ромба через сторону и угол: когда известны стороны и один из углов ромба, применяют следующие формулы:

Через сторону и половинный угол:

Через сторону и другую диагональ:

Сумма квадратов диагоналей равна квадрату стороны, умноженному на четыре D^2+d^2=4a^2. Отсюда можно вывести, что:

Через угол и другую диагональ:

Через площадь и другую диагональ: традиционной формулой для нахождения площади ромба считается S=a*h. Но относительно диагоналей она будет выглядеть S=1/2*D*d. После преобразований получаем:

Через периметр и другую диагональ. В этом случае формулу выведем самостоятельно. Т.к. ромб имеет равные стороны, чтобы найти одну из них, периметр делим на 4: a=P/4. Диагонали перпендикулярны друг другу и образуют прямой угол. Тогда одна из сторон и половины длин диагоналей образуют прямоугольный треугольник. Далее воспользуемся теоремой Пифагора. Для большой диагонали она будет выглядеть: D=2*(a^2-(d/2)^2)^1/2. Аналогично для нахождения малой диагонали: d=2*(a^2-(D/2)^2)^1/2.

Пример:

Найти меньшую диагональ ромба, если периметр равен 20 см, большая диагональ равна 8 см.

Дано: Р=20см, D=8 см. Найдем длину одной стороны ромба, разделив периметр на четыре a=20/4=5 см. Воспользуемся формулой пункта №3 и получим d=(4*5^2-8^2)^1/2=6 см.

Несмотря на кажущуюся простоту такой геометрической фигуры, как ромб, он таит в себе много интересных моментов. К нему применимы свойства параллелограмма, биссектрисы, прямоугольного, а иногда и равнобедренного треугольника. Зная формулы, легко можно решить задачи по нахождению диагоналей ромба.

Источник

Ромб — это четырехугольник, который является параллелограммом, сохраняет все его свойства, но кроме этого он еще и равносторонний. Так как все стороны ромба равны, а из свойств параллелограмма его противоположные углы также равны между собой, диагонали ромба не просто пересекаются в точке, которая делит их на две равные части каждую, а они всегда будут перпендикулярны по отношению друг к другу.

Когда в ромбе проводятся диагонали, они делят его на четыре конгруэнтных прямоугольных треугольника, катетами которого являются половины диагоналей. В любом из полученных прямоугольных треугольников можно, зная гипотенузу (сторона ромба), вычислить оба катета. Для этих целей используются тригонометрические отношения синуса и косинуса в прямоугольном треугольнике — так как оба катета, примем их временно за a и b, неизвестны, для вычислений понадобится один из острых углов в треугольнике.

Чтобы перевести эти формулы в параметры ромба, необходимо связать стороны треугольника со сторонами и диагоналями ромба, а также острый угол треугольника с углами ромба.

Сторона ромба, как было оговорено, становится гипотенузой треугольника, а половины диагоналей берут на себя роль катетов. Тогда в обратном порядке, чтобы найти полноценные диагонали, нужно будет каждый вычисленный катет увеличить в два раза.

Угол, используемый в синусе и косинусе для нахождения катетов и затем диагоналей ромба, является ничем иным как половинным углом самого ромба, так как диагонали ромба являются биссектрисами его углов. То есть будет справедливо следующее равенство:

α_ромба=2 α_{треугольника}
Или
α_ромба/2=α_{треугольника}

Теперь для выведения общей формулы диагоналей ромба через сторону ромба и его угол (кстати, выбор острого или тупого угла не сказывается на результате расчетов) выписанные замены должны быть подставлены в исходные формулы треугольника, с которых начинался алгоритм вычислений.