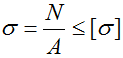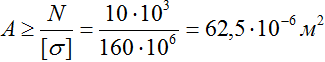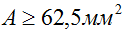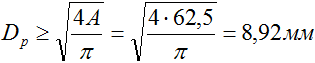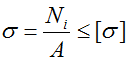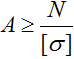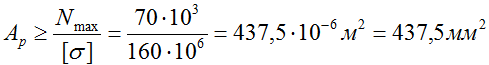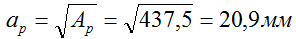Пример решения задачи по расчету минимального диаметра стального стержня обеспечивающего его прочность.
Задача
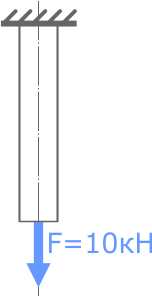
Подобрать по условию прочности диаметр стального стержня нагруженного продольной растягивающей силой F=10кН. Допустимые напряжения σ=160МПа.
Другие примеры решений >
Помощь с решением задач >
Решение
Для того чтобы стержень был прочным, нормальные напряжения σ в его поперечных сечениях не должны превышать заданных допустимых значений.
Условие прочности при продольном нагружении
где A — площадь поперечного сечения,
N – величина внутренней продольной силы, которая была определена ранее (N=10кН).
От диаметра, который мы будем рассчитывать, в данном выражении зависит только площадь A, поэтому получаем:
В квадратных миллиметрах площадь сечения представить проще:
То есть для того чтобы стержень был прочным, площадь его поперечного сечения независимо от формы должна быть не менее указанной величины.
Из формулы площади круга выражаем его расчетный диаметр
Это минимальный диаметр стержня, обеспечивающий его прочность.
Если в задании нет дополнительных условий, полученный размер можно округлить до целого миллиметра, но только в большую сторону.
Окончательно принимаем D=9мм.
Другие примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
Практическая
работа №1
Тема: Расчет
диаметра стержня круглого сечения.
Цель
работы: Выполнение
расчета и выбор диаметра стержня круглого сечения из условия прочности
Теоретический
материал
Все напряжения делятся на 2 группы:
I.
Напряжения по направлению:
1. σ (сигма) – нормальное напряжение
(рисунок 1, 2) – направлено перпендикулярно сечению, рассматривается в
деформации растяжения, сжатия, изгибов (продольных, поперечных)
Рисунок 1. Нормальное
напряжение Рисунок 2. Общее напряжение
2.
t (тay)- касательное
напряжение (рисунок 2) – направлено по касательной к сечению,
рассматривается в деформации кручения, сдвига и сложном виде деформации.
3. (po) – общее напряжение
(рисунок 3), находится по теореме Пифагора
II.
Напряжения по величине
1. Рабочее напряжение – напряжение, которое
возникает внутри конструкции под действием приложенных сил (рисунок 4).
Рисунок 4. Действие силы F на
стержень диаметром 20 мм
2.
Допустимое напряжение – напряжение, которое определяется по диаграмме
испытания материалов и при котором конструкция работает долговечно. Величина
рабочего напряжения должна быть меньше допустимого(табличного).
[]-допустимое нормальное напряжение
[]-допустимое касательное напряжение
3.
Предельное напряжение – напряжение, при котором конструкция разрушается.
— предельное нормальное напряжение
—
предельное касательное напряжение
Для решения задачи, в которой необходимо подобрать
размер поперечного сечения стержня рекомендуется следующая последовательность:
—
освободить
балку от связей, заменив их реакциями связей;
—
составить
уравнение равновесия и определить реакцию стержня, удерживающего балку в
равновесии;
—
из
условия прочности определить площадь поперечного сечения стержня;
—
определить
диаметр стержня.
Пример. Для
стержня, удерживающего балку в равновесии (рисунок 5), подобрать размер
круглого сечения из условия прочности. Для материала стержня (сталь Ст5)
принять: [σ]р
= 160МПа, [σ]с = 120МПа – допустимые напряжения на растяжение и
сжатие. На балку действуют внешний момент М=16кН, сила F=20кН на
участках а=1,5м, b=0,5м.
|
Дано: [σ]р [σ]с М=16кН, F=20кН , а=1,5м, b=0,5м. Подобрать |
|
Рисунок
5
Решение.
1.
Освобождаемся от связей, заменяем их реакциями, составляем расчетную схему
(рисунок 6).
Рисунок
6. Расчетная схема
2. Определяем
усилие в стержне СD —
продольную силу Nс,
препятствующую деформации стержня. Для этого составляем уравнение равновесия =0.
—
М+ Nс sin 30 (a+b) – F ·а=0
Nс = (М + F ·а) / sin 30 (a+b) =
(16 + 20·1,5)/0,5 (1,5+0,5) = 46 кН.
Реакция
связи направлена в сторону деформации, значит стержень СD
подвергается деформации растяжения.
3. Из условия
прочности на растяжение опреденляем диаметр стержня
; А ³ Nс / [σ]р,
для круга А= pd2 /4,
отсюда
pd2 = 4Nс / [σ]р ;
d = 
Принимаем d = 20мм.
Для обеспечения прочности
принимаем диаметр стержня 20 мм.
Обеспечивающие
средства:
1. методическое
руководство по выполнению работы;
2. таблица
тригонометрических функций;
3. индивидуальное
задание;
4. тетрадь
для практических работ;
5. карандаш,
линейка, транспортир, ластик, авторучка;
6. калькулятор.
Методические
рекомендации по выполнению работы:
1. Внимательно
изучить методические указания, предложенный теоретический материал.
2. В соответствии
с вариантом выполнить задание.
Для этого
необходимо:
—
полностью
переписать условие задания;
—
выполнить
задание в соответствии с методикой, приведенной выше;
—
располагать
действия в таком порядке, чтобы был виден логический ход выполнения работы.
3. Сделать выводы
о проделанной работе.
4. Ответить на
контрольные вопросы.
Литература:
1. Эрдеди
А.А. Техническая механика: учебник для студ.учреждений сред.проф.образования/
А.А. Эрдеди, Н.А. Эрдеди. – 4-е изд., стер. – М.: Издательский центр
«Академия», 2017.
2. Олофинская
В.П. Техническая механика. Курс лекций с вариантами практических и тестовых
заданий. — М.: ФОРУМ-ИНФРА-М, 2013.
3. Сафонова
Г.Г., Артюховская Т.Ю., Ермаков Д.А. Техническая механика. — М.: ИНФРА-М, 2013.
Порядок
выполнения заданий
1. По
исходным данным своего варианта начертить рисунок, соблюдая размеры.
2. Обозначить
на рисунке размеры а и b.
3. Освободить
балку от связей, заменив их реакциями связей;
4. Составить
уравнение равновесия и определить реакцию стержня, удерживающего балку в
равновесии;
5. Из условия
прочности определить площадь поперечного сечения стержня;
6. Определить
диаметр стержня.
Задания для выполнения работы
Для стержня, удерживающего балку в равновесии,
подобрать размер круглого сечения из условия прочности. Для материала стержня
(сталь Ст5) принять: [σ]р = 160МПа, [σ]с = 120МПа –
допускаемы напряжения на растяжение и сжатие. На балку действуют внешний момент
М, сила F на
участках а, b. Данные
для решения задачи представлены в таблице 1.
Таблица 1.
Исходные данные
|
вариант |
рисунок |
Исходные |
вариант |
рисунок |
Исходные |
||||||
|
F, кН |
М, кН·м |
b, м |
а, м |
F, кН |
М, кН·м |
b, м |
а, м |
||||
|
1 |
1 |
10 |
12 |
0,6 |
0,4 |
19 |
1 |
28 |
20 |
0,5 |
0,4 |
|
2 |
2 |
11 |
12 |
1,3 |
0,2 |
20 |
2 |
26 |
17 |
0,8 |
0,3 |
|
3 |
3 |
12 |
12 |
1,3 |
0,3 |
21 |
3 |
20 |
14 |
0,8 |
0,4 |
|
4 |
4 |
13 |
11 |
1,4 |
0,3 |
22 |
4 |
13 |
14 |
1,5 |
0,5 |
|
5 |
5 |
20 |
16 |
0,9 |
0,4 |
23 |
5 |
18 |
16 |
1 |
0,6 |
|
6 |
6 |
15 |
14 |
1,1 |
0,4 |
24 |
6 |
22 |
18 |
0,7 |
0,4 |
|
7 |
7 |
16 |
13 |
1,2 |
0,5 |
25 |
7 |
14 |
10 |
1,2 |
0,2 |
|
8 |
8 |
22 |
17 |
0,8 |
0,5 |
26 |
8 |
10 |
12 |
0,7 |
0,8 |
|
9 |
9 |
28 |
20 |
0,5 |
0,5 |
27 |
9 |
12 |
18 |
1,5 |
0,4 |
|
10 |
10 |
16 |
14 |
1,1 |
0,6 |
28 |
10 |
24 |
19 |
0,6 |
0,6 |
|
11 |
1 |
32 |
15 |
0,9 |
0,3 |
29 |
1 |
29 |
23 |
0,5 |
0,4 |
|
12 |
2 |
29 |
20 |
1,1 |
0,2 |
30 |
2 |
23 |
25 |
0,9 |
0,3 |
|
13 |
3 |
10 |
11 |
1,4 |
0,4 |
31 |
3 |
20 |
12 |
0,9 |
0,4 |
|
14 |
4 |
18 |
15 |
1 |
0,3 |
32 |
4 |
18 |
10,5 |
0,2 |
0,5 |
|
15 |
5 |
18 |
15 |
1 |
0,4 |
33 |
5 |
26 |
13 |
0,5 |
0,6 |
|
16 |
6 |
24 |
18 |
0,7 |
0,5 |
34 |
6 |
14 |
11 |
0,6 |
0,4 |
|
17 |
7 |
12 |
10 |
1,6 |
0,6 |
35 |
7 |
22 |
12 |
0,3 |
0,2 |
|
18 |
8 |
21 |
20 |
0,5 |
0,5 |
36 |
8 |
12 |
14 |
0,4 |
0,4 |
Выводы
Выводы
формулируются в свободной форме.
В выводах
необходимо отразить следующие моменты:
1) В какой
степени достигнута цель работы;
2) Какие
знания и умения приобретены в процессе выполнения работы.
Контрольные
вопросы
1. Поясните, в чем
заключается метод РОЗУ?
2. Перечислите
виды напряжений.
3. Каково правило знаков
нахождения продольной силы?
4. Напишите
формулу нахождения нормального напряжения.
5. Какие расчеты
можно выполнить из условия прочности?
iSopromat.ru
Пример решения задачи по расчету минимального диаметра стального стержня обеспечивающего его прочность.
Подобрать по условию прочности диаметр стального стержня нагруженного продольной растягивающей силой F=10кН. Допустимые напряжения σ =160МПа.
Для того чтобы стержень был прочным, нормальные напряжения σ в его поперечных сечениях не должны превышать заданных допустимых значений.
где A — площадь поперечного сечения,
N – величина внутренней продольной силы, которая была определена ранее (N=10кН).
От диаметра, который мы будем рассчитывать, в данном выражении зависит только площадь A, поэтому получаем:
В квадратных миллиметрах площадь сечения представить проще:
То есть для того чтобы стержень был прочным, площадь его поперечного сечения независимо от формы должна быть не менее указанной величины.
Из формулы площади круга выражаем его расчетный диаметр
Это минимальный диаметр стержня, обеспечивающий его прочность.
Если в задании нет дополнительных условий, полученный размер можно округлить до целого миллиметра, но только в большую сторону.
Окончательно принимаем D=9мм.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Источник
iSopromat.ru
Пример решения задачи по расчету размеров поперечного сечения прямого стального стержня по условию прочности на растяжение-сжатие.
Для прямого стержня постоянного сечения подобрать размер стороны a квадратного сечения по условию прочности. Материал стержня – сталь. Допустимые напряжения [ σ ]=160 МПа.
Полученные размеры принять согласно ГОСТ 6636.
Пример решения
Предыдущие пункты решения задачи
Рассматриваемый стержень нагружен исключительно продольными силами, поэтому для подбора размеров его поперечного сечения воспользуемся условием прочности при растяжении-сжатии.
где N – внутренние продольные силы (найдены ранее),
A — площадь поперечного сечения стержня.
Чтобы найти размеры поперечного сечения стержня рассчитаем площадь A. Для этого запишем условие прочности относительно площади:
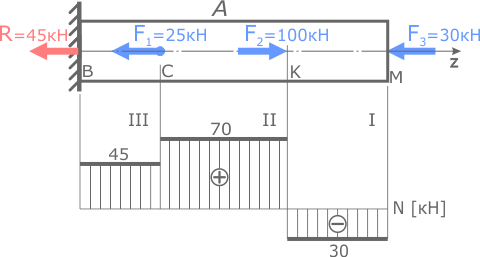
Площадь сечения в данном случае постоянна по всей длине стержня и должна обеспечивать прочность на всех его силовых участках. Поэтому расчет будем вести по самому нагруженному из них, т.е. где внутренняя сила максимальна (Nmax).
По построенной эпюре внутренних сил видно, что наиболее нагруженным является II участок, где N=Nmax=70кН.
Тогда расчетная площадь сечения стержня:
Таким образом для обеспечения необходимой прочности стержня площадь его поперечного сечения должна быть не менее 437,5 мм 2 .
Теперь, зная площадь квадрата, рассчитаем его сторону
Это соответственно минимальный размер поперечного сечения стержня, обеспечивающий его прочность.
В случаях, когда в задании не ставится дополнительных условий полученный размер можно округлить до целого миллиметра, но только в большую сторону.
По ГОСТ 6636 окончательно принимаем ближайший в сторону увеличения линейный размер а =22мм.
Все дальнейшие расчеты стержня будем вести по этому размеру.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Источник
Определяем диаметр вала из условия прочности



Условие прочности при кручении имеет вид
τmax = 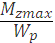
где Wp= πd 3 /16 ≈ 0,2d 3 – полярный момент сопротивления (момент сопротивления при кручении).
Наибольший по абсолютному значению крутящий момент возникает на втором участке вала:
Тогда требуемый диаметр вала определяется по формуле
d треб ≥ 
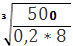
Округляя полученное значение до стандартного, принимаем диаметр вала равным d = 70 мм.
Определяем углы закручивания поперечных сечений A, B, C, D и E и строим эпюру углов закручивания
Сначала вычисляем крутильную жесткость стержня GIp, где G – модуль сдвига, а
Ip = πd 4 /32 ≈ 0,1 d 4 – полярный момент инерции. Получим
GIp = 0,8*10 4 *0,1 * 7 4 = 192*10 4 кН·см 2 .
Углы закручивания на отдельных участках стержня равны:
φAB = 
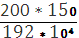
φBC = 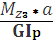
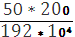
φCD = 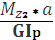
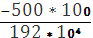
φDE = 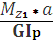

Угол закручивания в заделки равен нулю, то есть φA = 0. Тогда
Эпюра углов закручивания показана на рис. 9.1, в. Отметим, что в пределах длины каждого из участков вала угол закручивания изменяется по линейному закону.
Задачи на кручение «круглого» стержня
Жестко защемленный одним концом стальной стержень (модуль сдвига G = 0,8*10 4 кН/см 2 ) круглого поперечного сечения скручивается четырьмя моментами Мi (рис. 9.2).
· построить эпюру крутящих моментов;
· при заданном допускаемом касательном напряжении [τ] = 8 кН/см 2 из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм;
· построить эпюру углов закручивания поперечных сечений стержня.
Варианты расчетных схем к задаче на кручение стержня круглого сечения
Таблица 8.1. Исходные условия для самостоятельного решения
Источник
ПроСопромат.ру
Технический портал, посвященный Сопромату и истории его создания
Архив рубрики: Задачи на кручение
Проверочный и проектный расчеты при кручении
Задача. Для заданного стального бруса d=50мм (материал – сталь Ст3) построить эпюры крутящих моментов, углов поворота поперечных сечений. Проверить прочность бруса, если допускаемое касательное напряжение [τ]=30МПа. Подобрать для бруса кольцевое сечение при 

Строим эпюру МК
2.Строим эпюру углов поворота сечений. Углы поворота сечений определяем по формуле
Расчет ведем по сечениям от неподвижного конца – стены А, в которой угол поворота равен нулю φА=0. В формуле обязательно следует учитывать знаки крутящих моментов.
Модуль сдвига для Ст3 G = 0,8·10 5 МПа = 0,8·10 8 кПа.
Определим полярный момент инерции для круглого сечения:
Вычисляем углы поворота сечений — от стены А.
Если требуется перейти к градусной мере, то:
Далее вычисляем все последующие углы поворота, учитывая ранее найденные:

3.Проверим прочность бруса по формуле
Максимальный крутящий момент с эпюры МК = 0,75 кНм.
Определим полярный момент сопротивления сечения:
Тогда
4.Подбираем кольцевое сечение для вала с 
Наружный диаметр кольца определим по формуле проектного расчета для кольцевого сечения:
Тогда d = 0,8 · 60 = 48 мм.
Проверим прочность подобранного сечения. Полярный момент сопротивления для кольца:
5. Сравним варианты – круглое и кольцевое – по расходу материала
В задаче площадь круглого вала А = 19,6 см 2 , а у кольцевого сечения (полого) А = 10,7 см 2 , что позволяет говорить об экономии материала почти в два раза. Т.о. брус (вал) кольцевого сечения экономичнее равнопрочного сплошного.
Задача на кручение
Для вала определить диаметр, построить эпюры крутящих моментов и углов закручивания.
1) Определяем величины внутренних крутящих моментов M. Для этого разбиваем стержень на участки (I, II, III, IV) и производим расчёт M со свободного конца стержня. Крутящий момент M в сечении равен алгебраической сумме моментов, действующих на стержень с одной стороны (справа) от рассматриваемого сечения.
Расчёт M соответственно по участкам IV, III, II, I:
Зная числовые значения крутящих моментов M, строится эпюра M, при этом положительные значения M откладываются вверх, а отрицательные – вниз от горизонтальной линии.
2) Определяем диаметр стержня из условия прочности:



3) Производим расчет жесткости вала при кручении


4) Производим расчет 





Задача
Ступенчатый стержень нагружен крутящим моментом Т .При каком отношении 


Условие одинаковой прочности на участках будет выполнено в том случае ,если касательные напряжения будут одинаковы.
Определим касательные напряжения, обозначив крутящий момент в левой стене как 





Теперь составим уравнение деформаций — углов поворота. Начнем от правой стены В, в которой 



Полярные моменты инерции:


Составим уравнение статики для заданной схемы:

Теперь, решая (4) , (3) и (1), получим отношение 
Задача на расчет вала на прочность и жесткость при кручении
Для стального вала, нагруженного внешними крутящими моментами, построить эпюры внутренних крутящих моментов, определить размеры поперечного сечения в виде кольца (d/D=0,85) из условий прочности и жесткости, построить эпюры максимальных касательных напряжений, абсолютных и относительных углов поворота поперечных сечений.
Определим внутренние крутящие моменты. Расчет внутренних крутящих моментов проводится с помощью метода сечений.
Участок LK: МL= М4 = 5 кНм; МК=М4=5кНм.
Покажем эпюру крутящих моментов на рис.б.
Определяем размеры поперечного сечения вала из условия прочности и жесткости:

Тогда из условия прочности:
А из условия жесткости:
Для подобранного сечения вала его геометрические характеристики:
Рассчитаем касательные напряжения для участков:
Построим эпюру касательных напряжений на рис.в.
Расчет относительных углов поворота на участках:
Сначала определим жесткость сечения вала при кручении:
Эпюра θ показана на рис. г.
Определение угловых перемещений характерных сечений (идем от опоры В, в которой угол поворота равен 0):
Эпюра φ представлена на рис.д.
Задача на температурные напряжения при кручении
Стальные стержни 1 и 2 нагреваются на 
Определить максимальные напряжения.
При нагреве стержней на 
Напряжения, вызванные изменением температуры в стержне постоянного сечения, не зависят от его длины, площади поперечного сечения, а зависят от модуля упругости, коэффициента линейного расширения 

Эти напряжения создадут усилия:

Касательные напряжения:
Следует помнить, что при нагреве стержней в них возникают сжимающие напряжения, а при охлаждении – растягивающие. Эти напряжения, суммируясь с напряжениями от силовых факторов, могут значительно превышать допускаемые. Это обстоятельство следует учитывать при проектировании элементов конструкций.
Задача
К стальному валу приложены три известных момента:
Требуется: 1) установить, при каком значении Х угол поворота правого крайнего сечения вала равен нулю; 2) для найденного значения Х построить эпюру крутящих моментов; 3) при заданном значении [τ] определить диаметр вала из расчета на прочность и округлить его до ближайшей большей величины, соответственно равной 30, 35, 40, 45, 50, 60, 70, 80, 90, 100 мм; 4) построить эпюру углов поворота; 5) найти наибольший относительный угол закручивания (в градусах на 1м длины).
Решение: Обозначим границы участков русскими буквами А,……,Д.
I.Записываем условие, что угол поворота крайнего правого сечения (Д) вала равен нулю – исходя из условий задачи.
Данный угол поворота является суммой углов поворота вала на каждом участке:
Угол поворота на участке определяется по формуле:

G — модуль сдвига , 

Таким образом, 
Так как вал имеет постоянное поперечное сечение, то
Определяем внутренние крутящие моменты на участках методом сечений. Идем от свободного конца вала, на каждом участке мысленно проводим сечение и рассматриваем равновесие всегда правой отсеченной части:
Подставляем найденные значения моментов в уравнение (1) :
2. Строим эпюру крутящих моментов. Для этого подставляем в выражения для моментов Мк найденные значения Х.
Полученные значения откладываем в виде ординат на эпюре
3.Определяем диаметр вала из условия прочности:




[τ]=80 МПа — допускаемое касательное напряжение
Определяем диаметр:
Принимаем диаметр вала d=45 мм=4,5 см
4. Построение эпюры углов поворота начинаем от опоры и строим нарастающим итогом. Предварительно посчитаем жесткость вала:
Угол поворота в левой опоре равен нулю, поскольку в заделке поворота быть не может:
В последней точке угол поворота должен получиться равным нулю (по условию задачи), таким он и получился. Строим эпюру углов поворота.
5. Наибольший относительный угол закручивания определим по формуле:

Статически неопределимые задачи при кручении. Задача2
Требуется: 1) Построить эпюру крутящих моментов и подобрать размеры поперечных сечений заданной формы, соблюдая следующие соотношения между ними:
2) Построить эпюру углов поворота.
Сначала составляем уравнение статики для всего бруса:
Здесь два неизвестных, следовательно, требуется еще одно уравнение. Его получим, если сформулируем условие совместности деформаций всех трех участков бруса. Оно заключается в том, что поворот правого опорного сечения относительно левого опорного сечения для рассматриваемого бруса невозможен, поскольку оба его концы жестко защемлены:
Сократим на 
Выразим моменты инерции сечений разных форм с учетом заданных соотношений размеров:
Итак, все моменты инерции выражены через один параметр с, что позволит довести до числа решение уравнения (2′):
или после сокращения на с 4 :
С помощью метода сечений выразим неизвестные крутящие моменты через один из реактивных опорных моментов, например, через МА:
С учетом (а), (б) и (в) уравнение (2′′), будет:
откуда находим значение МА:
Тогда из (а), (б) и (в) найдем:
Эти результаты показаны в виде эпюры крутящих моментов.
Подбор размеров сечений производится по условиям прочности:
— на первом участке
Для круглого сечения
При заданном соотношении d=c:
— на втором участке
Для кольцевого сечения
Здесь мы должны учесть соотношения размеров, при которых и найдены внутренние усилия, то – есть
— на третьем участке
Для прямоугольного сечения 
По таблице α=0,246. И тогда Wк=2∙0,246∙с 3 .
Из условия прочности
Из трех требуемых значений «с» (0,023м, 0,04м и 0,046м) принимаем наибольшее с=0,046м и тогда проектные значения размеров сечений на разных участках должны быть
— на первом участке: круглое сечение диаметром d=0,046м,
— на втором участке: кольцевое сечение с внутренним диаметром d=0,046м, а внешним 
— на третьем участке: прямоугольное сечение шириной b=c=0,046м
и высотой h=2b=2∙0,046=0,092 м,
у которого Iк=β∙h∙b 3 =0,229∙0,092∙0,046 3 =205∙10 -8 м 4 .
2. Построение эпюры углов поворота.
Для этого вычисляются углы поворота сечений, расположенных на границах участков бруса (эти сечения на схеме обозначены цифрами в кружочках), они откладываются в виде ординат, вершины которых соединяются прямыми линиями. Так:
α0=0, поскольку крайнее левое сечение жестко защемлено и поворачиваться вокруг продольной оси z не может,
Равенство нулю угла поворота крайнего правого сечения, тоже жестко защемленного, служит контролем правильности всего решения задачи.
Статически неопределимые задачи при кручении. Задача1
Уравнение статики для всего бруса:
В этом уравнении два неизвестных (это реактивные моменты в опорах МА и МВ). Следовательно, задача один раз статически неопределима, и для ее решения необходимо составить дополнительное уравнение, выражающее факт совместности деформаций всех участков бруса.
Здесь можно рассуждать следующим образом: если удалить одну из опор, то брус станет статически определимым
Теперь крайнее правое сечение получило возможность поворачиваться. Но в заданной системе этот поворот невозможен. Поэтому величину МВ в удаленной опоре следует подобрать так, чтобы угол поворота опорного сечения равнялся нулю:
αВ=0 – это условие деформации.
Раскрывая его, будем иметь:
Тогда условие совместности деформаций (а) превращается в уравнение совместности деформаций:
В этом уравнении три неизвестных крутящих момента (по количеству участков бруса). Для их определения выразим крутящие моменты через заданные внешние скручивающие моменты М1, М2 и реактивные моменты, используя метод сечений. Так в любом сечении первого участка:
(
Далее, в любом сечении второго участка
Наконец, в любом сечении третьего участка:
Подставляя (b), © и (d) в уравнение (2), будем иметь:
В этом уравнении содержится одно-единственное неизвестное: это реактивный момент в левой опоре МА. Определив его из решения уравнения (2′), обратной подстановкой в формулы (b), © и (d) определим численные значения крутящих моментов 
Зная крутящие моменты, далее можно решить любую задачу прочности и жесткости бруса.
Кручение бруса тонкостенного замкнутого круглого сечения
Тонкостенное круглое сечение характеризуется средним радиусом Rср и толщиной стенки трубы δ
Считается, что касательные напряжения по толщине стенки распределяются равномерно и равны:
Угол закручивания
Кручение бруса прямоугольного сечения
Опыт показывает, что при кручении брусьев некруглого поперечного сечения сами сечения не остаются плоскими, то есть происходит депланация поперечных сечений. Исследовать напряженное и деформированное состояние таких брусьев при кручении методами сопротивления материалов не представляется возможным, так как в основе их лежит гипотеза плоских сечений (гипотеза Бернулли).
Задача о кручении бруса некруглого, в частности, прямоугольного сечения решена с помощью метода теории упругости, и на основе этого решения предложены простые расчетные формулы, имеющие ту же структуру, что и формулы для бруса круглого сечения, а именно:
Здесь: Wк=α∙h∙b 2 – момент сопротивления при кручении,
В этих формулах: b – меньшая из сторон прямоугольника,
h – большая сторона,
α, β – коэффициенты, значения которых приводятся в таблице в зависимости от отношения сторон h/b (эта таблица содержится в рубрике «Кручение», «Таблицы» или в любом учебнике сопротивления материалов).
Распределение касательных напряжений по прямоугольному сечению тоже отличается от распределения в круглом сечении:
Значения коэффициента γ Запись опубликована 05.09.2014 автором admin в рубрике Задачи, Задачи на кручение.
Источник
Из условия прочности находим искомый диаметр
и
,
oткуда
.
Удлинение участка
CD находим
по общей формуле
.
Здесь
– это площадь
трапеции mnrs, которая
равна
.
Следовательно,
.
Пример
14.
Стержень переменного
сечения с соотношением площадей
поперечных сечений A1/A2
=2 находится под действием сосредоточенных
сил и собственного веса (рис. а).
Материал стержня на всех участках
одинаков. Требуется построить эпюры
распределения продольной силы и
напряжений вдоль оси стержня и определить
перемещение сечения а–а.
Решение.
Строим эпюры
изменения продольной силы и напряжений
вдоль оси стержня. Собственный вес
стержня принято учитывать, заменяя его
распределенной по всей длине нагрузкой.
Интенсивность распределенной нагрузки
равна собственному весу, действующему
на единицу длины стержня, т. е.
на первом и втором
участках
,
на третьем участке
,
где
– объемный вес материала стержня.
Эпюры продольной
силы и напряжений строим, используя
метод сечений. Заметим, что угол наклона
эпюры продольной силы зависит от величины
q и, следовательно, при построении
эпюры N в масштабе угол ее наклона
на первом и втором участке должен быть
больше, чем на третьем участке, так как
A1 по условию больше, чем A2
(рис. б). Угол же наклона эпюры
напряжений зависит от объемного веса
g, и поэтому угол
наклона эпюры напряжений на всех участках
одинаков (рис. в).
Находим перемещение
(опускание) сечения а–а. Это
перемещение можно искать разными
способами. По первому
способу для определения перемещения
используем формулу
. Здесь F –
сосредоточенная сила, вызывающая
перемещение участка длиной l; G
– собственный вес рассматриваемого
участка. Эту формулу можно использовать
на участках постоянного сечения между
сосредоточенными силами. Отсчет надо
вести от неподвижного сечения, т.е.
заделки. Например, в рассматриваемой
задаче перемещение сечения а–а
складывается из удлинения участка
длиной l1, которое мы обозначим
, и удлинения
участка длиной
. При определении
удлинения
в формуле
сила F равна сумме F1, F2
и собственного веса всех расположенных
ниже участков. Вес участка стержня
длиной l1:
. Таким образом,
по формуле
.
Удлинение
происходит
под действием сосредоточенной силы,
состоящей из силы F2, веса
участков стержня, расположенных ниже
сечения а–а, и собственного веса
участка
. То есть
.
Окончательно
опускание сечения а–а равно
.
Если построена
эпюра распределения напряжений, то для
определения перемещения заданного
сечения удобно использовать второй
способ, применяя формулу
. В этой формуле
, а
– это площадь
эпюры напряжений. Таким образом, если
найти площадь двух трапеций на участке
между неподвижным сечением (заделкой)
и сечением а–а (заштрихованные
площади
и
эпюры
на рис. в)
и разделить полученную величину на
модуль упругости, мы получим искомое
перемещение сечения а–а:
.
При вычислении
перемещения обращайте внимание на
единицы измерения величин, входящих в
формулы. Рекомендуем окончательный
результат получить в сантиметрах.
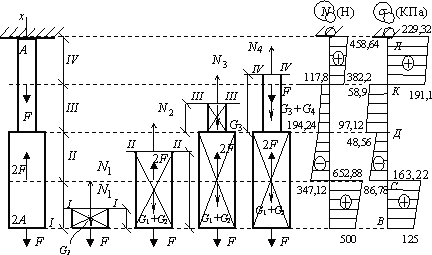
Пример
15.
Построить эпюры
нормальных сил и нормальных напряжений
для бруса, изображенного на рис. а.
Принять a = 0,4 м; площадь
поперечного сечения бруса на участках
III и IV
А = 20 см2; сосредоточенная
сила F = 0,5 кН, собственный
вес
= 0,0078 кг/см3
= 76,44 кН/м3.
Решение.
Для определения
внутренних усилий разбиваем брус с
прямолинейной осью на четыре участка.
Проводим сечение I
– I (рис. а) и
отбрасываем верхнюю часть бруса, заменяя
действие отброшенной части нормальной
силой N1 (рис.
б). Так как сечение I
–I может быть
проведено в любом месте участка I,
то длина оставшейся части участка будет
переменной величиной, и поэтому обозначим
ее через x (рис. б),
причем
. Запишем
уравнение равновесия, проектируя силы,
действующие на оставшуюся часть бруса,
на направление оси бруса:
а
б в г д
е ж
откуда
Через
обозначен
собственный вес оставшейся части бруса
первого участка, в пределах которого
площадь поперечного сечения равна 2А,
а длина оставшейся части обозначена
через x. Подставим
численные значения в полученную формулу:
.
Записанное выражение
показывает, что эпюра нормальных сил в
пределах первого участка представляет
собой наклонную прямую линию. Для
построения этой прямой определим
значение нормальной силы N1
в начале первого участка (x
= 0): N1(x
= 0) = 500 Н и в конце первого участка
(x = a=
0,5 м): N1 (х
= 0,5 м) =
Полученные значения
откладываем в масштабе в соответствующих
точках эпюры нормальных сил (рис. е).
Найденные точки соединяем прямой линией,
затем штрихуем первый участок эпюры
прямыми линиями, перпендикулярными к
оси бруса.
Проводим сечение
II – II и повторяем порядок расчета,
описанный выше для сечения I – I.
Переменная величина х участка II
– II будет изменяться в пределах
. Составим
уравнение равновесия (рис. в)
откуда
где
– собственный
вес части бруса, расположенного ниже
сечения II – II.
Окончательно имеем
Определяем значение
нормальной силы N2
в начале второго участка (х= 0,5 м):
и в конце этого же
участка (х = хmax =
1 м):
Полученные значения
N2 откладываем
в масштабе в начале и в конце второго
участка (рис. е).
Проводим сечение
III – III и для оставшейся части бруса
составляем уравнение равновесия (рис.
г)
откуда
где
– собственный
вес оставшейся части бруса третьего
участка;
– собственный
вес первого и второго участков.
Тогда для участка
где нормальная
сила N3 в
начале третьего участка будет N3(х=0)
= –194,2 Н; а в конце третьего участка
получаем N3 (х
= a = 0,5 м) = –117,8
Н. Найденные значения N3
переносим на эпюру нормальных сил.
И наконец,
рассматривая равновесие оставшейся
части бруса, после проведения сечения
IV – IV
получаем (рис. д)
откуда
где
Н –
собственный вес участков I – I и II
– II,
– собственный
вес третьего и оставшейся части четвертого
участков.
В этом случае имеем
т.е. в начале
четвертого участка N4
(х = 0,5 м) = 382,2 Н, а в конце этого
же участка N4
(х = 1 м) = 458,64 Н. Вычисленные значения
N4 откладываем
в масштабе на эпюре нормальных сил (рис.
е).
Эпюра нормальных
сил показывает, что первый и четвертый
участок подвержены растяжению, а второй
и третий – сжатию.
Для вычисления
значений нормальных напряжений
и построения
эпюры нормальных напряжений используем
формулу:
Эпюра нормальных
напряжений показывает, что самое большое
нормальное напряжение возникает в
сечении, проходящем через точку Л
четвертого участка (рис. ж), т.е. на
опоре.
Перемещения
поперечных сечений брусьев в статически
определимых задачах при растяжении-сжатии
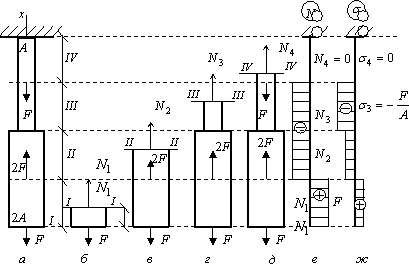
Пример
16.
Определить
перемещение нижнего конца стержня,
изображенного на рис. а. Задачу
решить без учета собственного веса
материала бруса. Принять
a
= 0,5 м; А = 10 см2; сосредоточенная
сила F = 10 кН.
Решение.
Для рассматриваемого случая эпюра
нормальных сил представлена на рис. е.
Для стержня со ступенчатым изменением
площади и нормальных сил перемещения
поперечных сечений вычисляются по
формуле (1.7). Рассматривая рис. а и
рис. е, запишем формулу для определения
перемещения нижнего конца стержня в
виде:
Знак «минус» в
ответе показывает, что общая длина
стержня уменьшится, т.е. нижний конец
стержня переместится вверх вдоль его
оси на величину
мм.
Пример
17.
Определить
перемещение нижнего конца стержня,
изображенного на рис. а. Принятьобъемный
вес материала стержня
= 76440 Н/м3.
Решение.
Для рассматриваемого
случая эпюра нормальных сил представлена
на рис. б.
Эпюра нормальных
сил построена с учетом сосредоточенных
внешних сил и с учетом собственного
веса материала бруса. Выделим на эпюре
нормальных сил (рис. б) ее постоянные
нормальные составляющие и треугольные
участки эпюры, учитывающие собственный
вес соответствующего участка. Разделение
составляющих эпюры нормальных сил на
рис. б произведено пунктирными
линиями.
Теперь перемещение
поперечного сечения от постоянной
составляющей эпюры нормальных сил будет
определяться по формуле
а перемещение от действия собственного
веса – по формуле
Для рассматриваемого
случая формула для определения перемещения
нижнего конца стержня будет иметь вид
Знак «+» показывает,
что общая длина стержня увеличится,
т.е. нижний конец стержня переместится
вниз вдоль его оси на величину
м
(рис. а).
Определим
перемещение сечения а – а (рис.
а). Для этого мысленно разрежем эпюру
нормальных сил в соответствующем сечении
а – а и отбросим нижнюю часть
эпюры. На основании оставшейся части
эпюры нормальных сил (рис. в) определяем
перемещение сечения а – а,
используя формулы
и
Полученный ответ
показывает, что поперечное сечение а
– а переместится вниз вдоль оси
стержня.
Пример
18.
Для стального
бруса квадратного сечения сжатого силой
Р с учетом собственного веса при
исходных данных приведенных ниже,
требуется (см. рис. а):
1. Определить
количество расчетных участков;
2. Составить
аналитические выражения для нормальных
сил Nz ,
нормальных напряжений
и вычислить
их значения для каждого из участков
с учетом их собственных весов;
3. Построить
эпюры Nz
и
;
4. Вычислить
перемещение верхнего конца колонны от
действия силы Р и собственного
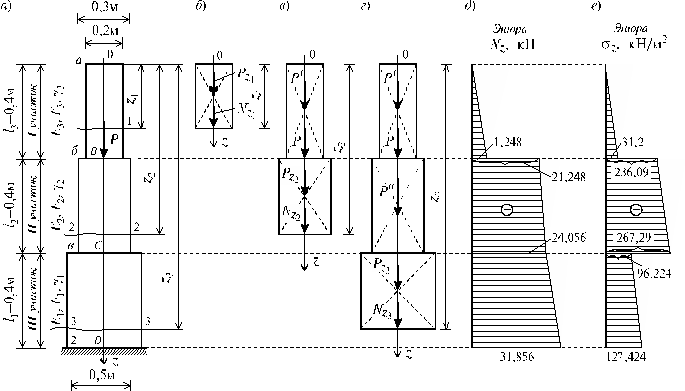
веса.
Дано: Р = 20 кН;
l1 = l2 = l3 = 0,4 м;
модуль упругости стали Е = кН/м2;
F1 =
м2; F2 = м2;
F3 = м2;
= 78
кН/м3 .
Решение.
1. Определение
количества участков.
Так как нормальная сила Nz
зависит от величин внешних сил, в данном
случае включающих в себя и собственный
вес колонны, а последний, в свою очередь,
от размеров поперечного сечения Fi
и объемного веса
g,
то границами участков следует назначать
те сечения, в которых приложены внешние
сосредоточенные силы и где происходит
скачкообразное изменение площади
поперечного сечения или объемного
веса материалов конструкций.
Исходя из
вышесказанного, учитывая
=const,
брус будет иметь три участка:
1 участок — от
0 до сечения В (где приложена сила
Р);
2 участок — от
сечения В до сечения С;
3 участок — от
сечения С до сечения D.
Следует заметить,
что при определении нормальных напряжений
используются те же участки.
2.
Составить аналитические выражения для
нормальных сил Nz,
нормальных напряжений sz
и вычислить их значения для каждого
из участков, с учетом их собственных
весов. Для
этого воспользуемся методом сечений.
1 участок (0 — В)
.
Проведя сечение
1 — 1
на расстоянии z1
от начала координат (точка 0),
рассмотрим равновесие верхней части.
При этом, к рассматриваемой части
прикладываются в центре ее тяжести
собственный вес и нормальная сила
, заменяющую
действие отброшенной нижней части
бруса на верхнюю рассматриваемую
(рис. б). Составив уравнение
равновесия рассматриваемой верхней
части колонны по оси z ,
получим:
.
В свою очередь,
собственный вес верхней части колонны
определяется следующим образом:
кН.
Тогда выражение
для нормальной силы будет иметь вид:
кН,
а для нормальных
напряжений
:
кН/м2.
Так как,
и
линейно зависят
от z1 ,
то для построения их графиков (эпюр)
достаточно определить значения этих
величин на границах участка, т.е.
при z1 = 0
при z1 = 0,4 м кН;
кН/м2.
Знаки минус при
и
указывают на
то, что принятое направление для этих
величин не совпадает с действительным,
т. к. в принятой схеме продольная сила
не растягивает, а сжимает первый участок.
2 участок (В — С)
.
Аналогично
предыдущему проводим сечение 2-2
на расстоянии z2
(рис. в). Для верхней части составляем
уравнение равновесия
.
В это уравнение
войдут: собственный вес первого участка
; собственный
вес отсеченной части второго участка
; сосредоточенная
сила Р = 20 кН, а также сила
.
Тогда уравнение
равновесия примет вид:
,
отсюда
=
=
кН.
Учитывая постоянство
площади поперечного сечения на втором
участке, выражение для нормального
напряжения может быть записано таким
образом:
кН/м2.
Вычислим значения
ординат
и
в граничных сечениях второго участка:
при z2 = 0,4 м
кН,
кН/м2;
при z2 = 0,8 м
кН,
кН/м2.
3 участок (С — D)
.
Составив уравнение
равновесия
(рис. г)
для верхней части бруса, получим:
,
откуда
кН.
Выражение для
напряжения:
кН/м2.
Вычислим значения
ординат
и
в граничных
сечениях третьего участка:
при z3
= 0,8 м (0,8) = -19,5 (0,8 + 0,43364) = -24,056
кН,
(0,8) = -78 (0,8 + 0,43364) = -96,224
кН/м2;
при z3
= 1,2 м (1,2) = -19,5 (1,2 + 0,43364) = -31,856
кН,
кН/м2.
3. Построение
эпюр Nz
и.
По причине линейной зависимости
нормальной силы и напряжений от координаты
z для
построения их эпюр достаточно значений
Nz
и
в
граничных сечениях каждого из участков
(см. рис. д, е). Необходимым
условием правильности построения этих
графиков является выполнение следующих
требований:
— скачок
в эпюре Nz
должен находиться в точке приложения
сосредоточенного усилия и быть равным
по величине значению этой силы;
— скачки
в эпюре
должны
совпадать с точками приложения внешней
силы Р и изменения площади поперечного
сечения колонны.
После анализа
полученных эпюр (рис. д, е)
легко можно убедиться, что построения
выполнены правильно.
4. Вычисление
перемещения верхнего конца колонны
от действия всех сил. Полное
перемещение согласно закону Гука
может быть вычислено по формуле
.
В данном случае
это выражение принимает следующий вид:
Так как величины
определенных интегралов равны площадям,
очерченным соответствующими
подынтегральными функциями, то для
вычисления перемещений
достаточно
вычислить площади эпюры Nz
на каждом из этих участков и
разделить их на Ei
Fi
. Следовательно,
.
Пример
19.
Найти закон
изменения площадей поперечного сечения
бруса равного сопротивления, испытывающего
растяжение под действием силы и
собственного веса.
Решение.
В каждом сечении бруса равного
сопротивления нормальные напряжения
должны быть равны постоянной величине
(). Запишем
условие равновесия элемента длиной dx:
или
Имеем dG –
собственный вес элемента бруса длиной
dx:
тогда
или
Интегрируя последнее
выражение, находим
где С –
произвольная постоянная интегрирования,
которая находится из граничных условий.
Окончательно запишем
Постоянную
интегрирования находим из условия, что
при х = 0 имеем А(х) = А0,
т.е. получаем
.
Таким образом,
закон изменения площади поперечного
сечения А(х) получает вид
,
т.е. в брусе равного
сопротивления площади поперечных
сечений изменяются по логарифмическому
закону.
Расчеты
на растяжение и сжатие статически
определимых стержневых систем
Пример
20.
Абсолютно жесткий
брус ВС (ЕВС =
) прикреплен
в точке С к неподвижному шарниру
(см. рис.), а в точке В поддерживается
стальной тягой АВ. В точке В
приложена вертикальная сила F
= 20 кН.
Подобрать сечение
тяги АВ и показать перемещение точки
В. Расчетное сопротивление стали
растяжению
коэффициент
условий работы
а модуль
упругости стали тяги АВ –
Решение.
Вырежем мысленно
узел В (рис. б) и составим для
него уравнения равновесия:
откуда
находим
откуда
Окончательно имеем
Следовательно,
брус ВС сжат силой N2, а
элемент АВ растянут силой N1.
Подбор сечения
тяги АВ проводим по формуле
откуда определяем
Предположим, что
тяга АВ имеет круглое поперечное
сечение, тогда An
= 1,44 см2 =
, откуда находим
r = 0,677 см и d =
1,35 см.
Определим удлинения
стержней АВ и СВ:
Таким образом,
точка В переместится в точку В/
по дуге окружности радиусом
, причем
расстояние между точками А и В/
будет равно
Пример
21.
Определить
из расчетов на прочность и жесткость
допускаемую силу F,
если []
= 120 МПа, []
= 1,7 мм, А1
= 2А,
А2
= А
= 5 см2,
l1
= l2
= l
= 1 м, Е
= 200 ГПа.
Р
е ш е н и е.
1.
Определение усилий в стержнях.
Из
условия равновесия бруса АС
имеем
,
,
;
,
,
.
2.
Расчет на прочность.
Находим
напряжения в стержнях
,
.
Как
видим, наиболее нагруженным является
2-й стержень, прочность которого
предопределяет прочность всей конструкции
в целом. Из условия прочности
находим
=
30 кН.
3.
Расчет на жесткость.
Вычисляем
деформации стержней
,
,
а
по ним перемещение точки С.
Из подобия треугольников В1А1В2
и С1А1С2
имеем:
В1В2/А1В2
= С1С2/А1С2
или
,
откуда
.
Записываем
условие жесткости
,
откуда
=
200×109×5×10-4×1,7×10-3/(8,5×1)=
20 кН.
Допускаемая
нагрузка из расчета на жесткость
получилась меньше, чем из расчета на
прочность, поэтому ее и принимаем в
качестве окончательной, т.е.
кН.
Пример
22.
К двум одинаковым
стержням приложена сила F. Установить,
при каком угле
конструкция
будет иметь наименьший вес?
Р е ш е н и е.
Вес конструкции
является функцией угла
, т.е.
.
Нам необходимо
установить такой угол, при котором
функция
принимает
минимальное значение. В теории оптимального
проектирования она называется целевой
функцией.
Для определения
веса стержневой системы нужно знать
площади сечений стержней. Из условия
равновесия узла С находим усилия в
стержнях:
,
,
,
а из условия
прочности – площади их поперечных
сечений:
,
откуда
.
Учитывая, что длины
стержней
, находим вес
конструкции (целевую функцию):
.
Функция
принимает
минимальное значение, когда
,
откуда
и
.
Определение
грузоподъемности статически определимой
конструкции, работающей на растяжение-сжатие.
Расчет по допускаемым напряжениям
При таком подходе
несущая способность конструкции
отождествляется с несущей способностью
наиболее нагруженного элемента.
Последовательность расчета при этом
выглядит следующим образом.
Составляются
уравнения статики и по числу лишних
неизвестных – дополнительные уравнения
совместности деформаций. Решая полученную
систему, определяют усилия в стержнях
и связанные с ними напряжения. Из
сопоставления напряжений в наиболее
нагруженном элементе с допустимой
величиной делается заключение о
надежности конструкции либо определяются
искомые величины (размеры сечения
стержней, допускаемая нагрузка).
Главная 




Определить диаметры круглых поперечных сечений стержней кронштейна (4.18), если [σ]=160 МПа.
Рис. 4.18
Усилия в стержнях определяются методом сечений путем вырезания узла A. Из уравнений проекций всех сил на оси y, x, получим:
;
.
Диаметры стержней определяются из условий прочности:



Версия для печати