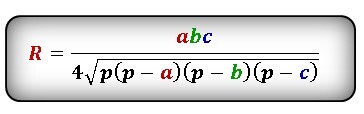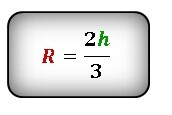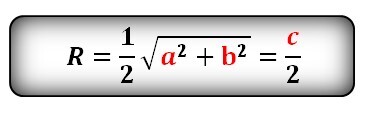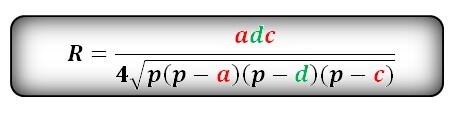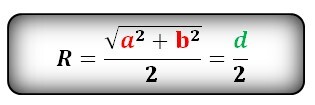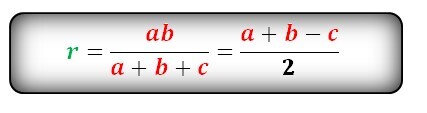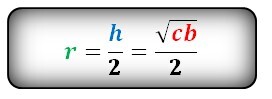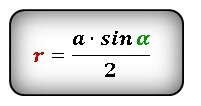Как найти диаметр окружности
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости.
Круг — часть плоскости, лежащая внутри окружности, а также сама окружность.
Если говорить проще, окружность — это замкнутая линия, как, например, обруч и велосипедное колесо. Круг — часть плоскости, ограниченная окружностью, как блинчик или вырезанный из картона кружок.
Диаметр — отрезок, который соединяет две точки окружности и проходит через ее центр.
Радиус — отрезок, который соединяет центр окружности и любую точку на ней.
Как узнать диаметр. Формулы
В данной теме нам предстоит узнать три формулы:
1. Общая формула.
Исходя из основных определений нам известно, что значение диаметра равно двум радиусам: D = 2 × R, где D — диаметр, R — радиус.
2. Если перед нами стоит задача найти диаметр по длине окружности
D = C : π, где C — длина окружности, π — это константа, которая равна отношению длины окружности к диаметру, она всегда равна 3,14.
Чтобы получить правильный ответ, можно поделить столбиком или использовать онлайн-калькулятор.
3. Если есть чертеж окружности
- Начертить внутри круга прямую горизонтальную линию. Ее месторасположение не играет значительной роли.
- Отметить точки пересечения прямой и окружности.
- Начертить при помощи циркуля две окружности одного радиуса (больше, чем радиус первоначальной окружности), первую — с центром в точке A, вторую — с центром в точке B.
- Провести прямую через две точки, в которых произошло пересечение. Отметить точки пересечения полученной прямой с окружностью. Диаметр равен этому отрезку.
- Теперь осталось измерить диаметр круга при помощи линейки. Получилось!
Эти простые формулы могут пригодиться не только на школьных уроках, но и если вы решите освоить профессию дизайнера интерьера, архитектора или модельера одежды.
Радиус и диаметр окружности
Окружность — это фигура в геометрии, которая состоит
из множества точек, расположенных на одинаковом
расстоянии от заданной точки (центра окружности).
Радиус окружности — это отрезок, который соединяет
центр окружности с какой-либо точкой окружности.
Диаметр окружности — это отрезок, который соединяет
две любые точки окружности, причем сам отрезок
должен проходить через центр окружности
Eсли от центра окружности провести
отрезки ко всем точкам окружности, то они будут иметь
одинаковую длину, то есть равны. В математике
такие отрезки называют радиусами.
Все радиусы окружности, как и диаметры окружности,
равны между собой, имеют одинаковую длину.
На рисунке выше изображена окружность, с центром в точке O.
OA = OB = OC — радиусы окружности;
BC = CO + OB — диаметр окружности;
Радиус окружности принято обозначать маленькой либо большой буквой, r или R.
Диаметр окружности обозначают буквой D.
Диаметр окружности условно состоит из двух
радиусов и равен длинам этих радиусов.
Длину радиуса окружности можно найти через диаметр окружности.
Для этого достаточно разделить на два длину диаметра окружности,
получившееся число и будет радиусом.
Формула радиуса окружности через диаметр:
Формула диаметра окружности через радиус:
Также, окружность, может быть вписанной в фигуру, описанной
около фигуры; или вообще может быть не вписана и не описана.
Формула радиуса окружности зависит от того находится фигура
внутри окружности, или окружность находится около фигуры.
Существует радиус вписанной окружности
и радиус описанной окружности.
Формулы радиуса вписанной и радиуса описанной окружностей
зависят в первую очередь от геометрической фигуры.
Радиус вписанной окружности — это радиус окружности,
которая вписана в геометрическую фигуру.
Радиус описанной окружности — это радиус окружности,
которая описана около геометрической фигуры.
Как посчитать диаметр окружности
Онлайн калькулятор
Как посчитать диаметр зная длину окружности
Чему равен диаметр если длина окружности ?
Каков диаметр (d) если длина окружности C?
Формула
d = C /π , где π ≈ 3.14
Пример
Если длина круга равна 5 см, то его диаметр примерно равен 1.59 см.
Как посчитать диаметр зная радиус окружности
Чему равен диаметр окружности если
Каков диаметр окружности (d) если её радиус r?
Формула
Пример
Если радиус круга равен 0.5 см, то его диаметр равен 1 см.
Как посчитать диаметр окружности зная её площадь
Чему равен диаметр окружности если
Каков диаметр окружности (d) если её площадь S?
Формула
d = √ 4S /π , где π ≈ 3.14
Пример
Если площадь круга равна 5 см 2 , то его диаметр примерно равен 2.52 см.
http://colibrus.ru/radius-i-diametr-okruzhnosti/
http://poschitat.online/diametr-okruzhnosti
Как найти диаметр окружности равнобедренного треугольника(см)?
Боковая сторона равнобедренного треугольника равна 4. Угол при вершине, противолежащий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника.
Решить задание можно несколькими способами. Можно исходить из теоремы косинусов,
Далее по теореме синусов считаем диаметр.
Можно считать и по другой схеме. Не через вычисление основания — с, а через угол при основании.
Есть и еще один вариант решения задачи.
Диаметр окружности описанной около равнобедренного треугольника находится по формуле: сторона делённая на синус угла противолежащего этой стороне.
Берём угол 120 градусов, синус 120 градусов равен синус 60 градусов, и равен корень из 3 делить на 2. По теореме косинусов можем найти противолежащую сторону. Получили что сторона равна корень из 48. Тогда делим корень из 48 на синус угла 120 градусов и получаем 8 см.
Теорема синусов
Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.
Нарисуем стандартный треугольник и запишем теорему формулой:
Формула теоремы синусов:
Докажем теорему с помощью формулы площади треугольника через синус его угла.
Из этой формулы мы получаем два соотношения:
На b сокращаем, воспользуемся правилом пропорции и получим:
Из этих двух соотношений получаем:
Теорема синусов для треугольника доказана.
Эта теорема пригодится, чтобы найти:
Стороны треугольника, если даны два угла и одна сторона.
Углы треугольника, если даны две стороны и один прилежащий угол.
Доказательство следствия из теоремы синусов
У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.
,где R — радиус описанной около треугольника окружности.
Так образовались три формулы радиуса описанной окружности:
Основной смысл следствия из теоремы синусов заключен в этой формуле:
Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.
Для доказательства следствия теоремы синусов рассмотрим три случая.
1. Угол ∠А = α — острый в треугольнике АВС.
Проведем диаметр BA1. В этом случае точка А и точка А1 лежат в одной полуплоскости от прямой ВС.
Используем теорему о вписанном угле и видим, что ∠А = ∠А1 = α. Треугольник BA1C — прямоугольный, в нём ∠ BCA1 = 90°, так как он опирается на диаметр BA1.
Чтобы найти катет a в треугольнике BA1C, нужно умножить гипотенузу BA1 на синус противолежащего угла.
BA1 = 2R, где R — радиус окружности
Для остроугольного треугольника с описанной окружностью теорема доказана.
2. Угол ∠А = α — тупой в треугольнике АВС.
Проведем диаметр окружности BA1. Точки А и A1 по разные стороны от прямой ВС. Четырёхугольник ACA1B вписан в окружность, и его основное свойство в том, что сумма противолежащих углов равна 180°.
Следовательно, ∠А1 = 180° — α.
Вспомним свойство вписанного в окружность четырёхугольника:
Также известно, что sin(180° — α) = sinα.
В треугольнике BCA1 угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом:
α = 2R sin (180° — α) = 2R sinα
Для тупоугольного треугольника с описанной окружностью теорема доказана.
Часто используемые тупые углы:
3. Угол ∠А = 90°.
В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности.
Для прямоугольного треугольника с описанной окружностью теорема доказана.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Примеры решения задач
Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал.
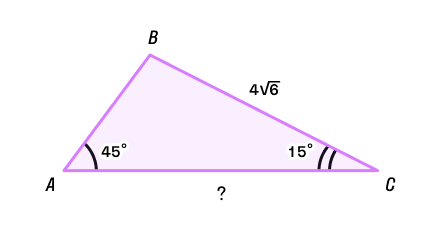
Пример 1. В треугольнике ABC ∠A = 45°,∠C = 15°, BC = 4√6. Найти AC.
Согласно теореме о сумме углов треугольника:
∠B = 180° — 45° — 15° = 120°
Сторону AC найдем по теореме синусов:
Пример 2. Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см соответственно. Найти угол, который расположен напротив данного катета.
Примем неизвестный угол за x. Тогда соотношение сторон выглядит так:
Ответ: угол составляет примерно 53,1°.
Запоминаем
Обычная теорема: стороны треугольника пропорциональны синусам противолежащих углов.
Расширенная теорема: в произвольном треугольнике справедливо следующее соотношение:
Радиус описанной и вписанной окружности: Формулы и примеры
На самом деле эту тему проходят еще в начальных классах обычной школы. И все, кто хорошо учился, сразу смогут сказать, о чем идет речь. Ну, или хотя бы точно понять, что РАДИУС как-то связан с окружностью.
Что такое радиус
И действительно:
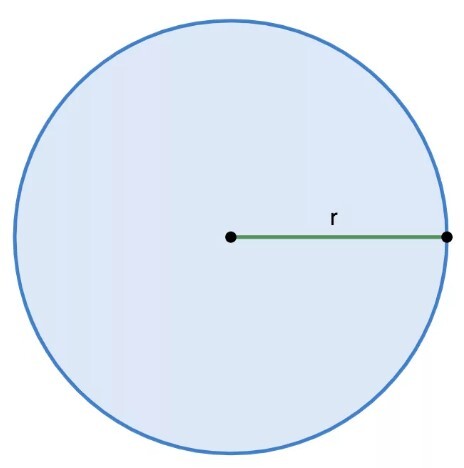
Радиус – это отрезок, который начинается в центре окружности и заканчивается в любой точке ее поверхности. В то же время так называется и длина этого отрезка.
Вот так это выглядит графически.
Само слово РАДИУС имеет латинские корни. Оно произошло от «radius», что можно перевести как «луч» или «спица колеса». Впервые этот математический термин ввел французский ученый П.Ромус. Было это в 1569 году.
Но потребовалось чуть более ста лет, чтобы слово РАДИУС прижилось и стало общепринятым.
Кстати, есть еще несколько значений слова РАДИУС:
- Размер охвата чего-нибудь или сфера распространения. Например, говорят «Огонь уничтожил все в радиусе 10 километров» или «ОН показал на карте радиус действия артиллерии»;
- В анатомии этим словом обозначают Лучевую кость предплечья.
Но, конечно, нас интересует РАДИУС как математический термин. А потому и продолжим говорить именно о нем.
Радиус и диаметр
Радиус в математике всегда обозначается латинской буквой «R» или «r». Принципиальной разницы, большую букву писать или маленькую, нет.
А два соединенных вместе радиуса, которые к тому же находятся на одной прямой, называются диаметром. Или по-другому:
Диаметр – это отрезок, который проходит через центр окружности и соединяет две противоположные точки на ее поверхности. По аналогии с радиусом под диаметром подразумевают и длину этого отрезка.
Обозначается диаметр также первой буквой своего слова – D или d.
Исходя из определения диаметра, можно сделать простой вывод, который одновременно является одной из базовых основ геометрии.
Длина диаметра равна удвоенной длине радиуса.
Примеры задач
Длина окружности равняется 87,92 см. Найдите ее радиус.
Используем первую формулу (через периметр):
Найдите радиус круга, если его площадь составляет 254,34 см 2.
Воспользуемся формулой, выраженной через площадь фигуры:
Формулы для радиуса описанной окружности
Найти радиус описанной окружности треугольника по сторонам
Формула радиуса описанной окружности треугольника (R ) :
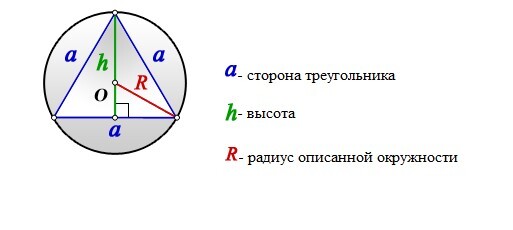
Найти радиус описанной окружности равностороннего треугольника по стороне или высоте
Формула радиуса описанной окружности равностороннего треугольника через его сторону:
Формула радиуса описанной окружности равностороннего треугольника через высоту:
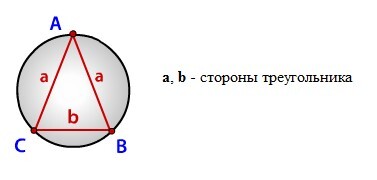
Найти радиус описанной окружности равнобедренного треугольника по сторонам
Зная стороны равнобедренного треугольника, можно по формуле, найти, радиус описанной окружности около этого треугольника.
Формула радиуса описанной окружности равнобедренного треугольника (R):
Найти радиус описанной окружности прямоугольного треугольника по катетам
Радиус описанной окружности прямоугольного треугольника равен половине его гипотенузы.
Формула радиуса описанной окружности прямоугольного треугольника (R):
Радиус описанной окружности трапеции по сторонам и диагонали
Формула радиуса описанной окружности равнобокой трапеции, (R)
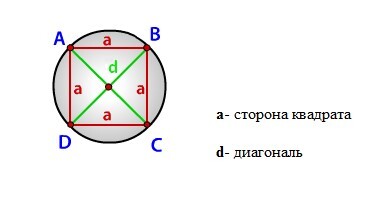
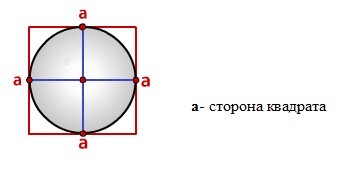
Найти радиус описанной окружности около квадрата
Радиус описанной окружности квадрата равен половине его диагонали
Формула радиуса описанной окружности квадрата (R):
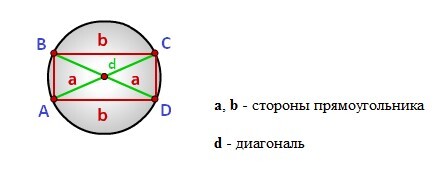
Радиус описанной окружности прямоугольника по сторонам
Радиус описанной окружности прямоугольника равен половине его диагонали
Формула радиуса описанной окружности прямоугольника (R):
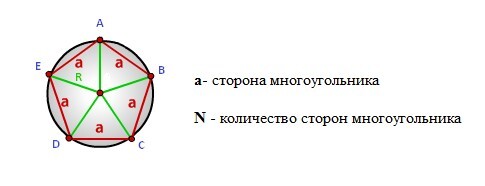
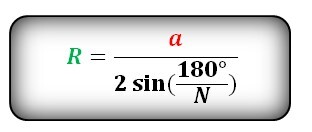
Радиус описанной окружности правильного многоугольника
Формула радиуса описанной окружности правильного многоугольника, (R):
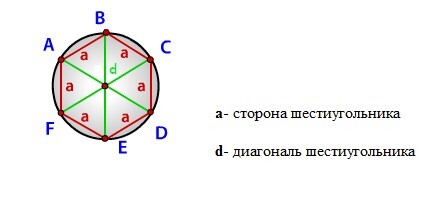
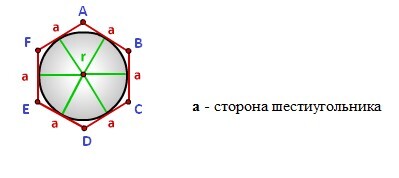
Радиус описанной окружности правильного шестиугольника
Радиус описанной окружности правильного шестиугольника (R):
Формулы для радиуса вписанной окружности
Радиус вписанной окружности в треугольник
Формула радиуса вписанной окружности в треугольник (r):
Радиус вписанной окружности в равносторонний треугольник
Формула для радиуса вписанной окружности в равносторонний треугольник (r):
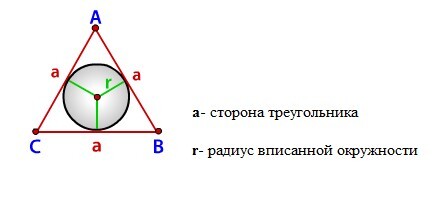
Радиус вписанной окружности равнобедренный треугольник
1. Формулы радиуса вписанной окружности если известны: стороны и угол
Формула радиуса вписанной окружности в равнобедренный треугольник через стороны (r ) :
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и угол (r ) :
2. Формулы радиуса вписанной окружности если известны: сторона и высота
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и высоту (r ) :
Радиус вписанной окружности в прямоугольный треугольник
Формула радиуса вписанной окружности в прямоугольный треугольник (r):
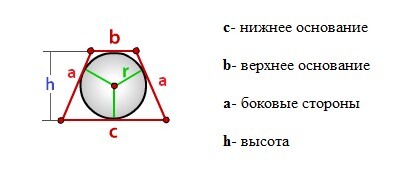
Радиус вписанной окружности в равнобочную трапецию
Формула радиуса вписанной окружности равнобочной трапеции (r):
Радиус вписанной окружности в квадрат
Формула радиуса вписанной окружности в квадрат (r):
Радиус вписанной окружности в ромб
1. Формулы радиуса вписанной окружности если известны: диагональ, стороны и угол
Формула радиуса вписанной окружности в ромб через диагонали (r ) :
Формула радиуса вписанной окружности в ромб через сторону и угол (r ) :
Формула радиуса вписанной окружности в ромб через диагональ и угол (r ) :
Формула радиуса вписанной окружности в ромб через диагональ и сторону (r ) :
2. Радиус вписанной окружности ромба, равен половине его высоты
Формула радиуса вписанной окружности в ромб (r ) :
Радиус вписанной окружности в правильный многоугольник
Формула радиуса вписанной окружности в правильный многоугольник, (r):
Радиус вписанной окружности в шестиугольник
Формула радиуса вписанной окружности в шестиугольник, (r):
Примеры задач
Дан треугольник со сторонами 5, 7 и 10 см. Вычислите радиус вписанной в него окружности.
Сперва вычислим площадь треугольника. Для этого применим формулу Герона:
Остается только применить соответствующую формулу для вычисления радиуса круга:
Боковые стороны равнобедренного треугольника равны 16 см, а основание 7 см. Найдите радиус вписанной в фигуру окружности.
Воспользуемся подходящей формулой, подставив в нее известные значения:
Всем спасибо и приятного просмотра! Если понравилась публикация подписывайтесь и ставьте палец вверх!
|
Боковая сторона равнобедренного треугольника равна 4. Угол при вершине, противолежащий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника. Решить задание можно несколькими способами. Можно исходить из теоремы косинусов, Далее по теореме синусов считаем диаметр. Можно считать и по другой схеме. Не через вычисление основания — с, а через угол при основании. Есть и еще один вариант решения задачи. Ответ: 8см. автор вопроса выбрал этот ответ лучшим Артём1234567897012 3 года назад Диаметр окружности описанной около равнобедренного треугольника находится по формуле: сторона делённая на синус угла противолежащего этой стороне. Берём угол 120 градусов, синус 120 градусов равен синус 60 градусов, и равен корень из 3 делить на 2. По теореме косинусов можем найти противолежащую сторону. Получили что сторона равна корень из 48. Тогда делим корень из 48 на синус угла 120 градусов и получаем 8 см. Знаете ответ? |
Вписанные и описанные треугольники. Еще две формулы площади треугольника. Теорема синусов
Вписанный треугольник — треугольник, все вершины которого лежат на окружности. Тогда окружность называется описанной вокруг треугольника.
Очевидно, расстояние от центра описанной окружности до каждой из вершин треугольника одинаково и равно радиусу этой окружности.
Вокруг любого треугольника можно описать окружность, причем только одну.
Окружность вписана в треугольник, если она касается всех его сторон. Тогда сам треугольник будет описанным вокруг окружности. Расстояние от центра вписанной окружности до каждой из сторон треугольника равно радиусу этой окружности.
В любой треугольник можно вписать окружность, причем только одну.
Рассмотрим важные теоремы, которые помогут нам при решении задач.
Теорема 1. Вокруг любого треугольника можно описать окружность, причем только одну. Ее центр – это точка пересечения серединных перпендикуляров к сторонам треугольника.
Иногда говорят, что окружность описана около треугольника. Это означает то же самое – все вершины треугольника лежат на окружности.
Доказательство этой теоремы здесь: Свойство серединных перпендикуляров.
Теорема 2. В любой треугольник можно вписать окружность, причем только одну. Ее центром является точка пересечения биссектрис треугольника.
Доказательство теоремы здесь: Свойства биссектрис треугольника.
Теорема 3. Центр окружности, описанной вокруг прямоугольного треугольника, лежит на середине гипотенузы, а радиус этой окружности равен половине гипотенузы.
Доказательство:
Медиана, проведенная к гипотенузе, равна ее половине, по свойству медианы прямоугольного треугольника.
Его доказательство можно найти здесь: Свойство медианы прямоугольного треугольника.
Поэтому середина гипотенузы – это точка, равноудаленная от вершины прямого угла и от концов гипотенузы, то есть от всех вершин прямоугольного треугольника.
Теорема 4.
Центр окружности, описанной вокруг остроугольного треугольника, лежит внутри этого треугольника.
Центр окружности, описанной вокруг прямоугольного треугольника, лежит на середине гипотенузы.
Центр окружности, описанной вокруг тупоугольного треугольника, лежит вне этого треугольника.
Теорема 5. Радиус окружности , вписанной в прямоугольный треугольник с катетами
и
и гипотенузой
, вычисляется по формуле:
Доказательство теоремы здесь: Радиус окружности, вписанной в прямоугольный треугольник.
В задачах ЕГЭ чаще всего встречаются вписанные и описанные правильные треугольники.
Напомним определение правильного многоугольника:
Правильным называется многоугольник, все стороны и все углы которого равны. Центры вписанной и описанной окружностей правильного многоугольника находятся в одной точке.
Из этого определения, понятно, что правильный треугольник – равносторонний. Для решения такого треугольника полезно уметь выводить формулы радиусов вписанной и описанной окружностей.
Теорема 6.
Для правильного треугольника со стороной а радиус описанной окружности равен
А радиус окружности, вписанной в правильный треугольник, равен
Докажем эту теорему.
У равностороннего треугольника медианы, биссектрисы, высоты и серединные перпендикуляры совпадают, и точка их пересечения является центром как вписанной, так и описанной окружностей.
Пусть в правильном треугольнике стороны
, точка О – центр вписанной и описанной окружностей,
— медианы и высоты. По свойству медиан треугольника, отрезки
в точке О делятся в отношении 2 : 1, считая от вершин. Тогда
Получаем, что
Из треугольника АВН получаем, что длина стороны
Тогда
Значит, формула радиуса окружности, описанной около правильного треугольника —
Формула радиуса окружности, вписанной в правильный треугольник
Как видим, часто геометрическая задача решается с помощью несложных формул, и помогает в этом алгебра.
Разберем задачи ОГЭ и ЕГЭ по теме: Вписанные и описанные треугольники.
Задача 1, тренировочная. Периметр правильного треугольника АВС равен 15. Найдите радиус вписанной и описанной окружностей.
Решение:
Длина стороны равностороннего треугольника равна
Радиусы – вписанной и
– описанной окружностей можно найти по формулам:
где
— сторона треугольника.
Значит,
Ответ:
Решая задачи по теме «Вписанные и описанные треугольники», мы часто пользуемся формулами площади треугольника, а также теоремой синусов.
Вот две полезные формулы для площади треугольника.
Площадь треугольника равна половине произведения его периметра на радиус вписанной окружности.
,
где — полупериметр,
— радиус окружности, вписанной в треугольник.
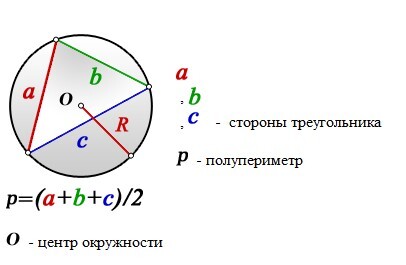
Есть и еще одна формула, применяемая в основном в задачах части :
где — стороны треугольника,
— радиус описанной окружности.
Для любого треугольника верна теорема синусов:
Теорема синусов:
R — радиус описанной окружности
Задача 2, ЕГЭ. Найдите диаметр окружности, вписанной в треугольник со сторонами 13, 14 и 15.
Решение:
Выразим площадь треугольника двумя разными способами:
где
– полупериметр треугольника, a
– его стороны.
Тогда , а диаметр окружности равен
Ответ: 8.
Задача 3, ЕГЭ. Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен . Найдите гипотенузу c этого треугольника. В ответе укажите
.
Решение:
Треугольник прямоугольный и равнобедренный. Значит, его катеты одинаковы. Пусть каждый катет равен . Тогда гипотенуза равна
.
Запишем площадь треугольника АВС двумя способами:
Приравняв эти выражения, получим, что . Поскольку
, получаем, что
.
Тогда .
В ответ запишем .
Ответ: 4.
Задача 4, ЕГЭ. В треугольнике сторона
равна
, а угол
равен
. Найдите радиус описанной около этого треугольника окружности.
Решение:
По теореме синусов
Тогда
Ответ: 7.
Задача 5, ЕГЭ. В треугольнике угол А равен
, а угол В –
. Найдите радиус окружности, описанной около треугольника
, если сторона
равна 10.
Решение:
Зная, что сумма углов треугольника равна , найдем угол С.
По теореме синусов
Значит,
Ответ: 10.
Задача 6, ЕГЭ. Сторона АС треугольника АВС с тупым углом В равна радиусу описанной около него окружности. Найдите угол В. Ответ дайте в градусах.
По теореме синусов,
Получаем, что . Угол
— тупой. Значит, он равен
.
Ответ: 150.
Задача 7, ЕГЭ. Боковые стороны равнобедренного треугольника равны , основание равно
. Найдите радиус описанной окружности этого треугольника.
Углы треугольника не даны. Что ж, выразим его площадь двумя разными способами.
, где
— высота треугольника. Ее найти несложно — ведь в равнобедренном треугольнике высота является также и медианой, то есть делит сторону
пополам. По теореме Пифагора найдем
.
Тогда .
Ответ: 25.
Задача 8, ОГЭ. В равнобедренном треугольнике основание
равно 10 см, а высота, проведенная к основанию, 12 см. Найдите периметр треугольника и радиус вписанной окружности.
Решение:
Высота , проведенная к основанию
, является медианой. Значит,
.
находится по теореме Пифагора из треугольника
:
Периметр треугольника – это сумма длин сторон, т.е.
Площадь треугольника
Радиус вписанной окружности r найдем по формуле
Ответ:
Задача 9, ОГЭ. Стороны и
треугольника
равны 6 и
соответственно, угол
. Найдите диаметр окружности, описанной около треугольника
.
Решение:
Найдем длину стороны по теореме косинусов, используя длины сторон
,
и косинус угла В, противолежащего стороне
:
Теперь воспользуемся теоремой синусов:
Значит, диаметр окружности, описанной около треугольника , равен 6.
Ответ: 6.
Задача 10. Найдите площадь прямоугольного треугольника, если радиус описанной окружности равен 5, а вписанной 1.
Решение:
Пусть длина радиуса описанной окружности , а длина радиуса вписанной окружности
Мы знаем, что , где
– полупериметр,
– стороны треугольника.
Значит,
Отсюда
Тогда
Ответ: 11.
Задача 11. Найдите площадь прямоугольного треугольника, если радиус вписанной окружности равен 2, а гипотенуза 10.
Решение:
Пусть радиус вписанной окружности , а гипотенуза
Мы знаем, что в прямоугольном треугольнике
Значит, отсюда
Площадь находится по формуле где
– полупериметр,
– стороны треугольника.
Ответ: 24.
Рассмотрим также задачу из 2 части ЕГЭ по математике.
Задача 12. Точка О – центр вписанной в треугольник окружности. Прямая
вторично пересекает описанную около треугольника
окружность в точке Р.
а) Докажите, что
б) Найдите площадь треугольника , если радиус окружности, описанной около треугольника
равен 10,
Решение:
а) Пусть О – центр вписанной окружности, значит,
и
– биссектрисы углов
и
соответственно, и
как вписанные углы, опирающиеся на одну и ту же дугу
Тогда
– внешний угол треугольника
, поэтому он равен сумме двух внутренних углов, не смежных с ним, т.е.
Значит, Что и требовалось доказать.
б) , следовательно, треугольник
– равнобедренный,
– основание,
Угол равен
, значит,
По теореме синусов для треугольника :
Тогда отрезок равен отрезку
, т.е.
.
Найдем угол С из треугольника :
как вписанные углы, опирающиеся на дугу
.
Площадь треугольника находится по формуле:
Ответ:
Задачи на вписанные и описанные треугольники особенно необходимы тем, кто нацелен на решения задания .
Если вам понравился наш материал — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Вписанные и описанные треугольники. Еще две формулы площади треугольника. Теорема синусов» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
08.05.2023
Окружность — это фигура в геометрии, которая состоит
из множества точек, расположенных на одинаковом
расстоянии от заданной точки (центра окружности).
Радиус окружности — это отрезок, который соединяет
центр окружности с какой-либо точкой окружности.Диаметр окружности — это отрезок, который соединяет
две любые точки окружности, причем сам отрезок
должен проходить через центр окружности
Eсли от центра окружности провести
отрезки ко всем точкам окружности, то они будут иметь
одинаковую длину, то есть равны. В математике
такие отрезки называют радиусами.
Все радиусы окружности, как и диаметры окружности,
равны между собой, имеют одинаковую длину.
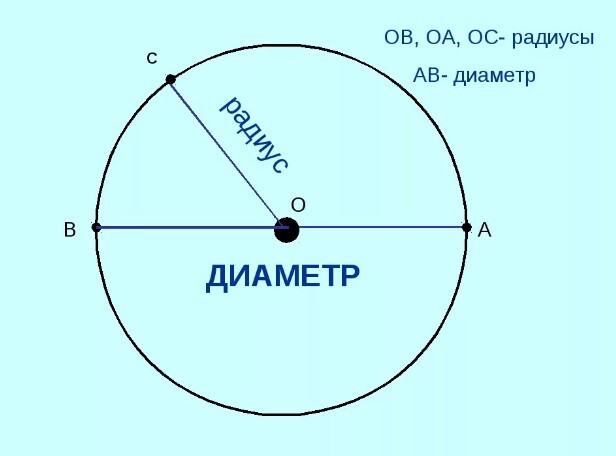
На рисунке выше изображена окружность, с центром в точке O.
OA = OB = OC — радиусы окружности;
BC = CO + OB — диаметр окружности;
Радиус окружности принято обозначать маленькой либо большой буквой, r или R.
Диаметр окружности обозначают буквой D.
Диаметр окружности условно состоит из двух
радиусов и равен длинам этих радиусов.
Длину радиуса окружности можно найти через диаметр окружности.
Для этого достаточно разделить на два длину диаметра окружности,
получившееся число и будет радиусом.
Формула радиуса окружности через диаметр:
[ R = D/2 ]
Формула диаметра окружности через радиус:
[ D = 2R ]
Также, окружность, может быть вписанной в фигуру, описанной
около фигуры; или вообще может быть не вписана и не описана.
Формула радиуса окружности зависит от того находится фигура
внутри окружности, или окружность находится около фигуры.
Существует радиус вписанной окружности
и радиус описанной окружности.
Формулы радиуса вписанной и радиуса описанной окружностей
зависят в первую очередь от геометрической фигуры.
Радиус вписанной окружности — это радиус окружности,
которая вписана в геометрическую фигуру.Радиус описанной окружности — это радиус окружности,
которая описана около геометрической фигуры.