Математика, 3 класс
Урок №33. Круг. Окружность (центр, радиус, диаметр)
Перечень вопросов, рассматриваемых в теме:
— что такое окружность и круг?
— какие элементы имеет окружность?
— чем отличается круг от окружности?
Глоссарий по теме:
Окружность — это замкнутая кривая, все точки которой одинаково удалены от центра.
Круг – это геометрическая фигура, которая ограничена окружностью.
Радиус- это отрезок, соединяющий центр окружности с любой точкой на окружности.
Диаметр – отрезок, который соединяет две точки окружности, проходящий через центр.
Основная и дополнительная литература по теме урока:
1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. с. 94-96.
2. Рудницкая В. Н. Тесты по тматематике:3 класс. М.:Издательство «Экзамен», 2016 с. 48-51.
3. Рудницкая В.Н. Контрольные работы по математике:3 класс. М.: Издательство»Экзамен», 2017, с. 49-54.
4. Рудницкая В. Н. КИМ ВПР. Математика .3 класс. М.: Издательство «Экзамен», 2018, с. 77-79.
Теоретический материал для самостоятельного изучения
С незапамятных времен люди используют в своей жизни круг.
1. Около 3300 года до нашей эры стали применять гончарный круг, делать круглую посуду – тарелки, вазы, кастрюли, горшки, сковородки. У посуды есть окружность (верхний край) и круг (дно).
2. Мы не можем представить свою жизнь без машин: автобус, велосипед, швейная, машинки, самолет, луноход, различные станки, подъемный кран…Они не похожи друг на друга, но присмотримся к ним повнимательнее. Есть у них у всех похожие части – детали, и одна из них – колесо. Сначала колеса были круглые и гладкие, чтобы по земле легко катились, а потом человек придумал много разных колес.
3. Круг и окружность широко применяются в архитектуре и искусстве: круглые арки, своды, купола. Круг – это форма кочевых шатров и поселений. Еще древние греки обнаружили, что с помощью циркуля и линейки можно построить множество фигур, включая шестиугольники, квадраты и другие правильные многоугольники, и создавать волшебные узоры.
4. Необозрима сфера применения круга в математике: тригонометрический круг, круги Эйлера, задачи на построение, круговые диаграммы и т.д. Многие приборы имеют круглую шкалу, в математике таким прибором является транспортир .
5. Картинки с волшебными кругами люди используют в медицинских целях, когда на них смотришь, кажется, что они двигаются. Если смотреть на них несколько минут, то проходит головная боль.
6. Также человек использует круг, как универсальный символ, означающий целостность, непрерывность, первоначальное совершенство. Три концентрических круга символизируют прошлое, настоящее и будущее; три сферы земли: землю, воздух и воду.
Круг в жизни человека имеет очень важную роль, и без использования круглых предметов обойтись невозможно.
Окружность и круг – удивительно гармоничные, совершенные, простые фигуры. Окружность – единственная замкнутая кривая, которая может “скользить сама по себе”, вращаясь вокруг центра, поэтому колеса делают круглыми, а не квадратными или треугольными.
Круг – это колесо. Колесо – это прогресс – движение вперед. Если остановится колесо, то остановится колесо Истории. Остановятся все виды транспорта, остановятся все часы и механизмы, фабрики и заводы.
Круг – символ цикличности, повторяемости. Все движется по кругу.
Круг дает ощущение взаимосвязи с Космосом.
Сама природа выбирает эту удобную и компактную форму как шар и круг.
Сравним две фигуры.
На 1 рисунке видим замкнутую кривую линию, на которой находятся точки К и С на одинаковых расстояниях от точки О.Такая замкнутая кривая называется окружностью. Точка О — центр окружности. Все точки, поставленные на окружности, находятся на одинаковом расстоянии от центра!
Есть специальный инструмент, который позволяет чертить окружности – это циркуль.
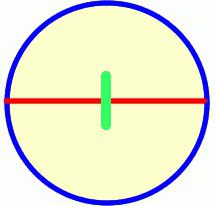
На рисунке 2 видим геометрическую фигуру, которая ограничена окружностью. Эта фигура называется круг.
Вывод: окружность — граница круга; круг — часть внутри окружности. В таблице указаны отличительные признаки круга и окружности:
Если соединить любую точку окружности с ее центром, то получится отрезок, который называется радиусом.
Если соединить 2 точки окружности, проходящих через центр, получится отрезок, который называется диаметром.
Диаметр делит круг на две равные части и все диаметры у окружности равной длины.

Задания тренировочного модуля:
1. Длина радиуса составляет 6 см. Чему равен диаметр окружности?
6см; 12 см; 3см.
Правильный ответ: 12см.
2. Заполните таблицу
|
радиус |
4 см |
3 см |
7 дм |
5 дм |
|
диаметр |
Правильный ответ:
|
радиус |
4 см |
3 см |
7 дм |
5 дм |
|
диаметр |
8 см |
6 см |
14 дм |
10 дм |
Как посчитать диаметр окружности
Онлайн калькулятор
Как посчитать диаметр зная длину окружности
Чему равен диаметр если длина окружности ?
Каков диаметр (d) если длина окружности C?
Формула
d = C /π , где π ≈ 3.14
Пример
Если длина круга равна 5 см, то его диаметр примерно равен 1.59 см.
Как посчитать диаметр зная радиус окружности
Чему равен диаметр окружности если
Каков диаметр окружности (d) если её радиус r?
Формула
Пример
Если радиус круга равен 0.5 см, то его диаметр равен 1 см.
Как посчитать диаметр окружности зная её площадь
Чему равен диаметр окружности если
Каков диаметр окружности (d) если её площадь S?
Формула
d = √ 4S /π , где π ≈ 3.14
Пример
Если площадь круга равна 5 см 2 , то его диаметр примерно равен 2.52 см.
Как найти диаметр окружности
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости.
Круг — часть плоскости, лежащая внутри окружности, а также сама окружность.
Если говорить проще, окружность — это замкнутая линия, как, например, обруч и велосипедное колесо. Круг — часть плоскости, ограниченная окружностью, как блинчик или вырезанный из картона кружок.
Диаметр — отрезок, который соединяет две точки окружности и проходит через ее центр.
Радиус — отрезок, который соединяет центр окружности и любую точку на ней.
Как узнать диаметр. Формулы
В данной теме нам предстоит узнать три формулы:
1. Общая формула.
Исходя из основных определений нам известно, что значение диаметра равно двум радиусам: D = 2 × R, где D — диаметр, R — радиус.
2. Если перед нами стоит задача найти диаметр по длине окружности
D = C : π, где C — длина окружности, π — это константа, которая равна отношению длины окружности к диаметру, она всегда равна 3,14.
Чтобы получить правильный ответ, можно поделить столбиком или использовать онлайн-калькулятор.
3. Если есть чертеж окружности
- Начертить внутри круга прямую горизонтальную линию. Ее месторасположение не играет значительной роли.
- Отметить точки пересечения прямой и окружности.
- Начертить при помощи циркуля две окружности одного радиуса (больше, чем радиус первоначальной окружности), первую — с центром в точке A, вторую — с центром в точке B.
- Провести прямую через две точки, в которых произошло пересечение. Отметить точки пересечения полученной прямой с окружностью. Диаметр равен этому отрезку.
- Теперь осталось измерить диаметр круга при помощи линейки. Получилось!
Эти простые формулы могут пригодиться не только на школьных уроках, но и если вы решите освоить профессию дизайнера интерьера, архитектора или модельера одежды.
Как вычислить диаметр окружности?
Для начала, давайте разберемся, что такое окружность и в чем ее отличие от круга. Возьмите ручку или карандаш красного цвета и нарисуйте на листке бумаги обычный круг. Закрасьте всю середину полученной фигуры синим карандашом. Красный контур, обозначающий границы фигуры, – это окружность. А вот синее содержимое внутри нее — и есть круг.
Размеры круга и окружности определяются диаметром. На красной линии, обозначающей окружность, отметьте две точки таким образом, чтобы они оказались зеркальным отражением друг друга. Соедините их линией. Отрезок обязательно пройдет через точку в центре окружности. Этот отрезок, соединяющий противоположные части окружности, и называется в геометрии диаметром.
Отрезок, который тянется не через центр окружности, но смыкается с ней противоположными концами, называется хордой. Следовательно, хорда, пролегающая через точку центра окружности, и является ее диаметром.
Расстояние от центральной точки до точки, отложенной на окружности, называется радиусом и обозначается буквой R. Знание величины радиуса помогает вычислить диаметр окружности одним несложным действием:
К примеру, радиус — 7 см. Умножаем 7 см на 2 и получаем величину, равную 14 см. Ответ: D заданной фигуры равен 14 см.
Иногда приходится определять диаметр окружности лишь по ее длине. Здесь необходимо применить специальную формулу, помогающую определить длину окружности. Формула L = 2 Пи * R, где 2 – это неизменная величина (константа), а Пи = 3,14. А так как известно, что R = D * 2, то формулу можно представить и другим способом
Данное выражение применимо и как формула диаметра окружности. Подставив известные в задаче величины, решаем уравнение с одним неизвестным. Допустим, длина равна 7 м. Следовательно:
Ответ: диаметр равен 21,98 метрам.
Если известно значение площади, то также можно определить диаметр окружности. Формула, которая применяется в данном случае, выглядит так:
D = 2 * (S / Пи) * (1 / 2)
S – в данном случае площадь фигуры. Допустим, в задаче она равна 30 кв. м. Получаем:
D = 2 * (30 / 3, 14) * (1 / 2) D = 9, 55414
При обозначенной в задаче величине, равной объему (V) шара, применяется следующая формула нахождения диаметра: D = (6 V / Пи) * 1 / 3.
Иногда приходится находить диаметр окружности, вписанной в треугольник. Для этого по формуле находим радиус представленной окружности:
R = S / p (S – площадь заданного треугольника, а p – периметр, разделенный на 2).
Полученный результат увеличиваем вдвое, учитывая, что D = 2 * R.
Нередко находить диаметр окружности приходится и в быту. К примеру, при определении размера кольца, что равносильно его диаметру. Для этого необходимо обмотать палец потенциального обладателя кольца ниткой. Отметить точки соприкосновения двух концов. Измерить линейкой длину от точки до точки. Полученное значение умножаем на 3,14, следуя формуле определения диаметра при известной длине. Так что, утверждение о том, что познания в геометрии и алгебре в жизни не пригодятся, не всегда соответствует действительности. А это является серьезным поводом для того, чтобы более ответственно относиться к школьным предметам.
http://skysmart.ru/articles/mathematic/diametr-okruzhnosti
http://fb.ru/article/64066/kak-vyichislit-diametr-okrujnosti
Содержание
- — Что такое диаметр и радиус окружности?
- — Как правильно чертить окружность?
- — Как обозначить радиус и диаметр?
- — Чему равна длина окружности?
Что такое диаметр и радиус окружности?
Круг — часть плоскости, ограниченная окружностью, как апельсин 🍊 и тарелка. Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус — отрезок, который соединяет центр окружности и любую точку на ней.
Как правильно чертить окружность?
Этапы построения:
Разделить стороны квадрата на две равные части, отметить буквами или цифрами. Через полученные точки провести центровую линию (штрихпунктирную) Сначала горизонтальную, затем вертикальную. Пересечение линий отметить точкой О – центр окружности. В точку О поставить ножку циркуля и начертить окружность.
Как обозначить радиус и диаметр?
R — радиус; D — диаметр; S — площадь круга.
Чему равна длина окружности?
Мы получили две важные формулы: С=πD и С=2πR, где С — длина окружности, R -радиус окружности, D — диаметр окружности.
Интересные материалы:
Кто любит кислую почву?
Кто придумал науку о почве?
Можно ли мел добавлять в почву?
Можно ли золой Раскислить почву?
Нужно ли Раскислять почву под огурцы?
Почему Красная почва?
Почему нужно беречь почвы?
Почему образуются различные типы почв?
Почему почва становится щелочной?
Почему Почва в теплице белеет?
Урок: математика (урок дан в рамках тематической проверки 17. 11. 2015) (УМК «Система Л.В.Занкова»)
Тема: «Диаметр окружности. Построение диаметра окружности».
Класс: 3
Тип урока: урок усвоения новых знаний
Форма проведения: урок- практикум
Формы организации учебно-познавательной деятельности: фронтальная, индивидуальная, групповая, в парах.
Оборудование:
- И.И. Аргинская, Е.И.Ивановская. Математика. Учебник для 3 класса: В 2 ч.- Самара: Издательство «Учебная литература»: Издательский дом «Фёдоров», 2012. , тетрадь.
- презентация к уроку, тренажёры, задания для практической работы в группах; тесты для каждого ученика.
- чертёжные инструменты: линейка, циркуль, карандаш;
- ножницы; цветная бумага, клей, конверты с кружками.
- нетбуки, классный компьютер, телевизор, документ камера.
Цель урока: познакомить с определением «диаметр окружности», научить строить на чертеже радиусы и диаметры окружности.
Задачи урока:
Образовательные: повторить понятия «радиус», «круг», «окружность»; познакомить с определением «диаметр окружности»; вывести основное свойство радиусов одной окружности; научиться находить и строить радиусы и диаметры на чертеже, обозначать их буквами.
Развивающие: развивать логическое мышление, математическую речь, умение осуществлять контроль и самоконтроль учебной деятедьности, развитие умений сравнивать и обобщать, расширять математический кругозор.
Воспитательные: воспитывать ответственное отношение к учебному труду, показать значение математических знаний в жизни человека.
Формируемые УУД:
Личностные УУД: развивать познавательную активность в процессе исследовательской деятельности, эмоциональную сферу, речь, умение общаться, работать в группах; уметь проводить самооценку на основе критерия успешности учебной деятельности.
Метапредметные:
Познавательные УУД: уметь ориентироваться в своей системе знаний: отличать новое от уже известного; добывать новые знания; находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке; развивать логическое мышление;
Коммуникативные УУД: уметь оформлять свои мысли в устной форме; слушать и понимать речь других; уметь работать в парах и группах; совместно договариваться о правилах поведения и общения и следовать им; развивать трудолюбие, дисциплинированность, уважение к одноклассникам;
Регулятивные УУД: уметь определять и формулировать цель на уроке с помощью учителя; проговаривать последовательность действий; работать по коллективно составленному плану; оценивать правильность выполнения действия на уровне адекватной оценки; планировать своё действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе оценки и учёта характера сделанных ошибок; высказывать своё мнение.
ХОД УРОКА
|
Этапы урока |
Деятельность учителя |
Деятельность учащихся |
|
1. Мотивация к учебной деятельности |
(Приветствие для учащихся) (Слайды 1-3) Проверь, дружок, Девиз нашего урока: Думать — коллективно! Решать — оперативно! Отвечать — доказательно! Бороться — старательно! И тогда открытия нас ждут обязательно! |
Психологически настраиваются на продуктивную деятельность. Дети читают стихотворение вместе с учителем |
|
2. Актуализация полученных ранее знаний. |
-Наш урок мы начнём с устного счёта. (Слайды 4-9) Ну-ка в сторону карандаши, Ни костяшек, ни ручек, ни мела. Устный счёт! Мы творим это дело Только силой ума и души! 1. Игра «Мотокрос» (круговые примеры) 2. Может ли быть у 2 велосипедов 5 колёс? (Да) 3. Для детского сада купили 4 двухколёсных велосипеда и 5 трёхколёсных велосипедов. Сколько всего колёс у всех велосипедов? (23 колеса) 4. Отгадайте ребус Откройте тетради. Запишите число (Слайд 10) 17 ноября. Классная работа.. — Ребята, посмотрите что изображено на доске? А что такое окружность? Как называется центральная точка? — А что такое радиус окружности? -Как его можно обозначить? -Сколько радиусов у этой окружности? -Постройте в своих тетрадях окружность r=2 см -Постройте на ней цветными карандашами 4 радиуса, обозначьте их буквами. — А сколько ещё радиусов можно провести в данной окружности? -Что можно о них сказать? (Слайд 11) -Как вы догадались? —Радиусы одной окружности равны.Это свойство радиусов одной окружности. |
3 человека работают индивидуально на оценку на нетбуках. А все остальные дети выполняют задания, которые они видят на экране телевизора Ответы детей: Окружность изображена. Окружность –это линия, которая является границей круга. Центр окружности, обозначается латинской буквой О. Радиус- это отрезок, который соединяет центр окружности с любой точкой на окружности. Радиус обозначается латинской буквой r или двумя буквами. -4 радиуса —В одной окружности можно провести большое количество радиусов. -Они равны. -Измерили. |
|
3. Выявление места и причины затруднения |
-Ребята, а отрезок РК –это радиус? (Слайд 12) — Если это не радиус, то как мы назовём отрезок РК? -Попробуйте сами дать опрелеление этому отрезку и попытайтесь построить его на своей окружности. —В чем затруднение? -Почему же возникло затруднение? |
—Нет, это не радиус. Дети рассуждают, предлагают свои варианты ответа на вопрос. Дети пытаются сформулировать определение . Не знаем определение и не можем правильно построить. |
|
4. Постановка целей и задач урока. |
-Какую цель вы поставите перед собой на уроке? Дети читают на слайде: (Слайд 13) — Отрезок РК- это диаметр. Сформулируйте тему нашего урока. Помощники. (Слайд 14) Оля, Лена и Костя дали свои определения понятию «диаметр». Оля: «Диаметр- это отрезок, который соединяет центр окружности с любой точкой окружности». Лена: «Диаметр – это отрезок, соединяющий две точки на окружности и проходящий через её центр». Костя: «Диаметр- это отрезок, который соединяет две любые точки окружности». -С кем из ребят совпадает твоё мнение? -Начертите на вашей окружности диаметр РК. Запишите в тетради: (Слайд 15) РК=d —Ребята, сравните радиус окружности и её диаметр. — Что вы можете сказать? -Как записать? Запишите в своих тетрадях d=r+r d=2r Физминутка для глаз (Слайд 16) -А сейчас проведем физминутку, пусть ваши глаза отдохнут. |
Определяют тему и цели самостоятельно. -Узнать как правильно называется этот отрезок, как правильно его надо строить. «Диаметр окружности. Построение диаметра окружности». Дети рассуждают над каждым высказыванием и приходят к выводу, что права Лена Чертят в тетрадях диаметр и обозначают его буквами РК. Записывают в тетрадях РК=d Диаметр равен двум радиусам. d=r+r d=2r Дети выполняют физкультминутку для глаз. |
|
5. Первичная проверка понимания. |
Ребята, перечислите все радиусы и диаметры на рисунке. (Слайд 17) Практическая работа в парах. (Слайд 18) При пересадке цветов у одного горшка не оказалось поддона. Наша задача узнать подойдёт ли пластиковая тарелочка в качестве поддона для нашего цветка?Радиус дна горшка 7см. Что нам надо сделать? Как мы это будем делать? |
Дети перечисляют Найти радиус или диаметр пластиковой тарелки. Выполняют самостоятельно задание. Измерили диаметр 16 см и разделили на 2. Вывод: тарелочка подойдёт в качестве поддона. |
|
6. Первичное закрепление |
Практическая работа в группах. (Слайд 19) -Ребята, а сейчас вы будете работать в группах. Каждая группа получит инструкцию по выполнению данного задания. Ваша задача распределить обязанности между участниками и четко следовать данной инструкции. А результат вашей работы мы увидим через 10-12 минут. -Оцените работу каждой группы. Физкультминутка (Слайд 20) |
Распределяют обязанности внутри группы, чертят и вырезают круги, а затем производят сборку готового изделия. У них должна получиться мишень для игры в «Дартс». Они вывешивают готовые мишени на доску. Оценивают правильность и аккуратность выполнения работы каждой группы. Выполняют движения под музыку. |
|
7. Контроль усвоения. |
Тест «Проверьте свои знания». (Слайд 21) А1. Как называется отрезок АВ на чертеже? 1) диаметр окружности 2) радиус окружности 3) центр окружности А2. Выберите верное продолжение высказывания. Диаметр окружности – это отрезок, который … 1) соединяет две любые точки окружности 2) соединяет центр окружности с любой точкой окружности 3) соединяет две точки окружности и проходит через центр окружности А3. Может ли окружность иметь два радиуса разной длины? 1) может 2) не может 3) затрудняюсь ответить Взаимопроверка в парах и правильные ответы на экране. Проверим как вы выполнили задание с помощью документкамеры. |
Работают с тестом, отмечают правильные ответы. Осуществляют взаимопроверку в парах. |
|
8. Рефлексия. |
(Слайд 22) -Какую цель на уроке вы перед собой ставили? -Удалось ли достичь цели? -Кто из вас смог сам открыть новое знание? Докажите. -Кто встретил трудности? В чем? Почему? -Теперь я вам предлагаю оценить свою работу на уроке. Перед вами в конвертах лежат кружки (зелёного, желтого и красного цвета) КРАСНЫЙ-Я все понял, но у меня есть еще вопросы. ЖЁЛТЫЙ -Я все понял, могу работать самостоятельно. ЗЕЛЁНЫЙ— Я все понял, могу объяснить другим. |
Ответы детей Учащиеся оценивают себя. |
|
9. Домашнее задание. |
-Что будете делать дома для того, чтобы знания закрепить? (Слайд 23) Откройте дневники, запишите домашнее задание: Спасибо за работу! Удачи в изучении математики! (Слайд 24) |
Выучим определение, что такое диаметр, потренируемся чертить окружность определённого радиуса и диаметра. |
Чтобы вопрос опубликовался, войди или зарегистрируйся
Восстановление пароля
Мы отправили письмо со ссылкой на смену пароля на username@mail.ru.
Если письма нет, проверь папку «Спам».
Чтобы вопрос опубликовался, войди или зарегистрируйся
Нужна регистрация на Учи.ру
«Ваш урок» теперь называется Учи.Ответы. Чтобы зайти на сайт, используй логин и пароль от Учи.ру. Если у тебя их нет, зарегистрируйся на платформе.