Как найти диаметр окружности вписанной в ромб

Какими свойствами обладает вписанная в ромб окружность? Как найти её радиус?

Центр вписанной в ромб окружности — точка пересечения его диагоналей.

Радиус вписанной в ромб окружности можно найти по общей формуле

где S — площадь ромба, p — его полупериметр.

Так как полупериметр ромба равен p=2a, где a — сторона ромба, эту формулу можно записать как

С учётом формул для нахождения площади ромба:

где α — угол ромба (причем α может быть как острым, так и тупым).

где d1и d2 — диагонали ромба.

Таким образом, еще две формулы радиуса вписанной в ромб окружности:

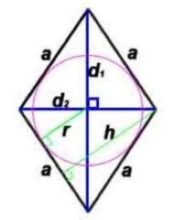
Так как диаметр вписанной окружности равен высоте ромба, радиус равен половине высоты ромба:

Если известно, что точка касания вписанной окружности делит сторону ромба на отрезки, то радиус можно выразить через длины этих отрезков.

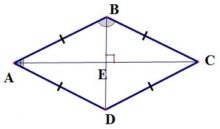
Так как диагонали ромба взаимно перпендикулярны и радиус, проведённый в точку касания, перпендикулярен стороне, то по свойству высоты прямоугольного треугольника из треугольника AOD имеем

Следовательно, радиус вписанной в ромб окружности есть среднее пропорциональное между отрезками, на которые делит сторону точка касания:

Окружность, вписанная в ромб

Вписанная в ромб окружность — это окружность, которая лежит внутри ромба и касается всех его сторон.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

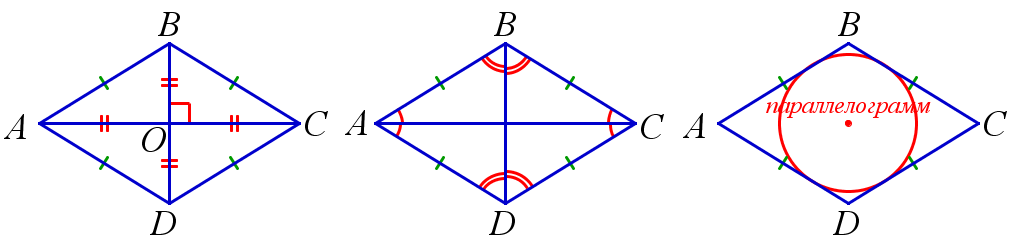
Окружность можно вписать в многоугольник, у которого равны суммы противолежащих сторон. Ромб соответствует этому условию, поэтому в ромб можно вписать окружность.

Свойства ромба и вписанной окружности

• в любой ромб можно вписать окружность;
• точка пересечения диагоналей ромба является центром окружности, вписанной в ромб.

Как найти радиус, основные способы

Радиус вписанной окружности, если известны диагонали и сторона

Радиус r вписанной в ромб окружности равен произведению его диагоналей, деленному на периметр или на сторону, умноженную на 4.

a — сторона ромба,

Р — периметр ромба.

У изображенного ромба АВСD сторона равна а. Большая диагональ BD равна (d_1), меньшая диагональ АС равна (d_2). Радиус вписанной окружности:

(r=frac{d_1d_2}{4a}=frac{BDcdot AC}{4cdot АВ}).

Если известны только диагонали ромба

Эту формулу можно получить из предыдущей.

Диагонали ромба пересекаются под прямым углом, делятся точкой пересечения пополам, и разбивают ромб на четыре прямоугольных треугольника.

Рассмотрим один из таких треугольников — ΔАВО. Сторона ромба АВ является гипотенузой ΔАВО.

Если известны диагонали ромба BD, равная (d_1) и АС, равная (d_2), то катеты ВО и АО ΔАВО будут равны (frac{d_1}2) и (frac{d_2}2) соответственно.

Выразим гипотенузу АВ треугольника АВО через его катеты ВО и АО.

Согласно теореме Пифагора (АВ=sqrt{ВО^2+АО^2}=sqrt{left(frac{d_1}2right)^2+left(frac{d_2}2right)^2}).

Подставив в формулу (r=frac{d_1d_2}p=frac{d_1d_2}{4a}) значение (а=sqrt{left(frac{d_1}2right)^2+left(frac{d_2}2right)^2}) и упростив выражение,

получаем (r=frac{d_1d_2}{2sqrt{left(d_1right)^2+left(d_2right)^2}}).

Если известны сторона и угол

Радиус окружности, вписанной в ромб, равен половине произведения его стороны и синуса любого внутреннего угла ромба.

Если известна высота ромба

Радиус вписанной в ромб окружности равен половине его высоты.

Из этой формулы следует, что высота ромба равна диаметру вписанной в него окружности.

Если известны площадь ромба и его сторона

Вычисление радиуса через отрезки m и n

Вписанная окружность касается стороны ромба. Точка касания делит сторону ромба на два отрезка. Пусть это будут отрезки m и n.

Диагонали ромба взаимно перпендикулярны, ΔАОD — прямоугольный. Высота ΔАОD к стороне АD равна радиусу вписанной в ромб АВСD окружности.

По свойству высоты прямоугольного треугольника, проведенной к гипотенузе, (ОК=sqrt{АКcdot КD}).

Следовательно, радиус вписанной в ромб окружности равен среднему пропорциональному между отрезками, на которые делит сторону ромба точка касания.

Задачи с решениями

Ромб – это параллелограмм, у которого все стороны равны. Следовательно, он наследует все свойства параллелограмма. А именно:

• Диагонали ромба взаимно перпендикулярны.
• Диагонали ромба являются биссектрисами его внутренних углов.

Окружность можно вписать в четырехугольник тогда и только тогда, когда суммы противоположных сторон равны.
Следовательно, в любой ромб можно вписать окружность. Центр вписанной окружности совпадает с центром пересечения диагоналей ромба.
Радиус вписанной окружности в ромб можно выразить несколькими способами

1 способ. Радиуса вписанной окружности в ромб через высоту

Высота ромба равна диаметру вписанной окружности. Это следует из свойства прямоугольника, который образуют диаметр вписанной окружности и высота ромба – у прямоугольника противолежащие стороны равны.

Следовательно формула радиуса вписанной окружности в ромб через высоту:

2 способ. Радиус вписанной окружности в ромб через диагонали

Площадь ромба можно выразить через радиус вписанной окружности
, где Р– периметр ромба. Зная, что периметр это сумма всех сторон четырехугольника имеем P=4×а. Тогда
Но площадь ромба  также равна половине произведения его диагоналей
Прировняв правые части формул площади, имеем следующее равенство
В результате получаем формулу, позволяющую вычислить радиус вписанной окружности в ромб чрез диагонали

3 способ. Радиус вписанной окружности в ромб через отрезки m и n

Точка F – точка касания окружности со стороной ромба, которая делит ее на отрезки AF и BF. Пусть AF=m, BF=n.
Точка O – центр пересечения диагоналей ромба и центр вписанной в него окружности.
Треугольник AOB – прямоугольный, так как диагонали ромба пересекаются под прямым углом.
, т.к. является радиусом, проведенным в точку касания окружности . Следовательно OF – высота треугольника AOB к гипотенузе. Тогда AF и BF – проекции катетов на гипотенузу.
Высота в прямоугольном треугольнике, опущенная на гипотенузу есть среднее пропорциональное между проекциями катетов на гипотенузу.

Формула радиуса вписанной окружности в ромб через отрезки равна корню квадратному из произведения этих отрезков, на которые делит сторону ромба точка касания окружности

Пример расчета радиуса окружности вписанной в ромб, если известны отрезки m и n
Найдите радиус описанной окружности в ромб, если точка касания делит сторону ромба на 9 и 4
Пусть ABCD-ромб, тогда AC и BD его диагонали.
Пусть точка O – это центр вписанной в ромб ABCD окружности.
Пусть точка F – точка касания окружности со стороной ромбаAB. Тогда. AF=9, BF=4
Применив ранее полученную формулу, получаем

Ромб — это параллелограмм, у которого все стороны равны. При этом трапеция обладает всеми свойствами четырехугольника и параллелограмма. Поэтому запоминать надо свойства, которые характерны для ромба.

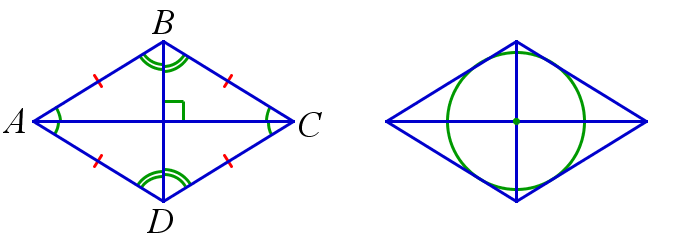
Свойства ромба:

1. Противоположные углы равны. На рисунке: ∠BAC=∠DAC=∠BCA=∠DCA, ∠ABD=∠CBD=∠ADB=∠CDB.
2. Диагонали точкой пересечения делятся пополам. На рисунке: точка E.
3. Диагонали ромба пересекаются под прямым углом. На рисунке: AC⊥BD
4. Диагонали ромба являются биссектрисами его углов.

Признаки ромба:

1. Если диагонали четырёхугольника перпендикулярны и делятся точкой пересечения пополам, то этот четырёхугольник – ромб. На рисунке: AC⊥BD,AO=CO,BO=DO
2. Если диагонали четырёхугольника лежат на биссектрисах его углов, то этот четырёхугольник – ромб. На рисунке: ∠BAC=∠DAC,∠BCA=∠DCA∠ABD=∠CBD,∠ADB=∠CDB.
3. Если четырёхугольник — это параллелограмм и в него можно вписать окружность, то этот четырёхугольник – ромб. На рисунке: AB||CD,BC||AD,ABCD – описанный.

Ромб и окружность

В ромб можно вписать окружность. Центром этой окружности является точка пересечения диагоналей ромба.

Радиус окружности, вписанной в ромб, можно найти по формуле: или где: a — длина стороны, d₁, d₂ –диагонали.

Четырёхугольник можно описать окружностью, если сумма его противолежащих углов равна 180°. Таким образом, ромб, вписанный в окружность – это квадрат. Центр окружности совпадает с точкой пересечения диагоналей.

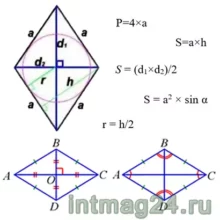
Основные формулы для ромба:

 Периметр: Площадь по стороне и высоте: Площадь по диагоналям: Радиус окружности, вписанной в ромб: или Площадь по стороне и радиусу вписанной окружности:

Площадь по стороне и углу:

где a — длина стороны, d₁, d₂ –диагонали, P-периметр, S-площадь,
h -высота, проведенная к противоположной стороне
α — угол между сторонами ромба.

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, вписанной в ромб. Также разберем примеры решения задач для закрепления изложенного материала.

Формулы вычисления радиуса вписанной в ромб окружности

Через диагонали и сторону

Радиус r вписанной в ромб окружности равняется произведению его диагоналей, деленному на сторону, умноженную на 4.

• d₁ и d₂ – диагонали ромба;
• a – сторона ромба.

Через диагонали

Радиус r вписанной в ромб окружности можно найти, зная только длины его обеих диагоналей:

Эту формулу можно получить, если сторону a в формуле выше выразить через диагонали (согласно одному из свойств ромба):

Через сторону и угол

Радиус окружности r, вписанной в ромб, равняется половине произведения его стороны и синуса любого угла.

Через высоту

Радиус вписанного в ромб круга равняется половине его высоты.

• h (или GF) – высота ромба;
• h = 2r.

Примеры задач

Задание 1
Известно, что диагонали ромба равны 6 и 8 см. Найдите радиус окружности, вписанной в него.

Решение
Применим соответствующую формулу, подставив в нее известные значения:

Задание 2
Вычислите радиус вписанного в ромб круга, если его сторона равна 11 см, а один из углов – 30°.

Решение
В данном случае мы можем воспользоваться последней из рассмотренных выше формул: