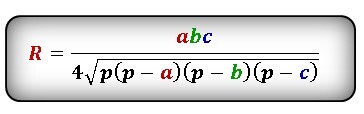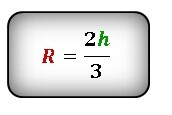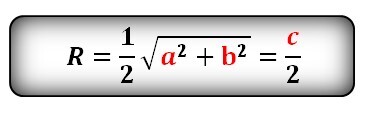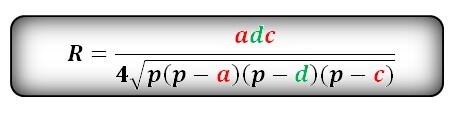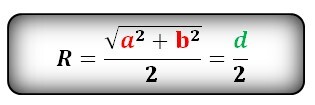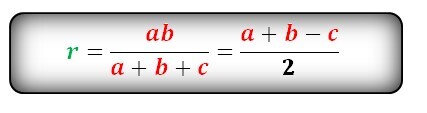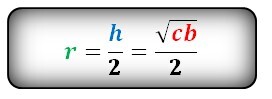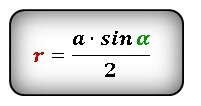|
Боковая сторона равнобедренного треугольника равна 4. Угол при вершине, противолежащий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника. Решить задание можно несколькими способами. Можно исходить из теоремы косинусов, Далее по теореме синусов считаем диаметр. Можно считать и по другой схеме. Не через вычисление основания — с, а через угол при основании. Есть и еще один вариант решения задачи. Ответ: 8см. автор вопроса выбрал этот ответ лучшим Артём1234567897012 3 года назад Диаметр окружности описанной около равнобедренного треугольника находится по формуле: сторона делённая на синус угла противолежащего этой стороне. Берём угол 120 градусов, синус 120 градусов равен синус 60 градусов, и равен корень из 3 делить на 2. По теореме косинусов можем найти противолежащую сторону. Получили что сторона равна корень из 48. Тогда делим корень из 48 на синус угла 120 градусов и получаем 8 см. Знаете ответ? |
Как найти диаметр окружности в равнобедренном треугольнике
Боковая сторона равнобедренного треугольника равна 22, угол при вершине, противолежащей основанию, равен Найдите диаметр описанной окружности этого треугольника.
Это задание ещё не решено, приводим решение прототипа.
Боковая сторона равнобедренного треугольника равна 1, угол при вершине, противолежащей основанию, равен 120°. Найдите диаметр описанной окружности этого треугольника.
Сумма двух равных углов при основании треугольника равна 60°, поэтому каждый из них равен 30°. Тогда по теореме синусов
Радиус описанной окружности равнобедренного треугольника
Радиус описанной окружности равнобедренного треугольника можно найти по одной из общих формул радиуса окружности, описанной около треугольника.
Используя свойства равнобедренного треугольника, можно также получить дополнительные формулы.
I. Радиус описанной около треугольника окружности можно найти по формуле
Площадь равнобедренного треугольника через длину основание a и боковую сторону b можно найти по формуле
соответственно, формула для нахождения радиуса описанной окружности для равнобедренного треугольника принимает вид:
верна и для равнобедренного треугольника.
Радиус описанной около равнобедренного треугольника окружности:
где a — основание, b — боковая сторона, α — угол при вершине, β — угол при основании.
III. Радиус описанной окружности в равнобедренном треугольнике можно найти непосредственно, без использования общих формул.
Например, в прямоугольном треугольнике AOF AO=R, AF=b/2, ∠FAO=α/2. Отсюда
IV. В равнобедренном тупоугольном треугольнике центр описанной окружности лежит вне треугольника, напротив его вершины.
Радиус находят по тем же формулам, что и для остроугольного треугольника.
V. В равнобедренном прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы, радиус равен половине гипотенузы (то есть половине основания треугольника).
Треугольник вписанный в окружность
Определение
Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.
На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.
ВD = FC = AE — диаметры описанной около треугольника окружности.
O — центр вписанной в треугольник окружности.
Формулы
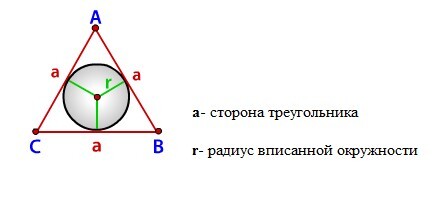
Радиус вписанной окружности в треугольник
r — радиус вписанной окружности.
- Радиус вписанной окружности в треугольник,
если известна площадь и все стороны:
Радиус вписанной окружности в треугольник,
если известны площадь и периметр:
Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:
Радиус описанной окружности около треугольника
R — радиус описанной окружности.
- Радиус описанной окружности около треугольника,
если известна одна из сторон и синус противолежащего стороне угла:
Радиус описанной окружности около треугольника,
если известны все стороны и площадь:
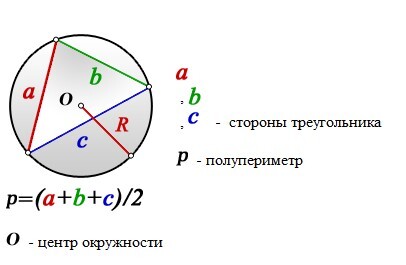
Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:
Площадь треугольника
S — площадь треугольника.
- Площадь треугольника вписанного в окружность,
если известен полупериметр и радиус вписанной окружности:
Площадь треугольника вписанного в окружность,
если известен полупериметр:
Площадь треугольника вписанного в окружность,
если известен высота и основание:
Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:
Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:
[ S = frac<1><2>ab cdot sin angle C ]
Периметр треугольника
P — периметр треугольника.
- Периметр треугольника вписанного в окружность,
если известны все стороны:
Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:
Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:
Сторона треугольника
a — сторона треугольника.
- Сторона треугольника вписанного в окружность,
если известны две стороны и косинус угла между ними:
Сторона треугольника вписанного в
окружность, если известна сторона и два угла:
Средняя линия треугольника
l — средняя линия треугольника.
- Средняя линия треугольника вписанного
в окружность, если известно основание:
Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:
Высота треугольника
h — высота треугольника.
- Высота треугольника вписанного в окружность,
если известна площадь и основание:
Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:
[ h = b cdot sin alpha ]
Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:
Свойства
- Центр вписанной в треугольник окружности
находится на пересечении биссектрис. - В треугольник, вписанный в окружность,
можно вписать окружность, причем только одну. - Для треугольника, вписанного в окружность,
справедлива Теорема Синусов, Теорема Косинусов
и Теорема Пифагора. - Центр описанной около треугольника окружности
находится на пересечении серединных перпендикуляров. - Все вершины треугольника, вписанного
в окружность, лежат на окружности. - Сумма всех углов треугольника — 180 градусов.
- Площадь треугольника вокруг которого описана окружность, и
треугольника, в который вписана окружность, можно найти по
формуле Герона.
Доказательство
Около любого треугольника, можно
описать окружность притом только одну.
окружность и треугольник,
которые изображены на рисунке 2.
окружность описана
около треугольника.
- Проведем серединные
перпендикуляры — HO, FO, EO. - O — точка пересечения серединных
перпендикуляров равноудалена от
всех вершин треугольника. - Центр окружности — точка пересечения
серединных перпендикуляров — около
треугольника описана окружность — O,
от центра окружности к вершинам можно
провести равные отрезки — радиусы — OB, OA, OC.
окружность описана около треугольника,
что и требовалось доказать.
Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.
http://colibrus.ru/treugolnik-vpisannyy-v-okruzhnost/
Как найти диаметр окружности равнобедренного треугольника(см)?
Боковая сторона равнобедренного треугольника равна 4. Угол при вершине, противолежащий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника.
Решить задание можно несколькими способами. Можно исходить из теоремы косинусов,
Далее по теореме синусов считаем диаметр.
Можно считать и по другой схеме. Не через вычисление основания — с, а через угол при основании.
Есть и еще один вариант решения задачи.
Диаметр окружности описанной около равнобедренного треугольника находится по формуле: сторона делённая на синус угла противолежащего этой стороне.
Берём угол 120 градусов, синус 120 градусов равен синус 60 градусов, и равен корень из 3 делить на 2. По теореме косинусов можем найти противолежащую сторону. Получили что сторона равна корень из 48. Тогда делим корень из 48 на синус угла 120 градусов и получаем 8 см.
Теорема синусов
Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.
Нарисуем стандартный треугольник и запишем теорему формулой:
Формула теоремы синусов:
Докажем теорему с помощью формулы площади треугольника через синус его угла.
Из этой формулы мы получаем два соотношения:
На b сокращаем, воспользуемся правилом пропорции и получим:
Из этих двух соотношений получаем:
Теорема синусов для треугольника доказана.
Эта теорема пригодится, чтобы найти:
Стороны треугольника, если даны два угла и одна сторона.
Углы треугольника, если даны две стороны и один прилежащий угол.
Доказательство следствия из теоремы синусов
У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.
,где R — радиус описанной около треугольника окружности.
Так образовались три формулы радиуса описанной окружности:
Основной смысл следствия из теоремы синусов заключен в этой формуле:
Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.
Для доказательства следствия теоремы синусов рассмотрим три случая.
1. Угол ∠А = α — острый в треугольнике АВС.
Проведем диаметр BA1. В этом случае точка А и точка А1 лежат в одной полуплоскости от прямой ВС.
Используем теорему о вписанном угле и видим, что ∠А = ∠А1 = α. Треугольник BA1C — прямоугольный, в нём ∠ BCA1 = 90°, так как он опирается на диаметр BA1.
Чтобы найти катет a в треугольнике BA1C, нужно умножить гипотенузу BA1 на синус противолежащего угла.
BA1 = 2R, где R — радиус окружности
Для остроугольного треугольника с описанной окружностью теорема доказана.
2. Угол ∠А = α — тупой в треугольнике АВС.
Проведем диаметр окружности BA1. Точки А и A1 по разные стороны от прямой ВС. Четырёхугольник ACA1B вписан в окружность, и его основное свойство в том, что сумма противолежащих углов равна 180°.
Следовательно, ∠А1 = 180° — α.
Вспомним свойство вписанного в окружность четырёхугольника:
Также известно, что sin(180° — α) = sinα.
В треугольнике BCA1 угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом:
α = 2R sin (180° — α) = 2R sinα
Для тупоугольного треугольника с описанной окружностью теорема доказана.
Часто используемые тупые углы:
3. Угол ∠А = 90°.
В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности.
Для прямоугольного треугольника с описанной окружностью теорема доказана.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Примеры решения задач
Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал.
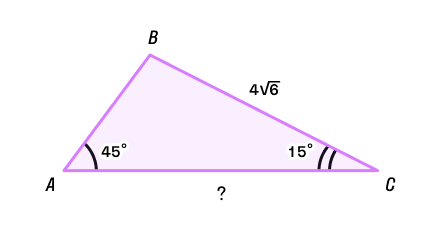
Пример 1. В треугольнике ABC ∠A = 45°,∠C = 15°, BC = 4√6. Найти AC.
Согласно теореме о сумме углов треугольника:
∠B = 180° — 45° — 15° = 120°
Сторону AC найдем по теореме синусов:
Пример 2. Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см соответственно. Найти угол, который расположен напротив данного катета.
Примем неизвестный угол за x. Тогда соотношение сторон выглядит так:
Ответ: угол составляет примерно 53,1°.
Запоминаем
Обычная теорема: стороны треугольника пропорциональны синусам противолежащих углов.
Расширенная теорема: в произвольном треугольнике справедливо следующее соотношение:
Радиус описанной и вписанной окружности: Формулы и примеры
На самом деле эту тему проходят еще в начальных классах обычной школы. И все, кто хорошо учился, сразу смогут сказать, о чем идет речь. Ну, или хотя бы точно понять, что РАДИУС как-то связан с окружностью.
Что такое радиус
И действительно:
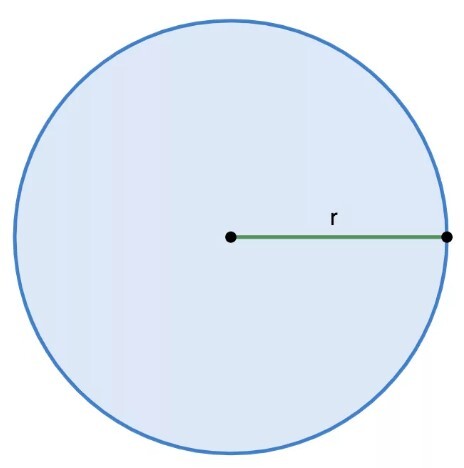
Радиус – это отрезок, который начинается в центре окружности и заканчивается в любой точке ее поверхности. В то же время так называется и длина этого отрезка.
Вот так это выглядит графически.
Само слово РАДИУС имеет латинские корни. Оно произошло от «radius», что можно перевести как «луч» или «спица колеса». Впервые этот математический термин ввел французский ученый П.Ромус. Было это в 1569 году.
Но потребовалось чуть более ста лет, чтобы слово РАДИУС прижилось и стало общепринятым.
Кстати, есть еще несколько значений слова РАДИУС:
- Размер охвата чего-нибудь или сфера распространения. Например, говорят «Огонь уничтожил все в радиусе 10 километров» или «ОН показал на карте радиус действия артиллерии»;
- В анатомии этим словом обозначают Лучевую кость предплечья.
Но, конечно, нас интересует РАДИУС как математический термин. А потому и продолжим говорить именно о нем.
Радиус и диаметр
Радиус в математике всегда обозначается латинской буквой «R» или «r». Принципиальной разницы, большую букву писать или маленькую, нет.
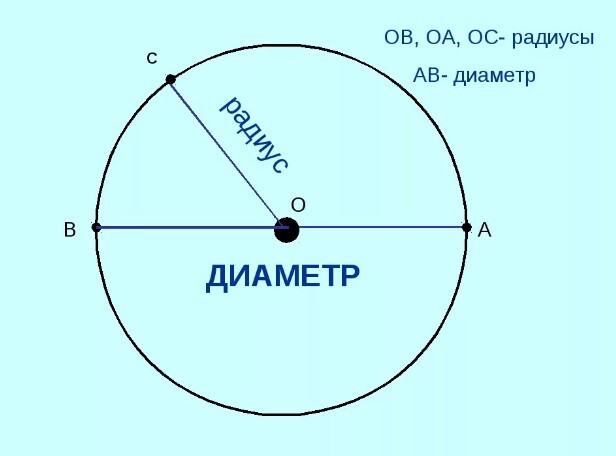
А два соединенных вместе радиуса, которые к тому же находятся на одной прямой, называются диаметром. Или по-другому:
Диаметр – это отрезок, который проходит через центр окружности и соединяет две противоположные точки на ее поверхности. По аналогии с радиусом под диаметром подразумевают и длину этого отрезка.
Обозначается диаметр также первой буквой своего слова – D или d.
Исходя из определения диаметра, можно сделать простой вывод, который одновременно является одной из базовых основ геометрии.
Длина диаметра равна удвоенной длине радиуса.
Примеры задач
Длина окружности равняется 87,92 см. Найдите ее радиус.
Используем первую формулу (через периметр):
Найдите радиус круга, если его площадь составляет 254,34 см 2.
Воспользуемся формулой, выраженной через площадь фигуры:
Формулы для радиуса описанной окружности
Найти радиус описанной окружности треугольника по сторонам
Формула радиуса описанной окружности треугольника (R ) :
Найти радиус описанной окружности равностороннего треугольника по стороне или высоте
Формула радиуса описанной окружности равностороннего треугольника через его сторону:
Формула радиуса описанной окружности равностороннего треугольника через высоту:
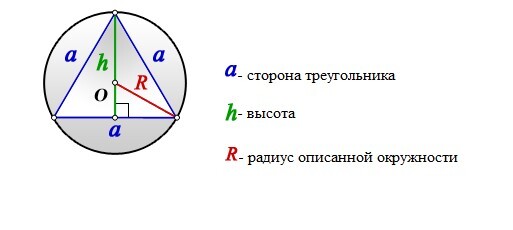
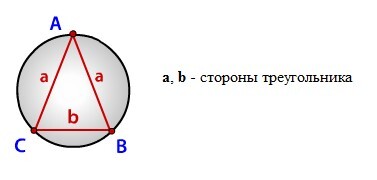
Найти радиус описанной окружности равнобедренного треугольника по сторонам
Зная стороны равнобедренного треугольника, можно по формуле, найти, радиус описанной окружности около этого треугольника.
Формула радиуса описанной окружности равнобедренного треугольника (R):
Найти радиус описанной окружности прямоугольного треугольника по катетам
Радиус описанной окружности прямоугольного треугольника равен половине его гипотенузы.
Формула радиуса описанной окружности прямоугольного треугольника (R):
Радиус описанной окружности трапеции по сторонам и диагонали
Формула радиуса описанной окружности равнобокой трапеции, (R)
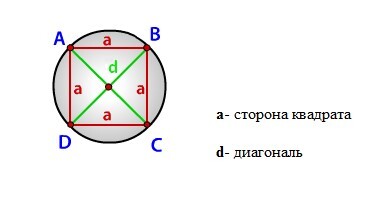
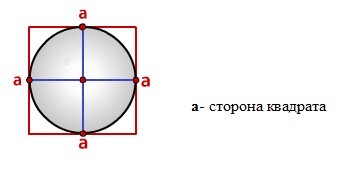
Найти радиус описанной окружности около квадрата
Радиус описанной окружности квадрата равен половине его диагонали
Формула радиуса описанной окружности квадрата (R):
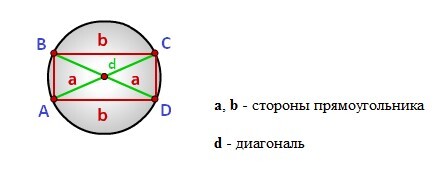
Радиус описанной окружности прямоугольника по сторонам
Радиус описанной окружности прямоугольника равен половине его диагонали
Формула радиуса описанной окружности прямоугольника (R):
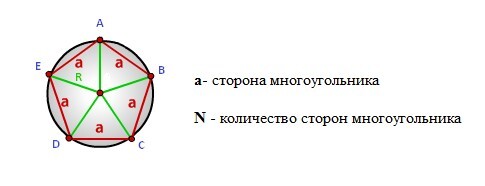
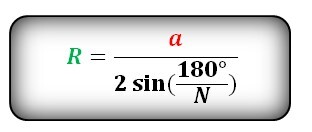
Радиус описанной окружности правильного многоугольника
Формула радиуса описанной окружности правильного многоугольника, (R):
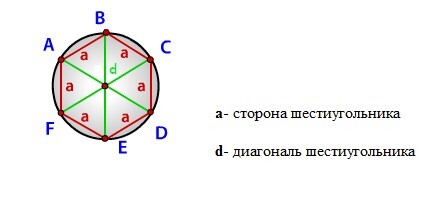
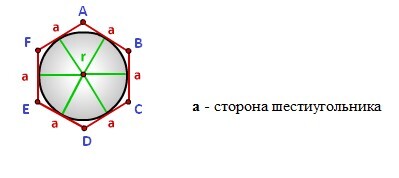
Радиус описанной окружности правильного шестиугольника
Радиус описанной окружности правильного шестиугольника (R):
Формулы для радиуса вписанной окружности
Радиус вписанной окружности в треугольник
Формула радиуса вписанной окружности в треугольник (r):
Радиус вписанной окружности в равносторонний треугольник
Формула для радиуса вписанной окружности в равносторонний треугольник (r):
Радиус вписанной окружности равнобедренный треугольник
1. Формулы радиуса вписанной окружности если известны: стороны и угол
Формула радиуса вписанной окружности в равнобедренный треугольник через стороны (r ) :
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и угол (r ) :
2. Формулы радиуса вписанной окружности если известны: сторона и высота
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и высоту (r ) :
Радиус вписанной окружности в прямоугольный треугольник
Формула радиуса вписанной окружности в прямоугольный треугольник (r):
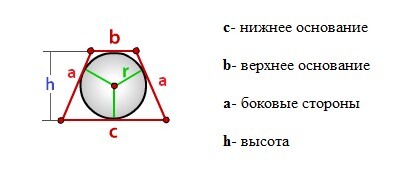
Радиус вписанной окружности в равнобочную трапецию
Формула радиуса вписанной окружности равнобочной трапеции (r):
Радиус вписанной окружности в квадрат
Формула радиуса вписанной окружности в квадрат (r):
Радиус вписанной окружности в ромб
1. Формулы радиуса вписанной окружности если известны: диагональ, стороны и угол
Формула радиуса вписанной окружности в ромб через диагонали (r ) :
Формула радиуса вписанной окружности в ромб через сторону и угол (r ) :
Формула радиуса вписанной окружности в ромб через диагональ и угол (r ) :
Формула радиуса вписанной окружности в ромб через диагональ и сторону (r ) :
2. Радиус вписанной окружности ромба, равен половине его высоты
Формула радиуса вписанной окружности в ромб (r ) :
Радиус вписанной окружности в правильный многоугольник
Формула радиуса вписанной окружности в правильный многоугольник, (r):
Радиус вписанной окружности в шестиугольник
Формула радиуса вписанной окружности в шестиугольник, (r):
Примеры задач
Дан треугольник со сторонами 5, 7 и 10 см. Вычислите радиус вписанной в него окружности.
Сперва вычислим площадь треугольника. Для этого применим формулу Герона:
Остается только применить соответствующую формулу для вычисления радиуса круга:
Боковые стороны равнобедренного треугольника равны 16 см, а основание 7 см. Найдите радиус вписанной в фигуру окружности.
Воспользуемся подходящей формулой, подставив в нее известные значения:
Всем спасибо и приятного просмотра! Если понравилась публикация подписывайтесь и ставьте палец вверх!
Диаметр окружности равен 2R
Формула радиуса описанной около треугольника окружности
R=abc:4 S
c -основание- нам известно, оно равно 12 .
Боковые стороны этого равнобедренного треугольника найдем по теореме Пифагора. Они равны по 3√5
Площадь S треугольника равна произведению высоты на половину основания:
S=6·3=18
Подставим в формулу найденные величины:
R=12·(3√5)²: 4·18=7,5
D=15
Боковая сторона равнобедренного треугольника равна 4. Угол при вершине, противолежащий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника.
Спрятать решение
Решение.
Воспользуемся теоремой косинусов:
(здесь a и b — боковые стороны равнобедренного треугольника, c — основание.
Диаметр описанной окружности найдем по обобщенной теореме синусов:
Ответ: 8.
Примечание.
Вместо того, чтобы искать основание треугольника, можно было найти угол при основании. Действительно, сумма углов при основании данного равнобедренного треугольника равна 60°. Эти углы равны, поэтому каждый из них равен 30°. Применяя обобщенную теорему синусов для боковой стороны и противолежащего ей угла, получаем:
Приведем решение Андрея Ларионова.
Угол при основании равен
Следовательно, дуга описанной окружности, на которую он опирается, равна 2 · 30° = 60°. Эту дугу стягивает боковая сторона треугольника.
Хорда, стягивающая дугу в 60°, равна радиусу окружности, поэтому радиус описанной окружности равен боковой стороне треугольника, тогда D = 2 · 4 = 8.