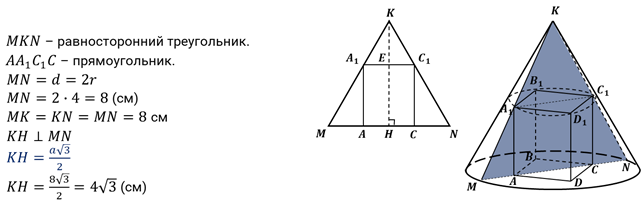
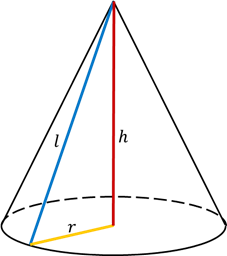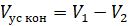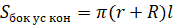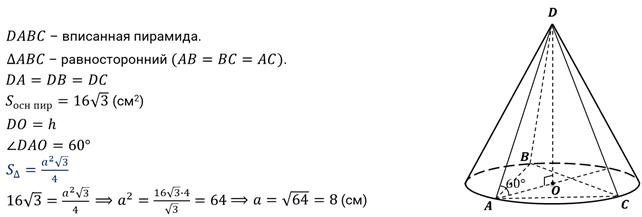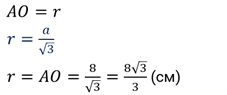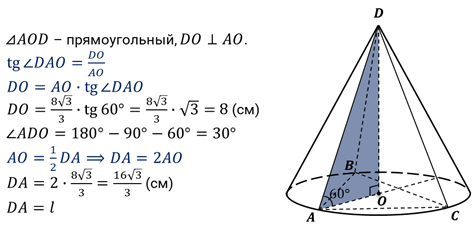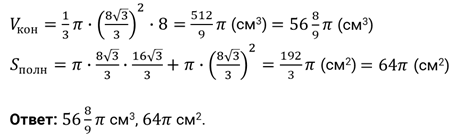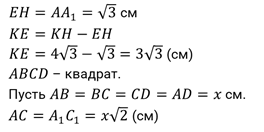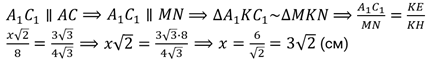Формулы для вычисления диаметра конуса. Пример решения геометрической задачи
Фигура конус является объектом изучения стереометрии. Основными свойствами конуса являются наличие у него объема и площади поверхности, которые можно вычислить с помощью линейных параметров. Одним из них является диаметр конуса. В данной статье покажем, как этот диаметр можно рассчитать по другим известным характеристикам фигуры.
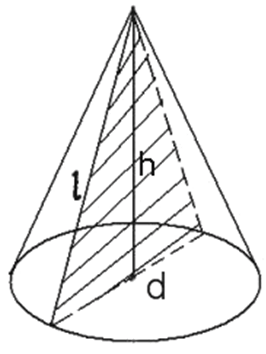
Круглый прямой конус
В общем случае конусом является фигура, построенная в результате движения отрезка вдоль некоторой кривой на плоскости, при этом второй конец отрезка зафиксирован в определенной точке пространства. Сам отрезок называется генератрисой, или образующей, а кривая — директрисой, или направляющей.
Согласно приведенному определению, кривая, которая ограничивает фигуру, может быть совершенно любого типа. Самыми известными из них являются парабола, гипербола, эллипс и окружность. В последнем случае говорят о круглом конусе.
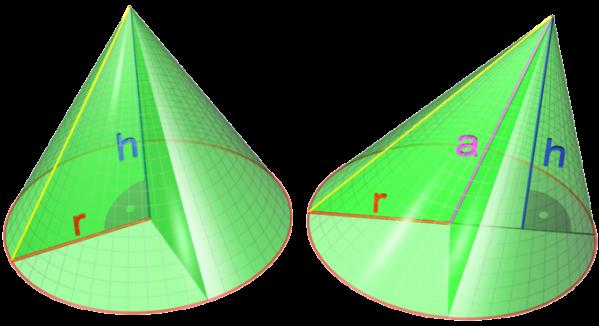
Круглый конус может быть наклонным и прямым. Обе фигуры показаны ниже на рисунке.
Здесь r — радиус окружности, которая ограничивает основание фигуры. Буквой h обозначена высота, которая представляет опущенный на основание из вершины конуса перпендикуляр. Буквой a обозначена ось конуса. Видно, что в случае прямой фигуры его высота совпадает с осью, то есть пересекает окружность в ее центре.
Помимо радиуса r и высоты h, важным линейным параметром конуса является длина его образующей g. Как было сказано, образующая — это отрезок, соединяющий директрису с высотой. Для прямого круглого конуса все образующие равны друг другу.
Далее в статье, раскрывая вопрос касательно того, как найти диаметр конуса, будет рассматриваться только конус круглый и прямой.
Вычисление диаметра фигуры через линейные параметры и угол при основании
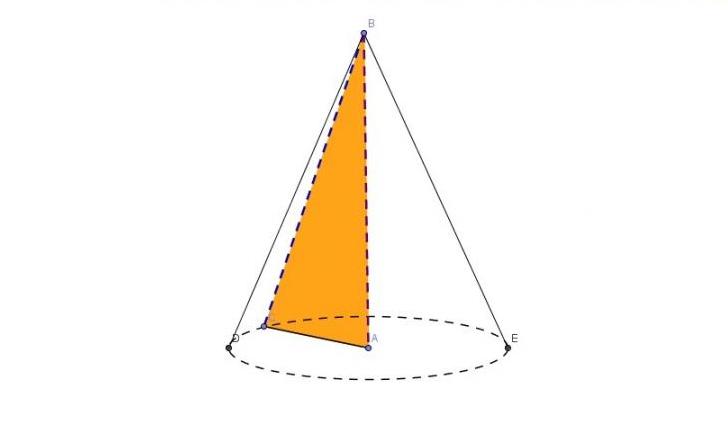
Описанную пространственную фигуру можно получить, если вращать вокруг любого катета прямоугольный треугольник. Этот факт демонстрирует рисунок ниже.
Из рисунка видно, что два катета AC и AB являются радиусом r и высотой h объемной фигуры соответственно. Генератриса g — это гипотенуза BC. Эти соответствия позволяют записать формулу диаметра конуса через известные g и h:
При записи этой формулы использовалась теорема Пифагора, а также определение диаметра, который в два раза больше радиуса основания конуса.
Если известен угол φ между основанием и любой из образующих g фигуры, тогда диаметр конуса можно определить по следующим формулам:
Оба равенства являются следствием применения определения тригонометрических функций тангенса и косинуса.
Вычисление диаметра через площадь поверхности и генератрису
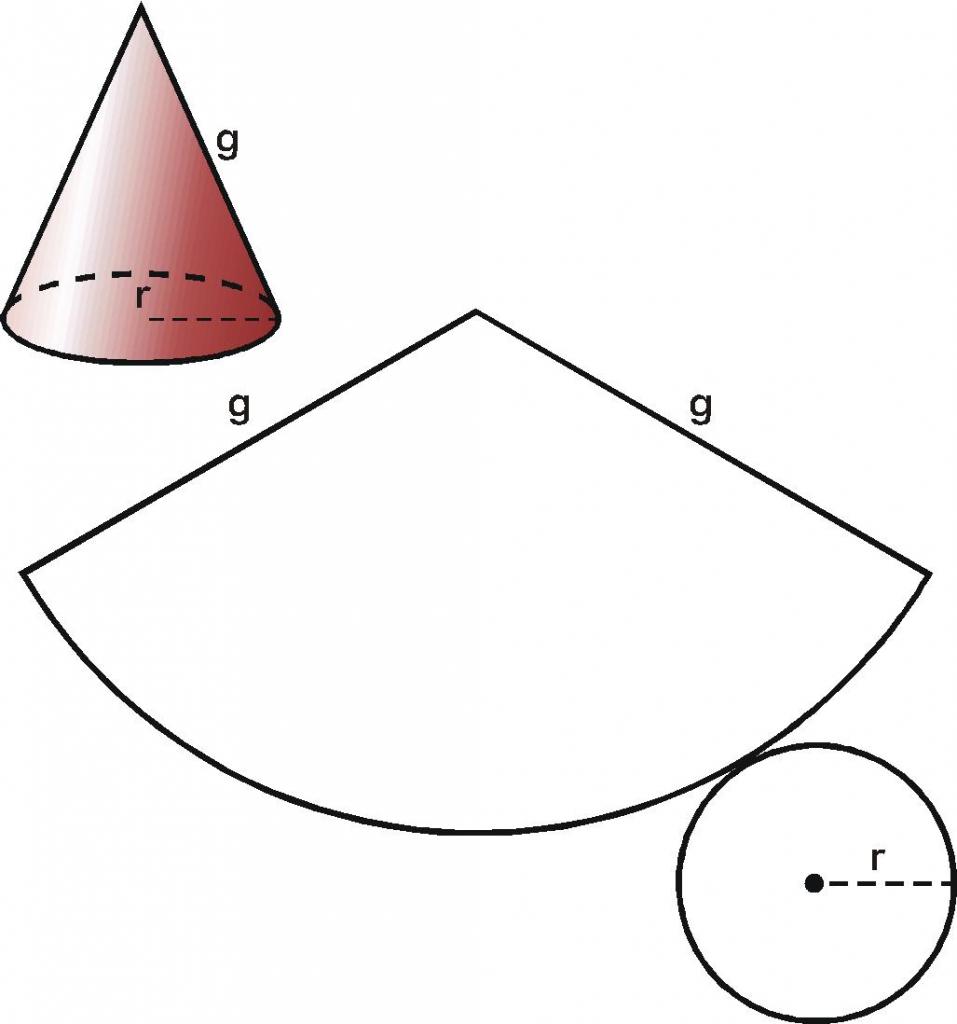
Поверхность рассматриваемого конуса образована конической поверхностью и круглым основанием. Развертка конуса показана ниже.
Общая площадь развертки определяется по следующей формуле:
Если известна площадь S и генератриса g, тогда это уравнение позволяет вычислить радиус фигуры, а значит, и ее диаметр. Заметим, что речь идет об уравнении второго порядка относительно радиуса r. Решать его следует с использованием дискриминанта. При решении, как правило, получаются два корня, один из которых отрицательный. Он должен быть отброшен, ввиду его не физического значения.
С использованием описанной методики в конце статьи будет решена задача, и будет получен ответ на вопрос о том, чему равен диаметр конуса.
Определение диаметра через объем и высоту
Теперь покажем, как найти диаметр конуса, зная его объем V и высоту h. Для этого необходимо вспомнить, что объем конуса, как и объем любой пирамиды, можно определить, пользуясь следующим равенством:
Здесь S — площадь основания. Поскольку площадь основания в рассматриваемом случае является площадью круга, то это выражение можно переписать в таком виде:
Остается выразить отсюда радиус и умножить его в два раза, и мы получим ответ на вопрос о том, как найти диаметр конуса через величины V и h. Имеем:
Заметим, что в правой части получается размерность длины. Это доказывает правильность полученной формулы.
Все записанные в статье формулы для диаметра d фигуры также являются справедливыми для радиуса, который будет в два раза меньше диаметра.
Задача на определение диаметра через известную площадь конуса и его образующую
Дан конус, площадь поверхности которого составляет 150 см 2 . Генератриса равна 14 см. Чему равен диаметр конуса?
Для получения ответа на поставленный вопрос используем описанную в статье методику. Сначала выпишем соответствующее уравнение:
При получении последнего равенства мы разделили левую и правую его части на число Пи. Рассчитываем дискриминант D. Имеем:
Полученный дискриминант приведен с точностью до 0,0001. Формула для корней уравнения r имеет следующий вид:
Очевидно, что один из корней будет отрицательным. Его не будем вычислять. Определим лишь искомый положительный радиус фигуры:
Чтобы найти диаметр конуса, остается умножить это значение на два и записать ответ: d = 5,674 см.
В конце отметим, что, зная два любых параметра круглого конуса прямого, можно определить любую его характеристику, включая объем и площадь поверхности.
Высота конуса равна .
В этой статье рассмотрим задачи на нахождение элементов конуса. Конечно же, их можно отнести к одним из самых простых задач, которые входят в открытый банк заданий ЕГЭ по математике.
Как и многие задачи этой части, решаются они в одно-два действия. Несмотря на то, что это это стереометрическая задача, для решения достаточно знать теорему Пифагора. Рассмотрим задачи:
Высота конуса равна 4, а диаметр основания — 6. Найдите образующую конуса.
Высота конуса равна 4, а длина образующей — 5. Найдите диаметр основания конуса.
Диаметр основания конуса равен 6, а длина образующей — 5. Найдите высоту конуса.
В будущем рассмотрим и другие задачи с конусами, не пропустите. Успехов вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Полный Видеокурс по РУССКОМУ ЯЗЫКУ!
ПРЕМИУМ-КУРС по математике на 100 баллов!
Замучили боль и скованность в мышцах спины?
Александр, позвольте одно БОЛЬШООООЕ , но принципиальное, замечание.
В изображении тел вращения (конус, цилиндр)показывать диаметр следует отрезком, соединяющим две точки окружности и проходящим через центр основания.
То, что изображено на Ваших рисунках, это — хорды. Почему?
Я объясняю своим ученикам так. Наш глаз позволяет видеть поверхность круглого тела чуть больше половины. Значит, если соединить основания двух образующих конуса (или)цилиндра на изображении (плоскостном рисунке), то получится хорда, и она будет отличной от диаметра.
Конечно, лучше это объяснять ученикам с помощью стереометрической модели. Но , надеюсь, Вы мою мысль поняли.
Конус. Площади поверхностей. Объём
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.
Получите невероятные возможности
Конспект урока «Конус. Площади поверхностей. Объём»
Напомним, что конус – это тело, полученное при вращении прямоугольного треугольника вокруг прямой, проходящей через один из его катетов.
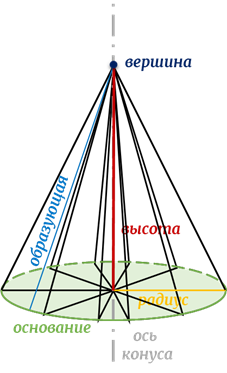
Назовём элементы конуса.
Осью конуса называется прямая вращения.
Основание конуса – круг радиуса 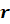
Радиус конуса 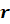
Вершина конуса – неподвижная вершина треугольника вращения.
Образующая конуса 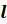
Высота конуса 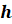
В конусе радиус основания 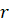
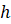
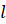
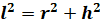
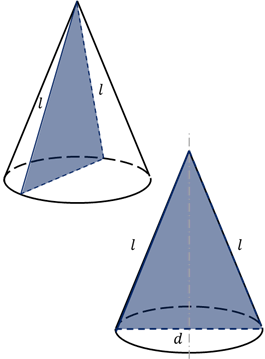
Сечение конуса плоскостью, проходящей через его вершину, представляет собой равнобедренный треугольник, у которого боковые стороны являются образующими конуса.
Осевым сечением конуса называется сечение конуса плоскостью, проходящей через его ось.
Осевое сечение конуса – равнобедренный треугольник, боковые стороны которого – образующие, а основание – диаметр основания конуса.
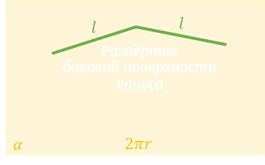
Боковую поверхность конуса, как и боковую поверхность цилиндра, можно развернуть на плоскость, разрезав её по одной из образующих. Развёрткой боковой поверхности конуса является круговой сектор.
Обратите внимание, радиус сектора равен образующей 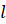
Площадь боковой поверхности конуса можно вычислить по следующим формулам:
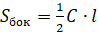
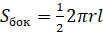
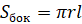
где 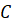
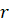
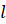
Площадь полной поверхности конуса равна сумме площади боковой поверхности конуса и площади его основания.
Тогда площадь полной поверхности конуса можно вычислить по формуле^
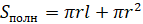
где 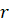
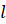
Объём конуса равен одной третьей произведения площади основания на высоту.
Тогда его можно вычислить по формуле:
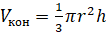
где 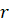
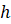
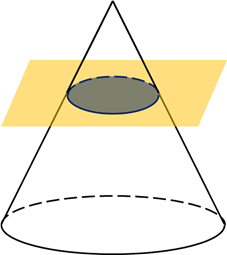
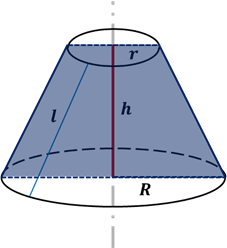
Плоскость, параллельная плоскости основания конуса, пересекает конус по кругу, а боковую поверхность – по окружности с центром на оси конуса. Эта плоскость разбивает конус на две части. Одна из частей (верхняя) представляет собой конус, а вторая (нижняя) называется усечённым конусом.
Усечённым конусом называется часть конуса, ограниченная его основанием и сечением, параллельным плоскости основания. Усечённый конус имеет ось, высоту 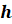
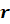
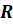
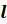
Площадь боковой поверхности усечённого конуса и объём усечённого конуса равен разности площадей боковых поверхностей и объёмов полного конуса и отсечённого.
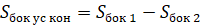
Площадь боковой поверхности усечённого конуса можно найти по следующим формулам:
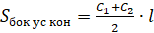
Объём усечённого конуса можно вычислить по следующим формулам:
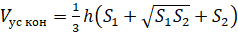
где 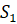
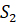
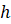
или 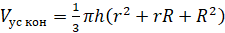
где 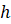
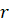
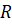
Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.
Задача первая. Радиус основания конуса равен 
Задача вторая. В конус вписана правильная треугольная пирамида с площадью основания 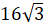
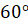
Задача третья. В равносторонний конус с радиусом основания, равным 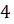
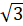
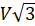
Задача четвёртая. Длины радиусов оснований и образующей усечённого конуса равны соответственно 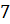
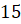
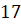
Фигура конус является объектом изучения стереометрии. Основными свойствами конуса являются наличие у него объема и площади поверхности, которые можно вычислить с помощью линейных параметров. Одним из них является диаметр конуса. В данной статье покажем, как этот диаметр можно рассчитать по другим известным характеристикам фигуры.
Круглый прямой конус
В общем случае конусом является фигура, построенная в результате движения отрезка вдоль некоторой кривой на плоскости, при этом второй конец отрезка зафиксирован в определенной точке пространства. Сам отрезок называется генератрисой, или образующей, а кривая — директрисой, или направляющей.
Согласно приведенному определению, кривая, которая ограничивает фигуру, может быть совершенно любого типа. Самыми известными из них являются парабола, гипербола, эллипс и окружность. В последнем случае говорят о круглом конусе.
Круглый конус может быть наклонным и прямым. Обе фигуры показаны ниже на рисунке.
Здесь r — радиус окружности, которая ограничивает основание фигуры. Буквой h обозначена высота, которая представляет опущенный на основание из вершины конуса перпендикуляр. Буквой a обозначена ось конуса. Видно, что в случае прямой фигуры его высота совпадает с осью, то есть пересекает окружность в ее центре.
Помимо радиуса r и высоты h, важным линейным параметром конуса является длина его образующей g. Как было сказано, образующая — это отрезок, соединяющий директрису с высотой. Для прямого круглого конуса все образующие равны друг другу.
Далее в статье, раскрывая вопрос касательно того, как найти диаметр конуса, будет рассматриваться только конус круглый и прямой.
Вычисление диаметра фигуры через линейные параметры и угол при основании
Описанную пространственную фигуру можно получить, если вращать вокруг любого катета прямоугольный треугольник. Этот факт демонстрирует рисунок ниже.
Из рисунка видно, что два катета AC и AB являются радиусом r и высотой h объемной фигуры соответственно. Генератриса g — это гипотенуза BC. Эти соответствия позволяют записать формулу диаметра конуса через известные g и h:
d = 2*√(g2 — h2)
При записи этой формулы использовалась теорема Пифагора, а также определение диаметра, который в два раза больше радиуса основания конуса.
Если известен угол φ между основанием и любой из образующих g фигуры, тогда диаметр конуса можно определить по следующим формулам:
d = 2*g*cos(φ);
d = 2*h/tg(φ)
Оба равенства являются следствием применения определения тригонометрических функций тангенса и косинуса.
Вычисление диаметра через площадь поверхности и генератрису
Поверхность рассматриваемого конуса образована конической поверхностью и круглым основанием. Развертка конуса показана ниже.
Общая площадь развертки определяется по следующей формуле:
S = pi*r2 + pi*r*g
Если известна площадь S и генератриса g, тогда это уравнение позволяет вычислить радиус фигуры, а значит, и ее диаметр. Заметим, что речь идет об уравнении второго порядка относительно радиуса r. Решать его следует с использованием дискриминанта. При решении, как правило, получаются два корня, один из которых отрицательный. Он должен быть отброшен, ввиду его не физического значения.
С использованием описанной методики в конце статьи будет решена задача, и будет получен ответ на вопрос о том, чему равен диаметр конуса.
Определение диаметра через объем и высоту
Теперь покажем, как найти диаметр конуса, зная его объем V и высоту h. Для этого необходимо вспомнить, что объем конуса, как и объем любой пирамиды, можно определить, пользуясь следующим равенством:
V = 1/3*S*h
Здесь S — площадь основания. Поскольку площадь основания в рассматриваемом случае является площадью круга, то это выражение можно переписать в таком виде:
V = 1/3*pi*r2*h
Остается выразить отсюда радиус и умножить его в два раза, и мы получим ответ на вопрос о том, как найти диаметр конуса через величины V и h. Имеем:
r = √(3*V/(pi*h));
d = 2*r = 2*√(3*V/(pi*h))
Заметим, что в правой части получается размерность длины. Это доказывает правильность полученной формулы.
Все записанные в статье формулы для диаметра d фигуры также являются справедливыми для радиуса, который будет в два раза меньше диаметра.
Задача на определение диаметра через известную площадь конуса и его образующую
Дан конус, площадь поверхности которого составляет 150 см2. Генератриса равна 14 см. Чему равен диаметр конуса?
Для получения ответа на поставленный вопрос используем описанную в статье методику. Сначала выпишем соответствующее уравнение:
S = pi*r2 + pi*r*g =>
r2 + 14*r — 150/3,14 = 0
При получении последнего равенства мы разделили левую и правую его части на число Пи. Рассчитываем дискриминант D. Имеем:
D = 142 — 4*1*(-150/3,14) = 387,0828
Полученный дискриминант приведен с точностью до 0,0001. Формула для корней уравнения r имеет следующий вид:
r = (-14±√D)/2
Очевидно, что один из корней будет отрицательным. Его не будем вычислять. Определим лишь искомый положительный радиус фигуры:
r = (-14+√387,0828)/2 = 2,837 см
Чтобы найти диаметр конуса, остается умножить это значение на два и записать ответ: d = 5,674 см.
В конце отметим, что, зная два любых параметра круглого конуса прямого, можно определить любую его характеристику, включая объем и площадь поверхности.
Фигура конус является объектом изучения стереометрии. Основными свойствами конуса являются наличие у него объема и площади поверхности, которые можно вычислить с помощью линейных параметров. Одним из них является диаметр конуса. В данной статье покажем, как этот диаметр можно рассчитать по другим известным характеристикам фигуры.
Круглый прямой конус
В общем случае конусом является фигура, построенная в результате движения отрезка вдоль некоторой кривой на плоскости, при этом второй конец отрезка зафиксирован в определенной точке пространства. Сам отрезок называется генератрисой, или образующей, а кривая — директрисой, или направляющей.
Согласно приведенному определению, кривая, которая ограничивает фигуру, может быть совершенно любого типа. Самыми известными из них являются парабола, гипербола, эллипс и окружность. В последнем случае говорят о круглом конусе.
Круглый конус может быть наклонным и прямым. Обе фигуры показаны ниже на рисунке.
Здесь r — радиус окружности, которая ограничивает основание фигуры. Буквой h обозначена высота, которая представляет опущенный на основание из вершины конуса перпендикуляр. Буквой a обозначена ось конуса. Видно, что в случае прямой фигуры его высота совпадает с осью, то есть пересекает окружность в ее центре.
Каждая объемная фигура, которая имеет конечные линейные размеры, обладает в пространстве некоторой…
Помимо радиуса r и высоты h, важным линейным параметром конуса является длина его образующей g. Как было сказано, образующая — это отрезок, соединяющий директрису с высотой. Для прямого круглого конуса все образующие равны друг другу.
Далее в статье, раскрывая вопрос касательно того, как найти диаметр конуса, будет рассматриваться только конус круглый и прямой.
Вычисление диаметра фигуры через линейные параметры и угол при основании
Описанную пространственную фигуру можно получить, если вращать вокруг любого катета прямоугольный треугольник. Этот факт демонстрирует рисунок ниже.
Из рисунка видно, что два катета AC и AB являются радиусом r и высотой h объемной фигуры соответственно. Генератриса g — это гипотенуза BC. Эти соответствия позволяют записать формулу диаметра конуса через известные g и h:
d = 2*√(g2 — h2)
При записи этой формулы использовалась теорема Пифагора, а также определение диаметра, который в два раза больше радиуса основания конуса.
Если известен угол φ между основанием и любой из образующих g фигуры, тогда диаметр конуса можно определить по следующим формулам:
d = 2*g*cos(φ);
d = 2*h/tg(φ)
Оба равенства являются следствием применения определения тригонометрических функций тангенса и косинуса.
Каждая объемная фигура, которая имеет конечные линейные размеры, обладает в пространстве некоторой…
Вычисление диаметра через площадь поверхности и генератрису
Поверхность рассматриваемого конуса образована конической поверхностью и круглым основанием. Развертка конуса показана ниже.
Общая площадь развертки определяется по следующей формуле:
S = pi*r2 + pi*r*g
Если известна площадь S и генератриса g, тогда это уравнение позволяет вычислить радиус фигуры, а значит, и ее диаметр. Заметим, что речь идет об уравнении второго порядка относительно радиуса r. Решать его следует с использованием дискриминанта. При решении, как правило, получаются два корня, один из которых отрицательный. Он должен быть отброшен, ввиду его не физического значения.
С использованием описанной методики в конце статьи будет решена задача, и будет получен ответ на вопрос о том, чему равен диаметр конуса.
Определение диаметра через объем и высоту
Теперь покажем, как найти диаметр конуса, зная его объем V и высоту h. Для этого необходимо вспомнить, что объем конуса, как и объем любой пирамиды, можно определить, пользуясь следующим равенством:
Все пространственные фигуры, которые изучает специальный раздел геометрии — стереометрия, можно…
V = 1/3*S*h
Здесь S — площадь основания. Поскольку площадь основания в рассматриваемом случае является площадью круга, то это выражение можно переписать в таком виде:
V = 1/3*pi*r2*h
Остается выразить отсюда радиус и умножить его в два раза, и мы получим ответ на вопрос о том, как найти диаметр конуса через величины V и h. Имеем:
r = √(3*V/(pi*h));
d = 2*r = 2*√(3*V/(pi*h))
Заметим, что в правой части получается размерность длины. Это доказывает правильность полученной формулы.
Все записанные в статье формулы для диаметра d фигуры также являются справедливыми для радиуса, который будет в два раза меньше диаметра.
Задача на определение диаметра через известную площадь конуса и его образующую
Дан конус, площадь поверхности которого составляет 150 см2. Генератриса равна 14 см. Чему равен диаметр конуса?
Для получения ответа на поставленный вопрос используем описанную в статье методику. Сначала выпишем соответствующее уравнение:
S = pi*r2 + pi*r*g =>
r2 + 1 r — 150/3,14 = 0
При получении последнего равенства мы разделили левую и правую его части на число Пи. Рассчитываем дискриминант D. Имеем:
D = 142 — 1*(-150/3,14) = 387,0828
Полученный дискриминант приведен с точностью до 0,0001. Формула для корней уравнения r имеет следующий вид:
r = (-14±√D)/2
Очевидно, что один из корней будет отрицательным. Его не будем вычислять. Определим лишь искомый положительный радиус фигуры:
r = (-14+√387,0828)/2 = 2,837 см
Чтобы найти диаметр конуса, остается умножить это значение на два и записать ответ: d = 5,674 см.
В конце отметим, что, зная два любых параметра круглого конуса прямого, можно определить любую его характеристику, включая объем и площадь поверхности.
Найди верный ответ на вопрос ✅ «Как найти диаметр основания конуса*помогите если длинна оброзующей 37 высота конуса = 12 …» по предмету 📙 Алгебра, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Главная » Алгебра » Как найти диаметр основания конуса*помогите если длинна оброзующей 37 высота конуса = 12
Высота конуса равна …
В этой статье рассмотрим задачи на нахождение элементов конуса. Конечно же, их можно отнести к одним из самых простых задач, которые входят в открытый банк заданий ЕГЭ по математике.
Как и многие задачи этой части, решаются они в одно-два действия. Несмотря на то, что это это стереометрическая задача, для решения достаточно знать теорему Пифагора. Рассмотрим задачи:
Высота конуса равна 57, а диаметр основания — 152. Найдите образующую конуса.
Рассмотрим осевое сечение конуса. По теореме Пифагора:
Ответ: 95
Как извлекать корень из большого числа читайте здесь.
Высота конуса равна 21, а длина образующей — 75 . Найдите диаметр основания конуса.
Диаметр основания конуса равен двум радиусам. Радиус мы можем найти по теореме Пифагора из прямоугольного треугольника:
Следовательно, диаметр основания конуса равен 144.
Ответ: 144
Диаметр основания конуса равен 56, а длина образующей — 100 . Найдите высоту конуса.
Рассмотрим осевое сечение конуса. По теореме Пифагора:
Ответ: 96
Высота конуса равна 4, а диаметр основания — 6. Найдите образующую конуса.
Посмотреть решение
Высота конуса равна 4, а длина образующей — 5. Найдите диаметр основания конуса.
Посмотреть решение
Диаметр основания конуса равен 6, а длина образующей — 5. Найдите высоту конуса.
Посмотреть решение
В будущем рассмотрим и другие задачи с конусами, не пропустите. Успехов вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Категория: Стереометрия КОНУС ЦИЛИНДР | ЕГЭ-№2
НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.