Сфера, шар, сегмент и сектор. Формулы и свойства сферы
Формула. Объём шара:
| V = | 4 | π R 3 = | 1 | π D 3 |
| 3 | 6 |
S = 4 π R 2 = π D 2
Уравнение сферы
x 2 + y 2 + z 2 = R 2
( x — x 0) 2 + ( y — y 0) 2 + ( z — z 0) 2 = R 2
Основные свойства сферы и шара
Секущая, хорда, секущая плоскость сферы и их свойства
d m между секущей плоскостью и центром сферы всегда меньше радиуса R:
m r такого круга можно найти по формуле:
где R — радиус сферы (шара), m — расстояние от центра шара до секущей плоскости.
Касательная, касательная плоскость к сфере и их свойства
Формула. Объём сегмента сферы с высотой h через радиус сферы R:
S = π R(2 h + √ 2 h R — h 2 )
Формула. Объём сектора V с высотой O1H (h) через радиус шара OH (R):
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Геометрия. 11 класс
Конспект урока
Геометрия, 11 класс
Урок №8. Сфера и шар
Перечень вопросов, рассматриваемых в теме:
- что такое сфера, какие у неё есть элементы (центр, радиус, диаметр сферы);
- что такое шар и его элементы;
- уравнение сферы;
- формула для нахождения площади поверхности сферы;
- взаимное расположение сферы и плоскости;
- теорема о радиусе сферы, который проведён в точку касания и теорему обратную данной.
Глоссарий по теме:
Окружность – множество точек плоскости, равноудалённых от данной точки. Данная точка называется центром окружности, расстояние от центра до любой точки окружности называется радиусом окружности.
Круг – это часть плоскости, ограниченная окружностью.
Сфера – это поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки, которую называют центром.
Тело, ограниченное сферой, называется шаром.
Шар можно описать и иначе. Шаром радиуса R с центром в точке О называется тело, которое содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем R (включая О), и не содержит других точек.
– уравнение сферы радиуса R и центром С(x0; y0; z0).
Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка – точкой касания.
Сегмент шара — это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегмента h называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента.
Сектором называется часть шара, ограниченная совокупностью всех лучей, исходящих из центра шара О и образующих круг на его поверхности с радиусом r.
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций : базовый и углубл. уровни – М. : Просвещение, 2014. – 255, сс. 136-142.
Шарыгин И.Ф., Геометрия. 10–11 кл. : учеб. для общеобразоват. учреждений– М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 77-84.
Открытые электронные ресурсы:
Теоретический материал для самостоятельного изучения
1. Основные теоретические факты
По аналогии с окружностью сферу рассматривают как множество всех точек равноудалённых от заданной точки, но только всех точек не плоскости, а пространства.
Рисунок 1 – Сфера с центром в точке О и радиусом R
Данная точка О называется центром сферы, а заданное расстояние – радиусом сферы (обозначается R). Любой отрезок, соединяющий центр и какую-нибудь точку сферы, также называется радиусом сферы. Отрезок, соединяющий две точки сферы и проходящий через центр, называется диаметром (обозначается D). D=2R.
Сферой называется поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки, которую называют центром.
Тело, ограниченное сферой, называется шаром.
Шар можно описать и иначе. Шаром радиуса R с центром в точке О называется тело, которое содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем R (включая О), и не содержит других точек.
Сферу можно получить ещё одним способом — вращением полуокружности вокруг её диаметра, а шар – вращением полукруга вокруг его диаметра.
2. Уравнение сферы
Прежде чем вывести уравнение сферы введем понятие уравнения поверхности в пространстве. Для этого рассмотрим прямоугольную систему координат Oxyz и некоторую поверхность F. Уравнение с тремя переменными x, y, z называется уравнением поверхности F, если этому уравнению удовлетворяют координаты любой точки поверхности F и не удовлетворяют координаты никакой другой точки.
Пусть сфера имеет центром точку С (x0; y0; z0) и радиус R. Расстояние от любой точки М (x; y; z) до точки С вычисляется по формуле:
МС=
Исходя из понятия уравнения поверхности, следует, что если точка М лежит на данной сфере, то МС=R, или МС 2 =R 2 , то есть координаты точки М удовлетворяют уравнению:
.
Это выражение называют уравнением сферы радиуса R и центром С(x0; y0; z0).
3. Взаимное расположение сферы и плоскости
Взаимное расположение сферы и плоскости зависит от соотношения между радиусом сферы R и расстояния от центра сферы до плоскости d.
1. Пусть dR. Если расстояние от центра сферы до плоскости меньше радиуса сферы, тогда сфера и плоскость пересекаются, и сечение сферы плоскостью есть окружность.
2. Пусть d=R. Если расстояние от центра сферы до плоскости равно радиусу сферы тогда сфера и плоскость имеют только одну общую точку, и в этом случае говорят, что плоскость касается сферы.
3. Пусть dR. Если расстояние от центра сферы до плоскости больше радиуса сферы, то сфера и плоскость не имеют общих точек.
Рассмотрим случай касания более подробно.
Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка – точкой касания.
Теорема (свойство касательной плоскости).
Радиус сферы, проведённый в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.
Теорема (признак касательной плоскости):
Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащей на сфере, то эта плоскость является касательной к сфере.
4. Основные формулы
Соотношение между радиусом сферы, радиусом сечения и расстоянием от центра сферы до плоскости сечения:
Формула для вычисления площади поверхности сферы и ее элементов:
S=4πR 2 – площадь сферы.
S = 2πRh – площадь поверхности сегмента сферы радиуса R с высотой h.
– площадь поверхности сектора с высотой h.
Примеры и разбор решения заданий тренировочного модуля
1. Площадь сечения шара, проходящего через его центр, равна 9 кв. м. Найдите площадь поверхности шара.
Площадь круга вычисляется по формуле: Sкр=πR 2 .
Площадь поверхности шара вычисляется по формуле: Sсф=4πR 2 . Радиус шара и радиуса сечения, проходящего через центр шара, одинаковые. Поэтому площадь поверхности шара в 4 раза больше площади его диаметрального сечения. То есть площадь поверхности шара равна 36.
2. Вычислите радиус круга, площадь которого равна площади сферы радиуса 5.
Площадь сферы равна Sсф=4πR 2 . То есть Sсф=100π.
По условию площадь круга некоторого радиуса r также равна 100π. Значит, r 2 =100, то есть r=10.
3. Все стороны треугольника АВС касаются сферы радиуса 5. Найти расстояние от центра сферы до плоскости треугольника, если АВ=13, ВС=14, СА=15
Окружность, вписанная в треугольник, является сечением сферы.
Найдем ее радиус.
Площадь треугольника с известными сторонами можно вычислить по формуле Герона:
С другой стороны, S=p·r.
Теперь найдем расстояние от центра шара до секущей плоскости.
4. Вершины прямоугольника лежат на сфере радиуса 10. Найти расстояние от центра сферы до плоскости прямоугольника, если его диагональ равна 16.
Так как вершины прямоугольника лежат на сфере, то окружность, описанная около прямоугольника, является сечением сферы.
Радиус окружности, описанной около прямоугольника, равен половине его диагонали, то есть r=8.
Диаметр шара. Калькулятор и формулы
Чтобы найти диаметр шара при помощи этого калькулятора, достаточно заполнить любую одну ячейку, введя известное значение, и нажать на кнопку расчета. Программа автоматически вычислит все остальные значения, которые отобразятся в ответе вместе с удобными и понятными формулами.
Введите данные:
Достаточно ввести только одно значение, остальное калькулятор посчитает сам.
http://resh.edu.ru/subject/lesson/4034/conspect/
http://calcon.ru/diametr-shara-kalkulyator-i-formuly/
Шар, рассматриваемый в трёхмерном пространстве, представляет собой объёмную геометрическую фигуру.
Любое правильное шаровидное тело состоит из совокупности точек эвклидова (3-хмерного) пространства,
которые находятся на расстоянии от одной из них не далее заданного. Точка, относительно которой
ведётся отсчёт и вокруг которой сосредоточены важные для этого пространственного тела отношения,
получила название центра шара.
Его поверхность, являющаяся своего рода оболочкой, ограничивающей
объём пространственного тела и представляющая совокупность равноудалённых от центра точек, названа
сферой. Расстояние между центром и любой точкой сферы – это радиус шара. Образуется шар, в геометрии
входящий в группу тел вращения, полным оборотом половины плоского круга вокруг своего диаметра,
одновременно выступающего и диаметром шара. Этот отрезок, называемый осью вращения, соединяет
противолежащие точки на поверхности фигуры, называемые полюсами. Одновременно диаметр проходит через
центральную точку шара.
- Диаметр шара через плошадь поверхности шара
- Диаметр шара через обьём шара
Способ вычисления диаметра шара при известном значении объёма фигуры
Диаметр шара, представляющий собой удвоенный радиус фигуры, может быть выведен из стандартной
формулы, связывающей его с площадью поверхности: S = 4πR² или S = πD². Отсюда выводим диаметр:
D = √(S ⁄ π)
где S — площадь поверхности шара
Цифр после
запятой:
Результат в:
Пример. Значение площади поверхности (сферы) конкретного шара S = 314.Тогда,
принимая в качестве константы с точностью до сотых π = 3,14, вычисляем диаметр: D = √(314 ⁄ 3,14) = √100 = 10.
Способ нахождения диаметра шара при заданном значении его объёма
Объём шара связан с радиусом фигуры формулой V = 4 ⁄ 3 * πR³. Радиус представляет собой половину
диаметра шара, то есть R = D ⁄ 2. Подставляя в формулу выраженный через диаметр радиус и выполняя
преобразование для выделения диаметра, получаем следующее выражение: V = 4 ⁄ 3 * π(D ⁄ 2)³, V = 4 ⁄
3* πD³ ⁄ 8, отсюда
D = ³√(6V / π)
где V — объём шара
Цифр после
запятой:
Результат в:
Пример. Для примера примем значение объёма шара равным 11,304. Здесь, беря константу
π с точностью до сотых (π = 3,14), получаем: D = ³√(6 * 11,304 / 3,14)
или, выполняя вычисление D=6.
В природе этот пространственный объект имеет множество реальных аналогов, поэтому его свойства и
параметры важны при решении массы научных задач в биологии, астрономии, физике. Ряд распространённых
инженерных, строительных задач также проводится с использованием геометрических вычислений,
связанных с шарообразными конструкциями. Нахождение диаметра шара – одна из них, и она может быть
выполнена несколькими различными способами. Описание двух вариантов вычислений здесь и
представлено.

Ответ или решение1
Лапина Анастасия
- Дана сфера, площадь поверхности которой равна 625 * π см². Требуется найти диаметр данной сферы, которого обозначим через D. Как известно, площадь поверхности сферы S при известном радиусе R можно найти по формуле S = 4 * π * R².
- Если учесть требование задания, то вместо этой формулы лучше пользоваться другой формулой определения площадь поверхности сферы, а именно, когда площадь поверхности сферы вычисляется через её диаметр. Так как диаметр сферы равен двум радиусам, то R = D / 2. Подставляя это в формулу, приведённую выше, имеем: S = 4 * π * (D / 2)² = 4 * π * D² / 2² = π * D².
- Итак, π * D² = 625 * π см². Поделим обе части этого равенства на π. Тогда, получим D² = 625 см², откуда D = √(625 см²) = 25 см.
Ответ: 25 см.
Диаметр
Диаметр круга или сферы – это хорда или линия, соединяющая две точки окружности, и проходящая через центр круга. Таким образом, диаметр – это два радиуса, расположенных по отношению друг к другу под углом 180° , так чтобы получить прямую линию.
Диаметр круга
Диаметр круга напрямую связан с радиусом и представляет собой его удвоенное значение. Но это не единственный способ вычислить диаметр. Зная площадь круга, можно конвертировать формулу, подставив вместо радиуса половину диаметра, и вывести значение последнего:
Точно также можно найти диаметр круга через длину окружности, разделив ее на 4π :
Диаметр сферы
Диаметр сферы – это точно такой же удвоенный радиус, как и диаметр круга. По сути, диаметр представляет собой ось вращения сферы, поэтому он напрямую связан с ее размерами. Помимо радиуса и диаметра, у сферы есть определенный объем, который она занимает в пространстве. Связь объема с диаметром выражается следующим образом:
Также вычислить диаметр сферы можно через ее площадь. Исходя из формулы площади сферы или шара следует, что его поверхность описывается произведением числа π на квадрат диаметра. Следовательно, диаметр сферы через ее площадь, трансформируя эту формулу, можно получить через извлечение квадратного корня из отношения площади сферы к числу π .
Как вычислить диаметр окружности
wikiHow работает по принципу вики, а это значит, что многие наши статьи написаны несколькими авторами. При создании этой статьи над ее редактированием и улучшением работали, в том числе анонимно, 45 человек(а).
Количество просмотров этой статьи: 1 223 125.
Вычислить диаметр окружности не составит труда, если вы знаете какие-либо другие ее размеры: радиус, длину окружности или площадь ограничиваемого ею круга. Диаметр можно вычислить, даже не зная этих размеров — при наличии начерченной окружности. Если вы хотите узнать, как вычислить диаметр окружности, следуйте указанным ниже шагам.
Как найти радиус и диаметр окружности через площадь круга?
Как найти радиус и диаметр окружности, если известна площадь круга?
Площадь круга вычисляется по формуле S=Пи*R^2, где R — радиус круга, а Пи — трансцендентная величина приблизительно равная 3,14 с недостатком, и равная 3,15 с избытком. Тогда средняя величина Пи=6.29/2=3,145, более точно Пи=3,14159. R=√(S/Пи), диаметр D=2*R=2*√(S/Пи). Например, при S=10 квадратных единиц R=√(10/Пи)=3,183. а D=6,366. .
Площадь круга мы можем вычислить по формуле, которая представлена ниже, где латинской буквой S обозначается площадь, буквой R — радиус, а π — является иррациональным числом равное 3,141592653589793238 46. Для использования в школьных расчётах число π округляется до второго знака после запятой, то есть 3,14
S = πR² или S = 3,14R²
Если в задании нам известна площадь круга то мы можем легко вычислить радиус по формуле:
R = √(S / π) или R = √(S / 3,14)
Чтобы вычислить диаметр круга нужно просто результат (радиус) умножить на 2:
D = 2√(S / π) или D = 2√(S / 3,14)
Для того, чтобы вычислить площадь круга, необходимо знать формулу S=πR², где S — это площадь круга, π — число Пи ( 3,1415926535. его обычно для вычислений округляют до 3,14 ), R — радиус круга.
Из этой формулы можно вывести формулу для вычисления радиуса круга через его площадь: R=√S/π.
Для того, чтобы вычислить радиус круга нужно извлечь корень квадратный ( √ ) из частного : площади круга, поделенной на число Пи.
Рассмотрим конкретный пример вычисления радиуса круга через его площадь:
Площадь круга равна 10 кв.см., найдем радиус круга: R=√10/3,14=1,78 см. Радиус круга, площадь которого равна 10 кв.см., равен 1,78 см.
Радиус круга равен половине его диаметра, то есть D=2R, где D — диаметр круга, а R — его радиус. Если в эту формулу подставить формулу радиуса круга через его площадь, то получим такую формулу для вычисления диаметра круга через его площадь: D=2√S/π.
То есть, для того, чтобы вычислить диаметр круга нужно извлечь корень квадратный ( √ ) из частного: площади круга, поделенной на число Пи, и полученный результат умножить на два.
Если мы вычислим диаметр круга с площадью 10 кв.см. по этой формуле, то получим результат 3,56 см.
Сфера, шар, сегмент и сектор. Формулы и свойства сферы
Определение.
Сфера (поверхность шара) — это совокупность всех точек в трехмерном пространстве, которые находятся на одинаковом расстоянии от одной точки, называемой центром сферы (О).
Сферу можно описать, как объёмную фигуру, которая образуется вращением окружности вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.
Определение.
Шар — это совокупность всех точек в трехмерном пространстве, расстояние от которых не превышает определенного расстояния до точки, называемой центром шара (О) (совокупность всех точек трехмерного пространства ограниченных сферой).
Шар можно описать как объёмную фигуру, которая образуется вращением круга вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.
Определение. Радиус сферы (шара) (R) — это расстояние от центра сферы (шара) O к любой точке сферы (поверхности шара).
Определение. Диаметр сферы (шара) (D) — это отрезок, соединяющий две точки сферы (поверхности шара) и проходящий через ее центр.
Формула. Объём шара:
| V = | 4 | πR3 = | 1 | πD3 |
| 3 | 6 |
Формула. Площадь поверхности сферы через радиус или диаметр:
S = 4πR2 = πD2
Уравнение сферы
1. Уравнение сферы с радиусом R и центром в начале декартовой системе координат:
x2 + y2 + z2 = R2
2. Уравнение сферы с радиусом R и центром в точке с координатами (x0, y0, z0) в декартовой системе координат:
(x — x0)2 + (y — y0)2 + (z — z0)2 = R2
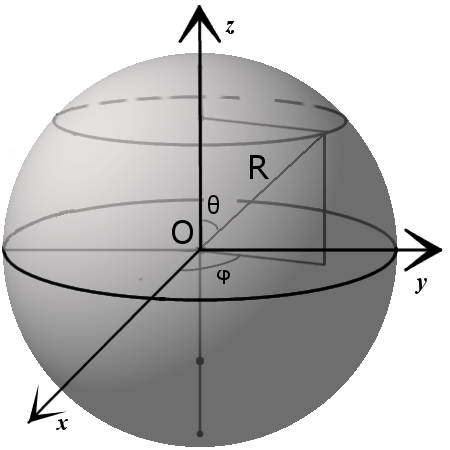
3. Параметрическое уравнение сферы с центром в точке (x0, y0, z0):
x = x0 + R · sin θ · cos φ
y = y0 + R · sin θ · sin φ
z = z0 + R · cos θ
где θ ϵ [0,π], φ ϵ [0,2π].
Определение. Диаметрально противоположными точками называются любые две точки на поверхности шара (сфере), которые соединены диаметром.
Основные свойства сферы и шара
1. Все точки сферы одинаково удалены от центра.
2. Любое сечение сферы плоскостью является окружностью.
3. Любое сечение шара плоскостью есть кругом.
4. Сфера имеет наибольший объём среди всех пространственных фигур с одинаковой площадью поверхности.
5. Через любые две диаметрально противоположные точки можно провести множество больших окружностей для сферы или кругов для шара.
6. Через любые две точки, кроме диаметрально противоположных точек, можно провести только одну большую окружность для сферы или большой круг для шара.
7. Любые два больших круга одного шара пересекаются по прямой, проходящей через центр шара, а окружности пересекаются в двух диаметрально противоположных точках.
8. Если расстояние между центрами любых двух шаров меньше суммы их радиусов и больше модуля разности их радиусов, то такие шары пересекаются, а в плоскости пересечения образуется круг.
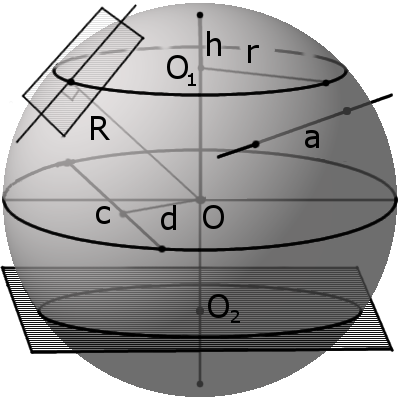
Секущая, хорда, секущая плоскость сферы и их свойства
Определение. Секущая сферы — это прямая, которая пересекает сферу в двух точках. Точки пересечения называются точками протыкания поверхности или точками входа и выхода на поверхности.
Определение. Хорда сферы (шара) — это отрезок, соединяющий две точки сферы (поверхности шара).
Определение. Секущая плоскость — это плоскость, которая пересекает сферу.
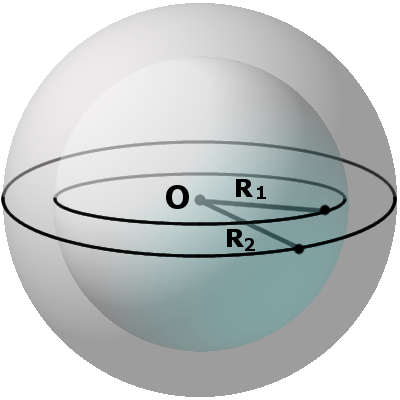
Определение. Диаметральная плоскость — это секущая плоскость, проходящая через центр сферы или шара, сечение образует соответственно большую окружность и большой круг. Большая окружность и большой круг имеют центр, который совпадают с центром сферы (шара).
Любая хорда, проходящая через центр сферы (шара) является диаметром.
Хорда является отрезком секущей прямой.
Расстояние d от центра сферы до секущей всегда меньше чем радиус сферы:
d < R
Расстояние m между секущей плоскостью и центром сферы всегда меньше радиуса R:
m < R
Местом сечения секущей плоскости на сфере всегда будет малая окружность, а на шаре местом сечения будет малый круг. Малая окружность и малый круг имеют свои центры, не совпадающих с центром сферы (шара). Радиус r такого круга можно найти по формуле:
r = √R2 — m2,
где R — радиус сферы (шара), m — расстояние от центра шара до секущей плоскости.
Определение. Полусфера (полушар) — это половина сферы (шара), которая образуется при ее сечении диаметральной плоскостью.
Касательная, касательная плоскость к сфере и их свойства
Определение.Касательная к сфере — это прямая, которая касается сферы только в одной точке.
Определение.Касательная плоскость к сфере — это плоскость, которая соприкасается со сферой только в одной точке.
Касательная пряма (плоскость) всегда перпендикулярна радиусу сферы проведенному к точке соприкосновения
Расстояние от центра сферы до касательной прямой (плоскости) равно радиусу сферы.
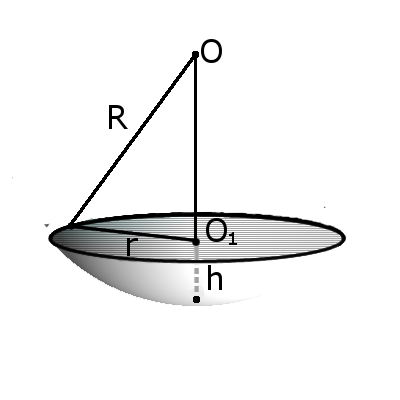
Определение. Сегмент шара — это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегмента h называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента.
Формула. Площадь внешней поверхности сегмента сферы с высотой h через радиус сферы R:
S = 2πRh
Формула. Объём сегмента сферы с высотой h через радиус сферы R:
Определение. Срез шара — это часть шара, которая образуется в результате его сечения двумя параллельными плоскостями и находится между ними.
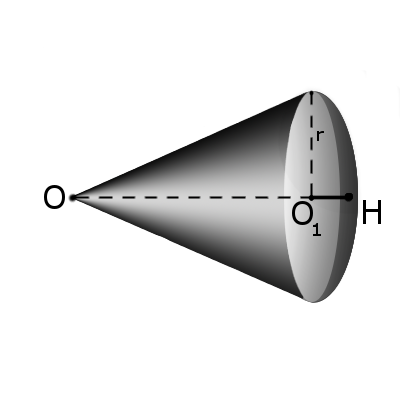
Определение. Сектором называется часть шара, ограниченная совокупностью всех лучей, исходящих из центра шара О и образующих круг на его поверхности с радиусом r.
Формула. Площадь поверхности сектора S с высотой O1H (h) через радиус шара OH (R):
S = πR(2h + √2hR — h2)
Формула. Объём сектора V с высотой O1H (h) через радиус шара OH (R):
Определение. Касательными сферами (шарами) называются любые две сферы (шара), которые имеют одну общую точку соприкосновения. Если расстояние между центрами больше суммы радиусов, то фигуры не касаются и не пересекаются.
Определение. Концентрическими сферами называются любые две сферы, которые имеют общий центр и радиусы различной длины.