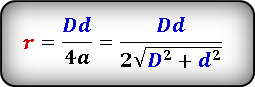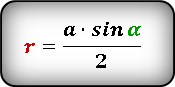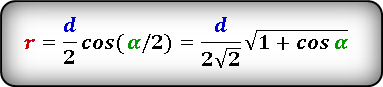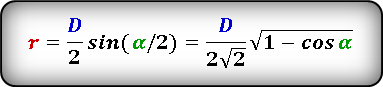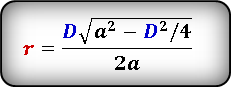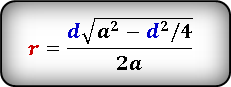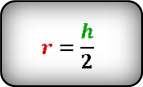Как найти диаметр вписанной окружности прямоугольного треугольника - Исправление недочетов и поиск решений вместе с Examum.ru

Все формулы для радиуса вписанной окружности

Радиус вписанной окружности в треугольник

a , b , c — стороны треугольника

p — полупериметр, p=( a + b + c )/2

Формула радиуса вписанной окружности в треугольник ( r ):

Радиус вписанной окружности в равносторонний треугольник

a — сторона треугольника

r — радиус вписанной окружности

Формула для радиуса вписанной окружности в равносторонний треугольник ( r ):

Радиус вписанной окружности равнобедренный треугольник

1. Формулы радиуса вписанной окружности если известны: стороны и угол

a — равные стороны равнобедренного треугольника

b — сторона ( основание)

α — угол при основании

О — центр вписанной окружности

r — радиус вписанной окружности

Формула радиуса вписанной окружности в равнобедренный треугольник через стороны ( r ) :

Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и угол ( r ) :

2. Формулы радиуса вписанной окружности если известны: сторона и высота

a — равные стороны равнобедренного треугольника

b — сторона ( основание)

h — высота

О — центр вписанной окружности

r — радиус вписанной окружности

Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и высоту ( r ) :

Узнать ещё

Знание — сила. Познавательная информация

Окружность, вписанная в прямоугольный треугольник

Если в задаче дана окружность, вписанная в прямоугольный треугольник, то ее решение может быть связано со свойством отрезков касательных, проведенных из одной точки, и теоремой Пифагора.

Кроме того, следует учесть, что радиус вписанной в прямоугольный треугольник окружности вычисляется по формуле

где a и b — длины катетов, c — гипотенузы.

Рассмотрим две задачи на вписанную в прямоугольный треугольник окружность.

Точка касания окружности, вписанной в прямоугольный треугольник, делит гипотенузу на отрезки 4 см и 6 см. Найти периметр и площадь треугольника и радиус окружности.

Дано: ∆ ABC, ∠C=90º,

окружность (O, r) — вписанная,

K, M, F — точки касания со сторонами AC, AB, BC,

1) По свойству отрезков касательных, проведенных из одной точки,

AK=AM=6 см,

2) AB=AM+BM=6+4=10 см,

3) По теореме Пифагора:

Второй корень не подходит по смыслу задачи. Значит, CK+CF=2 см, AC=8 см, BC=6 см.

Ответ: 24 см, 24 см², 2 см.

Найти площадь прямоугольного треугольника, гипотенуза которого равна 26 см, а радиус вписанной окружности — 4 см.

Дано:∆ ABC, ∠C=90º,

окружность (O, r) — вписанная,

K, M, F — точки касания со сторонами AC, AB, BC,

1) Проведем отрезки OK и OF.

(как радиусы, проведенные в точки касания).

Четырехугольник OKCF — прямоугольник (так как у него все углы — прямые).

А так как OK=OF (как радиусы), то OKCF — квадрат.

2) По свойству касательных, проведенных из одной точки,

3) AC=AK+KC=(x+4) см, BC=BF+CF=26-x+4=(30-x) см.

Окружность, вписанная в треугольник. Основное свойство биссектрисы угла

Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла

Определение 1 . Биссектрисой угла называют луч, делящий угол на две равные части.

Теорема 1 (Основное свойство биссектрисы угла) . Каждая точка биссектрисы угла находится на одном и том же расстоянии от сторон угла (рис.1).

Доказательство . Рассмотрим произвольную точку D , лежащую на биссектрисе угла BAC , и опустим из точки D перпендикуляры DE и DF на стороны угла (рис.1). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны острые углы DAF и DAE , а гипотенуза AD – общая. Следовательно,

что и требовалось доказать.

Теорема 2 (обратная теорема к теореме 1) . Если некоторая точка находится на одном и том же расстоянии от сторон угла, то она лежит на биссектрисе угла (рис.2).

Доказательство . Рассмотрим произвольную точку D , лежащую внутри угла BAC и находящуюся на одном и том же расстоянии от сторон угла. Опустим из точки D перпендикуляры DE и DF на стороны угла (рис.2). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE , а гипотенуза AD – общая. Следовательно,

что и требовалось доказать.

Определение 2 . Окружность называют окружностью, вписанной в угол , если она касается касается сторон этого угла.

Теорема 3 . Если окружность вписана в угол, то расстояния от вершины угла до точек касания окружности со сторонами угла равны.

Доказательство . Пусть точка D – центр окружности, вписанной в угол BAC , а точки E и F – точки касания окружности со сторонами угла (рис.3).

Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE (как радиусы окружности радиусы окружности ), а гипотенуза AD – общая. Следовательно

что и требовалось доказать.

Замечание . Теорему 3 можно сформулировать и по-другому: отрезки касательных касательных , проведенных к окружности из одной точки, равны.

Определение 3 . Биссектрисой треугольника называют отрезок, являющийся частью биссектрисы угла треугольника, и соединяющий вершину треугольника с точкой на противоположной стороне.

Теорема 4 . В любом треугольнике все три биссектрисы пересекаются в одной точке.

Доказательство . Рассмотрим две биссектрисы, проведённые из вершин A и C треугольника ABC , и обозначим точку их пересечения буквой O (рис. 4).

Опустим из точки O перпендикуляры OD , OE и OF на стороны треугольника. Поскольку точка O лежит на биссектрисе угла BAC , то в силу теоремы 1 справедливо равенство:

Поскольку точка O лежит на биссектрисе угла ACB , то в силу теоремы 1 справедливо равенство:

Следовательно, справедливо равенство:

откуда с помощью теоремы 2 заключаем, что точка O лежит на биссектрисе угла ABC . Таким образом, все три биссектрисы треугольника проходят через одну и ту же точку, что и требовалось доказать

Определение 4 . Окружностью, вписанной в треугольник , называют окружность, которая касается всех сторон треугольника (рис.5). В этом случае треугольник называют треугольником, описанным около окружности .

Следствие . В любой треугольник можно вписать окружность, причем только одну. Центром вписанной в треугольник окружности является точка, в которой пересекаются все биссектрисы треугольника.

Формулы для радиуса окружности, вписанной в треугольник

Формулы, позволяющие найти радиус вписанной в треугольник окружности , удобно представить в виде следующей таблицы.

a, b, c – стороны треугольника,
S – площадь,
r – радиус вписанной окружности,
p – полупериметр

a – сторона равностороннего треугольника,
r – радиус вписанной окружности

Фигура	Рисунок	Формула	Обозначения
Произвольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Прямоугольный треугольник

где
a, b, c – стороны треугольника,
S –площадь,
r – радиус вписанной окружности,
p – полупериметр
.

где
a, b, c – стороны треугольника,
r – радиус вписанной окружности,
p – полупериметр
.

где
a – сторона равностороннего треугольника,
r – радиус вписанной окружности

Произвольный треугольник

Равнобедренный треугольник

Равносторонний треугольник

Прямоугольный треугольник

Произвольный треугольник

где
a, b, c – стороны треугольника,
S –площадь,
r – радиус вписанной окружности,
p – полупериметр
.

где
a, b, c – стороны треугольника,
r – радиус вписанной окружности,
p – полупериметр
.

Равнобедренный треугольник

Равносторонний треугольник

где
a – сторона равностороннего треугольника,
r – радиус вписанной окружности

Прямоугольный треугольник

Вывод формул для радиуса окружности, вписанной в треугольник

Теорема 5 . Для произвольного треугольника справедливо равенство

где a, b, c – стороны треугольника, r – радиус вписанной окружности, – полупериметр (рис. 6).

с помощью формулы Герона получаем:

что и требовалось.

Теорема 6 . Для равнобедренного треугольника справедливо равенство

где a – боковая сторона равнобедренного треугольника, b – основание, r – радиус вписанной окружности (рис. 7).

то, в случае равнобедренного треугольника, когда

что и требовалось.

Теорема 7 . Для равностороннего треугольника справедливо равенство

где a – сторона равностороннего треугольника, r – радиус вписанной окружности (рис. 8).

то, в случае равностороннего треугольника, когда

что и требовалось.

Замечание . Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в равносторонний треугольник, непосредственно, т.е. без использования общих формул для радиусов окружностей, вписанных в произвольный треугольник или в равнобедренный треугольник.

Теорема 8 . Для прямоугольного треугольника справедливо равенство

Доказательство . Рассмотрим рисунок 9.

Поскольку четырёхугольник CDOF является прямоугольником прямоугольником , у которого соседние стороны DO и OF равны, то этот прямоугольник – квадрат квадрат . Следовательно,

В силу теоремы 3 справедливы равенства

Следовательно, принимая также во внимание теорему Пифагора, получаем

что и требовалось.

Замечание . Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в прямоугольный треугольник, с помощью общей формулы для радиуса окружности, вписанной в произвольный треугольник.

источники:

Окружность, вписанная в прямоугольный треугольник

http://www.resolventa.ru/uslugi/uslugischoolrost.htm

Источник

ВИДЕОУРОК

Вписанная окружность
прямоугольного треугольника.

Радиус окружности,
вписанной в прямоугольный треугольник,

можно найти по формуле:

где r –
искомый радиус, а и b – катеты,

с – гипотенуза треугольника.

Радиус вписанной в
прямоугольный треугольник окружности

равен произведению катетов, делённому на сумму
катетов и гипотенузы,

где r –
искомый радиус, а и b – катеты,

с – гипотенуза треугольника.

Радиус вписанной в
прямоугольный треугольник окружности равен площади этого треугольника, делённой
на полупериметр:

где р – полупериметр

ЗАДАЧА:

Точка касания окружности, вписанной в прямоугольный треугольник,
делит один из катетов на отрезки 2 см и 8 см,
отсчитывая от вершины прямого угла. Найдите периметр треугольника.

РЕШЕНИЕ:

Начертим чертёж:

ВМ
= ВN = х.

(2 + х)² + (2 + ² = (8
+ х)²,

х² + 4х + 4
+ 100 =

= х² + 16х + 64,

12х = 40,

х =
¹⁰/₃ (см).

Р = (2 + + (8 + ¹⁰/₃) + (¹⁰/₃ + 2) = 26²/₃ (см).

ЗАДАЧА:

Вписанная окружность прямоугольного треугольника АВС касается гипотенузы АВ в точке
К. Найдите радиус
вписанной окружности, если АК = 4 см, ВК
= 6 см.

РЕШЕНИЕ:

За свойством касательных имеем:

АК = АМ = 4 см,
ВК = ВN = 6 см.

Обозначим радиус вписанной окружности
через х:

СN = СM = NО = МО = х.

Тогда

АС =
(4 + х) см.
ВС = (6 + х) см,

АВ =
4 см +
6 см =
10 см.

По теореме Пифагора для треугольника АВС
можно записать соотношение:

(4 + х)² + (6 + х)² = 10².

Решим это квадратное уравнение:

16 + 8x + x²
+ 36 + 12x + x² = 100,

2x² + 20x + 52 – 100 = 0,

2x² + 20x – 48 = 0,

x² + 10x – 24 = 0,

x₁ = 2, x₂ = –10.

x₂не
удовлетворяет условию задачи.

ОТВЕТ: 2 см.

ЗАДАЧА:

Точка касания окружности, вписанной в прямоугольный треугольник,
делить гипотенузу на отрезки 8 см и 12
см. Найдите периметр треугольника.

РЕШЕНИЕ:

Начертим чертёж:

(8 + 12)²
= (8 + х)² + (12 + х)²,

400 = 64 + 16x + x²
+ x² + 24x + 144,

2x² + 40x – 192 = 0,

x² + 20x – 96 = 0,

x₁ = 4, x₂ = –24.

x₂не
подходит.

Р
= 8 + 12 + 12 + 4 + 4 + 8 = 48 (см).

ОТВЕТ: 48 см.

Описанная окружность
прямоугольного треугольника.

Центром окружности, описанной
вокруг прямоугольного треугольника, будет середина его гипотенузы.

Диаметр окружности,
описанной вокруг прямоугольного треугольника, равен его гипотенузе.

Медиана прямоугольного
треугольника, проведённая к его гипотенузе, равна половине гипотенузы и
является радиусом окружности, описанной около этого треугольника.

ОА = ОВ = ОС = R

Радиус описанной окружности равен половине
гипотенузы:

ЗАДАЧА:

Отрезок ВС – диаметр окружности, изображённой на рисунку.

Угол АВС = 55°.

Найдите
величину
угла АСВ
?

РЕШЕНИЕ:

ВС – диаметр,
поэтому ∠ ВАС = 90°,

∠ АСВ = 180° – (90° + 55°) = 35°.

ЗАДАЧА:

Перпендикуляр,
опущенный из точки окружности на его диаметр, делит диаметр на отрезки, разность
между которыми равна 5 см. Найдите радиус окружности, если длина перпендикуляра равна 6 см.

РЕШЕНИЕ:

Пусть АВ – диаметр окружности с
центром в точке О, СD ⊥ АВ,

где С – точка окружности,

СD = 6 см, АD = х см,

ВD – АD = 5 см.

Тогда

DВ = (х + 5) см.

Треугольник АСВ – прямоугольный (угол С прямой, так как
он вписанный и опирается на диаметр).

СD – перпендикуляр, проведений из вершины прямого угла на
гипотенузу. Тогда:

АD ∙ DВ = СD²,

х(х + 5) = 6²,

х²
+ 5х – 36 = 0,

x₁ = –9, x₂ = 4.

x₁не подходит.

Поэтому, АD = 4 см,

DВ = 4 + 5 = 9 (см).

АВ
= АD
+ DВ
=

=
4
+ 9 = 13 (см).

Тогда

r = АВ :
2 = 13 : 2 = 6,5 (см).

ОТВЕТ: 6,5 см

ЗАДАЧА:

Из точки на окружности проведены две перпендикулярные
хорды, разность между которыми равна 4 см. Найдите эти хорды, если радиус окружности равен 10
см.

РЕШЕНИЕ:

Пусть задана окружность радиуса R,

в
которой
проведены
хорды АВ и
АС (АВ ⊥ АС),

R = АО = ВО = СО =
10 см,

АС – АВ =
4
см.

Пусть АВ = х см, тогда

АС = (4
+ х) см.

Так как ∠ А = 90°, то треугольник
ВАС –
прямоугольный,
в
котором

ВС = 2ОВ= 2 ∙ 10 = 20 см.

Из
прямоугольного треугольника ВАС имеем:

АВ² + АС²
= ВС²,

х² + (4 + х)²
= 20²,

х² + 16 + 8х
+ х² = 400,

х² + 4х –
192 = 0,

х₁ = 12,

х₂
= –16 – не подходит.

Поэтому,
АВ = 12 см,

АС
= 4 + 12 = 16 (см).

ОТВЕТ: 12
см, 16 см

ЗАДАЧА:

Угол между биссектрисой и
медианой прямоугольного треугольника, проведёнными из вершины прямого угла,
равен 14°.
Найдите меньший угол этого треугольника.

РЕШЕНИЕ:

Начертим чертёж.

Так как треугольник
прямоугольный и медиана ВМ иcходит
из прямого угла В, то точка М является центром
описанной окружности вокруг треугольника
АВС.
Следовательно,

АМ
= МС = МВ = R,

где R –
радиус описанной окружности.

Найдём сначала угол МВС.
Учитывая, что BD – биссектриса, то

∠ DВС = ⁹⁰/₂ = 45°. Тогда

∠ МВС = ∠ МВD + ∠ DВС,

∠ МВС = 14° + 45° = 59°.

Рассмотрим
равнобедренный треугольник МВС со сторонами

МВ = МС,

в
котором углы при основании ВС равны, то есть

∠ С = ∠ МВС
= 59°.

Так
как сумма острых углов в прямоугольном треугольнике равна 90°, то

∠ А + ∠ С = 90°,

∠ А = 90° – ∠ С =

= 90° – 59° = 31°.

ЗАДАЧА:

Периметр
прямоугольного треугольника равен 72 м, а радиус вписанной в него окружности – 6 м. Найдите диаметр описанной окружности.

РЕШЕНИЕ:

DO = OF = OE = r = 6 м.

Поэтому AD =
AF =
6 м.

FC = EC, BD = BE (отрезки касательных, проведённых из
одной точки)

Пусть

BD = BE = x,

FC = EC = y,

Тогда

AB
= x + 6, AC = y + 6,

BC = x + y.

AB + AC + BC =

= x + 6 + y + 6
+ x + y = 72.

2x + 2y + 12 = 72,

2x + 2y = 60,

x + y = 30.

(x + y) – гипотенуза, или диаметр описанной окружности.

ОТВЕТ: 30 м.

ЗАДАЧА:

В окружности на расстоянии 6
см от его центра проведена хорда длинной 16
см. Найдите радиус окружности.

РЕШЕНИЕ:

Начертим чертёж:

Пользуясь теоремой
Пифагора, находим радиус.

ЗАДАЧА:

Две окружности, радиусы которых равны 4 см и 9 см, имеют внешнее касание. Найдите расстояние между
точками касания данных окружностей с их общей внешней касательной.

РЕШЕНИЕ:

ВК ⊥ АD, АК = 9 – 4 = 5 см.

Из ∆ ВКА:

Источник

$[r = frac{{a + b - c}}{2},]$

где a и b — длины катетов, c — гипотенузы.

Рассмотрим две задачи на вписанную в прямоугольный треугольник окружность.

Задача 1.

Дано: ∆ ABC, ∠C=90º,

окружность (O, r) — вписанная,

K, M, F — точки касания со сторонами AC, AB, BC,

BM=4 см, AM=6 см.

Найти:

$[{P_{Delta ABC,}}{S_{Delta ABC}},r.]$

Решение:

1) По свойству отрезков касательных, проведенных из одной точки,

AK=AM=6 см,

BF=BM=4 см,

CK=CF=x см.

2) AB=AM+BM=6+4=10 см,

AC=AK+CK=(6+x) см,

BC=BF+CF=(4+x) см.

3) По теореме Пифагора:

$[A{C^2} + B{C^2} = A{B^2}]$

$[{(6 + x)^2} + {(4 + x)^2} = {10^2}]$

$[36 + 12x + {x^2} + 16 + 8x + {x^2} = 100]$

$[2{x^2} + 20x - 48 = 0]$

$[{x^2} + 10x - 24 = 0]$

По теореме Виета,

$[{x_1} = 2,{x_2} = - 12.]$

Второй корень не подходит по смыслу задачи. Значит, CK+CF=2 см, AC=8 см, BC=6 см.

$[{P_{Delta ABC}} = AB + AC + BC,]$

$[{P_{Delta ABC}} = 10 + 8 + 6 = 24(cm),]$

$[{S_{Delta ABC}} = frac{1}{2}AC cdot BC,]$

$[{S_{Delta ABC}} = frac{1}{2} cdot 8 cdot 6 = 24(c{m^2}),]$

$[r = frac{{AC + BC - AB}}{2},]$

$[r = frac{{8 + 6 - 10}}{2} = 2(cm).]$

Ответ: 24 см, 24 см², 2 см.

Задача 2.

Дано:∆ ABC, ∠C=90º,

окружность (O, r) — вписанная,

K, M, F — точки касания со сторонами AC, AB, BC,

AB=26 см, r=4 см.

Найти:

$[{S_{Delta ABC}}]$

Решение:

1) Проведем отрезки OK и OF.

(как радиусы, проведенные в точки касания).

Четырехугольник OKCF — прямоугольник (так как у него все углы — прямые).

А так как OK=OF (как радиусы), то OKCF — квадрат.

2) По свойству касательных, проведенных из одной точки,

AM=AK=x см,

BF=BM=(26-x) см,

CF=CK=r=4 см.

3) AC=AK+KC=(x+4) см, BC=BF+CF=26-x+4=(30-x) см.

По теореме Пифагора,

$[A{C^2} + B{C^2} = A{B^2}]$

$[{(x + 4)^2} + {(30 - x)^2} = {26^2}]$

$[{x^2} + 8x + 16 + 900 - 60x + {x^2} = 676]$

$[2{x^2} - 52x + 240 = 0]$

$[{x^2} - 26x + 120 = 0]$

$[{x_1} = 20,{x_2} = 6.]$

Если AM=20 см, то AC=24 см, BC=10 см.

Если AM=6 см, то AC=10 см, BC=24 см.

$[4){S_{Delta ABC}} = frac{1}{2}AC cdot BC,]$

$[{S_{Delta ABC}} = frac{1}{2} cdot 24 cdot 10 = 120(c{m^2}).]$

Ответ: 120 см².

Источник

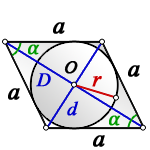
1. Формулы радиуса вписанной окружности если известны: диагональ, стороны и угол

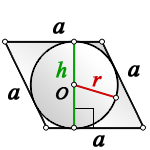
a — сторона ромба

D — большая диагональ

d — меньшая диагональ

α — острый угол

О — центр вписанной окружности

r — радиус вписанной окружности

Формула радиуса вписанной окружности в ромб через диагонали ( r ) :

Формула радиуса вписанной окружности в ромб через сторону и угол ( r ) :

Формула радиуса вписанной окружности в ромб через диагональ и угол ( r ) :

Формула радиуса вписанной окружности в ромб через диагональ и сторону ( r ) :

2. Радиус вписанной окружности ромба, равен половине его высоты

a — сторона ромба

h — высота

О — центр вписанной окружности

r — радиус вписанной окружности

Формула радиуса вписанной окружности в ромб ( r ) :

Источник

Тема: Окружность (Вписанная и описанная окружности)
Условие задачи полностью выглядит так:

694 Найдите диаметр окружности, вписанной в прямоугольный треугольник, если гипотенуза треугольника равна с, а сумма катетов равна m.

Задача из главы Окружность по предмету Геометрия из задачника Геометрия. 7-9 класс, Атанасян, Бутузов, Кадомцев, Позняк, Юдина (8 класс)

Если к данной задачи нет решения — не переживайте. Наши администраторы стараются дополнять сайт решениями для тех задач
и упражнения где это требуется и которые не даны в решебниках и сборниках с ГДЗ. Попробуйте зайти позже. Вероятно, вы найдете то, что искали

Рады приветствовать учеников всех учебных заведений всех возрастов на нашем сайте!
Здесь вы найдете решебники и решения задач бесплатно, без регистрации.

Источник