Как найти диапазон вещественных чисел

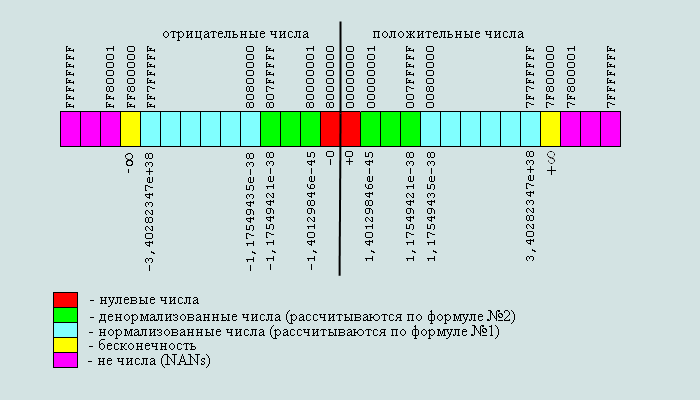
Вещественные числа обычно представляются в виде чисел с плавающей запятой. Числа с плавающей запятой — один из возможных способов представления действительных чисел, который является компромиссом между точностью и диапазоном принимаемых значений, его можно считать аналогом экспоненциальной записи чисел, но только в памяти компьютера.

Число с плавающей запятой состоит из набора отдельных двоичных разрядов, условно разделенных на так называемые знак (англ. sign), порядок (англ. exponent) и мантиссу (англ. mantis). В наиболее распространённом формате (стандарт IEEE 754) число с плавающей запятой представляется в виде набора битов, часть из которых кодирует собой мантиссу числа, другая часть — показатель степени, и ещё один бит используется для указания знака числа ( — если число положительное, — если число отрицательное). При этом порядок записывается как целое число в коде со сдвигом, а мантисса — в нормализованном виде, своей дробной частью в двоичной системе счисления. Вот пример такого числа из двоичных разрядов:

Знак
	Порядок	Мантисса
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	14	10	9	0

Знак — один бит, указывающий знак всего числа с плавающей точкой. Порядок и мантисса — целые числа, которые вместе со знаком дают представление числа с плавающей запятой в следующем виде:

, где — знак, — основание, — порядок, а — мантисса.
Десятичное число, записываемое как , где — число в полуинтервале , — степень, в которой стоит множитель ; в нормализированной форме модуль будет являться мантиссой, а — порядком, а будет равно тогда и только тогда, когда принимает отрицательное значение.
Например, в числе

Порядок также иногда называют экспонентой или просто показателем степени.

При этом лишь некоторые из вещественных чисел могут быть представлены в памяти компьютера точным значением, в то время как остальные числа представляются приближёнными значениями.

Более простым вариантом представления вещественных чисел является вариант с фиксированной точкой, когда целая и вещественная части хранятся отдельно. Например, на целую часть отводится всегда бит и на дробную отводится всегда бит. Такой способ в архитектурах процессоров не присутствует. Отдаётся предпочтение числам с плавающей запятой, как компромиссу между диапазоном допустимых значений и точностью.

Нормальная и нормализованная форма

Нормальной формой (англ. normal form) числа с плавающей запятой называется такая форма, в которой мантисса (без учёта знака) в десятичной системе находится на полуинтервале . Такая форма записи имеет недостаток: некоторые числа записываются неоднозначно (например, можно записать в 4 формах — , , , ), поэтому распространена также другая форма записи — нормализованная (англ. normalized), в которой мантисса десятичного числа принимает значения от (включительно) до (не включительно), а мантисса двоичного числа принимает значения от (включительно) до (не включительно). То есть в мантиссе слева от запятой до применения порядка находится ровно один знак. В такой форме любое число (кроме ) записывается единственным образом. Ноль же представить таким образом невозможно, поэтому стандарт предусматривает специальную последовательность битов для задания числа (а заодно и некоторых других полезных чисел, таких как и ).
Так как старший двоичный разряд (целая часть) мантиссы вещественного числа в нормализованном виде всегда равен «», то его можно не записывать, сэкономив таким образом один бит, что и используется в стандарте IEEE 754. В позиционных системах счисления с основанием большим, чем (в троичной, четверичной и др.), этого замечательного свойства нет (ведь целая часть там может быть не только единицей).

Типы чисел с плавающей точкой (по IEEE 754)

Число половинной точности (Binary16, Half precision)

Число́ полови́нной то́чности  — компьютерный формат представления чисел, занимающий в памяти половину машинного слова (в случае 32-битного компьютера — бит или байта). В силу невысокой точности этот формат представления чисел с плавающей запятой обычно используется в видеокартах, где небольшой размер и высокая скорость работы важнее точности вычислений.

Знак
	Порядок	Мантисса
0	0	0	0	0	0	1,	0	0	0	0	0	0	0	0	0	0
	14	10		9	0

Порядок записан со сдвигом . То есть чтобы получить актуально значение порядка нужно вычесть из него сдвиг. Сдвиг можно получить по формуле , где — число бит, отведенное на хранение порядка (в случае числа половинной точности ).

Ограничения точности

• Целые от нуля до передаются как есть.
• Целые от до округляются к ближайшему чётному целому.
• Целые от до округляются до ближайшего целого, делящегося нацело на четыре.
• Целые от до округляются до ближайшего целого, делящегося на восемь.
• Целые от до округляются до ближайшего целого, делящегося на шестнадцать.
• Целые от до округляются до ближайшего целого, делящегося на тридцать два.

Число одинарной точности (Binary32, Single precision, float)

Число́ одина́рной то́чности — компьютерный формат представления чисел, занимающий в памяти одно машинное слово (в случае 32-битного компьютера — бита или байта). Используется для работы с вещественными числами везде, где не нужна очень высокая точность.

Знак
	Порядок (8 бит)	Мантисса (23+1 бита)
0	0	0	0	0	0	0	0	0	1,	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	30	23		22	0

Порядок записан со сдвигом .

Число двойной точности (Binary64, Double precision, double)

Число́ двойно́й то́чности —
компьютерный формат представления чисел, занимающий в памяти два машинных слова (в случае 32-битного компьютера — бита или байт). Часто используется благодаря своей неплохой точности, даже несмотря на двойной расход памяти и сетевого трафика относительно чисел одинарной точности.

Знак
	Порядок (11 бит)	Мантисса (52+1 бит)
0	0	0	0	0	0	0	0	0	0	0	0	1,	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	62	52		51	0

Порядок записан со сдвигом .

Число четверной точности (Binary128, Quadruple precision)

Число́ четверно́й то́чности —
компьютерный формат представления чисел, занимающий в памяти четыре машинных слова (в случае 32-битного компьютера — бит или байт). Используется в случае необходимости крайне высокой точности.

Знак
	Порядок (15 бит)	Мантисса (112+1 бит)
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1,	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	126	112		111

Мантисса (112+1 бит)
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
0

Порядок записан со сдвигом .

Обычно этот формат реализуется программно, случаи аппаратной реализации крайне редки. Также не гарантируется поддержка этого типа в языках программирования, хотя кое-где она и реализована (например, компилятор gcc для архитектуры x86 позволяет использовать тип __float128, являющийся программной реализацией числа с четверной точностью).
В совокупности эти факторы делают Quadruple весьма экзотичным и редко встречающимся форматом чисел с плавающей запятой.

Диапазон значений чисел с плавающей запятой

Диапазон чисел, которые можно записать данным способом, зависит от количества бит, отведённых для представления мантиссы и показателя. Пара значений показателя (когда все разряды нули и когда все разряды единицы) зарезервирована для обеспечения возможности представления специальных чисел. К ним относятся ноль, значения NaN (Not a Number, «не число», получается как результат операций типа деления нуля на ноль) и .

Данная таблица только лишь примерно указывает границы допустимых значений, без учета возрастающей погрешности с ростом абсолютного значения и существования денормализованных чисел.

Название в IEEE 754	Название типа переменной в Си	Диапазон значений	Бит в мантиссе	Бит на переменную
Half precision	—	6,10×10-5..65504	11	16
Single presicion	float	-3,4×1038..3,4×1038	23	32
Double precision	double	-1,7×10308..1,7×10308	53	64
Extended precision	На некоторых архитектурах (например в сопроцессоре Intel) long double	-3,4×104932..3,4×104932	65	80

Особые значения чисел с плавающей точкой

Ноль (со знаком)

Как уже было оговорено выше, в нормализованной форме числа с плавающей точкой невозможно представить ноль. Поэтому для его представления зарезервированы специальные значения мантиссы и порядка — число считается нулём, если все его биты, кроме знакового, равны нулю. При этом в зависимости от значения бита знака ноль может быть как положительным, так и отрицательным.

Знак
	Порядок	Мантисса
0/1	0	0	0	0	0	1,	0	0	0	0	0	0	0	0	0	0	=
	14	10		9	0

Арифметика нуля со знаком

Арифметика отрицательного нуля аналогична таковой для любого отрицательного числа и понятна интуитивно. Вот несколько примеров:

• (если )

• (если )

Неопределенность (NaN)

NaN — это аббревиатура от фразы «not a number«. NaN является результатом арифметических операций, если во время их выполнения произошла ошибка (примеры см. ниже). В IEEE 754 NaN представлен как число, в котором все двоичные разряды порядка — единицы, а мантисса не нулевая.

Знак
	Порядок	Мантисса
0/1	1	1	1	1	1	1,	0/1	0/1	0/1	0/1	0/1	0/1	0/1	0/1	0/1	0/1	=
	14	10		9	0

Любая операция с NaN возвращает NaN. При желании в мантиссу можно записывать информацию, которую программа сможет интерпретировать. Стандартом это не оговорено и мантисса чаще всего игнорируется.

Как можно получить NaN?

• , где

Есть и другие способы получения NaN, подробности можно найти по ссылкам в соответствующем разделе.

По определению NaN ≠ NaN, поэтому, для проверки значения переменной нужно просто сравнить ее с собой.

Бесконечности

В число с плавающей запятой можно записать значение или . Как и нули со знаком, бесконечности позволяют получить хотя бы близкий к правильному результат вычисления в случае переполнения. Согласно стандарту IEEE 754 число с плавающей запятой считается равным бесконечности, если все двоичные разряды его порядка — единицы, а мантисса равна нулю. Знак бесконечности определяется знаковым битом числа.

Знак
	Порядок	Мантисса
0/1	1	1	1	1	1	1,	0	0	0	0	0	0	0	0	0	0	=
	14	10		9	0

Получить бесконечность можно при переполнении и при делении ненулевого числа на ноль. При этом

Денормализованные числа

Денормализованные числа (англ. denormalized/subnormal numbers) — это способ увеличить количество представимых числом с плавающей запятой значений около нуля, дабы повысить точность вычислений. Каждое значение денормализованного числа меньше самого маленького нормализованного («обычного») значения числа с плавающей запятой.
Согласно стандарту, если порядок равен своему минимальному значению (все его биты — нули, а истинное значение порядка равно его сдвигу) и все биты мантиссы равны нулю, то это . Если же мантисса не равна нулю, то это число с порядком, на единицу большим минимального (все биты порядка, кроме младшего — нули) и данной мантиссой, целая часть которой считается равной нулю, а не единице.

То есть число с плавающей запятой, при учете вышесказанного, можно задать следующим образом:

• , если (нормализованное число)

• , если (денормализованное число)

Где — бит знака, — последовательность битов мантиссы, — значение порядка (с учетом сдвига), — минимальное значение порядка, используемое для записи чисел (1 — сдвиг) , — минимальное значение порядка, которое он в принципе может принять (все биты нули, 0 — сдвиг).

Хоть денормализованные числа и позволяют бороться с погрешностями и обрабатывать очень маленькие значения, за эти возможности приходится дорого платить. Ввиду сложности денормализованные числа крайне редко реализуют на аппаратном уровне — вместо этого используются программные реализации, работающие значительно медленнее.

В современных процессорах обработка денормализованных чисел происходит в десятки раз медленнее, чем обработка нормализованных чисел. Ниже приведена часть таблицы из статьи Isaac Dooley, Laxmikant Kale «Quantifying the Interference Caused by Subnormal Floating-Point Values»^[1]

Производитель	Процессор	Замедление (разы)
IBM	PowerPC 970	2,4
AMD	Athlon	6,0
Intel	Pentium 3	15,8
AMD	Athlon 64	21,4
AMD	Opteron64	23,8
Intel	Core Duo	44,2
Intel	P4 Xeon	97,9
Intel	Pentium 4	131,0
Intel	Itanium 2	183,2
Sun	UltraSPARC IV	520,0

В таблице приведены наихудшие результаты тестирования среди всех использованных компиляторов (gcc, icc, xlc) со всеми доступными флагами оптимизации. Исследователи утверждают, что различие среднего случая с худшим незначительно.

Поскольку в стандартных форматах (одинарной и двойной точности) денормализованные числа получаются действительно очень маленькими и практически никак не влияют на результат некоторых вычислений (при этом заметно замедляя их скорость), то иногда они просто игнорируются. При этом используются два простых механизма, получивших называние Flush-to-zero (FTZ) и Denormals-are-zero (DAZ). Первый механизм заставляет операции возвращать ноль, как только становится ясно, что результат будет денормализованным. Второй механизм заставляет операции рассматривать поступающие на вход денормализованные числа как нули.
Ярким примером подобного «отсечения» денормализованных чисел могут послужить видеокарты, в которых резкое падение скорости вычислений в сотню раз недопустимо. Так же, например, в областях, связанных с обработкой звука, нет нужды в очень маленьких числах, поскольку они представляют столь тихий звук, что его не способно воспринять человеческое ухо.

В версии стандарта IEEE 754-2008 денормализованные числа (denormal или denormalized numbers) были переименованы в subnormal numbers, то есть в числа, меньшие «нормальных». Поэтому их иногда еще называют «субнормальными«.

Действия с числами с плавающей запятой

Умножение и деление

Самыми простыми для восприятия арифметическими операциями над числами с плавающей запятой являются умножение и деление. Для того, чтобы умножить два вещественных числа в нормализованной форме необходимо перемножить их мантиссы, сложить порядки, округлить и нормализовать полученное число.

Соответственно, чтобы произвести деление нужно разделить мантиссу делимого на мантиссу делителя и вычесть из порядка делимого порядок делителя. Затем точно так же округлить мантиссу результата и привести его к нормализованной форме.

Сложение и вычитание

Идея метода сложения и вычитания чисел с плавающей точкой заключается в приведении их к одному порядку. Сначала выбирается оптимальный порядок, затем мантиссы обоих чисел представляются в соответствии с новым порядком, затем над ними производится сложение/вычитание, мантисса результата округляется и, если нужно, результат приводится к нормализированной форме. Пример:

Выполним сложение чисел с плавающей точкой и смещенным порядком в 32-х разрядном формате   и .
Переведем   в машинный вид. Для этого сначала переведем его в двоичную систему счисления.
   
  

Нормализуем полученное двоичное число по правилам машинной арифметики.
   

Найдем смещенный порядок. Так как в условии говорится о 32-разрядном представлении, то смещение порядка равно .
          

Число отрицательное, следовательно, в бите знака будет стоять единица.

Итак, первое число в машинном 32-разрядном представлении с плавающей точкой будет иметь вид:
10000111 (жирным шрифтом выделен порядок числа, длина мантиссы — 23 бита).

Переведем второе число в машинный вид, совершая те же действия.

 = ,...  ...  
В качестве мантиссы будут сохранены первые  бита после запятой т.е. .
Очевидно, что порядок со смещением у второго числа будет таким же, как и у первого.

Второе число положительное, следовательно, бит знака будет содержать ноль.

Итак в машинном 32-разрядном представлении второе число будет иметь вид:

10000111
Далее в арифметических операциях будет использоваться число ,=, а не = видимо для упрощения(хотя это не совсем корректно).

Порядки у слагаемых равны, поэтому пропускаем шаг выравнивания порядков и проводим вычитание мантисс по правилам двоичной арифметики. В 
компьютере этим занимается арифметический сопроцессор, встроенный в центральный процессор машины.

,    

Приводим полученный результат к машинному виду. Для этого мы должны внести поправку в порядок — уменьшить его на единицу.
Знак результата —  положительный, следовательно, бит знака содержит ноль.

10000110

Проверим правильность наших вычислений. Переведем результат в десятичное представление.

Найдем реальный порядок результата, вычтя из него значение смещения .

Следовательно, число результата будет иметь вид:
      ,  

Результат наших вычислений верен, так как  -   .

Алгоритм получения представления вещественного числа в памяти ЭВМ

Покажем преобразование действительного числа для представления его в

памяти ЭВМ на примере величины типа Double.

Как видно из таблицы, величина этого типа занимает в памяти байт. На

рисунке ниже показано, как здесь представлены поля мантиссы и порядка (нумерация битов осуществляется справа налево):

Знак	Смещённый порядок	Мантисса
63	62..52	51..0

Можно заметить, что старший бит, отведенный под мантиссу, имеет номер

, т.е. мантисса занимает младшие бита. Черта указывает здесь на

положение двоичной запятой. Перед запятой должен стоять бит целой части

мантиссы, но поскольку она всегда равна , здесь данный бит не требуется и

соответствующий разряд отсутствует в памяти (но он подразумевается).

Значение порядка хранится здесь не как целое число, представленное в

дополнительном коде. Для упрощения вычислений и сравнения действительных

чисел значение порядка в ЭВМ хранится в виде смещенного числа, т.е. к

настоящему значению порядка перед записью его в память прибавляется

смещение. Смещение выбирается так, чтобы минимальному значению порядка

соответствовал нуль. Например, для типа Double порядок занимает бит и

имеет диапазон от до , поэтому смещение равно ₍₎

₍₎. Наконец, бит с номером указывает на знак числа.

Таким образом, из вышесказанного вытекает следующий алгоритм для

получения представления действительного числа в памяти ЭВМ:

1. перевести модуль данного числа в двоичную систему счисления;
2. нормализовать двоичное число, т.е. записать в виде M 2^p, где M —

   мантисса (ее целая часть равна ₍₎) и p — порядок, записанный в

   десятичной системе счисления;

3. прибавить к порядку смещение и перевести смещенный порядок в двоичную

   систему счисления;

4. учитывая знак заданного числа (0 — положительное; 1 — отрицательное),

   выписать его представление в памяти ЭВМ.

Пример. Запишем код числа ,.

1. Двоичная запись модуля этого числа имеет вид .
2. Имеем

   .

3. Получаем смещенный порядок . Далее имеем

   _{() ()}.

4. Окончательно
   

   1	10000000111	0011100001010000000000000000000000000000000000000000
   63	62..52	51..0

Очевидно, что более компактно полученный код стоит записать следующим

образом: C073850000000000₍₁₆₎.

Другой пример иллюстрирует обратный переход от кода действительного

числа к самому числу.

Пример. Пусть дан код 3FEC600000000000₍₁₆₎ или

0	01111111110	1100011000000000000000000000000000000000000000000000
63	62..52	51..0

1. Прежде всего замечаем, что это код положительного числа, поскольку в

   разряде с номером записан нуль. Получим порядок этого числа:

   _{() ()}; .

2. Число имеет вид , или

   ,.

3. Переводом в десятичную систему счисления получаем ,.

См. также

• Представление символов, таблицы кодировок
• Представление целых чисел: прямой код, код со сдвигом, дополнительный код

Примечания

Ссылки

Использованные материалы

На русском

• Википедия — Экспоненциальная запись
• Википедия — Число с плавающей запятой
• Википедия — Отрицательный и положительный ноль
• Хабрахабр — статья пользователя Yruslan «Что нужно знать про арифметику с плавающей запятой»
• Статья Лапшевой Е.Е. «Машинная арифметика с вещественными числами» Статья удалена

На английском

• Wikipedia — NaN
• Wikipedia — Floating point
• Wikipedia — IEEE 754-2008

Что стоит прочесть

• Материалы по стандарту IEEE 754 (англ.)
• Русский перевод стандарта IEEE 754

7.1 Вычисление границ диапазона для чисел одинарной точности ieee 754

Зная
формат чисел с одинарной точностью
стандарта IEEE 754 можно посчитать границы
диапазона представления действительных
чисел в этом формате. Для этого подставим
значения максимальных и минимальных
абсолютных чисел IEEE 754 в формулы №1 и
№2.

Минимальное
нормализованное число по (абсолютное)
00
80 00 00 = 2^-126∙(1+0/2²³)=
2^-126
≈ 1,17549435∙e^-38
80
80 00 00 = -2^-126∙(1+0/2²³)=-2^-126
≈ -1,17549435∙e^-38

Максимальное
денормализованое число (абсолютное)
00
7F FF FF = 2^-126∙(1-2^-23)
≈ 1,17549421∙e^-38
80
7F FF FF = -2^-126∙(1-2^-23)
≈ -1,17549421∙e^-38
Отсюда
видно что минимальное нормализированное
число граничит с максимальным
денормализированным.

Минимальное
денормализованное число (абсолютное)
00
00 00 01 = 2^-126∙
2^-23=
2^-149
≈ 1,40129846∙e^-45
80
00 00 01 = -2^-126∙
2^-23=
2^-149
≈ -1,40129846∙e^-45
Это
число граничит с нулем.

Максимальное
нормализированное число (абсолютное)
7F
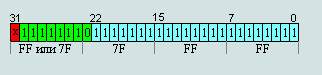
7F FF FF = 2¹²⁷∙(2-2^-23)
≈ 3,40282347∙e⁺³⁸
FF
7F FF FF = -2¹²⁷∙(2-2^-23)
≈ -3,40282347∙e⁺³⁸
Это
число граничит с бесконечностью.

7.2 Полный диапазон чисел одинарной точности (32 бит) по стандарту ieee754

Рис.4
.Диапазон чисел формата одинарной
точности (32 бита) представленных по
стандарту IEEE 754

7.3 Полный диапазон чисел двойной точности (64 бит) по стандарту ieee754

Рис.5
.Диапазон чисел формата двойной точности
(64 бита) представленных по стандарту
IEEE 754

7.4 Точность представления вещественных чисел в формате ieee754.

Числа
представленные в формате IEEE754 представляют
конечное множество, на которое отображается
бесконечное множество вещественных
чисел. Поэтому исходное число может
быть представлено в формате IEEE754 с
ошибкой.

Рис.6
Функция ошибки точности представления
числа в IEEE754

Абсолютная
максимальная ошибка для числа в формате
IEEE754 равна в пределе половине шага чисел.
Шаг чисел удваивается с увеличением
экспоненты двоичного числа на единицу.
То есть, чем дальше от нуля, тем шире шаг
чисел в формате IEEE754 по числовой оси.

Шаг
денормализованных чисел равен 2^(E-149)
(Single) и 2^(E-1074)
(Double).
Соответственно
предел макс. абсолютной ошибки будет
равен 1/2 шага числа: 2^(E-150)
(Single) и 2^(E-1075)
(Double).
Относительная ошибка в % будет
равна: (2^(E-150)/F)*100%(Single)
и (2^(E-1075)/F)*100%
(Double).

Шаг нормализованных чисел
равен 2^(E-150)
(Single) и 2^(E-1075)
(Double).
Соответственно
предел макс. абсолютной ошибки будет
равен 1/2 шага числа: 2^(E-151)
(Single) и 2^(E-1076)
(Double).
Относительная ошибка в % будет
равна: (2^(E-151)/F)*100%(Single)
и (2^(E-1076)/F)*100%
(Double).

Максимальная
относительная ошибка для денормализованного
числа(single/double):

Максимальная
относительная ошибка нормализованного
числа(single):

Максимальная
относительная ошибка нормализованного
числа(double):

Таблица 1. Максимальная возможная ошибка для чисел Single
IEEE754, hex	число, dec	абсолютная ошибка, dec	относительная, %
00000001	2-149 ≈1,401298e-45	2-150≈0,700649e-45	=50
00000002	2-148 ≈2,802597e-45	2-150≈0,700649e-45	=25
00000032	≈7,00649e-44	2-150≈0,700649e-45	=1
007FFFFF	≈1,175494e-38	2-150≈0,700649e-45	≈5,96e-6
00800001	≈1,175494e-38	2-149 ≈1,401298e-45	≈11,9209e-6
0DA24260	≈1,0e-30	2-123 ≈9,4039e-38	≈9,4039e-6
1E3CE508	≈1,0e-20	2-90 ≈8,0779e-28	≈8,0779e-6
2EDBE6FF	≈1,0e-10	2-57 ≈6,9389e-18	≈6,9389e-6
3F800000	≈1,0	2-23 ≈1,192e-7	≈11,9209e-6
41200000	≈10,0	2-20 ≈9,5367e-7	≈9,5367e-6
42C80000	≈1,0e+2	2-17 ≈7,6294e-6	≈7,62939e-6
501502F9	≈1,0e+10	210 ≈1,024e+3	≈10,24e-6
60AD78EC	≈1,0e+20	243 ≈8,7961e+12	≈8,7961e-6
7149F2CA	≈1,0e+30	276 ≈7,5558e+22	≈7,5558e-6
7F7FFFFF	≈+3,40282e+38	2104 ≈2,02824e+31	≈5,96e-6

Таблица 2. Максимальная возможная ошибка для чисел Double
IEEE754, hex	число, dec	абсолютная ошибка, dec	относительная, %
00000000 00000001	2-1074 ≈4,940656e-324	2-1075≈2,470328e-324	=50
00000000 00000002	2-1073 ≈9,881313e-324	2-1075≈2,470328e-324	=25
00000000 00000032	≈2,470328e-322	2-1075≈2,470328e-324	=1
000FFFFF FFFFFFFF	≈2,225073e-308	2-1075≈2,470328e-324	≈1,110223e-14
00100000 00000001	≈2,225074e-308	2-1074 ≈4,940656e-324	≈2,220446e-14
2B2BFF2E E48E0530	≈1,0e-100	2-385 ≈1,268971e-116	≈1,268971e-14
3FF00000 00000000	=1,0	2-52 ≈2,220446e-16	≈2,220446e-14
54B249AD 2594C37D	≈1,0e+100	2280 ≈1,942669e+84	≈1,942669e-14
6974E718 D7D7625A	≈1,0e+200	2612 ≈1,699641e+184	≈1,699641e-14
7FEFFFFF FFFFFFFF	≈1,79769e+308	2971 ≈1,99584e+292	≈1,110223e-14

Из
выше приведенного следует, что основная
масса чисел в формате IEEE754 имеет стабильную
небольшую относительную погрешность:
Максимально возможная относительная
погрешность для числа Single составляет
2^-23*100%
=11,920928955078125e-6 %
Максимально возможная
относительная погрешность для числа
Double составляет 2^-52*100%
=2,2204460492503130808472633361816e-14 %

Соседние файлы в папке вычМатКурсач

• #
• #
• #
• #
• #
• #

Вопросы занятия:

·       
представление
вещественных чисел в компьютере;

·       
множество
действительных чисел, представимых в памяти компьютера, дискретно, конечно и
ограничено;

·       
форматы
представления вещественных чисел.

Как вы помните из курса
математики, вещественные числа – это более широкий круг чисел,
появление которых возникло из необходимости измерения несоизмеримых величин.
Например, для извлечения корня, вычисления логарифмов, решения уравнений,
исследования функций и прочее.

Данное множество включает
в себя кроме целых чисел ещё и рациональные и иррациональные числа.

Понятие вещественного
числа прошло долгий путь определения и становления. Ещё в Древней Греции в
школе Пифагора было открыто существование несоизмеримых величин –
несоизмеримость стороны и диагонали квадрата – то есть было открыто наличие
иррациональных чисел.

Классическое определение
вещественным числам дал в восемнадцатом веке Исаак Ньютон.

Понятно, что в математике
множество вещественных чисел – бесконечно, непрерывно и не ограничено. Если
представить числовую ось, то между двумя точками на числовой оси лежит
бесконечное множество вещественных чисел.

Рассмотрим представление
вещественных чисел в компьютере. Как вы помните, числа в компьютере
представляются в двоичной системе счисления. Однако, в отличии от математики,
множество вещественных чисел в компьютере – дискретно, ограничено и конечно.
Опять же, как и в случае с целыми числами, из-за ограниченности размера ячейки
памяти.

Рассмотрим пример.

Из математики известно,
что дробь

 Здесь слово
«бесконечная» означает, что в десятичной записи бесконечной десятичной дроби
после запятой стоит бесконечное число десятичных знаков.

А слово «периодическая»
означает, что это такая дробь, в которой бесконечно повторяется одна или
несколько цифр. В нашем случае единица.

То есть обыкновенная
дробь

Выполним деление на
калькуляторе.

Итак, на табло
калькулятора мы видим конечное число единиц после запятой.

Первый разряд отведён под
знак числа. После запятой мы видим шестнадцать цифр, остальные не вместились в
разрядную сетку. То есть мы получили не точное десятичное значение дроби одна
девятая, а его сокращённое значение.

Следующее по величине
число, которое может быть отображено на табло калькулятора будет больше
предыдущего на величину, которая называется шагом числовой
последовательности.

То есть можно сделать вывод:
множество вещественных чисел, представимых в калькуляторе, дискретно, потому
что числа отделены друг от друга конечными отрезками.

Давайте узнаем будет ли
шаг в последовательности вещественных чисел на калькуляторе постоянной
величиной (как у целых чисел).

Вычислим выражение

То есть мы получили
число, которое больше предыдущего числа в тысячу раз.  Как и в прошлый раз,
наше число будет обрезанное.

Обратите внимание, шаг
числовой последовательности изменится. Он, по сравнению с предыдущем примером,
увеличится в тысячу раз.

То есть можно сделать вывод:
множество вещественных чисел, представимых в калькуляторе, дискретно с
переменной величиной шага между соседними числами.

Отметим на числовой
прямой точные значения вещественных чисел, которые можно представить на
калькуляторе. Как видим, точки будут размещаться неравномерно: ближе к нулю –
чаще, дальше от нуля – реже.

Все наши манипуляции с
калькулятором также действительны и для компьютера, только с переходом на
двоичную систему счисления и с учётом размера ячейки памяти компьютера.

В компьютере также,
вещественные числа расположены неравномерно.

Множество вещественных
чисел на калькуляторе и компьютере ограниченно и конечно из-за ограниченности
разрядной сетки.

То есть самое большое
число на разных калькуляторах будет различным. Так на самом простом
калькуляторе, самое большое вещественное число будет 999999999. Если увеличить
это число на единицу, то калькулятор выдаст сообщение об ошибке. На другом же
калькуляторе, более усовершенствованном, самое большое число будет больше и
если прибавить единицу, то вы получите следующий результат:

Для нас такая запись
означает: единица, умноженная на десять в шестнадцатой степени.

Данный формат записи
числа называют форматом с плавающей запятой, ранее мы рассматривали
примеры только с фиксированной запятой.

Число, стоящее перед
буквой е, называют мантиссой, число, стоящее после — порядком.
Буква Е – это основание десятичной системы счисления.

То есть всякое
вещественное число икс записывается в виде произведения мантиссы и основания
системы счисления в некоторой целой степени, которую называют порядком:

Например, число 25324
можно представить различными способами

Рассмотрим представление
0,25324 • 10⁵

Здесь мантисса m =
0,25324, а n = 5 – порядок.

 Порядок указывает, на
какое количество позиций и в каком направлении должна сместится десятичная
запятая в мантиссе.

Мантисса числа
для однозначности представления чисел с плавающей запятой должна иметь нормализованную
форму, а именно представлять собой правильную дробь с цифрой после запятой,
отличной от нуля;

Рассмотрим примеры
нормализованного представления чисел.

Числа в компьютере могут
представляться в формате как с фиксированной запятой, это, как правило, целые
числа, так и в формате с плавающей запятой.

Но важно понимать, что и
для числа, записанного в формате с плавающей запятой всегда есть ограничение –
есть определённое самое большое число. Для нашего калькулятора это число

Положительные и
отрицательные числа расположены симметрично относительно нуля. Следовательно,
максимальное и минимальное числа равны между собой по модулю.

Эти числа являются
целыми, но именно они ограничивают представление всех чисел: и целых, и
вещественных, на калькуляторе.

Для компьютера эти
ограничения конечно будут больше, но все равно будут. Как вы понимаете данное
ограничение зависит от разрядности ячейки памяти и от того сколько разрядов
выделяется под мантиссу и под порядок.

Вещественное число может
занимать в памяти компьютера 32 или 64 разряда. То есть наша ячейка в памяти
может состоять из 32 или 64 клеточек. При этом выделяются разряды для хранения
знака мантиссы, знака порядка, порядка и мантиссы.

Давайте разберёмся на
примере. Возьмём число 125 в десятичной системе счисления и запишем её в 32-разрядную
ячейку.

Мы записали двоичное
число в экспоненциальной форме.

Теперь перенесём всё в
клеточки ячейки памяти, размером 32 разряда.

Под знак и порядок
выделяется 8 клеточек, под знак и мантиссу 24.

Первую клеточку слева
выделяем под знак. Так как наше число положительное, то ставим цифру ноль. В
разделе Знак и порядок запишем число семь в двоичной системе счисления.
Оставшиеся клеточки заполним нулями.

Теперь переходим к
разделу Знак и мантисса. В первой слева снова ставим цифру ноль, которая
обозначает, что число положительное. Далее запишем наше число, а оставшиеся
клеточки заполним нулями.

Мы записали наше число в
тридцатидвухразрядную ячейку.

Диапазон представления
вещественных чисел определяется количеством разрядов, отведённых для хранения
порядка чисел, а точность – количеством разрядов, отведённых для хранения
мантиссы.

Диапазон вещественных
чисел ограничен, но он значительно шире, чем при представление целых чисел в
форме с фиксированной запятой.

Например, при
использовании 32-разрядной ячейки этот диапазон следующий:

Подводя итог нашего
урока, можно сделать следующий вывод, что бесконечное, непрерывное и не
ограниченное множество вещественных чисел в математике, в компьютерном
представлении превращается в дискретное, ограниченное и конечное множество.

Итоги урока.

вещественные числа в
компьютере представляются в формате с плавающей запятой.

всякое вещественное число
X записывается в виде произведения
мантиссы m и основания системы
счисления q в некоторой целой
степени n, которую называют
порядком.

Нормализованной формой
числа с плавающей запятой называется правильная дробь с
цифрой после запятой, отличной от нуля.

Диапазон представления
вещественных чисел определяется количеством
разрядов, отведённых для хранения порядка чисел, а точность – количеством разрядов,
отведённых для хранения мантиссы.

Помогите пожалуйста решить задачку

Определить диапазон представления вещественных чисел в
                              формате с плавающей запятой:
                              •   32 бита (8 бит порядок, 24 бита мантисса),
                              •   64 бита (11 бит порядок, 53 бита мантисса),
                              •   80 бит (15 бит порядок, 65 бита мантисса).

Гипермаркет знаний>>Информатика>>Информатика 9 класс>>Информатика: Числа в памяти компьютера

§ 17. Числа в памяти компьютера

Основные темы параграфа:

♦ представление целых чисел;
♦ размер ячейки и диапазон значений чисел;
♦ особенности работы компьютер с целыми числами;
♦ представление вещественных чисел;
♦ особенности работы компьютера с вещественными числами.

Любая информация в памяти компьютера представляется в двоичном виде: последовательностью нулей и единиц. Исторически первым типом данных, с которыми стали работать компьютеры были числа. Теперь это и числа, и тексты, и изображение, и звук. Работа с данными любого типа в конечном счете сводится к обработке двоичных чисел — чисел, записываемых с помощью двух цифр — 0 и 1. Поэтому современные компьютерные технологииназывают цифровыми технологиями.

В компьютере различаются два типа числовых величин: целые числа и вещественные числа. Различаются способы их представления в памяти компьютера.

Представление целых чисел

Часть памяти, в которой хранится одно число, будем называть ячейкой. Минимальная ячейка, в которой может храниться целое число, имеет размер 8 битов — 1 байт. Получим представление десятичного числа 25 в такой ячейке. Для этого нужно перевести число в двоичную систему счисления. Как это делается, вы уже знаете. Результат перевода:

25₁₀ = 11001₂.

Теперь осталось «вписать» его в восьмиразрядную ячейку (записать так называемое внутреннее представление числа). Делается это так:

00011001.

Число записывается «прижатым» к правому краю ячейки (в младших разрядах). Оставшиеся слева разряды (старшие) заполняются нулями.

Самый старший разряд — первый слева, хранит знак числа. Если число положительное, то в этом разряде ноль, если отрицательное — единица. Самому большому положительному целому числу соответствует следующий код:

01111111.

Чему он равен в десятичной системе? Можно расписать это число в развернутой форме и вычислить выражение. Но можно решить задачу быстрее. Если к младшему разряду этого числа прибавить единицу, то получится число 10000000. В десятичной системе оно равно 2⁷ = 128. Значит:

01111111₂ = 128 — 1 = 127.

Максимальное целое положительное число, помещающееся в 8-разрядную ячейку, равно 127.

Теперь рассмотрим представление целых отрицательных чисел. Как, например, в 8-разрядной ячейке памяти будет представлено число -25? Казалось бы, очевидным ответом является следующий: нужно в представлении числа 25 заменить старший разряд с 0 на 1. К сожалению, в компьютере все несколько сложнее.

Для представления отрицательных целых чисел используется дополнительный код.

Получить дополнительный код можно по следующему алгоритму:

1) записать внутреннее представление положительного числа X;
2) записать обратный код этого числа заменой во всех разрядах 0 на 1 и 1 на 0;
3) к полученному числу прибавить 1.

Определим по этим правилам внутреннее представление числа -25₁₀ в 8-разрядной ячейке:

1) 00011001
2) 11100110
3)             +1
    11100111 — это и есть представление числа -25.

В результате выполнения такого алгоритма единица в старшем разряде получается автоматически. Она и является признаком отрицательного значения.

Проверим полученный результат. Очевидно, что при сложении чисел +25 и -25 должен получиться ноль.

   00011001
 +11100111
1 00000000

Единица в старшем разряде, получаемая при сложении, выходит за границу ячейки и исчезает. В ячейке остается ноль!

Из этого примера теперь можно понять, почему представление отрицательного числа называется дополнительным кодом.

Представление восьмиразрядного отрицательного числа -X дополняет представление соответствующего положительного числа +Х до значения 2⁶.

Размер ячейки к диапазон значений чисел

Наибольшее по модулю отрицательное значение в 8-разрядной ячейке равно -2⁷ = -128.  Его внутреннее представление: 10000000. Таким образом, диапазон представления целых чисел в восьмиразрядной ячейке следующий:

-128 < X < 127, или -2⁷ < X < 2⁷ — 1.

Восьмиразрядное представление целых чисел обеспечивает слишком узкий диапазон значений. Если требуется больший диапазон, нужно использовать ячейки большего размера. Для 16-разрядной ячейки диапазон значений будет следующим:

-2¹⁵ <X < 2¹⁵ — 1, или -32 768 < X < 32 767.

Теперь становится очевидной обобщенная формула для диапазона целых чисел в зависимости от разрядности N ячейки:

-2^N-1 < X < 2^N-1-1.

Диапазон для 32-разрядной ячейки получается достаточно большим:

-2³¹ < Х < 2³¹ — 1, или
-2 147 483 648 < X < 2 147 483 647.

Особенности работы компьютера с целыми числами

Выполняя на компьютере вычисления с целыми числами, нужно помнить об ограниченности диапазона допустимых значений. Выход результатов вычислений за границы допустимого диапазона называется переполнением. Переполнение при вычислениях с целыми числами не вызывает прерывания работы процессора. Машина продолжает считать, но результаты могут оказаться неправильными.

Представление вещественных чисел

Целые и дробные числа в совокупности называются вещественными числами. В математике также используется термин «действительные числа». Решение большинства математических задач сводится к вычислениям с вещественными числами.

Всякое вещественное число (X) можно записать в виде произведения мантиссы m и основания системы счисления р в некоторой целой степени n, которую называют порядком:

X = m · рⁿ.

Например, число 25,324 можно записать в таком виде: 0,25324 · 10². Здесь m = 0,25324 — мантисса, n = 2 — порядок. Порядок указывает, на какое количество позиций и в каком направлении должна сместиться десятичная запятая в мантиссе.

Чаще всего для хранения вещественных чисел в памяти компьютера используется либо 32-разрядная, либо 64-разрядная ячейка. Первый вариант называется представлением с обычной точностью, второй — представлением с удвоенной точностью. В ячейке хранятся два числа в двоичной системе счисления: мантисса и порядок. Здесь мы не будем подробно рассматривать правила представления вещественных чисел. Отметим лишь основные следствия, вытекающие из этих правил, которые важно знать пользователю компьютера, занимающемуся математическими вычислениями.

Особенности работы компьютера с вещественными числами

1. Диапазон вещественных чисел ограничен. Но он значительно шире, чем для рассмотренного ранее способа представления целых чисел. Например, при использовании 32-разрядной ячейки этот диапазон следующий:

-3,4 · 10³⁸ < X < 3,4 · 10³⁸.

2. Выход за диапазон (переполнение) — аварийная ситуация для процессора, который прерывает свою работу.
3. Результаты машинных вычислений с вещественными числами содержат погрешность. При использовании удвоенной точности эта погрешность уменьшается.

Коротко о главном

В памяти компьютера целые числа представляются в двоичной системе счисления и могут занимать ячейку размером 8, 16, 32 и т. д. битов.

Диапазон значений целых чисел ограничен. Чем больше размер ячейки, тем шире диапазон.

При выходе результатов вычислений с целыми числами за допустимый диапазон работа процессора не прерывается. При этом результаты могут оказаться неверными.

Вещественные числа представляются в виде совокупности мантиссы и порядка в двоичной системе счисления. Обычный размер ячейки — 32 или 64 бита.

Результаты вычислений с вещественными числами приближенные. Переполнение приводит к прерыванию работы процессора.

Вопросы и задания

И. Семакин, Л. Залогова, С. Русаков, Л. Шестакова, Информатика, 9 класс
Отослано читателями из интернет-сайтов

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь — Образовательный форум.

Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки

©  Автор системы образования 7W и Гипермаркета Знаний — Владимир Спиваковский

При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов —
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других «взрослых» тем.

Разработка — Гипермаркет знаний 2008-

Ждем Ваши замечания и предложения на email:
По вопросам рекламы и спонсорства пишите на email: