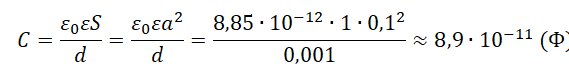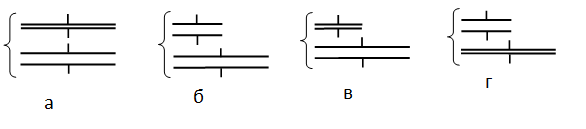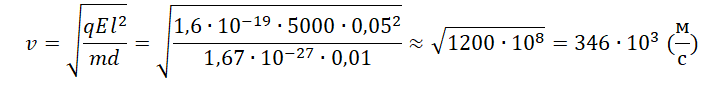Как найти диэлектрическую проницаемость в конденсаторе - Исправление недочетов и поиск решений вместе с Examum.ru

В этой статье мы расскажем о самых важных вещах, связанных с диэлектрической проницаемостью. Среди прочего, вы узнаете о важных ролях, которые она играет, и о её типичных значениях.

Простое объяснение

В повседневной жизни вы сталкиваетесь с различными веществами, такими как металлы, вода или кислород. Каждое из этих веществ по-разному реагирует на электрические поля.

Диэлектрическая проницаемость (диэлектрическая постоянная или абсолютная диэлектрическая проницаемость) ε описывает способность материала к поляризации электрическими полями и определяется следующим образом: ε = ε_r * ε₀ .

Здесь ε_r — относительная проницаемость, а ε₀ — электрическая постоянная (или диэлектрическая проницаемость вакуума).

Если понимать значение термина «проницаемость» буквально, то это мера того, насколько сильно материя «пропускает» электрическое поле. Поэтому проницаемость можно рассматривать как меру того, насколько материя может быть поляризована.

Диэлектрическая проницаемость вакуума

Особую роль играет диэлектрическая проницаемость вакуума (также называемая проницаемостью вакуума). В этом разделе мы расскажем вам о значении и единицах измерения проницаемости вакуума, о том, как она связана с другими константами, и о ее значении в контексте других важных законов.

Числовое значение и единица измерения

Диэлектрическая проницаемость вакуума ε₀ имеет значение 8,85418781762039 * 10^-12 или 8.85 * 10^-12, что более практично для расчетов. Единицей измерения константы является [ Ф·м⁻¹ ] или если выражать через основные единицы СИ [ м⁻³·кг⁻¹·с⁴·А² ].

Взаимосвязь с другими константами

Существует замечательная связь между электрической постоянно ε₀, магнитной постоянно μ‎₀ и скоростью света в вакууме с₀. То есть верно следующее соотношение: c₀² = 1 / ε₀ * μ‎₀ .

До 2019 года это уравнение точно определяло значение постоянной электрического поля. Однако в ходе пересмотра ситуация изменилась, и с 20 мая 2019 года как электрическая постоянная, так и магнитная постоянная имеют определенную погрешность измерения.

Это уравнение было первым указанием на то, что свет может быть электромагнитной волной.

Закон Кулона и электрический потенциал

Помимо связи со скоростью света, электрическая постоянная фигурирует в других важных законах электродинамики. К ним относятся, например:

Закон Кулона:

Электрический потенциал заряженной частицы : φ ( r ) = q / 4 * π * ε₀ * r .

В частности, закон Кулона является основой электростатики, поэтому константа электрического поля также имеет большое значение.

Диэлектрическая проницаемость: общий случай

В этом разделе мы рассмотрим общий случай. Мы объясним физический смысл абсолютной диэлектрической проницаемости с помощью электроизоляционных материалов и объясним, что такое относительная диэлектрическая проницаемость.

Диэлектрическая проницаемость диэлектриков

В электроизолирующих материалах (диэлектриках) электрические заряды связаны с атомами или молекулами. Поэтому они могут лишь немного перемещаться внутри атомов или молекул. Электрическое поле может изменить распределение заряда в диэлектрике двумя важными способами: деформацией и вращением. Даже если отдельные электрические заряды могут двигаться незначительно, совокупность всех движений определяет поведение электроизоляционного материала.

Поляризация

В зависимости от того, состоит ли материал из полярных или неполярных молекул, реакция на внешнее электрическое поле различна. С неполярной молекулой происходит растягивание (деформация), при котором поле индуцирует дипольный момент в каждой молекуле материала. Все эти дипольные моменты направлены в ту же сторону, что и электрическое поле.

В полярной молекуле, с другой стороны, происходит вращение, так что и здесь все дипольные моменты направлены в сторону электрического поля. В целом внешнее электрическое поле вызывает образование в материале большого количества диполей, все из которых ориентированы в том же направлении, что и внешнее поле. Таким образом, материал поляризуется. Поляризация P описывает, сколько дипольных моментов приходится на единицу объема материала.

Диэлектрическая проницаемость диэлектриков

Таким образом, поляризация диэлектрика вызывается электрическим полем. Возникающие направленные дипольные моменты, в свою очередь, создают электрическое поле, противодействующее внешнему полю. Таким образом, это противоположное поле ослабляет внешнее поле. В целом, связь между поляризацией и внешним электрическим полем сложная. Для многих веществ, так называемых линейных диэлектриков, поляризация пропорциональна полю. Применяется следующее соотношение:

P = ε₀ * χ * E , где

Здесь ε₀ — электрическая постоянная, а χ — электрическая поляризуемость. Электрическое поле E в этом уравнении является полным полем. Поэтому причиной этого могут быть частично свободные заряды и частично сама поляризация.. Свободные заряды — это все те носители заряда, которые не являются результатом поляризации. Таким образом, это полное электрическое поле очень трудно рассчитать, поскольку мы обычно не имеем информации о распределении поляризационных зарядов.

Для справки: χ — коэффициент, зависящий от химического состава, концентрации, структуры (в том числе от агрегатного состояния) среды, температуры, механических напряжений и т. д. (от одних факторов более сильно, от других слабее, конечно же и в зависимости от диапазона изменений каждого), и называемый (электрической) поляризуемостью (а чаще, по крайней мере для того случая, когда он выражается скаляром — диэлектрической восприимчивостью) данной среды.

Википедия

Электрическая индукция

Чтобы иметь возможность рассчитать электрическое поле даже в присутствии диэлектрика, вводится электрическая индукция D. В линейной среде: D = ε₀ * E + P = ε₀ * E + ε₀ * χ_e * E = ε₀ * ( 1 + χ_e ) * E и поэтому D также пропорциональна E.

Если вы объедините константы вместе ε = ε₀ * ( 1 + χ_e ), то получится: D = ε * E .

Постоянная ε и называется диэлектрической проницаемостью.

Относительная диэлектрическая проницаемость

Величина: ε_r = 1 + χ_e = ε / ε₀ называется относительной проницаемостью (также относительной диэлектрической проницаемостью). С его помощью полное электрическое поле в присутствии диэлектрика определяется следующим образом: E = D / ε = D / ε_r * ε₀ .

При постоянной электрической индукции относительная проницаемость, таким образом, определяет, насколько сильно ослабляется электрическое поле. Чем больше относительная проницаемость, тем больше ослабляется электрическое поле и, следовательно, уменьшается общая напряженность электрического поля.

Термин относительная проницаемость может привести к неправильному пониманию того, что относительная проницаемость для данного материала является константой. На самом деле, относительная проницаемость зависит от многих факторов. Среди них:

температура материала;
частота внешнего электрического поля;
напряженность внешнего электрического поля.

Для некоторых материалов относительная проницаемость дополнительно зависит от направления. Следовательно, в случае таких материалов это не просто число, а часто тензор второго порядка.

Особенно наглядную иллюстрацию влияния диэлектриков с разной относительной проницаемостью можно получить, поместив диэлектрик между двумя пластинами конденсатора. Если измерить электрическое напряжение на конденсаторе до и после введения диэлектрика, то можно обнаружить, что напряжение на конденсаторе уменьшается ровно на величину ε_r относительной диэлектрической проницаемости. Это следует непосредственно из уравнения: E = U / d для величины электрического поля между пластинами конденсатора, расположенными на расстоянии d друг от друга. Это также иллюстрирует, почему ε_r называется относительной проницаемостью. Напряжение на конденсаторе уменьшается на коэффициент ε_r за счет введения диэлектрика, по сравнению со случаем, когда между пластинами только вакуум.

Относительные диэлектрические проницаемости отдельных материалов

Наконец, мы приводим таблицу с типичными значениями относительной диэлектрической проницаемости (относительной диэлектрической проницаемости) различных материалов. Следует отметить, что в таких таблицах обычно указывается относительная проницаемость, а не сама абсолютная диэлектрическая проницаемость. Поэтому, если вы ищете таблицу для определения абсолютной диэлектрической проницаемости определенного материала, вы должны помнить, что приведенное там значение не является непосредственно той проницаемостью, которую вы ищете. Однако для заданного значения относительной проницаемости можно вычислить соответствующую абсолютную диэлектрическую проницаемость без особых дополнительных усилий. То есть нужно применять следующую уже известную нам формулу: ε = ε_r * ε₀ .

Вещество	ε_r
Вакуум	ровно 1
Гелий	1,000065
Медь	5,6
Воздух (сухой)	1,00059
Метанол	32,6
Бумага	1 – 4
Вода ( 20°C, 0 — 3 ГГц )	80
Вода ( 0°C, 0 — 1 ГГц )	88

Таблица 1. Относительная диэлектрическая проницаемость выбранных веществ
(если не указано иное: при 18°C и 50 Гц)

В предыдущем разделе мы упоминали, что относительная проницаемость зависит, помимо прочего, от температуры и частоты. Поэтому важно знать и температуру, и частоту, если вы хотите получить значение из таблицы. Например, относительная проницаемость воды при температуре 20°C и частоте 0 ГГц равна 80. Если температура 0°C, а частота та же, относительная проницаемость воды равна 88. Медь, с другой стороны, имеет относительную проницаемость 5,6. Это означает, что вода как среда уменьшит напряжение на конденсаторе в 80 раз, в то время как медь уменьшит его только в 5,6 раз.

Список использованной литературы

Курс физики для ФМШ при НГУ, раздел «Электромагнитное поле», гл. 2: «Диэлектрики».
Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. — М.: Мир, 1965.
Сивухин Д. В. Общий курс физики. — М.. — Т. III. Электричество.
Гольдштейн Л. Д., Зернов Н. В. Электромагнитные поля и волны. М.: Сов. радио, 1971. С. 11.

Источник

Определение

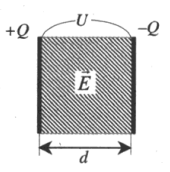
Конденсатор служит для накопления электрического заряда. Он представляет собой два проводника, разделенных слоем диэлектрика.

Плоский конденсатор — система двух разноименно заряженных пластин.

Разность потенциалов U (В) между обкладками конденсатора (напряжение между пластинами), определяется произведением напряженности создаваемого ими электрического поля на расстояние между ними:

U=Ed

Электроемкость конденсатора

Определение

Электрическая емкость — характеристика проводника, мера его способности накапливать электрический заряд.

Электроемкость обозначается как C. Единица измерения электрической емкости — Фарад (Ф).

Электроемкость конденсатора определяется формулой:

C=ε0εSd

ε0 — диэлектрическая постоянная, равная 8,85∙10^–12 Кл²/(Н∙м²);
ε — диэлектрическая проницаемость среды;
S (м²) — площадь каждой пластины.

Внимание! У воздушного конденсатора диэлектрическая проницаемость среды равна 1.

Связь между электроемкостью конденсатора, зарядом и напряжением определяется формулами:

C=QU=qU

Важно! Электроемкость конденсатора зависит только от площади его пластин, расстояния между ними и диэлектрической проницаемости среды. От заряда и напряжения эта величина не зависит.

Энергия конденсатора

Формула энергии конденсатора

Энергия конденсатора связана с его электроемкостью и вычисляется по следующим формулам:

Wэ=q22C=CU22

Подсказки к задачам

Конденсатор отключен от источника	q = q′
Конденсатор подключен к источнику	U = U′
Количество теплоты и энергия конденсатора	Q = ∆W_э

Пример №1. Вычислить электроемкость плоского воздушного конденсатора с квадратными пластинами со стороной 10 см, расположенными на расстоянии 1 мм друг от друга. Ответ округлить до десятых.

10 см = 0,1 м

1 мм = 0,001 м

Так как между обкладками конденсатора находится воздух, примем диэлектрическую проницаемость среды за единицу.

Площадь квадратной пластины равна квадрату ее стороны:

S = a²

Соединения конденсаторов

	Последовательное соединение	Параллельное соединение
Схема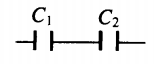
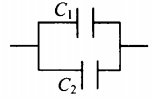Напряжение	U=U1+U2	U=U1=U2
Заряд	q=q1=q2	q=q1+q2
Электроемкость	1C=1C1+1C2	C=C1+C2

Подсказки к задачам

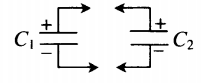
Два конденсатора, электроемкости которых C₁и C₂, заряжены до напряжения U₁и U₂. Найдите разность потенциалов после соединения конденсаторов одноименными полюсами.

Схема соединения конденсаторов одноименными полюсами:

Заряд системы после соединения:

q′
=C1U1+C2U2

Электрическая емкость системы:

C′
=C1+C2

Напряжение:

U′
=q′C′=C1U1+C2U2C1+C2

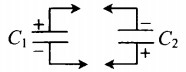
Два конденсатора, электроемкости которых C₁и C₂, заряжены до напряжения U₁и U₂. Найдите разность потенциалов после соединения конденсаторов разноименными полюсами.

Схема соединения конденсаторов разноименными полюсами:

Заряд системы после соединения:

q′
=C1U1−C2U2

Электрическая емкость системы:

C′
=C1+C2

Напряжение:

U′
=q′C′=C1U1−C2U2C1+C2

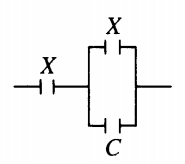
Пример №2. К конденсатору, электрическая емкость которого C = 16 пФ, подключают два одинаковых конденсатора емкостью X: один параллельно, а второй — последовательно (см. рисунок). Емкость образовавшейся батареи конденсаторов равна емкости C. Какова емкость X? Ответ округлите до десятых.

Электрическая емкость параллельного соединения равна:

Cпарал=X+C

Электроемкость последовательного соединения:

1Cпослед=1Cпарал+1X=1X+C+1X

Учтем, что суммарная электроемкость равна C:

1C=1X+C+1X

Преобразуем, умножим выражение на CX(X+C):

X(X+C)=CX+C(X+C)

Раскроем скобки:

X2+XC=CX+CX+C2

X2−CX−C2=0

Решив уравнение, получим: X = 25,9 пФ.

Разбор задач на тему «Заряженная частица в поле конденсатора»

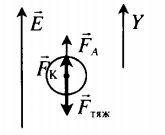
Шарик, находящийся в масле плотностью ρ, «висит» в поле плоского конденсатора. Плотность вещества шарика ρ_ш > ρ, его радиус r, расстояние между обкладками конденсатора d. Каков заряд шарика, если электрическое поле направлено вверх, а разность потенциалов между обкладками U?	Условие равновесия исходит из второго закона Ньютона: −Fтяж+−FK+−FA=0 ρ_ш > ρ, поэтому −Fтяж> −FA. В этом случае сила Кулона направлена вверх, а заряд шарика положительный. Схематически это можно отобразить так: Проекция второго закона Ньютона на ось ОУ: FK+FA=Fтяж Сила тяжести равна произведению объема на плотность шарика и на ускорение свободного падения: Fтяж=ρш43πr3g Архимедова сила равна произведению объема шарика на плотность масла и на ускорение свободного падения: FА=ρ43πr3g Сила Кулона: FK=qUd qUd+ρ43πr3g=ρш43πr3g q=(ρш43πr3g−ρ43πr3g)dU=4πr3gd(ρш−ρ)3U
Маленький шарик с зарядом q и массой m, подвешенный на невесомой нити с коэффициентом упругости k, находится между вертикальными пластинами воздушного конденсатора. Расстояние между обкладками конденсатора d. Какова разность потенциалов между обкладками конденсатора U, если удлинение нити ∆l?	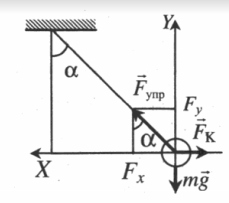Условие равновесия исходит из второго закона Ньютона: −Fтяж+−FK+−Fупр=0 Проекции на оси ОХ и ОУ соответственно: Fупрsinα−FK=0 Fупрcosα−mg=0 Отсюда: kΔlsinα=qUd kΔlcosα=mg Чтобы избавиться от угла α, возведем уравнения в квадрат и сложим их: (kΔl)2sin2α+(kΔl)2cos2α=(qUd)2+(mg)2 (kΔl)2(sin2α+cos2α)=(qUd)2+(mg)2 sin2α+cos2α=1 (kΔl)2=(qUd)2+(mg)2 U=dq√(kΔl)2−(mg)2
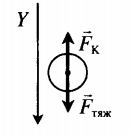
Пластины плоского конденсатора расположены горизонтально на расстоянии d друг от друга. Напряжение на пластинах конденсатора U. В пространстве между пластинами падает капля жидкости. Масса капли m, ее заряд q. Определите расстояние между пластинами. Влиянием воздуха на движение капли пренебречь.	Второй закон Ньютона в векторной форме: −Fтяж+−FK=0 Проекция на вертикальную ось: Fтяж−FK=0 Fтяж=mg FK=qUd mg=qUd d=qUmg
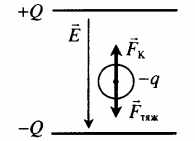
Между двумя параллельными горизонтально расположенными диэлектрическими пластинами создано однородное электрическое поле с напряженностью −E, направленное вертикально вниз. Между пластинами помещен шарик на расстоянии d от верхней пластины и b от нижней. Заряд шарика –q, масса m. Шарик освобождают, и он начинает двигаться. Через какой промежуток времени t шарик ударится об одну из пластин, если система находится в поле силы тяжести Земли?	Второй закон Ньютона в векторной форме: −Fтяж+−FK=m−a Согласно условию данной задачи, сила тяжести противоположно направлена силе Кулона. Построим рисунок: Если F_тяж> F_K, то шарик движется с ускорением вниз. Ускорение и перемещение в этом случае равны: a=mg−qEm s=b Если F_тяж< F_K, то шарик движется с ускорением верх. Ускорение и перемещение в этом случае равны: a=qE−mgm s=d Начальная скорость шарика равна нулю. Поэтому перемещение также равно: s=at22 Сделаем вычисления для случая F_тяж> F_K: at22=b mg−qEmt22=b t=√2bmmg−qE Выполняя вычисления для случая Сделаем вычисления для случая F_тяж< F_K, получим: t=√2bmqE−mg
Между двумя параллельными, вертикально расположенными диэлектрическими пластинами создано однородное электрическое поле, напряженность которого −E и направлена слева направо. Между пластинами помещен шарик на расстоянии b от левой пластины и d от правой. Заряд шарика –q, масса m. Шарик освобождают, и он начинает двигаться. Найдите смещение шарика по вертикали ∆h до удара об одну из пластин. Пластины имеют достаточно большой размер.	Второй закон Ньютона в векторной форме: −Fтяж+−FK=m−a Если сила Кулона направлена вправо, то s_x = d. Если сила Кулона направлена вправо, то s_x = b. Учитывая, что заряд меньше нуля, а вектор напряженности направлен вправо, делаем вывод, что кулоновская сила направлена влево. Из проекций второго закона Ньютона выразим проекции ускорения на оси ОХ и ОУ соответственно: ax=qEm ay=g Проекции перемещений на эти же оси: sx=axt22 sx=Δh=gt22 axt22=b Или: qEmt22=b Так как время движения шарика по вертикали и горизонтали одинаково: t2=2Δhg=2mbqE Δh=mbgqE

Задание EF17979

Введите ответ в поле ввода
Плоский конденсатор подключён к гальваническому элементу. Как изменятся при уменьшении зазора между обкладками конденсатора три величины: ёмкость конденсатора, величина заряда на его обкладках, разность потенциалов между ними?

Для каждой величины определите соответствующий характер изменения:

увеличится
уменьшится
не изменится

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения

1.Определить, от чего зависит емкость конденсатора, и как она изменится при уменьшении зазора между его обкладками.

2.Определить, от чего зависит величина заряда конденсатора, и как она изменится после уменьшения зазора между его обкладками.

3.Определить, от чего зависит разность потенциалов между обкладками конденсатора, и как она изменится при уменьшении зазора.

Решение

Емкость конденсатора определяется формулой:

C=ε0εSd

Следовательно, емкость имеет обратно пропорциональную зависимость от расстояния между обкладками. Если расстояние уменьшить, то емкость увеличится.

Вот как взаимосвязана электроемкость и заряд конденсатора:

C=qU

Мы выяснили, что электроемкость увеличивается. Следовательно, увеличится и заряд, так как они имеют прямо пропорциональную зависимость.

С учетом того, что плоский конденсатор подключен к гальваническому элементу, разность потенциалов никак не зависит от расстояния между обкладками. Поэтому величина U остается неизменной.

Ответ: 113

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18574

Воспользовавшись оборудованием, представленным на рис. 1, учитель собрал модель плоского конденсатора (рис. 2), зарядил нижнюю пластину положительным зарядом, а корпус электрометра заземлил. Соединённая с корпусом электрометра верхняя пластина конденсатора приобрела отрицательный заряд, равный по модулю заряду нижней пластины. После этого учитель сместил одну пластину относительно другой не изменяя расстояния между ними (рис. 3). Как изменились при этом показания электрометра (увеличились, уменьшились, остались прежними)? Ответ поясните, указав, какие явления и закономерности Вы использовали для объяснения. Показания электрометра в данном опыте прямо пропорциональны разности потенциалов между пластинами конденсатора.

Алгоритм решения

1.Проанализировать каждый этап эксперимента.

2.Установить, от чего зависит угол отклонения стрелки электрометра.

3.Выяснить, что поменяется при смещении одной пластины конденсатора относительно другой, и что при этом произойдет со стрелкой электрометра.

Решение

На первом рисунке стрелка и стержень электрометра, соединённые с нижней пластиной, но изолированные от корпуса, заряжаются положительно. Поэтому стрелка отклоняется на некоторый угол. В верхней пластине и металлическом корпусе электрометра происходит перераспределение свободных электронов таким образом, что верхняя пластина заряжается отрицательно.

На втором рисунке заряды пластин одинаковы по модулю и противоположны по знаку, пластины образуют конденсатор с ёмкостью:

C=ε0εSd

S — площадь перекрытия пластин, d — расстояние между ними, ε — диэлектрическая проницаемость диэлектрика между пластинами.

Характер изменения угла отклонения стрелки совпадает с изменением разности потенциалов между пластинами: при увеличении разности потенциалов увеличивается угол отклонения, при уменьшении разности потенциалов угол уменьшается.

На рисунке 3 площадь перекрытия пластин уменьшилась. Следовательно, уменьшилась электроемкость, которая имеет обратно пропорциональную зависимость от разности потенциалов:

C=qU

Заряд остается постоянным, поскольку система изолированная — заряду просто некуда деться. Поэтому с уменьшением электроемкость растет разность потенциалов. Поэтому показания электрометра увеличатся.

Ответ: Увеличатся

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18695

Ученик изучает свойства плоского конденсатора. Какую пару конденсаторов (см. рисунок) он должен выбрать, чтобы на опыте обнаружить зависимость ёмкости конденсатора от расстояния между его обкладками?

Алгоритм решения

Установить, какие величины в данном эксперименте должны быть переменными, а какие — постоянными.
Найти рисунок с парой конденсаторов, удовлетворяющий требованиям, выявленным в шаге 1.

Решение

Чтобы на опыте обнаружить зависимость ёмкости конденсатора от расстояния между его обкладками, нужно сохранить все величины постоянными, кроме самого расстояния. Поэтому площади обкладок должны быть одинаковыми, но расстояние между ними разными, как на рисунке 1.

Ответ: а

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18703

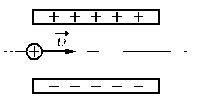
Протон влетает в электрическое поле конденсатора параллельно его пластинам в точке, находящейся посередине между пластинами (см. рисунок). Найдите минимальную скорость υ, с которой протон должен влететь в конденсатор, чтобы затем вылететь из него. Длина пластин конденсатора 5 см, расстояние между пластинами 1 см, напряжённость электрического поля конденсатора 5000 В/м. Поле внутри конденсатора считать однородным, силой тяжести пренебречь.

Ответ записать в км/с, округлив до десятков.

Алгоритм решения

1.Записать исходные данные и перевести единицы измерения величин в СИ.

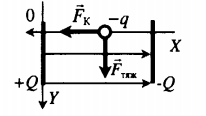
2.Выполнить рисунок. Указать направление движения протона и силы, действующие на него.

3.Выяснить, при каком условии протон успеет вылететь из конденсатора.

4.Выполнить решение в общем виде.

5.Подставить известные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

• Масса протона: m = 1,67∙10^–27 кг.

• Заряд протона: q = 1,6∙10^–19 Кл.

• Расстояние между обкладками конденсатора: d = 1 см.

• Длина пластин конденсатора: l = 5 см.

• Напряженность однородного поля внутри конденсатора: E = 5000 В/м.

1 см = 0,01 м

5 см = 0,05 м

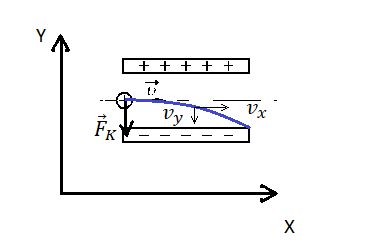
Сделаем рисунок:

Изначально протон обладает только горизонтальной скоростью v, равной v_x. Влетев в однородное электростатическое поле внутри конденсатора, протон обретает вертикальную компоненту скорости, которая растет за счет ускорения, придаваемого кулоновскими силами. Положительно заряженный протон притягивается нижней отрицательно зараженной пластиной конденсатора.

Чтобы протон вылетел из конденсатора, его горизонтальная компонента скорости должна быть достаточной для того, чтобы частица не притянулась к нижней пластине раньше. Время, которое понадобится протону для преодоления длины пластин конденсатора со скоростью v_x:

t=lvx=lv

Протон влетел в пространство между обкладками конденсатора на одинаковом расстоянии от них. Следовательно, прежде чем он упадет на нижнюю пластину, по оси OY он переместится на расстояние, равное 0,5d. Так как начальная компонента скорости равна нулю (мы пренебрегаем силой тяжести):

0,5d=at22

Протон вылетит из конденсатора, а не упадет на его пластину, если время горизонтального перемещения до конца пластин будет как минимум равно времени падения. Выразим время падения:

t=√da

Приравняем правые части уравнений времени и получим:

lv=√da

Отсюда скорость равна:

v=√al2d

Ускорение выразим из второго закона Ньютона:

FK=ma=qUd

a=qUmd

Но известно, что:

U=Ed

Поэтому:

a=qEdmd=qEm

Отсюда:

Минимальная скорость, с которой протон должен влететь в конденсатор, составляет 346∙10³ м/с. Округлим до десятков и переведем в км/с. Получим 350 км/с.

Ответ: 350

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 6k

Источник

Как найти диэлектрическую проницаемость

Чтобы правильно рассчитать параметры конденсаторов в процессе их разработки и производства, необходимо знать такой параметр как диэлектрическая проницаемость.

Инструкция

Диэлектрическая проницаемость ε(относительная) среды — это физическая величина, которая характеризует свойства диэлектрической (изолирующей) среды. Она связана с эффектом поляризации диэлектриков под воздействием электрического поля. Диэлектрическая проницаемостьε показывает, во сколько раз меньше сила взаимодействия электрических зарядов в какой-либо среде, чем в вакууме.

Чтобы определить диэлектрическую проницаемость вещества εr, сравните ёмкость конденсатора, взятого как тестовый, с заданным диэлектриком (Cx) и ёмкость этого же конденсатора, но в вакууме (Co): Ɛr = Cx/Co

Диэлектрическая проницаемость большинства газов, в том числе воздуха, в обычных условиях приближается к единице (из-за их низкой плотности). Большая часть твёрдых диэлектриков относительная имеет диэлектрическую проницаемость, которая лежит в диапазоне от 2 до 8. В статическом поле диэлектрическая постоянная воды имеет достаточно высокое значение — примерно 80.

Вещества с молекулами, которые обладают значительным электрическим диполем, имеют и большое значение диэлектрической проницаемости.К примеру, диэлектрическая проницаемость сегнетоэлектриков исчисляется десятками и сотнями тысяч.

Диэлектрическая проницаемость является одним из важнейших параметров при создании конденсаторов. Применение материалов, которые имеют высокую диэлектрическую проницаемостью, позволяет значительно снизить геометрические размеры конденсаторов.

Ёмкость электрических конденсаторов определяется по формуле: C= Ɛr*Ɛo*S/d
Где:

εr — диэлектрическая проницаемость изолятора между обкладками,

εо — электрическая постоянная,

S — площадь поверхности обкладок конденсатора,

d — промежуток между обкладками.

Диэлектрическая проницаемость принимается в расчет также при создании печатных плат.

Видео по теме

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

A dielectric medium showing orientation of charged particles creating polarization effects. Such a medium can have a lower ratio of electric flux to charge (more permittivity) than empty space

In electromagnetism, the absolute permittivity, often simply called permittivity and denoted by the Greek letter ε (epsilon), is a measure of the electric polarizability of a dielectric. A material with high permittivity polarizes more in response to an applied electric field than a material with low permittivity, thereby storing more energy in the material. In electrostatics, the permittivity plays an important role in determining the capacitance of a capacitor.

In the simplest case, the electric displacement field D resulting from an applied electric field E is

{displaystyle mathbf {D} =varepsilon mathbf {E} .}

More generally, the permittivity is a thermodynamic function of state.^[1] It can depend on the frequency, magnitude, and direction of the applied field. The SI unit for permittivity is farad per meter (F/m).

The permittivity is often represented by the relative permittivity ε_r which is the ratio of the absolute permittivity ε and the vacuum permittivity ε₀

${displaystyle kappa =varepsilon _{mathrm {r} }={frac {varepsilon }{varepsilon _{0}}}}$

This dimensionless quantity is also often and ambiguously referred to as the permittivity. Another common term encountered for both absolute and relative permittivity is the dielectric constant which has been deprecated in physics and engineering^[2] as well as in chemistry.^[3]

By definition, a perfect vacuum has a relative permittivity of exactly 1 whereas at standard temperature and pressure, air has a relative permittivity of κ_air ≈ 1.0006.

Relative permittivity is directly related to electric susceptibility (χ) by

otherwise written as

${displaystyle varepsilon =varepsilon _{mathrm {r} }varepsilon _{0}=(1+chi )varepsilon _{0}}$

The term «permittivity» was introduced in the 1880s by Oliver Heaviside to complement Thomson’s (1872) «permeability».^[4] Formerly written as p, the designation with ε has been in common use since the 1950s.

Units[edit]

The standard SI unit for permittivity is farad per meter (F/m or F·m⁻¹).^[5]

${displaystyle {frac {text{F}}{text{m}}}={frac {text{C}}{{text{V}}{cdot }{text{m}}}}={frac {{text{C}}^{2}}{{text{N}}{cdot }{text{m}}^{2}}}={frac {{text{C}}^{2}{cdot }{text{s}}^{2}}{{text{kg}}{cdot }{text{m}}^{3}}}={frac {{text{A}}^{2}{cdot }{text{s}}^{4}}{{text{kg}}{cdot }{text{m}}^{3}}}}$

Explanation[edit]

In electromagnetism, the electric displacement field D represents the distribution of electric charges in a given medium resulting from the presence of an electric field E. This distribution includes charge migration and electric dipole reorientation. Its relation to permittivity in the very simple case of linear, homogeneous, isotropic materials with «instantaneous» response to changes in electric field is:

where the permittivity ε is a scalar. If the medium is anisotropic, the permittivity is a second rank tensor.

In general, permittivity is not a constant, as it can vary with the position in the medium, the frequency of the field applied, humidity, temperature, and other parameters. In a nonlinear medium, the permittivity can depend on the strength of the electric field. Permittivity as a function of frequency can take on real or complex values.

In SI units, permittivity is measured in farads per meter (F/m or A²·s⁴·kg⁻¹·m⁻³). The displacement field D is measured in units of coulombs per square meter (C/m²), while the electric field E is measured in volts per meter (V/m). D and E describe the interaction between charged objects. D is related to the charge densities associated with this interaction, while E is related to the forces and potential differences.

Vacuum permittivity[edit]

The vacuum permittivity ε₀ (also called permittivity of free space or the electric constant) is the ratio D/E in free space. It also appears in the Coulomb force constant,

${displaystyle k_{text{e}}={frac {1}{4pi varepsilon _{0}}}}$

Its value is^[6]^[7]

${displaystyle varepsilon _{0} {stackrel {mathrm {def} }{=}} {frac {1}{c_{0}^{2}mu _{0}}}approx 8.854,187,8128(13)times 10^{-12}{text{ F/m }}}$

where

c₀ is the speed of light in free space,^[a]
µ₀ is the vacuum permeability.

The constants c₀ and μ₀ were both defined in SI units to have exact numerical values until the 2019 redefinition of the SI base units. Therefore, until that date, ε₀ could be also stated exactly as a fraction, ${displaystyle {tfrac {1}{c_{0}^{2}mu _{0}}}={tfrac {1}{35,950,207,149.472,7056pi }}{text{ F/m}}}$
even if the result was irrational (because the fraction contained π).^[9] In contrast, the ampere was a measured quantity before 2019, but since then the ampere is now exactly defined and it is μ₀ that is an experimentally measured quantity (with consequent uncertainty) and therefore so is the new 2019 definition of ε₀ (c₀ remains exactly defined before and since 2019).

Relative permittivity[edit]

The linear permittivity of a homogeneous material is usually given relative to that of free space, as a relative permittivity ε_r (also called dielectric constant, although this term is deprecated and sometimes only refers to the static, zero-frequency relative permittivity). In an anisotropic material, the relative permittivity may be a tensor, causing birefringence. The actual permittivity is then calculated by multiplying the relative permittivity by ε₀:

${displaystyle varepsilon =varepsilon _{mathrm {r} }varepsilon _{0}=(1+chi )varepsilon _{0},}$

where χ (frequently written χ_e) is the electric susceptibility of the material.

The susceptibility is defined as the constant of proportionality (which may be a tensor) relating an electric field E to the induced dielectric polarization density P such that

${displaystyle mathbf {P} =varepsilon _{0}chi mathbf {E} ,}$

where ε₀ is the electric permittivity of free space.

The susceptibility of a medium is related to its relative permittivity ε_r by

${displaystyle chi =varepsilon _{mathrm {r} }-1.}$

So in the case of a vacuum,

The susceptibility is also related to the polarizability of individual particles in the medium by the Clausius-Mossotti relation.

The electric displacement D is related to the polarization density P by

${displaystyle mathbf {D} =varepsilon _{0}mathbf {E} +mathbf {P} =varepsilon _{0}(1+chi )mathbf {E} =varepsilon _{mathrm {r} }varepsilon _{0}mathbf {E} .}$

The permittivity ε and permeability µ of a medium together determine the phase velocity v = c/n of electromagnetic radiation through that medium:

$varepsilon mu ={frac {1}{v^{2}}}.$

Practical applications[edit]

Determining capacitance[edit]

The capacitance of a capacitor is based on its design and architecture, meaning it will not change with charging and discharging. The formula for capacitance in a parallel plate capacitor is written as

${displaystyle C=varepsilon {frac {A}{d}}}$

where is the area of one plate, is the distance between the plates, and is the permittivity of the medium between the two plates. For a capacitor with relative permittivity kappa , it can be said that

${displaystyle C=kappa varepsilon _{0}{frac {A}{d}}}$

Gauss’s law[edit]

Permittivity is connected to electric flux (and by extension electric field) through Gauss’s law. Gauss’s law states that for a closed Gaussian surface, S,

${displaystyle Phi _{E}={frac {Q_{text{enc}}}{varepsilon _{0}}}=oint _{S}mathbf {E} cdot mathrm {d} mathbf {A} ,}$

where $Phi _{E}$ is the net electric flux passing through the surface, ${displaystyle Q_{text{enc}}}$ is the charge enclosed in the Gaussian surface, is the electric field vector at a given point on the surface, and is a differential area vector on the Gaussian surface.

If the Gaussian surface uniformly encloses an insulated, symmetrical charge arrangement, the formula can be simplified to

${displaystyle EAcos(theta )={frac {Q_{text{enc}}}{varepsilon _{0}}},}$

where theta represents the angle between the electric field lines and the normal (perpendicular) to S.

If all of the electric field lines cross the surface at 90°, the formula can be further simplified to

${displaystyle E={frac {Q_{text{enc}}}{varepsilon _{0}A}}.}$

Because the surface area of a sphere is $4pi r^{2}$ , the electric field a distance away from a uniform, spherical charge arrangement is

${displaystyle E={frac {Q}{varepsilon _{0}A}}={frac {Q}{varepsilon _{0}left(4pi r^{2}right)}}={frac {Q}{4pi varepsilon _{0}r^{2}}}.}$

This formula applies to the electric field due to a point charge, outside of a conducting sphere or shell, outside of a uniformly charged insulating sphere, or between the plates of a spherical capacitor.

Dispersion and causality[edit]

In general, a material cannot polarize instantaneously in response to an applied field, and so the more general formulation as a function of time is

${displaystyle mathbf {P} (t)=varepsilon _{0}int _{-infty }^{t}chi left(t-t'right)mathbf {E} left(t'right),dt'.}$

That is, the polarization is a convolution of the electric field at previous times with time-dependent susceptibility given by χ(Δt). The upper limit of this integral can be extended to infinity as well if one defines χ(Δt) = 0 for Δt < 0. An instantaneous response would correspond to a Dirac delta function susceptibility χ(Δt) = χδ(Δt).

It is convenient to take the Fourier transform with respect to time and write this relationship as a function of frequency. Because of the convolution theorem, the integral becomes a simple product,

${displaystyle mathbf {P} (omega )=varepsilon _{0}chi (omega )mathbf {E} (omega ).}$

This frequency dependence of the susceptibility leads to frequency dependence of the permittivity. The shape of the susceptibility with respect to frequency characterizes the dispersion properties of the material.

Moreover, the fact that the polarization can only depend on the electric field at previous times (i.e. effectively χ(Δt) = 0 for Δt < 0), a consequence of causality, imposes Kramers–Kronig constraints on the susceptibility χ(0).

Complex permittivity[edit]

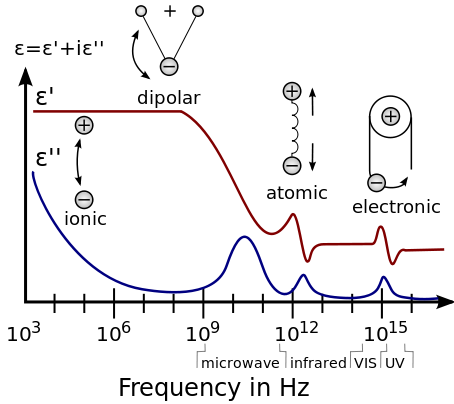
A dielectric permittivity spectrum over a wide range of frequencies. ε′ and ε″ denote the real and the imaginary part of the permittivity, respectively. Various processes are labeled on the image: ionic and dipolar relaxation, and atomic and electronic resonances at higher energies.^[10]

As opposed to the response of a vacuum, the response of normal materials to external fields generally depends on the frequency of the field. This frequency dependence reflects the fact that a material’s polarization does not change instantaneously when an electric field is applied. The response must always be causal (arising after the applied field), which can be represented by a phase difference. For this reason, permittivity is often treated as a complex function of the (angular) frequency ω of the applied field:

{displaystyle varepsilon rightarrow {hat {varepsilon }}(omega )}

(since complex numbers allow specification of magnitude and phase). The definition of permittivity therefore becomes

${displaystyle D_{0}e^{-iomega t}={hat {varepsilon }}(omega )E_{0}e^{-iomega t},}$

where

D₀ and E₀ are the amplitudes of the displacement and electric fields, respectively,
i is the imaginary unit, i² = −1.

The response of a medium to static electric fields is described by the low-frequency limit of permittivity, also called the static permittivity ε_s (also ε_DC):

${displaystyle varepsilon _{mathrm {s} }=lim _{omega rightarrow 0}{hat {varepsilon }}(omega ).}$

At the high-frequency limit (meaning optical frequencies), the complex permittivity is commonly referred to as ε_∞ (or sometimes ε_opt^[11]). At the plasma frequency and below, dielectrics behave as ideal metals, with electron gas behavior. The static permittivity is a good approximation for alternating fields of low frequencies, and as the frequency increases a measurable phase difference δ emerges between D and E. The frequency at which the phase shift becomes noticeable depends on temperature and the details of the medium. For moderate field strength (E₀), D and E remain proportional, and

${displaystyle {hat {varepsilon }}={frac {D_{0}}{E_{0}}}=|varepsilon |e^{-idelta }.}$

Since the response of materials to alternating fields is characterized by a complex permittivity, it is natural to separate its real and imaginary parts, which is done by convention in the following way:

${displaystyle {hat {varepsilon }}(omega )=varepsilon '(omega )-ivarepsilon ''(omega )=left|{frac {D_{0}}{E_{0}}}right|left(cos delta -isin delta right).}$

where

ε′ is the real part of the permittivity;
ε″ is the imaginary part of the permittivity;
δ is the loss angle.

The choice of sign for time-dependence, e^−iωt, dictates the sign convention for the imaginary part of permittivity. The signs used here correspond to those commonly used in physics, whereas for the engineering convention one should reverse all imaginary quantities.

The complex permittivity is usually a complicated function of frequency ω, since it is a superimposed description of dispersion phenomena occurring at multiple frequencies. The dielectric function ε(ω) must have poles only for frequencies with positive imaginary parts, and therefore satisfies the Kramers–Kronig relations. However, in the narrow frequency ranges that are often studied in practice, the permittivity can be approximated as frequency-independent or by model functions.

At a given frequency, the imaginary part, ε″, leads to absorption loss if it is positive (in the above sign convention) and gain if it is negative. More generally, the imaginary parts of the eigenvalues of the anisotropic dielectric tensor should be considered.

In the case of solids, the complex dielectric function is intimately connected to band structure. The primary quantity that characterizes the electronic structure of any crystalline material is the probability of photon absorption, which is directly related to the imaginary part of the optical dielectric function ε(ω). The optical dielectric function is given by the fundamental expression:^[12]

${displaystyle varepsilon (omega )=1+{frac {8pi ^{2}e^{2}}{m^{2}}}sum _{c,v}int W_{c,v}(E){bigl (}varphi (hbar omega -E)-varphi (hbar omega +E){bigr )},dx.}$

In this expression, W_c,v(E) represents the product of the Brillouin zone-averaged transition probability at the energy E with the joint density of states,^[13]^[14] J_c,v(E); φ is a broadening function, representing the role of scattering in smearing out the energy levels.^[15] In general, the broadening is intermediate between Lorentzian and Gaussian;^[16]^[17] for an alloy it is somewhat closer to Gaussian because of strong scattering from statistical fluctuations in the local composition on a nanometer scale.

Tensorial permittivity[edit]

According to the Drude model of magnetized plasma, a more general expression which takes into account the interaction of the carriers with an alternating electric field at millimeter and microwave frequencies in an axially magnetized semiconductor requires the expression of the permittivity as a non-diagonal tensor.^[18] (see also Electro-gyration).

${displaystyle mathbf {D} (omega )={begin{vmatrix}varepsilon _{1}&-ivarepsilon _{2}&0\ivarepsilon _{2}&varepsilon _{1}&0\0&0&varepsilon _{z}\end{vmatrix}}operatorname {mathbf {E} } (omega )}$

If ε₂ vanishes, then the tensor is diagonal but not proportional to the identity and the medium is said to be a uniaxial medium, which has similar properties to a uniaxial crystal.

Classification of materials[edit]

Classification of materials based on permittivity

ε_r″/ε_r′	Current conduction	Field propagation
0		perfect dielectric lossless medium
≪ 1	low-conductivity material poor conductor	low-loss medium good dielectric
≈ 1	lossy conducting material	lossy propagation medium
≫ 1	high-conductivity material good conductor	high-loss medium poor dielectric
∞	perfect conductor

Materials can be classified according to their complex-valued permittivity ε, upon comparison of its real ε′ and imaginary ε″ components (or, equivalently, conductivity, σ, when accounted for in the latter). A perfect conductor has infinite conductivity, σ = ∞, while a perfect dielectric is a material that has no conductivity at all, σ = 0; this latter case, of real-valued permittivity (or complex-valued permittivity with zero imaginary component) is also associated with the name lossless media.^[19] Generally, when σ/ωε′ ≪ 1 we consider the material to be a low-loss dielectric (although not exactly lossless), whereas σ/ωε′ ≫ 1 is associated with a good conductor; such materials with non-negligible conductivity yield a large amount of loss that inhibit the propagation of electromagnetic waves, thus are also said to be lossy media. Those materials that do not fall under either limit are considered to be general media.

Lossy medium[edit]

In the case of a lossy medium, i.e. when the conduction current is not negligible, the total current density flowing is:

${displaystyle J_{text{tot}}=J_{mathrm {c} }+J_{mathrm {d} }=sigma E+iomega varepsilon 'E=iomega {hat {varepsilon }}E}$

where

Note that this is using the electrical engineering convention of the Complex conjugate ambiguity; the physics/chemistry convention involves the complex conjugate of these equations.

The size of the displacement current is dependent on the frequency ω of the applied field E; there is no displacement current in a constant field.

In this formalism, the complex permittivity is defined as:^[20]^[21]

${displaystyle {hat {varepsilon }}=varepsilon 'left(1-i{frac {sigma }{omega varepsilon '}}right)=varepsilon '-i{frac {sigma }{omega }}}$

In general, the absorption of electromagnetic energy by dielectrics is covered by a few different mechanisms that influence the shape of the permittivity as a function of frequency:

First are the relaxation effects associated with permanent and induced molecular dipoles. At low frequencies the field changes slowly enough to allow dipoles to reach equilibrium before the field has measurably changed. For frequencies at which dipole orientations cannot follow the applied field because of the viscosity of the medium, absorption of the field’s energy leads to energy dissipation. The mechanism of dipoles relaxing is called dielectric relaxation and for ideal dipoles is described by classic Debye relaxation.
Second are the resonance effects, which arise from the rotations or vibrations of atoms, ions, or electrons. These processes are observed in the neighborhood of their characteristic absorption frequencies.

The above effects often combine to cause non-linear effects within capacitors. For example, dielectric absorption refers to the inability of a capacitor that has been charged for a long time to completely discharge when briefly discharged. Although an ideal capacitor would remain at zero volts after being discharged, real capacitors will develop a small voltage, a phenomenon that is also called soakage or battery action. For some dielectrics, such as many polymer films, the resulting voltage may be less than 1–2% of the original voltage. However, it can be as much as 15–25% in the case of electrolytic capacitors or supercapacitors.

Quantum-mechanical interpretation[edit]

In terms of quantum mechanics, permittivity is explained by atomic and molecular interactions.

At low frequencies, molecules in polar dielectrics are polarized by an applied electric field, which induces periodic rotations. For example, at the microwave frequency, the microwave field causes the periodic rotation of water molecules, sufficient to break hydrogen bonds. The field does work against the bonds and the energy is absorbed by the material as heat. This is why microwave ovens work very well for materials containing water. There are two maxima of the imaginary component (the absorptive index) of water, one at the microwave frequency, and the other at far ultraviolet (UV) frequency. Both of these resonances are at higher frequencies than the operating frequency of microwave ovens.

At moderate frequencies, the energy is too high to cause rotation, yet too low to affect electrons directly, and is absorbed in the form of resonant molecular vibrations. In water, this is where the absorptive index starts to drop sharply, and the minimum of the imaginary permittivity is at the frequency of blue light (optical regime).

At high frequencies (such as UV and above), molecules cannot relax, and the energy is purely absorbed by atoms, exciting electron energy levels. Thus, these frequencies are classified as ionizing radiation.

While carrying out a complete ab initio (that is, first-principles) modelling is now computationally possible, it has not been widely applied yet. Thus, a phenomenological model is accepted as being an adequate method of capturing experimental behaviors. The Debye model and the Lorentz model use a first-order and second-order (respectively) lumped system parameter linear representation (such as an RC and an LRC resonant circuit).

Measurement[edit]

The relative permittivity of a material can be found by a variety of static electrical measurements. The complex permittivity is evaluated over a wide range of frequencies by using different variants of dielectric spectroscopy, covering nearly 21 orders of magnitude from 10⁻⁶ to 10¹⁵ hertz. Also, by using cryostats and ovens, the dielectric properties of a medium can be characterized over an array of temperatures. In order to study systems for such diverse excitation fields, a number of measurement setups are used, each adequate for a special frequency range.

Various microwave measurement techniques are outlined in Chen et al..^[22] Typical errors for the Hakki-Coleman method employing a puck of material between conducting planes are about 0.3%.^[23]

Low-frequency time domain measurements (10⁻⁶ to 10³ Hz)
Low-frequency frequency domain measurements (10⁻⁵ to 10⁶ Hz)
Reflective coaxial methods (10⁶ to 10¹⁰ Hz)
Transmission coaxial method (10⁸ to 10¹¹ Hz)
Quasi-optical methods (10⁹ to 10¹⁰ Hz)
Terahertz time-domain spectroscopy (10¹¹ to 10¹³ Hz)
Fourier-transform methods (10¹¹ to 10¹⁵ Hz)

At infrared and optical frequencies, a common technique is ellipsometry. Dual polarisation interferometry is also used to measure the complex refractive index for very thin films at optical frequencies.

For the 3D measurement of dielectric tensors at optical frequency, Dielectric tensor tomography [1] can be used.

Notes[edit]

^ Current practice of standards organizations such as NIST and BIPM is to use c₀, rather than c, to denote the speed of light in vacuum according to ISO 31. In the original Recommendation of 1983, the symbol c was used for this purpose.^[8]

References[edit]

^ Landau, L. D.; Lifshitz, E. M.; Pitaevskii, L. P. (2009). Electrodynamics of continuous media. Elsevier Butterworth-Heinemann. ISBN 978-0-7506-2634-7. OCLC 756385298.
^ IEEE Standards Board (1997). «IEEE Standard Definitions of Terms for Radio Wave Propagation». IEEE STD 211-1997: 6.
^ Braslavsky, S.E. (2007). «Glossary of terms used in photochemistry (IUPAC recommendations 2006)» (PDF). Pure and Applied Chemistry. 79 (3): 293–465. doi:10.1351/pac200779030293. S2CID 96601716.
^ Fleming, John Ambrose (1910). The Principles of Electric Wave Telegraphy. p. 340..
^ International Bureau of Weights and Measures (2006), The International System of Units (SI) (PDF) (8th ed.), ISBN 92-822-2213-6, archived (PDF) from the original on 2021-06-04, retrieved 2021-12-16, p. 119
^ «2018 CODATA Value: vacuum electric permittivity». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
^ «Latest (2018) values of the constants (NIST)». Physics.nist.gov. 2019-05-20. Retrieved 2022-02-05.
^ «Special Publication 330, Appendix 2″ (PDF). NIST: 45. Archived from the original (PDF) on 2016-06-03..
^ «Latest (2006) values of the constants (NIST)». Physics.nist.gov. 2017-07-01. Retrieved 2018-11-20.
^ «Dielectric Spectroscopy». Archived from the original on 2006-01-18. Retrieved 2018-11-20.
^
Hofmann, Philip (2015-05-26). Solid State Physics (2 ed.). Wiley-VCH. p. 194. ISBN 978-3527412822.
^
Peter Y. Yu; Manuel Cardona (2001). Fundamentals of Semiconductors: Physics and Materials Properties. Berlin: Springer. p. 261. ISBN 978-3-540-25470-6.
^
José García Solé, Jose Solé, Luisa Bausa (2001). An introduction to the optical spectroscopy of inorganic solids. Wiley. Appendix A1, pp, 263. ISBN 978-0-470-86885-0.{{cite book}}: CS1 maint: multiple names: authors list (link)
^
John H. Moore; Nicholas D. Spencer (2001). Encyclopedia of chemical physics and physical chemistry. Taylor and Francis. p. 105. ISBN 978-0-7503-0798-7.
^
Solé, José García; Bausá, Louisa E; Jaque, Daniel (2005-03-22). Solé and Bausa. p. 10. ISBN 978-3-540-25470-6.
^
Hartmut Haug; Stephan W. Koch (1994). Quantum Theory of the Optical and Electronic Properties of Semiconductors. World Scientific. p. 196. ISBN 978-981-02-1864-5.
^
Manijeh Razeghi (2006). Fundamentals of Solid State Engineering. Birkhauser. p. 383. ISBN 978-0-387-28152-0.
^ Prati, E. (2003). «Propagation in Gyroelectromagnetic Guiding Systems». Journal of Electromagnetic Waves and Applications. 17 (8): 1177–1196. doi:10.1163/156939303322519810. S2CID 121509049.
^ Orfanidis, Sophocles J. «1: Maxwell’s Equations» (PDF). Electromagnetic Waves and Antennas. Rutgers University.
^ Seybold, John S. (2005). Introduction to RF Propagation. John Wiley & Sons. p. 22, eq. (2.6). ISBN 9780471743682.
^ Kaiser, Kenneth L. (2005). Electromagnetic Shielding. CRC Press. pp. 1–28, eqs. (1.80) and (1.81). ISBN 9780849363726.
^ Linfeng Chen; V. V. Varadan; C. K. Ong; Chye Poh Neo (2004). «Microwave theory and techniques for materials characterization». Microwave electronics. Wiley. p. 37. ISBN 978-0-470-84492-2.
^ Mailadil T. Sebastian (2008). Dielectric Materials for Wireless Communication. Elsevier. p. 19. ISBN 978-0-08-045330-9.

External links[edit]

Electromagnetism, a chapter from an online textbook

Источник

Диэлектрическая среда, показывающая ориентацию заряженных частиц, создающих эффекты поляризации. Такая среда может иметь более низкое отношение электрического потока к заряду (большую диэлектрическую проницаемость), чем пустое пространство

В электромагнетизме абсолютная диэлектрическая проницаемость, часто называемая просто диэлектрической проницаемостью и обозначается греческой буквой ε (эпсилон), является мерой электрической поляризуемости диэлектрика. Материал с высокой диэлектрической проницаемостью поляризуется больше в ответ на приложенное электрическое поле, чем материал с низкой диэлектрической проницаемостью, тем самым накапливая больше энергии в материале. В электростатике диэлектрическая проницаемость играет важную роль в определении емкости конденсатора.

В простейшем случае поле электрического смещения D { displaystyle mathbf {D}}, возникающее в результате приложенного электрического поля E { displaystyle mathbf {E}}равно

D = ε E. { displaystyle mathbf {D} = varepsilon mathbf {E}.}

В общем, диэлектрическая проницаемость — это термодинамическая функция состояния. Это может зависеть от частоты, величины и направления приложенного поля. Единица измерения диэлектрической проницаемости в системе СИ составляет фарад на метр (Ф / м).

Диэлектрическая проницаемость часто представлена относительной диэлектрической проницаемостью ε r { displaystyle varepsilon _ { textrm {r}}} ${ displaystyle varepsilon _ { textrm {r}}}$ , которая является отношением абсолютной диэлектрической проницаемости ε { displaystyle varepsilon}и вакуумной проницаемости ε 0 { displaystyle varepsilon _ {0}} $varepsilon _ {0}$

κ = ε r = ε ε 0 { displaystyle kappa = varepsilon _ { mathrm {r}} = { frac { varepsilon} { varepsilon _ {0}}}} ${ displaystyle kappa = varepsilon _ { mathrm {r}} = { frac { varepsilon} { varepsilon _ {0}}}}$

Эта безразмерная величина также часто бывает неоднозначно называют диэлектрической проницаемостью. Другой общий термин, встречающийся как для абсолютной, так и для относительной диэлектрической проницаемости, — это диэлектрическая проницаемость, которая не приветствуется в физике и технике, а также в химии.

По определению, идеальный вакуум имеет относительную диэлектрическую проницаемость ровно 1, тогда как при STP, воздух имеет относительную диэлектрическую проницаемость κ air = 1.0006.

Относительная диэлектрическая проницаемость напрямую связана с электрической восприимчивостью (χ) посредством

χ = κ — 1 { displaystyle chi = kappa -1}

иначе записывается как

ε знак равно ε р ε 0 знак равно (1 + χ) ε 0 { Displaystyle varepsilon = varepsilon _ { mathrm {r}} varepsilon _ {0} = (1+ chi) varepsilon _ {0 }} ${ displaystyle varepsilon = varepsilon _ { mathrm {r}} varepsilon _ {0} = (1+ chi) varepsilon _ {0}}$

Содержание

1 Единицы
2 Пояснение
3 Вакуумная диэлектрическая проницаемость
4 Относительная диэлектрическая проницаемость
5 Практическое применение
- 5.1 Определение емкости
- 5.2 Закон Гаусса
6 Дисперсия и причинно-следственная связь
- 6.1 Комплексная диэлектрическая проницаемость
- 6.2 Тензорная диэлектрическая проницаемость
- 6.3 Классификация материалов
- 6.4 Несущая среда
- 6.5 Квантово-механическая интерпретация
7 Измерение
8 См. Также
9 Примечания
10 Ссылки
11 Дополнительная литература
12 Внешние ссылки

Единицы

Стандартная единица измерения диэлектрической проницаемости в системе СИ — фарад на метр (Ф / м или Ф · м).

F m = CV ⋅ m = C 2 N ⋅ m 2 = C 2 ⋅ s 2 кг ⋅ м 3 { displaystyle { frac { text {F}} { text {m}}} = { frac { text {C}} {{ text {V}} { cdot} { text {m}}}} = { frac {{ text {C}} ^ {2}} {{ text {N}} { cdot} { text {m}} ^ {2}} } = { frac {{ text {C}} ^ {2} { cdot} { text {s}} ^ {2}} {{ text {kg}} { cdot} { text {m }} ^ {3}}}} ${ displaystyle { frac { text {F}} { text {m}}} = { frac { text {C}} {{ text {V}} { cdot} { text {m}}} } = { frac {{ text {C}} ^ {2}} {{ text {N}} { cdot} { text {m}} ^ {2}}} = { frac {{ текст {C}} ^ {2} { cdot} { text {s}} ^ {2}} {{ text {kg}} { cdot} { text {m}} ^ {3}}} }$

Объяснение

В электромагнетизме поле электрического смещения Dпредставляет собой распределение электрических зарядов в данной среде, возникающее в результате наличие электрического поля E . Это распределение включает миграцию заряда и электрическую дипольную переориентацию. Его отношение к диэлектрической проницаемости в очень простом случае линейных, однородных, изотропных материалов с «мгновенным» откликом на изменения электрического поля:

D = ε E { displaystyle mathbf {D} = varepsilon mathbf {E}}

, где диэлектрическая проницаемость ε является скаляром. Если среда анизотропна, диэлектрическая проницаемость является тензором второго ранга .

В общем, диэлектрическая проницаемость не является постоянной, так как она может меняться в зависимости от положения в среде, частоты поля применяется, влажность, температура и другие параметры. В нелинейной среде диэлектрическая проницаемость может зависеть от напряженности электрического поля. Диэлектрическая проницаемость как функция частоты может принимать действительные или комплексные значения.

В единицах СИ диэлектрическая проницаемость измеряется в фарадах на метр (Ф / м или А · с · кг · м). Поле смещения D измеряется в единицах кулонов на квадратный метр (Кл / м), а электрическое поле E измеряется в в на метр (В / м). D и E описывают взаимодействие между заряженными объектами. D связан с плотностями заряда, связанными с этим взаимодействием, тогда как E связан с силами и разностями потенциалов.

Диэлектрическая проницаемость вакуума

Диэлектрическая проницаемость вакуума ε 0 (также называемая диэлектрической проницаемостью свободного пространства или электрической постоянной ) равна соотношение D/Eв свободном пространстве. Он также появляется в постоянной кулоновской силы,

ke = 1 4 π ε 0 { displaystyle k _ { text {e}} = { frac {1} {4 pi varepsilon _ {0}} }} ${ displaystyle k _ { text {e}} = { frac {1} {4 pi varepsilon _ {0}}}}$

Его значение

ε 0 = def 1 c 0 2 μ 0 = 1 35 950 207 149,472 7056 π F / м ≈ 8,854 187 8176… × 10 — 12 F / м { displaystyle varepsilon _ {0} { stackrel { mathrm {def}} {=}} { frac {1} {c_ {0} ^ {2} mu _ {0}}} = { frac {1} {35 , 950 , 207 , 149.472 , 7056 pi}} { text {F / m}} приблизительно 8.854 , 187 , 8176 ldots times 10 ^ {- 12} { text {F / m}}} ${ displaystyle varepsilon _ {0} { stackrel { mathrm {def}} {=}} { frac {1 } {c_ {0} ^ {2} mu _ {0}}} = { frac {1} {35 , 950 , 207 , 149.472 , 7056 pi}} { text {F / m }} приблизительно 8,854 , 187 , 8176 ldots times 10 ^ {- 12} { text {F / m}}} $

где

c0- скорость света в свободном пространстве,
µ0- проницаемость вакуума.

Константы c 0 и μ 0 были определены в единицах СИ, чтобы иметь точные числовые значения до переопределения единиц СИ в 2019 году. (Аппроксимация во втором значении ε 0 выше проистекает из того, что π является иррациональное число.)

Относительная диэлектрическая проницаемость

Линейная диэлектрическая проницаемость однородного материала обычно дается относительно диэлектрической проницаемости свободного пространства, как относительная диэлектрическая проницаемость ε r (также c называется диэлектрическая проницаемость, хотя этот термин устарел и иногда относится только к статической относительной диэлектрической проницаемости при нулевой частоте). В анизотропном материале относительная диэлектрическая проницаемость может быть тензором, вызывающим двойное лучепреломление. Фактическая диэлектрическая проницаемость затем вычисляется путем умножения относительной диэлектрической проницаемости на ε 0:

ε = ε r ε 0 = (1 + χ) ε 0, { displaystyle varepsilon = varepsilon _ { mathrm {r}} varepsilon _ {0} = (1+ chi) varepsilon _ {0},} ${ displaystyle varepsilon = varepsilon _ { mathrm {r}} varepsilon _ {0} = (1+ chi) varepsilon _ {0},}$

где χ (часто пишется как χ e) — электрическая восприимчивость материала.

Восприимчивость определяется как константа пропорциональности (которая может быть тензором ), связывающая электрическое поле Eс индуцированным диэлектриком плотность поляризации Pтакая, что

P = ε 0 χ E, { displaystyle mathbf {P} = varepsilon _ {0} chi mathbf {E},} ${ displaystyle mathbf {P} = varepsilon _ {0} chi mathbf {E},}$

где ε 0 — электрическая проницаемость свободного пространства..

Восприимчивость среды связана с ее относительной диэлектрической проницаемостью ε r соотношением

χ = ε r — 1. { displaystyle chi = varepsilon _ { mathrm {r}} -1.} ${ displaystyle chi = varepsilon _ { mathrm {r}} -1.}$

Итак, в случае вакуума

χ = 0. { displaystyle chi = 0.}

Восприимчивость также связано с поляризуемостью отдельных частиц в среде посредством соотношения Клаузиуса-Моссотти.

. электрическое смещение Dсвязано с плотностью поляризации P по

D = ε 0 E + P = ε 0 (1 + χ) E = ε r ε 0 E. { displaystyle mathbf {D} = varepsilon _ {0} mathbf {E} + mathbf {P} = varepsilon _ {0} (1+ chi) mathbf {E} = varepsilon _ { mathrm {r}} varepsilon _ {0} mathbf {E}.} ${ displaystyle mathbf {D} = varepsilon _ {0} mathbf {E} + mathbf {P} = varepsilon _ {0} (1+ chi) mathbf {E} = varepsilon _ { mathrm {r}} varepsilon _ {0} mathbf {E}.}$

Диэлектрическая проницаемость ε и проницаемость µ среды вместе определяют фазовую скорость v = c / n электромагнитного излучения через эту среду:

ε μ = 1 v 2. { displaystyle varepsilon mu = { frac {1} {v ^ {2}}}.} $varepsilon mu = { frac {1} {v ^ {2}}}.$

Практическое применение

Определение емкости

Емкость конденсатора основана на на его дизайн и архитектуру, то есть он не изменится при зарядке и разрядке. Формула для емкости в конденсаторе с параллельными пластинами записывается как

C = ε A d { displaystyle C = varepsilon { frac {A} {d}}} ${ displaystyle C = varepsilon { frac {A} {d}}}$

где A { displaystyle A}— площадь одной пластины, d { displaystyle d}— расстояние между пластинами, а ε { displaystyle varepsilon}— диэлектрическая проницаемость среды между двумя пластинами. Для конденсатора с относительной диэлектрической проницаемостью κ { displaystyle kappa} kappa можно сказать, что

C = κ ε 0 A d { displaystyle C = kappa varepsilon _ { 0} { frac {A} {d}}} ${ displaystyle C = kappa varepsilon _ {0} { frac {A} {d}}}$

Закон Гаусса

Диэлектрическая проницаемость связана с электрическим потоком (и, как следствие, электрическим полем) через закон Гаусса. Закон Гаусса гласит, что для замкнутой гауссовой поверхности s

Φ E = Q enc ε 0 = ∮ s E ⋅ d A { displaystyle Phi _ {E} = { frac {Q_ { text {enc}}} { varepsilon _ {0}}} = oint _ {s} mathbf {E} cdot mathrm {d} mathbf {A}} ${ displaystyle Phi _ {E} = { frac {Q _ { text {enc}}} { varepsilon _ {0}}} = oint _ {s} mathbf {E} cdot mathrm {d} mathbf {A}}$

где Φ E { displaystyle Phi _ {E}} $Phi _ {E}$ — чистый электрический поток, проходящий через поверхность, Q enc { displaystyle Q _ { text {enc}}} ${ displaystyle Q _ { text {enc}}}$ равно заряд, заключенный в гауссовой поверхности, E { displaystyle mathbf {E}}— вектор электрического поля в данной точке на поверхности, и d A { displaystyle mathrm {d} mathbf {A}}— вектор дифференциальной площади на гауссовой поверхности.

Если гауссова поверхность равномерно охватывает изолированное симметричное расположение зарядов, формулу можно упростить до

EA cos ⁡ (θ) = Q enc ε 0 { displaystyle EA cos ( theta) = { frac {Q _ { text {enc}}} { varepsilon _ {0}}}} ${ displaystyle EA cos ( theta) = { frac {Q _ { text {enc}}} { varepsilon _ {0}}} }$

где θ { displaystyle theta} theta представляет собой угол между электрическими полями вектор и вектор площади.

Если все силовые линии электрического поля пересекают поверхность под углом 90 °, формулу можно упростить до

E = Q enc ε 0 A { displaystyle E = { frac {Q _ { text {enc}}} { varepsilon _ {0} A}}} ${ displaystyle E = { frac {Q _ { text {enc}}} { varepsilon _ {0} A}}}$

Поскольку площадь поверхности сферы равна 4 π r 2 { displaystyle 4 pi r ^ {2}} $4 pi r ^ {2}$ , электрическое поле на расстоянии r { displaystyle r}от однородного сферического заряда составляет

E = Q ε 0 A = Q ε 0 (4 π r 2) { displaystyle E = { frac {Q} { varepsilon _ {0} A}} = { frac {Q} { varepsilon _ {0} left (4 pi r ^ {2} right) }}} ${ displaystyle E = { frac {Q} { varepsilon _ {0} A}} = { frac {Q} { varepsilon _ {0} left (4 pi r ^ {2} right)}}}$

E = Q 4 π ε 0 r 2 = k Q r 2 { displaystyle E = { frac {Q} {4 pi varepsilon _ {0} r ^ {2}}} = { frac {kQ} {r ^ {2}}}} ${ displaystyle E = { frac {Q} {4 pi varepsilon _ {0} r ^ {2}}} = { frac {kQ} {r ^ {2}}}}$

где k { displaystyle k}— постоянная Кулона (∼ 9,0 × 10 9 м / F { displaystyle sim 9.0 times 10 ^ {9} { text {m}} / { text {F}}} ${ displaystyle sim 9.0 times 10 ^ {9} { text {m}} / { text {F}}}$ ). Эта формула применяется к электрическому полю, создаваемому точечным зарядом, вне проводящей сферы или оболочки, вне однородно заряженной изолирующей сферы или между пластинами сферического конденсатора.

Дисперсия и причинно-следственная связь

В общем, материал не может поляризоваться мгновенно в ответ на приложенное поле, поэтому более общая формулировка как функция времени:

P (t) = ε 0 ∫ — ∞ t χ (t — t ′) E (t ′) dt ′. { displaystyle mathbf {P} (t) = varepsilon _ {0} int _ {- infty} ^ {t} chi left (t-t ‘ right) mathbf {E} left ( t ‘ right) , dt’.} ${displaystyle mathbf {P} (t)=varepsilon _{0}int _{-infty }^{t}chi left(t-t'right)mathbf {E} left(t'right),dt'.}$

То есть поляризация представляет собой свертку электрического поля в предыдущие моменты времени с зависящей от времени восприимчивостью, определяемой как χ (Δt). Верхний предел этого интеграла можно расширить до бесконечности, если определить χ (Δt) = 0 для Δt < 0. An instantaneous response would correspond to a дельта-функции Дирака восприимчивости χ (Δt) = χδ (Δt).

Удобно взять преобразование Фурье по времени и записать это соотношение как функцию частоты. Благодаря теореме о свертке интеграл становится простым произведением

P (ω) = ε 0 χ (ω) E (ω). { displaystyle mathbf {P} ( omega) = varepsilon _ {0} chi ( omega) mathbf {E} ( omega).} ${ displaystyle mathbf {P} ( omega) = varepsilon _ {0} chi ( omega) mathbf {E} ( omega).}$

Эта частотная зависимость восприимчивости приводит к частотной зависимости диэлектрическая проницаемость. Форма восприимчивости по отношению к частоте характеризует дисперсионные свойства материала.

Более того, тот факт, что поляризация может зависеть только от электрического поля в предыдущие моменты времени (т.е. эффективно χ (Δt) = 0 для Δt < 0), a consequence of причинно-следственной связи, накладывает ограничения Крамерса – Кронига от восприимчивости χ (0).

Комплексная диэлектрическая проницаемость

Спектр диэлектрической проницаемости в широком диапазоне частот. Ε ′ и ε ″ обозначают действительную и мнимую части диэлектрической проницаемости соответственно. На изображении обозначены различные процессы: ионная и диполярная релаксация, а также атомные и электронные резонансы при более высоких энергиях.

В отличие от реакции вакуума, реакция обычных материалов на внешние поля обычно зависит от частота поля. Эта частотная зависимость отражает тот факт, что поляризация материала не изменяется мгновенно при приложении электрического поля. Отклик всегда должен быть причинным (возникающим после приложенного поля), который может быть представлен фазой разница. По этой причине диэлектрическая проницаемость i s часто рассматривается как комплексная функция (угловой) частоты ω приложенного поля:

ε → ε ^ (ω) { displaystyle varepsilon rightarrow { hat { varepsilon}} ( omega)}

(поскольку комплексные числа позволяют указать величину и фазу). Таким образом, определение диэлектрической проницаемости становится

D 0 e — i ω t = ε ^ (ω) E 0 e — i ω t, { displaystyle D_ {0} e ^ {- i omega t} = { hat { varepsilon}} ( omega) E_ {0} e ^ {- i omega t},} ${ displaystyle D _ {0} e ^ {- я omega t} = { hat { varepsilon}} ( omega) E_ {0} e ^ {- i omega t},}$

где

D0и E 0 — амплитуды смещения и электрического поля, соответственно,
i — мнимая единица, i = -1.

Реакция среды на статические электрические поля описывается низкочастотным пределом диэлектрической проницаемости, также называемым статическая диэлектрическая проницаемость ε s (также ε DC):

ε s = lim ω → 0 ε ^ (ω). { displaystyle varepsilon _ { mathrm {s}} = lim _ { omega rightarrow 0} { hat { varepsilon}} ( omega).} ${ displaystyle varepsilon _ { mathrm {s}} = lim _ { omega rightarrow 0} { hat { varepsilon}} ( omega).}$

На пределе высоких частот (имеется в виду оптический частот), комплексная диэлектрическая проницаемость обычно обозначается как ε ∞ (или иногда ε opt). На плазменной частоте и ниже диэлектрики ведут себя как идеальные металлы с поведением электронного газа. Статическая диэлектрическая проницаемость является хорошим приближением для переменных полей низких частот, и по мере увеличения частоты между D и E возникает измеримая разность фаз δ. Частота, при которой фазовый сдвиг становится заметным, зависит от температуры и характеристик среды. Для умеренной напряженности поля (E 0), D и E остаются пропорциональными, а

ε ^ = D 0 E 0 = | ε | е — я δ. { displaystyle { hat { varepsilon}} = { frac {D_ {0}} {E_ {0}}} = | varepsilon | e ^ {- i delta}.} ${ displaystyle { hat { varepsilon}} = { frac {D_ {0}} {E_ {0}}} = | varepsilon | e ^ {- i delta}.}$

Поскольку ответ Материал к переменным полям характеризуется комплексной диэлектрической проницаемостью, естественно разделить ее действительную и мнимую части, что сделано условно следующим образом:

ε ^ (ω) = ε ′ (ω) — i ε ″ (ω) = | D 0 E 0 | (cos ⁡ δ — я sin ⁡ δ). { displaystyle { hat { varepsilon}} ( omega) = varepsilon ‘( omega) -i varepsilon’ » ( omega) = left | { frac {D_ {0}} {E_ {0 }}} right | left ( cos delta -i sin delta right).} ${displaystyle {hat {varepsilon }}(omega)=varepsilon '(omega)-ivarepsilon ''(omega)=left|{frac {D_{0}}{E_{0}}}right|left(cos delta -isin delta right).}$

где

ε ′ — действительная часть диэлектрической проницаемости;
ε ″ — мнимая часть диэлектрической проницаемости;
δ — угол потерь.

Выбор знака для временной зависимости e диктует соглашение о знаке для мнимой части диэлектрической проницаемости. Используемые здесь знаки соответствуют знакам, обычно используемым в физике, тогда как для инженерного соглашения необходимо перевернуть все мнимые величины.

Комплексная диэлектрическая проницаемость обычно является сложной функцией частоты ω, поскольку она представляет собой наложенное описание явлений дисперсии, происходящих на нескольких частотах. Диэлектрическая проницаемость ε (ω) должна иметь полюсы только для частот с положительными мнимыми частями и, следовательно, удовлетворяет соотношениям Крамерса – Кронига. Однако в узких частотных диапазонах, которые часто изучаются на практике, диэлектрическая проницаемость может быть аппроксимирована частотно-независимой или модельными функциями.

На данной частоте мнимая часть ε ″ приводит к потерям поглощения, если она положительна (в приведенном выше соглашении о знаках), и к усилению, если она отрицательна. В более общем плане следует учитывать мнимые части собственных значений тензора анизотропной диэлектрической проницаемости.

В случае твердых тел сложная диэлектрическая функция тесно связана с зонной структурой. Первичной величиной, которая характеризует электронную структуру любого кристаллического материала, является вероятность поглощения фотона, которая напрямую связана с мнимой частью оптической диэлектрической функции ε (ω). Оптическая диэлектрическая проницаемость задается основным выражением:

ε (ω) = 1 + 8 π 2 e 2 m 2 ∑ c, v ∫ W c, v (E) (φ (ℏ ω — E) — φ (ℏ ω + E)) dx. { displaystyle varepsilon ( omega) = 1 + { frac {8 pi ^ {2} e ^ {2}} {m ^ {2}}} sum _ {c, v} int W_ {c, v} (E) { bigl (} varphi ( hbar omega -E) — varphi ( hbar omega + E) { bigr)} , dx.} ${ displaystyle varepsilon ( omega) = 1 + { frac {8 pi ^ {2} e ^ {2}} {m ^ {2}}} sum _ {c, v} int W_ {c, v} (E) { bigl (} varphi ( hbar omega -E) - varphi ( hbar omega + E) { bigr)} , dx.}$

В этом выражении W c, v (E) представляет собой произведение средней вероятности перехода для зоны Бриллюэна при энергии E с совместной плотностью состояний, Дж c, v (E); φ — функция уширения, отражающая роль рассеяния в размытии уровней энергии. В общем, уширение является промежуточным между лоренцевым и гауссовым ; для сплава он несколько ближе к гауссову из-за сильного рассеяния на статистических флуктуациях локального состава в нанометровом масштабе.

Тензорная диэлектрическая проницаемость

Согласно модели Друде намагниченной плазмы, более общее выражение, которое учитывает взаимодействие носителей с переменным электрическим полем на миллиметрах и Микроволновые частоты в аксиально намагниченном полупроводнике требуют выражения диэлектрической проницаемости в виде недиагонального тензора. (см. также Электрогирация ).

D (ω) = | ε 1 — i ε 2 0 i ε 2 ε 1 0 0 0 ε z | Е ⁡ (ω) { Displaystyle mathbf {D} ( omega) = { begin {vmatrix} varepsilon _ {1} — я varepsilon _ {2} 0 \ i varepsilon _ {2} varepsilon _ {1} 0 \ 0 0 varepsilon _ {z} \ end {vmatrix}} operatorname { mathbf {E}} ( omega)} ${ displaystyle mathbf {D} ( omega) = { begin {vmatrix} varepsilon _ {1} -i varepsilon _ {2} 0 \ i varepsilon _ {2} varepsilon _ {1} 0 \ 0 0 varepsilon _ {z} \ end {vmatrix}} operatorname { mathbf {E }} ( omega)}$

Если ε 2 исчезает, тогда тензор диагонален, но не пропорционален идентичности, и среда называется одноосной средой, которая имеет свойства, аналогичные одноосному кристаллу.

Классификация материалов

Классификация материалов на основе диэлектрической проницаемости

εr″ /εr′	Ток проводимость	Поле распространение
0		идеальный диэлектрик. среда без потерь
≪ 1	материал с низкой проводимостью. плохой проводник	среда с низкими потерями. хороший диэлектрик
≈ 1	проводящий материал с потерями	среда распространения с потерями
≫ 1	материал с высокой проводимостью. хороший проводник	среда с высокими потерями. плохой диэлектрик
∞	идеальный проводник

Материалы можно классифицировать в соответствии с их комплексными значениями pe Эмиттерность ε при сравнении ее действительной ε ′ и мнимой ε ″ составляющих (или, что то же самое, проводимости, σ, если учитывать в последнем). идеальный проводник имеет бесконечную проводимость, σ = ∞, а идеальный диэлектрик — это материал, который вообще не имеет проводимости, σ = 0; этот последний случай действительной диэлектрической проницаемости (или комплексной диэлектрической проницаемости с нулевой мнимой составляющей) также связан с названием среды без потерь. Обычно, когда σ / ωε ′ 1, мы считаем материал диэлектриком с низкими потерями (хотя и не совсем без потерь), тогда как σ / ωε ′ ≫ 1 ассоциируется с хорошим проводником; такие материалы с существенной проводимостью дают большое количество потерь, которые препятствуют распространению электромагнитных волн, поэтому их также называют средами с потерями. Материалы, не подпадающие ни под один из ограничений, считаются общедоступными.

Среда с потерями

В случае среды с потерями, т. Е. Когда ток проводимости не является незначительным, общая плотность протекающего тока составляет:

J tot = J c + J d = σ E + я ω ε ′ E знак равно я ω ε ^ E { Displaystyle J _ { text {tot}} = J _ { mathrm {c}} + J _ { mathrm {d}} = sigma E + i omega varepsilon ‘E = i omega { hat { varepsilon}} E} ${displaystyle J_{text{tot}}=J_{mathrm {c} }+J_{mathrm {d} }=sigma E+iomega varepsilon 'E=iomega {hat {varepsilon }}E}$

, где

Величина тока смещения зависит от частота ω приложенного поля E; в постоянном поле нет тока смещения.

В этом формализме комплексная диэлектрическая проницаемость определяется как:

ε ^ = ε ′ (1 — i σ ω ε ′) = ε ′ — i σ ω { displaystyle { hat { varepsilon }} = varepsilon ‘ left (1-i { frac { sigma} { omega varepsilon’}} right) = varepsilon ‘-i { frac { sigma} { omega}}} ${displaystyle {hat {varepsilon }}=varepsilon 'left(1-i{frac {sigma }{omega varepsilon '}}right)=varepsilon '-i{frac {sigma }{omega }}}$

В общем, поглощение электромагнитной энергии диэлектриками покрывается несколькими различными механизмами, которые влияют на форму диэлектрической проницаемости в зависимости от частоты:

Во-первых, это эффекты релаксации, связанные с постоянным и постоянным током. индуцированные молекулярные диполи. На низких частотах поле изменяется достаточно медленно, чтобы позволить диполям достичь равновесия до того, как поле заметно изменится. Для частот, на которых ориентация диполей не может следовать за приложенным полем из-за вязкости среды, поглощение энергии поля приводит к диссипации энергии. Механизм релаксации диполей называется диэлектрической релаксацией, а для идеальных диполей описывается классической релаксацией Дебая.
Во-вторых, резонансными эффектами, которые возникают из-за вращений или колебаний. атомов, ионов или электронов. Эти процессы наблюдаются вблизи их характерных частот поглощения.

. Вышеуказанные эффекты часто объединяются, чтобы вызвать нелинейные эффекты в конденсаторах. Например, диэлектрическое поглощение относится к неспособности конденсатора, который был заряжен в течение длительного времени, полностью разрядиться при кратковременном разряде. Хотя идеальный конденсатор будет оставаться при нулевом напряжении после разрядки, реальные конденсаторы будут развивать небольшое напряжение, явление, которое также называется замачиванием или действием батареи. Для некоторых диэлектриков, таких как многие полимерные пленки, результирующее напряжение может быть менее 1-2% от исходного напряжения. Однако в случае электролитических конденсаторов или суперконденсаторов.

квантово-механическая интерпретация

с точки зрения квантовой механики она может достигать 15–25%., диэлектрическая проницаемость объясняется атомным и молекулярным взаимодействиями.

На низких частотах молекулы полярных диэлектриков поляризованы приложенным электрическим полем, которое вызывает периодические вращения. Например, на частоте микроволны микроволновое поле вызывает периодическое вращение молекул воды, достаточное для разрыва водородных связей. Поле действует против связей, и энергия поглощается материалом в виде тепла. Вот почему микроволновые печи очень хорошо подходят для материалов, содержащих воду. Есть два максимума мнимой составляющей (показателя поглощения) воды, один на частоте микроволн, а другой на частоте далекого ультрафиолета (УФ). Оба этих резонанса находятся на более высоких частотах, чем рабочая частота микроволновых печей.

На умеренных частотах энергия слишком высока, чтобы вызвать вращение, но слишком мала, чтобы напрямую воздействовать на электроны, и поглощается в виде резонансных молекулярных колебаний. В воде здесь показатель поглощения начинает резко падать, а минимум мнимой диэлектрической проницаемости приходится на частоту синего света (оптический режим).

На высоких частотах (например, УФ и выше) молекулы не могут релаксировать, и энергия полностью поглощается атомами, возбуждая электронные уровни энергии. Таким образом, эти частоты классифицируются как ионизирующее излучение.

. Хотя выполнение полного ab initio (то есть из первых принципов) моделирования теперь возможно с вычислительной точки зрения, оно еще не нашло широкого применения. Таким образом, феноменологическая модель считается адекватным методом фиксации экспериментального поведения. модель Дебая и модель Лоренца используют линейное представление сосредоточенных параметров системы первого и второго порядка (соответственно, RC и LRC резонансный контур).

Измерение

Относительную диэлектрическую проницаемость материала можно определить с помощью различных статических электрических измерений. Комплексная диэлектрическая проницаемость оценивается в широком диапазоне частот с использованием различных вариантов диэлектрической спектроскопии, охватывающих почти 21 порядок величины от 10 до 10 герц. Кроме того, с помощью криостатов и сушильных шкафов диэлектрические свойства среды можно охарактеризовать по множеству температур. Для изучения систем для таких разнообразных полей возбуждения используется ряд измерительных установок, каждая из которых соответствует определенному диапазону частот.

Различные методы микроволновых измерений описаны в Chen et al. Типичные ошибки при использовании шайбы материала между проводящими плоскостями составляют около 0,3%.

Низкочастотные измерения во временной области (От 10 до 10 Гц)
Низкочастотные измерения в частотной области (от 10 до 10 Гц)
Отражательные коаксиальные методы (от 10 до 10 Гц)
Коаксиальный метод передачи (от 10 до 10 Гц)
Квазиоптические методы (от 10 до 10 Гц)
Терагерцовая спектроскопия во временной области (от 10 до 10 Гц)
Фурье — методы преобразования (от 10 до 10 Гц)

В инфракрасной и оптической частотах распространенным методом является эллипсометрия. Интерферометрия с двойной поляризацией также используется для измерения комплексного показателя преломления очень тонких пленок на оптических частотах.

См. Также

Примечания

Ссылки

Дополнительная литература

C. JF Bottcher, OC von Belle Paul Bordewijk (1973) Теория электрической поляризации: диэлектрическая поляризация, том 1, (1978) том 2, Elsevier ISBN 0-444-41579-3.
Артур фон Хиппель (1954) Диэлектрики и волны ISBN 0-89006-803-8
Редактор Артура фон Хиппеля (1966) Диэлектрические материалы и Приложения: статьи 22 авторов ISBN 0-89006-805-4.

Внешние ссылки

Электромагнетизм, глава из онлайн-учебника
Что все это захваченный заряд…, Другой подход к некоторым проблемам конденсаторов
Комплексная диэлектрическая проницаемость и показатель преломления для металлов
DrudeLorentz.com Онлайн-база данных по построению графиков и параметризации моделей диэлектрической проницаемости Друде-Лоренца обычных металлов

Источник

Простое объяснение

Диэлектрическая проницаемость вакуума

Числовое значение и единица измерения

Взаимосвязь с другими константами

Закон Кулона и электрический потенциал

Диэлектрическая проницаемость: общий случай

Диэлектрическая проницаемость диэлектриков

Поляризация

Электрическая индукция

Относительная диэлектрическая проницаемость

Относительные диэлектрические проницаемости отдельных материалов

Список использованной литературы

Электроемкость конденсатора

Энергия конденсатора

Подсказки к задачам

Соединения конденсаторов

Подсказки к задачам

Разбор задач на тему «Заряженная частица в поле конденсатора»

Как найти диэлектрическую проницаемость

Units[edit]

Explanation[edit]

Vacuum permittivity[edit]

Relative permittivity[edit]

Practical applications[edit]

Determining capacitance[edit]

Gauss’s law[edit]

Dispersion and causality[edit]

Complex permittivity[edit]

Tensorial permittivity[edit]

Classification of materials[edit]

Lossy medium[edit]

Quantum-mechanical interpretation[edit]

Measurement[edit]

See also[edit]

Notes[edit]

References[edit]

Further reading[edit]

External links[edit]

Содержание

Единицы

Объяснение

Диэлектрическая проницаемость вакуума

Относительная диэлектрическая проницаемость

Практическое применение

Определение емкости

Закон Гаусса

Дисперсия и причинно-следственная связь

Комплексная диэлектрическая проницаемость

Тензорная диэлектрическая проницаемость

Классификация материалов

Среда с потерями

квантово-механическая интерпретация

Измерение

См. Также

Примечания

Ссылки

Дополнительная литература

Внешние ссылки