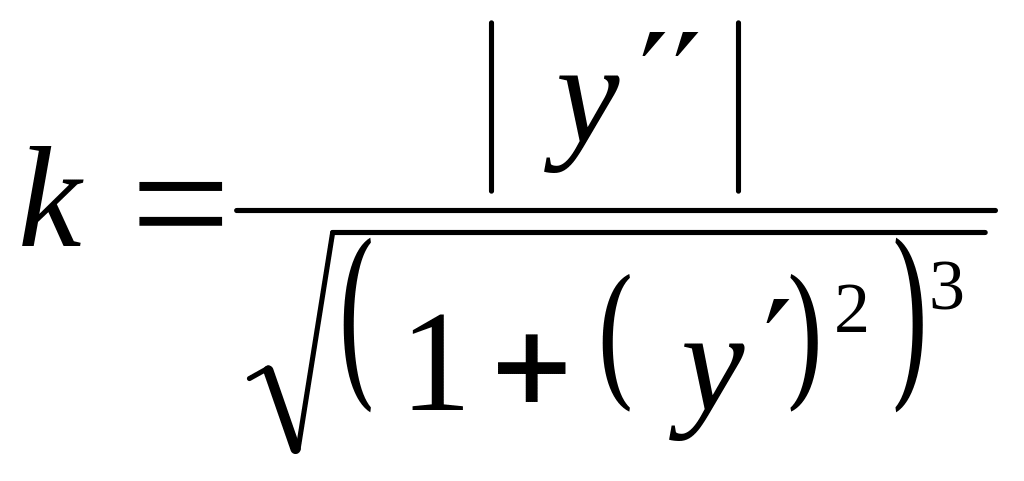Как найти дифференциал дуги - Исправление недочетов и поиск решений вместе с Examum.ru

Пусть
некоторая кривая на
заданном промежутке является гладкой
кривой, т. е. её производная непрерывна,
тогда:

если
плоская кривая отнесена к прямоугольной
системе координат и задана уравнением

,
то дифференциал длины дуги dl
выражается формулой

;

если
плоская кривая отнесена к прямоугольной
системе координат и задана уравнением

,
то дифференциал длины дуги dl
выражается формулой

;

если
плоская кривая отнесена к прямоугольной
системе координат и задана параметрически
системой уравнений

,
то дифференциал длины дуги dl
выражается формулой

где

,

;

если
плоская кривая отнесена к полярной
системе координат и задана уравнением

,
то дифференциал длины дуги dl
выражается формулой

где

С
геометрической точки зрения дифференциал
длины дуги можно представить длиной
соответствующего отрезка касательной
к линии в начальной точке дуги.

Пример.
Найти
дифференциал длины дуги кривой

.

Решение.
Представим уравнение кривой в виде

(знаки

в выражении у
указывают, что кривая симметрична оси
Ох).

Найдем
производную функции

тогда
дифференциал длины дуги данной кривой

Следовательно,

Пример.
Найти
дифференциал длины дуги кривой

.

Решение.
Найдем производную функции

тогда
дифференциал длины дуги данной кривой

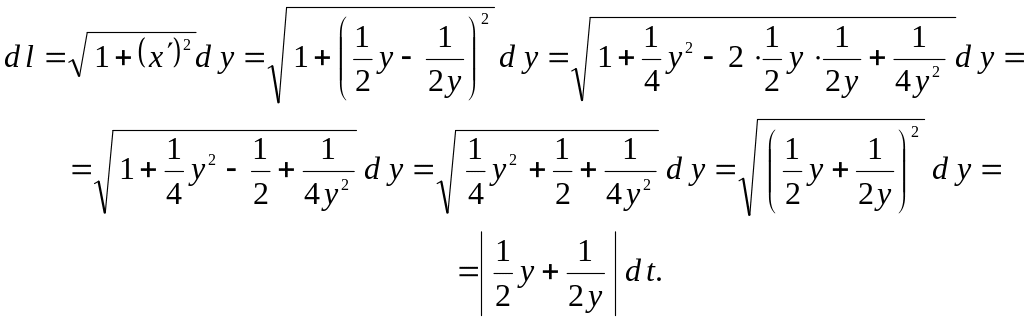
Следовательно,

Пример.
Найти
дифференциал длины дуги астроиды

.

Решение.
Дифференцируя по t,
получим

тогда
дифференциал длины дуги астроиды

Следовательно,

Пример.
Найти
дифференциал длины дуги логарифмической
спирали

.

Решение.
Найдем производную функции

:

тогда
дифференциал длины дуги логарифмической
спирали

Следовательно,

Упражнения.

Найти дифференциал длины дуги следующих
кривых:

;

2.18.Кривизна

Первая
производная

функции
f
(x)
характеризует
направление линии

,
а
вторая производная

устанавливает
меру её изогнутости, или искривленности.

Определение.
Углом
смежности дуги линии называется угол

между
касательными в ее конечных точках, а
отношение
угла смежности дуги

к ее длине

называется средней кривизной дуги

_ср.

Определение.
Кривизной
k

линии в некоторой ее точке называется
предел, к которому стремится средняя
кривизна

_ср
дуги
линии
при стремлении конечной точки дуги к
ее начальной точке, т. е.

В
частности, кривизна окружности радиуса
r
есть

_окр=

,
кривизна прямой равна нулю.

Если
плоская кривая отнесена к прямоугольной
системе координат и задана уравнением

,
то кривизна k

дуги выражается формулой

Eсли
плоская кривая отнесена к прямоугольной
системе координат и задана параметрически
системой уравнений

, то кривизна k

дуги выражается формулой

где

,

,

.

Если
плоская кривая отнесена к полярной
системе координат и задана уравнением

,
то кривизна k

дуги выражается формулой

где

,

.

Пример.
Найти
кривизну линии

в
точке с абсциссой

Решение.
Найдем значения производных первого и
второго порядков функции

в точке с абсциссой

Подставим
найденные значения

в
формулу

Следовательно,
кривизна
линии

в
точке с абсциссой

Пример.
Найти
кривизну циклоиды

в
точке

.

Решение.
Дифференцируя по t,
получим

Вычислим
значения производных в
точке

Подставляя
найденные значения

,

в формулу

имеем

Следовательно,
кривизна
циклоиды

в
точке

Пример.
Найти
кривизну кардиоиды

в
точке

.

Решение.
Найдем значение функции

в точке с абсциссой

Найдем
значения производных первого и второго
порядков функции

в точке с абсциссой

Подставим
значения

в
формулу

Следовательно,
кривизна
кардиоиды

в
точке

Упражнения.

Найти кривизну дуги в заданной точке
следующих линий:

,

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Содержание:

Формула парабол
Интегрирования по частям

По этой ссылке вы найдёте полный курс лекций по математике:

Пустьдана кривая , где функция f(x) имеет на отрезке (а, 6] непрерывную производную f'(x). Рассмотрим дугу этой кривой от точки Л (а, /(а)) до переменной точки (рис. 29). Тогда длина 5 дуги ^AM этой кривой будет функцией от ж и выразится формулой Так как подынтегральная функция непрерывна на отрезке [, то будем иметь .

Отсюда для дифференциала длины дуги ^ AM получаем формулу Геометрический смысл дифференциала длины дуги кривой заключается в том, что он равен длине отрезка MN касательной МТ, ограниченного точкой касания М(х, у) и точкой N(x + dx, у + dy) (рис. 29). При достаточно малом dx = Ах длина AS дуги ^ММ’ кривой У = f(x)t отвечающей приращению Ах = dx может считаться приближенно равной длине отрезка MN касательной МТ, проведенной в точке М к этой кривой, т. е.

Для случая задания кривой параметрическими уравнениями , где функции имеют непрерывные производные на отрезке [to» Т), получим Из этой формулы, в частности, следует, что если за параметр t взять длину S переменной дуги, т. е. положить то Если кривая задана уравнением в полярных координатах: где функция имеет непрерывную производную f) на отрезке Дифференциал длины дуги кривой Физические приложения определенного интеграла Масса и центр тяжести неоднородного стержня.

Приближенное вычисление определенных интегралов Формула парабол §15. Физические приложения определенного интеграла 15.1. Работа переменной силы Определим работу, которую произведет сила F при перемещении ею материальной точки М по прямой Ох из точки а в точку Ъ . Из физики известно, что если сила F постоянна, то работа А равна произведению величины F силы F на длину пути $ = ь — а, т. е. А = F • t, при условии, что сила направлена по прямой Ох.

Пусть величина силы F, действующей на материальную точку М по прямой Ох, является непрерывной функцией от г: на отрезке [a, ft] прямой Ох. Разобьем отрезок на п частей с длинами . На каждом частичном отрезке , Xk I возьмем произвольную точку и будем считать, что величинасилы F наэтом отрезке постоянна и равна F = Тогда при достаточно малом Лхк работа ЛАк будет приближенно равна а сумма даст приближенное значение работы А силы F на отрезке [a, ft].

Но так как Ап является интегральной суммой для функции F{x) на отрезке [a, ft], то за работу А силы F на отрезке [a, ft] естественно принять предел этой суммы при max Ахк О, который существует в силу непрерывности F(x) на [a, ft]. Таким образом, искомая работа А будет равна Пример 1. Нейти работу А, которая совершается при перемещении заряда qi из точки Af t, отстоящей от заряда q, на расстоянии , а точку , отстоящую от заряда ?t на расстоянии г2, считая, что заряд помещен в точке , принятой за начало отсчета.

Возможно вам будут полезны данные страницы:

Пусть электрические заряды q и q2 имеют одинаковые знаки, например, . Поэтому заряд q будет отталкивать заряд gj. По закону Кулона величина F силы F электростатического взаимодействия двух точечных электрических зарядов, находящихся а вакууме, рвана где г — рвсстояние между зарядами, к — коэффициент пропорциональности. Применяя формулу (1), нейдем Масса и центр тяжести неоднородного стержня Пустьдан неоднородный стержень, расположенный на отрезке [а, 6] оси Ох, линейная плотность р = р(х) которого известна.

Разобьем отрезок [а, Ь] точками на частичные отрезки на каждом из которых возьмем по одной произвольной точке , и составим сумму п .

Так как каждое слагаемое этой суммы является приближенным значением массы части стержня на отрезке ж*],тоуказаннуюсуммуестественно принять за приближенное значение массы всего стержня. Поэтому массу то воего стержня определим как предел сумм при стремлении к нулю шах 0, т. е. как интеграл.

Таким образом, масса то стержня равна Для определения центра тяжести неоднородного стержня используем формулу для координаты центра системы материальных точек , имеющих массы т и расположенных в точках , хп оси Ох. Координата хс центра тяжести этой системы находится по формуле Разобьем отрезок [а,д] точками а на частичные отрезки [ и вычислим массу части стержня, расположенной на этом отрезке. По формуле (2) имеем т.

Применив формулу среднего значения к этому интегралу, получим, что Допуская, что масса то* сосредоточена в точке отрезка , неоднородный стержень можно рассматривать как систему материальных точек с массами то*, расположенных в точках Iк отрезка [а, Ъ]. Так как то по формуле (3) найдем приближенное выражениедл я координаты хс центра тяжести неоднородного стержня: — Выражение, стоящее в числителе правой части (4), является интегральной суммой для функции хр(х) на отрезке (а, 6]. Поэтому координату хс центра тяжести неоднородного стержня определим по формуле Пример 2.

Найти координату хе центра тяжести неоднородного стержня, линейная пло1ность которого А Находим массу данного стержня Искомая координата центра тяжести равна § 16. Приближенное вычисление определенных интегралов При решении физических задач приходатся иметь дело с определенными интегралами от непрерывных функций, первообразные которых не выражаются через элементарные функции. Это приводит к необходимости получения приближенных формул для вычисления Определенных интегралов.

Приведем две из них, а именно, формулу

трапеций и формулу парабол. 16.1. Формула трапеций Пусть требуется вычислить интеграл и с помощью прямых х) построим п прямолинейных трапеций (рис. 30). Сумма площадей этих трапеций приближенно равна площади криволинейной трапеции, т. е. где — соответственно основания трапеций, — их высоты. Таким образом, получена приближенная формула + Замечен не.

Если функция f(x) имеет на {о, 6] непрерывную производную иторого порядка f»(z), то абсолютная величина погрешности не превосходит числа которая называется формулой трапеций. Эта формула тем точнее, чем больше п. Пример 1. Пользуясь формулой трапеций, вычислить приближенно интеграл при 4 Разобьем отрезок (0,1) на 10 равных частей точками . и вычислим приближенно значения функции в этих точках: Применяя формулу трапеций, получим Г Оценим погрешность полученного результата.

Так как На отрезке [0,1J имеем а значит . Поэтому погрешность получен-ного результата не превосходит величины Дифференциал длины дуги кривой Физические приложения определенного интеграла Масса и центр тяжести неоднородного стержня Приближенное вычисление определенных интегралов Формула парабол Точное значение данного интеграла легко находим по формуле Ньютона—Лейбница: Абоолютная ошибка результата, полученного по формуле трапеций, меньше 0,0007, что находится в со-1 ответствии с приведенной выше оценкой погрешности.

Формула парабол

Вычислим сначала площадь Q криволинейной трапеции, ограниченной дугой параболыу + С,проходящейчерезточки (рис.31). Площадь будет равна Разобьем отрезок [а, 6) на 2п (четное число) равных отрезков точками и представим интеграле виде суммы Проведем через точки прямые, параллельные оси Оу и обозначим через Л^2п-1»точки пересечения этих прямых с кривой у = /(х), а их ординаты обозначимчрез Через каждые три точки проведем параболу с вертикальной осью симметрии. В результате получим п криволинейных трапеций, ограниченных сверху параболами (рис. 32).

Так как площадь частичной криволинейной трапеции, отвечающей отрезку приближенно равна площади соответствующей «параболической» трапеции, то, учитывая , что длина h отрезка [ равна ^, по формуле (1) имеем где Подставляя в правую часть равенства (2) вместо интегралов их приближенные значения, получаем приближенную формулу Эта формула называется формулой парабол или формулой Симпсона. 3«и»*аки« . Если функция f(x) имеет на отрезке [о, 6) непрерывную производнуючетверто го порядка /IV(*). то абсолютная величина погрешности формулы Симпсона не больше чем Погрешность формулы Симпсона с ростом п уменьшается быстрее, чем погрешность формулы трапеций.

Поэтому формула Симпсона позволяет получить большую точность, чем формула трапеций. Пример 2. Вычислить приближенно интеграл по формуле Симпсона при 2п = 4. М Разобьем отрезок (0,1] на четыре равных части точками и вычислим приближенно значения функции точках: По формуле Симпсона находим 1 Оценим погрешность полученного результата. Подынтегральная функция y имеет производную четвертого порядка , для которой получаем Погрешность результата не превосходит величины .

Сравнивая приближенное значение интеграла с точным, приходим к выводу, что абсолютная ошибка результата, полученного по формуле Симпсона, меньше 0,0001, что соответствует полученной выше оценке погрешности. > Эти примеры показывают, что формула Симпсона дает более точные приближенные значения определенных интегралов, чем формула трапеций. Упражнения Вычислить определенные интегралы, пользуясь формулой Ньютона—Лейбница.

Интегрирования по частям

Интегрирования по частям, вычислите следующие интегралы: Вычисление пжнцаде й 27. Вычислите площадьфигуры, ограниченной параболой у = х2+2х-3 и прямой у = х+3. 28. Вычислите плошадь фигуры, ограниченной параболой у = 2х — х2 и прямой у = -х. 29. Вычислите площадьфигуры, ограниченной параболой у = х2 — 1, прямой х = 2 и осями координат. 30. Вычислите площадьфигуры, ограниченной параболами у = х2 -Зх-4 и у = 4+Зх-х2. 31.

Вычислите площадьфигуры, ограниченной прямыми у = х- 1, у = 1 и кривой у = In х. 32. Вычислите площадь фигуры, ограниченной кривыми у = еГг, у = е* и прямой х = 1. 33. Вычислите площадь фигуры, ограниченной кривой у = х3, прямой у = 8 и осью Оу. 34. Вычислите площадь фигуры, ограниченной астроидой х = a cos31, у = a sin’i (а > 0). 35. Вычислите площадь фигуры, ограниченной одной аркой циклоиды х = a(t — sin t), у = а(1 — cos/), а > 0, и осьюабцисс. 36. Найдите площадь фигуры, ограниченной кардиоидой х = а(2 cos t — cos 21), у = а(2 sin t — sin 2/), a > 0. 37. Найдите площадь фигуры, ограниченной кривой р = a sin у 38.

Найдите площадь фигуры, ограниченной кривой р = a sin 2 39. Найдите площадь фигуры, ограниченной кривой р = 2 + sin Дифференциал длины дуги кривой Физические приложения определенного интеграла Масса и центр тяжести неоднородного стержня Приближенное вычисление определенных интегралов Формула парабол Вычисление объемов тел 40. Найдите объем тела, образованного вращением вокруг оси Ох одной полуволны синусоиды у = sin х (0 ^ х ^ *). 41.

Найдите объем тела, образованного вращением вокруг оси Ох кривой у = sin2 х ( 42. Найдите объем эллипсоида, образованного вращением эллипса ^ + = 1 покруг оси Ох. 43. Найдите объем тела, образованного вращением вокруг оси Ох площадки, ограниченной осью Ох и параболой у = ах — х2 (а > 0) 44. Найдите объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной параболой у = х2, осью Оу и прямой у = 1. 45.

Найдите объем сегмента, отсекаемого плоскостью х = а от эллипгич еского параболоида k + li = x’ 46. Найдите объем тела, ограниченного однополостным гиперболоидом ^ + Ц? — = 1 и плоскостями Вычисление длин дуг 47. Вычислите длину дуги параболы у = у от точки (0,0) до точки (1,5). • 48. Вычислите длину дуги полукубической параболы у = от начала координат до точки 4(1,1). 49. Найдите длину дуги кривой у = In х от х = >/3 до х — /8. / 50. Найдите дли ну дуги кривой у = In sin х отх = у дох = §. 51. Найдите длину кривой х — a cos3 t,y = a sin31 (о > 0) (астроида). 52.

Найдите длину дуги кривой х = у — t, у = t2 + 2 от t — 0 до t = 3. 53. Найдите длину дуги кривой х = е* cos *, у = е* sin t от t — 0 до t = In х. 54. Найдите длину дуги логарифмической спирали р = ае*(а > 0), находящейся внутри круга 55. Найдите длину кривой р = a sin 50. Найдите длину первого витка спирали Архимеда р =

Лекции:

Дифференциальное уравнение Бернулли
Биномиальное распределение
Координаты вектора
Определение производной
Первый замечательный предел: пример решения
Формулы двойного угла
Сумма ряда
Метод Якоби
Метод интегрирования
Свойства функций, имеющих конечный предел

Источник

Наталья Игоревна Восковская

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Определение длины дуги кривой

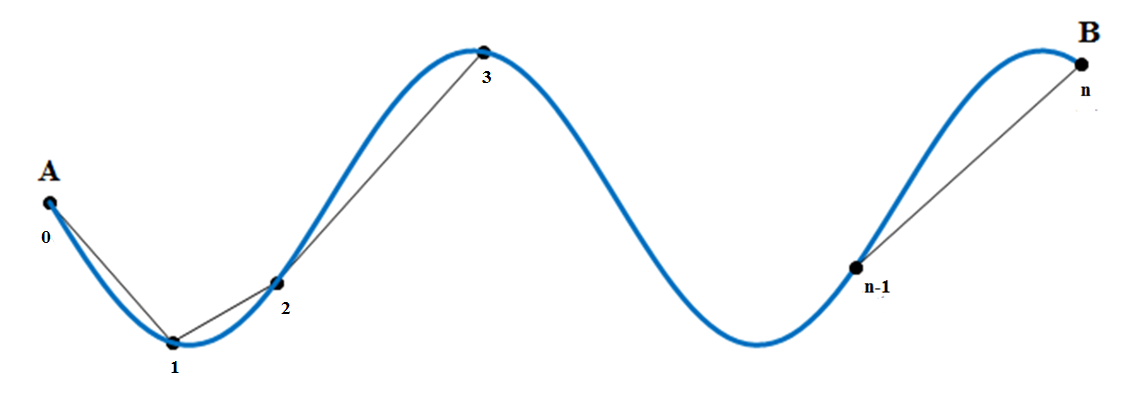
Рассмотрим в пространстве дугу $cup AB$ некоторой кривой. Точками $M_{0} $, $M_{1} $, $M_{2} $, …. , $M_{n-1} $, $M_{n} $ разобьем её на $n$ произвольных последовательных участков. Соединим соседние точки отрезками прямых и получим вписанную в дугу $cup AB$ ломаную, в которой $M_{0} $ совпадает с точкой $A$, а $M_{n} $ совпадает с точкой $B$. Эта ломаная состоит из звеньев $M_{0} M_{1} $, $M_{1} M_{2} $, …. , $M_{i-1} M_{i} $, …. , $M_{n-1} M_{n} $.

Обозначим длины звеньев этой ломаной следующим образом: длина $M_{0} M_{1} =Delta ; l_{1} $, длина $M_{1} M_{2} =Delta ; l_{2} $, …. , длина $M_{i-1} M_{i} =Delta ; l_{i} $, …. , длина $M_{n-1} M_{n} =Delta ; l_{n} $. Тогда периметр этой ломаной $l_{n} =Delta ; l_{1} +Delta ; l_{2} +ldots +Delta ; l_{i} +ldots +Delta ; l_{n} $ или просто $l_{n} =sum limits _{i=1}^{n}Delta ; l_{i} $.

Сдай на права пока
учишься в ВУЗе

Вся теория в удобном приложении. Выбери инструктора и начни заниматься!

Получить скидку 3 000 ₽

Будем уменьшать длины всех звеньев за счет увеличения их количества. При этом форма ломаной будет приближается к форме дуги кривой.

На этом основании длина дуги кривой определяется так: длиной $l$ дуги называется предел, к которому стремится периметр вписанной в эту дугу ломаной при неограниченном увеличении числа её звеньев и при стремлении к нулю наибольшей из длин её звеньев.

Соответствующее выражение имеет вид: $l=mathop{lim }limits_{max ; Delta ; l_{i} to 0} sum limits _{i=1}^{n}Delta ; l_{i} $.

Определение

Кривые, для которых этот предел существует, называются спрямляемыми.

Формулы для длины дуги плоской кривой

Пусть кривая задана между своими точками $A$ и $B$ на отрезке $left[a,; bright]$ уравнением в явном виде $y=fleft(xright)$, где $fleft(xright)$ — непрерывная функция с непрерывной первой производной на этом отрезке. В этом случае длина дуги кривой между точками точками $A$ и $B$ вычисляется по формуле $l=int limits _{a}^{b}sqrt{1+y’^{2} } cdot dx $.

«Длина дуги и ее производная» 👇

Задача 1

Найти длину дуги цепной линии $y=frac{1}{2} cdot left(e^{x} +e^{-x} right)$ на отрезке $left[0,; 1right]$.

Находим производную:

[y’=left(frac{1}{2} cdot left(e^{x} +e^{-x} right)right)^{{‘} } =frac{1}{2} cdot left(e^{x} -e^{-x} right).]

Вычисляем:

[1+y’^{2} =1+left(frac{1}{2} cdot left(e^{x} -e^{-x} right)right)^{2} =1+frac{1}{4} cdot left(e^{2cdot x} -2cdot e^{x} cdot e^{-x} +e^{-2cdot x} right)=]

[=1+frac{1}{4} cdot left(e^{2cdot x} -2+e^{-2cdot x} right)=frac{1}{4} cdot left(e^{x} +e^{-x} right)^{2} ;]

[sqrt{1+y’^{2} } =frac{1}{2} cdot left(e^{x} +e^{-x} right).]

Находим длину дуги:

[l=int limits _{a}^{b}sqrt{1+y’^{2} } cdot dx =int limits _{0}^{1}frac{1}{2} cdot left(e^{x} +e^{-x} right)cdot dx =frac{1}{2} cdot left[e^{x} -e^{-x} right]_{0}^{1} =]

[=frac{1}{2} cdot left(left(e^{1} -e^{-1} right)-left(e^{0} -e^{-0} right)right)=frac{e-e^{-1} }{2} .]

Пусть кривая задана параметрическими уравнениями $x=xleft(tright)$ и $y=yleft(tright)$, $alpha le tle beta $. Предположим, что функции $x=xleft(tright)$ и $y=yleft(tright)$ и их производные непрерывны при $alpha le tle beta $, причем $x’left(tright)ne 0$. В этом случае длина дуги кривой вычисляется по формуле $l=int limits _{alpha }^{beta }sqrt{left(x’left(tright)right)^{2} +left(y’left(tright)right)^{2} } cdot dt $.

Задача 2

Найти длину одной арки циклоиды $x=t-sin t$, $y=1-cos t$, $0le tle 2cdot pi $.

Находим производные:

[x’=left(t-sin tright)^{{‘} } =1-cos t; y’=left(1-cos tright)^{{‘} } =sin t.]

Вычисляем:

[left(x’right)^{2} +left(y’right)^{2} =left(1-cos tright)^{2} +left(sin tright)^{2} =2cdot left(1-cos tright)=4cdot sin ^{2} frac{t}{2} .]

Находим длину дуги:

[l=int limits _{0}^{2cdot pi }sqrt{4cdot sin ^{2} frac{t}{2} } cdot dt =2cdot int limits _{0}^{2cdot pi }sin frac{t}{2} cdot dt =-4cdot left[cos frac{t}{2} right]_{0}^{2cdot pi } =]

[=-4cdot left(cos frac{2cdot pi }{2} -cos frac{0}{2} right)=-4cdot left(-1-1right)=8.]

Пусть кривая задана в полярных координатах $rho =rho left(phi right)$, $alpha le phi le beta $. Предположим, что функция $rho =rho left(phi right)$ и её производная непрерывны при $alpha le phi le beta $. В этом случае длина дуги кривой вычисляется по формуле $l=int limits _{alpha }^{beta }sqrt{rho ^{2} +rho ‘^{2} } cdot dphi $.

Задача 3

Найти длину кардиоиды $rho =1+cos phi $.

Так как кардиоида симметрична относительно полярной оси, то изменяя полярный угол $phi $ от $0$ до $pi $, мы получим половину длины кардиоиды.

Находим производную: $rho ‘=-sin phi $.

Вычисляем:

[rho ^{2} +rho ‘^{2} =left(1+cos phi right)^{2} +left(-sin phi right)^{2} =2cdot left(1+cos phi right).]

Находим половину длины кардиоиды:

[frac{l}{2} =int limits _{0}^{pi }sqrt{2cdot left(1+cos phi right)} cdot dphi =2cdot int limits _{0}^{pi }cos frac{phi }{2} cdot dphi =4cdot left[sin frac{phi }{2} right]_{0}^{pi } =4cdot sin frac{pi }{2} =4.]

Полная длина кардиоиды $l=8$.

Производная и дифференциал дуги

Пусть в формуле $l=int limits _{a}^{b}sqrt{1+left(f’left(xright)right)^{2} } cdot dx $ для длины дуги кривой, заданной в виде $y=fleft(xright)$, $ale xle b$, нижняя граница интеграла $a$ остается постоянной, а верхняя граница изменяется и равна $x$.

При этом длина дуги $lleft(xright)=int limits _{a}^{x}sqrt{1+left(f’left(tright)right)^{2} } cdot dt $ будет функцией верхней границы (переменная интегрирования переобозначена, чтобы не путать её с верхней границей).

В соответствии с теоремой о производной интеграла по верхней границе производная этой функции имеет вид $l’left(xright)=sqrt{1+left(f’left(xright)right)^{2} } $.

Отсюда получаем дифференциал дуги:

$dlleft(xright)=l’left(xright)cdot dx=sqrt{1+left(f’left(xright)right)^{2} } cdot dx$, откуда $dl=sqrt{1+y’^{2} } cdot dx$ или $dl=sqrt{dx^{2} +dy^{2} } $.

При параметрическом задании функции $x=xleft(tright)$ и $y=yleft(tright)$, $alpha le tle beta $ дифференциал дуги имеет вид $dl=sqrt{left(x’left(tright)right)^{2} +left(y’left(tright)right)^{2} } cdot dt$.

При задании функции в полярных координатах $rho =rho left(phi right)$, $alpha le phi le beta $ дифференциал дуги имеет вид $dl=sqrt{rho ^{2} +rho ‘^{2} } cdot dphi $.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Пусть на отрезкеЗадана дифференцируемая функция, графи

Ком которой является дуга(рис. 15.11). ОтрезокРазобьем на и частей точкамиЭтим точкам будут соответствовать точки,

ДугиСоединим их отрезками прямых. Ломаную

Называют вписанной в дугу. Периметр этой ломаной обозначим через, т. е.

Длиной дуги называется предел периметра вписанной в нее ломаной, когда число звеньев Мк.)Мк неограниченно возрастает, а длина наибольшего из них стремится к нулю:

Где X — длина наибольшего звена

Будем отсчитывать длину дуги от некоторой ее точки, например, от точки А; пусть в точке М (х, у) длина дуги АМ равна /, а в точке Мх + Дх, у + Ау)

Длина дуги АМ’ равна /+Д/, где А1 — длина дуги ММ’ (рис. 15.12). Очевидно, 1 = 1 (х), бесконечно малая дуга линии и стягивающая ее хорда эквивалентны:

Дифференциал длины дуги плоской кривой, заданной уравнением у = /(х), выражается формулой

<11 = л]с1х2 +ф2.

Эта формула имеет простой геометрический смысл: она выражает теорему Пифагора

Для бесконечно, малого треугольника МШ (рис. 15.12, <й=МТ, Д/ = ММ’). Дифференциал дуги пространственной кривой выражается формулой

<11 = -^сЬ2 + дуг; + дг2.

< Предыдущая		Следующая >

Источник

Формулы длины дуги регулярной кривой

Лемма. Пусть жорданова кривая регулярна и ell(t) — длина дуги этой кривой, ограниченной точками M(a) и M(b) . Тогда функция ell(t) дифференцируема на отрезке [a;b] , причем для всех имеем:

$ell'(t)= sqrt{bigl(varphi'(t)bigr)^2+ bigl(psi'(t)bigr)^2},.$

(8)

Доказательство. Возьмем любое tin[a;b] и дадим приращение Delta t такое, что t+Delta tin[a;b] . Положим для определенности Delta t>0 . Соответствующее приращение функции ell(t) , т. е. ell(t+Delta t)-ell(t) , равно длине дуги кривой, ограниченной точками M(t) и M(t+Delta t) . В силу неравенств (6) и (7) пункта 2 имеем:

$sqrt{alpha^2+beta^2}cdotDelta tleqslant Deltaellleqslant sqrt{A^2+B^2}cdotDelta t,,$

где alpha и beta — наименьшие значения функций bigl|varphi'(t)bigr| и bigl|psi'(t)bigr| на отрезке [t;t+Delta t] , а и — наибольшие значения этих функций на том же отрезке. Но тогда

$sqrt{alpha^2+beta^2}leqslant frac{Deltaell}{Delta t} leqslantsqrt{A^2+B^2},.$

Перейдем к пределу при Delta tto0 . В силу непрерывности функций varphi'(t) и psi'(t) в точке получаем, что

$lim_{Delta tto0}alpha= lim_{Delta tto0}A= varphi'(t),qquad lim_{Delta tto0}beta= lim_{Delta tto0}B= psi'(t),$

а потому

$ell'(t)= lim_{Delta tto0}frac{Deltaell}{Delta t}= sqrt{bigl(varphi'(t)bigr)^2+ bigl(psi'(t)bigr)^2},.$

Итак, лемма доказана.

Из этой леммы следует, что

$dell= ell'(t),dt= sqrt{bigl(varphi'(t)bigr)^2+ bigl(psi'(t)bigr)^2},dt,.$

(9)

Геометрический смысл формулы дифференциала длины дуги криво

Так как dx=varphi'(t),dt и dy=psi'(t),dt , то формулу (9) можно переписать в виде $dell=sqrt{(dx)^2+(dy)^2}$ .

Геометрический смысл этой формулы ясен из рисунка 50, где Deltaell — участок дуги, a dell —соответствующий отрезок касательной. Мы будем называть dell дифференциалом длины дуги кривой.

Теорема 2. Если жорданова кривая $Gammacolon begin{cases}x=varphi(t),\ y=psi(t),end{cases}aleqslant tleqslant b$ . регулярна, то ее длина выражается формулой

$ell(Gamma)= intlimits_{a}^{b}! sqrt{bigl(varphi'(t)bigr)^2+ bigl(psi'(t)bigr)^2},dt,.$

(10)

Доказательство. Так как $ell'(t)= sqrt{bigl(varphi'(t)bigr)^2+ bigl(psi'(t)bigr)^2}$ , то ell(t) — первообразная для $sqrt{bigl(varphi'(t)bigr)^2+ bigl(psi'(t)bigr)^2}$ , а тогда ell(Gamma) равна разности значений первообразной, т. е.

$ell=ell(b)-ell(a)= intlimits_{a}^{b}! sqrt{bigl(varphi'(t)bigr)^2+ bigl(psi'(t)bigr)^2},dt,.$

Теорема доказана.

Полученную формулу можно переписать в следующих видах:

$ell= intlimits_{a}^{b}dell,,$

(10′)

$ell= intlimits_{a}^{b}! sqrt{x_t^{prime2}+y_t^{prime2}}dt,,$

(10″)

или

$ell= intlimits_{a}^{b}! sqrt{(dx)^2+(dy)^2},.$

(10″‘)

Пример 1. Найти длину дуги астроиды $begin{cases}x=acos^3t,,\ y=asin^3t,, end{cases}0leqslant tleqslant2pi$

Решение. Данная кривая симметрична относительно обеих координатных осей (см. рис. 48), поэтому достаточно найти длину четверти дуги, расположенной в первом квадранте $left(0 leqslant t leqslant frac{pi}{2}right)$ .

Найдем производные: $x'_t=-3acos^2tsin{t},,~~ y'_t=3asin^2tcos{t}$ . Вычислить сумму их квадратов:

$x_t^{prime2}+y_t^{prime2}= 9a^2cos^2t sin^2t,bigl(cos^2t+ sin^2tbigr)= 9a^2cos^2t sin^2t,.$

Учитывая сказанное выше, найдем четверть длины астроиды:

$frac{1}{a},ell= 3aintlimits_{0}^{pi/2} sin{t}cos{t},dt= ldots= left.{3acdot frac{sin^2t}{2}}right|_{0}^{pi/2}= frac{3}{2},a,.$

Длина всей кривой $ell=4cdot frac{3}{2},a=6a$ . Она мало отличается от 2pi a , т. е. от длины окружности, описанной вокруг астроиды.

Частные случаи формулы длины кривой

Рассмотрим некоторые частные случаи общей формулы (10) пункта 3. Если кривая Gamma задана явным уравнением y=f(x), a leqslant x leqslant b , то ее можно представить параметрическими уравнениями

$begin{cases}x=t,\ y=f(t),end{cases} a leqslant t leqslant b.$

В этом случае

$ell(Gamma)= intlimits_{a}^{b}! sqrt{1+bigl(f'(t)bigr)^2},dt= intlimits_{a}^{b}! sqrt{1+bigl(f'(x)bigr)^2},dx,.$

(11)

Полученную формулу записывают короче в виде

$ell= intlimits_{a}^{b}! sqrt{1+y_x^{prime2}},dx,.$

(11′)

Значит,

$dell= sqrt{1+y_x^{prime2}},dx,.$

(12)

Пример 2. Вычислить длину дуги цепной линии $y= frac{e^x+e^{-x}}{2}$ , взятой от точки x=0 до точки x=1 (рис. 51).

График цепной линии (гиперболического косинуса)

Решение. Найдём производную $y'= frac{e^{x}-e^{-x}}{2}$ . Вычислить подкоренное выражение

$1+y'^2= 1+ frac{1}{4}(e^x-e^{-x})^2= frac{4+e^{2x}-2+ e^{-2x}}{4}= left(frac{e^x+e^{-x}}{2}right)^2$

Длина ell указанного отрезка цепной линии будет

$ell= intlimits_{0}^{1} frac{e^x+e^{-x}}{},dx= left.{frac{e^x-e^{-x}}{2}}right|_{0}^{1}= frac{e-e^{-1}}{2},.$

Длина дуги кривой в полярных координатах

Рассмотрим теперь случай, когда кривая Gamma задана в полярных координатах уравнением rho=f(varphi) , где alpha leqslant varphi leqslant beta , причем функция на отрезке [alpha;beta] имеет непрерывную производную f'(varphi) .

Так как декартовы координаты связаны с полярными координатами точек плоскости соотношениями $begin{cases}x=rhocosvarphi,,\ y=rhosinvarphi,,end{cases}$ , полярное уравнение данной кривой можно записать в виде параметрических уравнений: $begin{cases} x=f(varphi) cosvarphi,,\ y=f(varphi) sinvarphi,,end{cases}$ ; отсюда находим:

$begin{cases}x'_{varphi}= f'(varphi)cosvarphi- f(varphi)sinvarphi,;\ y'_{varphi}= f'(varphi)sinvarphi+ f(varphi)cosvarphi,.end{cases}$ Поэтому

$begin{aligned}x'_{varphi}+y'_{varphi}&= f'^2(varphi) cos^2varphi- 2f'(varphi)cosvarphi, f(varphi)sinvarphi+ f^2(varphi)sin^2varphi+ f'^2(varphi)sin^2varphi,,+\ &phantom{=,}+, 2 f'(varphi)sinvarphi, f(varphi)cosvarphi+ f^2(varphi)cos^2varphi=\ &= f'^2(varphi)+ f^2(varphi)= rho_{varphi}^{prime2}+ rho^2.end{aligned}$

В силу формулы (10) пункта 3 получаем формулу длины дуги кривой в полярных координатах:

$ell= intlimits_{alpha}^{beta}! sqrt{rho_{varphi}^{prime2}+ rho^2},dvarphi,.$

(13)

График кардиоиды в полярной системе координат

Пример 3. Вычислить длину кардиоиды rho=a(1+cosvarphi) .

Решение. Данная функция rho четная, следовательно, кривая расположена симметрично относительно полярной оси (рис. 52). Поэтому сначала найдем половину длины дуги данной кривой, для которой полярный угол varphi изменяется от до , после чего удвоим полученный результат:

$begin{aligned}ell&= 2intlimits_{0}^{pi}! sqrt{rho_{varphi}^{prime2}+ rho^2},dvarphi=\ &= 2intlimits_{0}^{pi}! sqrt{a^2sin^2varphi+ a^2(1+cosvarphi)^2},dvarphi=\ &= 4aintlimits_{0}^{pi} cos frac{varphi}{2},dvarphi= left.{8asin frac{varphi}{2}}right|_{0}^{pi}=8a,.end{aligned}$

Приращение угла и функции в полярной системе координат

Из формулы (13) получаем выражение для дифференциала дуги, заданной полярным уравнением

$dell= sqrt{(drho)^2+rho^2(dvarphi)^2},.$

(14)

Геометрическую иллюстрацию этой формулы дает рисунок 53. На этом рисунке —дуга рассматриваемой кривой, — дуга окружности с центром в точке и радиусом rho , rhoDeltavarphi — длина дуги , Заменяя rhoDeltavarphi,~ Deltarho и Deltaell соответственно на rho dvarphi,~drho и dell ; рассматриваем криволинейный треугольник ABC как прямоугольный с катетами и dvarphi и гипотенузой dell Тогда

$dell= sqrt{(drho)^2+rho^2(dvarphi)^2},.$

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник