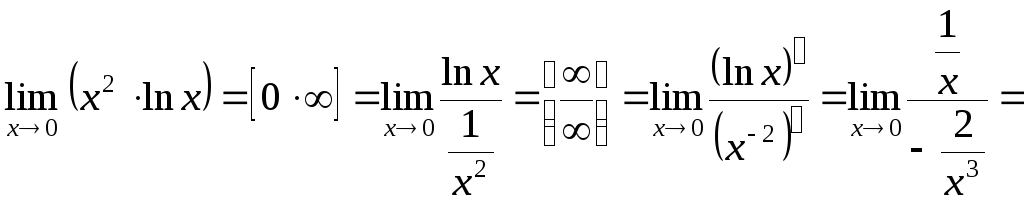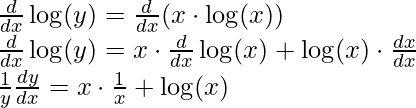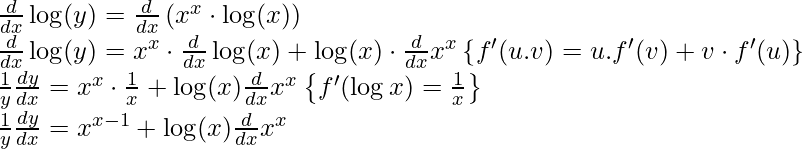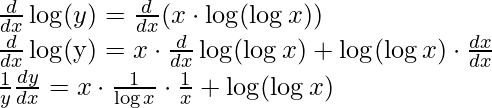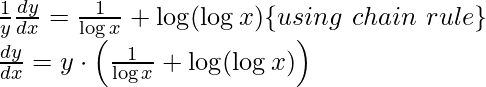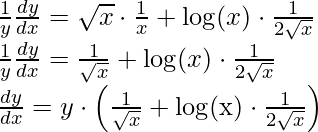Как найти дифференциал функции натурального логарифма - Исправление недочетов и поиск решений вместе с Examum.ru

Простое объяснение принципов решения логарифмического дифференцирования и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.

Алгоритм решения логарифмического дифференцирования

В некоторых случаях нахождение производной функции значительно упрощается, если сначала произвести логарифмирование исходной функции, а уже затем произвести дифференцирование. Такой приём носит название логарифмического дифференцирования.

Правило нахождения степенно-показательной функции

$(u^{v})' = u^{v}cdotln ucdot v' + vcdot u^{v - 1}cdot u'$

Таблица основных производных

Нужна помощь в написании работы?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Заказать работу

Примеры решения логарифмического дифференцирования

Задача

Найти производную функции $y = frac{(x^{2} + 2)cdotsqrt[4]{(x - 1)^{3}}cdot e^{x}}{(x + 5)^{3}}$ .

Решение

Найдём логарифм функции

$ln y = ln{x^{2} + 2} + frac{3}{4}ln(x - 1) + x - 3ln(x + 5)$ .

Дифференцируем это равенство по :

$frac{1}{y}y' = frac{1}{x^{2} + 2}cdot2x + frac{3}{4}cdotfrac{1}{x - 1} + 1 - 3cdotfrac{1}{x + 5}$

Выразим :

$y' = ycdotleft(frac{2x}{x^{2} + 2} + frac{3}{4(x - 1)} + 1 - frac{3}{x + 5}right) = frac{(x^{2} + 2)cdotsqrt[4]{(x - 1)^{3}}cdot e^{x}}{(x + 5)^{3}}cdotleft(frac{2x}{x^{2} + 2} + frac{3}{4(x - 1)} + 1 - frac{3}{x + 5}right)$

Ответ

$y' = frac{(x^{2} + 2)cdotsqrt[4]{(x - 1)^{3}}cdot e^{x}}{(x + 5)^{3}}cdotleft(frac{2x}{x^{2} + 2} + frac{3}{4(x - 1)} + 1 - frac{3}{x + 5}right)$

Задача

Найти производную функции $y = (sin2x)^{x^{2} + 1}$ .

Решение

Используя формулу $(u^{v})' = u^{v}cdotln ucdot v' + vcdot u^{v - 1}cdot u'$ , получаем:

$y' = (sin2x)^{x^{2} + 1}cdotlnsin2xcdot2x + (x^{2} + 1)cdot(sin2x)^{x^{2}}cdotcos2xcdot2$

Ответ

$y' = (sin2x)^{x^{2} + 1}cdotlnsin2xcdot2x + (x^{2} + 1)cdot(sin2x)^{x^{2}}cdotcos2xcdot2$

Задача

Найти производную функции $y = lnfrac{x}{1 - x^{4}}$ .

Решение

Найдём логарифм функции

$[ln y = ln{x} - ln(1 - x^{4})]$

Дифференцируем это равенство по :

$[y' = frac{1}{x} - frac{1}{1 - x^{4}}(1 - x^{4})' = frac{1}{x} + frac{4x^{3}}{1 - x^{4}} = frac{1 + 3x^{4}}{x(1 - x^{4})}]$

Ответ

$y' = frac{1 + 3x^{4}}{x(1 - x^{4})}$

Задача

Найти производную функции

$[y = lnfrac{x}{sqrt{1 + x^{2}}}]$

Решение

Найдём логарифм функции

$[ln y = ln{x} - frac{1}{2}ln(1 + x^{2})]$

Дифференцируем это равенство по :

$[y' = frac{1}{x} - frac{1}{2}frac{1}{1 + x^{2}}cdot2x = frac{1}{x(1 + x^{2})}]$

Ответ

$[y' = frac{1}{x(1 + x^{2})}]$

Задача

Найти производную функции

$[y = lnfrac{1 + x}{1 - x}]$

Решение

Найдём логарифм функции

Дифференцируем это равенство по :

$[y' = frac{1}{1 + x}cdot(1 + x)' - frac{1}{1 - x}cdot(1 - x)' = frac{1}{1 + x} + frac{1}{1 - x} = frac{2}{1 - x^{2}}]$

Ответ

$[y' = frac{2}{1 - x^{2}}]$

Задача

Найти производную функции $y = (x + 5)^{2}(2x - 7)^{3}(x - 2)(x + 3)$ .

Решение

Найдём логарифм функции

Дифференцируем это равенство по :

$[frac{1}{y}y' = frac{2}{x + 5} + frac{3}{2x - 7}cdot2 + frac{1}{x - 2} + frac{1}{x + 3}]$

Выразим :

$[y' = ycdotleft(frac{2}{x + 5} + frac{3}{2x - 7}cdot2 + frac{1}{x - 2} + frac{1}{x + 3}right) =]$

$[= (x + 5)^{2}(2x - 7)^{3}(x - 2)(x + 3)cdotleft(frac{2}{x + 5} + frac{3}{2x - 7}cdot2 + frac{1}{x - 2} + frac{1}{x + 3}right)]$

Ответ

$[y' = (x + 5)^{2}(2x - 7)^{3}(x - 2)(x + 3)cdotleft(frac{2}{x + 5} + frac{3}{2x - 7}cdot2 + frac{1}{x - 2} + frac{1}{x + 3}right)]$

Задача

Найти производную функции

$[y = frac{sqrt[4]{x^{2} + 7x - 8}cdotsqrt[6]{x^{4} - 1}}{sqrt[3]{x^{3} - 3x^{2} + x - 4}}]$

Решение

Найдём логарифм функции

$[ln y = frac{1}{4}cdotfrac{1}{x^{2} + 7x - 8}(2x + 7) + frac{1}{6}cdotfrac{1}{x^{4} - 1}4x^{3} -]$

$[-frac{1}{3}cdotfrac{1}{x^{3} - 3x^{2} + x - 4}cdot(3x^{2} - 6x +1)]$

Дифференцируем это равенство по :

$[frac{1}{y}y' = frac{1}{4}cdotfrac{1}{x^{2} + 7x - 8}(2x + 7) + frac{1}{6}cdotfrac{1}{x^{4} - 1}4x^{3} -]$

$[-frac{1}{3}cdotfrac{1}{x^{3} - 3x^{2} + x - 4}cdot(3x^{2} - 6x + 1)]$

Выразим :

$[y' = ycdotfrac{1}{4}cdotfrac{1}{x^{2} + 7x - 8}(2x + 7) + frac{1}{6}cdotfrac{1}{x^{4} - 1}4x^{3} -]$

$[-frac{1}{3}cdotfrac{1}{x^{3} - 3x^{2} + x - 4}cdot(3x^{2} - 6x + 1) =]$

$[y' = frac{sqrt[4]{x^{2} + 7x - 8}cdotsqrt[6]{x^{4} - 1}}{sqrt[3]{x^{3} - 3x^{2} + x - 4}}ast]$

$[ast(frac{1}{4}cdotfrac{1}{x^{2} + 7x - 8}(2x + 7) + frac{1}{6}cdotfrac{1}{x^{4} - 1}4x^{3} -]$

$[-frac{1}{3}cdotfrac{1}{x^{3} - 3x^{2} + x - 4}cdot(3x^{2} - 6x + 1))]$

Ответ

$[y' = frac{sqrt[4]{x^{2} + 7x - 8}cdotsqrt[6]{x^{4} - 1}}{sqrt[3]{x^{3} - 3x^{2} + x - 4}}ast]$

$[ast(frac{1}{4}cdotfrac{1}{x^{2} + 7x - 8}(2x + 7) + frac{1}{6}cdotfrac{1}{x^{4} - 1}4x^{3} -]$

$[-frac{1}{3}cdotfrac{1}{x^{3} - 3x^{2} + x - 4}cdot(3x^{2} - 6x + 1))]$

Задача

Найти производную функции

$[y = x^{x}, (x > 0)]$

Решение

Возьмём натуральные логарифмы от обеих частей равенства, получим:

Дифференцируем это равенство по :

$[frac{1}{y}y' = ln x + frac{1}{x}]$

$[frac{1}{y}y' = ln x + 1]$

Выразим :

$[y' = ycdot(ln x + 1) = x^{x}cdot(ln x + 1)]$

Ответ

$[y' = x^{x}cdot(ln x + 1)]$

Задача

Найти производную функции

$[y = (sin x)^{cos x}, (pi < x > 0)]$

Решение

Возьмём натуральные логарифмы от обеих частей равенства, получим:

Дифференцируем это равенство по :

$[frac{1}{y}y' = -sin xcdotlnsin x + cos xcdotfrac{1}{sin x}cdotcos x]$

Выразим :

$[y' = ycdot(-sin xcdotlnsin x + cos xcdotfrac{1}{sin x}cdotcos x) =]$

$[= (sin x)^{cos x}cdot(-sin xcdotlnsin x + cos xcdotfrac{1}{sin x}cdotcos x) =]$

$[= (sin x)^{cos x}cdotleft(-sin xcdotlncos x + frac{cos^{2}x}{sin x}right)]$

Ответ

$[y' = (sin x)^{cos x}cdotleft(-sin xcdotlncos x + frac{cos^{2}x}{sin x}right)]$

Задача

Найти производную функции

$[y = sqrt{frac{ax + b}{cx + d}}]$

Решение

Найдём логарифм функции

$[ln y = frac{1}{2}left[ln(ax + b) - ln(cx + d)right]]$

Дифференцируем это равенство по :

$[frac{1}{y}y' = frac{1}{2}cdotleft[frac{1}{ax + b}cdot a - frac{1}{cx + d}cdot cright]]$

Выразим :

$[y' = ycdotfrac{1}{2}cdotleft[frac{1}{ax + b}cdot a - frac{1}{cx + d}cdot cright] =]$

$[y' = sqrt{frac{ax + b}{cx + d}}cdotfrac{1}{2}cdotleft[frac{1}{ax + b}cdot a - frac{1}{cx + d}cdot cright] =]$

$[y' = frac{ad - bc}{2(ax + b)(cx + d)}cdotsqrt{{frac{ax + b}{cx + d}}}]$

Ответ

$[y' = frac{ad - bc}{2(ax + b)(cx + d)}cdotsqrt{{frac{ax + b}{cx + d}}}]$

Источник

Логарифмическое дифференцирование

При
вычислении производной от логарифма
произведения, частного, степени или
корня, для упрощения нахождения
производной проводят предварительное
преобразование (см. Пример 10(и)).

В
ряде случаев для нахождения производной
целесообразно заданную функцию сначала
прологарифмировать (по умолчанию имеется
в виду натуральный логарифм). Затем
найти производную от этого логарифма
и по ней отыскать производную от заданной
функции. Такой прием называется
логарифмическим
дифференцированием.

Метод логарифмического
дифференцирования позволяет легко
найти производную показательно-степенной
функции вида

где

и
– дифференцируемые функции аргумента
.

Пример 14.

Найти
производную функции
.

Решение.

Прологарифмируем
обе части функции и преобразуем выражение:

Теперь дифференцируем
уравнение, как неявно заданную функцию:

;

Так
как
,
то окончательно получаем:

Производные высших порядков

Производной
2-го порядка от функции

называется производная от её первой
производной, т.е.

Аналогично,
производной 3-го порядка от функции
называется
производная от её второй производной,
т.е.

Таким
образом, производной
-го
порядка от функции

называется производная от производной
-го
порядка, т.е.

Следовательно,
для нахождения производной
-го
порядка необходимо последовательно
найти производную первого, затем второго,
затем третьего и т.д. до-го
порядка.

Пример 15.

Найти
третью производную
функции
.

Решение.

;

2.3. Дифференциал функции

Из определения
производной и свойств пределов следует,
что если

то ,

где
–
бесконечно малая величина ().

Выражаем
и получаем, что:.
Так как,
то в дальнейшем ее можно не учитывать
и мы получим:

Главная
часть приращения функции, линейная
относительно приращения независимой
переменной
,
называется дифференциалом
функции
и обозначаетсяили:

Т.
к. дифференциал
,
то дифференциал
функции равен произведению производной
функции на дифференциал аргумента:

Таким
образом, для нахождения дифференциала
функции, необходимо найти производную

и умножить её
на дифференциал независимой переменной
.

Пример
16.

Найти
дифференциал функции
.

Решение.

2.4. Применение дифференциального исчисления функции одной переменной

2.4.1. Применение производной при вычислении пределов.

Правило Лопиталя

При
вычислении предела функции подстановка
предельного значения аргумента часто
приводит к неопределенностям вида
,,
от которых невозможно избавиться при
помощи ранее изученных приемов. Теорема,
известная под названиемправило
Лопиталя,
является одним из основных инструментов
для раскрытия таких неопределенностей.

Правило
Лопиталя:
Пусть в некоторой окрестности точки
функцииидифференцируемы и.
Еслииодновременно являются бесконечно малыми
или бесконечно большими функциями при
,
то

при условии, что
предел отношения производных существует.

Эта
теорема справедлива также и для
односторонних пределов, и в случае,
когда
.

В
некоторых случаях раскрытие
неопределенностей вида
может потребовать неоднократного
применения правила Лопиталя.

Неопределенности

,,,,,

сводятся к
неопределенностям вида
путем алгебраических преобразований.

Пример 17.

Вычислить с помощью
правила Лопиталя пределы:

а); б); в).

Решение.

а)

б)

в)
.

Обозначим
искомый предел через
и прологарифмируем выражение:

;

или

Тогда:

Так
как
,
то искомый предел.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Содержание:

Суть метода логарифмического дифференцирования
Производная показательно-степенной функции

Для функций вида $y(x)=frac{u_{1}(x) cdot u_{2}(x) cdot ldots cdot u_{k}(x)}{v_{1}(x) cdot v_{2}(x) cdot ldots cdot v_{m}(x)}$ для упрощения нахождения
производной рациональнее использовать логарифмическое дифференцирование.

Суть метода логарифмического дифференцирования

Суть такого дифференцирования заключается в следующем: вначале находится
логарифм заданной функции, а уже затем
вычисляется от него производная. Пусть задана некоторая функция
$y=f(x)$. Прологарифмируем левую и правую части данного выражения:

$$ln y=ln f(x)$$

Далее продифференцируем полученное равенство при условии, что
$y$ является функцией от $x$, то есть найдем
производную сложной функции:

$$(ln y)^{prime}=(ln f(x))^{prime} Rightarrow frac{1}{y} cdot y^{prime}=(ln f(x))^{prime}$$

А тогда, выражая искомую производную $y^{prime}$, в
результате имеем:

$$y^{prime}=y cdot(ln f(x))^{prime}$$

Пример

Задание. Найти производную функции
$y=frac{(x+2)^{2}(x-4) sqrt{x^{2}+1}}{(x-2)^{3}(x-4)^{5}}$

Решение. Если находить производную данной функции, используя
таблицу производных и
правила дифференцирования, то процесс будет очень трудоемким. Производную будем находить с помощью логарифмического
дифференцирования. Прологарифмируем левую и правую части заданной функции:

$$ln y=ln frac{(x+2)^{2}(x-4) sqrt{x^{2}+1}}{(x-2)^{3}(x-4)^{5}}$$

Используя свойства логарифмов, преобразуем правую часть полученного равенства к следующему виду:

$$begin{array}{c}
ln frac{(x+2)^{2}(x-4) sqrt{x^{2}+1}}{(x-2)^{3}(x-4)^{5}}= \
=ln left[(x+2)^{2}(x-4) sqrt{x^{2}+1}right]-ln left[(x-2)^{3}(x-4)^{5}right]= \
=ln (x+2)^{2}+ln (x-4)+ln sqrt{x^{2}+1}-ln (x-2)^{3}-ln (x-4)^{5}= \
=2 ln (x+2)+ln (x-4)+frac{1}{2} ln left(x^{2}+1right)-3 ln (x-2)-5 ln (x-4)= \
=2 ln (x+2)-4 ln (x-4)+frac{1}{2} ln left(x^{2}+1right)-3 ln (x-2)
end{array}$$
$$ln y=2 ln (x+2)-4 ln (x-4)+frac{1}{2} ln left(x^{2}+1right)-3 ln (x-2)$$

Дифференцируем левую и правую часть последнего равенства, не забывая, что
$y$ является функцией переменной
$x$:

$$begin{array}{c}
(ln y)^{prime}=left(2 ln (x+2)-4 ln (x-4)+frac{1}{2} ln left(x^{2}+1right)-3 ln (x-2)right)^{prime} \
frac{y^{prime}}{y}=(2 ln (x+2))^{prime}-(4 ln (x-4))^{prime}+left(frac{1}{2} ln left(x^{2}+1right)^{prime}-right. \
-(3 ln (x-2))^{prime}=2(ln (x+2))^{prime}-4(ln (x-4))^{prime}+frac{1}{2}left(ln left(x^{2}+1right)right)^{prime}- \
-3(ln (x-2))^{prime}=2 cdot frac{1}{x+2} cdot(x+2)^{prime}-4 cdot frac{1}{x-4} cdot(x-4)^{prime}+ \
+frac{1}{2} cdot frac{1}{x^{2}+1} cdotleft(x^{2}+1right)^{prime}-3 cdot frac{1}{x-2} cdot(x-2)^{prime}= \
=frac{2}{x+2}-frac{4}{x-4}+frac{x}{x^{2}+1}-frac{3}{x-2}
end{array}$$

Итак,

$$frac{y^{prime}}{y}=frac{2}{x+2}-frac{4}{x-4}+frac{x}{x^{2}+1}-frac{3}{x-2}$$

Отсюда

$$y^{prime}=yleft(frac{2}{x+2}-frac{4}{x-4}+frac{x}{x^{2}+1}-frac{3}{x-2}right)$$

Подставляя вместо функции $y$ ее выражение,
окончательно будем иметь, что

$$y^{prime}=frac{(x+2)^{2} sqrt{x^{2}+1}}{(x-2)^{3}(x-4)^{4}}left(frac{2}{x+2}-frac{4}{x-4}+frac{x}{x^{2}+1}-frac{3}{x-2}right)$$

Ответ. $y^{prime}=frac{(x+2)^{2} sqrt{x^{2}+1}}{(x-2)^{3}(x-4)^{4}}left(frac{2}{x+2}-frac{4}{x-4}+frac{x}{x^{2}+1}-frac{3}{x-2}right)$

Производная показательно-степенной функции

Рационально использовать логарифмическое дифференцирование и при нахождении
производной показательно-степенной
(или степенно-показательной) функции или «функции в степени функция», то есть в случае, когда заданная функция имеет
вид $y(x)=u(x)^{v(x)}$. Логарифмируем левую и правую часть:

$$ln y(x)=ln u(x)^{v(x)}$$
$$ln y(x)=v(x) cdot ln u(x)$$

Тогда

$$(ln y(x))^{prime}=(v(x) cdot ln u(x))^{prime}$$

Производную в левой части равенства находим как производную сложной функции, а в правой — как производную произведения:

$$begin{array}{c}
frac{y^{prime}(x)}{y(x)}=v^{prime}(x) cdot ln u(x)+v(x) cdot frac{u^{prime}(x)}{u(x)} Rightarrow \
Rightarrow y^{prime}(x)=y(x) cdotleft(v^{prime}(x) cdot ln u(x)+v(x) cdot frac{u^{prime}(x)}{u(x)}right)
end{array}$$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Найти производную функции $y(x)=(sin x)^{x}$

Решение. Применим логарифмическое дифференцирование:

$$begin{array}{l}
ln y(x)=ln (sin x)^{x} \
ln y(x)=x ln (sin x)
end{array}$$

Тогда, продифференцировав левую и правую часть, будем иметь:

$$begin{array}{c}
(ln y(x))^{prime}=(x ln (sin x))^{prime} \
frac{y^{prime}(x)}{y(x)}=(x)^{prime} cdot ln sin x+x cdot(ln sin x)^{prime}= \
=1 cdot ln sin x+x cdot frac{1}{sin x} cdot(sin x)^{prime}=ln sin x+frac{x}{sin x} cdot cos x= \
=ln sin x+x cdot operatorname{ctg} x
end{array}$$

Отсюда получаем, что

$$y^{prime}(x)=y(x)(ln sin x+x operatorname{ctg} x)=(sin x)^{x} cdot(ln sin x+x operatorname{ctg} x)$$

Ответ. $y^{prime}(x)=(sin x)^{x} cdot(ln sin x+x operatorname{ctg} x)$

Читать дальше: производная степенно-показательной функции.

Источник

Определение натурального логарифма

Определение.

Натуральным мы будем называть логарифм с основанием .

Напоминание: Что такое ? Давайте вспомним. Итак, рассмотрим функцию . Число иррациональное. В чем его особенность? К графику касательная в точке наклонена под градусом к оси . Рис. 1.

Рис. 1. Касательная к графику функции

Так вот, если касательная наклонена под градусом к оси , то основание этой функции есть число .

Производная в точке : .

И то есть скорость роста функции в точке равна значению функции в этой же точке.

Мы вспомнили, что такое число – основание натурального логарифма.

Теперь дадим строгое определение и обозначение.

Определение.

Натуральным логарифмом (обозначается ln) называется логарифм по основанию .

Несколько примеров, чтобы привыкнуть к новому обозначению.

Примеры:

Итак, мы дали строгое определение натуральному логарифму и привели несколько примеров.

Теперь изучим логарифмическую функцию с натуральным основанием, то есть

Функция y=ln x

Функция . Во-первых, допускаются только положительные значения . Напомним, ≈2,72 – иррациональное число. Для начала, чтобы построить график, используем таблицу.

	1
	0	1	2	-1	-2

Если ;

то вычисляем:

;

Если , то

Таким образом, построим график функции по точкам и понимаем характер изменения функции: рис. 2.

Рис. 2. График функции

Прочтем график функции и перечислим ее свойства:

Свойства функции y=ln x

Вот график:

Рис. 3. График функции

Функция определена, когда ;

Функция возрастает на всей области определения (0,∞);

Функция не ограничена ни снизу, ни сверху;

Не существует ,

Функция непрерывна;

;

Функция выпукла. Если рассмотреть отрезок (A;B), то функция находится над отрезком;

Функция дифференцируема. То есть в любой точке есть касательная.

Дифференцирование функции y=ln x

Логарифмическую функцию с натуральным основанием можно дифференцировать. Давайте научимся это делать.

Для этого докажем формулу .

Доказательство.

Мы знаем, что ;

Значит, производная от сложной функции ^′;

Также знаем основное логарифмическое тождество:

;

Продифференцируем тождество :

Выразим :

Формула доказана. Теперь дифференцировать логарифмические функции с натуральным основанием мы можем.

В итоге имеем две важные формулы:

;

Значит, мы умеем решать любые типовые задачи на производную логарифмической функции с основанием .

Некоторые примеры на нахождение производной

Найти производную.

Типовая задача на нахождение производной в точке

Найти производную функции в точке:

Дано:

Найти:

Решение:

1. Напомним формулу производной от дроби:

Найдем отдельно производные от числителя и знаменателя:

;

3. Можно упрощать, а можно просто подставить 0.

Ответ:

Задача на касательную

Найти касательную:

Дано:

Найти: уравнение касательной к данной прямой в данной точке

Решение.

У нас есть стандартная методика.

Есть уравнение касательной:

Все действия данной методики направлены на то, чтобы найти нужные нам элементы касательной:

Находим точку касания. Так как , то

Точка касания найдена.

Находим производную в любой точке

Находим производную в конкретной точке :

Находим уравнение касательной:

– таково уравнение касательной.

Теперь дадим иллюстрацию на чертеже:

Как построить график функции ?

Надо стандартную кривую сдвинуть влево на единицу по оси (рис. 4).

Рис. 4. Иллюстрация примера

Получим кривую. Ее асимптота . Получили и саму кривую и касательную. То есть, иллюстрация дана.

Итак, мы познакомились с натуральными логарифмами, изучили функцию y=ln x. На следующем уроке мы рассмотрим дифференцирование показательной и логарифмической функций.

Список литературы

Мордкович А.Г. Алгебра и начала математического анализа. – М.: Мнемозина.
Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. – М.: Дрофа.
Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала математического анализа. – М.: Просвещение.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

Ru.wikipedia.org (Источник).
Mathprofi.ru (Источник).
Ru.wikipedia.org (Источник).

Домашнее задание

1. Найти производную функции:

а) ;

б) .

a) Найти уравнение касательной к прямой в точке ;

б) Найти уравнение касательной к прямой в точке .

3. Алгебра и начала анализа, Мордкович А.Г.: № 1648, 1656.

Источник

Logarithmic differentiation helps to find the derivatives of complicated functions, using the concept of logarithmic. Sometimes finding the differentiation of the function is very tough but differentiating the logarithm of the same function is very easy, then in such cases, the logarithmic differentiation formula is used.

In calculus, the differentiation of some complex functions is found first by taking log and then finding the logarithmic derivative of that function. In this article, we will learn about Logarithmic Differentiation in detail.

What is Logarithmic Differentiation?

Method of finding the derivative of a function by first taking the logarithm and then differentiating is called logarithmic differentiation. This method is specially used when the function is type y = f(x)^g(x). In this type of problem where y is a composite function, we first need to take a logarithm, making the function log (y) = g(x) log (f(x)). This creates a situation where the differentiation of the exponent function was quite tricky but after taking the log on both sides of the equation, we can easily differentiate it using logarithm properties and the chain rule. This method is also known as Composite exponential function differentiation. This approach allows us to calculate the derivative of complex exponential functions efficiently.

Logarithmic differentiation uses the chain rule of differentiation and is generally used to differentiate functions of form f(x)g(x), f(x)/g(x), f(x)^g(x), and others.

Read More: Laws of Logarithms

Logarithmic Differentiation Formula

Logarithmic differentiation of a function f(x) is found by dividing the differentiation of the function, by the function. The formula used is shown below,

d / dx [log f(x)] = f'(x) / f(x)

Logarithmic formulas are very useful in solving logarithmic differentiation. Some of the important logarithmic properties used are,

log XY = log X + log Y
log X/Y = log X – log Y
log X^Y = Y log X
log_YX = (log X) / (log Y)

Note: Logarithmic differentiation rules are only valid for the positive functions only because logarithm of negative function is undefined.

Applications of Log Differentiation

Log differentiation found its application while solving various differentiation problems. Various types of problems where Log Differentiation is used are discussed below,

Product of Functions (Product Rule)

The differentiation of any function which is a product of two functions can easily be calculated using logarithmic differentiation.

Suppose we have to find differentiation of f(x) where, f(x) = g(x) × h(x) then by using concept of logarithmic differentiation,

f(x) = g(x) × h(x)

Taking log on both sides,

log f(x) = log (g(x) × h(x))

log f(x) = log g(x) + log h(x) [Using property log (XY) = log (X) + log (Y)]

Differentiating both sides with respect to x,

d/dx [log f(x)] = d/dx [log g(x)] + d/dx [log h(x)]

f'(x)/f(x) = g'(x)/g(x) + h'(x)/h(x)

f'(x) = f(x) [g'(x)/g(x) + h'(x)/h(x)]

f'(x) = f(x) [(h(x)×g'(x) + g(x)×h'(x))/ (g(x)×h(x))]

f'(x) = g(x)×h(x) [h(x)×g'(x) + g(x)×h'(x)] / g(x)×h(x)

f'(x) = h(x)×g'(x) + g(x)×h'(x)

The result obtained above is the “Leibniz rule” and is commonly known as the “Product rule“.

Division of Functions (Quotient Rule)

The differentiation of any function which is in form of a division of two functions can easily be calculated using logarithmic differentiation.

Suppose one has to find the differentiation of f(x) where f(x) = g(x) / h(x) by using the concept of logarithmic. differentiation,

f(x) = g(x)/h(x)

Taking log on both sides,

log f(x) = log [g(x)/h(x)]

log f(x) = log g(x) – log h(x) [Using property log (X/Y) = log (X) – log (Y)]

Differentiating both sides with respect to x,

d/dx [log f(x)] = d/dx [log g(x)] – d/dx [log h(x)]

f'(x)/f(x) = g'(x)/g(x) – h'(x)/h(x)

f'(x) = f(x)[g'(x)/g(x) – h'(x)/h(x)]

f'(x) = f(x) [(g'(x)×h(x) – g(x)×h'(x))/(g(x)×h(x))]

f'(x) = g(x)/h(x) [g'(x)×h(x) – g(x)×h'(x)]/g(x)×h(x)

f'(x) = [g'(x)×h(x) – g(x)×h'(x)] / h²(x)

The result obtained above is commonly known as the “Quotient rule“.

Exponential Functions

The differentiation of any function which is in exponential form can easily be calculated using logarithmic differentiation.

Suppose we have to find differentiation of f(x) where, f(x) = g(x)^h(x) then by using concept of logarithmic differentiation,

f(x) = g(x)^h(x)

Taking log on both sides

log f(x) = log [g(x)^h(x)]

log f(x) = h(x) × log (g(x)) [Using property log (X^Y) = Ylog (X)]

Differentiating both sides with respect to x,

d/dx [log f(x)] = d/dx [h(x) × log g(x)]

f'(x)/f(x) = h(x) × d/dx log g(x) + log g(x) × d/dx h(x) [Using uv rule of differentiation]

f'(x)/f(x) = h(x) × g'(x)/g(x) + log g(x) × h'(x)

f'(x)/f(x) = [h(x) × g'(x) + g(x) × h'(x) × log g(x)] / g(x)

f'(x) = f(x) [h(x)×g'(x) + g(x)×h'(x)×log g(x)] / g(x)

f'(x) = g(x)^h(x)[h(x)×g'(x) + g(x)×h'(x)×log g(x)] / g(x)

f'(x) = g(x)^h(x)-1 [h(x)×g'(x) + g(x)×h'(x)×log g(x)]

Method to Solve Logarithmic Functions

The steps involved in differentiating a logarithmic function are summarized below,

Take log on both sides,
Use logarithmic properties to simplify the function,
Now differentiate the equation with respect to x,
Simplify the obtained equation,
Substitute back the value of y.

Following the above result one can easily find the differentiation of logarithmic functions.

Also, Check

Advanced Differentiation

Implicit Differentiation

Differentiation and Integration Formula

Solved Examples on Logarithmic Differentiation

Example 1: Find the derivative of x^x.

Solution:

Let y = x^x

Step 1: Taking log on both sides

log(y) = log(x^x)

Step 2: Use logarithmic property to simplify the equation

log(y) = x ⋅ log(x) [Using property log(a^b) = b⋅ log(a)]

Step 3: Now differentiate the equation with respect to x,

$frac{d}{d x} log (y)=frac{d}{d x}(x cdot log (x)) \ frac{d}{d x} log (y)=x cdot frac{d}{d x} log (x)+log (x) cdot frac{d x}{d x} \ frac{1}{y} frac{d y}{d x}=x cdot frac{1}{x}+log (x)$

Step 4: Simplify the obtained equation

$frac{d y}{d x}=y(1+log (x))$

Step 5: Substitute back the value of y

$frac{d y}{d x}=x^{x}(1+log (x))$

Example 2: Find the derivative of $x^{left(x^{x}right)}$ ?

Solution:

Given,

y = $x^{left(x^{x}right)}$

Step 1: Taking log on both sides,

log(y) = log( $x^{left(x^{x}right)}$ )

Step 2: Use logarithmic property to simplify the equation

log(y) = x^x⋅ log(x) [Using property log(a^b) = b⋅ log(a)]

Step 3: Differentiating both sides with respect to x,

$frac{d}{d x} log (y)=frac{d}{d x}left(x^{x} cdot log (x)right) \ frac{d}{d x} log (y)=x^{x} cdot frac{d}{d x} log (x)+log (x) cdot frac{d}{d x} x^{x}left{f^{prime}(u . v)=u . f^{prime}(v)+v cdot f^{prime}(u)right} \ frac{1}{y} frac{d y}{d x}=x^{x} cdot frac{1}{x}+log (x) frac{d}{d x} x^{x} left{f^{prime}(log x)=frac{1}{x}right}\ frac{1}{y} frac{d y}{d x}=x^{x-1}+log (x) frac{d}{d x} x^{x}$

Step 4: Simplify the obtained equation,

Since now we know the derivative of x^x, We will substitute here directly.

$frac{1}{y} frac{d y}{d x}=x^{x-1}+log x cdot x^{x}(1+log x) \ frac{d y}{d x}=yleft(x^{x-1}+log x cdot x^{x}(1+log x)right)$

Step 5: Substitute back the value of y

$frac{d y}{d x}=x^{left(x^{x}right)}left(x^{x-1}+log x cdot x^{x}(1+log x)right)$

Example 3: Find the derivative of y = (log x)^x.

Solution:

Given,

y = (logx)^x

Step 1: Taking log on both sides,

log(y) = log((logx)^x)

Step 2: Use logarithmic property to simplify the equation

log(y) = x ⋅ log(logx) [using property log(a^b) = b⋅ log(a)]

Step 3: Differentiating both sides with respect to x,

$frac{d}{d x} log (y)=frac{d}{d x}(x cdot log (log x)) \ frac{d}{d x} log (mathrm{y})=x cdot frac{d}{d x} log (log x)+log (log x) cdot frac{d x}{d x} \ frac{1}{y} frac{d y}{d x}=x cdot frac{1}{log x} cdot frac{1}{x}+log (log x)$

Step 4: Simplify the obtained equation,

$frac{1}{y} frac{d y}{d x}=frac{1}{log x}+log (log x) { using~chain~rule } \ frac{d y}{d x}=y cdotleft(frac{1}{log x}+log (log x)right)$

Step 5: Substitute back the value of y

$frac{d y}{d x}=(log x)^{x} cdotleft(frac{1}{log x}+log (log x)right)$

Example 4: Find the derivative of y = x^√x.

Solution:

Given,

y = x^√x

Step 1: Taking log on both sides,

log(y) = log(x^√x)

Step 2: Use logarithmic property to simplify the equation

log(y) = √x⋅ log(x) [using property log(a^b) = b⋅ log(a)]

Step 3: Differentiating both sides with respect to x,

$frac{d}{d x} log (y)=frac{d}{d x}(sqrt{x} cdot log (x))\ frac{d}{d x} log (mathrm{y})=sqrt{x} cdot frac{d}{d x} log (mathrm{x})+log (x) cdot frac{d sqrt{x}}{d x}$

Step 4: Simplify the obtained equation,

$frac{1}{y} frac{d y}{d x}=sqrt{x} cdot frac{1}{x}+log (x) cdot frac{1}{2 sqrt{x}} \ frac{1}{y} frac{d y}{d x}=frac{1}{sqrt{x}}+log (x) cdot frac{1}{2 sqrt{x}} \ frac{d y}{d x}=y cdotleft(frac{1}{sqrt{x}}+log (mathrm{x}) cdot frac{1}{2 sqrt{x}}right)$

Step 5: Substitute back the value of y

$frac{d y}{d x}=mathrm{x}^{sqrt{x}} cdotleft(frac{1}{sqrt{x}}+log (mathrm{x}) cdot frac{1}{2 sqrt{x}}right)$

FAQs on Logarithmic Differentiation

Question 1: What is the Formula of Logarithmic Differentiation?

Answer:

Logarithmic Differentiation of a function f(x) is found by dividing the differentiation of the function by the function itself. i.e.

d/dx [log f(x)] = f ‘(x)/f(x)

Logarithmic differentiation of a function is calculated using the chain rule of differentiation. These functions are also used to solve exponential functions.

Question 2: When Logarithmic Differentiation is used?

Answer:

Logarithmic differentiation is used when one need to find the differentiation of the complex function, such as, multiplication or division of two fucntions, a function in power of another function, etc. Logarithmic differentiation solves such types of complex functions very easily.

Question 3: What are the Examples of Log Differentiation?

Answer:

Logarithmic differentiation is used to solve different functions, such as, exponential e^{cos x}, product (x + 5)³ (x² + 2)³, exponent (cos x)^{sin x} , etc.

Question 4: What are the Different Rules of Logarithmic Differentiation?

Answer:

Logarithmic differentiation uses the following rules to obtain the differentiation of the complex functions, such as,

Product Rule

Quotient Rule

Exponential Rule

Источник