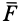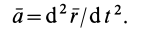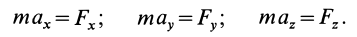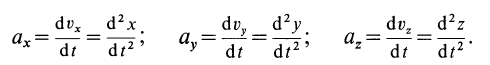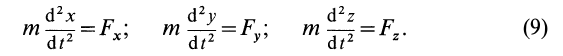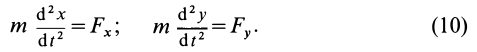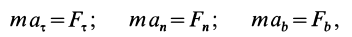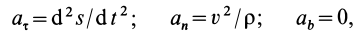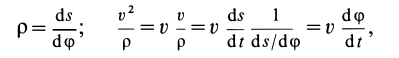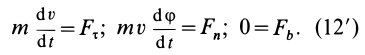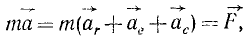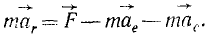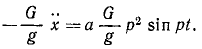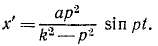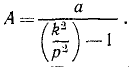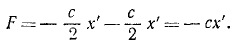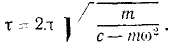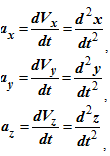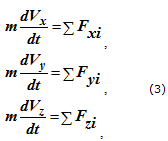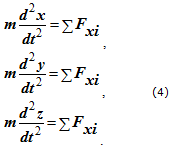Содержание:
Дифференциальные уравнения движения материальной точки:
Используя основной закон динамики, можно вывести дифференциальные уравнения движения материальной точки в различных системах координат. По аксиоме о связях и силах реакций связей можно получить дифференциальные уравнения движения и несвободной точки так же, как и для свободной, только ко всем приложенным к точке силам надо добавить силы реакций связей.
Силы реакций связей при движении точки могут зависеть в общем случае не только от вида наложенных на точку связей и приложенных к ней сил, но и от характера ее движения, например от ее скорости при движении в воздухе или в какой-либо другой сопротивляющейся среде. В дальнейшем не будем делать различия между свободной и несвободной материальными точками. Обозначая равнодействующую всех заданных сил и сил реакций связей
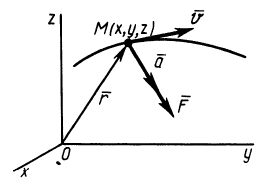
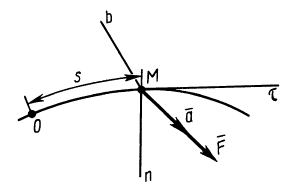
Из кинематики точки известно, что ускорение 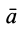
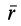
Дифференциальное уравнение движения материальной точки в векторной форме имеет вид
Если спроецировать обе части уравнений (7) или (8) на координатные оси, то можно получить дифференциальные уравнения движения точки в проекциях на эти оси.
В декартовой системе координат в общем случае
Проекции ускорения на координатные оси можно выразить через вторые производные по времени от координат движущейся точки:
Рис. 3
Дифференциальные уравнения движения материальной точки в прямоугольной декартовой системе координат имеют вид
Частные случаи дифференциального уравнения движения материальной точки
Если известно, что материальная точка движется в одной и той же плоскости, то, принимая ее за координатную плоскость 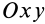
Так как 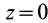
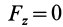
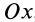
Так как при движении 
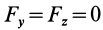
где 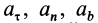
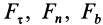
где 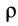
Второе уравнение из (12) можно преобразовать:
где 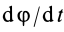
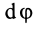
Дифференциальные уравнения (12) можно представить в виде
Рис. 4
Эта форма дифференциальных уравнений движения точки удобна при исследовании некоторых случаев полета снарядов и ракет, особенно по траектории, лежащей в плоскости. Тогда 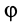
Дифференциальные уравнения движения точки можно представить в любой другой системе координат. Для этого надо знать выражения проекций ускорения на эти оси координат.
Дифференциальные уравнения относительного движения точки
Кориолисовыми силами инерции называют две векторные величины, имеющие размерность силы и добавляемые к силам, приложенным к материальной частице, для определения ее относительного ускорения
Все дифференциальные уравнения движения, с которыми мы ознакомились в этой главе, относятся к абсолютному движению, т. е. к движению по отношению к инерциальной системе отсчета. Для написания дифференциальных уравнений движения точки (или частицы) относительно подвижных осей подставим в основное уравнение динамики (123) вместо абсолютного ускорения точки его выражение (110):
откуда
Векторную величину
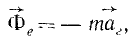
имеющую размерность силы, равную произведению массы материальной частицы на ее переносное ускорение и направленную противоположно этому ускорению, называют переносной силой инерции Кориолиса.
Векторную величину
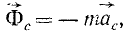
равную произведению массы материальной частицы на ее кориолисово ускорение и направленную противоположно этому ускорению, называют поворотной силой инерции Кориолиса.
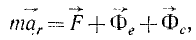
или в проекциях на оси координат:
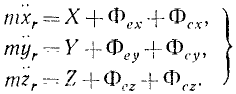
Таким образом, относительное движение материальной точки можно описать такими же (по форме) дифференциальными уравнениями, как и абсолютное, но к действующим на точку силам нужно прибавить две кориолисовы силы инерции: переносную и поворотную.
Эти величины следует отличать от даламберовых сил инерции (см. гл. XX), введение которых позволяет решать задачи динамики методом статики.
Пример решения задачи №1
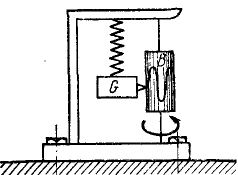
Определить амплитуду вынужденных колебаний в относительном движении вибрографа для записи вертикальных колебаний фундамента (рис. 171), совершающего вместе с фундаментом колебания по закону χ = a sin pt, если вес груза равен G и жесткость пружины с.
Рис. 171
Решение. Рама жестко соединена с фундаментом и участвует в его колебаниях, как и вращающийся барабан В, на котором груз G, перемещаясь вверх и вниз, записывает колебания фундамента. Вертикальные перемещения х’ груза G по отношению к раме являются относительными и по отношению к барабану, если пренебречь его вращением. Уравнение этих относительных перемещений можно составить как уравнение абсолютного движения, если к заданным силам добавить переносную кориолисову силу, равную и противоположную произведению вектора переносного ускорения на массу груза. Переносная сила инерции груза равна
Напишем дифференциальное уравнение относительных колебаний груза, сократив на m:
x’ + k2χ’ = ар2 sin pt.
где 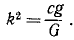
Амплитуда этих колебаний тем менее отличается от амплитуды колебаний фундамента, чем меньше собственная частота k прибора сравнительно с частотой р, т. е. чем меньше жесткость пружины и чем больше масса груза.
Ответ.
- Заказать решение задач по теоретической механике
Пример решения задачи №2
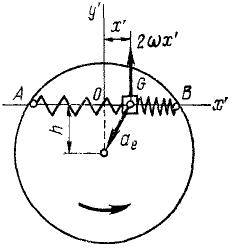
Ползун G (рис. 172) может скользить по хорде AB равномерно вращающегося горизонтального диска, к точкам А и В которой он прикреплен двумя одинаковыми пружинами жесткостью 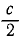
Рис. 172
Решение. Построим оси подвижной системы координат с началом в точке О (в положении относительного равновесия ползуна), направив Ox’ но хорде.
Определим силы, действующие на ползун. Если ползун отклонится от равновесного положения О на величину х’, то одна из пружин сожмется, а другая растянется. Согласно закону Гука сила каждой из пружин пропорциональна деформации х’ и направлена к точке О. Следовательно, на ползун действует активная сила
Кроме активной силы, надо учесть действие кориолисовых сил: Φe—переносной и Φc-поворотной.
Переносная сила инерции равна произведению массы т ползуна на его переносное ускорение: 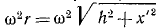
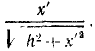
Поворотная сила Кориолиса равна произведению массы ползуна иа кориолисово ускорение 2ωx’ и направлена против этого ускорения. Таким образом, чтобы определить направление поворотной силы Кориолиса, надо вектор относительной скорости повернуть на 90° против переносного вращения. Находим, что поворотная сила инерции действует перпендикулярно AB и проекция ее на Ox’ равна нулю.
При найденных значениях активных сил и кориолисовых сил дифференциальное уравнение относительного движения ползуна по хорде имеет вид:
mх’ = — cx’ + mω2x’= — (с—mω2)x’.
Это уравнение выражает гармоническое колебание с периодом
Ответ. 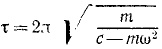
Пример решения задачи №3
Составить дифференциальное уравнение относительного движения ползуна, описанного в предыдущей задаче, считая, что при его движении вдоль хорды AB возникает трение, пропорциональное нормальному давлению на хорду.
Решение. Нормальное давление обусловлено поворотной силой инерции и нормальной составляющей переносной силы инерции.
Поворотная сила ползуна Φс=2mωx’ переменна по величине и направлению. Она направлена перпендикулярно к хорде AB, но в сторону положительных значений у’, если точка G движется в сторону отрицательных значений х’, т. е, если х’ < 0, и, наоборот, в сторону отрицательных у’, если х’ положительно. А так как сила трения направлена всегда против относительной скорости, то силу трения, обусловленную давлением Φс, мы вполне определим по величине и по знаку выражением
— f2mωx’.
Нормальная составляющая переносной силы инерции ползуна постоянна по величине и всегда направлена в сторону положительных у’. Чтобы ее определить, надо 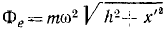
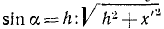
mх’ =— (с—mω2) x’ — fm (2ωx’ ± ω2h),
причем знак второго слагаемого в скобках надо брать положительным при х’ < 0 и отрицательным при х’ > 0. Решение такого уравнения при движении точки G влево и вправо получается, конечно, различным. Если Л — 0 и хорда является диаметром, то вместо кулонова трения получается вязкое демпфирование, зависящее от скорости.
- Две основные задачи динамики точки
- Прямолинейное движение точки
- Криволинейное движение материальной точки
- Движение несвободной материальной точки
- Сложное движение точки
- Сложение движение твердого тела
- Кинематика сплошной среды
- Аксиомы классической механики
Механической
системой называется совокупность
материальных точек или тел, положение
и движение которых зависят от положения
и движения всех остальных точек.
Механическая
система может быть образована из
свободных точек, движение которых не
ограничено какими-либо геометрическими
связями. Примером механической системы
из точек с геометрическими связями
служит любой механизм.
силы, действующие
на точки несвободной механической
системы, можно подразделить на активные
силы
и реакции связей
.
с другой стороны, действующие на точки
системы силы можно подразделить на
внешниеи на внутренние
.
Внутренними силами взаимодействуют
между собой точки данной системы.
Внешними силами действуют на точки
системы точки или тела, не входящие в
данную систему. Главный вектори главный момент
всех внутренних сил системы относительно
любого центра равны нулю:
;
(7.1)
.
(7.2)
Для n
точек механической системы можно
записать n
дифференциальных уравнений движения
в векторной форме типа
(7.3) или 3n
дифференциальных уравнения движения
в проекциях на координатные оси вида:
;
;
.
(7.4)
Чтобы найти
уравнение движения механической системы
под действием заданных сил, необходимо
проинтегрировать при известных начальных
условиях систему дифференциальных
уравнений второго порядка, что сопряжено
с большими трудностями.
Дифференциальные
уравнения движения механической системы
можно использовать для вывода общих
теорем динамики, с помощью которых можно
решать задачи о движении материальной
точки или механической системы, установить
зависимость между основными динамическими
характеристиками механического движения
материальных тел.
8. Теорема о движении центра масс.
Центром масс или
центром инерции системы является
геометрическая точка, положение которой
определяется в каждый момент времени:
,
,
,
(8.1) где М – масса системы,
равная сумме масс всех точек системы;
mk—
масса произвольной точки Mk;
xk,
yk,
zk
– координаты
произвольной точки Mk
системы.
В однородном поле
земного тяготения центр масс совпадает
с центром тяжести.
Центр масс существует
для любой механической системы независимо
от действующих сил.
Центр масс системы
движется как материальная точка, масса
которой равна массе всей системы и к
которой приложен все внешние силы,
действующие на систему (теорема о
движении центра масс).
,
(8.2) где М—масса
системы;
ac—ускорение
центра масс;
—
главный вектор всех внешних сил системы.
Теорема о движении
центра масс имеет два следствия, которые
определяют закон сохранения движения
центра масс.
Рисунок 18
1. Если главный вектор всех
внешних сил, действующих на систему,
равен нулю, то центр масс системы будет
находиться в покое или двигаться
равномерно и прямолинейно.
В автомобиле (рис.
18) действие газов на поршень двигателя
является внутренней силой. Внешние силы
– это сила тяжести автомобиля
,
нормальна реакция дороги,
сила трениямежду колесами автомобиля и дороги. При
отсутствии сцепления колес с дорогой
(=0)
действие внутренних сил не может изменить
закона движения центра масс. Если,
,
то поэтому.
При начальной скорости центра масс,
центр масс будет оставаться в покое.
2. Если сумма
проекций всех внешних сил, действующих
на систему, на какую-либо ось равна нулю,
то проекция скорости центра масс на
данную ось будет оставаться постоянной.
Если
,
то,
поэтому.
Если в начальный момент времени,
то учитывая, что,
координата центра масс остается
постоянной (xc=const).
Для человека, стоящего на абсолютно
гладкой горизонтальной поверхности
(рис. 19), внешними силами является его
вес
и нормальная реакция
.
Сила трения на гладкой поверхности
отсутствует, т.е.,xc=const.На
гладкой поверхности человек может
подпрыгнуть в вертикальном направлении,
так как в проекции на ось у теорема о
движении масс
п
>0, т.е. центр масс может переместиться
по вертикали. Перемещение по горизонтали
будет возможно при действии силы трения
скольжения (рис. 19,б). Применяя теорему
о движении центра масс, можно решать
прямую и обратную задачи динамики
поступательного движения в следующей
последовательности:
имеет вид
.
При отталкивании от земли за счет
деформации мышцR>P,
1. выбрать систему
координат;
2. изобразить все
внешние силы;
3. записать теорему
о движении центра масс в проекции на
ось координат;
4. определить
искомые величины в соответствии с
условиями задачи.
ПРИМЕР 10.
Определить действие
фундамента кривошипного пресса при
холостом ходе, если кривошип ОА=r
вращается с постоянной угловой скоростью
,
длина кривошипа АВ=,
вес фундамента и корпусаG1,
вес кривошипа
G2,
вес штампа В
G3.
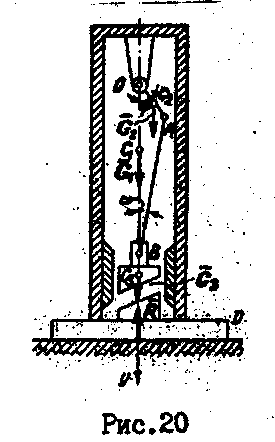
В начальный момент кривошип занимал
вертикальное нижнее положение (рис.
20).
РЕШЕНИЕ.
1. На пресс действуют
внешние силы: сила тяжести корпуса с
фундаментом
,
кривошипа,
штампаи нормальная реакция грунта
.
Запишем теорему о движении центра масс
системы в проекции на ось у:
,
(1) где.
(2)
3. Выразим ординату
ус
центра масс
,
(3) гдеG=G1+G2+G3.
Угол поворота
кривошипа
.
y1=OC1=const;
y2=OC2cos=0,5rcos
;
y3=OAcos+ABcos
+BC3=2cos
+
cos
+BC3;
где
ВС3=const.
Из
ОАВ:
;
;
.
Если разложить
в ряд, отбросив члены ряда, содержащие
в степени выше второй, получим
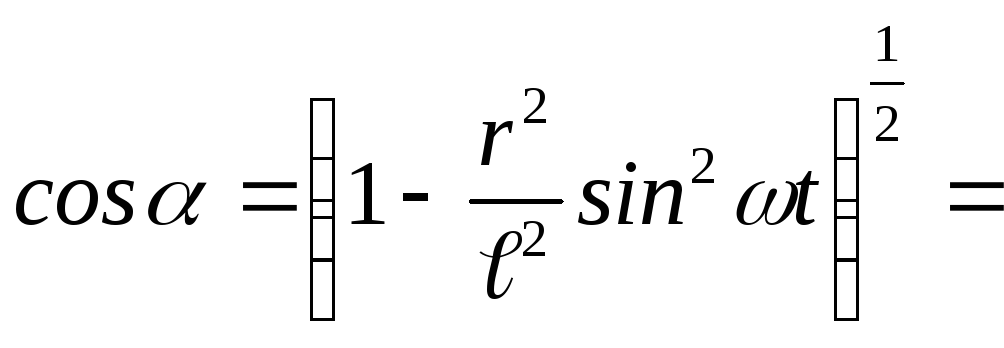
;
тогда;

(4)
Продифференцируем
(4) дважды по времени и подставим в (1)
;
(5)
;
отсюда находим нормальную реакцию
грунта, а следовательно, величину
давления на фундамент в зависимости от
угла поворота кривошипа
.
ПРИМЕР 11.
Механическая
система состоит из прямоугольной
вертикальной плиты 1 массой m1=18кг,
движущейся вдоль горизонтальных
направляющих, и груза D
массой m2=6кг.
В момент времени t0=0,
когда плита двигалась со скоростью
u0=2м/с,
груз начал двигаться вдоль желоба в
соответствии с уравнением S=AD=0,4sin(t2)
(S—в
метрах, t—в
секундах (рис. 21)). Определить скорость
плиты в момент времени t1=1с.
Р
1. Внешними силами,
действующими на систему, являются вес
пластины
,
вес грузаи нормальная реакция поверхности
.
2. Применим теорему
о движении центра масс в проекции на
ось х:
.
(1) Так как,
,
то.
(2)
3. Выразим произведение
,
где х1,
х2
– абсциссы плиты и груза.
.
Тогда.
(3) Продифференцируем (3) по времени,
(4) где— искомая скорость плиты.
При t=0
u1=u0;
.
Следовательно,
С1=(m1+m2)u0.
(5) С учетом (2), (4) и (5) получим
,
откуда находим скорость плиты.
При t1=1c
м/с.
Соседние файлы в предмете Теоретическая механика
- #
- #
- #
- #
Составление систем дифференциальных уравнений движения материальной точки, на которую действует некоторая система сил для определения движения точки под действием этих сил.
Пусть на материальную точку действует некоторая система сил и требуется определить движение точки под действием этих сил.
Уравнение второго закона динамики для материальной точки массой m запишется в виде
m∙ a = ΣFi (1)
где a — ускорение точки;
Fi — силы, действующие на точку, включая реакции связей.
Спроецировав уравнение (1) на декартовы оси координат, получим систему из трех уравнений
m∙ ax = ΣFxi
m∙ ay = ΣFyi (2)
m∙ az = ΣFzi
где ax , ay , az — проекции ускорения точки на декартовы оси координат;
Fxi , Fyi , Fzi — проекция i<-той силы на соответствующую ось.
Учитывая, что
получаем систему дифференциальных уравнений первого порядка относительно проекций скорости точки
или второго порядка относительно координат точки
Спроецировав уравнение (1) на естественные оси координат, получим следующую систему уравнений
где aτ и an — касательное и нормальное ускорение точки;
Fτi , Fni , Fbi — проекции i-той силы на касательную, нормаль и бинормаль соответственно.
Учитывая, что
aτ = dV/dt,
an = V2/ρ,
ab = 0
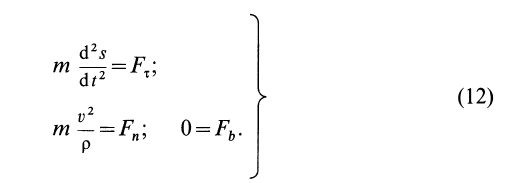
получим:
mdV/dt = ΣFτi
mV2/ρ = ΣFni (5)
0 = ΣFbi
В зависимости от того, что известно о движении точки, дифференциальные уравнения записывают или в декартовых или в естественных координатах.
- Пример решения задачи по теме
- Интегрирование дифференциальных уравнений движения
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее