Содержание:
- Случай независимой переменной
- Случай зависимой переменной
Пусть функция $y=f(x)$ зависит от переменной
$x$ и дифференцируема в точке
$x$. Может оказаться, что в точке
$x$ дифференциал
$d y=f^{prime}(x) d x$, рассматриваемый как функция от
$x$, есть также дифференцируемая функция. Тогда существует
дифференциал от дифференциала $d(dy)$ данной функции,
который называется дифференциалом второго порядка функции $y=f(x)$.
Дифференциал второго порядка обозначается следующим образом:
$d^2y=d(dy)$
Аналогично определяются дифференциалы более высоких порядков.
Определение
Дифференциалом
$n$-го порядка
$d_ny$ функции
$y=f(x)$ называется дифференциал от дифференциала
$(n-1)$-го порядка этой функции, то есть
$$d^{n} y=dleft(d^{n-1} yright)$$
Получим формулы, выражающие дифференциалы высших порядков. Рассмотрим несколько случаев.
Случай независимой переменной
Пусть $y=f(x)$ — функция независимой переменной
$x$, имеющая дифференциалы любого порядка.
Первый дифференциал функции
$$d y=f^{prime}(x) d x$$
где $dx=Delta x$ — некоторое приращение независимой
переменной $x$, которое мы задаем сами и которое не
зависит от $x$. По определению
$$d^{2} y=d(d y)=dleft(f^{prime}(x) d xright)$$
Переменной является аргумент $x$. Значит, для
дифференциала величина $dx$ является постоянной и
поэтому может быть вынесена за знак дифференциала. То есть дифференциал второго порядка
$$d^{2} y=dleft(f^{prime}(x) d xright)=d x cdot dleft(f^{prime}(x)right)$$
Для вычисления дифференциала $dleft(f^{prime}(x)right)$ применим формулу
дифференциала первого порядка к функции $f^{prime}(x)$. Тогда получим:
$$dleft(f^{prime}(x)right)=left(f^{prime}(x)right)^{prime} cdot d x=d x cdot f^{prime prime}(x) d x=f^{prime prime}(x)(d x)^{2}=f^{prime prime}(x) d x^{2}$$
Итак,
$$d^{2} y=f^{prime prime}(x) d x^{2}$$
Рассматривая последовательно дифференциалы все более высокого порядка, получим формулу дифференциала
$n$-го порядка:
$$d^{n} y=f^{n}(x) d x^{n}$$
Пример
Задание. Найти дифференциал третьего порядка функции $y(x)=4x^3-12x+5$
Решение. По формуле
$$d^{3} y=y^{prime prime prime}(x) d x^{3}$$
Найдем третью производную заданной функции:
$$begin{array}{c}
y^{prime}(x)=left(4 x^{3}-12 x+5right)^{prime}=left(4 x^{3}right)^{prime}-(12 x)^{prime}+(5)^{prime}= \
4left(x^{3}right)^{prime}-12(x)^{prime}+0=4 cdot 3 x^{2}-12 cdot 1=12 x^{2}-12 \
y^{prime prime}(x)=left(y^{prime}(x)right)^{prime}=left(12 x^{2}-12right)^{prime}=left(12 x^{2}right)^{prime}-(12)^{prime}= \
=12left(x^{2}right)^{prime}-0=12 cdot 2 x=24 x \
y^{prime prime prime}(x)=left(y^{prime prime}(x)right)^{prime}=(24 x)^{prime}=24(x)^{prime}=24
end{array}$$
Тогда
$$d^{3}y=24dx^3$$
Ответ. $d^{3}y=24dx^3$
Случай зависимой переменной
Пусть задана дифференцируемая функция $y=f(u(x))$. Тогда
$$d y=f^{prime}(u) d u$$
где $d u=u^{prime}(x) d x$ в общем случае не является постоянной величиной.
Поэтому дифференциал от функции $f^{prime}(u) d u$ берем как дифференциал от произведения
$$d^{2} y=dleft(f^{prime}(u) d uright)=dleft(f^{prime}(u)right) cdot d u+f^{prime}(u) cdot d(d u)=f^{prime prime}(u) d u^{2}+f^{prime}(u) d^{2} u$$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти дифференциал второго порядка
$d^{2}u$ функции $f(u)=sqrt{u}$, где
$u(x)=3x+7$ и $x$ — независимая переменная.
Решение. Решим пример разными способами и сравним ответы.
1-ый способ. Согласно формуле, имеем, что искомый дифференциал
$$d^{2} y=f^{prime prime}(u) d u^{2}+f^{prime}(u) d^{2} u$$
Найдем все необходимые компоненты формулы. Из условия имеем:
$$begin{array}{c}
f^{prime}(u)=(sqrt{u})^{prime}=frac{1}{2 sqrt{u}} \
f^{prime prime}(u)=left(f^{prime}(u)right)^{prime}=left(frac{1}{2 sqrt{u}}right)^{prime}=frac{1}{2} cdotleft(u^{-frac{1}{2}}right)^{prime}= \
=frac{1}{2} cdotleft(-frac{1}{2}right) cdot u^{-frac{3}{2}}=-frac{1}{4 sqrt{u^{3}}} \
d u=d(3 x+7)=(3 x+7)^{prime} d x=left[(3 x)^{prime}+(7)^{prime}right] d x= \
=left[3(x)^{prime}+0right] d x=3 cdot 1 cdot d x=3 d x \
d^{2} u=d(3 d x)=d x cdot d(3)=d x cdot 0=0
end{array}$$
А тогда:
$$begin{aligned}
d^{2} y=&-frac{1}{4 sqrt{u^{3}}} d u^{2}+frac{1}{2 sqrt{u}} cdot 0=-frac{1}{4 sqrt{u^{3}}} cdot(3 d x)^{2}=\
&=-frac{9}{4 sqrt{u^{3}}} d x^{2}=-frac{9}{4 sqrt{(3 x+7)^{3}}} d x^{2}
end{aligned}$$
2-ой способ. Из того, что $f(u)=sqrt{u}$ и
$u(x)=3 x+7$, получаем:
$$f(x)=sqrt{3 x+7}$$
А тогда
$$d^{2} y=f^{prime prime}(x) d x^{2}$$
Найдем вторую производную функции $f(x)=sqrt{3 x+7}$:
$$f^{prime}(x)=(sqrt{3 x+7})^{prime}=frac{1}{2 sqrt{3 x+7}} cdot(3 x+7)^{prime}=$$
$$=frac{1}{2 sqrt{3 x+7}} cdotleft[(3 x)^{prime}+(7)^{prime}right]=frac{1}{2 sqrt{3 x+7}} cdotleft[3(x)^{prime}+0right]=$$
$$=frac{3 cdot 1}{2 sqrt{3 x+7}}=frac{3}{2 sqrt{3 x+7}}$$
$$f^{prime prime}(x)=left(f^{prime}(x)right)^{prime}=left(frac{3}{2 sqrt{3 x+7}}right)^{prime}=frac{3}{2}left((3 x+7)^{-frac{1}{2}}right)^{prime}=$$
$$=frac{3}{2} cdotleft(-frac{1}{2}right) cdot(3 x+7)^{-frac{3}{2}} cdot(3 x+7)^{prime}=$$
$$=-frac{3}{4 sqrt{(3 x+7)^{3}}} cdotleft[(3 x)^{prime}+(7)^{prime}right]=-frac{3}{4 sqrt{(3 x+7)^{3}}} cdot 3(x)^{prime}=$$
$$=-frac{3 cdot 3 cdot 1}{4 sqrt{(3 x+7)^{3}}}=-frac{9}{4 sqrt{(3 x+7)^{3}}}$$
Окончательно имеем:
$$d^{2} y=-frac{9}{4 sqrt{(3 x+7)^{3}}} d x^{2}$$
Ответ. $d^{2} y=-frac{9}{4 sqrt{(3 x+7)^{3}}} d x^{2}$
Читать дальше: производная функции, заданной неявно.
Дифференциалы различных порядков
Щебетун Виктор
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Что такое дифференциал функции
Определение
Дифференциалом функции называется произведение производной этой функции на приращение независимой переменной.
Дифференциал функции обозначается dy и имеет запись вида:
$dy = f ‘(x) Delta $х
Пусть дана функция y = f(x), где х — независимая переменная. Дифференциал этой функции есть некоторая функция от х но от х зависит только первый сомножитель f ‘(x) второй же сомножитель dx является приращением независимой переменной x и от значения этой переменной не зависит.
dy = f ‘(x)dx
Функция dy есть функция от x и называется дифференциалом.
Что такое второй, третий дифференциал
Определение
Дифференциал от дифференциала функции называется вторым дифференциалом или дифференциалом второго порядка этой функции и обозначается d2y.
$d^2y = d(dy)$
Определение
Третьим дифференциалом или дифференциалом третьего порядка функции называется дифференциал от ее второго дифференциала:
$d^3y = d(d2y) = f »'(x)dx^3$
Что такое дифференциал n-го порядка
Определение
Дифференциалом n-го порядка является дифференциал от дифференциала (n-1)-го порядка:
$d^ny = d(d^{n-1}y)$
Пользуясь дифференциалами различных порядков, производную любого порядка можно представить как отношение дифференциалов соответствующего порядка:
[f'(x)=frac{dx}{dy} ]
[f^{n} (x)=frac{d^{n} y}{dx^{n} } ]
Пример 1
Найти дифференциал функции.
[d(2x^{3} +1)]
Решение.
По правилу дифференцирования, дифференциал суммы равен сумме дифференциалов функций.
[d(2x^{3} +1)=d(2x^{3} )+d(1)]
Найдем производные данных функций и добавим к ним знак дифференциала. Производная второй функции так же как и дифференциал равна 0.
[d(2x^{3} +1)=6x^{2} dx]
«Дифференциалы различных порядков» 👇
Пример 2
Найти дифференциал второго порядка функции.
[y(x)=x^{3} -arccos x]
Решение.
- По определению дифференциала, дифференциал второго порядка равен:
- Продифференцируем данную функцию по х:
- Вычислим вторую производную
- Подставим полученную производную в формулу дифференциала второго порядка:
[d^{2} y=y»(x)dx^{2} ]
[y'(x)=(x^{3} -arccos x)’=(x^{3} )’-(arccos x)’=3x^{2} +frac{1}{sqrt{1-x^{2} } } ]
[y»(x)=left(3x^{2} +frac{1}{sqrt{1-x^{2} } } right)^{{‘} } =6x+left((1-x^{2} )^{-frac{1}{2} } right)^{{‘} } =6x-frac{1}{2} (1-x^{2} )^{-frac{3}{2} } (1-x^{2} )’]
[y»(x)=6x+x(1-x^{2} )^{-frac{3}{2} } ]
[d^{2} y=y»(x)dx^{2} =left(6x+x(1-x^{2} )^{-frac{3}{2} } right)dx^{2} =left(6x+frac{x}{sqrt[{}]{(1-x^{2} )^{3} } } right)dx^{2} ]
Пример 3
Найти дифференциал второго порядка функции заданной неявно.
[xy-y^{2} =3]
Решение.
- Перенесем все члены функции в одну сторону
- Найдем первый дифференциал dy
- Дифференциал разности равен разности дифференциалов
- Распишем дифференциал произведения и вычислим
- Выразим dy
- Вычислим дифференциал второго порядка по свойству частного:
- Выполним замену dy
[xy-y^{2} -3=0]
[dleft(xy-y^{2} right)-dleft(3right)=0]
[dleft(xyright)-dleft(y^{2} right)-dleft(3right)=0]
[dleft(xright)cdot y+xdy-dleft(y^{2} right)-dleft(3right)=0]
[ydx+xdy-2ydy-0=0]
[dyleft(x-2yright)=-ydx]
[dy=-frac{ydx}{x-2y} ]
[d^{2} y=d(dy)=dleft(-frac{ydx}{x-2y} right)]
[d^{2} y=dleft(-frac{y}{x-2y} right)dx=frac{d(-y)(x-2y)-(-y)cdot d(x-2y)}{left(x-2yright)^{2} } dx]
[d^{2} y=frac{-dy(x-2y)+ycdot d(x)-2dy}{left(x-2yright)^{2} } dx]
[d^{2} y=frac{-frac{-ydxleft(x-2yright)}{x-2y} +ydx-2ydy}{left(x-2yright)^{2} } dx]
[d^{2} y=frac{ydx+ydx-2ydy}{left(x-2yright)^{2} } dx=frac{2ydx-2yleft(-frac{ydx}{x-2y} right)}{left(x-2yright)^{2} } dx]
[d^{2} y=frac{2ydx+frac{2y^{2} }{x-2y} }{left(x-2yright)^{2} } dx=frac{2ydx+2y^{2} }{left(x-2yright)^{3} } dx]
[d^{2} y=frac{2y(x+2y)+2y^{2} }{left(x-2yright)^{3} } dx^{2} =frac{2xy+4y^{2} +2y^{2} }{left(x-2yright)^{3} } dx^{2} =frac{2xy+6y^{2} }{left(x-2yright)^{3} } dx^{2} ]
[d^{2} y=frac{2yleft(x+3yright)dx^{2} }{left(x-2yright)^{3} } ]
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 15.12.2022
-
Дифференциал функции
Дифференциал
(первого порядка) функции
—это главная
часть ее приращения, линейная относительно
приращения аргумента. Дифференциал
аргумента равен его приращению:
.
Дифференциал функции равен произведению
ее производной на дифференциал аргумента.
Основные
свойства дифференциала:
1.
,
где-const.
2.
.
3.
.
4.
.
5.
,
.
6.
,
.
Форма дифференциала первого порядка
не зависит от того, является аргумент
функции независимой переменной или
функцией другого аргумента. В этом
состоит свойствоинвариантности
формы дифференциала первого порядка.
Дифференциалом
второго порядка
функции
называется дифференциал от дифференциала
первого порядка:.
Аналогично
определяется дифференциал
третьего порядка:
.Дифференциал
n-го
порядка:
.
Если
и
— независимая переменная, то дифференциалы
высших порядков вычисляются по формулам:
,
,…..,
.
Если
,
,
то,
где дифференцирование функциивыполняется по переменной
.
Это имеет место и для дифференциалов
более высоких порядков.
.
Дифференциалы
второго и более высоких порядков не
обладают свойством инвариантности
формы.
Геометрически
дифференциал представляет собой
приращение ординаты касательной к
графику функции в точке
.
Если
приращение аргумента мало по абсолютной
величине, то
и
.
Таким образом, дифференциал функции
может применяться для приближенных
вычислений.
Абсолютная
величина разности между истинным
значением какой-либо величины
и ее приближенным значением
называется
абсолютной погрешностью и
обозначается
.
Абсолютная
величина отношения абсолютной погрешности
к истинному значению называется
относительной
погрешностью
и обозначается
.
Относительная погрешность обычно
выражается в процентах.
Если
приращение функции заменить ее
дифференциалом, то получим приближенное
значение приращения
.
В этом случае абсолютная погрешность
равна,
а относительная погрешность будет.
С
помощью дифференциала функции вычисляют
абсолютную погрешность функции
,
если известна абсолютная погрешностьаргумента. В практических задачах
значения аргумента находятся с помощью
измерений, и его абсолютная погрешность
считается известной.
Пусть
требуется вычислить значение функции
при
некотором значении аргумента,
истинная величина которого нам известна,
но дано его приближенное значениес абсолютной погрешностью
,
.
Тогда
.
Отсюда
видно, что
.
Относительная
погрешность функции
выражается формулой

Пример
1. Найти
дифференциал функции
.
Решение:
.
Пример
2. Найти все
дифференциалы функции
.
Решение:
,
,
,
,
.
Пример
3. Найти
для неявно заданной функции
.
Решение: Функция
задана неявно. Находим первую производную
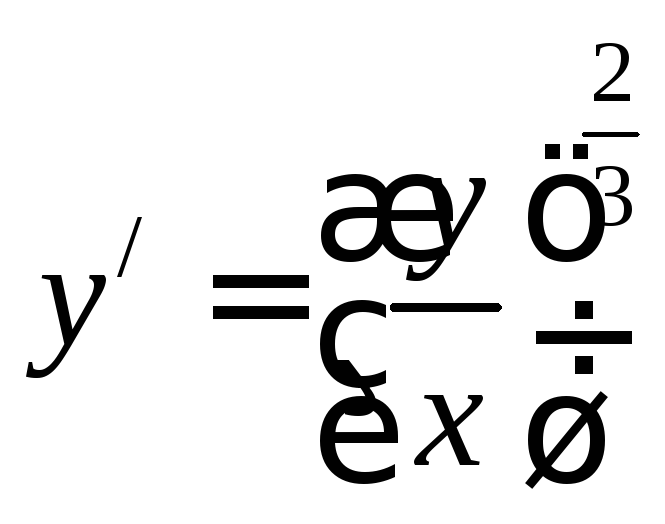
тогда

Вычислим вторую
производную

отсюда
.
Пример
4. Выразить
дифференциал сложной функции через
независимую переменную и дифференциал:
,
,
.
Решение:
.

Пример
5. Вычислить
приближенное значение
.
Решение:
Рассмотрим функцию
.
Полагая,
и применяя формулу
,
получим:

Пример
6. Вычислить
приближенное значение площади круга,
радиус которого равен 3,02 м.
Решение:
Воспользуемся формулой
.
Полагая
,
,
имеем.
Следовательно, приближенное значение
площади круга составляет.
Пример
7. Для функции
найти приращение ординаты касательной
и приращение функции при переходе
аргументаот значения
к
.
Решение:
согласно геометрическому смыслу
дифференциала, приращению ординаты
касательной соответствует дифференциал
функции
.
При
и
получим
.
Приращение функции
находим по формуле
.
Следовательно,
приращение ординаты касательной равно
0,7, а приращение функции 0,71. Т. к.
,
то.
Пример
8. Найти
дифференциал и приращение функции
в точке
и
.
Найти абсолютную и относительную
погрешности значения функции при замене
приращения функции ее дифференциалом.
Решение:
Имеем:
,
.
При
и
получим:
,
.
Абсолютная
погрешность
,
а относительная погрешность.
Пример
9. При измерении
сторона куба
оказалась равной 4 см. При этом максимально
возможная погрешность измерениянаходится в пределах
см.
Определить абсолютную и относительную
погрешности при вычислении объема куба.
Решение:
Объем куба равен
см
.
Возможная
неточность измерения
.
Отсюда
абсолютная погрешность
.
Относительная
погрешность
.
Пример
10. Найти
приближенно
.
Решение:
Полагаем
,
тогда,
.
Если
принять
,
то,
.
Найти дифференциалы
указанных порядков от функций:
1.
,
-?.
Ответ:.
2.
,
-?
Ответ:.
3.
,
-?
Ответ:.
4.
,
-?
Ответ:.
5.
,
,
,
-? Ответ:
.
,
.
6.
,
-?
Ответ:
.
7.
,
-? Ответ:
.
8.
,
-? Ответ:
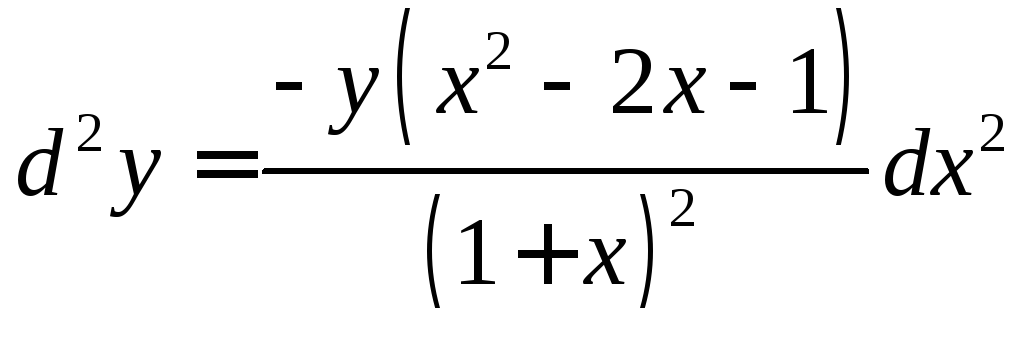
9.
-? Ответ:
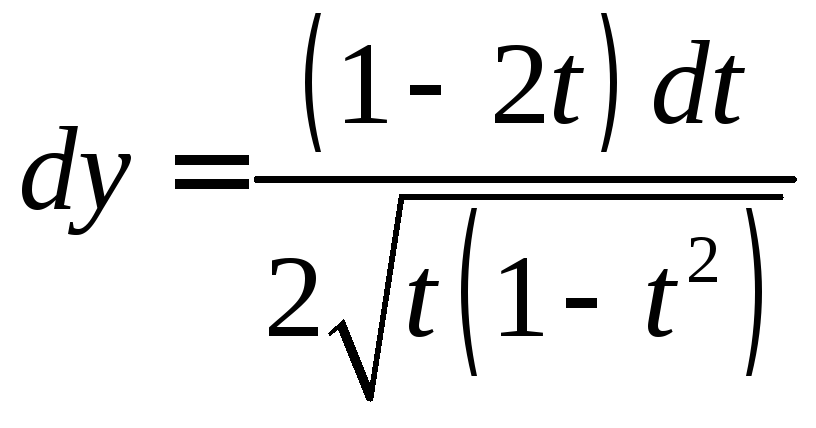
10.
-? Ответ:
.
11.
,
-? Ответ:
.
12.
,
-? Ответ:
.
13.
,
.
-?
Ответ:,
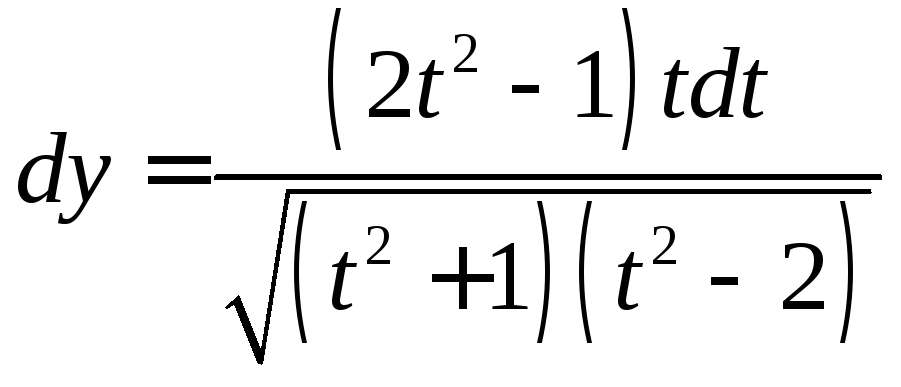
14.
,
,
-?
Ответ:
,
.
15.
-?
Найти приближенное
значение:
16.
.
Ответ: 0,811.
17.
.
Ответ: 1,035.
18.
.
Ответ: 0,078.
19.
.
Ответ: 1,9938.
20.
.
Ответ: 2,02.
21.
.
Ответ:3,03.
22.
.
Ответ:.
23.
.
Ответ:.
24.
.
Ответ: 0,1.
25.
.
Ответ:.
26.
Определить, на сколько приблизительно
увеличится объем шара, если его радиус
см
увеличить на 0,2см. Ответ: 565.
27.
Вычислить приближенное значение площади
круга, радиус которого равен 3,02 м.
Ответ:
.
28.
Сравнить приращение и дифференциал
функции
.
Ответ:
,
.
29.
Вычислить
,
для функции
при
и
.
Ответ:
,
.
30. Найти приближенное
значение объема шара радиуса 2,01 м.
Ответ:
.
31.
Найти приближенное значение
из уравнения:
.
Ответ:
.
32.
Найти приближенно значение объема шара
радиуса
.
Ответ:
.
33.
Ребра куба увеличены на 1см. При этом
дифференциал
объема
куба оказался равным 12 см
.
Найти первоначальную длину ребер.
Ответ: 2 см.
34.
Радиус круга увеличен на 1см. Дифференциал
площади круга оказался при этом равным
см
.
Найти первоначальную величину радиуса.
Ответ: 3 см.
35.
Определить приблизительно относительную
погрешность при вычислении поверхности
сферы, если при определении ее радиуса
относительная погрешность составила
.
Ответ:.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
14.02.201535.92 Mб149Сборник рецептур.djvu
- #
- #
Дифференциалом функции
называется главная (линейная по
) часть приращения функции. Чтобы понять данное определение, рассмотрим следующий рисунок.
На рисунке изображён график функции
и
касательной
к ней в точке
.
Дадим аргументу функции
некоторое приращение
,
тогда функция
также получит некоторое приращение
.
Величина
называется
дифференциалом функции
.
При этом, из графика следует, что
равно приращению ординаты касательной, проведённой в точке
к функции
.
Именно поэтому дифференциалом называют линейную часть приращения функции, т.е. приращение ординаты касательной.
Из рисунка следует, что угол наклона касательной
,
который она образует с положительным направлением оси
и
— равны. Кроме того, тангенс угла наклона касательной равен значению производной функции в точке касания:
Из треугольника
следует, что:
Таким образом, дифференциал функции выражается следующей формулой:
Рассмотрим ещё такой момент: из рисунка следует, что
, причем
. Причем, чем меньше
, тем меньший вклад в величину
вносит значение
. Т.е. при достаточно малых значениях
, можно считать, что
. Данное соотношение позволяет вычислять приближенное значение функции в точке
, если известно её значение в точке
.
Дифференциал высшего порядка (например порядка
) определяется как дифференциал от дифференциала
-ого порядка:
Например, дифференциал второго порядка вычисляется следующим образом:
Аналогичным образом получаем формулу для вычисления дифференциала
-ого порядка:
где
—
-ая производная функции
по переменной
.
Пару слов стоит сказать о вычислении дифференциала функции многих переменных, который в этом случае называется
полным дифференциалом. Полный дифференциал функции, зависящей от
-переменных
определяется по формуле:
Выражения для дифференциалов высших порядков функции многих переменных можно получить исходя из общей формулы:
В общем случае, для возведения суммы в
-ую степень необходимо воспользоваться формулой бинома Ньютона. Рассмотрим процесс получения формулы полного дифференциала второго порядка функции двух переменных:
Наш онлайн калькулятор способен вычислить дифференциалы разных порядков для любых функций одной или нескольких переменных с описанием подробного решения на русском языке.
Дифференциалы высших порядков
Например, для функции, зависящей от одной переменной второй и третий дифференциалы находятся по формулам:
При вычислении дифференциалов высших порядков очень важно запомнить, что величина не зависит от
то есть относительно переменной дифференцирования является константой, поэтому при дифференцировании по
величину
следует рассматривать как постоянный множитель.
При
-й дифференциал неинвариантен (в отличие от дифференциала первого порядка), то есть выражение
зависит в общем случае от того, рассматривается ли переменная
как независимая, либо как некоторая промежуточная функция другого переменного, например,
Примеры вычисления дифференциалов высших порядков
ПРИМЕР 1
| Задание | Найти дифференциал второго порядка функции |
| Решение | Согласно определению, искомый дифференциал равен:
Найдем вторую производную заданной функции: Тогда, искомый дифференциал |
| Ответ |
ПРИМЕР 2
| Задание | Найти дифференциал |
| Решение | Искомый дифференциал найдем по формуле:
Третья производная заданной функции: Тогда |
| Ответ |
| Понравился сайт? Расскажи друзьям! | |




