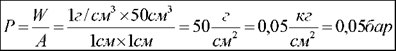From Wikipedia, the free encyclopedia
In fluid dynamics, dynamic pressure (denoted by q or Q and sometimes called velocity pressure) is the quantity defined by:[1]
where (in SI units):
- q is the dynamic pressure in pascals (i.e., kg/(m*s2),
- ρ (Greek letter rho) is the fluid mass density (e.g. in kg/m3), and
- u is the flow speed in m/s.
It can be thought of as the fluid’s kinetic energy per unit volume.
For incompressible flow, the dynamic pressure of a fluid is the difference between its total pressure and static pressure. From Bernoulli’s law, dynamic pressure is given by
where p0 and ps are the total and static pressures, respectively.
Physical meaning[edit]
Dynamic pressure is the kinetic energy per unit volume of a fluid. Dynamic pressure is one of the terms of Bernoulli’s equation, which can be derived from the conservation of energy for a fluid in motion.[1]
At a stagnation point the dynamic pressure is equal to the difference between the stagnation pressure and the static pressure, so the dynamic pressure in a flow field can be measured at a stagnation point.[1]
Another important aspect of dynamic pressure is that, as dimensional analysis shows, the aerodynamic stress (i.e. stress within a structure subject to aerodynamic forces) experienced by an aircraft travelling at speed 



Dynamic pressure can also appear as a term in the incompressible Navier-Stokes equation which may be written:
By a vector calculus identity (
so that for incompressible, irrotational flow (


Uses[edit]
A flow of air through a venturi meter, showing the columns connected in a U-shape (a manometer) and partially filled with water. The meter is «read» as a differential pressure head in cm or inches of water and is equivalent to the difference in velocity head.
The dynamic pressure, along with the static pressure and the pressure due to elevation, is used in Bernoulli’s principle as an energy balance on a closed system. The three terms are used to define the state of a closed system of an incompressible, constant-density fluid.
When the dynamic pressure is divided by the product of fluid density and acceleration due to gravity, g, the result is called velocity head, which is used in head equations like the one used for pressure head and hydraulic head. In a venturi flow meter, the differential pressure head can be used to calculate the differential velocity head, which are equivalent in the adjacent picture. An alternative to velocity head is dynamic head.
Compressible flow[edit]
Many authors define dynamic pressure only for incompressible flows. (For compressible flows, these authors use the concept of impact pressure.) However, the definition of dynamic pressure can be extended to include compressible flows.[2][3]
For compressible flow the isentropic relations can be used (also valid for incompressible flow):

Where:
See also[edit]
- Pressure
- Pressure head
- Hydraulic head
- Total dynamic head
- Drag, lift and pitching moment coefficients
- Derivations of Bernoulli equation
References[edit]
- L. J. Clancy (1975), Aerodynamics, Pitman Publishing Limited, London. ISBN 0-273-01120-0
- Houghton, E.L. and Carpenter, P.W. (1993), Aerodynamics for Engineering Students, Butterworth and Heinemann, Oxford UK. ISBN 0-340-54847-9
- Liepmann, Hans Wolfgang; Roshko, Anatol (1993), Elements of Gas Dynamics, Courier Dover Publications, ISBN 0-486-41963-0
Notes[edit]
- ^ a b c Clancy, L.J., Aerodynamics, Section 3.5
- ^ Clancy, L.J., Aerodynamics, Section 3.12 and 3.13
- ^ «the dynamic pressure is equal to half rho vee squared only in incompressible flow.»
Houghton, E.L. and Carpenter, P.W. (1993), Aerodynamics for Engineering Students, Section 2.3.1
External links[edit]
- Definition of dynamic pressure on Eric Weisstein’s World of Science
Эта тема была удалена. Только пользователи с правом управления темами могут её видеть.
В данном посте опишу теорию гидравлики простыми словами, чтобы понимать принципы поведения воды в трубе.
Как показала практика, многие работающие с системами автоматического полива люди, имеют ошибочное представление о поведении воды в трубопроводе. Так что опытным монтажникам думаю так же будет полезна данная статья.
Гидравлика изучает поведение жидкости, как в положении покоя, так и при ее движении. Грамотно спроектированная система трубопровода, значительно снижает количество проблем в течение всего жизненного цикла работы системы полива. Поддерживая скорость потока в определенных пределах, вы сможете увеличить значительно срок службы всей системы в целом.
Неверно спроектированная система с неправильными расчетами может привезти к поломке трубопровода, в случаях гидроудара и наводнению на участке.
Грамотный проектировщик учтет же при расчете все факторы, которые будут так или иначе влиять на работу системы, что позволит избежать аварий и существенных поломок в будущем.
Вдобавок неправильное проектное решение по поливу, заставит вас тратить излишнюю воду, а, следовательно, и деньги. Гидравлический анализ системы важен для уменьшения финансовых рисков, увеличения эффективности проекта и для того чтобы избавиться от излишних затрат.
Вода, подчиняясь законам гравитации, стекает в самые низкие точки поверхности и создает на этой поверхности давление. Давление -сила тяжести объема воды на данную площадь.
где Р- давление килограмм на квадратный сантиметр,
F- сила в килограммах,
А- площадь в квадратных сантиметрах
Сила давления в измеряемой точке создается столбом воды находящимся выше этой точки. Для примера на площади равной 1 см2, сила будет просто зависеть от высоты водного столба. Чем больше высота столба воды, больше веса воды действующего на дно, больше сила а, следовательно, и давление. Давление выражается, из выше сказанного, как килограмм на сантиметр квадратный или кг/см2 равный 1 бару.
Пример: На дне сосуда с 1 см2 площадью в основании и высотой водяного столба 50 см- давление будет равно:
Эта связь между давлением и изменением высоты водяного столба известно как напор в метрах. Используя эту закономерность, мы в дальнейшем сможем легко определять статическое (покоя) давление в любом месте трубопровода.
Статическое давление
Статическое давление- характеризует свойства воды когда она в покое т.е она не движется.
Динамическое давление- свойство воды, характеризующее ее при ее движении в заданном направлении по трубопроводу для обеспечения, например полива. Параметры двигающейся воды, с которыми мы будем в дальнейшем иметь дело это расход и давление.
Итак, статическое давление воды мы имеем в закрытой системе (перекрытые клапана) при неподвижном потоке воды. Значения давления в этом случае меняются только с изменением высоты водного уровня. Статическое давление показывает потенциал давления, с которым система сможет работать.
Следует запомнить, что значение статического давления на плоской местности остается постоянным и действующим с одинаковой силой во всех направлениях. Перепады высот оказывают влияние на его значение. Повышение высоты снижает, а снижение высоты повышает уровень статического давления.
Как только мы открываем, клапан или кран, вода начинает двигаться и, в этом случае, мы уже имеем дело с динамическим давлением. В этом случае появляются новые потери давления, а именно потери давления на трение по трубопроводу и местные потери (фитинги, обратные клапана, электромагнитные клапана и т.д.). Шероховатость стенок трубы, турбулентность — вот лишь та малая часть явлений, которые отрицательным образом сказываются на значении давления в трубопроводе при движении воды от магистрали к дождевателям.
Динамическое давление
Динамическое давление или «рабочее давление» отличается от статического тем, что оно зависит от потерь связанных с движением воды, и его необходимо также учитывать, как и изменение статического давления связанного с изменением высоты. Динамическое давление непосредственно связанно с расходом или тем количеством воды, которое проходит по трубе или в месте местного сопротивления.
С увеличением количества воды протекающего по трубопроводу, увеличивается скорость движения потока, увеличивая потери в давлении. Можно найти ряд таблиц с потерями на трение, учитывающих диаметры трубопровода, его материал и скорость потока воды. А также вы всегда сможете найти таблицу местных потерь давления в зависимости от расхода в каталогах производителей поливочного оборудования.
ВАЖНО!!
Самое частое заблуждение и стереотип даже у опытных людей, много лет работающих с системами автоматического полива- это святая вера в то, что ПРИ ПОСЛЕДОВАТЕЛЬНОМ ЗАУЖЕНИЕМ ДИАМЕТРА ТРУБОПРОВОДА- СОХРАНЯЕТСЯ ИЛИ УВЕЛИЧИВАЕТСЯ ДАВЛЕНИЕ. Это не ТАК.
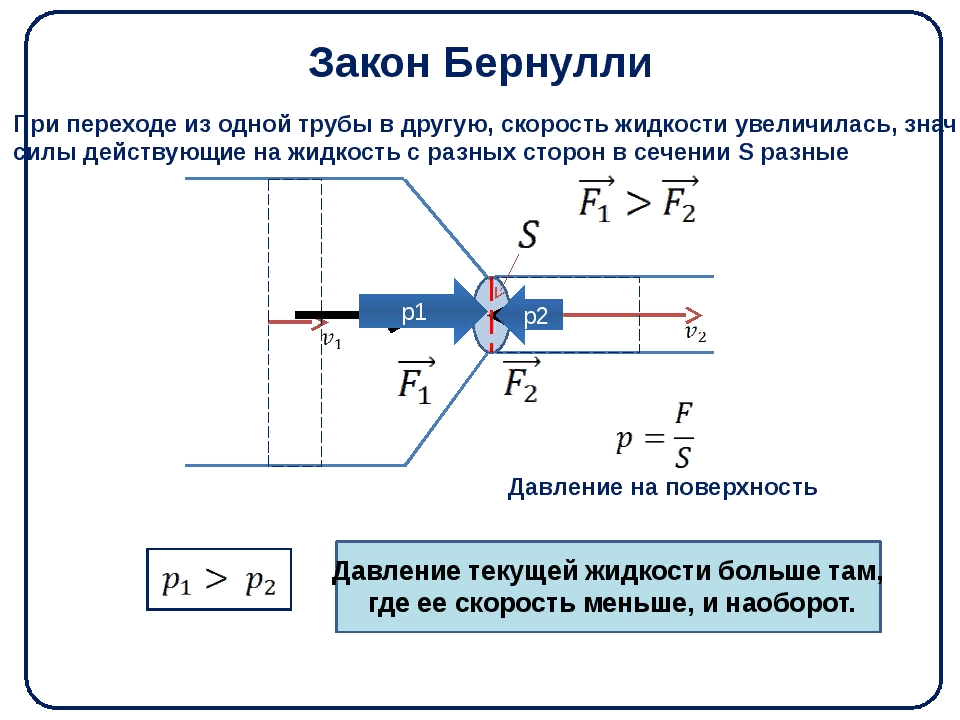
Увеличение скорости течения жидкости при переходе из участка трубы с большей площадью поперечного сечения в участок трубы с меньшей площадью поперечного сечения означает, что жидкость движется с ускорением.
Согласно второму закону Ньютона, причиной ускорения является сила. Этой силой в данном случае является разность сил давления, действующих на текущую жидкость в широкой и узкой частях трубы. Следовательно, в широкой части трубы давление жидкости должно быть больше, чем в узкой.
Закон Бернулли
Скорость потока (м3/ч, л/с), значение с которым вода двигается через компоненты трубопровода системы полива, очень важный фактор в анализе гидравлического расчета. Чем быстрее вода движется по трубе, тем выше потери на трение. Слишком большие скорости потока воды могут, также быть причинами других проблем (гидравлические удары, выход из строя запорного оборудования и т.д.).
Опытным путем и с помощью расчетов установлено, что скорость потока равная 1,5 м/с, является оптимальной для движения воды по пластиковым трубам. Дальнейшее увеличение скорости потока, приводит к непропорциональному увеличению значения потерь давления, порой в разы, что может привести к неприятным последствиям, когда на отдаленных зонах вы будете иметь давление, при котором полив осуществляться будет некорректно. А также, при скоростях меньших или равных 1,5 м/с, в системе снижается вероятность появления повреждений, связанных с гидравлическим ударом.
Напомню, что в сервисе по проектированию систем автоматического полива IRRISketch весь гидравлический расчёт делается автоматически, но знать азы всё равно полезно даже опытным работникам.
Ссылка на регистрацию http://bit.ly/irrismax
💪💪💪👍👍👍
@polivmax Всё очень доступно объяснил, спасибо:+1:
@polivmax Очень интересно написано. Но возник вопрос принципиального характера.
В статье утверждается, что резкое повышение скорости потока жидкости (воды) при неправильно проведенном гидравлическом расчете может стать причиной гидравлического удара. Что актуально только в замкнутых системах, типа систем отопления. Именно поэтому в таких системах предусмотрены группы безопасности, которые уберегают замкнутые системы от явлений такого рода. Единственная часть системы полива, в которой возможно возникновение гидавлического удара- это ее напорная часть (магистраль), но напорная часть расчитавыется по максимальному расходу и выполняется трубопроволом одного сечения по всей ее длине. За исключением разве что отводов к гидрантам, но это уже обусловлено экономической целесообразностью.
А вот механизм происхождения гидравлического удара, причиной которого является резкое повышение скорости потока в локальном трубопроводе, в котором и предусмотрено постепенное заужение сечения трубопровода в системе автополива мне не понятен (если разве, что исполнитель не установит всего один дождеватель на линию).
P.S. возможность автоматического проведения гидравлического расчета есть не только в упомянутом серсисе. Такая возможность должна быть как сам-собой разумеющийся факт. В ином случае смысла в таком сервисе нет совсем никакого, разве что, рисовать разметку расположения траншей.
@Eween Всё верно по поводу единого диаметра магистрали. вот только проблема в том, что не многие даже этот диаметр подбирают верно из-за этого уже в магистрали скорость потока превышает 2,5мс. Лично встречал и не раз.
Что же касается сервиса. Опять же для новичков информация не очевидная. Многие в голом автокаде делают и считают гидравлику в ручную. Я сам до того года именно так и делал, хотя знаю кучу специализированных программ. Совсем скоро иррискетч будет считать гидравлику так как не считает ни один подобный сервис.
@Eween
Да опасности возникновения гидравлического удара в системах автополива подвергаются в первую очередь запорные механизмы, эл.магнитные клапаны, клапаны быстрого доступа к воде, и другие завтворы, латеральная часть вне зоны риска, т.к потребители воды не запираются механически. Да и на современных клапанах обеспечена защита от гидроудара благодаря их плавному закрытию. Но никто не отменял кавитации в зонах с резким увеличением скорости потока (на тех самых заужениях с переходом диаметра). Поэтому все-таки не превышать скорость потока очень даже полезно, учитывая то что все собирается зачастую на компрессионых соединениях, которые не так надёжны как паечные. Вообщем, как говорится, соблюдайте скоростной режим:blush:
@filprots Именно так. не однократно видел (даже на видео заснял) как хвалёный ирритековский фитинг от гидроудара срывает на отводе насоса после закрытия гидранта (водяной розетки). так кто в моменте свыше 30атм как я понимаю может создаваться при гидроударе
На мое удивление, до сих пор, БОЛЬШОЕ кол-во профессионалов с пеной у рта пытаются доказать, что заужением диаметра они повышают давление в системе.
@polivmax Теперь мне кажется, что данная статья направлена не ликвидацию безграмотности в среде поливщиков, а на продвижение названанной программы. А про то что, эта программа будет считать так, как ни одна другая, это мне напоминает презентацию K- Pain. Там мы тоже слышали, что они горы свернут))))
@Eween Именно на ЛИКБЕЗ. Упоминание программы, которая, по моему мнению, адекватнее и удобнее аналогов — это то же ликбез. В любом случае это обмен опытом, а право выбора остаётся за каждым.
Так же никто не мешает рекомендовать другие программы, которые считает нужным.
@Eween те в школе в 10 классе нас задолго готовили к появлению Irrisketch?!)) вот это поворот :astonished: )))))))))))))))
- @polivmax процитировал лишь некоторые основы гидродинамики, на примере закона Бернулли. Да, многие программы, тот же ProContractor, RainCAD могут просчитать потери давления в линии на магистрали и узлах, но речь ведь не об этом. Речь о том что неправильный расчет приводит к преждевременному износу узлов системы, сокращая ее фактический срок эксплуатации. Многие специалисты даже не стесняются: выкладывают мп ротатор на котором 5-6 атмосфер, говорят о какой то экономической целесообразности, преимуществах мп перед остальными соплами а по факту что мы имеем — огромный перерасход воды, и дороговизну замены этих сопел, аргумент таких специалистов один — НУ ГАЗОН ЖЕ ЗЕЛЕНЫЙ — значит мы все правильно делаем)
Одно дело когда программа автоматически все делает за тебя, другое дело это понимание процесса. Знание элементарных законов — только возвысит вас в глазах вашего заказчика как специалиста. У меня такие случае были — на объекте установлен был скважинный насос и надо было проверить его хар-ки. Хорошо что у меня всегда с собой расходомер. Произвел замеры и установил рабочую точку в 2,5бар и 33л/мин.. Заказчик меня уверял в том что если из системы убрать гидроаккумулятор то давление возрастет (учитывая даже то, замеры я производил до аккумулятора прямо на выходе из скважины). Да так напористо и уже на повышенных тонах доказывал, что я даже немного стал сомневаться в своей правоте, но не отступил и оказался прав. Получил респект от заказчика и вот уже третий объект сотрудничаем, думаю если бы я тогда слился, заказчик все равно оказался бы не прав — но мнение обо мне у него уже было бы как о сомнительном специалисте.
@polivmax Про чреватость большой скорости потока понятно, но как-то не раскрыта тема меньшей скорости потока и что будет если везде будут как в магистрали, так и в веткахлиниях большие диаметры(типа на всякий пожарный) — скорость потока малая, давление хорошее. Как забабахать всё 40-50 диаметром — точно не ошибёшься!
@Lema а как же гидроудар?
Пользователь @Sergei написал в Основные законы гидравлики:
@Lema а как же гидроудар?
Чем больше диаметр труб, тем ниже скорость потока воды, и, соответственно, гидроудар.
Хотите гидроудар? Повысьте скорость потока в трубах. Хотите повысить скорость потока? Заужайте диаметр.
Ещё гидроудар может быть от резкого скачка давления. От чего в данном случае может быть скачок в трубах большого диаметра как-то не понятно.
@Lema Я не очень понял в чём суть вопроса и вопрос ли это?
Если я правильно понял, то с запасом можно хоть 110 диаметр заложить там, где и 32 подойдёт. Тут главный вопрос в экономической составляющей.
Пользователь @polivmax написал в Основные законы гидравлики:
Я не очень понял в чём суть вопроса и вопрос ли это?
Да, конечно вопрос.
Я про экономическую составляющую понимаю. Конечно труба большего диаметра дороже, но, вопрос в другом, чревато ли ещё чем-то завышение диаметра кроме цены и удобстваскорости монтажа?
Просто может я чего-то не знаю.
@Lema При скорости потока менее 0,2 мс есть вероятность застаивания воды и отложений в трубах
@Lema труба большего диаметра при размотке сильнее бьет по голове)))))
Уравнение Бернулли Статическое и динамическое давление

Вследствие наличия сил притяжения взаимное смещение частиц жидкости сопровождается некоторым сопротивлением, которое подобно механическому трению между мелкими частицами твердого вещества и называется внутренним трением, или вязкостью, жидкости. Вязкость жидкости проявляется, например, сопротивлением при помешивании жидкости, замедлением при падении в жидкости предметов и т. д.
Рассмотрим вначале стационарное течение идеальной жидкости (идеальной называется несжимаемая жидкость, не имеющая вязкости; стационарным называется течение, при котором величина скорости в любой точке жидкости со временем не изменяется). Установим для этих условий соотношение между давлением р в жидкости, скоростью движения v ее частиц и положением их в поле силы тяжести, характеризуемое высотой Л над некоторым уровнем отсчета (рис. 2).
Уравнение Бернулли
В соответствии с законом сохранения энергии полная энергия некоторой массы m (имеющей объем V) идеальной жидкости при течении остается неизменной, так как в ней отсутствуют потери на внутреннее трение.
Полная энергия составляется из потенциальной энергии давления (Еn = pV), потенциальной энергии тяжести (E«п = mgh) и кинетической энергии (Ек = mυ2/2). На основании сказанного: pV + mgh + (mυ2/2) = const.
Соответственно для каких-либо двух положений массы т идеальной жидкости, например в точках А и Б (рис. 2):
p1V + mgh1 + (mυ21/2) = p2V + mgh2 + (mυ2/2)
Если предпоследнее уравнение разделить почленно на объем V жидкости, то учитывая, что m/V есть плотность ρ жидкости, получим:
p + ρgh +(ρυ2/2) = const.
Это и есть уравнение Бернулли.
Для движения жидкости в горизонтальных трубках силу тяжести можно не учитывать и тогда уравнение Бернулли принимает вид:
p +(ρυ2/2)const
Из этого уравнения следует вывод, называемый правилом Бернулли: давление невязкой жидкости, текущей по горизонтальной трубе, выше там, где скорость ее меньше, и наоборот.
Пример расчета по формуле
Рассмотрим течение жидкости по трубе с неодинаковым сечением. Течение называется непрерывным, если через любое сечение трубы в единицу времени протекает одинаковое количество (объем) жидкости. При этом скорость движения жидкости на участках трубы обратно пропорциональна площади их сечений.
Действительно не трудно доказать, что объем V0 жидкости, протекающей в единицу времени через любое сечение трубы, может быть выражен произведением площади S сечения трубы на скорость υ течения жидкости: V0=Sυ. По условию этот объем постоянен для любого сечения трубы, следовательно,
V0 = Sυ = const.
т. е. произведение скорости течения жидкости на поперечное сечение струи есть величина постоянная. Это соотношение называют уравнением неразрывности струи.
Если обозначить сечение и скорость движения на участках трубы соответственно S1 и υ1 S2 и υ2, то согласно сказанному:
S1υ1 = S2υ2, откуда υ1/υ2 = S2/S1.
Скорость течения жидкости в трубе с переменным сечением обратно пропорциональна площади этих сечений.
При этом в соответствии с правилом Бернулли на участках меньшего сечения трубы давление будет ниже, на участках большего сечения — выше (рис. , а). Поясним механизм этого явления. При переходе на участок трубы меньшего сечения (линия ab на рис. , б) частицы жидкости ускоряются, на что затрачивается часть силы Р4, создающей давление на более широком участке (по условию равновесия частиц жидкости Р1= Р2+Fу, где Р2 — сила, создающая давление на суженном участке, Fу — сила, обеспечивающая ускорение частиц).
Наоборот, при переходе на участок с большим сечением (линия cd на рис. 82, б) частицы жидкости набегают на лежащую впереди и более медленно двигающуюся массу жидкости и, затормаживаясь, создают дополнительную силу Fт, повышающую давление на более широком участке (аналогично P3=P2 + Fт).
Можно подобрать условия, при которых давление жидкости в суженном участке трубы станет ниже атмосферного и тогда в этом месте струя будет обладать всасывающим действием. Всасывающее действие струи газа, пара или воды, выходящей из суженного отверстия с большой скоростью, используется в ряде приборов, применяемых в медицинской практике (ингалятор, водоструйный насос и др.).
Паровой ингалятор
Это прибор для вдыхания жидких лекарственных веществ в распыленном виде. Он состоит из кипятильника В, стакана К с лекарственной жидкостью и вставленной в него тонкой трубкой Т и направляющего патрубка С. Струя пара выходит из трубки кипятильника с большой скоростью. Вследствие этого давление около ее отверстия падает и лекарственная жидкость, всасываясь по трубке Т, поступает в струю, распыляется и, смешиваясь с паром, вдыхается больным через патрубок С
Водоструйный насос состоит из стеклянного сосуда Н, в который впаяно три трубки. Трубка имеет на конце коническое сужение. Насос присоединяется к водоводу и колбе К, из которой производится отсасывание. Вода, имеющая достаточно высокое давление, выходит из суженного конца трубки 1 с большей скоростью. Давление у отверстия трубки резко снижается и в сосуд А через трубку 2 засасывается воздух или жидкость, которые вместе с водой удаляются через трубку 3. Водоструйный насос удобен тем, что он не имеет вращающихся частей, требующих смазки, бесшумен и гигиеничен. Поэтому он часто применяется в лабораториях, операционных и т. п.
В уравнении Бернулли давление р называется статическим давлением рс жидкости. Оно может быть измерено обычным манометром, который двигается вместе с жидкостью, или практически при помощи неподвижной манометрической трубки, плоскость отверстия которой расположена параллельно направлению движения жидкости.
Второй член уравнения Бернулли (ρυ2/2)также имеет размерность давления и называется динамическим давлением рд в жидкости. Сумма статического и динамического давлений называется полным давлением р в жидкости:
р = рс + рд
Для измерения его применяют манометрическую трубку, изогнутую под прямым углом и помещенную отверстием навстречу движению жидкости. Частицы жидкости, заходящие в отверстие трубки полностью тормозятся в ней: скорость υ2 частиц жидкости в отверстии рав няется нулю: υ2=0. Тогда по уравнению Бернулли
р1 + (ρυ21/2) = р2 + (ρυ22/2) = р2
Следовательно, давление р2 в трубке:
р2 = р1 + (ρυ1/2)
где р1 — давление и υ1 — скорость движущейся жидкости
Если в струю жидкости поставить рядом две такие трубки, то разность уровней в трубках будет соответствовать динамическому давлению. На этом основан способ измерения скорости движения жидкости или газа В струю погружают две скрепленные вместе измерительные трубки, прямую и изогнутую (подобное устройство называется трубкой Пито), которые соединяются с U= образным манометром. Манометр покажет динамическое давление, по величине которого, пользуясь приведенной выше формулой, вычисляют искомую скорость:
υ = √(2pд/ρ)
Статья на тему Уравнение Бернулли
|
ρ gh = |
ρυ 2 |
+ ρ gh |
||
|
1 |
2 |
2 |
||
|
где υ — скорость истечения из отверстия. Сокращая на ρ и введя h = h1 − h2 |
— высоту |
|||
|
открытой поверхности жидкости над отверстием, получаем: |
||||
|
υ 2 |
= gh, î ò êóäà υ = 2gh |
(55.5) |
||
|
2 |
Эта формула называется формулой Торричелли.
Итак, скорость истечения жидкости из отверстия, расположенного на глубине h под открытой поверхностью, совпадает со скоростью, которую приобретает любое тело, падая с высоты h. Следует помнить, что этот результат получен в предположении, что жидкость идеальна. Для реальных жидкостей скорость истечения будет меньше, причем тем сильнее отличается от значения (55.5), чем больше вязкость жидкости.
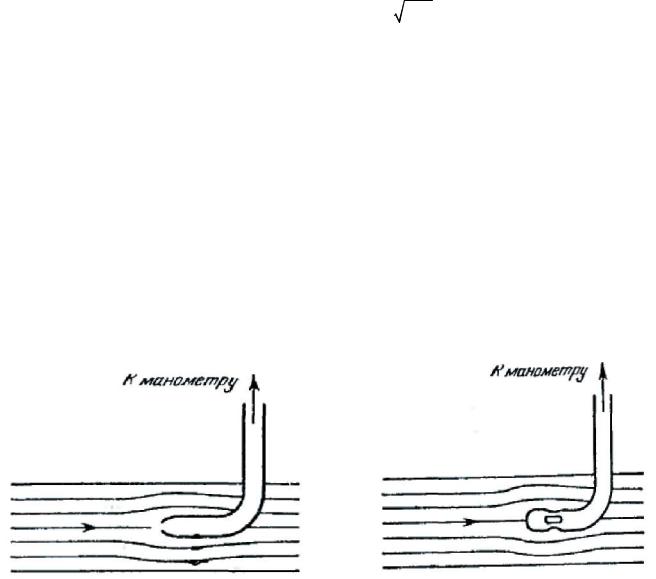
В предыдущем параграфе мы выяснили, что давление в жидкости связано с величиной скорости течения. Введение в жидкость прибора для измерения давления нарушает характер движения жидкости, а следовательно, может изменить и величину измеряемого давления. Поместим в жидкость изогнутую манометрическую трубку с входным отверстием, обращенным навстречу потоку (рис. 148). Такую трубку называют трубкой Пито. Рассмотрим линию тока, упирающуюся своим концом в центр отверстия трубки. Скорость вдоль рассматриваемой линии тока будет изменяться от υ для невозмущенного потока на больших расстояниях от трубки до нуля непосредственно перед отверстием. Согласно уравнению Бернулли давление перед отверстием
Рис 148 Рис. 149 (а следовательно, и в манометрической трубке) будет превышать давление в невозмущенном
потоке р на величину ρυ 2 / 2 . Следовательно, манометр, соединенный с трубкой Пито, покажет давление, равное
|
p′ = p + |
ρυ 2 |
(56.1) |
|
2 |
||
|
Имеющее размерность давления слагаемое ρυ 2 / 2 называют динамическим давлением. |
||
|
Давление p принято называть статическим. Давление p′ |
равное сумме статического и |
динамического давлений, называется полным давлением. Таким образом, с помощью трубки Пито можно измерять полное давление (56.1).
Если в тонкой изогнутой трубке сделать боковые отверстия, то скорость (а следовательно, и давление) вблизи таких отверстий будет мало отличаться от скорости (и давления)
152

невозмущенного потока (рис. 149), Поэтому манометр, присоединенный к такой трубке, называемой зондом, покажет статическое давление в жидкости p.
Зная полное и статическое давления, можно найти динамическое давление ρυ 2 / 2 , а следовательно, и скорость течения υ (плотность жидкости предполагается известной). Если трубку Пито и зонд смонтировать вместе, как показано на рис. 150, и подсоединить к разным коленам дифференциального манометра (т. е. манометра, измеряющего разность давлений), то показания манометра будут непосредственно давать динамическое давление. Проградуировав манометр в значениях скорости υ , можно получить прибор для измерения скорости течения жидкости.
Рис. 150
§57. Применение к движению жидкости закона сохранения импульса
К жидкостям и газам, как и к другим телам, применим закон сохранения импульса. Используем этот закон для решения некоторых задач.
Реакция текущей жидкости на стенки изогнутой трубы. Предположим, что в изогнутой трубе установился стационарный поток несжимаемой жидкости (рис. 151). Для простоты возьмем трубу постоянного сечения S. Тогда в силу неразрывности струи скорость в каждом сечении будет одинакова по величине и равна υ .
Рис. 151
Рассмотрим объем изогнутого участка трубы, ограниченного сечениями S1 и S2. За время t в этот объем будет втекать через сечение S1 количество жидкости Sυ t , обладающее
импульсом1 K1 = ρ Sυv1 t . Одновременно из этого объема будет вытекать через сечение S2
1 Давление обозначается той же буквой р, что и импульс. Поэтому в случаях, когда могут возникнуть недоразумения, мы будем обозначать именно буквой К.
153

такое же количество жидкости, обладающее импульсом K2 = ρ Sυv2 t . Таким образом, стенки изогнутого участка трубы сообщают за время t текущей мимо них жидкости приращение
|
импульса |
K = K2 − K1 = ρ Sυ (v2 − v1 ) |
t |
. Как мы знаем, приращение импульса тела за единицу |
времени равно действующей на тело силе. Следовательно, стенки трубы действуют на жидкость
|
f = |
K ρ Sυ (v2 |
− v1 ) |
|
с силами, равнодействующая которых равна |
t |
. По третьему закону Ньютона |
|
текущая жидкость действует на стенки трубы с силами, равнодействующая которых равна |
||
|
fr = ρ Sυ (v1 − v2 ) |
(57.1) |
Силу fr называют реакцией текущей жидкости на стенки трубы.
Реакция вытекающей струи. Струя жидкости, вытекающая из отверстия в сосуде (рис. 152),
уносит с собой за время t импульс K = ρ Sυv t ( ρ — плотность жидкости, S — площадь отверстия, v — скорость истечения струи). Этот импульс сообщается вытекающей жидкости
|
сосудом. По третьему закону Ньютона сосуд получает от вытекающей жидкости за время |
t |
|
|
импульс, равный — K, т. е. испытывает действие силы |
||
|
fr = − |
K = −ρ Sυv |
(57.2) |
|
t |
Рис. 152
Эта сила называется реакцией вытекающей струи. Если сосуд поставить на тележку, то под действием силы fr он придет в движение в направлении, противоположном направлению струи.
Найдем величину силыfr, воспользовавшись выражением (55.5) для скорости истечения жидкости из отверстия:
|
fr = ρ Sυ 2 = 2ghρ S |
(57.3) |
Если бы, как это может показаться на первый взгляд, сила fr совпадала по величине с силой гидростатического давления, которое жидкость оказывала бы на пробку, закрывающую отверстие, то fr была бы равна ghpS.
На самом деле сила fr оказывается в 2 раза большей. Это объясняется тем, что возникающее при вытекании струи движение жидкости в сосуде приводит к перераспределению давления, причем давление вблизи стенки, лежащей против отверстия, оказывается несколько большим, чем вблизи стенки, в которой сделано отверстие.
На реакции вытекающей струи газа основано действие реактивных двигателей и ракет. Реактивное движение, не нуждаясь для своего осуществления в наличии атмосферы, используется для полетов в космическое пространство.
Основоположником теории межпланетных сообщений является выдающийся русский ученый и изобретатель К Э. Циолковский (1857—1935). Он дал теорию полета ракеты и обосновал возможность применения реактивных аппаратов для межпланетных сообщений. В частности, Циолковским была разработана теория движения составных ракет, в которых каждая последующая ступень вступает в действие после того, как предыдущая ступень, израсходовав
154

полностью топливо, отделится от ракеты. Идеи Циолковского получили дальнейшее развитие и были осуществлены советскими учеными и инженерами, обеспечившими ведущую роль Советского Союза в освоении и изучении космического пространства,
§58. Силы внутреннего трения
Идеальная жидкость, т. е. жидкость без трения, является абстракцией. Всем реальным жидкостям и газам в большей или меньшей степени присуща вязкость или внутреннее трение. Вязкость проявляется в том, что возникшее в жидкости или газе движение после прекращения действия причин, его вызвавших, постепенно прекращается.
Для выяснения закономерностей, которым подчиняются силы внутреннего трения, рассмотрим следующий опыт. В жидкость погружены две параллельные друг другу пластины (рис. 153), линейные размеры которых значительно превосходят расстояние между ними d. Нижняя пластина удерживается на месте, верхняя приводится в движение относительно нижней
с некоторой скоростью υ0 . Опыт дает, что для перемещения верхней пластины с постоянной
скоростью υ0 необходимо действовать на нее с вполне определенной постоянной по величине силой f. Раз пластина не получает ускорения, значит, действие этой силы уравновешивается равной ей по величине противоположно направленной силой, которая, очевидно, есть сила трения, действующая
Рис. 153.
на пластину при ее движении в жидкости. Обозначим ее fтр.
Варьируя скорость пластины υ0 площадь пластин S и расстояние между ними d, можно получить, что
|
fò ð =η |
υ0 |
S |
(58.1) |
|
|
d |
||||
где η — коэффициент пропорциональности, зависящий от природы и состояния (например, температуры) жидкости и называемый коэффициентом внутреннего трения или коэффициентом вязкости, или просто вязкостью жидкости (газа).
Нижняя пластина при движении верхней также оказывается подверженной действию силы
|
f |
ò ð |
′ |
, равной по величине |
f |
ò ð . Для того чтобы нижняя пластина оставалась неподвижной, силу |
||
|
fò ð′ |
необходимо уравновесить с помощью силы |
f ′ |
. |
||||
Таким образом, при движении двух погруженных в жидкость пластин друг относительно друга между ними возникает взаимодействие, характеризуемое силой (58.1). Воздействие пластин друг на друга осуществляется, очевидно, через жидкость, заключенную между пластинами, передаваясь от одного слоя жидкости к другому. Если в любом месте зазора провести мысленно плоскость, параллельную пластинам (см. пунктирную линию на рис. 153), то можно утверждать. Что часть жидкости, лежащая над этой плоскостью, действует на часть
155

|
жидкости, лежащую под плоскостью, с силой |
f |
′ |
, а часть жидкости, лежащая под плоскостью, |
|
ò ð |
в свою очередь действует на часть жидкости, лежащую над плоскостью, с силой fò ð , причем
величина fò ð и fò ð′ определяется формулой (58.1). Таким образом, формула (58.1) определяет не только силу трения, действующую на пластины, но и силу трения между соприкасающимися частями жидкости.
Если исследовать скорость частиц жидкости в разных слоях, то оказывается, что она изменяется в направлении z перпендикулярном к пластинам (рис. 153), по линейному закону
|
υ (z) = |
υ0 |
z |
(58.2) |
|
|
d |
||||
Частицы жидкости, непосредственно соприкасающиеся с пластинами, как бы прилипают к ним и имеют такую же скорости как и сами пластины, Согласно формуле (58.2)
Использовав равенство (58.3), формуле (58.1) для силы внутреннего трения можно придать вид
|
fò ð =η |
dυ |
S |
(58.4) |
|
dz |
dυ
Величина dz показывает, как быстро изменяется скорость в направлении оси z, и называется градиентом скорости (точнее, это—модуль градиента скорости; сам градиент — вектор).
Формула (58.4) была нами получена для случая, когда скорость изменяется по линейному закону (в этом случае градиент скорости является постоянным). Оказывается, что эта формула остается справедливой и для любого другого закона изменения скорости при переходе от слоя к
слою. В этом случае для определения силы трения между двумя граничащими друг с другом dυ
слоями нужно брать значение градиента dz в том месте, где проходит воображаемая поверхность раздела слоев. Так, например, при движении жидкости в круглой трубе скорость равна нулю у стенок трубы, максимальна на оси трубы и, как можно показать, при не слишком больших скоростях течения изменяется вдоль любого радиуса по закону
|
υ = υ0 |
− |
r2 |
|||
|
1 |
(58.5) |
||||
|
R |
2 |
||||
где R — радиус трубы, υ0 — скорость па оси трубы, υ — скорость на расстоянии z от оси трубы (рис. 154). Проведем в жидкости мысленно цилиндрическую поверхность радиуса r Части жидкости, лежащие по разные стороны от этой поверхности, действуют друг на друга с силой, величина которой в расчете на единицу поверхности равна
f = η dυ = η 2υ0r dr R2
т, е. возрастает пропорционально расстоянию поверхности раздела от оси трубы (знак «—», получающийся при дифференцировании (58.5) по r, мы опустили, поскольку формула (58.4) дает лишь модуль силы внутреннего трения).
156
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В физике давление — это сила, деленная на единицу площади. Сила, в свою очередь, является ускорением массы раз. Это объясняет, почему зимний авантюрист безопаснее на льду сомнительной толщины, если он лежит на поверхности, а не стоит прямо; сила, которую он оказывает на лед (его масса, умноженная на ускорение вниз под действием силы тяжести), одинакова в обоих случаях, но если он лежит ровно, а не на двух ногах, эта сила распределяется по большей площади, тем самым уменьшая давление на лед.
Приведенный выше пример имеет дело со статическим давлением — то есть, ничего в этой «проблеме» не движется (и, надеюсь, так и останется!). Динамическое давление отличается, включая движение объектов через жидкости — то есть жидкости или газы — или поток самих жидкостей.
Общее уравнение давления
Как уже отмечалось, давление — это сила, деленная на площадь, а сила — это масса, умноженная на ускорение. Массу ( м ), однако, также можно записать как произведение плотности ( ρ ) и объема ( V ), поскольку плотность — это просто масса, деленная на объем. То есть, поскольку ρ = m / V , m = ρV . Кроме того, для обычных геометрических фигур объем, деленный на площадь, просто дает высоту.
Это означает, что, например, для столба жидкости, стоящего в цилиндре, давление ( P ) может быть выражено в следующих стандартных единицах:
Р = {мг выше {1pt} A} = {ρVg выше {1pt} A} = ρg {V выше {1pt} A} = ρgh
Здесь h — глубина ниже поверхности жидкости. Это показывает, что давление на любой глубине жидкости на самом деле не зависит от количества жидкости; Вы могли бы быть в небольшом аквариуме или океане, а давление зависит только от глубины.
Динамическое давление
Жидкости, очевидно, не просто сидят в резервуарах; они двигаются, часто прокачиваясь по трубам, чтобы добраться с места на место. Движущиеся жидкости оказывают давление на объекты внутри них так же, как и стоячие жидкости, но переменные меняются.
Возможно, вы слышали, что полная энергия объекта представляет собой сумму его кинетической энергии (энергии его движения) и его потенциальной энергии (энергии, которую он «запасает» при весенней нагрузке или находясь далеко над землей), и что это общее число остается постоянным в замкнутых системах. Аналогичным образом, полное давление жидкости представляет собой ее статическое давление, определяемое выражением ρgh, полученным выше, добавляемое к динамическому давлению, определяемому выражением (1/2) ρv 2.
Уравнение Бернулли
Вышеприведенный раздел представляет собой вывод критического уравнения в физике с последствиями для всего, что движется в жидкости или испытывает сам поток, включая самолеты, воду в водопроводной системе или бейсбольные мячи. Формально это
P_ {total} = ρgh + {1 вышеуказанный {1pt} 2} ρv ^ 2
Это означает, что, если жидкость поступает в систему через трубу с заданной шириной и на заданной высоте и покидает систему через трубу с другой шириной и на разной высоте, общее давление системы может оставаться постоянным.
Это уравнение опирается на ряд допущений: что плотность жидкости ρ не изменяется, что поток жидкости устойчив и что трение не является фактором. Даже с этими ограничениями, уравнение чрезвычайно полезно. Например, из уравнения Бернулли вы можете определить, что когда вода выходит из канала, диаметр которого меньше, чем у его точки входа, вода будет двигаться быстрее (что, вероятно, интуитивно понятно; реки демонстрируют большую скорость при прохождении через узкие каналы).) и его давление при более высокой скорости будет ниже (что, вероятно, не является интуитивным). Эти результаты вытекают из вариации уравнения
P_1 — P_2 = {1 выше {1pt} 2} ρ ({v_2} ^ 2 — {v_1} ^ 2)
Таким образом, если слагаемые положительны, а скорость на выходе больше скорости на входе (то есть, v 2 > v 1 ), давление на выходе должно быть ниже, чем давление на входе (то есть P 2 < P 1 ).