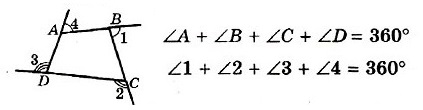Как найти диагональ четырехугольника
Четырехугольником называется фигура, состоящая из четырех сторон и углов, прилежащих к ним. К числу таких фигур относятся прямоугольник, трапеция, параллелограмм. В ряде задач по геометрии требуется найти диагональ одной из этих фигур.
Инструкция
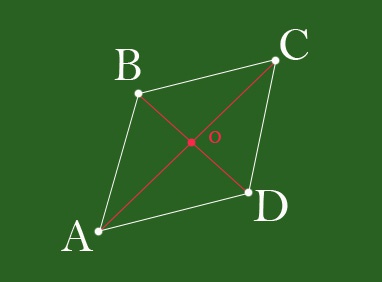
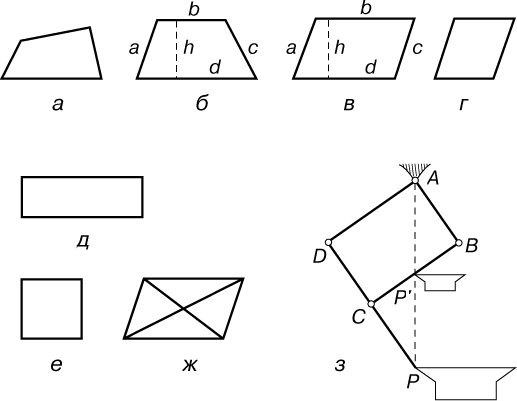
Диагональю четырехугольника называется отрезок, соединяющий его противоположные углы. У четырехугольника имеются две диагонали, которые между собой пересекаются в одной точке. Диагонали иногда бывают равными, как у прямоугольника и квадрата, а иногда имеют различную длину, как, например, у трапеции. Способ нахождения диагонали зависит от фигуры.Постройте прямоугольник со сторонами a и b и двумя диагоналями d1 и d2. Из свойств прямоугольника известно, что его диагонали между собой равны, пересекаются в одной точке и делятся в ней пополам. Если известны две стороны прямоугольника, то его диагонали найдите следующим образом: d1=√a^2+b^2=d2.Частным случаем прямоугольника является квадрат, у которого диагональ равна a√2. Кроме того, диагональ можно найти, зная площадь квадрата. Она равна: S = d^2/2.Отсюда длину диагонали вычислите по формуле: d = √2S.
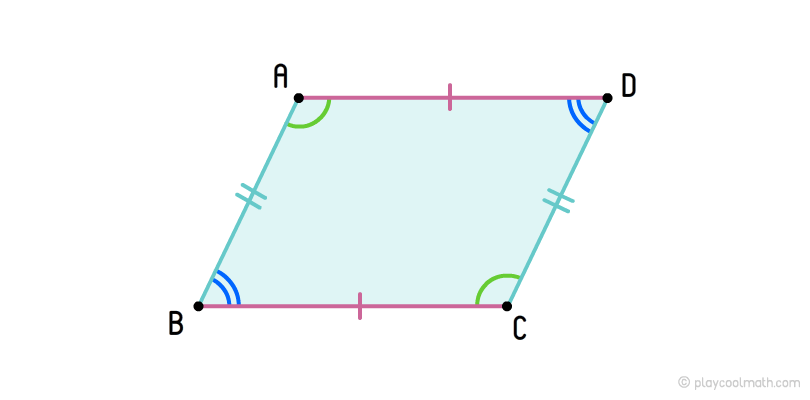
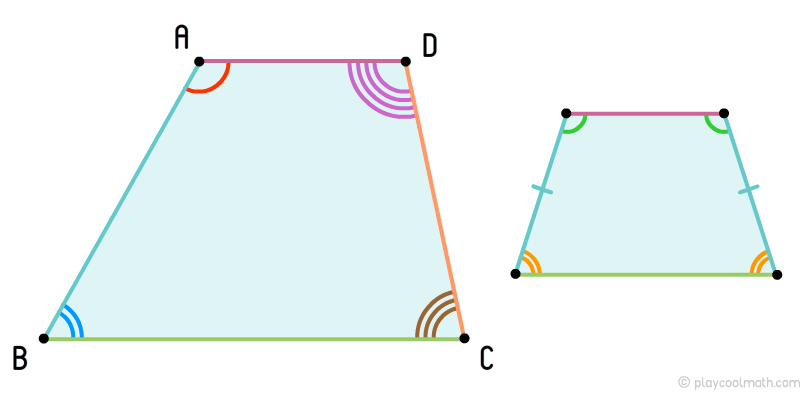
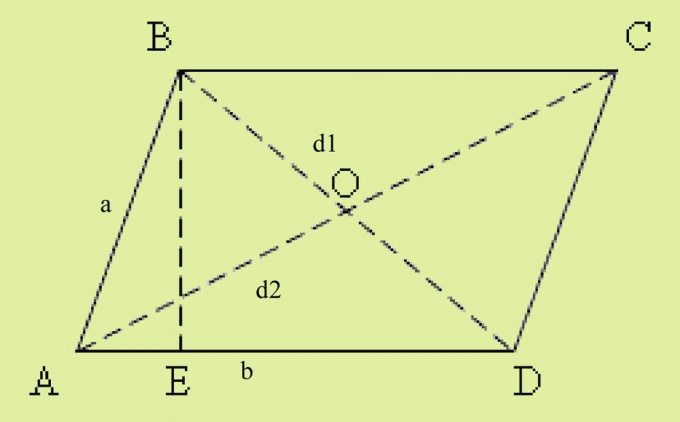
Несколько иным образом решайте задачу, когда дан не прямоугольник, а параллелограмм. У этой фигуры, в отличие от прямоугольника или квадрата, равны между собой не все углы, а только противоположные. Если в условии задача присутствует параллелограмм со сторонами a и b и заданным между ними углом, как показано на рисунке к шагу, то диагональ найдите, используя теорему косинусов: d^2 = a^2+b^2-2ab*cosα.Параллелограмм, имеющий равные стороны, называется ромбом. Если по условиям задачи необходимо найти диагональ этой фигуры, то потребуются значения его второй диагонали и площади, поскольку диагонали этой фигуры неравны. Формула площади ромба выглядит следующим образом: S = d1*d2/2.Отсюда d2 равна удвоенной площади фигуры, деленной на d1: d2 = 2S/d1.
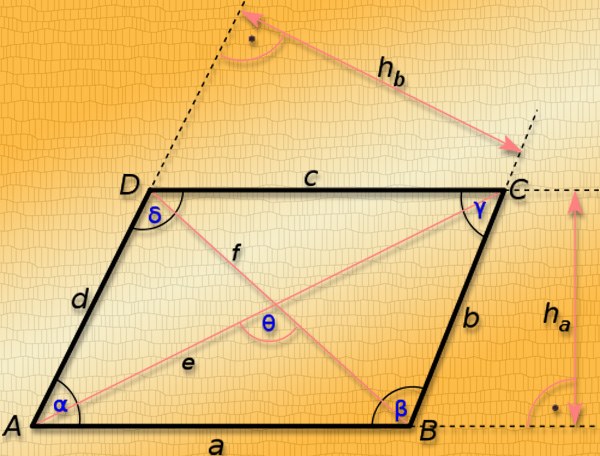
При вычислении площади трапеции придется воспользоваться тригонометрической функцией синуса. Если данная фигура является равнобочной, то, зная ее первую диагональ d1 и угол между двумя диагоналями AOD, как показано на рисунке к шагу, найдите вторую по следующей формуле: d2 = 2S/d1*sinφ. В данном случае рассматриваем трапецию ABCD.Существует также прямоугольная трапеция, диагональ которой найти несколько проще. Зная длину боковой стороны этой трапеции, совпадающей с ее высотой, а также нижнее основание, найдите ее диагональ, пользуясь обычной теоремой Пифагора. А именно сложите квадраты этих величин, а затем из результата извлеките квадратный корень.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Четырехугольники
теория по математике 📈 планиметрия
Четырехугольник – это геометрическая фигура, состоящая из четырех точек, никакие три из которых не лежат на одной прямой, и отрезков, последовательно соединяющих эти точки.
Выпуклый четырехугольник
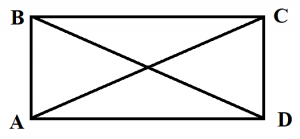
Четырехугольник называется выпуклым, если он находится в одной полуплоскости (то есть все его стороны расположены только с одной стороны прямой, прямая НЕ разбивает фигуру) относительно прямой, содержащей любую его сторону. На рисунке показан выпуклый четырехугольник АВСD.

Диагональ четырехугольника – отрезок, соединяющий любые две не соседние вершины. На рисунке 2 диагоналями являются отрезки АС и BD.
Виды и свойства выпуклых четырехугольников
Сумма углов выпуклого четырехугольника равна 360 градусов.
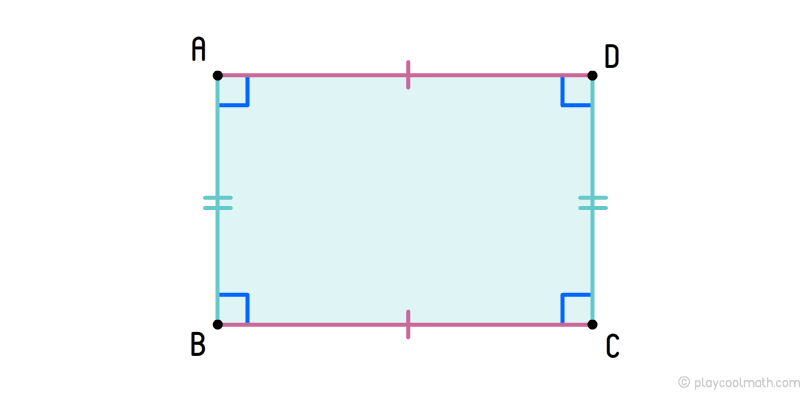
Прямоугольник
Прямоугольник – это четырехугольник, у которого все углы прямые.

- Противоположные стороны прямоугольника равны (АВ=CD, ВС=АD).
- Диагонали прямоугольника равны (АС=ВD).
- Диагонали пересекаются и точкой пересечения делятся пополам.
- Периметр прямоугольника – это сумма длин всех сторон: Р=(а + b) × 2, где а и b соседние (смежные) стороны прямоугольника
- Площадь прямоугольника – это произведение длин соседних (смежных) сторон, формула для нахождения площади прямоугольника:
S=ab, где a и b соседние стороны прямоугольника.
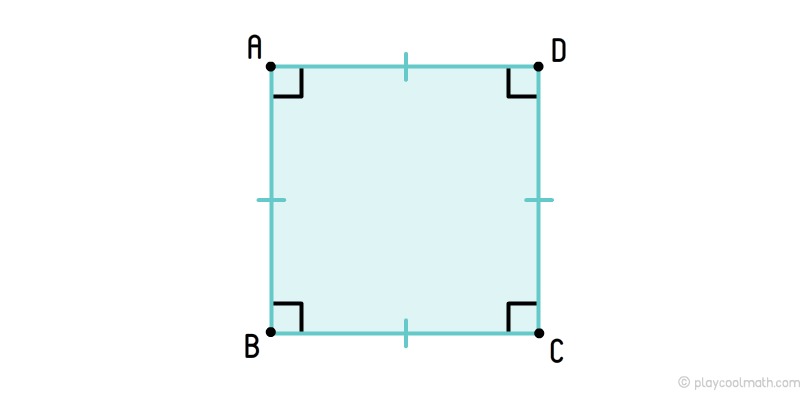
Квадрат
Квадрат – это прямоугольник, у которого все стороны равны.
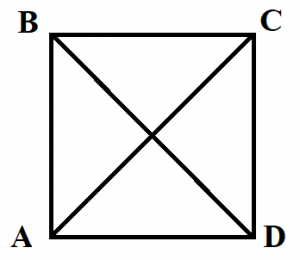
- Диагонали квадрата равны (BD=AC).
- Диагонали квадрата пересекаются под углом 90 градусов.
- Диагонали квадрата точкой пересечения делятся пополам (BO=OD, AO=OC).
- Периметр квадрата – это сумма длин всех сторон. Так как все стороны квадрата равны, то его можно найти по формуле Р=4×а, где а — длина стороны квадрата.
- Площадь квадрата – это произведение длин соседних сторон, формула для нахождения площади прямоугольника S=a 2 , где a — длина стороны квадрата.
Параллелограмм
Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны.
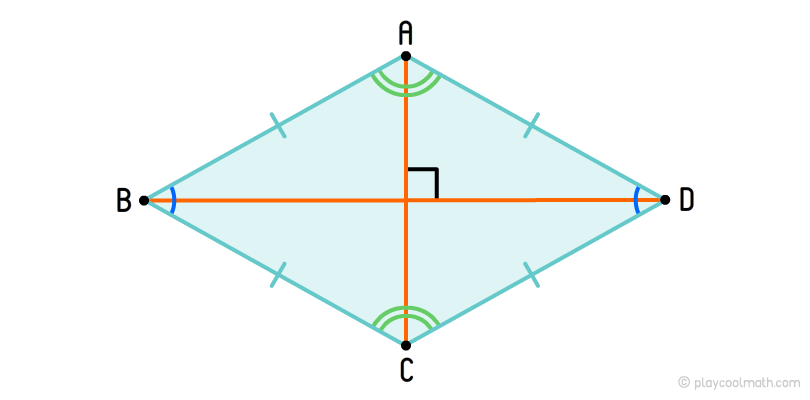
Ромб – это параллелограмм, у которого все стороны равны.
Трапеция
Трапеция – это четырехугольник, у которого только две противоположные стороны параллельны. Параллельные стороны называются основаниями трапеции, а две другие стороны – боковыми сторонами трапеции.
Виды трапеций
Трапеция называется прямоугольной, если у нее боковая сторона перпендикулярна основаниям. Прямоугольная трапеция имеет два прямых угла.
углы А и С равны по 90 градусов
Средняя линия трапеции
Сделаем чертеж параллелограмма и покажем на нем биссектрисы углов, которые пересекаются в точке N.
Угол ANB равен углу NАD как накрест лежащие при параллельных прямых ВС и АD и секущей AN. А по условию углы BАN и NАD равны (AN биссектриса). Следовательно, углы BАN и BNА равны. Значит, треугольник ABN является равнобедренным, у него АВ= BN.
Аналогично, через равенство углов CND, ADN и CDN доказывается, что треугольник CND является равнобедренным, у него CN=DC.
По условию задачи мы имеем параллелограмм, а по свойству параллелограмма – противолежащие стороны равны, т.е. АВ=СD, значит, АВ=BN=NC=CD. Таким образом, мы доказали, что BN=NC, т.е. N – середина ВС.
Ответ: см. решение
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите боковую сторону АВ трапеции ABCD, если углы АВС и BCD равны соответственно 30 0 и 135 0 , а СD =17
Сделаем чертеж, выполнив на нём дополнительные построения – высоты АМ и СН, которые равны как расстояния между параллельными сторонами трапеции.
Рассмотрим треугольник CНD, где CD=17, угол Н=90 0 , следовательно, треугольник прямоугольный. Найдем величину угла DCН, 135 0 – 90 0 =45 0 (так как провели высоту CН). Отсюда следует, что угол D=45 0 , так как треугольник прямоугольный. Значит, треугольник является равнобедренным (углы D и DCН равны по 45 градусов).
Найдем катеты CН и DН по теореме Пифагора, как катет равнобедренного треугольника по формуле с=а √ 2 , где с=17. Следовательно, CН = 17 √ 2 . . = 17 √ 2 2 . . .
Рассмотрим прямоугольный треугольник АВМ, где угол В равен 30 градусов, а катет АМ= CН= 17 √ 2 2 . . . Зная, что катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы, найдем АВ (она будет в два раза больше катета). АВ=2 × 17 √ 2 2 . . =17 √ 2
Ответ: см. решение
pазбирался: Даниил Романович | обсудить разбор | оценить
Основания трапеции равны 7 и 11, а высота равна 7. Найти площадь этой трапеции.
Для нахождения площади трапеции в справочном материале есть формула
S = a + b 2 . . h , для которой у нас известны и основания, и высота. Подставим в неё эти значения и вычислим: S = 7 + 11 2 . . ∙ 7 = 18 2 . . ∙ 7 = 9 ∙ 7 = 63
pазбирался: Даниил Романович | обсудить разбор | оценить
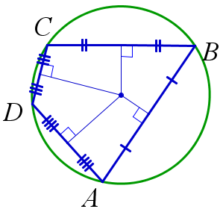
Радиус вписанной в квадрат окружности равен 22 √ 2 . Найти диагональ этого квадрата.
Для начала надо сделать построения на чертеже, чтобы увидеть, как располагаются известные и неизвестные элементы и чем они еще могут являться на чертеже.
Обозначим диагональ АВ, точкой О – центр окружности, С – один из углов квадрата. Покажем расстояние от центра окружности до стороны квадрата – радиус r. Если радиус равен 22 √ 2 , то сторона квадрата будет в два раза больше, т.е. 44 √ 2 .
Рассмотрим прямоугольный треугольник АВС, который является равнобедренным (так как по условию дан квадрат) и боковые стороны равны по 44 √ 2 . Нам надо найти диагональ, т.е. гипотенузу данного треугольника. Вспомним, что для нахождения гипотенузы равнобедренного треугольника есть формула с=а √ 2 , где с – гипотенуза, а – катет. Подставим в неё наши данные:
с=44 √ 2 × √ 2 =44 √ 4 =44 × 2=88
pазбирался: Даниил Романович | обсудить разбор | оценить
Площадь четырехугольника можно вычислить по формуле S= d 1 d 2 s i n a 2 . . , где d 1 и d 2 длины диагоналей четырехугольника, а – угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d 1 , если d 2 =16, sin a= 2 5 . . , a S=12,8
Для выполнения данного задания надо подставить все известные данные в формулу:
12,8= d 1 × 16 × 2 5 . . 2 . .
В правой части можно сократить 16 и 2 на 2: 12,8= d 1 × 8 × 2 5 . . 1 . .
Теперь умножим 8 на дробь 2 5 . . , получим 3,2: 12,8= d 1 × 3 , 2
Найдем неизвестный множитель, разделив 12,8 на 3,2: d 1 =12,8:3,2=4
pазбирался: Даниил Романович | обсудить разбор | оценить
На плане изображен дачный участок по адресу: п. Сосновка, ул. Зеленая, д. 19 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.
При входе на участок слева от ворот находится гараж. Справа от ворот находится сарай площадью 24 кв.м, а чуть подальше – жилой дом. Напротив жилого дома расположены яблоневые посадки. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, и огород с теплицей внутри (огород отмечен на плане цифрой 6). Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м. Между гаражом и сараем находится площадка, вымощенная такой же плиткой. К участку подведено электричество. Имеется магистральное газоснабжение.
Задание №1
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырех цифр без пробелов, запятых и других символов.
| Объекты | яблони | теплица | сарай | жилой дом |
| Цифры |
Решение
Для решения 1 задачи работаем с текстом и планом одновременно:
при входе на участок слева от ворот находится гараж (слева от входа находится объект под номером 2), итак, гараж — 2. Справа от ворот находится сарай площадью 24 кв.м (справа объект под номером 1), сарай – номер 1. А чуть подальше – жилой дом, следовательно, жилой дом – объект под номером 7. Напротив жилого дома расположены яблоневые посадки, на плане они обозначены цифрой 3. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, на плане видим, что к объекту под номером 4 ведет дорожка, значит баня – 4. Огород с теплицей внутри (огород отмечен на плане цифрой 6), в огороде расположена теплица – объект 5.
Итак, получили следующее:
1 – сарай; 2 – гараж; 3 – яблоневые посадки; 4 – баня; 5 – теплица; 6 – огород; 7 – жилой дом.
Заполняем нашу таблицу:
| Объекты | яблони | теплица | сарай | жилой дом |
| Цифры | 3 | 5 | 1 | 7 |
Записываем ответ: 3517
Задание №2
Плитки для садовых дорожек продаются в упаковках по 6 штук. Сколько упаковок плиток понадобилось, чтобы выложить все дорожки и площадку между сараем и гаражом?
Решение
Для начала надо определить, как обозначены дорожки, которые надо выложить плиткой, на плане. На плане они показаны серым цветом (мы их обведём голубым цветом).
Теперь ищем в условии задачи, что сказано про плитки и дорожки: «Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м».
Сосчитаем, сколько клеточек (плиток) на плане, получаем 65. Зная по условию задачи 1, что плитки продаются в упаковках по 6 штук, разделим 65 на 6. Заметим, что 65 на 6 не делится, получается приблизительно 10,8…Учитывая, что упаковки не делятся, округляем до большего целого числа, нам понадобится 11 упаковок.
Задание №3
Найдите расстояние от жилого дома до теплицы (расстояние между двумя ближайшими точками по прямой) в метрах.
Решение
Из задания 1 знаем, что жилой дом обозначен на плане цифрой 7, а теплица цифрой 5. Следовательно, на плане находим эти объекты и расстояние между двумя ближайшими точками по прямой (обозначим это голубым цветом). Видим, что это расстояние – 2 клетки. На плане показано, что длина стороны одной клетки равна 2 метра, значит, расстояние между двумя этими объектами равно 4 метра.
Задание №4
Найдите площадь, которую занимает гараж. Ответ дайте в квадратных метрах.
Решение
Найдем на плане гараж, это объект под номером 2. Гараж имеет прямоугольную форму, следовательно, нам надо найти площадь прямоугольника. Для этого надо найти длину и ширину. На плане показано, что длина стороны 1 клетки равна 2 метра, значит, длина гаража равна 8 м (4 клетки), а ширина — 6 м (3 клетки).
Зная ширину и длину, находим площадь гаража: 6х8=48 кв.м
Задание №5
Хозяин участка решил покрасить весь забор вокруг участка (только с внешней стороны) в зелёный цвет. Площадь забора равна 232 кв.м., а купить краску можно в одном из двух ближайших магазинов. Цена и характеристика краски и стоимость доставки заказа даны в таблице.
| Номер магазина | Расход краски | Масса краски в одной банке | Стоимость одной банки краски | Стоимость доставки заказа |
| 1 | 0,25 кг/кв.м | 6 кг | 3000 руб. | 500 руб. |
| 2 | 0,4 кг/кв.м | 5 кг | 1900 руб. | 800 руб. |
Во сколько рублей обойдется наиболее дешёвый вариант покупки с доставкой?
Решение
Определим, сколько килограммов краски понадобится для покраски забора площадью 232 кв.м:
1 магазин: 232х0,25=58 кг
2 магазин: 232х0,4=92,8 кг
Вычислим количество банок краски, которое надо купить, зная массу краски в 1 банке:
1 магазин: 58:6=9,7…; так как банки продаются целиком, то надо 10 банок (округляем до наибольшего целого числа)
2 магазин: 92,8:5=18,56; значит надо 19 банок.
Вычислим стоимость краски в каждом магазине плюс доставка:
1 магазин: 10х3000+500=30500 руб.
2 магазин: 19х1900+800=36900 руб.
Из решения задачи видно, что в 1 магазине купить краску выгоднее. Следовательно, наиболее дешёвый вариант покупки с доставкой будет стоить 30500 рублей.
Ответ: см. решение
pазбирался: Даниил Романович | обсудить разбор | оценить
Многоугольник. Нахождение диагоналей вписанного четырехугольника. Теорема Птоломея.
Обозначим стороны вписанного четырехугольника ABCD через a, b, с, d и его диагонали через x и y .Проведем AK ^ BС и СL ^ AD.
Так как сумма противоположных углов вписанного четырехугольника равна 2d, то, если угол B острый, угол D должен быть тупым.
Поэтому из треугольников ABС и ADС можем написать:
x 2 = a 2 + b 2 – 2b . BK [1];
x 2 = с 2 + d 2 + 2d . DL [2].
Прямоугольные треугольники ABK и СDL подобны, т.к. они содержат по равному острому углу (углы B и СDL равны, потому что каждый из них служит дополнением до 2d к углу ADС).
Из их подобия выводим:
откуда BK . с = DL . a [3].
Таким образом, мы получим три уравнения с тремя неизвестными x, BK и DL.
Чтобы исключить BK и DL , уравняем в первых двух уравнениях последние члены, для чего умножим уравнение [1] на сd , а уравнение [2] на ab .
Сложив затем результаты и, приняв во внимание уравнение [3], найдем:
(ab + сd)x 2 = a 2 сd + b 2 сd + с 2 ab + d 2 ab =aс(ad + bс) + bd(bс+ad)=(aс + bd)(ad+bс),
.
Заметим, что в числителе подкоренной величины первый множитель — сумма произведений противоположных сторон, а второй — сумма произведений сторон, сходящихся в концах определяемой диагонали, знаменатель же представляет сумму произведений сторон, сходящихся в концах другой диагонали.
После этого мы можем, по аналогии, написать следующую формулу для диагонали y:
.
Следствие 1.
Произведение диагоналей вписанного четырехугольника равно сумме произведений противоположных сторон.
Действительно, перемножив выражения, выведенные для x и для y, получим:
.
Это предложение известно под именем теоремы Птоломея.
Следствие 2.
Отношение диагоналей вписанного четырехугольника равно отношению суммы произведений сторон, сходящихся в концах первой диагонали, к сумме произведений сторон, сходящихся в концах второй диагонали.
Действительно, разделив те же два равенства, найдем:
.
Эти два следствия удобны для запоминания. Из них можно обратно вывести формулы для x и y (перемножением или делением равенств, определяющих xy и x/y).
Геометрия. Урок 4. Четырехугольники
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
- Определение четырехугольника
- Выпуклые четырехугольники
- Параллелограмм
Определение четырехугольника
Четырехугольником называется фигура, которая состоит из четырех точек (вершин) и четырех отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться.
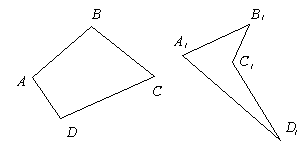
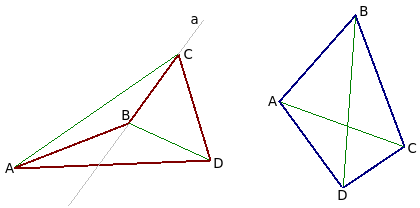
Четырехугольники бывают выпуклые ( A B C D ) и невыпуклые ( A 1 B 1 C 1 D 1 ) .
Выпуклые четырехугольники
В задачах ОГЭ встречаются выпуклые четырехугольники, поэтому подробно изучим их.
Смежные стороны – соседние стороны, которые выходят из одной вершины. Пары смежных сторон: A B и A D , A B и B C , B C и C D , C D и A D .
Противолежащие стороны – несмежные стороны (соединяют разные вершины). Пары противолежащих сторон: A B и C D , B C и A D .
Противолежащие вершины – вершины, не являющиеся соседними (лежат друг напротив друга). Пары противолежащих вершин: A и C , B и D .
Диагонали четырехугольника – отрезки, соединяющие противолежащие вершины. A C и B D – диагонали четырехугольника A B C D .
Диагонали выпуклого четырехугольника пересекаются в одной точке.
Площадь произвольного выпуклого четырехугольника можно найти по формуле:
S = 1 2 d 1 d 2 ⋅ sin φ
где d 1 и d 2 – диагонали четырехугольника, φ – угол между диагоналями (острый или тупой – не важно).
Рассмотрим более подробно некоторые виды выпуклых четырехугольников.
Класс параллелограммов : параллелограмм, ромб, прямоугольник, квадрат.
Класс трапеций : произвольная трапеция, прямоугольная трапеция, равнобокая (равнобедренная) трапеция.
Параллелограмм
Параллелограмм – четырехугольник, у которого противолежащие стороны попарно параллельны.
Свойства параллелограмма:
- Противолежащие стороны равны.
- Противоположные углы равны.
- Диагонали точкой пересечения делятся пополам.
- Сумма углов, прилежащих к одной стороне, равна 180 ° .
- Сумма квадратов диагоналей равна сумме квадратов сторон. d 1 2 + d 2 2 = 2 ( a 2 + b 2 )
Площадь параллелограмма можно найти по трём формулам.
Как произведение стороны и высоты, проведенной к ней.
Поскольку стороны имеют разные длины, то высоты, которые к ним проведены, тоже будут иметь разные длины.
Как произведение двух смежных (соседних) сторон на синус угла между ними.
Как полупроизведение диагоналей на синус угла между ними.
Ромб – параллелограмм, у которого все стороны равны.
Свойства ромба:
- Диагонали пересекаются под прямым углом.
- Диагонали являются биссектрисами углов, из которых выходят.
- Сохраняются все свойства параллелограмма.
Площадь ромба можно найти по трём формулам.
Как произведение стороны ромба на высоту ромба.
Как квадрат стороны ромба на синус угла между двумя сторонами.
Как полупроизведение диагоналей ромба.
Прямоугольник
Прямоугольник – это параллелограмм, у которого все углы равны 90 ° .
Свойства прямоугольника:
- Диагонали прямоугольника равны.
- Сохраняются все свойства параллелограмма.
Площадь прямоугольника можно найти по двум формулам:
Как произведение двух смежных (соседних) сторон прямоугольника.
Как полупроизведение диагоналей (так как они обе равны, обозначим их буквой d ) на синус угла между ними.
Квадрат
Квадрат – прямоугольник, у которого все стороны равны.
Свойства квадрата:
- Сохраняет свойства ромба.
- Сохраняет свойства прямоугольника.
Площадь квадрата можно вычислить по двум формулам:
Как квадрат стороны.
Как полупроизведение квадратов диагоналей (диагонали в квадрате равны).
Трапеция
Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие нет.
Стороны, которые параллельны друг другу называются основаниями , другие две стороны называются боковыми сторонами .
B C и A D – основания, A B и C D – боковые стороны трапеции A B C D .
Свойства трапеции:
сумма углов, прилежащих к боковой стороне, равна 180 ° .
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Средняя линия параллельна основаниям. Её длина находится по формуле: m = a + b 2
Площадь трапеции можно найти по двум формулам:
Как полусумму оснований на высоту. Поскольку полусумма оснований есть средняя линия трапеции, можно найти площадь трапеции как произведение средней линии на высоту.
Как полупроизведение диагоналей на синус угла между ними.
Виды трапеций
Прямоугольная трапеция – трапеция, у которой два угла прямые.
Равнобокая (равнобедренная) трапеция – трапеция, у которой боковые стороны равны.
Свойство равнобокой трапеции: углы при основании равны
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с четырехугольниками
http://www.calc.ru/Mnogougolnik-Nakhozhdeniye-Diagonaley-Vpisannogo-Chetyrekhug.html
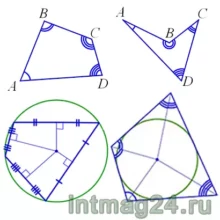
Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три точки не лежат на одной прямой.
Четырехугольники бывают выпуклые, если они расположены в одной полуплоскости относительно прямой, которая содержит одну из его сторон (ABCD) и невыпуклые (A1B1C1D1).
Если любые две противолежащие точки выпуклого четырёхугольника соединить между собой отрезком, то весь отрезок будет лежать внутри многоугольника. Для невыпуклого четырёхугольника это не выполняется (рисунок ниже).
Диагонали выпуклого четырёхугольника лежат внутри него и пересекаются. Одна из диагоналей невыпуклого четырёхугольника лежит снаружи, а другая внутри него, и эти диагонали не пересекаются.
Определения для четырехугольника
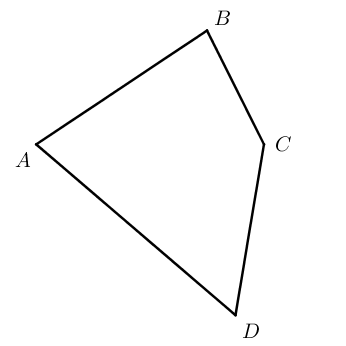
Данный четырёхугольник обозначается ABCD.
- Точки A, B, C, D называются его вершинами, а отрезки AB, BC, CD, DA – его сторонами.
- Смежные стороны – соседние стороны, имеющие общую вершину. Пары смежных сторон: AB и AD, AB и BC, BC и CD, CD и AD.
- Противолежащие стороны – несмежные стороны, не имеющие общих вершин. Пары противолежащих сторон: AB и CD, BC и AD.
Диагонали четырехугольника – отрезки, соединяющие противолежащие вершины. AC и BD – диагонали четырехугольника ABCD.
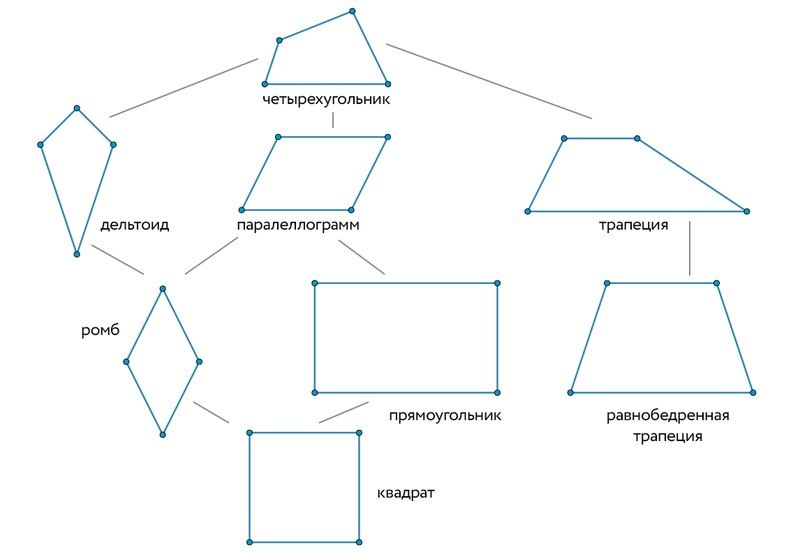
Виды четырехугольников:
Если рассмотреть схему, то каждый следующий четырехугольник обладает всеми свойствами предыдущего. Поэтому запоминать надо совсем немного.
Трапеция — это четырехугольник, у которого две противолежащие стороны параллельны, а две другие не параллельны. Трапеции бывают: произвольная, равносторонняя, прямоугольная.
Параллелограмм — это четырехугольник у которого противолежащие стороны параллельны. В параллелограмме:
— противоположные стороны и противоположные углы равны.
— диагонали параллелограмма делятся точкой пересечения пополам.
Соответственно, если четырехугольник обладает этими свойствами, то он является параллелограммом.
Прямоугольник — это параллелограмм, у которого все углы прямые. Прямоугольник является частным случаем параллелограмма, поэтому обладает всеми его свойствами.
Ромб — это параллелограмм, у которого все стороны равны. Ромб является частным случаем параллелограмма, поэтому обладает всеми его свойствами. В ромбе:
— противоположные углы равны,
— диагонали точкой пересечения делятся пополам,
— диагонали взаимно перпендикулярны,
— диагонали ромба являются биссектрисами углов.
Квадрат — это прямоугольник, у которого все стороны равны. Квадрат является частным случаем прямоугольника и частным случаем ромба, поэтому обладает всеми их свойствами. В квадрате:
— все углы равны 90 градусов,
— диагонали точкой пересечения делятся пополам,
— диагонали взаимно перпендикулярны,
— диагонали являются биссектрисами углов,
— диагонали равны.
Свойства углов четырехугольника
- Сумма углов четырёхугольника равна 360°
- Сумма внешних углов четырехугольника, взятых по одному при каждой вершине, равна 360°.
- Не существует четырёхугольников, у которых все углы острые или все углы тупые.
- Каждый угол четырёхугольника всегда меньше суммы трёх остальных углов.
Свойства сторон четырехугольника
- Каждая сторона четырехугольника меньше суммы всех его других сторон.
- Сумма диагоналей меньше его периметра.
Четырехугольник и окружность
Четырехугольник вокруг окружности.
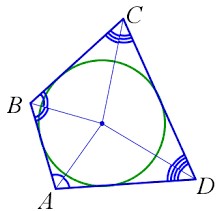
- Четырехугольник называется описанным, если существует окружность, касающаяся всех его сторон.
- В четырёхугольник можно вписать окружность, если суммы его противолежащих сторон равны (AB+CD=AD+BC).
- Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника.
Четырехугольник внутри окружности.
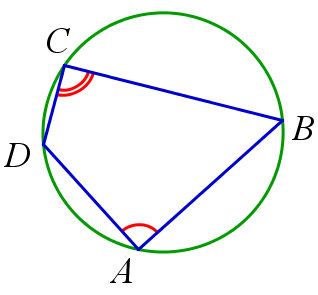
- Вписанный четырёхугольник — это четырёхугольник, все вершины которого лежат на одной окружности. Эта окружность называется описанной.
- Вокруг четырёхугольника можно описать окружность, если сумма двух его противоположных углов равна 180°.
- Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника.
- Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон (AC*BD=AB*CD+AD*BC).
Частные случаи:
- Параллелограмм, вписанный в окружность – это прямоугольник, центр окружности совпадает с точкой пересечения диагоналей.
- Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.
- Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной.
Диагонали четырехугольника
- Диагонали выпуклого четырёхугольника пересекаются в одной точке.
- Две противоположные стороны четырёхугольника перпендикулярны тогда и только тогда, когда сумма квадратов двух других противоположных сторон равна сумме квадратов диагоналей.
- Диагонали четырёхугольника перпендикулярны тогда и только тогда, когда суммы квадратов противоположных сторон равны.
Периметр и площадь четырехугольника
Периметр четырёхугольника равен сумме длин всех его сторон: где a, b, c, d – длины сторон четырёхугольника.
Площадь произвольного выпуклого четырёхугольника можно найти по формуле: где d1 и d2— диагонали четырёхугольника, a — угол между диагоналями.
Площадь вписанного четырёхугольника может быть вычислена по формуле: 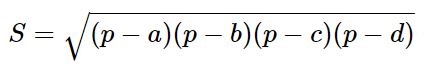
Площадь описанного четырёхугольника равна произведению его полупериметра на радиус вписанной окружности:
В предыдущем уроке мы познакомились с треугольниками. Узнали, какие треугольники бывают, чем друг от друга отличаются и какие общие признаки соответствуют для всех треугольников. В этом уроке мы узнаем, что такое четырехугольник. Начнем наш урок с определения четырехугольника.
Четырехугольник — это четырехугольная геометрическая фигура, образованная замкнутой ломаной линией, состоящей из четырех отрезков. Точки в четырехугольнике называются вершинами, отрезки называются сторонами или гранями четырехугольника.
Четырехугольник включает себя такие простейшие фигуры
- Четыре точки (A, B, C, D);
- Четыре отрезка (AB, BC, CD, DA);
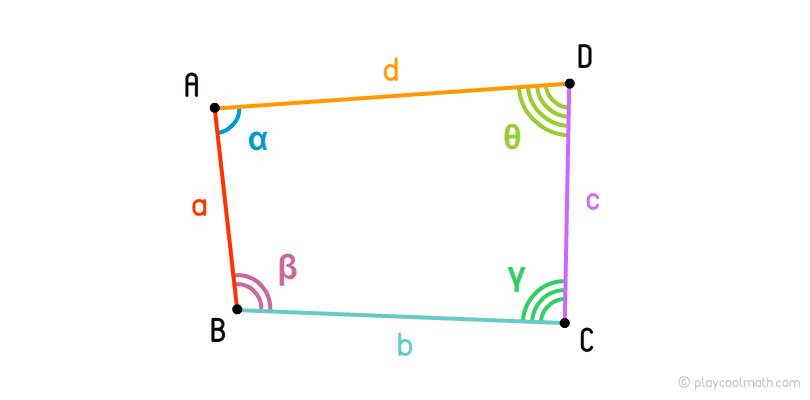
- Четыре угла (α, β, γ, θ);
- Замкнутая ломаная линия (ABCD).
Вершины четырехугольника
Вершины четырехугольника обозначают заглавными латинскими буквами. Четырехугольник обозначается последовательностью вершин. На рисунке у нас четырехугольник ABCD.
Стороны четырехугольника
Стороны четырехугольника (или еще их называют грани или ребра) обозначаются строчными латинскими буквами. На рисунке мы обозначили стороны четырехугольника буквами a, b, c, d. Также стороны треугольника можно обозначать в виде отрезков, например a = AB, b = BC, c = CD, d = DA. Стороны, которые относятся к одной вершине, называются смежными сторонами. На рисунке для вершины A мы имеем смежные стороны DA и AB
Углы четырехугольника
Углы, как мы знаем, обозначают строчными греческими буквами. На рисунке углы четырехугольника обозначены как α, β, γ, θ, где α = DAB, β = ABC, γ = BCD, θ = CDA. Каждый угол четырехугольника имеет противолежащий угол, например, на рисунке угол α имеет противолежащий угол γ, а для β противолежащий угол θ.
Диагонали четырехугольника
Диагональ четырехугольника — это отрезок, соединяющий противоположные вершины четырехугольника.
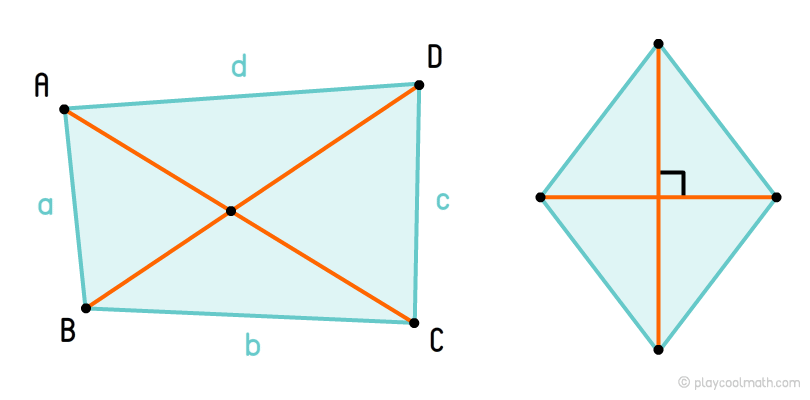
Всего у четырехугольника две диагонали. На рисунке отрезки AC и BD — это диагонали четырехугольника ABCD.
Если диагонали четырехугольника пересекаются под прямым углом, то такой четырехугольник называется ортодиагональным.
Биссектрисы четырехугольника
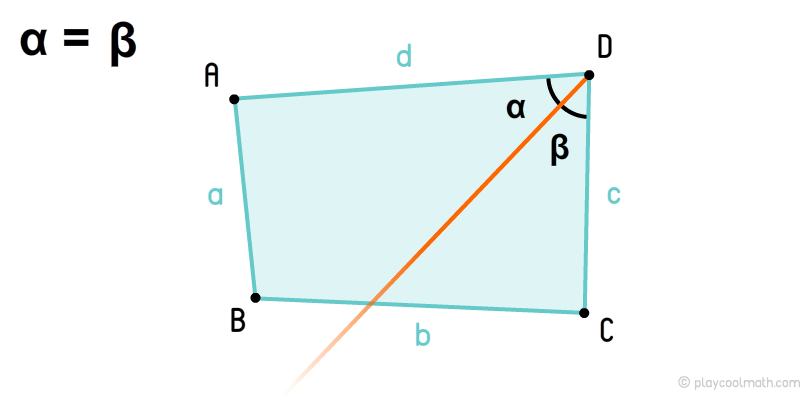
Биссектриса четырехугольника — это луч, разделяющий угол вершины на два равных угла.
В лекции по треугольникам мы подробно описали, как можно найти биссектрису для вершины с помощью транспортира.
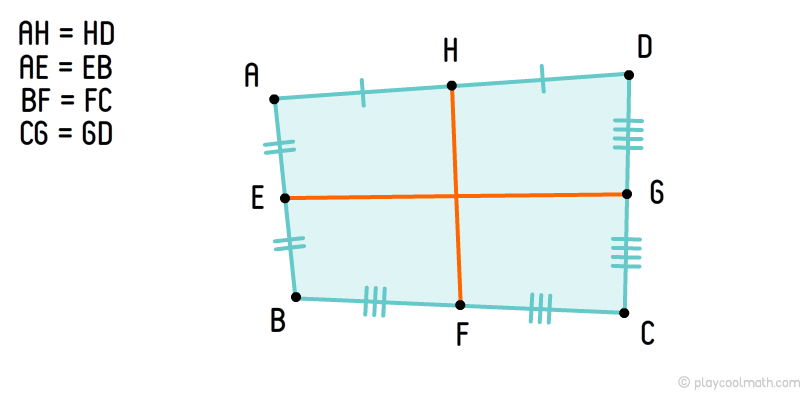
Средние линии четырехугольника
Средняя линия четырехугольника — это отрезок, соединяющий противоположные стороны через их середины.
Чтобы нарисовать среднюю линию необходимо все стороны четырехугольника разбить на два равных отрезка и найти середины. Середины противоположных сторон необходимо соединить отрезками, которые и будут средними линиями четырехугольника.
Классификация треугольников
Выпуклые четырехугольники
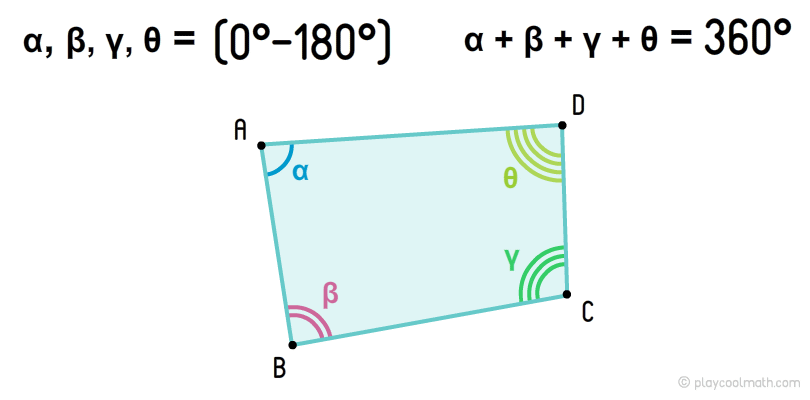
Выпуклый четырехугольник — это четырехугольник, у которого все углы выпуклые (от 0° до 180°, не включая эти значения). Сумма всех углов выпуклого четырехугольника всегда равна 360°
Невыпуклые или вогнутые четырехугольники
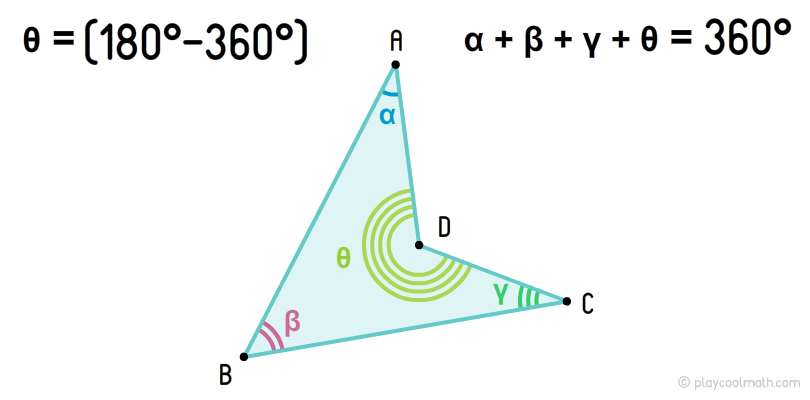
Вогнутый четырехугольник — это четырехугольник, у которого один угол вогнутый (от 180° до 360°, не включая эти значения). Сумма всех углов вогнутого четырехугольника всегда равна 360°
Самопересекающиеся четырехугольники
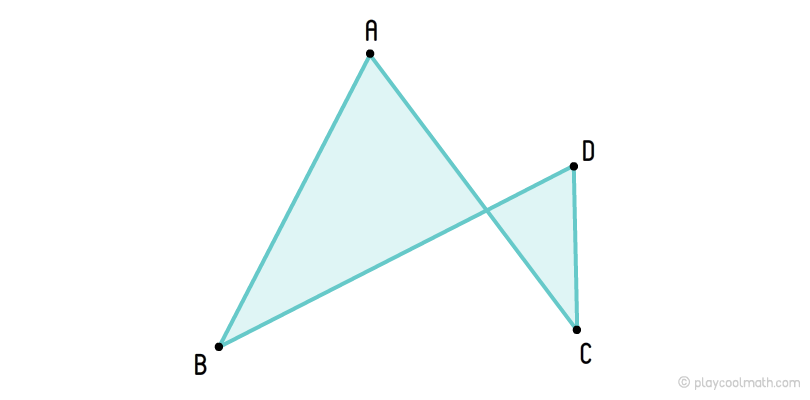
Самопересекающийся четырехугольник — это четырехугольник, у которого противоположные стороны пересекаются.
Визуально самопересекающийся четырехугольник похож на два треугольника у которых стороны лежать на двух пересекающихся линиях, а точка пересечения это общая вершина для треугольников.
Виды треугольников и их свойства
Параллелограмм
Параллелограмм — это четырехугольник, у которого противоположные стороны параллельны и равны. У параллелограмма противоположные углы равны.
Прямоугольник
Прямоугольник — это параллелограмм с равными углами. Прямоугольник — это четырехугольник, у которого противоположные стороны параллельны и равны. Все углы прямоугольника равны 90°.
Ромб
Ромб — это параллелограмм с равными сторонами. Ромб — это ортодиагональный четырехугольник, у которого все стороны равны и противоположные стороны параллельны.
Квадрат
Квадрат — это прямоугольник с равными сторонами. Квадрат — это выпуклый четырехугольник, у которого все стороны и углы равны. Все углы квадрата равны 90°.
Трапеция
Трапеция — это четырехугольник, у которого две противоположные стороны параллельны. Эти стороны называют основанием трапеции, остальные стороны называют бедрами трапеции.
Трапеция, у которой бедра равны, называют равнобедренной трапецией. У равнобедренной трапеции углы у оснований равны. На рисунке справа изображена равнобедренная трапеция.
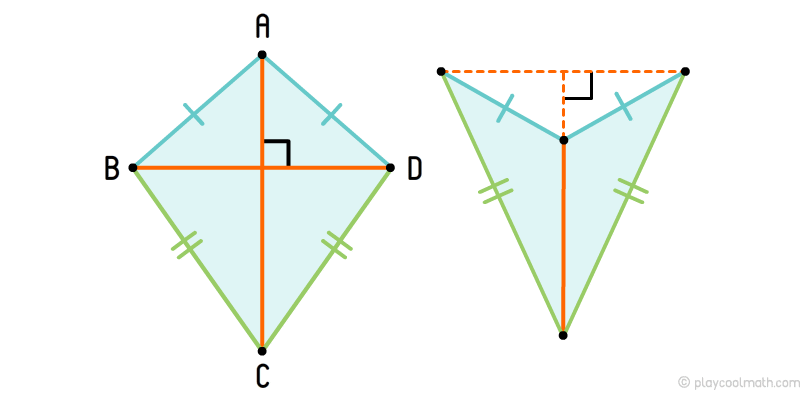
Дельтоид
Дельтоид — это ортодиагональный четырёхугольник, у которого смежные стороны для противоположных углов равны.
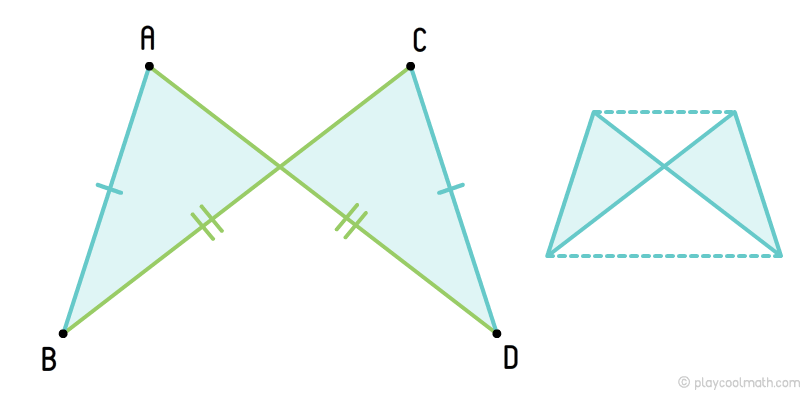
Антипараллелограмм
Антипараллелограмм (контрпараллелограмм) — это самопересекающийся четырехугольник, у которого противоположные стороны равны но не параллельны.
Если провести выпуклую геометрическую фигуры через вершины антипараллелограмма, то у нас получится равнобедренная трапеция.
Как вписать окружность в четырехугольник?
Окружность, касающаяся всех четырех сторон четырехугольника, называется вписанной окружностью четырехугольника. В четырехугольник можно вписать окружность только при одном условии, что суммы противоположных сторон равны. Если условие равенства противоположных сторон не выполняется, то в такой четырехугольник невозможно вписать окружность.
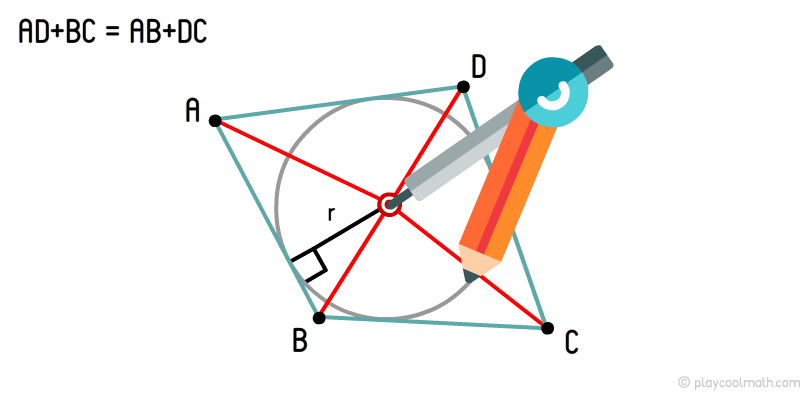
Как описать четырехугольник окружностью?
Окружность, проходящая по всем вершинам четырехугольника, называется описанной окружностью. Если сумма противоположных углов равна 180°, то такой четырехугольник можно описать окружностью. В случае, если данное условие не выполняется, то такой четырехугольник невозможно описать окружностью.
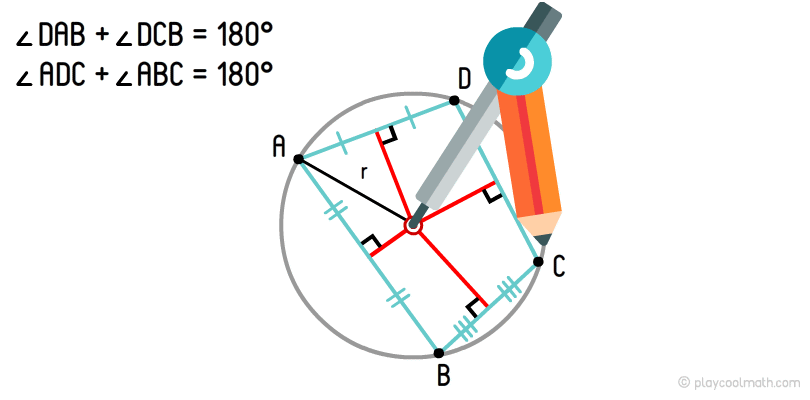
Мы уже рисовали описанную окружность для треугольника. Алгоритм для описания окружности для четырехугольника такой же. На рисунке хорошо видно, как из середины сторон мы провели перпендикуляры и нашли точку пересечения. С помощью штангенциркуля выставляем радиус от центра до любой вершины и круговым движением рисуем описанную окружность четырехугольника.
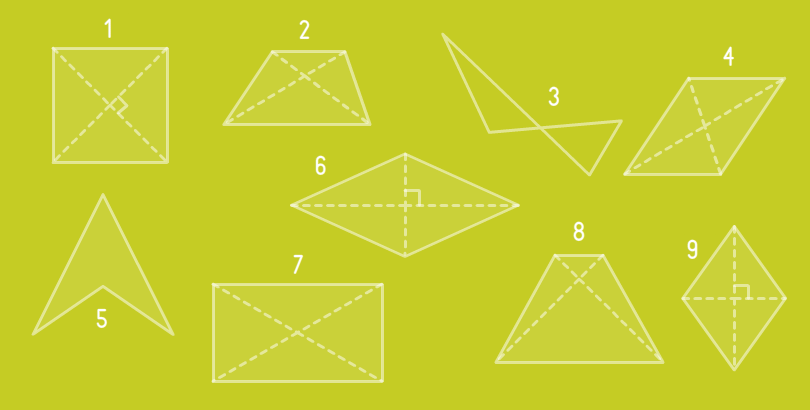
Найди ортодиагональные четырехугольники.
- #1
- #6
- #9
Совет 1: Как обнаружить диагональ четырехугольника
Четырехугольником именуется фигура, состоящая из четырех сторон и углов, прилежащих к ним. К числу таких фигур относятся прямоугольник, трапеция, параллелограмм. В ряде задач по геометрии требуется обнаружить диагональ одной из этих фигур.
Инструкция
1. Диагональю четырехугольника именуется отрезок, соединяющий его противоположные углы. У четырехугольника имеются две диагонали, которые между собой пересекаются в одной точке. Диагонали изредка бывают равными, как у прямоугольника и квадрата, а изредка имеют разную длину, как, скажем, у трапеции. Метод нахождения диагонали зависит от фигуры.Постройте прямоугольник со сторонами a и b и двумя диагоналями d1 и d2. Из свойств прямоугольника знаменито, что его диагонали между собой равны, пересекаются в одной точке и делятся в ней напополам. Если вестимы две стороны прямоугольника, то его диагонали обнаружьте дальнейшим образом: d1=?a^2+b^2=d2.Частным случаем прямоугольника является квадрат, у которого диагональ равна a?2. Помимо того, диагональ дозволено обнаружить, зная площадь квадрата. Она равна: S = d^2/2.Отсель длину диагонали вычислите по формуле: d = ?2S.
2. Несколько другим образом решайте задачу, когда дан не прямоугольник, а параллелограмм. У этой фигуры, в различие от прямоугольника либо квадрата, равны между собой не все углы, а только противоположные. Если в условии задача присутствует параллелограмм со сторонами a и b и заданным между ними углом, как показано на рисунке к шагу, то диагональ обнаружьте, применяя теорему косинусов: d^2 = a^2+b^2-2ab*cos?.Параллелограмм, имеющий равные стороны, именуется ромбом. Если по условиям задачи нужно обнаружить диагональ этой фигуры, то понадобятся значения его 2-й диагонали и площади, от того что диагонали этой фигуры неравны. Формула площади ромба выглядит дальнейшим образом: S = d1*d2/2.Отсель d2 равна удвоенной площади фигуры, деленной на d1: d2 = 2S/d1.
3. При вычислении площади трапеции придется воспользоваться тригонометрической функцией синуса. Если данная фигура является равнобочной, то, зная ее первую диагональ d1 и угол между двумя диагоналями AOD, как показано на рисунке к шагу, обнаружьте вторую по дальнейшей формуле: d2 = 2S/d1*sin?. В данном случае рассматриваем трапецию ABCD.Существует также прямоугольная трапеция, диагональ которой обнаружить несколько проще. Зная длину боковой стороны этой трапеции, совпадающей с ее высотой, а также нижнее основание, обнаружьте ее диагональ , пользуясь обыкновенной теоремой Пифагора. А именно сложите квадраты этих величин, а после этого из итога извлеките квадратный корень.
Совет 2: Как обнаружить диагональ ромба
У ромба стороны равны и попарно параллельны. Его диагонали пересекаются под прямым углом и делятся точкой пересечения на равные части. Эти свойства легко разрешают обнаружить величину диагоналей ромба.
Инструкция
1. Обозначим вершины ромба буквами латинского алфавита A, B, C и D для комфорта обсуждения. Точку пересечения диагоналей обычно обозначают буквой O. Длину ребра ромба обозначим буквой a. Величину угла BCD, тот, что равен углу BAD, обозначим α.
2. Обнаружим величину короткой диагонали. Потому что диагонали пересекаются под прямым углом, то треугольник COD является прямоугольным. Половина короткой диагонали OD является катетом этого треугольника и может быть обнаружена через гипотенузу CD, а также угол OCD.Диагонали ромба являются также биссектрисами его углов, следственно угол OCD равен α/2.Таким образом, OD = BD/2 = CD*sin(α/2). То есть, короткая диагональ BD = 2a*sin(α/2).
3. Аналогичным образом, из того, что треугольник COD прямоугольный, можем выразить величину OC (а это половина длинной диагонали).OC = AC/2 = CD*cos(α/2)Величина длинной диагонали выражается дальнейшим образом: AC =2a*cos(α/2)
Обратите внимание!
Ромб с прямыми углами именуется квадратом.Из прямоугольности треугольника COD, как и остальных 3 треугольников, образованных диагоналями и сторонами ромба, вытекает еще такое качество ромба: AC²+BD²=4a²
Полезный совет
Зная диагонали, легко обнаружить площадь ромба. Традиционно для этого их и вычисляют. Площадь ромба равна половине произведения его диагоналей.
Совет 3: Как обнаружить диагональ в параллелограмме
Вычислить диагональ параллелограмма бывает нужно не только при подготовке домашнего задания. Это может потребоваться, скажем, в бумажной пластике либо при создании архитектурного плана.
Вам понадобится
- Оборудование Бумага Линейка Карандаш Транспортир Таблица синусов и косинусов Математические представления: Свойства параллелограмма Свойства высоты треугольника Извлечение квадратного корня Теоремы синусов и косинусов
Инструкция
1. Постройте параллелограмм с заданными параметрами. В условиях обязаны быть заданы длины сторон параллелограмма и правда бы один угол.
2. Припомните, чему равна сумма квадратов диагоналей параллелограмма. Она равна удвоенной сумме квадратов его сторон, которые вам вестимы.
3. Обозначьте параллелограмм АBCD. Стороны параллелограмма обозначьте как a и b. Диагонали обозначьте как d1 и d2. Из угла В к стороне АD опустите высоту и обозначьте точку ее пересечения со стороной AD как Е. Внутри параллелограмма у вас получился прямоугольный треугольник АВЕ.
4. Обнаружьте высоту BЕ. Вам вестим угол А и гипотенуза АВ. AE = a*sinА
5. Вычислите длину отрезка АЕ. Он равен AE=a*cosA.
6. Вычислите отрезок ЕD, тот, что равен разности стороны AD и отрезка AE.
7. Вычислите гипотенузу прямоугольного треугольника BED, которая единовременно является диагональ ю d1. Она будет равна квадратному корню из суммы квадратов сторон BE и ED.
8. Обнаружьте квадрат 2-й диагонали. Он будет равняться удвоенной сумме квадратов сторон минус квадрат теснее знаменитой диагонали. Извлеките квадратный корень.
Обратите внимание!
При построении параллелограмма сурово следуйте заданным параметрам и пользуйтесь инструментами. При расчетах пользуйтесь таблицами синусов и косинусов.
Полезный совет
В прямоугольнике и квадрате диагонали равны. Квадрат диагонали прямоугольника равен сумме квадратов его сторон. В квадрате диагональ равна квадратному корню, извлеченному из удвоенного квадрата стороны. Диагонали ромба являются биссектрисами его углов.
Совет 4: Как обнаружить диагональ в прямоугольнике
Прямоугольник – плоская геометрическая фигура. Прямоугольник – это четырехугольник, у которого все углы прямые. Как же обнаружить диагональ квадрата, если вестимы длины его сторон?
Инструкция
1. Поделим прямоугольник диагональю на два равных треугольника. В этом случае диагональ будет являться гипотенузой этих треугольников. А, как вестимо из теоремы Пифагора, квадрат гипотенузы равен сумме квадратов катетов.Выходит, для поиска диагонали прямоугольника нужно:обнаружить сумму квадратов сторон прямоугольника а2 + b2, где а и b – длины сторон прямоугольника;извлечь из полученного итога квадратный корень.Пример:Определим длину диагонали прямоугольника со сторонами 3 и 4 см.Находим сумму квадратов сторон прямоугольника 32 + 42 = 9 + 16 = 25.Извлечь из полученного итога квадратный корень – длина диагонали равна 5 см.
Видео по теме
Обратите внимание!
Диагонали прямоугольника равны. Если обнаружена длина одной, то длина 2-й будет безусловно такой же.
Совет 5: Как обнаружить диагональ у квадрата
Квадрат – прекрасная и простая плоская геометрическая фигура. Это прямоугольник с равными сторонами. Как же обнаружить диагональ квадрата , если знаменита длина его стороны?
Инструкция
1. Диагональ квадрата обнаружить довольно легко, воспользовавшись теоремой Пифагора.Поделим квадрат диагональ ю на два равных треугольника. В этом случае диагональ будет являться гипотенузой одного из треугольников. А, как знаменито, квадрат гипотенузы равен сумме квадратов катетов.Рассматривая. что катеты – стороны квадрата и они равны, формула для расчета диагонали квадрата по его стороне дюже примитивна:длина диагонали квадрата равна длине его стороны умноженной на корень из 2-х.
Видео по теме
Полезный совет
Если точность математического итога не дюже значима, то взамен корня из 2-х дозволено применять его примерное значение 1,41.
Совет 6: Как обнаружить диагональ параллелограмма, если даны стороны
Параллелограмм – это четырехугольник, противоположные стороны которого параллельны. Прямые, соединяющие его противоположные углы, именуются диагоналями. Их длина зависит не только от длин сторон фигуры, но и от величин углов в вершинах этого многоугольника, следственно без познания правда бы одного из углов вычислить длины диагоналей дозволено только в исключительных случаях. Таковыми являются частные случаи параллелограмма – квадрат и прямоугольник.
Инструкция
1. Если длины всех сторон параллелограмма идентичны (a), то эту фигуру дозволено назвать еще и квадратом. Величины всех его углов равны 90°, а длины диагоналей (L) идентичны и могут быть рассчитаны по теореме Пифагора для прямоугольного треугольника. Умножьте длину стороны квадрата на корень из двойки – итог и будет длиной всякой из его диагоналей: L=a*?2.
2. Если о параллелограмме знаменито, что он является прямоугольником с указанными в условиях длиной (a) и шириной (b), то и в этом случае длины диагоналей (L) будут равны. И тут тоже задействуйте теорему Пифагора для треугольника, в котором гипотенузой является диагональ, а катетами – две смежные стороны четырехугольника. Желанную величину рассчитайте извлечением корня из суммы возведенных в квадрат ширины и высоты прямоугольника: L=?(a?+b?).
3. Для всех остальных случаев умения одних только длин сторон хватит лишь для определения величины, включающей в себя длины сразу обеих диагоналей – сумма их квадратов по определению равна удвоенной сумме квадратов длин сторон. Если же в дополнение к длинам 2-х смежных сторон параллелограмма (a и b) знаменит еще и угол между ними (?), то это дозволит рассчитать длины всего отрезка, соединяющего противоположные углы фигуры. Длину диагонали (L?), лежащей наоборот знаменитого угла, обнаружьте по теореме косинусов – сложите квадраты длин смежных сторон, от итога отнимите произведение этих же длин на косинус угла между ними, а из полученной величины извлеките квадратный корень: L? = ?(a?+b?-2*a*b*cos(?)). Для нахождения длины иной диагонали (L?) дозволено воспользоваться свойством параллелограмма, приведенным в начале этого шага – удвойте сумму квадратов длин 2-х сторон, от итога отнимите квадрат теснее рассчитанной диагонали, а из полученного значения извлеките корень. В всеобщем виде эту формулу дозволено записать так: L? = ?(a?+b?- L??) = ?(a?+b?-(a?+b?-2*a*b*cos(?))) = ?(a?+b?-a?-b?+2*a*b*cos(?)) = ?(2*a*b*cos(?)).
Совет 7: Как обнаружить вторую диагональ ромба
Ромбом дозволено назвать параллелограмм, диагонали которого делят напополам углы, лежащие в вершинах фигуры. Помимо этого свойства диагонали ромба знаменательны тем, что являются осями симметрии многоугольника, пересекаются только под прямым углом, а исключительная всеобщая точка делит всякую из них на два равных отрезка. Эти свойства дозволяют легко рассчитать длину одной из диагоналей, если знаменита длина иной и еще какой-либо параметр фигуры – размер стороны, угол в одной из вершин, площадь и т.д.
Инструкция
1. Если помимо длины одной из диагоналей (l) о рассматриваемом четырехугольнике вестимо, что он является частным случаем ромба – квадратом, никаких расчетов изготавливать не придется. В этом случае длины обеих диагоналей идентичны – примитивно приравняйте желанную величину (L) к знаменитой: L=l.
2. Познание длины стороны ромба (a) в дополнение к длине одной из диагоналей (l) дозволит рассчитать длину иной (L) по теореме Пифагора. Это допустимо потому, что две половины пересекающихся диагоналей образуют со стороной ромба прямоугольный треугольник. Половины диагоналей в нем являются катетами, а сторона – гипотенузой, следственно равенство, вытекающее из теоремы Пифагора дозволено записать так: a? = (l/2)? + (L/2)?. Для применения в расчетах преобразуйте его к такому виду: L = ?(4*a?-l?).
3. При вестимой величине одного из углов (?) ромба и длине одной из диагоналей (l) для нахождения величины иной (L) разглядите тот же прямоугольный треугольник. Тангенс половины вестимого угла в нем будет равен отношению длины противолежащего катета – половины диагонали l – к прилежащему – половине диагонали L: tg(?/2) = (l/2)/(L/2) = l/L. Следственно для вычисления желанной величины используйте формулу L = l/tg(?/2).
4. Если в условиях задачи приведена длина периметра (P) ромба и размер его диагонали (l), формулу вычисления длины 2-й (L) дозволено свести к равенству, использованному во втором шаге. Для этого поделите периметр на четверку и замените этим выражением длину стороны в формуле: L = ?(4*(P/4)?-l?) = ?(P?/4-l?).
5. В начальных условиях помимо длины одной из диагоналей (l) может быть приведена и площадь (S) фигуры. Тогда для вычисления длины 2-й диагонали ромба (L) используйте дюже примитивный алгорифм – удвойте площадь и поделите полученное значение на длину знаменитой диагонали: L = 2*S/l.
Совет 8: Как обнаружить крупную диагональ параллелограмма
Диагонали четырехугольника соединяют противоположные его вершины, деля фигуру на пару треугольников. Дабы обнаружить огромную диагональ параллелограмма , необходимо произвести ряд вычислений согласно исходным данным задачи.
Инструкция
1. Диагонали параллелограмма владеют рядом свойств, познание которых помогает в решении геометрических задач. В точке пересечения они делятся напополам, являясь биссектрисами пары противоположных углов фигуры, меньшая диагональ – для тупых углов, а огромная – острых. Соответственно, при рассмотрении пары треугольников, которые получаются из 2-х смежных сторон фигуры и одной из диагоналей, половина иной диагонали – это еще и медиана.
2. Треугольники, образованные половинами диагоналей и двумя параллельными сторонами параллелограмма , подобны. Помимо того, любая диагональ делит фигуру на два идентичных треугольника, графически симметричных касательно совместного основания.
3. Дабы обнаружить огромную диагональ параллелограмма , дозволено воспользоваться общеизвестной формулой соотношения суммы квадратов 2-х диагоналей и удвоенной суммы квадратов длин сторон. Она является прямым следствием из свойств диагоналей:d1? + d2? = 2•(a? + b?).
4. Пускай d2 – огромная диагональ , тогда формула преобразуется к виду:d2 = ?(2•(a? + b?) – d1?).
5. Примените эти познания на практике. Пускай задан параллелограмм со сторонами a=3 и b=8. Обнаружьте крупную диагональ , если вестимо, что она на 3 см огромнее меньшей.
6. Решение.Запишите формулу в всеобщем виде, введя знаменитые из начальных данных величины a и b:d1? + d2? = 2•(9 + 64) = 146.
7. Выразите длину меньшей диагонали d1 через длину большей согласно условию задачи:d1 = d2 – 3.
8. Подставьте это выражение в первое уравнение:(d2 – 3)? + d2? = 146
9. Возведите значение в скобке в квадрат:d2? – 6•d2 + 9 + d2? = 1462•d2? – 6•d2 – 135 = 0
10. Решите полученное квадратное уравнение касательно переменной d2 через дискриминант:D = 36 + 1080 = 1116.d2 = (6 ± ?1116)/4 ? [9,85; -6,85].Видимо, что длина диагонали – правильная величина, следственно, она равна 9,85 см.
Совет 9: Как подтвердить что ABCD параллелограмм
Геометрия всецело построена на теоремах и доказательствах. Дабы подтвердить, что произвольная фигура ABCD является параллелограммом, надобно знать определение и знаки этой фигуры.
Инструкция
1. Параллелограммом в геометрии именуется фигура с четырьмя углами, у которой параллельны противоположные стороны. Таким образом, ромб, квадрат и прямоугольник являются разновидностями этого четырехугольника.
2. Докажите, что две из противолежащих сторон равны и параллельны касательно друг друга. В параллелограмме ABCD это знак выглядит так: AB=CD и AB||CD. Нарисуйте диагональ АС. Полученные треугольники окажутся равными по второму знаку. АС – всеобщая сторона, углы ВАС и АСD, также как и ВСА и CAD, равны как лежащие накрест при параллельных прямых AB и CD (дано в условии). Но потому что эти накрест лежащие углы относятся и к сторонам AD и BC, значит эти отрезки также лежат на параллельных прямых, что и подвергалось доказательству.
3. Значимым элементами доказательства, что ABCD параллелограмм, являются диагонали, потому что в этой фигуре при пересечении в точке O они делятся на равные отрезки (AO=OC, BO=OD). Треугольники AOB и COD равны, потому что равны их стороны в связи с данными условиями и вертикальные углы. Из этого следует, что и углы DBA и CDB также как и CAB и ACD равны.
4. Но эти же углы являются накрест лежащими при том, что прямые AB и CD параллельны, а роль диагонали исполняет секущая. Доказав таким образом, что и два других образованных диагоналями треугольники равны, вы получите, что данный четырехугольник параллелограмм.
5. Еще одно качество, по которому дозволено подтвердить, что четырехугольник ABCD – параллелограмм звучит так: противоположные углы этой фигуры равны, то есть угол B равен углу D, а угол C равен A. Сумма углов треугольников, которые мы получим, если проведем диагональ AC, равна 180°. Исходя из этого получаем, что сумма всех углов данной фигуры ABCD равна 360°.
6. Припомнив данные задачи, дозволено легко осознать, что угол A и угол D в сумме составят 180°, подобно угол C + угол D = 180°. В тоже время эти углы являются внутренними, лежат на одной стороне, при соответствующих им прямых и секущих. Отсель следует, что прямые BC и AD параллельны, и приведенная фигура является параллелограммом.
















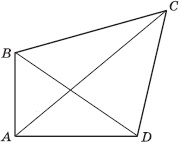 Данный четырёхугольник обозначается ABCD.
Данный четырёхугольник обозначается ABCD.