Как найти директрису гиперболы онлайн

bold{mathrm{Basic}}	bold{alphabetagamma}	bold{mathrm{ABGamma}}	bold{sincos}	bold{gedivrightarrow}	bold{overline{x}spacemathbb{C}forall}	bold{sumspaceintspaceproduct}	bold{begin{pmatrix}square&square\square&squareend{pmatrix}}	bold{H_{2}O}
square^{2} x^{square} sqrt{square} nthroot[msquare]{square} frac{msquare}{msquare} log_{msquare} pi theta infty int frac{d}{dx} ge le cdot div x^{circ} (square) |square| (f:circ:g) f(x) ln e^{square} left(squareright)^{‘} frac{partial}{partial x} int_{msquare}^{msquare} lim sum sin cos tan cot csc sec alpha beta gamma delta zeta eta theta iota kappa lambda mu nu xi pi rho sigma tau upsilon phi chi psi omega A B Gamma Delta E Z H Theta K Lambda M N Xi Pi P Sigma T Upsilon Phi X Psi Omega sin cos tan cot sec csc sinh cosh tanh coth sech arcsin arccos arctan arccot arcsec arccsc arcsinh arccosh arctanh arccoth arcsech begin{cases}square\squareend{cases} begin{cases}square\square\squareend{cases} = ne div cdot times < > le ge (square) [square] ▭:longdivision{▭} times twostack{▭}{▭} + twostack{▭}{▭} — twostack{▭}{▭} square! x^{circ} rightarrow lfloorsquarerfloor lceilsquarerceil overline{square} vec{square} in forall notin exist mathbb{R} mathbb{C} mathbb{N} mathbb{Z} emptyset vee wedge neg oplus cap cup square^{c} subset subsete superset supersete int intint intintint int_{square}^{square} int_{square}^{square}int_{square}^{square} int_{square}^{square}int_{square}^{square}int_{square}^{square} sum prod lim lim _{xto infty } lim _{xto 0+} lim _{xto 0-} frac{d}{dx} frac{d^2}{dx^2} left(squareright)^{‘} left(squareright)^{»} frac{partial}{partial x} (2times2) (2times3) (3times3) (3times2) (4times2) (4times3) (4times4) (3times4) (2times4) (5times5) (1times2) (1times3) (1times4) (1times5) (1times6) (2times1) (3times1) (4times1) (5times1) (6times1) (7times1) mathrm{Радианы} mathrm{Степени} square! ( ) % mathrm{очистить} arcsin sin sqrt{square} 7 8 9 div arccos cos ln 4 5 6 times arctan tan log 1 2 3 — pi e x^{square} 0 . bold{=} +

Подпишитесь, чтобы подтвердить свой ответ

Подписаться

Войдите, чтобы сохранять заметки

Войти

Номер Строки

Примеры

• frac{y^2}{25}-frac{x^2}{9}=1
  

• центр:frac{(x+3)^2}{25}-frac{(y-4)^2}{9}=1
  

• ось:-frac{(y-3)^2}{25}+frac{(x+2)^2}{9}=1
  

• фокусы:4x^2-9y^2-48x-72y+108=0
  

• вершины:x^2-y^2=1
  

• эксцентриситет:x^2-y^2=1
  

• асимптоты:x^2-y^2=1
  

• Показать больше

Описание

Пошаговый расчет центра Гиперболы, оси, фокусов, вершин, эксцентриситета и асимптот

hyperbola-function-calculator

ru

Блог-сообщения, имеющие отношение к Symbolab

My Notebook, the Symbolab way

Math notebooks have been around for hundreds of years. You write down problems, solutions and notes to go back…

Read More

Введите Задачу

Сохранить в блокнот!

Войти

Гипербола: формулы, примеры решения задач

Определение гиперболы, решаем задачи вместе

Определение гиперболы. Гиперболой называется множество всех точек плоскости, таких, для которых модуль разности расстояний от двух точек, называемых фокусами, есть величина постоянная и меньшая, чем расстояние между фокусами.

Каноническое уравнение гиперболы имеет вид:

,

где a и b — длины полуосей, действительной и мнимой.

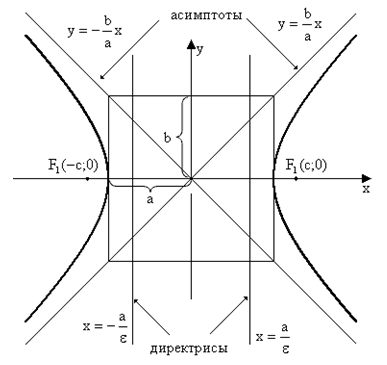
На чертеже ниже фокусы обозначены как и .

На чертеже ветви гиперболы — бордового цвета.

При a = b гипербола называется равносторонней.

Пример 1. Составить каноническое уравнение гиперболы, если его действительная полуось a = 5 и мнимая = 3.

Решение. Подставляем значения полуосей в формулу канонического уравения гиперболы и получаем:

.

Точки пересечения гиперболы с её действительной осью (т. е. с осью Ox) называются вершинами. Это точки (a, 0) (- a, 0), они обозначены и надписаны на рисунке чёрным.

Точки и , где

,

называются фокусами гиперболы (на чертеже обозначены зелёным, слева и справа от ветвей гиперболы).

называется эксцентриситетом гиперболы.

Гипербола состоит из двух ветвей, лежащих в разных полуплоскостях относительно оси ординат.

Пример 2. Составить каноническое уравнение гиперболы, если расстояние между фокусами равно 10 и действительная ось равна 8.

Если действительная полуось равна 8, то её половина, т. е. полуось a = 4 ,

Если расстояние между фокусами равно 10, то число c из координат фокусов равно 5.

То есть, для того, чтобы составить уравнение гиперболы, потребуется вычислить квадрат мнимой полуоси b.

Подставляем и вычисляем:

Получаем требуемое в условии задачи каноническое уравнение гиперболы:

.

Пример 3. Составить каноническое уравнение гиперболы, если её действительная ось равна 48 и эксцентриситет .

Решение. Как следует из условия, действительная полуось a = 24 . А эксцентриситет — это пропорция и так как a = 24 , то коэффициент пропорциональности отношения с и a равен 2. Следовательно, c = 26 . Из формулы числа c выражаем квадрат мнимой полуоси и вычисляем:

.

Результат — каноническое уравнение гиперболы:

Если — произвольная точка левой ветви гиперболы () и — расстояния до этой точки от фокусов , то формулы для расстояний — следующие:

.

Если — произвольная точка правой ветви гиперболы () и — расстояния до этой точки от фокусов , то формулы для расстояний — следующие:

.

На чертеже расстояния обозначены оранжевыми линиями.

Для каждой точки, находящейся на гиперболе, сумма расстояний от фокусов есть величина постоянная, равная 2a.

Прямые, определяемые уравнениями

,

называются директрисами гиперболы (на чертеже — прямые ярко-красного цвета).

Из трёх вышеприведённых уравнений следует, что для любой точки гиперболы

,

где — расстояние от левого фокуса до точки любой ветви гиперболы, — расстояние от правого фокуса до точки любой ветви гиперболы и и — расстояния этой точки до директрис и .

Пример 4. Дана гипербола . Составить уравнение её директрис.

Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется найти эксцентриситет гиперболы, т. е. . Вычисляем:

.

Получаем уравнение директрис гиперболы:

Многие задачи на директрисы гиперболы аналогичны задачам на директрисы эллипса. В уроке «Эллипс» это пример 7.

Характерной особенностью гиперболы является наличие асимптот — прямых, к которым приближаются точки гиперболы при удалении от центра.

Асимптоты гиперболы определяются уравнениями

.

На чертеже асимптоты — прямые серого цвета, проходящие через начало координат O.

Уравнение гиперболы, отнесённой к асимптотам, имеет вид:

, где .

В том случае, когда угол между асимптотами — прямой, гипербола называется равнобочной, и если асимптоты равнобочной гиперболы выбрать за оси координат, то её уравнение запишется в виде y = k/x , то есть в виде уравения обратной пропорциональной зависимости.

Пример 5. Даны уравнения асимптот гиперболы и координаты точки , лежащей на гиперболе. Составить уравнение гиперболы.

Решение. Дробь в уравнении асимптот гиперболы — это пропорция, следовательно, нужно сначала найти коэффициент пропорциональности отношения . Для этого подставляем в формулу канонического уравнения гиперболы координаты точки M x и y и значения числителя и знаменателя из уравнения асимптоты, кроме того, умножаем каждую дробь в левой части на коэффициент пропорциональности k.

.

Теперь имеем все данные, чтобы получить каноническое уравнение гиперболы. Получаем:

Гипербола обладает оптическим свойством, которое описывается следующим образом: луч, исходящий из источника света, находящегося в одном из фокусов гиперболы, после отражения движется так, как будто он исходит из другого фокуса.

Решить задачи на гиперболу самостоятельно, а затем посмотреть решения

Пример 6. Фокусы эллипса расположены на оси Ox симметрично относительно начала координат. Составить каноническое уравнение эллипса, если:

1) b = 4 , а один из фокусов в точке (5; 0)

2) действительная ось 6, расстояние между фокусами 8

3) один из фокусов в точке (-10; 0), уравнения асимптот гиперболы

Гипербола и её свойства

Гипербола и её форма.

Гиперболой мы назвали линию, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением
$$
frac>>-frac>>=1.label
$$

Из этого уравнения видно, что для всех точек гиперболы (|x| geq a), то есть все точки гиперболы лежат вне вертикальной полосы ширины (2a) (рис. 8.6). Ось абсцисс канонической системы координат пересекает гиперболу в точках с координатами ((a, 0)) и ((-a, 0)), называемых вершинами гиперболы. Ось ординат не пересекает гиперболу. Таким образом, гипербола состоит из двух не связанных между собой частей. Они называются ее ветвями. Числа (a) и (b) называются соответственно вещественной и мнимой полуосями гиперболы.

Рис. 8.6. Гипербола.

Для гиперболы оси канонической системы координат являются осями симметрии, а начало канонической системы — центром симметрии.

Доказательство аналогично доказательству соответствующего утверждения для эллипса.

Для исследования формы гиперболы найдем ее пересечение с произвольной прямой, проходящей через начало координат. Уравнение прямой возьмем в виде (y=kx), поскольку мы уже знаем, что прямая (x=0) не пересекает гиперболу. Абсциссы точек перечения находятся из уравнения
$$
frac>>-fracx^<2>>>=1.
$$
Поэтому, если (b^<2>-a^<2>k^ <2>> 0), то
$$
x=pm frac<sqrt-a^<2>k^<2>>>.
$$
Это позволяет указать координаты точек пересечения ((ab/v, abk/v)) и ((-ab/v, -abk/v)), где обозначено (v=(b^<2>-a^<2>k^<2>)^<1/2>). В силу симметрии достаточно проследить за движением первой из точек при изменении (k) (рис. 8.7).

Рис. 8.7. Пересечение прямой и гиперболы.

Числитель дроби (ab/v) постоянен, а знаменатель принимает наибольшее значение при (k=0). Следовательно, наименьшую абсциссу имеет вершина ((a, 0)). С ростом (k) знаменатель убывает, и (x) растет, стремясь к бесконечности, когда (k) приближается к числу (b/a). Прямая (y=bx/a) с угловым коэффициентом (b/a) не пересекает гиперболу, и прямые с большими угловыми коэффициентами ее тем более не пересекают. Любая прямая с меньшим положительным угловым коэффициентом пересекает гиперболу.

Если мы будем поворачивать прямую от горизонтального положения по часовой стрелке, то (k) будет убывать, (k^<2>) расти, и прямая будет пересекать гиперболу во все удаляющихся точках, пока не займет положения с угловым коэффициентом (-b/a).

К прямой (y=-bx/a) относится все, что было сказано о (y=bx/a): она не пересекает гиперболу и отделяет прямые, пересекающие ее, от не пересекающих. Из приведенных рассуждений вытекает, что гипербола имеет вид, изображенный на рис. 8.7.

Прямые с уравнениями (y=bx/a) и (y=-bx/a) в канонической системе координат называются асимптотами гиперболы.

Каноническое уравнение гиперболы по двум точкам

Две точки с координатами

Первая координата

Вторая координата

Каноническое уравнение гиперболы

Большая полуось гиперболы

Малая/мнимая полуось гиперболы

Эксцентриситет гиперболы

Фокальный параметр

Фокальное расстояние

Перицентрическое расстояние

Уравнение гиперболы в каноническом виде имеет вот такой вид. Так же как и при расчете уравнения эллипса по двум точкам, мы можем по двум точкам однозначно построить гиперболу, выраженную через вышеуказанную формулу. Используя универсальный калькулятор расчет кривой второго порядка на плоскости по точкам, мы легко определим значения и Кроме этого, зная эти параметры можно рассчитать следующее: Большая полуось — расстояние от центра гиперболы, до одной из вершин Фокальное расстояние — расстояние от центра гиперболы до одного из фокусов Мнимая полуось — расстояние от вершины гиперболы до асимптоты вдоль направления параллельного оси ординат Связь между тремя параметрами выражена в одной формуле Эксцентриситет — коэффициент, численно равный, отношению фокусного расстояния к большой полуоси гиперболы Перицентрическое расстояние — расстояние от фокуса до ближайшей вершины гиперболы Примеры задач Cоставить каноническое уравнение гиперболы по двум точкам Вводим данные в поля ввода. Можем писать как выражение, учитвая что квадратный корень обозначается sqrt, а можем сначала получить численные значения и подставить уже окончательные результаты. В результате получим Каноническое уравнение гиперболы Большая полуось гиперболы Малая/мнимая полуось гиперболы Эксцентриситет гиперболы Фокальный параметр Фокальное расстояние Перицентрическое расстояние Есть небольшая погрешность в вычислениях, вместо 2.9999999999 должно быть 3. Но думаю, что клиенты отнесутся с снисхождением, к одной десяти миллионной погрешности. источники: http://univerlib.com/analytic_geometry/second_order_lines_and_surfaces/hyperbola/ http://abakbot.ru/online-2/365-giper-poin

Пусть дана некоторая парабола (x^2+3y=16). Требуется найти уравнение директрисы для этой параболы. Нет, директриса — это не директор-женщина в вашей школе. Это такая специальная прямая, что каждая точка параболы равноудалена от фокуса параболы и директрисы. Ну вам об этом лучше не думать — просто вставьте уравнение параболы в калькулятор как показано в примере. И вы получите все что вам требуется. Справа приведет пример параболы и ее директрисы (прямая горизонтальная линия). Вы можете воспользоваться нашим примером — кликните на пиктограмму копирования и код запроса будет добавлен в калькулятор. вам остается только нажать кнопку «Решить». Что может быть проще? Ну и на всякий случай — определение параболы:
Пара́бола (греч. παραβολή — приложение) — геометрическое место точек, равноудалённых от данной прямой (называемой директрисой параболы) и данной точки (называемой фокусом параболы).

directrix of parabola x^2+3y=16

 

Похожие публикации: калькулятор

This calculator will find either the equation of the hyperbola from the given parameters or the center, foci, vertices, co-vertices, (semi)major axis length, (semi)minor axis length, latera recta, length of the latera recta (focal width), focal parameter, eccentricity, linear eccentricity (focal distance), directrices, asymptotes, x-intercepts, y-intercepts, domain, and range of the entered hyperbola. Also, it will graph the hyperbola. Steps are available.

Related calculators:

Parabola Calculator,
Circle Calculator,
Ellipse Calculator,
Conic Section Calculator



3.7.2. Директрисы гиперболы

У гиперболы, как и у эллипса, две директрисы, и определяются они точно так же.

В каноническом положении  директрисы расположены между ветвями

гиперболы и задаются теми же уравнениями , где «эпсилон» – эксцентриситет

данной гиперболы.

В нашей задаче:

Более того, для гиперболы справедлива абсолютно такая же теорема:

Гипербола – есть множество всех точек плоскости, таких, что отношение расстояния от каждой точки до фокуса к расстоянию от неё до

соответствующей (ближайшей) директрисы равно эксцентриситету:

То есть, для любой точки  гиперболы отношение её

расстояния до фокуса  к расстоянию от неё же до ближайшей директрисы  равно эксцентриситету: . Для пары  и любой точки  гиперболы (ради разнообразия я выбрал демонстрационную точку

дальней ветви) отношение такое же:

К слову, у параболы с её единственным фокусом и единственной директрисой по определению эти длины

относятся «один к одному», поэтому эксцентриситет любой параболы и равен единице.

Ответ: искомая линия представляет собой гиперболу  с

центром симметрии в точке  и повёрнутую на  относительно своего канонического положения. Каноническое уравнение: , фокусы: , эксцентриситет: , асимптоты: , директрисы: .

Но я вас просто так не отпущу – всё-таки разберу второй способ приведения линии  к каноническому виду. Осуществим поворот системы  на угол   радиан против часовой

стрелки и её параллельный перенос в точку . Тогда в системе  уравнение примет вид: .

Чертёж будет выглядеть точно так же, как и чертежи выше – с той поправкой, что гиперболу мы изобразим в системе . Соответственно, все вычисления будут проводиться в новых координатах, и переменные

следует записывать со значком  «тильда»: . В частности, асимптоты запишутся

так: , а директрисы – так: .

Очень хотелось упростить и даже вообще не рассматривать эту задачу, но она взята из конкретной контрольной работы, причём, заочного отделения.

Поэтому пришлось с упорным занудством разобрать все-все-все тонкости и технические приёмы.

Налью вам стакан молока за вредность и предложу задачу для самостоятельного решения, она проще:)

Задача 110

Найти уравнение геометрического места точек, для каждой из которых отношение расстояния до точки  к расстоянию до прямой  постоянно и равно . Сделать точный чертеж.

Подумайте, о какой это точке и о какой прямой шепчет условие Краткое решение и чертёж в конце книги.

И теперь вы готовы! (в хорошем смысле:))

– готовы рассмотреть суперзадачу, к которой я вас морально и технически готовил чуть ли не с первых параграфов темы.

…анекдот тут ещё вспомнился садистский про готовку, но, пожалуй, не буду – он неэтичный

3.8. Приведение уравнения к каноническому виду

3.7.1. Директрисы эллипса

| Оглавление |



Автор: Aлeксaндр Eмeлин