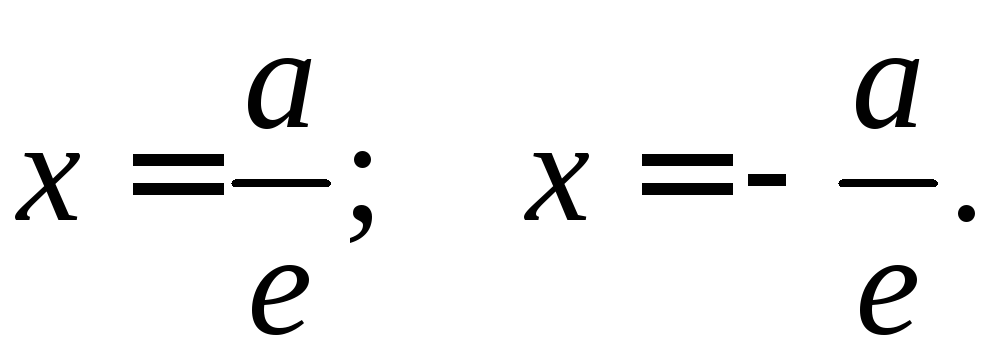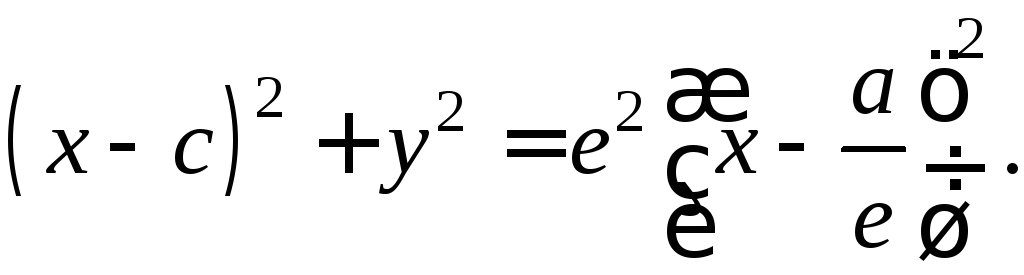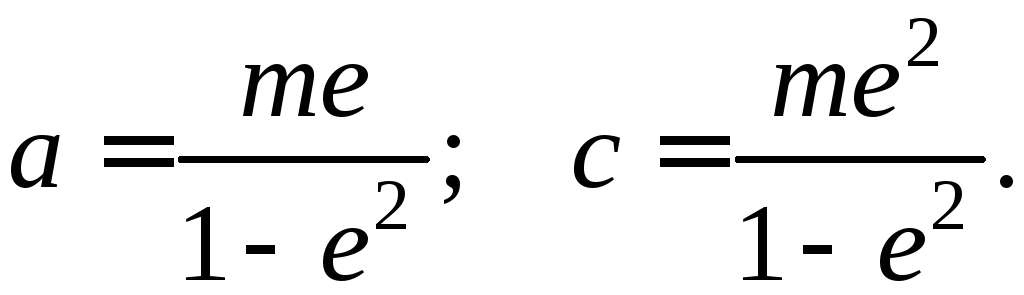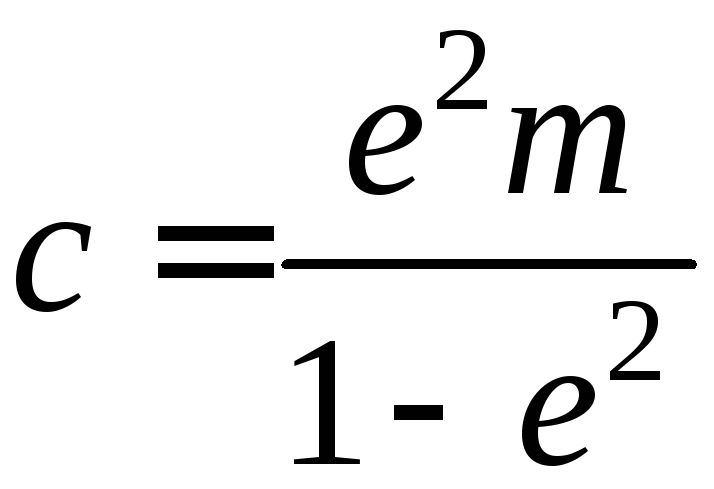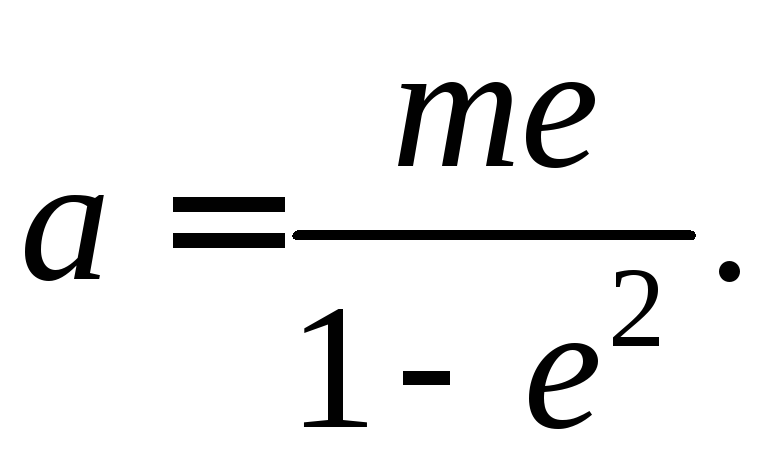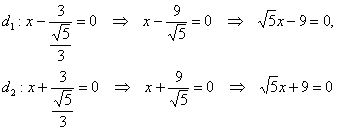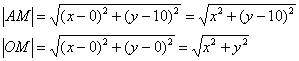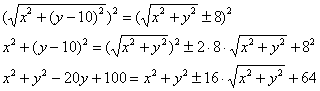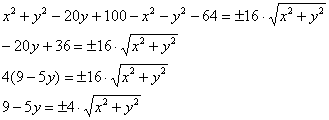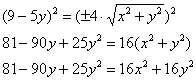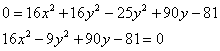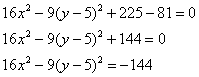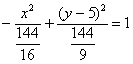Как найти директрису окружности

05.2. Эксцентриситет и директрисы конических сечений

Эксцентриситет и директрисы конических сечений

Изучение кривых второго порядка окажется неполным, если обойти вниманием некоторые их замечательные свойства, используемые в разнообразных приложениях.

Для эллипса, отличного от окружности, а также для гиперболы и параболы обнаруживается универсальное свойство: существует прямая, называемая директрисой (в зависимости от типа кривой их может быть одна или две), для которой отношение расстояния от точек этих кривых до фокуса к расстоянию до отвечающей этому фокусу директрисы есть величина постоянная.

Как известно, в частном случае это свойство справедливо для параболы согласно ее определению. Покажем также справедливость данного свойства для эллипса и гиперболы. Введем предварительно в рассмотрение параметр, характеризующий форму эллипса и гиперболы.

Эксцентриситетом эллипса (гиперболы) будем называть величину

(5.8)

Где с – половина фокусного расстояния эллипса (гиперболы), а – длина большей полуоси эллипса (длина действительной полуоси гиперболы).

Учитывая, что половина фокусного расстояния с и длины полуосей связаны известными соотношениями:

Для эллипса

Для гиперболы

Получим формулы вычисления эксцентриситета этих кривых по параметрам канонических уравнений:

для эллипса (5.9)

для гиперболы (5.10)

Очевидно, что эксцентриситет эллипса меньше единицы, а эксцентриситет гиперболы – больше единицы. Если длины полуосей эллипса близки друг к другу, то его эксцентриситет неограниченно приближается к нулю, а эллипс – к окружности.

Эксцентриситет эллипса характеризует его «сплюснутость»: чем он ближе к единице, тем более эллипс «вытянут» вдоль оси абсцисс. На рис. 5.12 показано семейство эллипсов, у которых при постоянной длине большой полуоси а малая полуось меняется.

Рис. 5.12. Влияние величины эксцентриситета
на форму эллипса.

Как по заданным длинам полуосей а и b с помощью циркуля и линейки найти фокусы гиперболы?

Изобразите семейство гипербол, у которых мнимая ось постоянна, а действительная полуось а меняется.

Эксцентриситет гиперболы также характеризует «сплюснутость» кривой. Ветви гиперболы расположены между асимптотами

и

Если действительная ось гиперболы совпадает с осью Ох (рис. 5.13), то величина угла между асимптотами будет уменьшаться с уменьшением b при постоянном a, и чем меньше отношение для гиперболы, тем меньше ее эксцентриситет е. На рис. 5.13 показано семейство гипербол, у которых при постоянной длине действительной полуоси a малая полуось b меняется.

Рис. 5.13. Влияние величины эксцентриситета
на форму гиперболы.

При определении параболы мы уже столкнулись с описанием этого геометрического места точек с помощью вспомогательной прямой, называемой директрисой. Такая прямая полезна также при изучении свойств эллипса и гиперболы. Более того, сами понятия эллипса и гиперболы могут быть введены через описание их свойств по отношению к директрисам и фокусам.

Будем называть директрисами эллипса, у которого большая полуось расположена вдоль оси Ох, прямые

.

Эти прямые расположены (рис.5.14) вне эллипса (так как ) на одинаковом расстоянии от его центра перпендикулярно оси Ох.

Рис. 5.14. Директрисы эллипса.

Точки эллипса обладают интересным свойством, которое мы сформулируем в виде теоремы.

ТЕОРЕМА 1. Для любой точки эллипса отношение ее расстояния до фокуса к расстоянию до
Соответствующей директрисы равно эксцентриситету.

Пусть d1 и d2 – расстояния от произвольной точки эллипса до директрис и соответственно (рис. 5.15). Расстояние от этой точки до фокуса будет , а до фокуса =, где, как известно, и – фокальные радиусы. Теорема утверждает:

Ранее уже получено: . Учитывая, что , будем иметь:

.

Так как директрисы перпендикулярны главной оси эллипса, то расстояния d1 и d2 находятся как длины отрезков, параллельных оси Ох:

Рис. 5.15. Расстояния от точки эллипса до фокуса
и соответствующей директрисы.

Что и требовалось доказать.

Директрисы для гиперболы вводятся так же, как и для эллипса.

Будем называть директрисами гиперболы, у которой действительная ось расположена на оси Ох, прямые

Эти прямые располагаются (рис. 5.16) между ветвями гиперболы (так как ) на расстоянии от ее центра перпендикулярно оси Ох.

Рис. 5.16. Директрисы гиперболы.

Докажем теорему, отражающую свойства директрис гиперболы.

ТЕОРЕМА 2. Для любой точки М(Х,У) гиперболы отношение ее расстояния до фокуса к расстоянию до соответствующей директрисы равно эксцентриситету е.

Для доказательства теоремы следует выделить четыре случая:

1. Точка располагается на левой ветви гиперболы, при этом рассматриваются фокус и директриса .

2. Точка находится на левой ветви гиперболы, при этом берутся фокус и директриса .

3. Точка принадлежит правой части гиперболы, при этом рассматриваются фокус и директриса .

4. Точка взята на правой ветви гиперболы, при этом используются фокус и директриса .

Рассуждения во всех этих случаях аналогичны. Выделим один из них, например, четвертый (рис. 5.17).

Рис. 5.17. Свойства директрис и фокусов гиперболы.

Для этого случая

Такой же результат мы получим в трех других случаях, что и доказывает теорему.

Сформулируем без доказательства теорему, которая позволяет по-новому определить эллипс и гиперболу.

ТЕОРЕМА 3. Геометрическое место точек М, для которых отношение е модуля радиус-вектора к расстоянию d точек М до заданной прямой есть величина постоянная, является эллипсом при и гиперболой при .

Точка F называется фокусом кривой, радиус-вектор –фокальным радиус–вектором, а упомянутая прямая – директрисой.

Таким образом, есть векторное уравнение эллипса при , либо гиперболы, если , а для оно определяет параболу.

Постройте семейство кривых при фиксированном е и различных d.

Полученный результат означает, что задание параметров e и d однозначно определяет эллипс, гиперболу, параболу.

Эллипс, гипербола и парабола, как уже отмечалось, могут быть получены путем конических сечений. Обоснование этому дает следующая теорема, которую мы приводим также без доказательства.

ТЕОРЕМА 4. Для всякой линии, будь то эллипс (включая окружность), гипербола или парабола, может быть найден такой круговой конус и такая плоскость, что пересечением конуса с этой плоскостью будет являться именно данная кривая.

Связь между этими линиями имеет и алгебраическое обоснование: все они задаются уравнениями второй степени. Можно доказать, что в любой прямоугольной системе координат уравнения таких кривых имеют вид

Где A, B,C, D,E и F – числа, причем

Каков геометрический смысл этого условия?

Справедливо и обратное утверждение: любое алгебраическое уравнение второй степени

Каким будет геометрический образ этого уравнения, когда левая его часть раскладывается на множители?

Определяет эллипс, гиперболу или параболу, если только левая часть уравнения не раскладывается на множители.

Вот почему для эллипса, гиперболы и параболы используется обобщающее название: кривые второго порядка.

Кривые второго порядка — определение и построение с примерами решения

Содержание:

Геометрической фигурой или просто фигурой на плоскости называется множество точек. Задать фигуру — значит указать, из каких точек плоскости она состоит. Одним из важных способов задания фигуры на плоскости является ее задание при помощи уравнений с двумя неизвестными. Произвольное уравнение с двумя неизвестными х и у записывается в виде

1. Если точка М(а,Ь) принадлежит фигуре Ф, то координаты (а,Ь) являются решениями уравнения
2. если пара чисел (c,d) является решением уравнения F(x,y) = 0, то точка N(c,d) принадлежит фигуре Ф.

Это определение в более компактной записи выглядит следующим образом. Уравнение называется уравнением фигуры, если , то есть (а, b) — решение уравнения F(x,y) = 0.

Из определения уравнения фигуры следует, что фигура Ф состоит только из тех точек плоскости, координаты которых являются решениями уравнения , т.е. уравнение фигуры задает эту фигуру.

Возможны два вида задач:

1. дано уравнение и надо построить фигуру Ф, уравнением которой является ;
2. дана фигура Ф и надо найти уравнение этой фигуры.

Первая задача сводится к построению графика уравнения и решается, чаще всего, методами математического анализа.

Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:

1. Задать фигуру геометрически, т.е. сформулировать условие, которому удовлетворяют только точки фигуры (довольно часто определение фигуры содержит такое условие);
2. Записать в координатах условие, сформулированное в первом пункте.

Эллипс

Эллипсом называется линия, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек , есть величина постоянная (большая, чем расстояние между ).

Точки называются фокусами эллипса. Обозначив расстояние между фокусами через 2с, а сумму расстояний от точек эллипса до фокусов через 2а, имеем с b. В этом случае а называется большой полуосью, a b — малой.

Если а =Ь, то уравнение (7.3) можно переписать в виде:

(7.5)

Это уравнение окружности с центром в начале координат. Эллипс (3) можно получить из окружности (4) сжатием плоскости к оси Ох. Пусть на плоскости выбрана прямоугольная система координат Оху. Тогда преобразование, переводящее произвольную точку М(х,у) в точку координаты которой задаются формулами будет окружность (4) переводить в эллипс, заданный соотношением

Число называется эксцентриситетом эллипса. Эксцентриситет характеризует форму эллипса: чем ближе к нулю, тем больше эллипс похож на окружность; при увеличении становится более вытянутым

Фокальными радиусами точки М эллипса называются отрезки прямых, соединяющие эту точку с фокусами . Их длины и задаются формулами Прямые называются директрисами эллипса. Директриса называется левой, а — правой. Так как для эллипса и, следовательно, левая директриса располагается левее левой вершины эллипса, а правая — правее правой вершины.

Директрисы обладают следующим свойством: отношение расстояния г любой точки эллипса от фокуса к ее расстоянию d до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е.

Гипербола

Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек есть величина постоянная (не равная нулю и меньшая, чем расстояние между ).

Точки называются фокусами гиперболы. Пусть по-прежнему расстояние между фокусами равно 2с. Модуль расстояний от точек гиперболы до фокусов обозначим через а. По условию, а 0) (рис. 9.7). Ось абсцисс проведём через фокус F перпендикулярно директрисе. Начало координат расположим посередине между фокусом и директрисой. Пусть А — произвольная точка плоскости с координатами (х, у) и пусть . Тогда точка А будет лежать на параболе, если r=d, где d- расстояние от точки А до директрисы. Фокус F имеет координаты .

Тогда А расстояние Подставив в формулу r=d, будем иметь. Возведя обе части равенства в квадрат, получим

или

(9.4.1)

Уравнение (9.4.1)- каноническое уравнение параболы. Уравнения также определяют параболы.

Легко показать, что уравнение , определяет параболу, ось симметрии которой перпендикулярна оси абсцисс; эта парабола будет восходящей, если а > 0 и нисходящей, если а О. Для этого выделим полный квадрат:

и сделаем параллельный перенос по формулам

В новых координатах преобразуемое уравнение примет вид: где р — положительное число, определяется равенством .

Пример:

Пусть заданы точка F и прямая у =-1 (рис. 9.8). Множество точек Р(х, y) для которых расстояние |PF| равно расстоянию, называется параболой. Прямая у = -1 называется директрисой параболы, а точка F — фокусом параболы. Чтобы выяснить, как располагаются точки Р, удовлетворяющие условию, запишем это равенство с помощью координат: , или после упрощения . Это уравнение геометрического места точек, образующих параболу (рис. 9.8).

Кривые второго порядка на плоскости

Кривой второго порядка называется фигура на плоскости, задаваемая в прямоугольной системе координат уравнением второй степени относительно переменных х и у:

где коэффициенты А, В и С не равны одновременно нулю

Любая кривая второго порядка на плоскости принадлежит к одному из типов: эллипс, гипербола, парабола, две пересекающиеся прямые, 2 параллельные прямые, прямая, точка, пустое множество.

Кривая второго порядка принадлежит эллиптическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют одинаковые знаки: АС>0.

Кривая второго порядка принадлежит гиперболическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют противоположные знаки: АС 2с. Точка М(х,у) принадлежит эллипсу тогда и только тогда, когда ее координаты удовлетворяют уравнению

которое называют каноническим уравнением эллипса.

Число а называют большей полуосью эллипса, число — мень-

шей полуосью эллипса, 2а и 2b — соответственно большей и меньшей осями эллипса. Точки называют вершинами эллипса, а — его фокусами (рис. 12).

Координатные оси являются осями симметрии эллипса, а начало координат — его центром симметрии. Центр симметрии эллипса называется центром эллипса.

Замечание. Каноническое уравнение эллипса можно рассматривать и в случае b>а. Оно определяет эллипс с большей полуосью b, фокусы которого лежат на оси Оу.

В случае а=b каноническое уравнение эллипса принимает вид и определяет окружность радиуса а с центром в начале координат.

Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большей оси.

Так, в случае а>b эксцентриситет эллипса выражается формулой:

Эксцентриситет изменяется от нуля до единицы и характеризует форму эллипса. Для окружности Чем больше эксцентриситет, тем более вытянут эллипс.

Пример:

Показать, что уравнение

является уравнением эллипса. Найти его центр, полуоси, вершины, фокусы и эксцентриситет. Построить кривую.

Решение:

Дополняя члены, содержащие х и у соответственно, до полных квадратов, приведем данное уравнение к каноническому виду:

— каноническое уравнение эллипса с центром в точке большей полуосью а=3 и меньшей полуосью

Найдем эксцентриситет эллипса:

Для вычисления вершин и фокусов удобно пользовать новой прямоугольной системой координат, начало которой находится в точке а оси параллельны соответственно осям Ох, Оу и имеют те же направления (осуществили преобразование параллельного переноса). Тогда новые координаты точки будут равны ее старым координатам минус старые координаты нового начала, т.е.

В новой системе координат координаты вершин и фокусов гиперболы будут следующими:

Переходя к старым координатам, получим:

Построим график эллипса.

Задача решена.

Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.

Так же, как и для эллипса, геометрическое свойство точек гиперболы выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину обозначим через 2а: 2а

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Урок 11

Директрисы эллиПса и гиПерболы.

Директрисы эллиПса и гиПерболы.

оПреДеление. Две Прямые, ПерПенДикулярные большой оси эллиПса и расПоложенные симметрично относительно центра на расстоянии а/e от него, называются Директрисами эллиПса (гДе а — большая Полуось эллиПса, e — эксцентриситет)

оПреДеление. Две Прямые, ПерПенДикулярные Действительной оси гиПерболы и расПоложенные симметрично относительно центра на расстоянии а/e от него, называются Директрисами гиПерболы (гДе а — Действительная Полуось, e — эксцентриситет)

уравнения Директрис эллиПса и гиПерболы имеют виД: х= ± а/e.

с Помощью Понятия Директрисы и эксцентриситета можно сформулировать общее свойство, Присущее эллиПсу и гиПерболе.

теорема. если r — расстояние от Произвольной точки м эллиПса (гиПерболы) До какого-нибуДь фокуса, d — расстояние от этой же точки До соответствующей этому фокусу Директрисы, то отношение r/d есть Постоянная величина, равная эксцентриситету эллиПса (гиПерболы).

Данное свойство можно Положить в основу общего оПреДеления этих линий: множество точек, Для которых отношение расстояний До фокуса и До соответствующей Директрисы является величиной Постоянной, равной e, есть эллиПс, если e 1.

возникает воПрос, что ПреДставляет собой множество точек, При условии e=1. оказывается, это новая линия второго ПоряДка, называемого Параболой.

оПреДеление. Параболой называется множество всех точек Плоскости, кажДая из которых нахоДится на оДинаковом расстоянии от Данной точки, называемой фокусом, и от Данной Прямой, называемой Директрисой и не ПрохоДящей через фокус.

Пусть м(х,у) — Произвольная точка Параболы. обозначим через r расстояние от точки м До фокуса f, через d — расстояние от точки м До Директрисы, а через P — расстояние от фокуса До Директрисы.

величину P называют Параметром Параболы. точка м лежит на Параболе, если r=P.

уравнение Параболы: у 2 =2Pх (каноническое уравнение).

исслеДуем форму Параболы По ее каноническому уравнению (Для не отрицательных значений у):

если х у 2 =2Pх у 2 =-2Pх х 2 =2Pу х 2 =-2Pу

Пример. Дано уравнение Параболы у 2 =6х. составьте уравнение ее Директрисы и найти коорДинаты фокуса.

решение. сравнивая Данное уравнение с каноническим уравнением Параболы, Получим, что 2р=6, откуДа р=3. так как фокус Параболы имеет коорДинаты (р/2;0), а Директриса — уравнение х=-р/2, то Для Данной Параболы Получаем: коорДинаты фокуса (1,5; 0) и уравнение Директрисы х=-1,5.

уПражнения .

1. составьте уравнение Параболы с вершиной в начале коорДинат и уравнение Директрисы Параболы, если известно, что осью симметрии является ось ох и что точка Пересечения Прямых у=х и у=2-х лежит на Параболе. (ответ: у 2 =х и х=-0,25)
2. Даны точки а(-1;0) и в(2;0). точка м(х;у) Движется так, что в треугольнике амв угол авм остается вДвое больше угла мав. оПреДелить траекторию точки м. (ответ: гиПербола)
3. Доказать, что если оси Двух Парабол взаимно ПерПенДикулярны и Параболы Пересекаются в четырех точках, то эти точки Пересечения лежат на оДной окружности.

Автор: Вяликова Мария Владимировна — учитель математики и информатики высшей квалификационной категории МАОУ Пролетарская СОШ Новгородского района Новгородской области

Две
прямые, перпендикулярные оси эллипса,
на которой расположены его фокусы, и
отстоящие от центра эллипса на расстоянии

,
где
а
— большая
полуось эллипса, а
е
— его
эксцентриситет, называются директрисами
эллипса.

Окружность,
для которой е
= 0 не имеет директрис

т.е. понятие директрис дается только
для эллипса.

Если
эллипс задан каноническим уравнением,
причем

(т.е. фокусы расположены на оси Ох)
то уравнения директрис имеют вид:

Так как

;
то
,
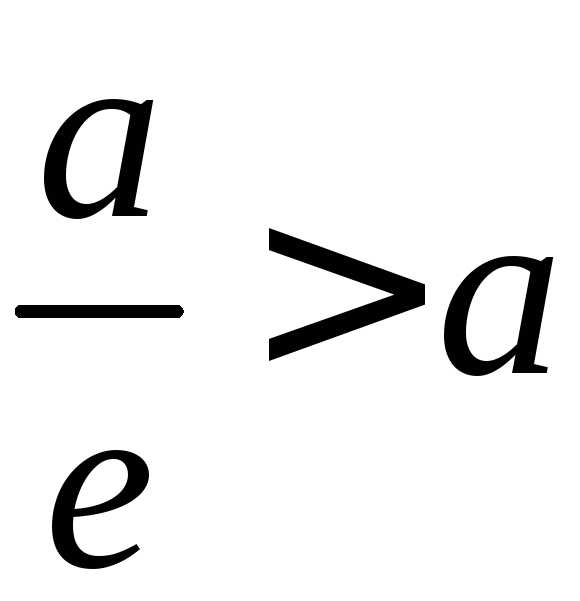
и, значит, директрисы эллипса отстоят
от его центра дальше, чем вершины (см.
рис.). Фокус и директриса эллипса,
расположенные по одну сторону от меньшей
оси эллипса, называются соответствующими
друг другу.

Таким
образом, фокусы
соответствует
директриса
,
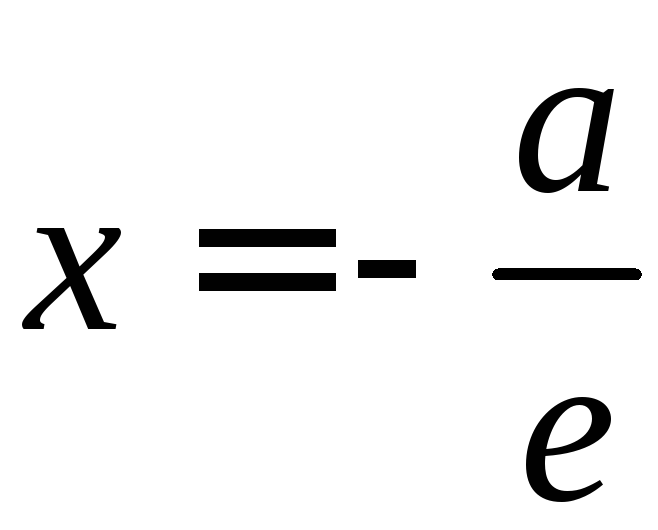
а фокусу
— директриса.

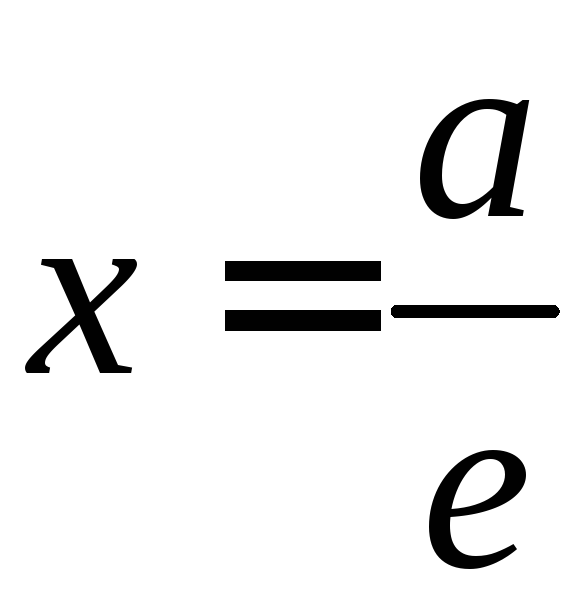
Теорема.
Для того чтобы точка лежала на эллипсе,
необходимо и достаточно, чтобы отношение
расстояния от этой точки до фокуса
эллипса к расстоянию от той же точки до
директрисы, соответствующей рассматриваемому
фокусу, было равно эксцентриситету
эллипса.

Доказательство:
Необходимость. Рассмотрим, например,
фокус
и соответствующую ему директрису.
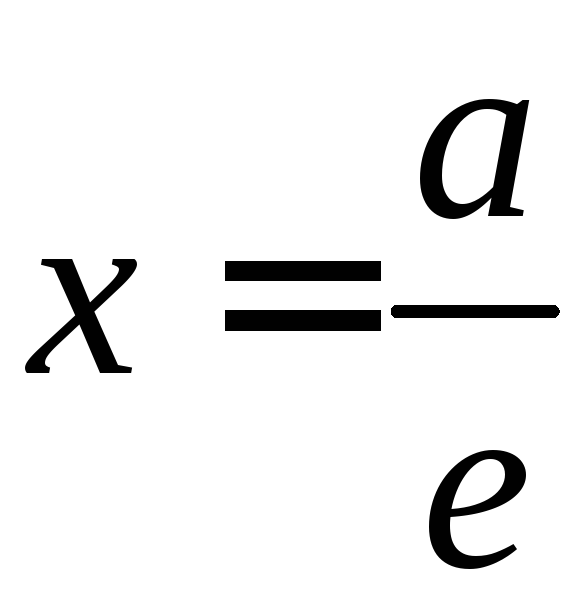
Расстояниеот точкиМ(х,
у)
до

ф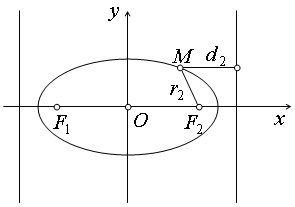окусавычисляется по формуле.

Расстояние
от той же точкиМ(х,
у)
эллипса до прямой
вычисляется по формуле.

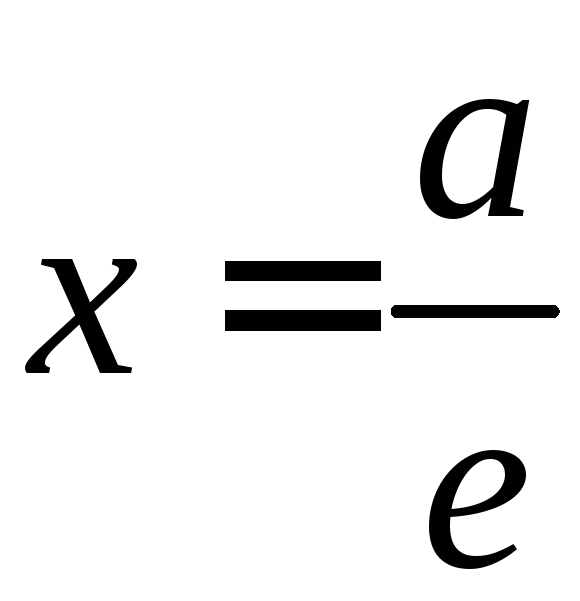
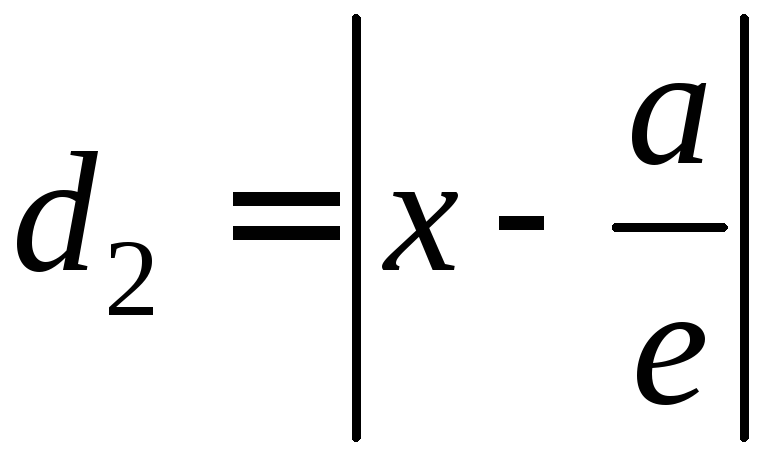
Итак:
.

Отсюда

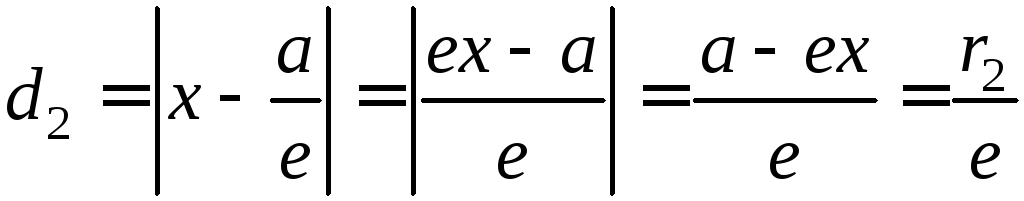
Теорема доказана.

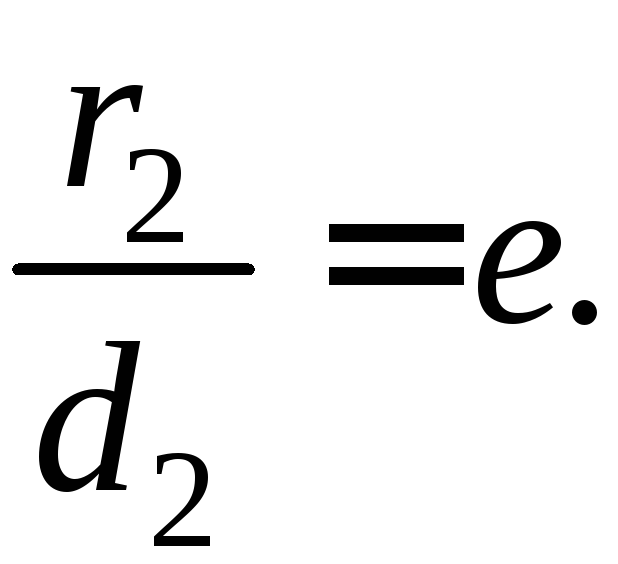
Аналогично
доказывается, что
,
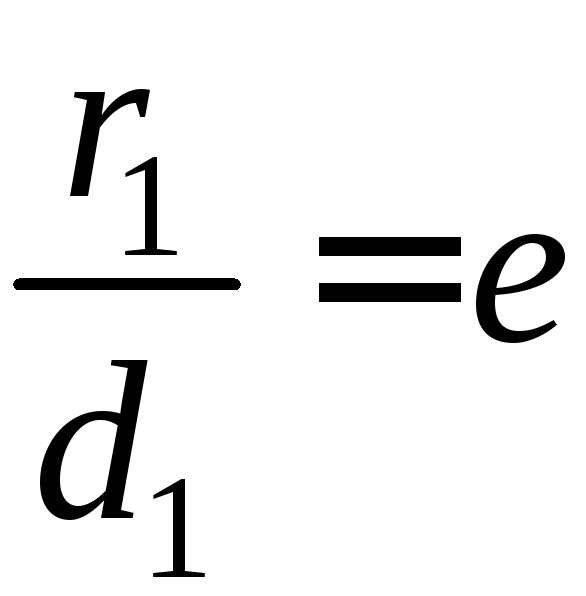
где,
есть расстояние от точкиМ
до фокуса
,
а— расстояние от той же точки до директрисы,
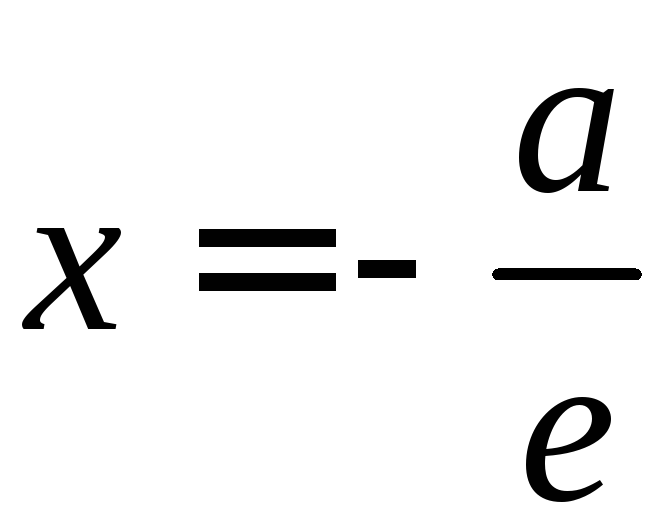
соответствующей фокусу.

Доказательство
достаточности.

Возьмем
каноническое уравнение эллипса, где a
>
b.
Рассмотрим, например, фокус
этого эллипса и соответствующую ему
директрису.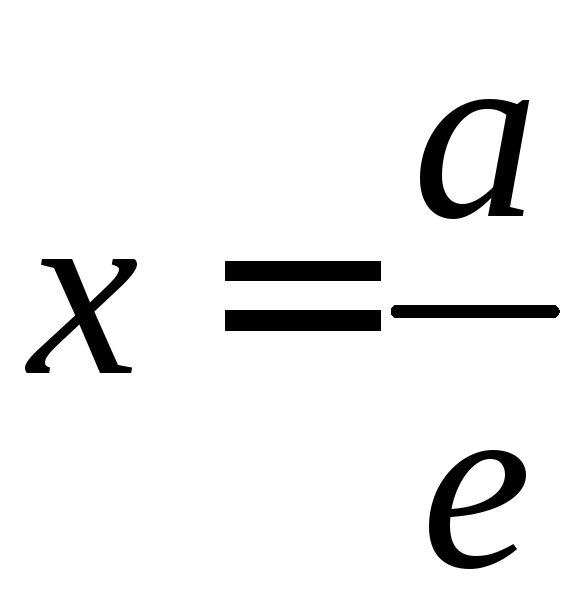

Пусть
М(х,
у)
такая точка, что

,

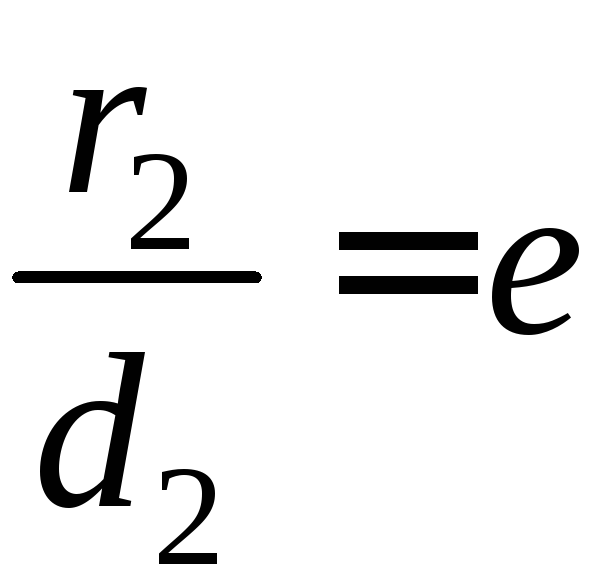
где
— расстояние от точкиМ
до фокуса
,
а— расстояние от точкиМ
до директрисы
.

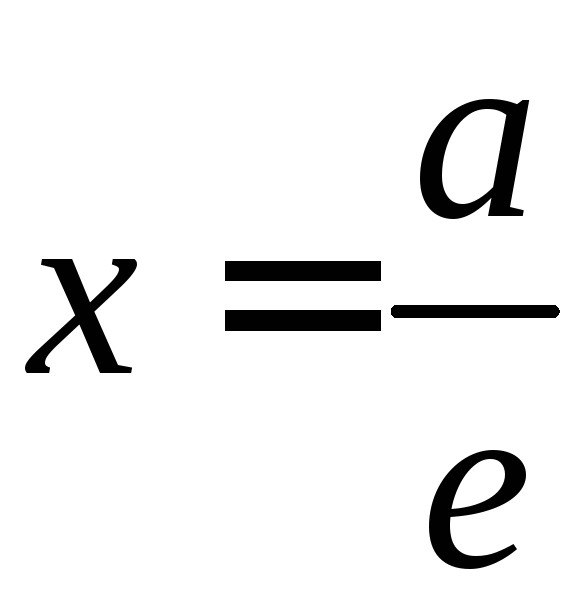
Докажем,
что точка М(х,у)
лежит на эллипсе.

В самом деле, т.к.

;

,

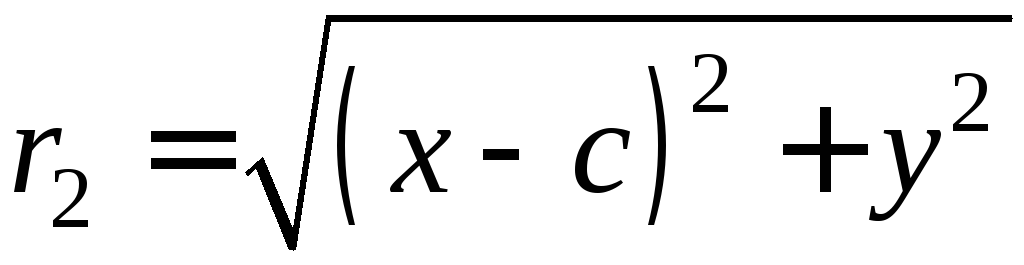
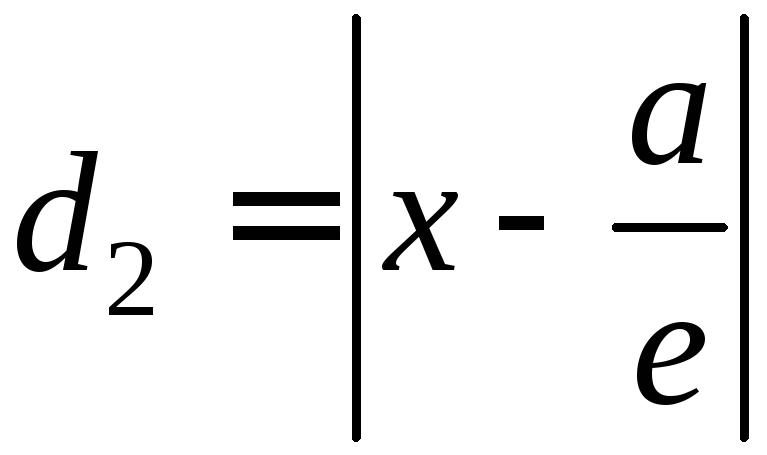
то из соотношения

или
,

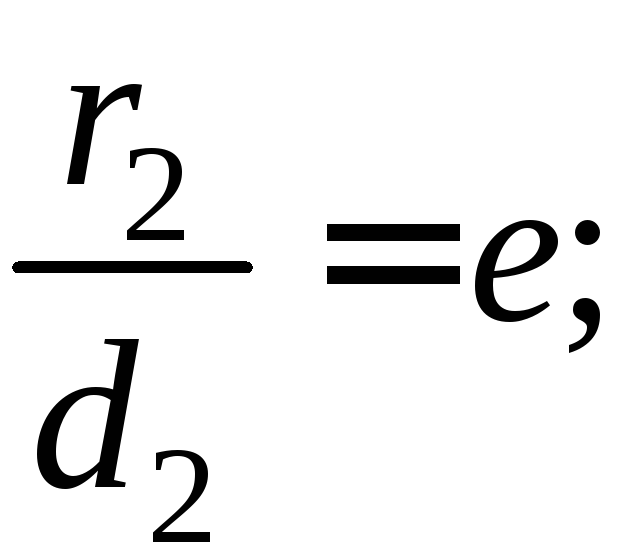
находим:

Упрощая
это уравнение, получим
.
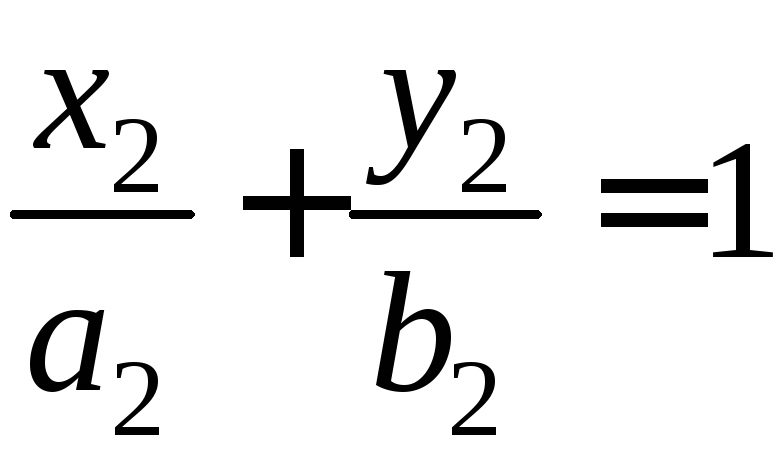
А это означает, что точкаМ(х,
у)
ежит на эллипсе.

Расстояние
m
от фокуса эллипса до его директрисы
равно

,

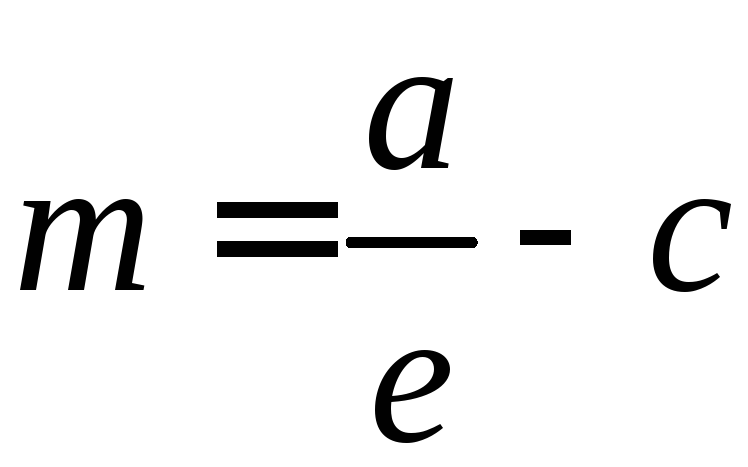
а эксцентриситет
определяется формулой:

.

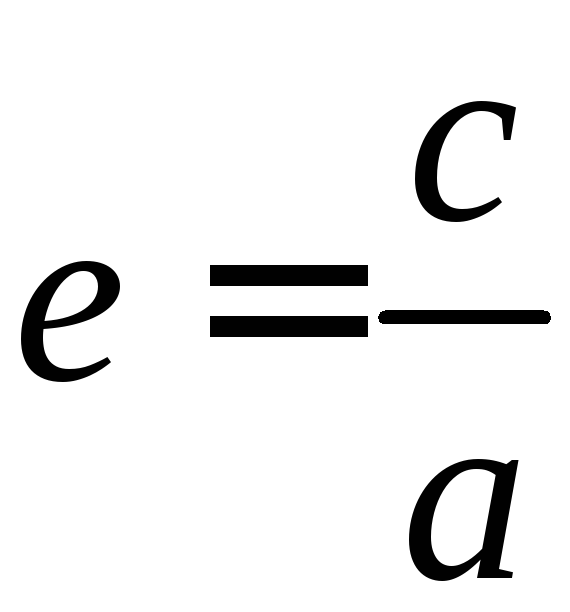
Из
этих соотношений находим

Отсюда
следует, что если на плоскости задана
произвольно точка
,
прямая, не проходящая через эту точку(отстоящая от точкина расстоянии
)
и задано произвольное положительное
число е,
меньшее 1, то существует эллипс, для
которого точка
— фокус, заданная прямая – директриса,
ае
—
эксцентриситет. Центр этого эллипса
находится на расстоянии

от точки
(по одну сторону с точкойот данной прямой), а большая полуось

Отсюда
и из только что доказанной теоремы
следует, что эллипс можно определить
как геометрическое место точек, для
каждой из которых отношение расстояния
от данной точки
к расстоянию до данной прямой,
не проходящей через точку,
равно данному положительному числу,
меньшему 1.

Исключением
является окружность, которая данным
свойством не обладает.

§ 106. Параметрические уравнения эллипса

Пусть
дан эллипс каноническим уравнением
.
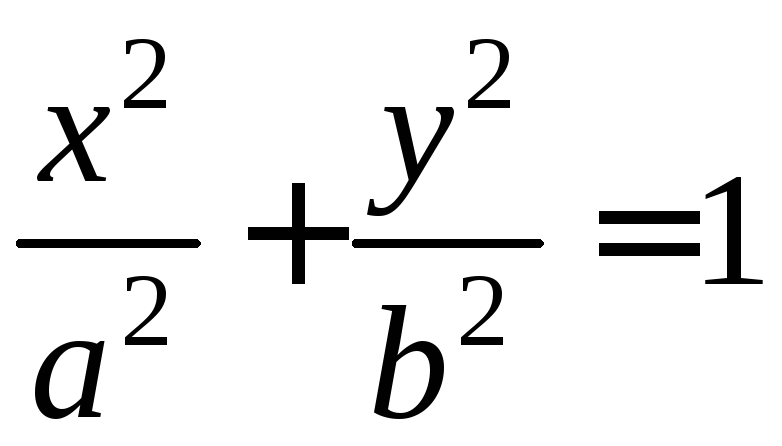
(1)

Рассмотрим
окружность

,
(2)

которая
переходит в данный эллипс в результате
сжатия

(3)

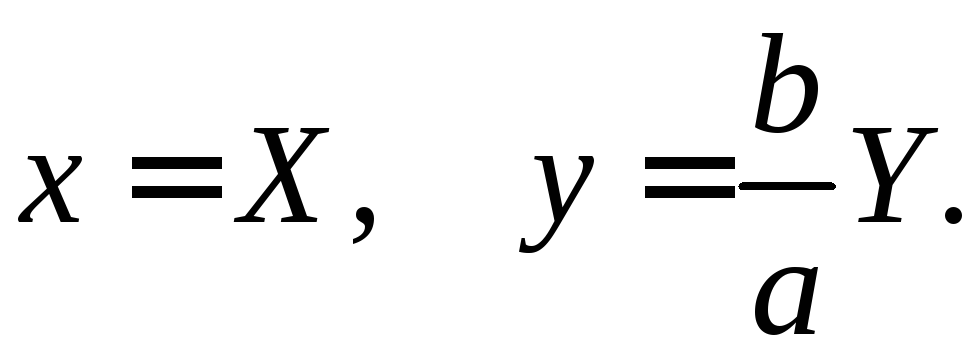
Пусть
М(х,
у)
– произвольная точка данного эллипса,
— ее образ на окружности. Обозначим черезугол от положительного направления осиОх
до луча ОР.

Тогда

и, следовательно,

.

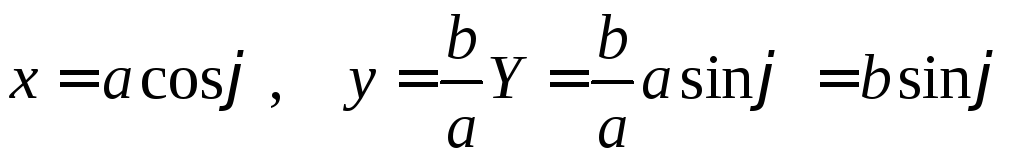
У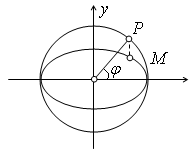равнения

И являются
параметрическими уравнениями эллипса.

Параметр
называется эксцентрическим углом точки
эллипса. Если задана точкаэллипса,
то для нахождениянадо построить
окружность на большей оси эллипса как
на диаметре и через точку М
провести прямую, параллельную малой
оси эллипса.

Точка
пересечения этой прямой с окружностью,
лежащая по ту же сторону от большей оси
эллипса, что и точкаМ,
является прообразом точки М(х,у)
при равномерном сжатии
Угол от осиОх
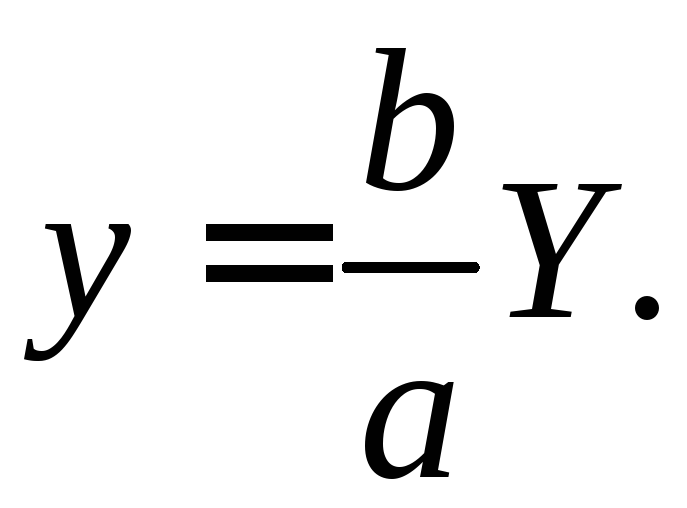
до луча ОР
и являются эксцентрическим углом
,
соответствующим взятой точкиМ
на эллипсе (см. рис.).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #



3.7.1. Директрисы эллипса

Да, они есть не только у параболы! – и эта прямая обрела тысячи горячих поклонников J.

…Ну что же, шалуны, завидуйте, у эллипса их две!

Директрисами эллипса называются две прямые, параллельные малой оси и отстоящие от неё на расстоянии , где  – большая полуось, а  – эксцентриситет данного эллипса.

Директрисы лежат вне эллипса и в каноническом положении  задаются

уравнениями . Для нашего героя :

Так и есть, первая директриса полностью совпала с прямой . Более того,

в условии задачи фактически сформулирован следующая теорема аналитической геометрии:

Эллипс – есть множество всех точек плоскости, таких, что отношение расстояния до каждой точки от фокуса к расстоянию от неё до соответствующей

(ближайшей) директрисы равно эксцентриситету:
То есть, для любой точки  эллипса отношение её расстояния до фокуса  к расстоянию от неё же до ближайшей директрисы  в точности равно эксцентриситету:

Со вторым фокусом и директрисой история аналогичная, какую бы точку  эллипса мы ни взяли – будет справедливо отношение: .

И не забываем об ответе: искомое геометрическое место точек представляет собой  эллипс   с фокусами , эксцентриситетом  и директрисами  , .

Похожий пример для самостоятельного решения:

Задача 108

Найти уравнение геометрического места точек, для каждой из которых отношение расстояния до точки  к расстоянию до прямой  постоянно и

равно . Выполнить чертеж. Привести уравнение линии к каноническому виду,

найти фокусы, эксцентриситет, асимптоты и директрисы, если они существуют.

Повышаем техническую сложность и знакомимся с новым материалом:

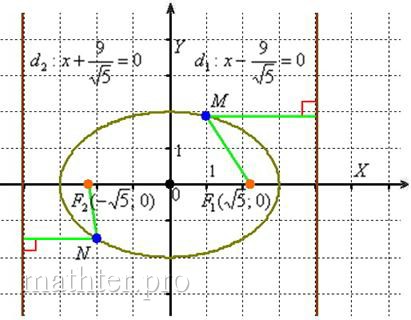
Задача 109

Составить уравнение линии, для каждой из которых разность расстояний до точек  и  по модулю равна 8. Привести уравнение

к каноническому виду и выполнить чертёж. Найти асимптоты, фокусы, эксцентриситет и директрисы, если они существуют.

…здесь уже из условия понятно, о какой кривой идёт речь

Решение: пусть точка  принадлежит искомой линии.

Тогда:

По условию,   или:

Корни? Модуль? Застрелитесь! Ерунда!

От модуля избавляемся немедленно:

Теперь нужно избавиться от радикалов. Возводить в квадрат сразу – идея плохая (можете попробовать), поэтому разведём корни по углам

ринга:

Ну вот, теперь совсем другое дело, возводим обе части в квадрат:

Успехи есть, но один корень остался, да ещё и со знаком «+–». Оставим нашего зловреда в одиночестве и максимально упростим левую часть

уравнения:

Возводим в квадрат обе части ещё раз, и заметьте, как попутно и совершенно спокойно исчезает знак «+–»:

Перебросим всё направо и «развернём» уравнение:

Получено уравнение линии 2-го порядка в общем виде. Выделяем полный квадрат при переменной «игрек»,

для этого вынесем «минус девять» за скобку:

Далее внутри скобки искусственно добавляем +25 (в целях применения формулы на следующем шаге) и, чтобы уравнение не изменилось, за скобками нужно прибавить :

Хорошо осмыслите выполненное действие! – фишка распространённая.

Собираем квадрат разности и допиливаем константы:

Вот тебе и раз. По всем признакам мыльная опера должна была закончиться гиперболой , но у нас «лишний» минус. Выполним проверку и раскроем скобки (что желательно сделать в любом

случае)… нет, всё верно – получается исходное общее уравнение .

Изменим знаки у обеих частей:

Уже ближе к правде, но «минус» оказался «не на своём месте». Из параграфа о повороте и переносе гиперболы вспоминаем, что это означает поворот данной кривой на 90 градусов относительно своего канонического положения.

Но давайте сначала доведём до ума уравнение. Делим обе части на 144:

и завершающий тонкий тюнинг:

 – получены «хорошие» значения полуосей – отличный признак!
 – вот она, долгожданная гипербола, удовлетворяющая условию задачи,

которое фактически представляет собой… определение гиперболы!

Едем дальше:

По условию требуется сначала привести уравнение к каноническому виду, и только потом выполнить чертёж. Дабы не

превысить точку кипения серого вещества, применим упрощенную схему. Однако случай всё равно не самый простой. Центр симметрии нашей подопечной

находится в точке , и, кроме того, она повёрнута на 90 градусов вокруг

этой точки

В «чайниковском» способе сначала удобно осуществить параллельный перенос линии  в начало координат: . И

только потом повернуть гиперболу на 90 градусов по часовой стрелке (относительно начала

координат), при этом значения полуосей меняются местами, а знак «минус» переносится к переменной «игрек»: .

Если же сначала повернуть гиперболу вокруг точки , то уравнение

запишется в виде , и после переноса получится тот же результат .

Не забывая про асимптоты ,

выполним чертёж:

Ещё раз, где изначально расположена гипербола? В точке  (центр симметрии), ветви направлены вверх и вниз. И если по условию вам требуется построить график  , то руководствуйтесь разобранным

ранее алгоритмом.

Но работать гораздо удобнее с приведённым уравнением. Найдём фокусы:
 – самостоятельно проанализируйте, что в неканоническом положении фокусы

находятся в точках .

Вычислим эксцентриситет:

3.7.2. Директрисы гиперболы

3.7. Задачи с линиями второго порядка

| Оглавление |



Автор: Aлeксaндр Eмeлин