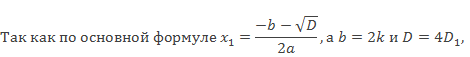Содержание:
- § 1 Понятие квадратного уравнения
- § 2 Решение квадратных уравнений
- § 3 Решение квадратного уравнения по формуле с четным вторым коэффициентом
- § 4 Краткие итоги урока
§ 1 Понятие квадратного уравнения
В этом уроке выведем формулы для решения квадратных уравнений с чётным вторым коэффициентом и научимся решать такие квадратные уравнения, используя эти формулы.
Квадратным уравнением называют уравнение вида ax2 + bx +c=0, где a называют первым или старшим коэффициентом, b – вторым коэффициентом или коэффициентом при х, с – свободным членом, х – переменная, причём a ≠ 0.
Чтобы решить квадратное уравнение, необходимо найти дискриминант D по формуле
D = b2 – 4ac
Если в квадратном уравнении коэффициент b- четное число, то это уравнение можно представить в виде ax2 + 2kx + c=0, где b=2k, k – целое число.
§ 2 Решение квадратных уравнений
Выведем формулы для решения квадратного уравнения с четным вторым коэффициентом. Для этого в основную формулу для решения квадратного уравнения вместо второго коэффициента b подставим 2k.
Найдем дискриминант.
D = b2 – 4ac = (2k)2 – 4ac = 4k2 – 4ac.
Вынесем за скобки 4 и получим D = 4(k2 – ac).
Обозначим выражение в скобках за D1. Тогда D1 = k2 – ac, а D = 4D1.
Видно, что число корней уравнения зависит от D1. Если D1 больше нуля, то уравнение имеет два корня.
Разделим числитель и знаменатель на 2. После всех преобразований формула примет вид
Корни х1 и х2 зависят только от знака квадратного корня в числителе, поэтому
А если дискриминант D1 равен нулю? Уравнение будет иметь один корень.
Вместо коэффициента b подставим 2k.
§ 3 Решение квадратного уравнения по формуле с четным вторым коэффициентом
Рассмотрим решение квадратного уравнения 5х2 –16 х + 3 = 0 как по основной формуле, так и по формуле с четным вторым коэффициентом. А затем сделаем некоторые выводы.
Итак, сначала выпишем коэффициенты a = 5, b= –16, с = 3.
Найдем дискриминант D по формуле D = b2 – 4ac.
Подставив в неё значения коэффициентов, получим D= (–16)2 – 4 ∙ 5 ∙ 3 = 196,дискриминант больше нуля D>0, значит, уравнение имеет два корня, используя соответствующие формулы, вычисляем:
Так как коэффициент b= –16 четное число, то можно решить это уравнение по формулам решения квадратного уравнения с четным вторым коэффициентом.
В нашем уравнении 5х2 –16х + 3 = 0, k = –16:2= –8.
Найдем дискриминант D1.
D1 = k2 –ac= (–8)2 – 5 ∙ 3 = 49, он больше нуля D1 >0, уравнение имеет два корня, которые находим по соответствующим формулам:
Заметим, что корни получились одинаковые х1 = 0,2; х2 = 3.
Однако есть преимущества в использовании формул решения квадратного уравнения с четным вторым коэффициентом.
Во-первых, при нахождении дискриминанта в квадрат возводится не число b, не второй коэффициент, а его половина и вычитается из этого квадрата не 4ac, а просто ac
Во-вторых, при нахождении корней в знаменателе не 2a, а просто a.
В-третьих, дискриминант, находимый по формуле с четным вторым коэффициентом, то есть D1, в 4 раза меньше дискриминанта D.
Если квадратное уравнение с четным вторым коэффициентом b=2k и с коэффициентом a= 1, т.е. является приведенным x2 + 2kx +c=0, то решить уравнение можно ещё проще. Находим дискриминант по формуле D1 = k2 – c.
Если он больше нуля D1 >0, то корни находим по формулам:
Если дискриминант равен нулю D1=0, то будет один корень х = –k.
Рассмотрим решение квадратного уравнения х2 +10 х–5600 = 0 как по основной формуле, так и по формуле решения квадратного уравнения с четным вторым коэффициентом, являющееся приведенным.
Выпишем коэффициенты a = 1, b= 10, с = – 5600.
Найдем дискриминант D по формуле D = b2 – 4ac.
D = (10)2 – 4 ∙ 1 ∙ (–5600) = 22500, D > 0, дискриминант положительный, значит, уравнение имеет два корня, используя соответствующие формулы, получим значения корней:
Так как коэффициент b = 10 четное число, то можно решить это уравнение по формуле решения квадратного уравнения с четным вторым коэффициентом. Заметим, что в уравнении коэффициент a=1.
Уравнение является приведенным.
k = 10 : 2 = 5.
Найдем дискриминант D1.
§ 4 Краткие итоги урока
Важно запомнить:
Если квадратное уравнение ax2 + bx + c = 0 с четным вторым коэффициентом, то есть второй коэффициент можно представить в виде b = 2k, k – целое число, то уравнение лучше решить по соответствующим формулам. При решении поступают следующим образом:
1.Находят дискриминант D1 по формуле D1 = k2 – ac. Значение дискриминанта зависит от коэффициентов a, k , с.
2.Сравнивают дискриминант D1 с нулём.
3.Если дискриминант больше нуля, то уравнение ax2 + 2kx +c=0 имеет два корня
Если дискриминант меньше нуля, корней нет.
4.Если квадратное уравнение ax2 + bx + c = 0 с четным вторым коэффициентом и является приведенным x2 + 2kx + c = 0, коэффициенты a= 1, b = 2k, k – целое число, то уравнение решают следующим образом:
1)Находят дискриминант D1 по формуле D1 = k2 – c.
2)Сравнивают дискриминант D1 с нулём.
3)Если дискриминант больше нуля, то уравнение x2 + 2kx +c=0 имеет два корня
Если дискриминант равен нулю, то х = –k.
Если дискриминант меньше нуля, корней нет.
Список использованной литературы:
- Макарычев Ю.Н., Н.Г. Миндюк, Нешков К.И., Суворова С.Б., под редакцией Теляковского С.А. Алгебра: учебник для 8 кл. общеобразоват. учреждений. — М.: Просвещение, 2013.
- Мордкович А.Г. Алгебра. 8 кл.: В двух частях. Ч.1: Учеб. для общеобразоват. учреждений. — М.: Мнемозина.
- Рурукин А.Н. Поурочные разработки по алгебре: 8 класс.- М.: ВАКО, 2010.
- Алгебра 8 класс: поурочные планы по учебнику Ю.Н. Макарычева, Н.Г. Миндюк, К.И. Нешкова, С.Б. Суворовой/ Авт.-сост. Т.Л. Афанасьева, Л.А. Тапилина. – Волгоград: Учитель, 2005.
Как найти дискрименант
В школьной программе часто приходится сталкиваться с решением квадратного уравнения типа: ax² + bx + c = 0, где а, b — первый и второй коэффициенты квадратного уравнения, с — свободный член. С помощью значения дискриминанта можно понять, есть ли у уравнения решения или нет, а если есть, то сколько.

Инструкция
Как найти дискриминант? Существует формула его нахождения: D = b² — 4ac. При этом, если D > 0, уравнение имеет два действительных корня, которые вычисляются по формулам:
x1 = (-b + VD)/2a,
x2 = (-b — VD)/2a,
где V означает квадратный корень.
Чтобы понять формулы в действии, решите несколько примеров.
Пример: x² — 12x + 35 = 0, в данном случае а = 1, b — (-12), а свободный член с — + 35. Найдите дискриминант: D = (-12)^2 — 4*1*35 = 144 — 140 = 4. Теперь найдите корни:
X1 = (-(-12) + 2)/2*1 = 7,
x2 = (-(-12) — 2)/2*1 = 5.
При а > 0, x1 < x2, при a < 0, x1 > x2, что означает если дискриминант больше нуля: существуют вещественные корни, график квадратичной функции пересекает ось ОX в двух местах.
Если D = 0, то решение одно:
x = -b/2a.
Если второй коэффициент квадратного уравнения b представляет собой четное число, то целесообразно найти дискриминант, деленный на 4. При этом формула примет следующий вид:
D/4 = b²/4 — ac.
Например, 4x^2 — 20x + 25 = 0, где a = 4, b = (- 20), с = 25. При этом D = b² — 4ac = (20)^2 — 4*4*25 = 400-400 = 0. Квадратный трехчлен имеет два равных корня, найдем их по формуле x = -b/2a = — (-20)/2*4 = 20/8 = 2,5. Если дискриминант равен нулю, значит существует один вещественный корень, график функции пересекает ось OX в одном месте. При этом, если а > 0, график располагается выше оси OX, а если a < 0, ниже этой оси.
При D < 0 вещественных корней не существует. Если дискриминант меньше нуля, значит не существует вещественных корней, а только комплексные корни, график функции не пересекает ось ОX. Комплексные числа — расширение множества вещественных чисел. Комплексное число можно представить как формальную сумму x + iy, где x и y — вещественные числа, i — мнимая единица.
Обратите внимание
В уравнении вида ax²+bx+c=0 необходимым условием является неравенство а нулю.
Если а равно единице, то уравнение называют приведенным.
Если а не равно одному, то -неприведенным. Если один из коэффициентов b, с или оба равны , то квадратное уравнение называется неполным
Источники:
- если дискриминант равен 1
- Квадратные уравнения на Сёзнайке
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Квадратные уравнения решаются по формулам Виета и способом Дискриминанта(D). Начнём с того что мы должны понять как выглядит квадратное уравнение.
ax²+bx+c.
a, b и c — это какие либо цифры. а Всегда стоит перед x², b стоит перед x, а c-это свободные член и он стоит без всего(то есть просто цифра). Почему мы должны запомнить перед кем они стоят, а не просто их последовательность? Все просто, они могут стоят и в другом порядке, то есть:
bx+ax²+c.
Если бы мы просто запомнили что первое-это а второе b, а третье с, то мы бы сделали ошибку.
Теперь перейдём к самим формулам. D(Дискриминант это вспоминающий элемент) давайте его вычислим:
D=b²-4*a*c
Опять повторю, место a, b и c должны быть цифры!
После того как мы все это вычалили, у нас получается число.
Если число D:
D > 0, то уравнение имеет 2 различных корня!
D = 0, то уравнение имеет 1 корень!
D < 0, то уравнение не имеет корней!
Допустим у нас получилось что D > 0, то вычислим корни.
x₁=(-b+√D)/(2*a)
x₂=(-b-√D)/(2*a)
Вот и все, только запомните, что если D=0, корень 1.
Что такое квадратные уравнения?
А теперь подробно с примерами обсудим квадратные уравнения.
Любые уравнения, сводящиеся к виду (ax^2+bx+c=0), называются квадратными. Где буквы ( b,; с) — любые числа, (aneq0). Почему (aneq0) мы обсудим ниже.
Обратите внимание на порядок слагаемых в квадратном уравнении:
(a) — всегда стоит первая и обязательно умножается на (x^2), она называется старшим коэффициентом (или первым);
(b) — принадлежит второму слагаемому и всегда умножается просто на переменную (x), это у нас второй коэффициент;
(c) — называют свободным членом, она не умножается ни на какую переменную.
В дальнейшем старайтесь приводить квадратное уравнение к виду (ax^2+bx+c=0), чтобы слагаемые стояли именно в таком порядке. Это очень важно при решении уравнений, и поможет избежать множества ошибок.
Потренируемся определять значения коэффициентов ( a, ; b,; с), чтобы запомнить порядок:
Пример 1
$$2x^2+3x+4=0;$$
$$a=2 quad b=3 quad c=4.$$
Пример 2
$$5x^2-3x-0,7=0;$$
$$a=5 quad b=-3 quad c=-0,7.$$
Пример 3
$$-x^2+2x+10=0;$$
Минус перед (x^2) можно представить в виде (-x^2=-1*x^2). Единицу обычно не пишут, поэтому минус перед первым слагаемым означает, что (a=-1):
$$a=-1 quad b=2 quad c=10.$$
Пример 4
$$3+x^2-5x=0;$$
Слагаемые стоят в неправильном порядке. Так коэффициенты находить неудобно, поэтому переставим все слагаемые в нужном порядке. От перемены мест слагаемых сумма не меняется:
$$x^2-5x+3=0;$$
$$a=1 quad b=-5 quad c=3.$$
Пример 5
$$2x^2-3x=0;$$
В уравнении нет свободного члена (c), поэтому он будет равен (0):
$$a=2 quad b=-3 quad c=0.$$
Пример 6
$$-4x^2+1=0;$$
А здесь уже нет второго коэффициента (b):
$$a=-4 quad b=0 quad c=1.$$
Уравнения, приведенные в примерах №5 и 6, называются неполными квадратными уравнениями, так как в них коэффициенты (b) или (c) равны нулю.
А вот если в уравнении коэффициенты ( a, ; b,; с) не равны 0, то такое уравнение называется полным.
От того, полное ли квадратное уравнение или неполное, зависит, как мы будем его решать. Начнем с неполных уравнений, они немного легче, но почему-то как раз в них все часто ошибаются.
Неполные квадратные уравнения
Неполное квадратное уравнение — это уравнение, в котором один из коэффициентов (b) или (c) равен нулю, (aneq0).
Как решать квадратное уравнение (ax^2+bx=0)?
Рассмотрим уравнение, в котором (c=0), оно будет иметь вид:
$$ax^2+bx=0;$$
Чтобы его решить, нужно вынести общий множитель (x) за скобки:
$$x(ax+b)=0;$$
И вспомнить правило, что произведение равно нулю, когда хотя бы один из множителей равен нулю. Здесь два множителя: (x) и ((ax+b)). Приравниваем их к нулю и решаем каждое по-отдельности:
$$x=0;$$
Тут решать-то нечего, сразу дан корень.
Второе:
$$ax+b=0;$$
Обычное линейное уравнение:
$$ax=-b;$$
$$x=frac{-b}{a};$$
Получили, что уравнение имеет сразу два корня:(x=0) и (x=frac{-b}{a}).
Разберем на примере:
Пример 7
$$2x^2+8x=0;$$
Выносим общий множитель (x):
$$x(2x+8)=0;$$
$$quad x_1=0 quad и quad 2x+8=0;$$
$$2x+8=0;$$
$$2x=-8;$$
$$x_2=-4.$$
Ответ: (x_1=0 quad и quad x_2=-4.)
Как решать квадратное уравнение (ax^2+с=0)?
Вот с такими уравнениями надо быть очень внимательными. Важно помнить, что любое число (выражение), возведенное в квадрат, всегда больше или равно нуля, оно не может быть отрицательным.
Общая схема решения уравнений вида (ax^2+с=0):
- Выражаем (x^2) из уравнения:
$$ax^2+c=0;$$
$$ax^2=-c;$$
$$x^2=frac{-c}{a};$$ -
Если (-frac{c}{a} geq 0):
$$x_1=sqrt{-frac{c}{a}};$$
$$x_2=-sqrt{-frac{c}{a}};$$ -
Если (-frac{c}{a} lt 0):
РЕШЕНИЙ НЕТ.
Пример 8
$$2x^2-8=0;$$
$$2x^2=8;$$
$$x^2=frac{8}{2};$$
$$x^2=4;$$
$$x=pmsqrt{4};$$
$$x_1=2;$$
$$x_2=-2;$$
Ответ: (x_1=2 quad и quad x_2=-2.)
Пример 9
$$4x^2+36=0;$$
$$2x^2=-36;$$
$$x^2=frac{-36}{2}=-18;$$
Так как (-18 < 0), а (x^2) не может быть отрицательным, то это уравнение не имеет корней.
Ответ: Нет корней.
Пример 10
$$frac{1}{2}x^2-frac{1}{18}=0;$$
$$frac{1}{2}x^2=frac{1}{18};$$
Чтобы избавиться от (frac{1}{2}), умножим уравнение слева и справа на (2):
$$x^2=frac{2}{18};$$
$$x^2=frac{1}{9};$$
$$x=pmsqrt{frac{1}{9}};$$
$$x_1=frac{1}{3};$$
$$x_2=-frac{1}{3};$$
Ответ: (x_1=frac{1}{3} quad и quad x_2=-frac{1}{3}.)
Решение квадратных уравнений через дискриминант
Квадратные уравнения (ax^2+bx+c=0), у которых все коэффициенты ( a, ; b,; с) не равны 0, называются полными квадратными уравнениями.
Чтобы их решать, нужно уметь находить дискриминант квадратного уравнения. Ничего страшного в этом нет, несмотря на странное называние. Дискриминантом уравнения (ax^2+bx+c=0) называют выражение:
$$D=b^2-4ac;$$
- Если дискриминант получился больше нуля ((D ge 0)), то квадратное уравнение имеет два корня, которые можно найти по формулам:
$$x_1=frac{-b+sqrt{D}}{2a};$$
$$x_2=frac{-b-sqrt{D}}{2a};$$ - Если дискриминант равен нулю ((D=0)), то квадратное уравнение имеет один корень:
$$x=frac{-b}{2a};$$ - Если дискриминант меньше нуля ((D<0)), то квадратное уравнение не имеет корней.
Примеры квадратных уравнений
Пример 11
$$2x^2-9x+4=0;$$
Прежде чем решать уравнение, я рекомендую выписать все коэффициенты:
$$a=2 quad b=-9 quad c=4.$$
Используя значения коэффициентов, можем посчитать дискриминант:
$$D=b^2-4ac=(-9)^2-4*2*4=81-32=49;$$
Ура, дискриминант посчитан и он больше нуля! Значит корней будет два, найдем их по формулам:
$$x_1=frac{-b+sqrt{D}}{2a}=frac{-(-9)+sqrt{49}}{2*2}=frac{9+7}{4}=frac{16}{4}=4;$$
$$x_2=frac{-b-sqrt{D}}{2a}=frac{-(-9)—sqrt{49}}{2*2}=frac{9-7}{4}=frac{2}{4}=frac{1}{2};$$
Ответ: (x_1=4 quad и quad x_2=frac{1}{2}.)
Пример 12
$$10x^2+x-21=0;$$
$$a=10 quad b=1 quad c=-21.$$
$$D=b^2-4ac=1^2-4*10*(-21)=1+840=841;$$
$$x_1=frac{-b+sqrt{D}}{2a}=frac{-1+sqrt{841}}{2*10}=frac{-1+29}{20}=frac{28}{20}=frac{7}{5};$$
$$x_2=frac{-b-sqrt{D}}{2a}=frac{-1-sqrt{841}}{2*10}=frac{-1-29}{20}=frac{-30}{20}=frac{-3}{2};$$
Ответ: (x_1=frac{7}{5} quad и quad x_2=-frac{3}{2}.)
Пример 13
$$(x-7)^2=2x^2+11x+23;$$
Это уравнение еще нужно привести к стандартному виду, для этого раскроем скобки по формуле «квадрат разности» ((a-b)^2=a^2-2ab+b^2):
$$x^2-14x+49=2x^2+11x+23;$$
Перекинем все слагаемые в левую часть, не забывая при этом менять знак на противоположный:
$$x^2-14x+49-2x^2-11x-23=0;$$
Приводим подобные слагаемые:
$$-x^2-25x+26=0;$$
$$a=-1 quad b=-25 quad c=26.$$
$$D=b^2-4ac=(-25)^2-4*(-1)*26=625+104=729;$$
$$x_1=frac{-b+sqrt{D}}{2a}=frac{-(-25)+sqrt{729}}{2*(-1)}=frac{25+27}{-2}=frac{52}{-2}=-26;$$
$$x_2=frac{-b-sqrt{D}}{2a}=frac{-(-25)-sqrt{729}}{2*(-1)}=frac{25-27}{-2}=frac{-2}{-2}=1;$$
Ответ: (x_1=-26 quad и quad x_2=1.)
Пример 14
$$3x^2+7x+6=0;$$
$$a=3 quad b=7 quad c=6.$$
$$D=b^2-4ac=7^2-4*3*6=49-72=-23;$$
Стоп! Дискриминант получился отрицательный, это означает, что у этого квадратного уравнения не будет корней.
Ответ: Нет корней.
Пример 15
$$4x^2-4x+1=0;$$
$$a=4 quad b=-4 quad c=1.$$
$$D=b^2-4ac=(-4)^2-4*4*1=16-16=0;$$
Дискриминат получился равен нулю. В этом случае у квадратного уравнения будет всего один корень, который можно найти по формуле:
$$x=frac{-b}{2a}=frac{-(-4)}{2*4}=frac{4}{8}=frac{1}{2};$$
Ответ: (x=frac{1}{2}.)
Полезно знать! Если дискриминант получился равен нулю, то перед вами формула полного квадрата. Это значит, что квадратный многочлен можно разложить по формуле ((apm b)^2=a^2pm 2ab+b^2).
И пример №15 можно решить, используя эту формулу:
$$4x^2-4x+1=0;$$
$$(2x-1)^2=0;$$
Квадрат равен нулю только в том случае, если выражение под квадратом равно нулю:
$$2x-1=0;$$
$$2x=1;$$
$$x=frac{1}{2};$$
Ответ получили точно такой же, как и при решении через дискриминант.
Дискриминант деленный на 4
Квадратные уравнения иногда удобно решать по упрощенной формуле дискриминанта. Но применять ее можно не во всех случаях, а только, если коэффициент (b) в уравнении (ax^2+bx+c=0) четный (делится на 2).
Итак, представим, что коэффициент (b) четный, тогда дискриминант можно посчитать по формуле:
$$D_4=left(frac{b}{2}right)^2-ac;$$
А корни уравнения находятся по формулам:
$$x_1=frac{-frac{b}{2}+sqrt{D_4}}{a};$$
$$x_2=frac{-frac{b}{2}-sqrt{D_4}}{a};$$
Кстати, обычный дискриминант (D) отличается от (D_4) в 4 раза:
$$D_4=frac{D}{4}=frac{b^2-4ac}{4}=frac{b^2}{4}-frac{4ac}{4}=left(frac{b}{2}right)^2-ac;$$
Поэтому (D_4) называют «дискриминантом деленным на 4».
Эти формулы нужны, чтобы, когда это возможно, сократить вычисления. Разберем на примере:
Пример 16
$$7x^2-20x-1067=0;$$
$$a=7 quad b=-20 quad c=-1067.$$
(b=-20) — четный, поэтому воспользуемся дискриминантом деленным на 4:
$$D_4=left(frac{b}{2}right)^2-ac=left(frac{-20}{2}right)^2-7*(-1067)=(-10)^2+7469=100+7469=7569;$$
$$x_1=frac{-frac{b}{2}+sqrt{D_4}}{a}=frac{-frac{-20}{2}+sqrt{7569}}{7}=frac{10+87}{7}=frac{97}{7};$$
$$x_2=frac{-frac{b}{2}-sqrt{D_4}}{a}=frac{-frac{-20}{2}-sqrt{7569}}{7}=frac{10-87}{7}=frac{-77}{7}=-11;$$
Ответ: (x_1=frac{97}{7} quad и quad x_2=-11.)
Возникает вопрос, зачем вообще нужен этот (D_4), если все можно считать через обычный дискриминант? Если бы мы считали пример №16 как обычно, то наш дискриминант, который и так получился не маленьким — ((D_4=7659)), был бы в четыре раза больше. А чем больше числа, тем сложнее расчеты.
Теорема Виета для решения квадратных уравнений
Теорема Виета — это еще один способ упростить решение полных квадратных уравнений. Ее очень часто используют для решения несложных квадратных уравнений в уме и для анализа квадратного многочлена, особенно это актуально в сложных заданиях с параметром в ЕГЭ.
Прежде чем сформулировать теорему Виета, познакомимся с приведенными квадратными уравнениями.
Приведенное квадратное уравнение
Квадратные уравнения (ax^2+bx+c=0), у которых коэффициент (a) при (x^2) равен (1), называют приведенными.
Например:
$$x^2+4x-3=0;$$
$$x^2-140x-65=0;$$
Любое полное квадратное уравнение всегда можно свести к приведенному. Для этого надо поделить все уравнение на коэффициент (a):
Пример 17
Привести квадратное уравнение к приведенному.
$$3x^2-15x+9=0;$$
Разделим уравнение на (a=3). (Так можно делать: если левую и правую части уравнения поделить на одно и то же число, то корни уравнения от этого не изменятся.)
$$frac{3x^2-15x+9}{3}=frac{0}{3};$$
В результате каждое слагаемое поделится на (3):
$$frac{3x^2}{3}-frac{15x}{3}+frac{9}{3}=0;$$
$$x^2-5x+3=0;$$
Формулы Виета
Сумма корней приведенного квадратного уравнения (x^2+bx+c=0) равна второму коэффициенту (b) со знаком минус, а произведение корней равно свободному члену (c).
Пусть (x_1), и (x_2) — корни квадратного уравнения (x^2+bx+c=0), тогда справедливы формулы:
$$ begin{cases}
x_1+x_2=-b; \
x_1*x_2=c. \
end{cases}$$
На первый взгляд может показаться, что это очень запутанно, но на самом деле, теорема Виета часто помогает решить уравнение в уме. Попробуем на практике:
Пример 18
$$x^2+4x+3=0;$$
$$a=1 quad b=4 quad c=3.$$
Воспользуемся теоремой Виета и выпишем формулы:
$$ begin{cases}
x_1+x_2=-b; \
x_1*x_2=c. \
end{cases}$$
Подставим коэффициенты:
$$ begin{cases}
x_1+x_2=-4; \
x_1*x_2=3. \
end{cases}$$
Нужно найти такие (x_1) и (x_2), которые удовлетворяют и первому, и второму уравнениям в системе. Подобрать корни достаточно просто: рассмотрим второе уравнение, какие два числа дают при умножении (3ку)?
Либо: (3=1*3);
Либо: (3=(-1)*(-3)).
Осталось проверить, будут ли найденные множители удовлетворять первому уравнению в системе, просто подставим их:
$$1+3 neq -4;$$
$$-1+(-3) = -4;$$
Вот мы и нашли корни системы уравнений: (x_1=-1) и (x_2=-3). А самое главное, мы нашли корни исходного квадратного уравнения.
Ответ: (x_1=-1 quad и quad x_2=-3.)
Если потренироваться, то все эти вычисления можно легко проводить в уме, если коэффициенты небольшие. Главное запомнить, что произведение корней должно быть равно свободному члену (c), а сумма корней равна ((-b)).
Теорема Виета, если (aneq1)
По теореме Виета можно решать не только приведенные квадратные уравнения (у которых (a=1)). Но перед тем, как применять формулы Виета, надо привести уравнение к приведенному, поделив на первый коэффициент (a):
$$ax^2+bx+c=0; quad mid :a$$
$$frac{ax^2}{a}+frac{bx}{a}+frac{c}{a};$$
$$x^2+frac{b}{a}*x+frac{c}{a};$$
Получили приведенное квадратное уравнение, для которого можно записать формулы Виета, где вторым коэффициентом будет (frac{b}{a}), а свободным членом (frac{c}{a}):
$$ begin{cases}
x_1+x_2=-frac{b}{a}; \
x_1*x_2=frac{c}{a}. \
end{cases}$$
Пример 19
$$12x^2+x-1=0;$$
$$a=12 quad b=1 quad c=-1.$$
Коэффициент (a=12 neq 1), поэтому разделим все уравнение на (a=12):
$$12x^2+x-1=0; quad mid :12$$
$$x^2+frac{1}{12}x-frac{1}{12}=0;$$
$$a=1 quad b=frac{1}{12} quad c=-frac{1}{12}.$$
Теорема Виета:
$$ begin{cases}
x_1+x_2=-frac{1}{12}; \
x_1*x_2=-frac{1}{12}. \
end{cases}$$
Подбираем корни:
$$x_1=-frac{1}{3};$$
$$x_2=frac{1}{4};$$
Ответ: (x_1=-frac{1}{3} quad и quad x_2=frac{1}{4}.)
Теорема Виета удобна, когда у квадратного уравнения небольшие коэффициенты и можно легко подобрать корни. В остальных случаях лучше пользоваться дискриминантом.