Решение квадратных уравнений
6 июля 2011
Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.
Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0.
Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:
- Не имеют корней;
- Имеют ровно один корень;
- Имеют два различных корня.
В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант.
Дискриминант
Пусть дано квадратное уравнение ax2 + bx + c = 0. Тогда дискриминант — это просто число D = b2 − 4ac.
Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:
- Если D < 0, корней нет;
- Если D = 0, есть ровно один корень;
- Если D > 0, корней будет два.
Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:
Задача. Сколько корней имеют квадратные уравнения:
- x2 − 8x + 12 = 0;
- 5x2 + 3x + 7 = 0;
- x2 − 6x + 9 = 0.
Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8)2 − 4 · 1 · 12 = 64 − 48 = 16
Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 32 − 4 · 5 · 7 = 9 − 140 = −131.
Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6)2 − 4 · 1 · 9 = 36 − 36 = 0.
Дискриминант равен нулю — корень будет один.
Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.
Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.
Корни квадратного уравнения
Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:
Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D < 0, корней нет — ничего считать не надо.
Задача. Решить квадратные уравнения:
- x2 − 2x − 3 = 0;
- 15 − 2x − x2 = 0;
- x2 + 12x + 36 = 0.
Первое уравнение:
x2 − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2)2 − 4 · 1 · (−3) = 16.
D > 0 ⇒ уравнение имеет два корня. Найдем их:
Второе уравнение:
15 − 2x − x2 = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2)2 − 4 · (−1) · 15 = 64.
D > 0 ⇒ уравнение снова имеет два корня. Найдем их
[begin{align} & {{x}_{1}}=frac{2+sqrt{64}}{2cdot left( -1 right)}=-5; \ & {{x}_{2}}=frac{2-sqrt{64}}{2cdot left( -1 right)}=3. \ end{align}]
Наконец, третье уравнение:
x2 + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 122 − 4 · 1 · 36 = 0.
D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:
[x=frac{-12+sqrt{0}}{2cdot 1}=-6]
Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.
Неполные квадратные уравнения
Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:
- x2 + 9x = 0;
- x2 − 16 = 0.
Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:
Уравнение ax2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.
Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.
Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax2 + c = 0. Немного преобразуем его:
Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c/a) ≥ 0. Вывод:
- Если в неполном квадратном уравнении вида ax2 + c = 0 выполнено неравенство (−c/a) ≥ 0, корней будет два. Формула дана выше;
- Если же (−c/a) < 0, корней нет.
Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c/a) ≥ 0. Достаточно выразить величину x2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.
Теперь разберемся с уравнениями вида ax2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:
Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:
Задача. Решить квадратные уравнения:
- x2 − 7x = 0;
- 5x2 + 30 = 0;
- 4x2 − 9 = 0.
x2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x1 = 0; x2 = −(−7)/1 = 7.
5x2 + 30 = 0 ⇒ 5x2 = −30 ⇒ x2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.
4x2 − 9 = 0 ⇒ 4x2 = 9 ⇒ x2 = 9/4 ⇒ x1 = 3/2 = 1,5; x2 = −1,5.
Смотрите также:
- Теорема Виета
- Следствия из теоремы Виета
- Тест на тему «Значащая часть числа»
- Метод коэффициентов, часть 1
- Однородные тригонометрические уравнения: общая схема решения
- Задача B4: строительные бригады
в котором хотя бы один из коэффициентов b или c равен нулю. Следовательно, неполное квадратное уравнение может иметь вид:
Чтобы решить уравнение вида ax 2 + bx = 0 , надо разложить левую часть уравнения на множители, вынеся x за скобки:
Произведение может быть равно нулю только в том случае, если один из множителей равен нулю, значит:
Неполные квадратные уравнения вида ax 2 + bx = 0, где b ≠ 0, решаются разложением левой части на множители. Такие уравнения всегда имеют два корня, один из которых равен нулю.
Пример 1. Решите уравнение:
Пример 2. Решите уравнение:
Чтобы решить уравнение вида ax 2 + c = 0 , надо перенести свободный член уравнения c в правую часть:
В этом случае уравнение не будет иметь корней, так как квадратный корень нельзя извлечь из отрицательного числа.
Если данное неполное уравнение будет иметь вид x 2 — c = 0 , то сначала опять переносим свободный член в правую часть и получаем:
Неполное квадратное уравнение вида ax 2 + c = 0, где c ≠ 0, либо не имеет корней, либо имеет два корня, которые являются противоположными числами.
Пример 1. Решите уравнение:
Пример 2. Решите уравнение:
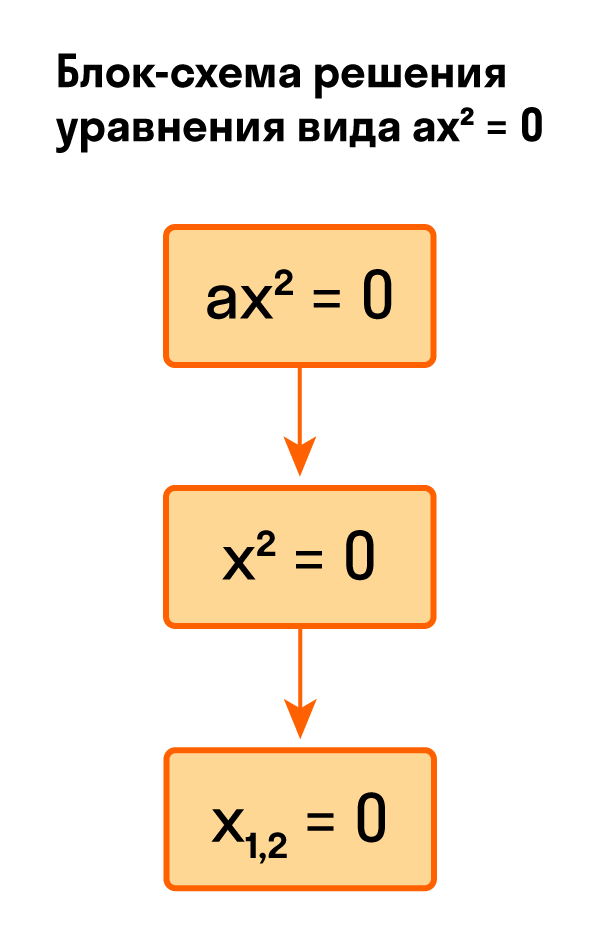
Уравнение вида ax 2 = 0 всегда имеет только один корень: x = 0. Так как a ≠ 0, то из ax 2 = 0 следует, что x 2 = 0, значит, и x = 0. Любое другое значение x не будет являться корнем данного уравнения.
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Степень уравнения можно определить по наибольшей степени, в которой стоит неизвестное. Если неизвестное стоит во второй степени — это квадратное уравнение.
Квадратное уравнение — это ax² + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.
Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b² − 4ac. А вот свойства дискриминанта:
Неполное квадратное уравнение — это уравнение вида ax² + bx + c = 0, где хотя бы один из коэффициентов b или c равен нулю.
- Если b = 0, то квадратное уравнение принимает вид ax² + 0x+c=0 и оно равносильно ax² + c = 0.
- Если c = 0, то квадратное уравнение выглядит так ax² + bx + 0 = 0, иначе его можно написать как ax² + bx = 0.
- Если b = 0 и c = 0, то квадратное уравнение выглядит так ax² = 0.
Такие уравнения отличаются от полного квадратного тем, что их левые части не содержат слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения.
Решение неполных квадратных уравнений
Как мы уже знаем, есть три формулы неполных квадратных уравнений:
- ax² = 0, ему отвечают коэффициенты b = 0 и c = 0;
- ax² + c = 0, при b = 0;
- ax² + bx = 0, при c = 0.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).
Как решить уравнение ax² = 0
Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax² = 0.
Уравнение ax² = 0 равносильно x² = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x² = 0 является нуль, так как 0² = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.
Таким образом, неполное квадратное уравнение ax² = 0 имеет единственный корень x = 0.
Пример 1. Решить −5x² = 0.
- Замечаем, что данному уравнению равносильно x2 = 0, значит исходное уравнение имеет единственный корень — нуль.
- По шагам решение выглядит так:
Записывайся на дополнительные уроки по математике онлайн, с нашими лучшими преподавателями! Для учеников с 1 по 11 класса!
Как решить уравнение ax² + с = 0
Обратим внимание на неполные квадратные уравнения вида ax² + c = 0, в которых b = 0, c ≠ 0. Мы знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный.
Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. То есть одно и то же, только с другими цифрами.
Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax² + c = 0:
- перенесем c в правую часть: ax² = — c,
- разделим обе части на a: x² = — c/а.
Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи.
Если — c/а 0, то корни уравнения x² = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а)² = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а)² = — c/а. Ура, больше у этого уравнения нет корней.
В двух словах
Неполное квадратное уравнение ax² + c = 0 равносильно уравнению ax² + c = 0, которое:
- не имеет корней при — c/а 0.
Пример 1. Найти решение уравнения 9x² + 4 = 0.
- Перенесем свободный член в правую часть:
Разделим обе части на 9:
Ответ: уравнение 9x² + 4 = 0 не имеет корней.
Пример 2. Решить -x² + 9 = 0.
- Перенесем свободный член в правую часть:
Разделим обе части на -1:
Ответ: уравнение -x² + 9 = 0 имеет два корня -3; 3.
Как решить уравнение ax² + bx = 0
Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.
Квадратное уравнение без с непривычно решать только первые несколько примеров. Запомнив алгоритм, будет значительно проще щелкать задачки из учебника.
Неполное квадратное уравнение ax² + bx = 0 можно решить методом разложения на множители. Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x.
Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.
Таким образом, неполное квадратное уравнение ax² + bx = 0 имеет два корня:
Пример 1. Решить уравнение 2x² — 32x = 0
- Вынести х за скобки
Ответ: х = 0 и х = 16.
Пример 2. Решить уравнение 3x² — 12x = 0
Разложить левую часть уравнения на множители и найти корни:
Формула нахождения корней неполного квадратного уравнения
В алгебре при решении задач возникает необходимость найти корни неполного квадратного уравнения, формулы которых требуется выводить. Этот процесс занимает время. Математики позаботились об оптимизации вычислений и предлагают специальные методики для расчетов. Однако перед их использованием нужно изучить теорию.
Общие сведения
Уравнением квадратного вида (квадратичной функцией) называется выражение, состоящее из неизвестных (переменных) и известных (констант) величин, основным условием которого является наличие второй степени при неизвестном значении. Математическая запись имеет такой вид: Mt^2+Nt+C=0, где М, N и С — некоторые константы.
Корнем квадратичного тождества называются такие значения переменных, которые обращают его в истинное равенство. Иными словами, при подстановке величин, полученных при его решении, правая часть равенства эквивалентна левой. Для правильного применения алгоритма поиска корней нужно знать классификацию квадратичных функций с переменными.
Классификация квадратных уравнений
Математики классифицируют квадратичные многочлены с переменными на два вида. К ним относятся следующие:
Первая группа включает все три константы (М, N и С). Вторая группа делится на три типа:
- Без коэффициента перед неизвестной первой степени (N), но с наличием С.
- Без С, но N включен в равенство.
- Без N и С.
В первом случае уравнение записывается в таком виде: Mt^2+Nt+C=0. Если коэффициент N отсутствует, то запись видоизменится таким образом: Mt^2+С=0. При этом достаточно сократить обе части на константу перед переменной, возведенной во вторую степень. Когда отсутствует постоянный коэффициент «С», то выражение записывается в такой форме: Mt^2+Nt=0. Для решения достаточно разложить его на множители, что приведет к понижению степени.
Однако наиболее интересный случай — наличие только компонента «Mt^2». Этот тип решается очень просто, поскольку переменная всегда равна нулевому значению. Хотя в некоторых заданиях она имеет сложную структуру, то есть M(t+1)^2. Пример сводится к полному квадратному уравнению и решается стандартным способом. Далее необходимо разобрать основные методики решения полных и неполных квадратичных функций.
Полные типы
В случаях когда квадратичная функция содержит все элементы (Mt^2+Nt+C=0), к ней можно применить три методики нахождения корней. К ним относятся следующие:
- Формулы корней через величину дискриминанта.
- Теорема Виета.
- Разложение на множители.
Далее требуется разобрать каждый из случаев подробно, а также ознакомиться с методикой решения тождества квадратичной формы с переменными.
Соотношения для определения корней
Формулы позволяют решать полные квадратные уравнения, используя новую величину, которая называется дискриминантом. Она обозначается латинской литерой «D» и раcчитывается по следующей формуле: D=(-N)^2-4МС. Следует отметить, что при подсчете возможны такие варианты значений D:
- D 1: переменная может принимать два значения.
В последнем случае корни необходимо находить по двум формулам: t1=[-N-(D)^0.5]/(2M) и t1=[-N+(D)^0.5]/(2M). Алгоритм решения имеет следующий вид:
- Написать квадратичное тождество с переменными.
- Произвести математические преобразования.
- Определить D и проанализировать его величину, которая показывает количество решений или их отсутствие.
- Рассчитать корни по формулам.
- Проверить найденные величины на четвертом шаге алгоритма, подставив их в исходное уравнение.
- Отсеять ложные значения, то есть числа, приводящие к пустому множеству.
Однако не во всех случаях рекомендуется использовать способ нахождения корней посредством этих соотношений. Для этих целей математики предлагают использовать одно утверждение, называемое теоремой Виета.
Теорема Виета
Коэффициент при старшей степени может быть равен единице, то есть t^2+Nt+C=0. В этом случае необязательно определять величину D, высчитывая ее по формулам. Существует способ намного проще. Он основан на определении корней при помощи теоремы Виета, которая имеет два положения (условия):
- Сумма t1 и t2 равна N, взятому с противоположным знаком.
- Произведение t1 и t2 эквивалентно константе «С».
Алгоритм решения уравнения квадратичной формы существенно упрощается. Он имеет следующий вид:
- Записать тождество.
- Решить систему, состоящую из двух выражений, или методом подбора значений переменных (в основном используется последний вариант).
- Записать результат.
- Выполнить проверку, подставив корни в исходное выражение.
Во втором пункте нужно использовать два условия суммы и произведения корней. Однако существует метод, который проще теоремы Виета и определения переменных по формулам.
Разложение на множители
Методика разложения квадратичной функции на простые множители применяется не только при нахождении корней, но и во многих задачах. Суть ее состоит в использовании формул сокращенного умножения для понижения степенного показателя при переменной. Соотношения разложения на множители, необходимые для решения квадратных уравнений, имеют такой вид:
- Выделение квадрата: математические преобразования для образования соответствующих множителей, которые возможно вынести за скобку или записать в виде формулы сокращенного умножения.
- Разность квадратов двух величин: t^2-m^2=(t-m)(t+m).
- Квадрат суммы 2 числовых значений: (t+m)^2=(t+m)(t+m)=t^2+2t+m^2.
- Квадратичная разность двух чисел: (t-m)^2=(t-m)(t-m)=t^2-2t+m^2.
Для подробной иллюстрации первого соотношения нужно разобрать пример выражения: t^2+2t+1=0. Для выделения квадрата необходимо в левой части прибавить и отнять единицу, то есть t^2+2t+1+(1-1)=0. Следует отметить, что равенство не поменяется, поскольку 1-1=0. Результат имеет такой вид: (t+1)^2-1=0. Последнее соотношение — формула разности, то есть (t+1-1)(t+1+1)=0.
Неполные квадратичные функции
Квадратичные функции неполного вида с неизвестными встречаются в физико-математических дисциплинах достаточно часто. Вычислить значения их корней можно двумя способами:
- Разложить на множители.
- Через дискриминант.
В основном используется первый метод при решении уравнений, поскольку второй добавляет больше вычислений. При использовании дискриминанта нужно дополнительно его рассчитывать, а затем подставлять в соответствующие соотношения. Однако необходимо знать о двух способах решения, а также уметь их применять на практике.
Вынесение компонентов
Методика разложения на множители, позволяющая решать неполные квадратные уравнения, простая и эффективная. Она выполняется по двум направлениям, которые зависят от самих коэффициентов. В первом случае необходимо рассмотреть тождество «Mt^2+С=0». Алгоритм нахождения его корней имеет следующий вид:
- 5t^2-125=0.
- 5(t^2-25)=0.
- t^2-25=0.
- t^2-25=(t-5)(t+5)=0.
- t1=-5 и t2=5. Подстановка: 5*(-5)^2-125=0 и 5*(5)^2-125=0. Корни являются истинными значениями, так как не превращают равенство в пустое множество.
Решить квадратное уравнение без «С» (Mt^2+Nt=0) также просто, поскольку в этом случае необходимо воспользоваться определенной методикой. Она имеет такой вид:
- Вынести при необходимости за скобку константу, которая является общим множителем: M[t^2+(N/M)t]=0.
- Сократить обе части равенства на «М»: t^2+(N/M)t=0.
- Вынести «t»: t[t+(N/M)]=0.
- Решить оба уравнения: t1=0 и t2=-N/M.
- Выполнить проверку, подставив решения в исходное выражение.
Далее нужно разобрать нахождение корней уравнения 2t^2-2t=0 при помощи описанной методики. Ее практическая реализация имеет такой вид:
Следует отметить, что при использовании метода разложения квадратного тождества с переменными на множители, происходит понижение степени. Этот подход можно применить и к выражениям с высшими показателями.
Вычисление дискриминанта
Решение неполного уравнения квадратичной формы через дискриминант осуществляется таким же образом, как и с полным. В формулу подставляются значения коэффициентов и рассчитывается величина «D». Затем вычисляются корни равенства.
Однако существует небольшая поправка для тождества такого типа: t1=(-N-(D)^0.5)/М и t2=(-N+(D)^0.5)/М. Алгоритм для примера «t^2-9=0» выглядит таким образом:
Существуют различные вариации тождеств, но вся методика сводится к подстановочным операциям в соответствующие формулы через дискриминант.
Таким образом, неполные квадратные уравнения решаются двумя способами, но оптимальный из них — разложение на множители для понижения степени при неизвестной.
источники:
http://skysmart.ru/articles/mathematic/nepolnye-kvadratnye-uravneniya
http://na5.club/matematika/formula-nahozhdeniya-kornej-nepolnogo-kvadratnogo-uravneniya.html
Квадратным уравнением называется уравнение вида ax2+bx+c=0, где х – переменная, a, b, c некоторые числа, причем a≠0. Обычно его называют полным квадратным уравнением.
Если в таком уравнении один из коэффициентов b или c равен нулю, либо оба одновременно равны нулю, то такое уравнение называется неполным квадратным уравнением.
Неполное квадратное уравнение при b=0: ax2+c=0
Для решения такого вида уравнения надо выполнить перенос коэффициента с в правую часть, затем найти квадрат переменной (делим обе части на одно и то же число), найти два корня уравнения, либо доказать, что корней нет (если х2 равен отрицательному коэффициенту; знаем, что квадрат любого числа равен только положительному числу).
Пример №1. Решить уравнение:
5х2–45=0
Выполним перенос числа –45 в правую часть, изменяя знак на противоположный: 5х2=45; найдем переменную в квадрате, поделив обе части уравнения на 5: х2=9. Видим, что квадрат переменной равен положительному числу, поэтому уравнение имеет два корня, находим их устно, извлекая квадратный корень из числа 9, получим –3 и 3. Оформляем решение уравнения обычным способом:
5х2–45=0
5х2=45
х2=9
Ответ: х=±3 или можно записать ответ так: х1=–3, х2=3 (обычно меньший корень записывают первым).
Пример №2. Решить уравнение:
–6х2–90=0
Выполним решение уже известным способом: –6х2=90. х2=–15 Здесь видим, что квадрат переменной равен отрицательному числу, а это значит, что уравнение не имеет корней. Ответ: нет корней.
Пример №3. Решить уравнение:
х2–100=0
Здесь мы видим в левой части уравнения формулу сокращенного умножения (разность квадратов двух выражений). Поэтому, можем разложить данное выражение на множители, и найти корни уравнения: (х–10)(х+10)=0. Соответственно, вспомним, что произведение двух множителей равно нулю тогда, когда хотя бы один из множителей равен нулю, то есть х–10=0 или х+10=0. Откуда имеем два корня х1=10, х2=–10.
Неполное квадратное уравнение при с=0: ax2+bx=0
Данного вида уравнение решается способом разложения на множители – вынесением за скобки переменной. Данное уравнение всегда имеет два корня, один из которых равен нулю. Рассмотрим данный способ на примерах.
Пример №4. Решить уравнение:
х2+8х=0
Выносим переменную х за скобки: х(х+8)=0. Получаем два уравнения х=0 или х+8=0. Отсюда данное уравнение имеет два корня – это 0 и –8.
Пример №5. Решить уравнение:
3х2–12х=0
Здесь кроме переменной можно вынести за скобки еще и коэффициент 3, который является общим множителем для данных в уравнении коэффициентов. Получим: 3х(х–4)=0. Получаем два уравнения 3х=0 и х–4=0. Соответственно и два корня – нуль и 4.
Неполное квадратное уравнение с коэффициентами b и с равными нулю: ax2=0
Данное уравнение при любых значениях коэффициента а будет иметь один корень, равный нулю.
Пример №6. Решить уравнение:
–14х2=0
Обе части уравнения делим на (–14) и получаем х2=0, откуда соответственно и единственный корень – нуль.
Пример №6. Решить уравнение:
23х2=0
Также делим обе части на 23 и получаем х2=0. Значит, корень уравнения – нуль.
Даниил Романович | Просмотров: 8.7k
Например, для трехчлена (3x^2+2x-7), дискриминант будет равен (2^2-4cdot3cdot(-7)=4+84=88). А для трехчлена (x^2-5x+11), он будет равен ((-5)^2-4cdot1cdot11=25-44=-19).
Дискриминант обозначается буквой (D) и часто используется при решении квадратных уравнений. Также по значению дискриминанта можно понять, как примерно выглядит график квадратичной функции (см. ниже).
Дискриминант и корни квадратного уравнения
Значение дискриминанта показывает количество корней квадратного уравнения:
— если (D) положителен – уравнение будет иметь два корня;
— если (D) равен нулю – только один корень;
— если (D) отрицателен – корней нет.
Это не надо учить, к такому выводу несложно прийти, просто зная, что квадратный корень из дискриминанта (то есть, (sqrt{D}) входит в формулу для вычисления корней квадратного уравнения: (x_{1}=)(frac{-b+sqrt{D}}{2a}) и (x_{2}=)(frac{-b-sqrt{D}}{2a}). Давайте рассмотрим каждый случай подробнее.
Если дискриминант положителен
В этом случае корень из него – это некоторое положительное число, а значит (x_{1}) и (x_{2}) будут различны по значению, ведь в первой формуле (sqrt{D}) прибавляется, а во второй – вычитается. И мы имеем два разных корня.
Пример: Найдите корни уравнения (x^2+2x-3=0)
Решение:
|
(x^2+2x-3=0) |
Выписываем коэффициенты: |
|
|
(a=1;) (b=2;) (c=-3;) |
Вычисляем дискриминант по формуле (D=b^2-4ac) |
|
|
(D=2^2-4cdot1cdot(-3)=) |
Найдем корни уравнения |
|
|
(x_{1}=)(frac{-2+sqrt{16}}{2cdot1})(=)(frac{2}{2})(=1) (x_{2}=)(frac{-2-sqrt{16}}{2cdot1})(=)(frac{-6}{2})(=-3) |
Получили два различных корня из-за разных знаков перед (sqrt{D}) |
Ответ: (x_{1}=1); (x_{2}=-3)
На графике квадратичной функции положительный дискриминант будет означать пересечение функции с осью икс ровно в двух точках – корнях уравнения. И это логично. Вдумайтесь – если уравнение (x^2+2x-3=0) имеет корни (x_{1}=1) и (x_{1}=-3), значит при подстановке (1) и (-3) вместо икса, левая часть станет нулем. А значит, если те же самые единицу и минус тройку подставить в функцию (y=x^2+2x-3) получим (y=0). То есть, функция (y=x^2+2x-3) проходит через точки ((1;0)) и ((-3;0)) (подробнее смотри статью Как построить график функции).

Если дискриминант равен нулю
А сколько корней будет, если дискриминант равен нулю? Давайте рассуждать.
Формулы корней выглядят так: (x_{1}=)(frac{-b+sqrt{D}}{2a}) и (x_{2}=)(frac{-b-sqrt{D}}{2a}). И если дискриминант – ноль, то и корень из него тоже ноль. Тогда получается:
(x_{1}=)(frac{-b+sqrt{D}}{2a})(=)(frac{-b+sqrt{0}}{2a})(=)(frac{-b+0}{2a})(=)(frac{-b}{2a})
(x_{2}=)(frac{-b-sqrt{D}}{2a})(=)(frac{-b-sqrt{0}}{2a})(=)(frac{-b-0}{2a})(=)(frac{-b}{2a})
То есть, значения корней уравнения будут совпадать, потому что прибавление или вычитание нуля ничего не меняет.
Пример: Найдите корни уравнения (x^2-4x+4=0)
Решение:
|
(x^2-4x+4=0) |
Выписываем коэффициенты: |
|
|
(a=1;) (b=-4;) (c=4;) |
Вычисляем дискриминант по формуле (D=b^2-4ac) |
|
|
(D=(-4)^2-4cdot1cdot4=) |
Находим корни уравнения |
|
|
(x_{1}=)(frac{-(-4)+sqrt{0}}{2cdot1})(=)(frac{4}{2})(=2) (x_{2}=)(frac{-(-4)-sqrt{0}}{2cdot1})(=)(frac{4}{2})(=2) |
Получили два одинаковых корня, поэтому нет смысла писать их по отдельности – записываем как один. |
Ответ: (x=2)
На графике квадратичной функции нулевой дискриминант означает одну точку пересечения функции с осью икс. Все аналогично изложенному выше: два корня – две точки пересечения, один корень – одна. В частности, функция (y=x^2-4x+4) будет выглядеть вот так:

Если дискриминант отрицателен
В этом случае корень из дискриминанта извлечь нельзя (т.к. квадратный корень из отрицательного числа – невычислим), а значит и корни квадратного уравнения мы вычислить не можем.
Пример: Найдите корни уравнения (x^2+x+3=0)
Решение
|
(x^2+x+3=0) |
Выписываем коэффициенты: |
|
|
(a=1;) (b=1;) (c=3;) |
Вычисляем дискриминант по формуле (D=b^2-4ac) |
|
|
(D=1^2-4cdot1cdot3=) |
Находим корни уравнения |
|
|
(x_{1}=)(frac{-1+sqrt{-11}}{2cdot1})(=…) (x_{2}=)(frac{-1-sqrt{-11}}{2cdot1})(=…) |
Оба корня содержат невычислимое выражение (sqrt{-11}), значит, и сами не вычислимы |
Ответ: нет корней.
То есть, отсутствие корней у квадратного уравнения с отрицательным дискриминантом – не чья-то случайная придумка. Это не потому что «в учебнике так написано», а действительно правда: невозможно найти такое число, чтоб при подстановке его вместо икса в выражение (x^2+x+3) получился ноль.
Матхак: заметим, что если вы решаете обычное квадратное уравнение или неравенство и получаете отрицательный дискриминант, стоит проверить решение еще раз, так как это не частая ситуация в школьном курсе математики.
Ну, а на графиках все просто: нет корней – нет точек пересечения с осью икс!

Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Дискриминант
квадратного уравнения
Поддержать сайт
Мы уже разобрали,
как решать квадратные уравнения.
Теперь давайте более подробно рассмотрим, что называют
дискриминантом квадратного уравнения.
Вернемся к нашей формуле для нахожденя корней квадратного уравнения.
Запомните!
Выражение «b2 − 4ac», которое находится под корнем,
принято называть дискриминантом и обозначать буквой «D».
По-другому, через дискриминант формулу нахождения корней квадратного уравнения можно записать так:
x1;2 = , где «D = b2 − 4ac»
По одной из версий термин «Дискриминант» произошел от латинского discriminantis, что означает «отличающий» или «различающий».
В зависимости от знака «D» (дискриминанта)
квадратное уравнение может иметь два, один или ни одного корня. Рассмотрим все три случая.
I случай
D > 0
(дискриминант больше нуля)
2x2 + 5x −7 = 0
D = b2 − 4ac
D = 52 − 4 · 2 · (−7)
D = 25 + 56
D = 81
D > 0
x1;2 =
x1;2 =
x1;2 =
| x1 = |
x2 = |
| x1 = |
x2 = |
| x1 = 1 |
x2 = −3 |
| x1 = 1 |
x2 = −3 |
Ответ: x1 = 1;
x2 = −3
Вывод: когда «D > 0» в квадратном уравнении два корня.
II случай
D = 0
(дискриминант равен нулю)
16x2 − 8x + 1 = 0
D = b2 − 4ac
D = (−8)2 − 4 · 16 · 1
D = 64 − 64
D = 0
x1;2 =
x1;2 =
x1;2 =
x =
x =
Ответ: x =
Вывод: когда «D = 0» в квадратном уравнении один корень.
III случай
D < 0
(дискриминант меньше нуля)
9x2 − 6x + 2 = 0
D = b2 − 4ac
D = (−6)2 − 4 · 9 · 2
D = 36 − 72
D = −36
D < 0
x1;2 =
x1;2 =
Ответ: нет действительных корней
Вывод: когда «D < 0» в квадратном уравнении нет корней.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий: