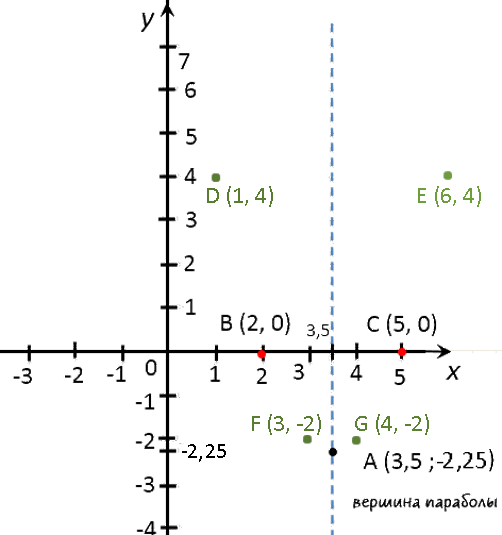В этой статье мы поговорим о том, что такое квадратичная функция, научимся строить ее график и определять вид графика в зависимости от знака дискриминанта и знака старшего коэффициента.
Итак.
Функция вида 

В уравнении квадратичной функции:
a — старший коэффициент
b — второй коэффициент
с — свободный член.
Графиком квадратичной функции является квадратичная парабола, которая для функции 
Обратите внимание на точки, обозначенные зелеными кружками — это, так называемые «базовые точки». Чтобы найти координаты этих точек для функции 
Внимание! Если в уравнении квадратичной функции старший коэффициент 

График функции 
Для нахождения координат базовых точек составим таблицу:
Обратите внимание, что график функции 

Итак, мы заметили:
Если старший коэффициент a>0, то ветви параболы напрaвлены вверх.
Если старший коэффициент a<0, то ветви параболы напрaвлены вниз.
Второй параметр для построения графика функции — значения х, в которых функция равна нулю, или нули функции. На графике нули функции 

Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты точек пересечения графика функции 

В случае квадратичной функции 

Теперь внимание!
В процессе решения квадратного уравнения мы находим дискриминант: 
И здесь возможны три случая:
1. Если 



2. Если 



3. Если 



Если 
Следовательно, зная направление ветвей параболы и знак дискриминанта, мы уже можем в общих чертах определить, как выглядит график нашей функции.
Следующий важный параметр графика квадратичной функции — координаты вершины параболы:
Прямая, проходящая через вершину параболы параллельно оси OY является осью симметрии параболы.
И еще один параметр, полезный при построении графика функции — точка пересечения параболы 
Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы 

То есть точка пересечения параболы с осью OY имеет координаты (0;c).
Итак, основные параметры графика квадратичной функции показаны на рисунке:
Рассмотрим несколько способов построения квадратичной параболы. В зависимости от того, каким образом задана квадратичная функция, можно выбрать наиболее удобный.
1. Функция задана формулой 
Рассмотрим общий алгоритм построения графика квадратичной параболы на примере построения графика функции
1. Направление ветвей параболы.
Так как 
2. Найдем дискриминант квадратного трехчлена

Дискриминант квадратного трехчлена больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ.
Для того, чтобы найти их координаты, решим уравнение:

3. Координаты вершины параболы:
4. Точка пересечения параболы с осью OY: (0;-5),и ей симметричная относительно оси симметрии параболы.
Нанесем эти точки на координатную плоскость, и соединим их плавной кривой:
Этот способ можно несколько упростить.
1. Найдем координаты вершины параболы.
2. Найдем координаты точек, стоящих справа и слева от вершины.
Воспользуемся результатами построения графика функции
Кррдинаты вершины параболы
Ближайшие к вершине точки, расположенные слева от вершины имеют абсциссы соответственно -1;-2;-3
Ближайшие к вершине точки, расположенные справа имеют абсциссы соответственно 0;1;2
Подставим значения х в уравнение функции, найдем ординаты этих точек и занесем их в таблицу:
Нанесем эти точки на координатную плоскость и соединим плавной линией:
2. Уравнение квадратичной функции имеет вид 

или в уравнении квадратичной функции 

Построим для примера график функции 
Вспомним линейные преобразования графиков функций. Чтобы построить график функции 
- сначала построить график функции
,
- затем одинаты всех точек графика умножить на 2,
- затем сдвинуть его вдоль оси ОХ на 1 единицу вправо,
- а затем вдоль оси OY на 4 единицы вверх:
Теперь рассмотрим построение графика функции 

Выделим в уравнении функции полный квадрат:
Следовательно, координаты вершины параболы: 
3. Уравнение квадратичной функции имеет вид y=(x+a)(x+b)
Построим для примера график функции y=(x-2)(x+1)
1. Вид уравнения функции позволяет легко найти нули функции — точки пересечения графика функции с осью ОХ:
(х-2)(х+1)=0, отсюда
2. Координаты вершины параболы:
3. Точка пересечения с осью OY: с=ab=(-2)(1)=-2 и ей симметричная.
Нанесем эти точки на координатную плоскость и построим график:
График квадратичной функции.
Перед вами график квадратичной функции вида .
Кликните по чертежу.
Подвигайте движки.
Исследуйте зависимость
— ширины графика функции от значения коэффициента
,
— сдвига графика функции вдоль оси
от значения
,
— сдвига графика функции вдоль оси
от значения
— направления ветвей параболы от знака коэффициента
— координат вершины параболы от значений
и
:
Скачать таблицу квадратичная функция
И.В. Фельдман, репетитор по математике.
Прежде чем перейти к разбору квадратичной функции рекомендуем вспомнить, что называют
функцией в математике.
Если вы прочно закрепите общие знания о функции (способы задания, понятие графика)
дальнейшее изучение других
видов функций будет даваться значительно легче.
Что называют квадратичной функцией
Запомните!
Квадратичная функция — это функция вида
y = ax2 + bx + c,
где a,
b и с — заданные числа.
Другими словами можно сказать, что если в функции старшая (то есть самая большая) степень,
в которой стоит «x» — это «2»,
то перед нами квадратичная функция.
Рассмотрим примеры квадратичных функций и определим, чему в них равны коэффициенты «a»,
«b» и «с».
| Квадратичная функция | Коэффициенты |
|---|---|
| y = 2x2 − 7x + 9 |
|
| y = 3x2 − 1 |
|
| y = −3x2 + 2x |
|
Как построить график квадратичной функции
Запомните!
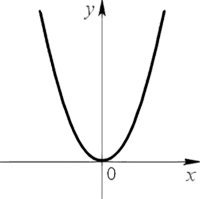
График квадратичной функции называют параболой.
Парабола выглядит следующим образом.
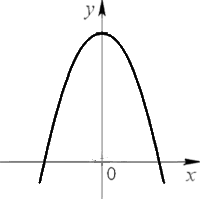
Также парабола может быть перевернутой.
Существует четкий алгоритм действий при построении графика квадратичной функции.
Рекомендуем при построении параболы всегда следовать этому порядку действий, тогда вы сможете избежать ошибок при построении.
Чтобы было проще понять этот алгоритм, сразу разберем его на примере.
Построим график квадратичной функции «y = x2 −7x + 10».
- Направление ветвей параболы
Запомните!
Если «a > 0», то ветви направлены вверх.
Если «a < 0», то ветви направлены вниз.
В нашей функции «a = 1», это означает, что ветви параболы направлены вверх.
- Координаты вершины параболы
Запомните!
Чтобы найти «x0»
(координата вершины по оси «Ox»)
нужно использовать формулу:Найдем «x0» для нашей функции «y = x2 −7x + 10».
Теперь нам нужно найти «y0»
(координату вершины по оси «Oy»).
Для этого нужно подставить найденное значение «x0» в исходную функцию.
Вспомнить, как найти значение функции можно в уроке
«Как решать задачи на функцию» в подразделе
«Как получить значение функции».y0(3,5) =
(3,5)2 − 7 ·3,5 + 10 = 12,25 − 24,5 + 10 =−12,25 + 10 = −2,25
Выпишем полученные координаты вершины параболы.
(·) A (3,5; −2,25) — вершина параболы.
Отметим вершину параболы на системе координат.
Проведем через отмеченную точку ось симметрии, так как парабола — это симметричный график
относительно оси «Oy». - Нули функции
Для начала давайте разберемся, что называют нулями функции.
Запомните!
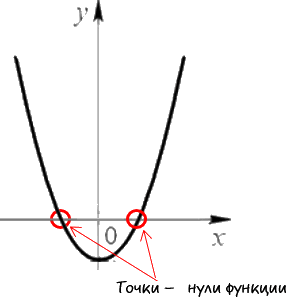
Нули функции — это точки пересечения графика функции с осью «Ox»
(осью абсцисс).Наглядно нули функции на графике выглядят так:
Свое название нули функции получили из-за того, что у этих точек координата
по оси «Oy» равна нулю.Теперь давайте разберемся, как до построения графика функции рассчитать координаты точек нулей функции.
Запомните!
Чтобы найти координаты точек нулей функции, нужно в исходную функцию подставить вместо
«y = 0».Подставим в заданную функцию «y = x2 −7x + 10»
вместо «y = 0» и решим полученное
квадратное уравнение
относительно
«x» .0 = x2 −7x + 10
x2 −7x + 10 = 0x1;2 =
7 ±
√49 − 4 · 1 · 102 · 1 x1;2 =
x1;2 =
x1 = x2 =
x1 = x2 =
x1 = 5 x2 = 2
Мы получили два корня в уравнении, значит, у нас две точки пересечения
с осью «Ox».
Назовем эти точки и выпишем их координаты.- (·) B (5; 0)
- (·) C (2; 0)
Отметим полученные точки («нули функции») на системе координат.
- Дополнительные точки для построения графика
Возьмем четыре произвольные числовые значения для «x».
Целесообразно брать целые числовые значения на оси «Ox»,
которые наиболее близки к оси
симметрии. Числа запишем в таблицу в порядке возрастания.x 1 3 4 6 y Для каждого выбранного значения «x»
рассчитаем «y».- y(1) = 12 − 7 · 1 + 10 = 1 − 7 + 10 =
4 -
y(3) = 32 − 7 · 3 + 10 = 9 − 21 + 10 =
−2 -
y(4) = 42 − 7 · 4 + 10 = 16 − 28 + 10 =
−2 -
y(6) = 62 − 7 · 6 + 10 = 36 − 42 + 10 =
4
Запишем полученные результаты в таблицу.
x 1 3 4 6 y 4 −2 −2 4 Отметим полученные точки графика на системе координат (зеленые точки).
Теперь мы готовы построить график.
На забудьте после построения подписать график функции. - y(1) = 12 − 7 · 1 + 10 = 1 − 7 + 10 =
Краткий пример построения параболы
Рассмотрим другой пример построения графика квадратичной функции.
Только теперь запишем алгоритм построения коротко без подробностей.
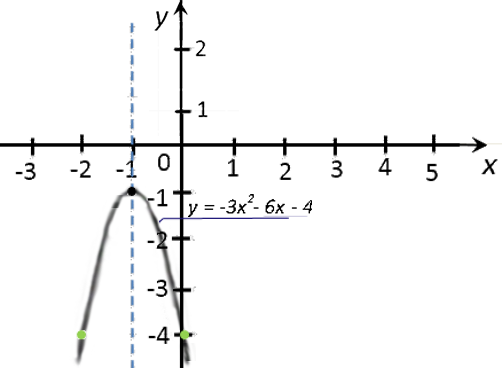
Пусть требуется построить график функции
«y = −3x2 − 6x − 4».
- Направление ветвей параболы
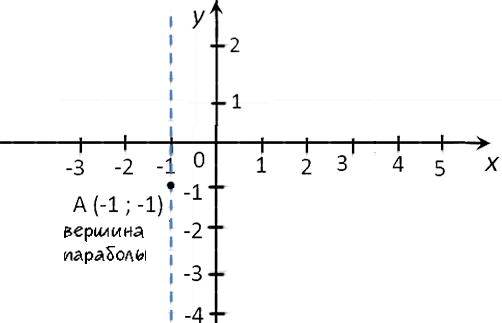
- Координаты вершины параболы
x0 =
x0 = == −1
y0(−1) = (−3) · (−1)2 − 6 · (−1) − 4 =
−3 · 1 + 6 − 4 = −1(·) A (−1; −1)
— вершина параболы.
- Нули функции
Точки пересечения с осью «Ox» (y = 0).
0 = −3x2 − 6x − 4
−3x2 − 6x − 4 = 0 |·(−1)
3x2 + 6x + 4 = 0
x1;2 =
−6 ±
√62 − 4 · 3 · 42 · 1 x1;2 =
x1;2 =
Ответ: нет действительных корней.Так как корней нет, значит, график функции не пересекает ось
«Ox». - Вспомогательные точки для: «x = −3»;
«x = −2»;
«x = 0»;
«x = 1». Подставим в исходную функцию
«y = −3x2 − 6x − 4».- y(−3) = −3 · (−3)2 − 6 · (−3) − 4
= −3 · 9 + 18 − 4 = −27 + 14 = −13 -
y(−2) = −3 · (−2)2 − 6 · (−2) − 4
= −3 · 4 + 12 − 4 = −12 + 12 − 4 = −4 -
y(0) = −3 · 02 − 6 · 0 − 4
= −4 -
y(1) = −3 · 12 − 6 · 1 − 4
= −3 −6 − 4 = −13
x −3 −2 0 1 y −13 −4 −4 −13 - y(−3) = −3 · (−3)2 − 6 · (−3) − 4
«a = −3» — ветви параболы направлены вниз.
Отметим вспомогательные точки. Отмечаем на системе координат только те точки, которые
не выходят за масштаб нашей системы координат, то есть точки
«(−2; −4)» и «(0; −4)».
Построим и подпишем график функции.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
В уравнении квадратичной функции:
a – старший коэффициент
b – второй коэффициент
с — свободный член.
Графиком квадратичной функции является квадратичная парабола, которая для функции 
Точки, обозначенные зелеными кружками – это, так
называемые «базовые точки». Чтобы найти координаты этих точек для
функции 
Внимание! Если в уравнении квадратичной функции старший коэффициент 

График функции 
Для нахождения координат базовых точек составим таблицу:
Обратите внимание, что график функции 

Итак, мы заметили:
Если старший коэффициент a>0, то ветви параболы напрaвлены вверх.
Если старший коэффициент a<0, то ветви параболы напрaвлены вниз.
Второй параметр для построения графика функции – значения х, в которых функция равна нулю, или нули функции. На графике нули функции 

Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты точек пересечения графика функции 

В случае квадратичной функции 

В процессе решения квадратного уравнения находим дискриминант: 
И здесь возможны три случая:
1. Если 


,то график функции выглядит как-то так:
2. Если 


,то график функции выглядит примерно так:
3. Если ,то уравнение



Если ,то график функции выглядит примерно так:
Следующий важный параметр графика квадратичной функции – координаты вершины параболы:
Прямая, прохдящая через вершину параболы параллельно оси OY является осью симметрии паработы.
И еще один параметр, полезный при построении графика функции – точка пересечения параболы 
Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы 

То есть точка пересечения параболы с осью OY имеет координаты (0;c).
Итак, основные параметры графика квадратичной функции показаны на рисунке:
Функция вида y=ax2+bx+c, где а, b, с – некоторые числа, причем, а≠0 число, х – переменная, называется квадратичной функцией.
Графиком квадратичной функции является парабола, она имеет вершину и две ветви, которые могут быть направлены либо вверх, либо вниз (рис.1). Красной точкой обозначена вершина параболы, из которой выходят ветви. Её координаты по графику – (3; –4). Направление ветвей зависит от значения коэффициента «а», то есть, если «а» – положительное число, то ветви направлены вверх; если число «а» – отрицательное, то ветви направлены вверх. На данном рисунке ветви направлены вверх, значит коэффициент «а» у формулы, которая задает эту функцию – положительное число. Коэффициент «с» показывает ординату (у) точки пересечения ветви параболы с осью у. Так, на рисунке №1 парабола пересекает ось у в точке (5;0), значит коэффициент с=5.
Рисунок №1.
Вершина параболы. Формула.
Чтобы найти координаты вершины параболы (х0; у0), надо воспользоваться формулой:
х0=−b2a
для нахождения у0 можно просто подставить значение х0 в формулу данной функции y0=ax2+bx+c вместо х.
Рассмотрим это на примере конкретно заданной функции.
Пример №1
Найти вершину параболы, заданной формулой у=2х2 – 8х + 5.
Найдем, чему равны коэффициенты: а=2; b= – 8
Подставим их в формулу и вычислим значение х0:
х0=−b2a=82∙2=84=2
Теперь в заданную по условию формулу вместо х подставим найденное значение у0=2∙22 – 8∙2 + 5=8 – 16 + 5= –3
Итак, мы нашли координаты вершины параболы: (2; –3).
Ответ: (2; –3).
Нули параболы
Значения х, при которых функция принимает значения, равные нулю, называются нулями функции. Другими словами, Значения абсцисс (х) точек пересечения ветвей параболы с осью х, называются нулями функции. На рисунке №1 точки координаты точек пересечения ветвей параболы с осью х следующие: (1;0) и (5;0). Значит, нули функции – это значения х, равные 1 и 5.
Рассмотрим, как найти нули функции не по рисунку, а по заданной формуле.
Пример №2
Найти нули функции у=х2 +4х – 5
Так как нули функции это абсциссы точек пересечения ветвей параболы с осью х, то их координаты будут (х;0), то есть у=0. Значит, вместо у подставляем нуль в нашу формулу 0=х2 +4х – 5 и получаем квадратное уравнение, решив которое, мы и найдем значения нулей функции:
х2 +4х – 5=0
а=1, b=4, с= –5
D=b2 – 4ac=42 – 4∙1∙(−5)=36
x=−b±√D2a
x=−4±√362; х1=–5; х2=1
Значит, нули функции равны –5 и 1
Ответ: –5 и 1
Примечание к заданию по нахождению нулей функции без графика
Если дискриминант уравнения отрицательный, значит, нулей функции нет, то есть парабола не пересекает ось х (вершина находится выше неё, если ветви направлены вверх и ниже, если ветви направлены вниз).
Рассмотрим нахождение соответствия рисунков парабол, расположенных в системе координат значениям а и с.
Пример №3
Для выполнения данного задания на соответствие необходимо сначала поработать с графиками, подписав на них, какими – отрицательными или положительными являются коэффициенты а и с.
Теперь можно выполнить соответствие:
Ответ: 231
Пример №4
Рассмотрим еще пример на соответствие
В данном задании рассмотрим коэффициенты в формулах и подчеркнем их: так, в формуле под буквой А коэффициент а=-2, т.е. отрицательный, значит, ветви направлены вниз, а это график под номером 2. В формулах под буквами Б и В первые и третьи коэффициенты одинаковые, значит, сравнить по рисунку их невозможно, следовательно, будем сравнивать по расположению вершины (справа или слева от оси у), а именно х0.
Итак, найдем х0 для формулы «Б»:
х0=−b2a=−42∙2=−44=−1
Видим, что х0 отрицательное, значит, вершина расположена слева от оси у, а это рисунок 3. Ну и осталось привести в соответствие В и 1.
Запишем в таблицу
Ответ: 231
Задание 11OM21R
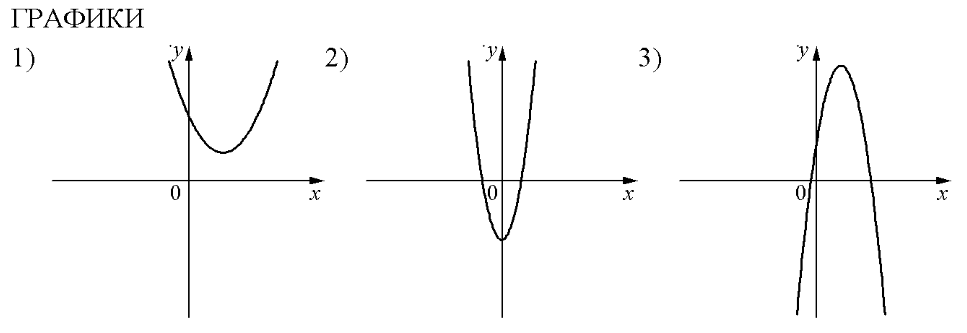
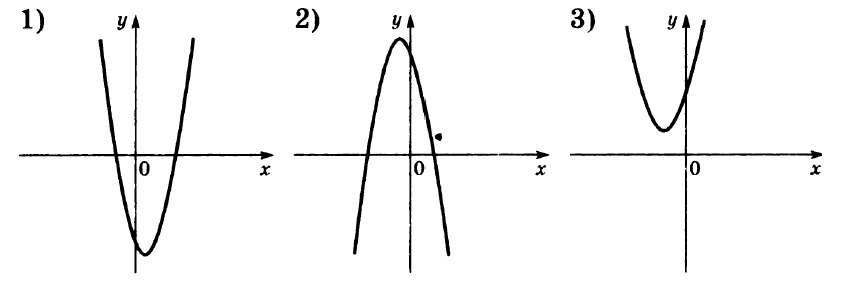
На рисунках изображены графики функций вида . Установите соответствие между знаками коэффициентов а и с и графиками функций.
КОЭФФИЦИЕНТЫ
А) a>0, с >0 Б) а<0; с>0 В) а>0, с<0
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
Решение
На рисунках в задании изображены параболы. Вспомним, что обозначают коэффициенты а и с: а – направление ветвей (a<0 – ветви вниз; а>0 – ветви вверх); коэффициент с показывает ординату точку пересечения параболы с осью х (с >0 – пересечение в положительном направлении; с<0 – пересечение в отрицательном направлении).
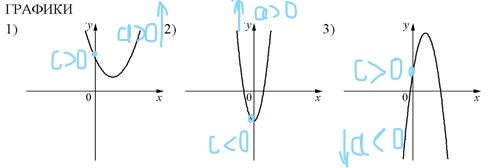
Теперь поработаем с графиками и подпишем на каждом из них соответствующие коэффициенты.
Теперь расставим в соответствии с указанными коэффициентами:
А) a>0, с >0 – это график №1
Б) а<0; с>0 – это график №3
В) а>0, с<0 – это график №2
Ответ: 132
pазбирался: Даниил Романович | обсудить разбор
Задание OM1105o
Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) у=–х2–4х–3 Б) у=–х2+4х–3 В) у=х2+4х+3
Сразу обратим внимание на вариант В. Эта функция единственная, имеющая положительный коэффициент при х2 (здесь а=1, т.е. а>0). При а>0 график параболы направлен ветками вверх. Такой график имеется только один – под №3. Кроме того, можно обратить внимание на коэфициент с. Она равен 3, т.е. с>0. Это указывает на то, что парабола должна пересечь ось Оу выше начала координат. Что и отображено на графике В. Получаем соответствие: В–3.
Оба других графика – 1-й и 2-й – пересекают ось Оу ниже начала координат, что соответствует значению с=–3<0 в обоих случаях.
Далее надежнее всего вычислить вершины оставшихся двух парабол из уравнений А и Б по формуле -b/2a. Видим, что случае А (- (-4)) / (2 • -1) = -2, следовательно, вершина левее оси Y, так как x0 отрицателен, значит, А-1, а Б-2.
Ответ: 123
pазбирался: Даниил Романович | обсудить разбор
Задание OM1101o
На рисунках изображены графики функций вида
y = ax² + bx + c
Установите соответствие между знаками коэффициентов a и c и графиками функций.
Коэффициенты:
А) a > 0, c > 0
Б) a < 0, c > 0
В) a > 0, c < 0
Графики:
Мы вспоминаем, за что отвечают коэффициенты a и b при построении графиков функции вида
y = ax² + bx + c
Коэффициент a определяет направление ветвей параболы: если a > 0, то ветви направлены вверх, а если a < 0, то ветви направлены вниз.
Таким образом, мы видим, что только у второй параболы ветви направлены вниз, а значит a < 0.
У первой и третьей ветви направлены вверх, то есть a > 0.
Далее мы смотрим, на что влияет коэффициент c.
Коэффициент c отвечает за положение параболы относительно оси x, или же отвечает за сдвиг по оси y, а именно:
если c > 0, то вершина параболы расположена выше оси х
если c < 0, то вершина параболы расположена ниже оси x
Так, у первой параболы c < 0, у второй и третьей c > 0.
Из всего вышеперечисленного можно найти ответ:
А) 3
Б) 2
В) 1
Ответ: 321
pазбирался: Даниил Романович | обсудить разбор
Даниил Романович | Просмотров: 10.7k
Home » 8 класс » Как построить параболу? Что такое парабола? Как решаются квадратные уравнения?
Урок: как построить параболу или квадратичную функцию?
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Парабола — это график функции описанный формулой ax2+bx+c=0.
Чтобы построить параболу нужно следовать простому алгоритму действий:
1 ) Формула параболы y=ax2+bx+c,
если а>0 то ветви параболы направленны вверх,
а<0 то ветви параболы направлены вниз.
Свободный член c эта точке пересекается параболы с осью OY;
2 ) Вершина параболы, ее находят по формуле x=(-b)/2a, найденный x подставляем в уравнение параболы и находим y;
3) Нули функции или по другому точки пересечения параболы с осью OX они еще называются корнями уравнения. Чтобы найти корни мы уравнение приравниваем к 0 ax2+bx+c=0;
Виды уравнений:
a) Полное квадратное уравнение имеет вид ax2+bx+c=0 и решается по дискриминанту;
b) Неполное квадратное уравнение вида ax2+bx=0. Чтобы его решить нужно вынести х за скобки, потом каждый множитель приравнять к 0:
ax2+bx=0,
х(ax+b)=0,
х=0 и ax+b=0;
c)Неполное квадратное уравнение вида ax2+c=0. Чтобы его решить нужно неизвестные перенести в одну сторону, а известные в другую. x =±√(c/a);
Как решать квадратные уравнения посмотреть тут.
4) Найти несколько дополнительных точек для построения функции.
ПРАКТИЧЕСКАЯ ЧАСТЬ
И так теперь на примере разберем все по действиям:
Пример №1:
y=x2+4x+3
c=3 значит парабола пересекает OY в точке х=0 у=3. Ветви параболы смотрят вверх так как а=1 1>0.
a=1 b=4 c=3 x=(-b)/2a=(-4)/(2*1)=-2 y= (-2)2+4*(-2)+3=4-8+3=-1 вершина находится в точке (-2;-1)
Найдем корни уравнения x2+4x+3=0
По дискриминанту находим корни
a=1 b=4 c=3
D=b2-4ac=16-12=4
x=(-b±√(D))/2a
x1=(-4+2)/2=-1
x2=(-4-2)/2=-3
Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=-2
х -4 -3 -1 0
у 3 0 0 3
Подставляем вместо х в уравнение y=x2+4x+3 значения
y=(-4)2+4*(-4)+3=16-16+3=3
y=(-3)2+4*(-3)+3=9-12+3=0
y=(-1)2+4*(-1)+3=1-4+3=0
y=(0)2+4*(0)+3=0-0+3=3
Видно по значениям функции,что парабола симметрична относительно прямой х=-2
Пример №2:
y=-x2+4x
c=0 значит парабола пересекает OY в точке х=0 у=0. Ветви параболы смотрят вниз так как а=-1 -1<0.
a=-1 b=4 c=0 x=(-b)/2a=(-4)/(2*(-1))=2 y=-(2)2+4*2=-4+8=4 вершина находится в точке (2;4)
Найдем корни уравнения -x2+4x=0
Неполное квадратное уравнение вида ax2+bx=0. Чтобы его решить нужно вынести х за скобки, потом каждый множитель приравнять к 0.
х(-x+4)=0, х=0 и x=4.
Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=2
х 0 1 3 4
у 0 3 3 0
Подставляем вместо х в уравнение y=-x2+4x значения
y=02+4*0=0
y=-(1)2+4*1=-1+4=3
y=-(3)2+4*3=-9+13=3
y=-(4)2+4*4=-16+16=0
Видно по значениям функции,что парабола симметрична относительно прямой х=2
Пример №3
y=x2-4
c=4 значит парабола пересекает OY в точке х=0 у=4. Ветви параболы смотрят вверх так как а=1 1>0.
a=1 b=0 c=-4 x=(-b)/2a=0/(2*(1))=0 y=(0)2-4=-4 вершина находится в точке (0;-4)
Найдем корни уравнения x2-4=0
Неполное квадратное уравнение вида ax2 +c=0. Чтобы его решить нужно неизвестные перенести в одну сторону, а известные в другую. x =±√(c/a)
x2=4
x1=2
x2=-2
Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=0
х -2 -1 1 2
у 0 -3 -3 0
Подставляем вместо х в уравнение y= x2-4 значения
y=(-2)2-4=4-4=0
y=(-1)2-4=1-4=-3
y=12-4=1-4=-3
y=22-4=4-4=0
Видно по значениям функции,что парабола симметрична относительно прямой х=0
Подписывайтесь на канал на YOUTUBE, чтобы быть в курсе всех новинок и готовится с нами к экзаменам.