Загрузить PDF
Загрузить PDF
В кубическом уравнении наивысшим показателем степени является 3, у такого уравнения 3 корня (решения) и оно имеет вид 
-
1
-
2
-
3
Разложите на множители (на произведение двух биномов) квадратное уравнение (если возможно). Многие квадратные уравнения вида
можно разложить на множители. Такое уравнение получится, если вынести
за скобки. В нашем примере:[4]
-
4
-
5
Используйте ноль и корни квадратного уравнения в качестве решений кубического уравнения. У квадратных уравнений два корня, а у кубических — три. Два решения вы уже нашли — это корни квадратного уравнения. Если же вы вынесли «х» за скобки, третьим решением будет
.[6]
Реклама
-
1
-
2
-
3
Разделите каждый множитель
на каждый множитель
. В итоге получится множество дробей и несколько целых чисел; корнями кубического уравнения будет одно из целых чисел или отрицательное значение одного из целых чисел.[9]
- В нашем примере разделите множители
(1 и 2) на множители
(1, 2, 3 и 6). Вы получите:
,
,
,
,
и
. Теперь в этот список добавьте отрицательные значения полученных дробей и чисел:
,
,
,
,
,
,
,
,
,
,
и
. Целыми корнями кубического уравнения являются какие-то числа из этого списка.
- В нашем примере разделите множители
-
4
Подставьте целые числа в кубическое уравнение. Если при этом равенство соблюдается, подставленное число является корнем уравнения. Например, подставьте в уравнение
:[10]
-
5
Реклама
-
1
-
2
Вычислите нулевой дискриминант по специальной формуле. Чтобы решить кубическое уравнение с помощью дискриминанта, нужно произвести ряд непростых вычислений, но если правильно выполнять все действия, этот метод станет незаменимым для решения наиболее сложных кубических уравнений. Сначала вычислите
(нулевой дискриминант) — это первая необходимая нам величина; для этого подставьте соответствующие значения в формулу
.[13]
-
3
Вычислите первый дискриминант по формуле
. Первый дискриминант
— это вторая важная величина; чтобы ее вычислить, подставьте соответствующие значения в указанную формулу.[14]
-
4
-
5
-
6
Реклама
Об этой статье
Эту страницу просматривали 409 893 раза.
Была ли эта статья полезной?
Решения кубических уравнений с вещественными коэффициентами. Универсальные методы. Дискриминант кубического уравнения. Формула Виета для кубического уравнения.
Кубическим уравнением называется уравнение вида
- ax3 + bx2 + cx +d = 0 , (1)
- где a, b,c ,d — постоянные коэффициенты, а х — переменная.
Мы рассмотрим случай, когда коэффициенты являются веществеными числами.
Корни кубического уравнения. Нахождение корней (решение) кубического уравнения.
Число х называется корнем кубического уравнения (1), если при его подстановке уравнение (1) обращается в верное равенство.
Кубическое уравнение имеет не более трех корней (над комплексным полем всегда три корня, с учетом кратности) . И всегда имеет хотя бы 1 (вещественный) корень. Все возможные случаи состава корней легко определить с помощью знака дискриминанта кубического уравнения, т.е.:
Δ= -4b3d + b2c2 — 4ac3 + 18abcd — 27a2d2 (Да, это дискриминант кубического уравнения)
Итак, возможны только 3 следующих случая:
- Δ > 0 — тогда уравнение имеет 3 различных корня. (Для продвинутых — три различных вещественных корня)
- Δ < 0 — уравнение имеет лишь 1 корень. (1 вещественный и пару комплексно сопряженных корней)
- Δ = 0 — хотя бы 2 корня уравнения совпадают. Т.е. мы имеем дело либо с уравнением с 2умя совпадающими корнями, и еще 1ним отличным от них, либо с уравнением с 3емя совпадающими корнями. (В любом случае все корни вещественные. И уравнение имеет 3 совпадающих корня, тогда и только тогда, когда результант его и его второй производной равен нулю)
На практике часто , решение кубических уравнений упирается в разложении их на множители. Т.е. алгоритм приблизительно следующий: угадываем один корень, пусть это будет корень α. Затем делим многочлен на (х- α), (если α корень, то он должен поделиться без остатка). Ну а дальше мы имеем дело с обычным квадратным уравнением. Но угадать можно только рациональный корень, и то, если коэффициенты подобраны удачным образом, так что этот корень просто угадывается. Мы же рассмотрим универсальные методы решения кубичесих уравнений.
Формула Кардано решения кубических уравнений (нахождения корней).
Это формула для нахождения корней канонической формы кубического уравнения. (Над полем комлексных чисел).
Канонической формой кубического уравнения называется уравнение вида
y3 + py + q = 0 (2)
К такому виду можно привести любое кубическое уравнение вида (1) с помощью следующей замены:
- x= y — b/3a (3)
- p= — b2/3a2 + c/a
- q= 2b3/27a3 — bc/3a2 + d/a
Итак, приступим к вычислению корней. Найдем следующие величины:
- Q=(p/3)3 + (q/2)2
- α = (-q/2 + Q1/2)1/3
- β = (-q/2 — Q1/2)1/3
Дискриминант уравнения (2) в этом случае равен
Δ = — 108Q
Дискриминант исходного уравнения (1) будет иметь тот же знак , что и вышеуказанный дискриминант. Корни уравнения (2) выражаются следующим образом:
- y1= α + β
- y2= — (α + β)/2 + (31/2(α — β)/2)i
- y3 =- (α + β)/2 — (31/2(α — β)/2)i
Соответственно, если Q>0, то уравнения (2) и (1) будут иметь лишь 1 (вещественный) корень, y1. Подставим его в (3) и найдем х для уравнения (1). (если вас интересуют также мнимые корни, то просто вычислите еще и y2, y3 и подставьте их в (3).
Если Q<0, то уравнение (2), как и уравнение (1) имеет три различных вещественных корня, но для их вычисления нужно уметь извлекать квадратный корень из отрицательного числа. Если вы это умеете, то проделайте расчеты, получите три корня y1, y2, y3 и подставьте их в (3).
Если же Q =0, то все корни уравнений (1) и (2) вещественные, причем как минимум 2 корня каждого из уравнений совпадают. При этом имеем
- α = β, и
- y1=2α,
- y2= y3 = — α.
Аналогично подставляем в (3) и получаем ответ.
Тригонометрическая формула Виета решения кубических уравнений (нахождения корней).
Эта формула находит решения приведенного кубического уравнения, то есть уравнения вида
x3 + ax2 + bx +c = 0 (4)
Очевидно, любое уравнение вида (1) можно привести к виду (4), просто поделив его на коэффициент а.
Итак, алгоритм применения этой формулы:
1. Вычисляем
- Q=(a2— 3b)/9
- R=(2a3 — 9ab + 27c)/54
2. Вычисляем
S = Q3 — R2
3. a) Если S>0, то вычисляем
φ=(arccos(R/Q3/2))/3
И наше уравнение имеет 3 корня (вещественных):
- x1= — 2(Q)1/2cos(φ) — a/3
- x2= — 2(Q)1/2cos(φ+2π/3) — a/3
- x3= — 2(Q)1/2cos(φ-2π/3) — a/3
б) Если S<0, то заменим тригонометрические функции гиперболическими.
Вычисляем
φ=(Arch( |R|/|Q|3/2)/3
Тогда единственный корень (вещественный): x1= -2sgn(R)*|Q|1/2*ch(φ) — a/3
Для тех, кого интересуют также и мнимые корни:
- x2= sgn(R)*|Q|1/2*ch(φ) — a/3 +(3|Q|)1/2 sh(φ)i
- x3= sgn(R)*|Q|1/2*ch(φ) — a/3 -(3|Q|)1/2sh(φ)i
ГДЕ:
- ch(x)=(ex+e-x)/2
- Arch(x) = ln(x + (x2-1)1/2)
- sh(x)=(ex-e-x)/2
- sgn(x) — знак х
в) Если S=0,то уравнение имеет меньше трех различных решений:
- x1= -2*R1/3 — a/3
- x2=x3=R1/3 — a/3
Кубическим называют уравнение, в котором только одна переменная представлена в третьей степени. Такие выражения в любом случае имеют от одного до трех корней. Значения, которые получаются при решении таких уравнений, могут быть равными друг другу или комплексными, если их не более двух.
Решение кубических уравнений – это решение уравнений, имеющих вид: [boldsymbol{a y^{3}+b y^{2}+c y+d=0}].
В уравнении такого типа a не равно 0, вместо b,c,d могут быть любые однозначные числа.
Данный вид уравнения имеет как минимум один корень – y1.
Решение таких равнений может осуществляться разными способами. Оно может преобразовываться в стандартное квадратное уравнение. В таком случае предстоит выбрать один из трех вариантов решения квадратного уравнения:
- разложение на множители;
- применение формул для квадратных уравнений;
- метод дополнения.
Решение кубических уравнений может осуществляться посредством формулы Кардано, а также теоремы Виета. Теорема Виета применяется для решения последней, четвертой степени.
Решение кубических уравнений с двумя членами
Уравнение будет иметь вид: [boldsymbol{a y^{3}+b=0}]
Для решения необходимо преобразовать его: [y^{3}=b / a=0]
Деление на a предполагает вместо нее любую цифру, кроме 0. После преобразования можно применить формулы для решения кубических уравнений, например, сокращенного умножения суммы кубов:
y3=b/a=0
(y+3√b/a)(y2—3√b/a*y+3√(b/a)2)=0
В результате из первой скобки выводим:
y=-3√b/a
во второй скобке получаем выражение – трехчлен:
y2-3√b/a*y+3√(b/a)2
Методы решения кубических уравнений возвратного вида
Алгоритм решения кубического уравнения возвратного вида отличается от предыдущего, так как оно выглядит следующим образом:
[boldsymbol{a y^{3}+b y^{2}+b y+a=0}]
В этом уравнении переменные a и b – это коэффициенты.
Первым делом при решении таких уравнений в математике выполняется группировка:
ay3+by2+by+a=a(y3+1)+b(y2+y)=a(y+1)(y2-y+1)+by(y+1)=(y+1)(ay2+y(b-a)+a)
В полученном выражении корень равен y=-1. Исходя из этого, чтобы получить корень квадратного трехчлена ay2+y(b-a)+a, потребуется найти дискриминант.
Определение
Дискриминант – произведение квадратов разностей корней в различных вариаций.
Решение кубических уравнений в составе которых рациональные корни
Предположим, что y=0. В этом случае он будет корнем уравнения, которое выглядит следующим образом:
ay3+by2+cy+d=0
При условии, что в уравнении свободные члены, d=0. Преобразуем уравнение и получим:
ay3+by2+cy=0
Решение кубических уравнений такого вида предполагает вынесение y за скобку. В итоге получается уравнение вида:
y(ay2+by+c)=0
Рассмотрим на конкретном примере, как решить кубическое уравнение с подробным решением:
5y3+2y2+4y=0
Решение:
Первым делом стоит упростить уравнение.
5y3+2y2+4y=0
Получим уравнение вида:
y(5y2+2y+4)=0
y=0, так как является корнем выражения.
Следующий шаг – поиск корней квадратного трехчлена 5y2+2y+4, который мы получили после упрощения. Для поиска приравняем к нулю и будем использовать дискриминант.
В ходе решения кубического уравнения с дискриминантом получим:
D=22-2*5*4=-38
Так как в ответе мы получили отрицательное значение, корней у данного трехчлена нет, значит x=0.
Если в уравнениях вида ay3+by2+cy+d=0 коэффициентами являются целые числовые значения, то при решении таких уравнений и нахождении его значения мы может получить иррациональные корни.
В случае, когда a не равно 0, при умножении на a2 каждой составляющей уравнения происходит замещение переменных, и получается: x=ay
ay3+by2+cy+d=0
Каждую составляющую выражения умножаем на a2:
a3*y3+b*a2*y2+c*a*a*y+d*a2=0
Учитывая, что решение кубических уравнений с подробным решением предполагает замещение переменных x=ay, то:
x2+b*x2+c*a*x+d*a2
Полученное уравнение является кубическим. В таких уравнениях корни могут быть разными – и целыми, и рациональными. Чтобы привести такое уравнение к тождественному равенству, потребуется подставить делители в полученное равенство. В этом случае полученный x1 будет корнем, и в то же время корнем начального уравнения:
x1=y1/a
Чтобы найти значение корней квадратного трехчлена, потребуется многочлен ay3+by2+cy+d разделить на y-y1.
Рассмотрим решение кубических уравнений такого вида на примере.
Пример:
Решить уравнение [x 3-3 x 2-13 x+15=0].
Решение:
Ищем первый корень перебором чисел: [0, pm1, pm2, pm3, pm5, pm15] и подстановкой в уравнение. В результате находим, что 1 является корнем. Тогда делим левую часть этого уравнения на двухчлен x-1 и получаем:
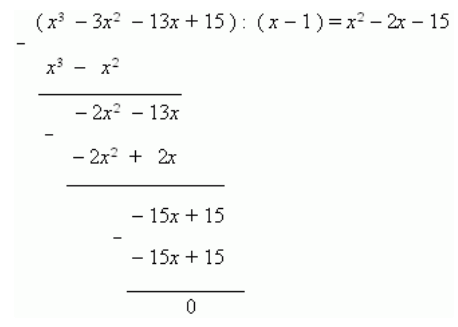
Теперь, решая квадратное уравнение: [x 2-2 x-15=0], находим оставшиеся два корня: x1=-3 и x2=5.
Ответ: 1; -3; 5.
Такой способ решения кубических уравнений используется для преобразования и решения возвратных уравнений. Из приведенного примера видно, что корнем является -1, значит, левую часть можно разделить на x+1. После того, как эти действия выполнены, можно находить корни квадратного трехчлена. Если рациональные корни отсутствуют, необходимо находить иные методы решения и разложения многочлена на множители.
Решение кубического уравнения с помощью формулы Кардано
Есть еще один способ — формула Кардано для решения кубических уравнений.
Если взять уравнение вида B0y3+B1y2+B2y+B3=0, то A1=B1/B0, A2=B2/B0, A3=B3/B0.
Z=-A21/3+A2
P=2A31/27-A1A2/3+A3.
Выведенные значение Z и P подставим в формулу Кардано.
X=3√-P/2+√P2/4+Z3/27+3√-P/2-+√P2/4+Z3/27
В итоге подбор кубических корней должен соответствовать значению –Z/3. В этом случае корни исходного уравнения будут выглядеть следующим образом:
y=x-A1/3
Применить формулу Кордано можно на примере для наглядности.
Пример
Решить уравнение [x^{3}+6 x^{2}+3 x-10=0]
Решение
Данное уравнение легко решается и без применения формулы Кардано. Легко подобрать корень [x=1]. Делением
[x=1] левой части уравнения по схеме Горнера получаем:
[begin{array}{r}+begin{array}{r}1&6&3&-10\0&1*1=1&7*1=7&10*1=10\end{array}
\hlinebegin{array}{r}1quadquadquad&7quadquadquad&10quadquadquadquad&0end{array}end{array}]
Следовательно, [x^{2}+7 x+10=0]. Решая это квадратное уравнение, получаем
[x=frac{-7 pm sqrt{7^{2}-4 * 1 * 10}}{2} Leftrightarrow x_{1}=-2, quad x_{2}=-5]
А теперь найдем корни исходного уравнения по формуле Кардано. Для данного уравнения [a=1, b=6, c=3, d=-10].
Замена переменной [x=y-frac{b}{3 a}=y-frac{6}{3}=y-2] приводит исходное уравнение к виду [y^{3}+p
y+q=0], где:
[p=frac{3 a c-b^{2}}{3 a^{2}}=frac{3 * 1 * 3-6^{2}}{3 * 1^{2}}=-9, quad q=\frac{2 b^{3}-9 a b c+27 a^{2}
d}{27 a^{3}}=frac{2 * 6^{3}-9 * 1 * 6 * 3+27 * 1^{2} *(-10)}{27 * 1^{3}}=0]
Вычислим дискриминант этого уравнения:
[Delta=left(frac{q}{2}right)^{2}+left(frac{p}{3}right)^{3}=left(frac{0}{2}right)^{2}+left(-frac{9}{3}right)^{3}=-27]
Так [Delta] каноническое уравнение имеет 3 действительных корня. Поскольку [q=0 Rightarrow
varphi=frac{pi}{2}=>]
[y_{1}=2 sqrt{-frac{p}{3}} * cos left(frac{varphi}{3}right)=2 sqrt{-frac{-9}{3}} * cos
left(frac{frac{pi}{2}}{3}right)=2 sqrt{3} * cos left(frac{pi}{6}right)=2 sqrt{3} *
frac{sqrt{3}}{2}=3,\y_{2}=2 sqrt{-frac{p}{3}} * cos left(frac{varphi}{3}+frac{2 pi}{3}right)=2
sqrt{3} * cos left(frac{frac{pi}{2}}{3}+frac{2 pi}{3}right)=2 sqrt{3} * cos left(frac{5
pi}{6}right)=-2 sqrt{3} * frac{sqrt{3}}{2}=-3,\y_{3}=2 sqrt{-frac{p}{3}} * cos
left(frac{varphi}{3}+frac{4 pi}{3}right)=2 sqrt{3} * cos left(frac{frac{pi}{2}}{3}+frac{4
pi}{3}right)=2 sqrt{3} * cos left(frac{3 pi}{2}right)=0.]
В данном случае для корней начального уравнения мы получим:
x1=y1-2=3-2=1;
x2=y2-2=-3-2=-5;
x3=y3-2=0-2=-2.
Получаем ответы: 1, -5, -2.
Нет времени решать самому?
Наши эксперты помогут!
Общее решение кубического уравнения, если известен один из корней
За исходное уравнение возьмем следующее:
y3+ay2+by+c=0
Предположим, что a,b,c являются действительными цифровыми значениями. Известный корень пометим, как y1. В таком случае, если произвести деление начального уравнения y3+ay2+by+c=0 на y-y1 получим квадратное уравнение. При решении такого уравнения удастся найти еще два корня – y2 и y3.
Чтобы доказать это, преобразуем кубический многочлен следующим образом:
y3+ay2+by+c=(y-y1)(y-y2)(y-y3)
При решении таких уравнений часто допускаются ошибки. Их решение – это сложное, многократное преобразование, которое требует точного знания формул и математических законов. Чтобы избежать ошибок и погрешностей, потребуется применить не только практические навыки, но и теоретические знания. Для решения кубических уравнений можно использовать специальный онлайн калькулятор. Принцип его действия основан на формуле Кардано. В том случае, если один или несколько коэффициентов такого уравнения равны нулю, или между ними присутствует определенная зависимость, решение будет более простым.
Чтобы научиться решать подобные уравнения, необходимо рассматривать примеры и тренироваться на их решении разными способами.
Решения кубических уравнений с вещественными коэффициентами. Универсальные методы. Дискриминант кубического уравнения. Формула Виета для кубического уравнения.
Решения кубических уравнений с вещественными коэффициентами. Универсальные методы. Дискриминант кубического уравнения. Формула Виета для кубического уравнения.
Кубическим уравнением называется уравнение вида
- ax 3 + bx 2 + cx +d = 0 , (1)
- где a, b,c ,d — постоянные коэффициенты, а х — переменная.
Мы рассмотрим случай, когда коэффициенты являются веществеными числами.
Корни кубического уравнения. Нахождение корней (решение) кубического уравнения.
Число х называется корнем кубического уравнения (1), если при его подстановке уравнение (1) обращается в верное равенство.
Кубическое уравнение имеет не более трех корней (над комплексным полем всегда три корня, с учетом кратности) . И всегда имеет хотя бы 1 (вещественный) корень. Все возможные случаи состава корней легко определить с помощью знака дискриминанта кубического уравнения, т.е.:
Δ= -4b 3 d + b 2 c 2 — 4ac 3 + 18abcd — 27a 2 d 2 (Да, это дискриминант кубического уравнения)
Итак, возможны только 3 следующих случая:
- Δ > 0 — тогда уравнение имеет 3 различных корня. (Для продвинутых — три различных вещественных корня)
- Δ 3 + py + q = 0 (2)
К такому виду можно привести любое кубическое уравнение вида (1) с помощью следующей замены:
- x= y — b/3a (3)
- p= — b 2 /3a 2 + c/a
- q= 2b 3 /27a 3 — bc/3a 2 + d/a
Итак, приступим к вычислению корней. Найдем следующие величины:
Дискриминант уравнения (2) в этом случае равен
Дискриминант исходного уравнения (1) будет иметь тот же знак , что и вышеуказанный дискриминант. Корни уравнения (2) выражаются следующим образом:
Соответственно, если Q>0, то уравнения (2) и (1) будут иметь лишь 1 (вещественный) корень, y1. Подставим его в (3) и найдем х для уравнения (1). (если вас интересуют также мнимые корни, то просто вычислите еще и y2, y3 и подставьте их в (3).
Если Q 3 + ax 2 + bx +c = 0 (4)
Очевидно, любое уравнение вида (1) можно привести к виду (4), просто поделив его на коэффициент а.
Итак, алгоритм применения этой формулы:
3. a) Если S>0, то вычисляем
И наше уравнение имеет 3 корня (вещественных):
Тогда единственный корень (вещественный): x1= -2sgn(R)*|Q| 1/2 *ch(φ) — a/3
Для тех, кого интересуют также и мнимые корни:
- ch(x)=(e x +e -x )/2
- Arch(x) = ln(x + (x 2 -1) 1/2 )
- sh(x)=(e x -e -x )/2
- sgn(x) — знак х
в) Если S=0,то уравнение имеет меньше трех различных решений:
Консультации и техническая
поддержка сайта: Zavarka Team
Решение кубических уравнений
Кубическое уравнение, содержащее коэффициенты с действительным корнем, остальные два считаются комплексно-сопряженной парой. Будут рассмотрены уравнения с двучленами и возвратные, а также с поиском рациональных корней. Вся информация будет подкреплена примерами.
Решение двучленного кубического уравнения вида A x 3 + B = 0
Кубическое уравнение, содержащее двучлен, имеет вид A x 3 + B = 0 . Его необходимо приводить к x 3 + B A = 0 с помощью деления на А , отличного от нуля. После чего можно применять формулу сокращенного умножения суммы кубов. Получаем, что
x 3 + B A = 0 x + B A 3 x 2 — B A 3 x + B A 2 3 = 0
Результат первой скобки примет вид x = — B A 3 , а квадратный трехчлен — x 2 — B A 3 x + B A 2 3 , причем только с комплексными корнями.
Найти корни кубического уравнения 2 x 3 — 3 = 0 .
Решение
Необходимо найти х из уравнения. Запишем:
2 x 3 — 3 = 0 x 3 — 3 2 = 0
Необходимо применить формулу сокращенного умножения. Тогда получим, что
x 3 — 3 2 = 0 x — 3 3 2 6 x 2 + 3 3 2 6 x + 9 2 3 = 0
Раскроем первую скобку и получим x = 3 3 2 6 . Вторая скобка не имеет действительных корней, потому как дискриминант меньше нуля.
Ответ: x = 3 3 2 6 .
Решение возвратного кубического уравнения вида A x 3 + B x 2 + B x + A = 0
Вид квадратного уравнения — A x 3 + B x 2 + B x + A = 0 , где значения А и В являются коэффициентами. Необходимо произвести группировку. Получим, что
A x 3 + B x 2 + B x + A = A x 3 + 1 + B x 2 + x = = A x + 1 x 2 — x + 1 + B x x + 1 = x + 1 A x 2 + x B — A + A
Корень уравнения равен х = — 1 , тогда для получения корней квадратного трехчлена A x 2 + x B — A + A необходимо задействовать через нахождение дискриминанта.
Решить уравнение вида 5 x 3 — 8 x 2 — 8 x + 5 = 0 .
Решение
Уравнение является возвратным. Необходимо произвести группировку. Получим, что
5 x 3 — 8 x 2 — 8 x + 5 = 5 x 3 + 1 — 8 x 2 + x = = 5 x + 1 x 2 — x + 1 — 8 x x + 1 = x + 1 5 x 2 — 5 x + 5 — 8 x = = x + 1 5 x 2 — 13 x + 5 = 0
Если х = — 1 является корнем уравнения, тогда необходимо найти корни заданного трехчлена 5 x 2 — 13 x + 5 :
5 x 2 — 13 x + 5 = 0 D = ( — 13 ) 2 — 4 · 5 · 5 = 69 x 1 = 13 + 69 2 · 5 = 13 10 + 69 10 x 2 = 13 — 69 2 · 5 = 13 10 — 69 10
Ответ:
x 1 = 13 10 + 69 10 x 2 = 13 10 — 69 10 x 3 = — 1
Решение кубических уравнений с рациональными корнями
Если х = 0 , то он является корнем уравнения вида A x 3 + B x 2 + C x + D = 0 . При свободном члене D = 0 уравнение принимает вид A x 3 + B x 2 + C x = 0 . При вынесении х за скобки получим, что уравнение изменится. При решении через дискриминант или Виета оно примет вид x A x 2 + B x + C = 0 .
Найти корни заданного уравнения 3 x 3 + 4 x 2 + 2 x = 0 .
Решение
3 x 3 + 4 x 2 + 2 x = 0 x 3 x 2 + 4 x + 2 = 0
Х = 0 – это корень уравнения. Следует найти корни квадратного трехчлена вида 3 x 2 + 4 x + 2 . Для этого необходимо приравнять к нулю и продолжить решение при помощи дискриминанта. Получим, что
D = 4 2 — 4 · 3 · 2 = — 8 . Так как его значение отрицательное, то корней трехчлена нет.
Ответ: х = 0 .
Когда коэффициенты уравнения A x 3 + B x 2 + C x + D = 0 целые, то в ответе можно получить иррациональные корни. Если A ≠ 1 , тогда при умножении на A 2 обеих частей уравнения проводится замена переменных, то есть у = А х :
A x 3 + B x 2 + C x + D = 0 A 3 · x 3 + B · A 2 · x 2 + C · A · A · x + D · A 2 = 0 y = A · x ⇒ y 3 + B · y 2 + C · A · y + D · A 2
Приходим к виду кубического уравнения. Корни могут быть целыми или рациональными. Чтобы получить тождественное равенство, необходимо произвести подстановку делителей в полученное уравнение. Тогда полученный y 1 будет являться корнем. Значит и корнем исходного уравнения вида x 1 = y 1 A . Необходимо произвести деление многочлена A x 3 + B x 2 + C x + D на x — x 1 . Тогда сможем найти корни квадратного трехчлена.
Найти корни заданного уравнения 2 x 3 — 11 x 2 + 12 x + 9 = 0 .
Решение
Необходимо произвести преобразование с помощью умножения на 2 2 обеих частей, причем с заменой переменной типа у = 2 х . Получаем, что
2 x 3 — 11 x 2 + 12 x + 9 = 0 2 3 x 3 — 11 · 2 2 x 2 + 24 · 2 x + 36 = 0 y = 2 x ⇒ y 3 — 11 y 2 + 24 y + 36 = 0
Свободный член равняется 36 , тогда необходимо зафиксировать все его делители:
± 1 , ± 2 , ± 3 , ± 4 , ± 6 , ± 9 , ± 12 , ± 36
Необходимо произвести подстановку y 3 — 11 y 2 + 24 y + 36 = 0 , чтобы получить тождество вида
1 3 — 11 · 1 2 + 24 · 1 + 36 = 50 ≠ 0 ( — 1 ) 3 — 11 · ( — 1 ) 2 + 24 · ( — 1 ) + 36 = 0
Отсюда видим, что у = — 1 – это корень. Значит, x = y 2 = — 1 2 .
Далее следует деление 2 x 3 — 11 x 2 + 12 x + 9 на x + 1 2 при помощи схемы Горнера:
| x i | Коэффициенты многочлена | |||
|---|---|---|---|---|
| 2 | — 11 | 12 | 9 | |
| — 0 . 5 | 2 | — 11 + 2 · ( — 0 . 5 ) = — 12 | 12 — 12 · ( — 0 . 5 ) = 18 | 9 + 18 · ( — 0 . 5 ) = 0 |
2 x 3 — 11 x 2 + 12 x + 9 = x + 1 2 2 x 2 — 12 x + 18 = = 2 x + 1 2 x 2 — 6 x + 9
После чего необходимо найти корни квадратного уравнения вида x 2 — 6 x + 9 . Имеем, что уравнение следует привести к виду x 2 — 6 x + 9 = x — 3 2 , где х = 3 будет его корнем.
Ответ: x 1 = — 1 2 , x 2 , 3 = 3 .
Алгоритм можно применять для возвратных уравнений. Видно, что — 1 – это его корень, значит, левая часть может быть поделена на х + 1 . Только тогда можно будет найти корни квадратного трехчлена. При отсутствии рациональных корней применяются другие способы решения для разложения многочлена на множители.
Решение кубических уравнений по формуле Кардано
Нахождение кубических корней возможно при помощи формулы Кардано. При A 0 x 3 + A 1 x 2 + A 2 x + A 3 = 0 необходимо найти B 1 = A 1 A 0 , B 2 = A 2 A 0 , B 3 = A 3 A 0 .
После чего p = — B 1 2 3 + B 2 и q = 2 B 1 3 27 — B 1 B 2 3 + B 3 .
Полученные p и q в формулу Кардано. Получим, что
y = — q 2 + q 2 4 + p 3 27 3 + — q 2 — q 2 4 + p 3 27 3
Подбор кубических корней должен удовлетворять на выходе значению — p 3 . Тогда корни исходного уравнения x = y — B 1 3 . Рассмотрим решение предыдущего примера, используя формулу Кардано.
Найти корни заданного уравнения 2 x 3 — 11 x 2 + 12 x + 9 = 0 .
Решение
Видно, что A 0 = 2 , A 1 = — 11 , A 2 = 12 , A 3 = 9 .
Необходимо найти B 1 = A 1 A 0 = — 11 2 , B 2 = A 2 A 0 = 12 2 = 6 , B 3 = A 3 A 0 = 9 2 .
Отсюда следует, что
p = — B 1 2 3 + B 2 = — — 11 2 2 3 + 6 = — 121 12 + 6 = — 49 12 q = 2 B 1 3 27 — B 1 B 2 3 + B 3 = 2 · — 11 2 3 27 — — 11 2 · 6 3 + 9 2 = 343 108
Производим подстановку в формулу Кордано и получим
y = — q 2 + q 2 4 + p 3 27 3 + — q 2 — — q 2 4 + p 3 27 3 = = — 343 216 + 343 2 4 · 108 2 — 49 3 27 · 12 3 3 + — 343 216 — 343 2 4 · 108 2 — 49 3 27 · 12 3 3 = = — 343 216 3 + — 343 216 3
— 343 216 3 имеет три значения. Рассмотрим их ниже.
— 343 216 3 = 7 6 cos π + 2 π · k 3 + i · sin π + 2 π · k 3 , k = 0 , 1 , 2
Если k = 0 , тогда — 343 216 3 = 7 6 cos π 3 + i · sin π 3 = 7 6 1 2 + i · 3 2
Если k = 1 , тогда — 343 216 3 = 7 6 cosπ + i · sinπ = — 7 6
Если k = 2 , тогда — 343 216 3 = 7 6 cos 5 π 3 + i · sin 5 π 3 = 7 6 1 2 — i · 3 2
Необходимо произвести разбиение по парам, тогда получим — p 3 = 49 36 .
Тогда получим пары: 7 6 1 2 + i · 3 2 и 7 6 1 2 — i · 3 2 , — 7 6 и — 7 6 , 7 6 1 2 — i · 3 2 и 7 6 1 2 + i · 3 2 .
Преобразуем при помощи формулы Кордано:
y 1 = — 343 216 3 + — 343 216 3 = = 7 6 1 2 + i · 3 2 + 7 6 1 2 — i · 3 2 = 7 6 1 4 + 3 4 = 7 6 y 2 = — 343 216 3 + — 343 216 3 = — 7 6 + — 7 6 = — 14 6 y 3 = — 343 216 3 + — 343 216 3 = = 7 6 1 2 — i · 3 2 + 7 6 1 2 + i · 3 2 = 7 6 1 4 + 3 4 = 7 6
x 1 = y 1 — B 1 3 = 7 6 + 11 6 = 3 x 2 = y 2 — B 1 3 = — 14 6 + 11 6 = — 1 2 x 3 = y 3 — B 1 3 = 7 6 + 11 6 = 3
Ответ: x 1 = — 1 2 , x 2 , 3 = 3
При решении кубических уравнений можно встретить сведение к решению уравнений 4 степени методом Феррари.
Решение кубических уравнений — методы и примеры вычислений
История и формулировки
Кубические уравнения составлялись ещё в Древней Греции и Египте. Археологами были найдены клинописные таблицы XVI века до нашей эры, содержащие описание возможного их решения. Вычислением кубов занимался Гиппократ, пытавшийся свести задачу к нахождению отрезков с помощью чертёжных инструментов. Архимед использовал для поиска ответа пересечение двух конусов.
Впервые методы решения такого рода уравнений были описаны в китайском учебнике «Математика в девяти книгах», составленном во втором столетии до нашей эры. В седьмом веке Омар Хайям на основании своих работ приходит к выводу, что решение уравнений третьей степени может иметь более одного ответа.
Математик Шараф ад-Дин публикует тракт об уравнениях, в котором описывает восемь различных типов кубических выражений, имеющих положительное решение. В своих вычислениях он использует численную аппроксимацию. Учёный не только разработал подход для решения с использованием производной функции и экстремумов, но и понял важность дискриминанта многочлена при нахождении кубов.
В 1530 году итальянский математик Никколо Тарталья разрабатывает методику решения, которой он после поделился с Джероламо Кардано. Согласно этому способу нужно было извлекать квадратный корень из отрицательного числа. Параллельно с этими исследованиями, основоположник символической алгебры Франсуа Виет, предлагает свой способ решения кубического равенства с тремя корнями. Позднее его работу описал и обосновал Рене Декарт.
Уравнением третьей степени называют выражение вида: a*y 3 + d*y 2 + c*y + n = 0. В математике оно называется кососимметрическим. Число y, значение которого необходимо найти, при подстановке превращает формулу в тождество. Называется оно корнем уравнения или просто решением. Кроме этого, y ещё является и корнем многочлена куба.
Таким образом, в кубических уравнениях стоит только одна переменная в третьей степени. Они всегда имеют три корня. При этом ответы могут быть равны друг другу и даже быть комплексными (но не более двух).
Формула квадратного уравнения
Используется при решении простейшего равенства методом разложения кубического уравнения на множители. Когда последний член равен нулю, решить такую задачу можно по методу квадратных уравнений. При n = 0, уравнение примет вид :
a*y 3 + d*y 2 + c*y + n = 0.
В полученном выражении каждый член представлен произведением на неизвестное, поэтому переменную y можно вынести за скобки: y*(d*y 2 + c) = 0. Уравнение в скобках является классическим квадратным, которое можно решать несколькими способами:
- разложением на множители;
- с использованием формулы корней квадратного уравнения;
- методом дополнения.
При выборе первого варианта разложение выполняют следующим образом. Например, необходимо решить равенство вида: *y 2 — 11*y — 16 = 0. Квадратный член можно записать в виде двух множителей: 3*y и y. Поэтому их можно записать сразу как произведение в скобках: (3 * + n) * (y + n) = 0. Так как определённый член можно записать в виде произведения 2*2 или 1*4, то формулу можно представить как (3 *y +1) * (y — 16).
Если раскрыть скобки, то получится равенство 3*y 2 — 12 *y + y + 16. Решением (-12*y + y) будет (-11*y). Как раз тот член, который нужен. Используя же произведение 2*2 — искомый член найти не получится.
Равенство раскладывают на два множителя: (3*y +1) (х — 16) = 0. Согласно аксиоме произведение двух членов равно нулю только тогда, когда хотя бы один из них равен нулю. Приравняв каждое выражение в скобках к нулю, можно записать два равенства: 3*y + 1 = 0 и y — 16 = 0. При решении каждого из них получится два ответа: y = 1/3 и y = 16.
Для проверки результата необходимо оба возможных решения подставить в формулу. Так как для квадратного уравнения существует только два решения, а для кубического три, то в этом случае третьим ответом будет ноль. Поэтому решением уравнения будет три корня: 0, 1/3, 16.
Но проще и нагляднее всего использовать второй вариант. Формула корней кубического уравнения имеет вид: y = ((-d + (d 2 — 4*a*c) ½ ) / 2*a и y = ((-d — (d 2 — 4*a*c) ½ ) / 2*a. Корни квадратного уравнения и будут ответом для кубического. Например, 5*y 2 — 7*y — 14 = 0. Приняв, что a = 5, d = -7, c = — 14 и подставив числовые значения, будет верным запись: y = 1 4 / 5 и y = -1. Дробное решение и отрицательное будет являться корнями кубического равенства.
Разложение на множители
Если определённый член не равен нулю, то посчитать игрек при помощи квадратных уравнений невозможно. В этом случае используется метод разложения на свободные множители. Например, 2 * y 3 + 9 * y 2 +13 * y + 6 = 0. Чтобы разложить кубическое уравнение на множители и определить неизвестное, придерживаются следующего порядка:
- Вычисляют множитель кубического коэффициента и свободного члена. Это те числа, которые при умножении друг на друга дают исходное число. Например, цифру шесть можно представить перемножением 6*1 и 2*3, то есть множителями шести являются: 1, 2, 3, 6. Коэффициентом кубического члена является двойка, соответственно её множители — цифры один и два.
- Выполняют деление множителей кубического члена на цифры разложения свободного. В результате действия получится набор, состоящий из дробных частей и целых чисел, при этом они могут быть и отрицательными. Для уравнения 2 * y 3 + 9 * y 2 +13 * y + 6 = 0 такой набор будет состоять из 1, -1, ½, -½, 1/3, -1/3, 1/6, -1/6, 2, -2, 2/3, -2/3 .
- Определяют ряды чисел, в которых существуют рациональные решения кубического выражения. Для рассматриваемого примера они будут следующие: -1*2 = -2; 9 + (-2) = 7; (-1) * 7 = -7; 13 +(-7) = 6; (-1)*6 = -6; 6+(-6) = 0 .
Вычисление рационального числа операция долгая и требующая внимания. Поэтому для быстрого нахождения ответа используется деление по схеме Горнера. По этой схеме выполняют деление целых цифр на коэффициенты всех членов равенства. Если в ответе получается только целая часть, то эти числа считаются вариантами решения. Таким методом можно находить и иррациональные выражения.
Чтобы освоить способ Горнера, необходимо тщательно в нём разобраться. Способ заключается в делении коэффициентов многочлена без учёта степенных показателей. Вычитание заменяется сложением как при делении в столбик. То есть уравнение, впрочем, как и неравенство, вида y 3 + 2*y 2 — 4 *y + 8, записывается как 1 2 -4 8 с необходимым делимым. В результате должен получиться многочлен с остатком. Если он будет нулевым, то одним из ответов уравнения и будет делимое .
Использование дискриминанта
Дискриминант степенного выражения представляет произведение квадратов разностей корней в различных сочетаниях. Другими словами, берут пару, состоящую из любых корней уравнения, вычитают друг из друга и возводят в квадрат. Это и будет один множитель. Затем берут другую пару и повторяют действия. Таким образом, перебирают все варианты.
При решении кубических равенств используют значения коэффициентов. Например, для уравнения y 3 — 3* y 2 + 3* y — 1, они будут равны: a = 1, d = -3, c = 3, n = -1. Затем вычисляют дельта нулевое. Это ключевая величина, которая после подставляется в формулу. В примере, Δ0 = d 2 — 3 * a * c, определяют как (-3) 2 — 3 * (1) * (3) = 9 − 3 * 3 = 0 .
Затем находят дельта один. Δ1 = 2 * d 3 — 9 * a * d * c + 27 * a 2 * n. Подставив значения в формулу, вычисляют Δ1:
2 (-3) 3 — 9 (1)(-3)*(3) + 27 (1) 2 * (-1) = 2 (-27) — 9 (-9) + 27 (-1) = -54 + 81 — 27 = 81 − 81 = 0 = Δ 1.
Используя найденное, по аналогии с квадратичным равенством находят дискриминант: d 2 — 4 * a * c. Применительно к кубическому виду применяется правило, что показатель отрицательный, когда уравнение может иметь только одно решение. Если же его значение равно нулю — одно или два. Уравнение кубического вида всегда должно иметь хотя бы одно решение, так как его график должен проходить через ось икс.
Так как в примере дельта-ноль и один равны нулю, то можно использовать следующее выражение:
- Δ1 2 — 4 * Δ0 3 / — 27 *a 2 ;
- (0) 2 — 4 * (0) 3 / — 27 * (1) 2 ;
- (0−0) / 27;
- Δ = 0.
Исходя из этого, уравнение имеет два решения. Вычислив С, можно определить возможные решения уравнения. Заменив по мере необходимости дельты, решается равенство:
C = ((Δ 1 2 — 4 Δ 0 3 ) +Δ) / 2) ½ = (((0 — 0) + 0)/2) ½ = 0.
Корни куба определяются по формуле: u n C + Δ0/(u n C)) / 3*a, где u = (-1 + √(-3))/2, а n равно одному, двум или трём. Если подставить эти значения в равенство, и оно будет верным, то эта цифра и является возможным решением уравнения. Этот способ показательный, но довольно сложный. Но если его понять, то проблем с решением уравнений любой сложности возникнуть не должно.
Теорема Виета и двучлен
Выражение вида: a*y 3 + d = 0 называется двухчленным или неполным уравнением. Для его решения нужно равенство привести к виду: y 3 + d/a = 0. Затем используя формулу сокращённого умножения для суммы кубов можно записать:
(y + 3 √ d/a) * (y 2 − ( 3 √ d/a)* y + 3 √ (d/a) 2 ) = 0.
Из первого множителя и находят значение игрека. Оно будет равно 3 √ d/a, ведь второй множитель — это квадратный трёхчлен с корнями комплексного вида.
Для проверки рациональных равенств удобно применять теорему Виета. Согласно ей корни уравнения связаны с коэффициентами выражениями:
- y1 + y2 + y3 = — d/a;
- y1 * y2 + y2 * y3 + y1 * y3 = c/a;
- y1 * y2 * y3 = — n/a.
Используя теорему, некоторые уравнения можно решить даже устно. Например, y 3 + 2y — 24 = 0. Решение выполняется в следующей последовательности:
- записывают теорему применительно к равенству;
- определяют знаки корней;
- раскладывают определённый член.
Частным случаем применения теоремы являются тригонометрические формулы для кубического равенства:
S = Q 3 — R 2 , где Q = (a2 — 3d)/9, а R = (2 а 3 — 9ad + 27c) / 54.
В зависимости от знака S применяется одна из следующих формул : φ = (arcos (R/Q 3/2 ))/3 и φ = (arcos (ЇRЇ/Q 3/2 ))/3. Первое выражение справедливо при S > 0 и имеет три корня: y 1 = -2 (Q) ½ * cos (φ) — a/3; y 2 = — (Q) ½ cos (φ + 2p /3) — a/3; y 3 = -2 (Q) ½ * cos (φ — 2p/3) — a/3. А второе при S ½ * ch (φ) — a/3. В случае же когда S=0,то уравнение имеет следующие корни: y 1= -2*R1 /3 — a/3; y 2= y 3 =R1/3 — a/3.
Теорему Виета можно использовать и для наивысшей, четвёртой степени, при которой ещё существует аналитическое решение.
Подробный онлайн-калькулятор
Вычисление корней требует внимательности и усердия. Чтобы быстро находить решение, нужно не только знание теории, но и практические занятия. Конечно же, знать формулы и уметь решать уравнения нужно самому.
Но при самостоятельном вычислении существует вероятность допущения ошибки. Поэтому на помощь приходят своего рода решебники-онлайн. Они умеют не только точно и быстро определять корни равенства, но и показывать подробное вычисление. Благодаря этому можно не просто получить правильный ответ, но и разобраться в решении, понять различные нюансы, проверить свои знания.
Из наиболее популярных интернет-порталов, позволяющих найти корни кубического уравнения онлайн, можно выделить: mathforyou. net, allcalc.ru, wedmath.ru, kontrolnaya-radota.ru. Воспользоваться такими сайтами-решателями сможет любой пользователь, даже не имеющий представление о методах решения уравнений.
Для этого нужно просто заполнить предлагаемые на странице поля и нажать кнопку «Рассчитать» или «Решить». Калькулятор сам на основании запрограммированных формул, чаще всего по методу Вието — Кардано, выполнит расчёт и выведет на экран ответ. Кроме этого, будет предложено подробное решение с описанием. На этих сайтах также можно посмотреть и примеры решений, формулы, теоремы.
http://zaochnik.com/spravochnik/matematika/systems/reshenie-kubicheskih-uravnenij/
http://nauka.club/matematika/reshenie-kubicheskikh-uravneniy.html
This article is about cubic equations in one variable. For cubic equations in two variables, see cubic plane curve.
Graph of a cubic function with 3 real roots (where the curve crosses the horizontal axis at y = 0). The case shown has two critical points. Here the function is f(x) = 1/4(x3 + 3x2 − 6x − 
In algebra, a cubic equation in one variable is an equation of the form
in which a is nonzero.
The solutions of this equation are called roots of the cubic function defined by the left-hand side of the equation. If all of the coefficients a, b, c, and d of the cubic equation are real numbers, then it has at least one real root (this is true for all odd-degree polynomial functions). All of the roots of the cubic equation can be found by the following means:
- algebraically: more precisely, they can be expressed by a cubic formula involving the four coefficients, the four basic arithmetic operations, square roots and cube roots. (This is also true of quadratic (second-degree) and quartic (fourth-degree) equations, but not for higher-degree equations, by the Abel–Ruffini theorem.)
- trigonometrically
- numerical approximations of the roots can be found using root-finding algorithms such as Newton’s method.
The coefficients do not need to be real numbers. Much of what is covered below is valid for coefficients in any field with characteristic other than 2 and 3. The solutions of the cubic equation do not necessarily belong to the same field as the coefficients. For example, some cubic equations with rational coefficients have roots that are irrational (and even non-real) complex numbers.
History[edit]
Cubic equations were known to the ancient Babylonians, Greeks, Chinese, Indians, and Egyptians.[1][2][3] Babylonian (20th to 16th centuries BC) cuneiform tablets have been found with tables for calculating cubes and cube roots.[4][5] The Babylonians could have used the tables to solve cubic equations, but no evidence exists to confirm that they did.[6] The problem of doubling the cube involves the simplest and oldest studied cubic equation, and one for which the ancient Egyptians did not believe a solution existed.[7] In the 5th century BC, Hippocrates reduced this problem to that of finding two mean proportionals between one line and another of twice its length, but could not solve this with a compass and straightedge construction,[8] a task which is now known to be impossible. Methods for solving cubic equations appear in The Nine Chapters on the Mathematical Art, a Chinese mathematical text compiled around the 2nd century BC and commented on by Liu Hui in the 3rd century.[2] In the 3rd century AD, the Greek mathematician Diophantus found integer or rational solutions for some bivariate cubic equations (Diophantine equations).[3][9] Hippocrates, Menaechmus and Archimedes are believed to have come close to solving the problem of doubling the cube using intersecting conic sections,[8] though historians such as Reviel Netz dispute whether the Greeks were thinking about cubic equations or just problems that can lead to cubic equations. Some others like T. L. Heath, who translated all of Archimedes’ works, disagree, putting forward evidence that Archimedes really solved cubic equations using intersections of two conics, but also discussed the conditions where the roots are 0, 1 or 2.[10]
Graph of the cubic function f(x) = 2x3 − 3x2 − 3x + 2 = (x + 1) (2x − 1) (x − 2)
In the 7th century, the Tang dynasty astronomer mathematician Wang Xiaotong in his mathematical treatise titled Jigu Suanjing systematically established and solved numerically 25 cubic equations of the form x3 + px2 + qx = N, 23 of them with p, q ≠ 0, and two of them with q = 0.[11]
In the 11th century, the Persian poet-mathematician, Omar Khayyam (1048–1131), made significant progress in the theory of cubic equations. In an early paper, he discovered that a cubic equation can have more than one solution and stated that it cannot be solved using compass and straightedge constructions. He also found a geometric solution.[12][a] In his later work, the Treatise on Demonstration of Problems of Algebra, he wrote a complete classification of cubic equations with general geometric solutions found by means of intersecting conic sections.[13][14] Khayyam made an attempt to come up with an algebraic formula for extracting cubic roots. He wrote:
“We have tried to express these roots by algebra but have failed. It may be, however, that men who come after us will succeed.”[15]
In the 12th century, the Indian mathematician Bhaskara II attempted the solution of cubic equations without general success. However, he gave one example of a cubic equation: x3 + 12x = 6x2 + 35.[16] In the 12th century, another Persian mathematician, Sharaf al-Dīn al-Tūsī (1135–1213), wrote the Al-Muʿādalāt (Treatise on Equations), which dealt with eight types of cubic equations with positive solutions and five types of cubic equations which may not have positive solutions. He used what would later be known as the «Ruffini-Horner method» to numerically approximate the root of a cubic equation. He also used the concepts of maxima and minima of curves in order to solve cubic equations which may not have positive solutions.[17] He understood the importance of the discriminant of the cubic equation to find algebraic solutions to certain types of cubic equations.[18]
In his book Flos, Leonardo de Pisa, also known as Fibonacci (1170–1250), was able to closely approximate the positive solution to the cubic equation x3 + 2x2 + 10x = 20. Writing in Babylonian numerals he gave the result as 1,22,7,42,33,4,40 (equivalent to 1 + 22/60 + 7/602 + 42/603 + 33/604 + 4/605 + 40/606), which has a relative error of about 10−9.[19]
In the early 16th century, the Italian mathematician Scipione del Ferro (1465–1526) found a method for solving a class of cubic equations, namely those of the form x3 + mx = n. In fact, all cubic equations can be reduced to this form if one allows m and n to be negative, but negative numbers were not known to him at that time. Del Ferro kept his achievement secret until just before his death, when he told his student Antonio Fior about it.
Niccolò Fontana Tartaglia
In 1535, Niccolò Tartaglia (1500–1557) received two problems in cubic equations from Zuanne da Coi and announced that he could solve them. He was soon challenged by Fior, which led to a famous contest between the two. Each contestant had to put up a certain amount of money and to propose a number of problems for his rival to solve. Whoever solved more problems within 30 days would get all the money. Tartaglia received questions in the form x3 + mx = n, for which he had worked out a general method. Fior received questions in the form x3 + mx2 = n, which proved to be too difficult for him to solve, and Tartaglia won the contest.
Later, Tartaglia was persuaded by Gerolamo Cardano (1501–1576) to reveal his secret for solving cubic equations. In 1539, Tartaglia did so only on the condition that Cardano would never reveal it and that if he did write a book about cubics, he would give Tartaglia time to publish. Some years later, Cardano learned about del Ferro’s prior work and published del Ferro’s method in his book Ars Magna in 1545, meaning Cardano gave Tartaglia six years to publish his results (with credit given to Tartaglia for an independent solution). Cardano’s promise to Tartaglia said that he would not publish Tartaglia’s work, and Cardano felt he was publishing del Ferro’s, so as to get around the promise. Nevertheless, this led to a challenge to Cardano from Tartaglia, which Cardano denied. The challenge was eventually accepted by Cardano’s student Lodovico Ferrari (1522–1565). Ferrari did better than Tartaglia in the competition, and Tartaglia lost both his prestige and his income.[20]
Cardano noticed that Tartaglia’s method sometimes required him to extract the square root of a negative number. He even included a calculation with these complex numbers in Ars Magna, but he did not really understand it. Rafael Bombelli studied this issue in detail[21] and is therefore often considered as the discoverer of complex numbers.
François Viète (1540–1603) independently derived the trigonometric solution for the cubic with three real roots, and René Descartes (1596–1650) extended the work of Viète.[22]
Factorization[edit]
If the coefficients of a cubic equation are rational numbers, one can obtain an equivalent equation with integer coefficients, by multiplying all coefficients by a common multiple of their denominators. Such an equation
with integer coefficients, is said to be reducible if the polynomial on the left-hand side is the product of polynomials of lower degrees. By Gauss’s lemma, if the equation is reducible, one can suppose that the factors have integer coefficients.
Finding the roots of a reducible cubic equation is easier than solving the general case. In fact, if the equation is reducible, one of the factors must have degree one, and thus have the form
with q and p being coprime integers. The rational root test allows finding q and p by examining a finite number of cases (because q must be a divisor of a, and p must be a divisor of d).
Thus, one root is 
(The coefficients seem not to be integers, but must be integers if p / q is a root.)
Then, the other roots are the roots of this quadratic polynomial and can be found by using the quadratic formula.
Depressed cubic[edit]
Cubics of the form
are said to be depressed. They are much simpler than general cubics, but are fundamental, because the study of any cubic may be reduced by a simple change of variable to that of a depressed cubic.
Let
be a cubic equation. The change of variable
gives a cubic (in t) that has no term in t2.
After dividing by a one gets the depressed cubic equation
with
The roots 

for 
Discriminant and nature of the roots[edit]
The nature (real or not, distinct or not) of the roots of a cubic can be determined without computing them explicitly, by using the discriminant.
Discriminant[edit]
The discriminant of a polynomial is a function of its coefficients that is zero if and only if the polynomial has a multiple root, or, if it is divisible by the square of a non-constant polynomial. In other words, the discriminant is nonzero if and only if the polynomial is square-free.
If r1, r2, r3 are the three roots (not necessarily distinct nor real) of the cubic 
The discriminant of the depressed cubic 
The discriminant of the general cubic 
It is the product of 
It follows that one of these two discriminants is zero if and only if the other is also zero, and, if the coefficients are real, the two discriminants have the same sign. In summary, the same information can be deduced from either one of these two discriminants.
To prove the preceding formulas, one can use Vieta’s formulas to express everything as polynomials in r1, r2, r3, and a. The proof then results in the verification of the equality of two polynomials.
Nature of the roots[edit]
If the coefficients of a polynomial are real numbers, and its discriminant 
This can be proved as follows. First, if r is a root of a polynomial with real coefficients, then its complex conjugate is also a root. So the non-real roots, if any, occur as pairs of complex conjugate roots. As a cubic polynomial has three roots (not necessarily distinct) by the fundamental theorem of algebra, at least one root must be real.
As stated above, if r1, r2, r3 are the three roots of the cubic 
If the three roots are real and distinct, the discriminant is a product of positive reals, that is 
If only one root, say r1, is real, then r2 and r3 are complex conjugates, which implies that r2 – r3 is a purely imaginary number, and thus that (r2 – r3)2 is real and negative. On the other hand, r1 – r2 and r1 – r3 are complex conjugates, and their product is real and positive.[23] Thus the discriminant is the product of a single negative number and several positive ones. That is 
Multiple root[edit]
If the discriminant of a cubic is zero, the cubic has a multiple root. If furthermore its coefficients are real, then all of its roots are real.
The discriminant of the depressed cubic 


and a double root
In other words,
This result can be proved by expanding the latter product or retrieved by solving the rather simple system of equations resulting from Vieta’s formulas.
By using the reduction of a depressed cubic, these results can be extended to the general cubic. This gives: If the discriminant of the cubic 
- either, if
the cubic has a triple root
-
- and
- or, if
the cubic has a double root
-
- and a simple root,
- and thus
Characteristic 2 and 3[edit]
The above results are valid when the coefficients belong to a field of characteristic other than 2 or 3, but must be modified for characteristic 2 or 3, because of the involved divisions by 2 and 3.
The reduction to a depressed cubic works for characteristic 2, but not for characteristic 3. However, in both cases, it is simpler to establish and state the results for the general cubic. The main tool for that is the fact that a multiple root is a common root of the polynomial and its formal derivative. In these characteristics, if the derivative is not a constant, it is a linear polynomial in characteristic 3, and is the square of a linear polynomial in characteristic 2. Therefore, for either characteristic 2 or 3, the derivative has only one root. This allows computing the multiple root, and the third root can be deduced from the sum of the roots, which is provided by Vieta’s formulas.
A difference with other characteristics is that, in characteristic 2, the formula for a double root involves a square root, and, in characteristic 3, the formula for a triple root involves a cube root.
Cardano’s formula[edit]
Gerolamo Cardano is credited with publishing the first formula for solving cubic equations, attributing it to Scipione del Ferro and Niccolo Fontana Tartaglia. The formula applies to depressed cubics, but, as shown in § Depressed cubic, it allows solving all cubic equations.
Cardano’s result is that, if
is a cubic equation such that p and q are real numbers such that 
where 



See § Derivation of the roots, below, for several methods for getting this result.
As shown in § Nature of the roots, the two other roots are non-real complex conjugate numbers, in this case. It was later shown (Cardano did not know complex numbers) that the two other roots are obtained by multiplying one of the cube roots by the primitive cube root of unity 

![{displaystyle varepsilon _{1}{sqrt[{3}]{u_{1}}}+varepsilon _{2}{sqrt[{3}]{u_{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02e0bcb38519295e82e15d08fab015ad7aad313c)
![{displaystyle varepsilon _{2}{sqrt[{3}]{u_{1}}}+varepsilon _{1}{sqrt[{3}]{u_{2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c765895e69b164dd7bc0b67dc06a5d5227ff3633)
If 
In casus irreducibilis, Cardano’s formula can still be used, but some care is needed in the use of cube roots. A first method is to define the symbols 
![{displaystyle {sqrt[{3}]{{~}^{~}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24d9ec8c0118de0d1a1c4002b6edfa9a90209ddf)
The second way for making Cardano’s formula always correct, is to remark that the product of the two cube roots must be –p / 3. It results that a root of the equation is
In this formula, the symbols 
![{displaystyle {sqrt[{3}]{{~}^{~}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24d9ec8c0118de0d1a1c4002b6edfa9a90209ddf)

This formula for the roots is always correct except when p = q = 0, with the proviso that if p = 0, the square root is chosen so that C ≠ 0. However, the formula is useless in these cases as the roots can be expressed without any cube root. Similarly, the formula is also useless in the other cases where no cube root is needed, that is when 
This formula is also correct when p and q belong to any field of characteristic other than 2 or 3.
General cubic formula[edit]
A cubic formula for the roots of the general cubic equation (with a ≠ 0)
can be deduced from every variant of Cardano’s formula by reduction to a depressed cubic. The variant that is presented here is valid not only for real coefficients, but also for coefficients a, b, c, d belonging to any field of characteristic different of 2 and 3.
The formula being rather complicated, it is worth splitting it in smaller formulas.
Let
(Both 



Then let
where the symbols 
![{displaystyle {sqrt[{3}]{{~}^{~}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24d9ec8c0118de0d1a1c4002b6edfa9a90209ddf)


With these conventions, one of the roots is
The other two roots can be obtained by changing the choice of the cube root in the definition of C, or, equivalently by multiplying C by a primitive cube root of unity, that is –1 ± √–3/2. In other words, the three roots are
where ξ = –1 + √–3/2.
As for the special case of a depressed cubic, this formula applies but is useless when the roots can be expressed without cube roots. In particular, if 



Trigonometric and hyperbolic solutions[edit]
Trigonometric solution for three real roots[edit]
When a cubic equation with real coefficients has three real roots, the formulas expressing these roots in terms of radicals involve complex numbers. Galois theory allows proving that when the three roots are real, and none is rational (casus irreducibilis), one cannot express the roots in terms of real radicals. Nevertheless, purely real expressions of the solutions may be obtained using trigonometric functions, specifically in terms of cosines and arccosines.[25] More precisely, the roots of the depressed cubic
are[26]
This formula is due to François Viète.[22] It is purely real when the equation has three real roots (that is 
This formula can be straightforwardly transformed into a formula for the roots of a general cubic equation, using the back-substitution described in § Depressed cubic.
The formula can be proved as follows: Starting from the equation t3 + pt + q = 0, let us set t = u cos θ. The idea is to choose u to make the equation coincide with the identity
For this, choose 

Combining with the above identity, one gets
and the roots are thus
Hyperbolic solution for one real root[edit]
When there is only one real root (and p ≠ 0), this root can be similarly represented using hyperbolic functions, as[27][28]
If p ≠ 0 and the inequalities on the right are not satisfied (the case of three real roots), the formulas remain valid but involve complex quantities.
When p = ±3, the above values of t0 are sometimes called the Chebyshev cube root.[29] More precisely, the values involving cosines and hyperbolic cosines define, when p = −3, the same analytic function denoted C1/3(q), which is the proper Chebyshev cube root. The value involving hyperbolic sines is similarly denoted S1/3(q), when p = 3.
Geometric solutions[edit]
Omar Khayyám’s solution[edit]
Omar Khayyám’s geometric solution of a cubic equation, for the case m = 2, n = 16, giving the root 2. The intersection of the vertical line on the x-axis at the center of the circle is happenstance of the example illustrated.
For solving the cubic equation x3 + m2x = n where n > 0, Omar Khayyám constructed the parabola y = x2/m, the circle that has as a diameter the line segment [0, n/m2] on the positive x-axis, and a vertical line through the point where the circle and the parabola intersect above the x-axis. The solution is given by the length of the horizontal line segment from the origin to the intersection of the vertical line and the x-axis (see the figure).
A simple modern proof is as follows. Multiplying the equation by x/m2 and regrouping the terms gives
The left-hand side is the value of y2 on the parabola. The equation of the circle being y2 + x(x − n/m2) = 0, the right hand side is the value of y2 on the circle.
Solution with angle trisector[edit]
A cubic equation with real coefficients can be solved geometrically using compass, straightedge, and an angle trisector if and only if it has three real roots.[30]: Thm. 1
A cubic equation can be solved by compass-and-straightedge construction (without trisector) if and only if it has a rational root. This implies that the old problems of angle trisection and doubling the cube, set by ancient Greek mathematicians, cannot be solved by compass-and-straightedge construction.
Geometric interpretation of the roots[edit]
Three real roots[edit]
For the cubic (1) with three real roots, the roots are the projection on the x-axis of the vertices A, B, and C of an equilateral triangle. The center of the triangle has the same x-coordinate as the inflection point.
Viète’s trigonometric expression of the roots in the three-real-roots case lends itself to a geometric interpretation in terms of a circle.[22][31] When the cubic is written in depressed form (2), t3 + pt + q = 0, as shown above, the solution can be expressed as
Here 

For the non-depressed case (1) (shown in the accompanying graph), the depressed case as indicated previously is obtained by defining t such that x = t − b/3a so t = x + b/3a. Graphically this corresponds to simply shifting the graph horizontally when changing between the variables t and x, without changing the angle relationships. This shift moves the point of inflection and the centre of the circle onto the y-axis. Consequently, the roots of the equation in t sum to zero.
One real root[edit]
In the Cartesian plane[edit]
The slope of line RA is twice that of RH. Denoting the complex roots of the cubic as g ± hi, g = OM (negative here) and h = √tan ORH = √slope of line RH = BE = DA.
When the graph of a cubic function is plotted in the Cartesian plane, if there is only one real root, it is the abscissa (x-coordinate) of the horizontal intercept of the curve (point R on the figure). Further,[32][33][34] if the complex conjugate roots are written as g ± hi, then the real part g is the abscissa of the tangency point H of the tangent line to cubic that passes through x-intercept R of the cubic (that is the signed length OM, negative on the figure). The imaginary parts ±h are the square roots of the tangent of the angle between this tangent line and the horizontal axis.[clarification needed]
In the complex plane[edit]
With one real and two complex roots, the three roots can be represented as points in the complex plane, as can the two roots of the cubic’s derivative. There is an interesting geometrical relationship among all these roots.
The points in the complex plane representing the three roots serve as the vertices of an isosceles triangle. (The triangle is isosceles because one root is on the horizontal (real) axis and the other two roots, being complex conjugates, appear symmetrically above and below the real axis.) Marden’s theorem says that the points representing the roots of the derivative of the cubic are the foci of the Steiner inellipse of the triangle—the unique ellipse that is tangent to the triangle at the midpoints of its sides. If the angle at the vertex on the real axis is less than π/3 then the major axis of the ellipse lies on the real axis, as do its foci and hence the roots of the derivative. If that angle is greater than π/3, the major axis is vertical and its foci, the roots of the derivative, are complex conjugates. And if that angle is π/3, the triangle is equilateral, the Steiner inellipse is simply the triangle’s incircle, its foci coincide with each other at the incenter, which lies on the real axis, and hence the derivative has duplicate real roots.
Galois group[edit]
Given a cubic irreducible polynomial over a field K of characteristic different from 2 and 3, the Galois group over K is the group of the field automorphisms that fix K of the smallest extension of K (splitting field). As these automorphisms must permute the roots of the polynomials, this group is either the group S3 of all six permutations of the three roots, or the group A3 of the three circular permutations.
The discriminant Δ of the cubic is the square of
where a is the leading coefficient of the cubic, and r1, r2 and r3 are the three roots of the cubic. As 

A3. In other words, the Galois group is A3 if and only if the discriminant is the square of an element of k.
As most integers are not squares, when working over the field Q of the rational numbers, the Galois group of most irreducible cubic polynomials is the group S3 with six elements. An example of a Galois group A3 with three elements is given by p(x) = x3 − 3x − 1, whose discriminant is 81 = 92.
Derivation of the roots[edit]
This section regroups several methods for deriving Cardano’s formula.
Cardano’s method[edit]
This method is due to Scipione del Ferro and Tartaglia, but is named after Gerolamo Cardano who first published it in his book Ars Magna (1545).
This method applies to a depressed cubic t3 + pt + q = 0. The idea is to introduce two variables u and v such that u + v = t and to substitute this in the depressed cubic, giving
At this point Cardano imposed the condition 3uv + p = 0. This removes the third term in previous equality, leading to the system of equations
Knowing the sum and the product of u3 and v3, one deduces that they are the two solutions of the quadratic equation
so
The discriminant of this equation is 
So (without loss of generality in choosing u or v):
As u + v = t, the sum of the cube roots of these solutions is a root of the equation. That is
is a root of the equation; this is Cardano’s formula.
This works well when 

The other roots of the equation can be obtained by changing of cube root, or, equivalently, by multiplying the cube root by each of the two primitive cube roots of unity, which are 
Vieta’s substitution[edit]
Vieta’s substitution is a method introduced by François Viète (Vieta is his Latin name) in a text published posthumously in 1615, which provides directly the second formula of § Cardano’s method, and avoids the problem of computing two different cube roots.[35]
Starting from the depressed cubic t3 + pt + q = 0, Vieta’s substitution is t = w – p/3w.[c]
The substitution t = w – p/3w transforms the depressed cubic into
Multiplying by w3, one gets a quadratic equation in w3:
Let
be any nonzero root of this quadratic equation. If w1, w2 and w3 are the three cube roots of W, then the roots of the original depressed cubic are w1 − p/3w1, w2 − p/3w2, and w3 − p/3w3. The other root of the quadratic equation is 
Lagrange’s method[edit]
In his paper Réflexions sur la résolution algébrique des équations («Thoughts on the algebraic solving of equations»),[36] Joseph Louis Lagrange introduced a new method to solve equations of low degree in a uniform way, with the hope that he could generalize it for higher degrees. This method works well for cubic and quartic equations, but Lagrange did not succeed in applying it to a quintic equation, because it requires solving a resolvent polynomial of degree at least six.[37][38][39]
Apart from the fact that nobody had previously succeeded, this was the first indication of the non-existence of an algebraic formula for degrees 5 and higher; as was later proved by the Abel–Ruffini theorem. Nevertheless, modern methods for solving solvable quintic equations are mainly based on Lagrange’s method.[39]
In the case of cubic equations, Lagrange’s method gives the same solution as Cardano’s. Lagrange’s method can be applied directly to the general cubic equation ax3 + bx2 + cx + d = 0, but the computation is simpler with the depressed cubic equation, t3 + pt + q = 0.
Lagrange’s main idea was to work with the discrete Fourier transform of the roots instead of with the roots themselves. More precisely, let ξ be a primitive third root of unity, that is a number such that ξ3 = 1 and ξ2 + ξ + 1 = 0 (when working in the space of complex numbers, one has 
be the discrete Fourier transform of the roots. If s0, s1 and s2 are known, the roots may be recovered from them with the inverse Fourier transform consisting of inverting this linear transformation; that is,
By Vieta’s formulas, s0 is known to be zero in the case of a depressed cubic, and −b/a for the general cubic. So, only s1 and s2 need to be computed. They are not symmetric functions of the roots (exchanging x1 and x2 exchanges also s1 and s2), but some simple symmetric functions of s1 and s2 are also symmetric in the roots of the cubic equation to be solved. Thus these symmetric functions can be expressed in terms of the (known) coefficients of the original cubic, and this allows eventually expressing the si as roots of a polynomial with known coefficients. This works well for every degree, but, in degrees higher than four, the resulting polynomial that has the si as roots has a degree higher than that of the initial polynomial, and is therefore unhelpful for solving. This is the reason for which Lagrange’s method fails in degrees five and higher.
In the case of a cubic equation, 






In the case of the depressed cubic, one has 





Computation of S and P[edit]
A straightforward computation using the relations ξ3 = 1 and ξ2 + ξ + 1 = 0 gives
This shows that P and S are symmetric functions of the roots. Using Newton’s identities, it is straightforward to express them in terms of the elementary symmetric functions of the roots, giving
with e1 = 0, e2 = p and e3 = −q in the case of a depressed cubic, and e1 = −b/a, e2 = c/a and e3 = −d/a, in the general case.
Applications[edit]
Cubic equations arise in various other contexts.
In mathematics[edit]
- Angle trisection and doubling the cube are two ancient problems of geometry that have been proved to not be solvable by straightedge and compass construction, because they are equivalent to solving a cubic equation.
- Marden’s theorem states that the foci of the Steiner inellipse of any triangle can be found by using the cubic function whose roots are the coordinates in the complex plane of the triangle’s three vertices. The roots of the first derivative of this cubic are the complex coordinates of those foci.
- The area of a regular heptagon can be expressed in terms of the roots of a cubic. Further, the ratios of the long diagonal to the side, the side to the short diagonal, and the negative of the short diagonal to the long diagonal all satisfy a particular cubic equation. In addition, the ratio of the inradius to the circumradius of a heptagonal triangle is one of the solutions of a cubic equation. The values of trigonometric functions of angles related to
satisfy cubic equations.
- Given the cosine (or other trigonometric function) of an arbitrary angle, the cosine of one-third of that angle is one of the roots of a cubic.
- The solution of the general quartic equation relies on the solution of its resolvent cubic.
- The eigenvalues of a 3×3 matrix are the roots of a cubic polynomial which is the characteristic polynomial of the matrix.
- The characteristic equation of a third-order constant coefficients or Cauchy–Euler (equidimensional variable coefficients) linear differential equation or difference equation is a cubic equation.
- Intersection points of cubic Bézier curve and straight line can be computed using direct cubic equation representing Bézier curve.
- Critical points of a quartic function are found by solving a cubic equation (the derivative set equal to zero).
- Inflection points of a quintic function are the solution of a cubic equation (the second derivative set equal to zero).
In other sciences[edit]
- In analytical chemistry, the Charlot equation, which can be used to find the pH of buffer solutions, can be solved using a cubic equation.
- In thermodynamics, equations of state (which relate pressure, volume, and temperature of a substances), e.g. the Van der Waals equation of state, are cubic in the volume.
- Kinematic equations involving linear rates of acceleration are cubic.
- The speed of seismic Rayleigh waves is a solution of the Rayleigh wave cubic equation.
- The steady state speed of a vehicle moving on a slope with air friction for a given input power is solved by a depressed cubic equation.
Notes[edit]
- ^ In O’Connor, John J.; Robertson, Edmund F., «Omar Khayyam», MacTutor History of Mathematics archive, University of St Andrews one may read This problem in turn led Khayyam to solve the cubic equation x3 + 200x = 20x2 + 2000 and he found a positive root of this cubic by considering the intersection of a rectangular hyperbola and a circle. An approximate numerical solution was then found by interpolation in trigonometric tables. The then in the last assertion is erroneous and should, at least, be replaced by also. The geometric construction was perfectly suitable for Omar Khayyam, as it occurs for solving a problem of geometric construction. At the end of his article he says only that, for this geometrical problem, if approximations are sufficient, then a simpler solution may be obtained by consulting trigonometric tables. Textually: If the seeker is satisfied with an estimate, it is up to him to look into the table of chords of Almagest, or the table of sines and versed sines of Mothmed Observatory. This is followed by a short description of this alternate method (seven lines).
- ^ Here,
is not the discriminant of the equation, but its opposite.
- ^ More precisely, Vieta introduced a new variable w and imposed the condition w(t + w) = p/3. This is equivalent with the substitution t = p/3w – w, and differs from the substitution that is used here only by a change of sign of w. This change of sign allows getting directly the formulas of § Cardano’s formula.
References[edit]
- ^ Høyrup, Jens (1992), «The Babylonian Cellar Text BM 85200 + VAT 6599 Retranslation and Analysis», Amphora: Festschrift for Hans Wussing on the Occasion of his 65th Birthday, Birkhäuser, pp. 315–358, doi:10.1007/978-3-0348-8599-7_16, ISBN 978-3-0348-8599-7
- ^ a b Crossley, John; W.-C. Lun, Anthony (1999). The Nine Chapters on the Mathematical Art: Companion and Commentary. Oxford University Press. p. 176. ISBN 978-0-19-853936-0.
- ^ a b Van der Waerden, Geometry and Algebra of Ancient Civilizations, chapter 4, Zurich 1983 ISBN 0-387-12159-5
- ^ Cooke, Roger (8 November 2012). The History of Mathematics. John Wiley & Sons. p. 63. ISBN 978-1-118-46029-0.
- ^ Nemet-Nejat, Karen Rhea (1998). Daily Life in Ancient Mesopotamia. Greenwood Publishing Group. p. 306. ISBN 978-0-313-29497-6.
- ^ Cooke, Roger (2008). Classical Algebra: Its Nature, Origins, and Uses. John Wiley & Sons. p. 64. ISBN 978-0-470-27797-3.
- ^ Guilbeau (1930, p.
states that «the Egyptians considered the solution impossible, but the Greeks came nearer to a solution.»
- ^ a b Guilbeau (1930, pp. 8–9)
- ^ Heath, Thomas L. (April 30, 2009). Diophantus of Alexandria: A Study in the History of Greek Algebra. Martino Pub. pp. 87–91. ISBN 978-1578987542.
- ^ Archimedes (October 8, 2007). The works of Archimedes. Translation by T. L. Heath. Rough Draft Printing. ISBN 978-1603860512.
- ^ Mikami, Yoshio (1974) [1913], «Chapter 8 Wang Hsiao-Tung and Cubic Equations», The Development of Mathematics in China and Japan (2nd ed.), New York: Chelsea Publishing Co., pp. 53–56, ISBN 978-0-8284-0149-4
- ^ A paper of Omar Khayyam, Scripta Math. 26 (1963), pages 323–337
- ^ J. J. O’Connor and E. F. Robertson (1999), Omar Khayyam, MacTutor History of Mathematics archive, states, «Khayyam himself seems to have been the first to conceive a general theory of cubic equations.»
- ^ Guilbeau (1930, p. 9) states, «Omar Al Hay of Chorassan, about 1079 AD did most to elevate to a method the solution of the algebraic equations by intersecting conics.»
- ^ Berggren, J. L. (2017-01-18). Episodes in the Mathematics of Medieval Islam. Springer. ISBN 978-1-4939-3780-6.
- ^ Datta, Bibhutibhushan; Singh, Avadhesh Narayan (2004), «Equation of Higher Degree», History of Hindu Mathematics: A Source Book, vol. 2, Delhi, India: Bharattya Kala Prakashan, p. 76, ISBN 81-86050-86-8
- ^ O’Connor, John J.; Robertson, Edmund F., «Sharaf al-Din al-Muzaffar al-Tusi», MacTutor History of Mathematics archive, University of St Andrews
- ^ Berggren, J. L. (1990), «Innovation and Tradition in Sharaf al-Dīn al-Ṭūsī’s Muʿādalāt», Journal of the American Oriental Society, 110 (2): 304–309, doi:10.2307/604533, JSTOR 604533
- ^ O’Connor, John J.; Robertson, Edmund F., «Fibonacci», MacTutor History of Mathematics archive, University of St Andrews
- ^ Katz, Victor (2004). A History of Mathematics. Boston: Addison Wesley. p. 220. ISBN 9780321016188.
- ^ La Nave, Federica; Mazur, Barry (2002), «Reading Bombelli», The Mathematical Intelligencer, 24 (1): 12–21, doi:10.1007/BF03025306, S2CID 189888034
- ^ a b c Nickalls, R.W.D. (July 2006). «Viète, Descartes, and the cubic equation» (PDF). Mathematical Gazette. 90 (518): 203–208. doi:10.1017/S0025557200179598. S2CID 124980170.
- ^ Pratt, Orson (1866). New and Easy Method of Solution of the Cubic and Biquadratic Equations: Embracing Several New Formulas, Greatly Simplifying this Department of Mathematical Science. Longmans, Green, Reader, and Dyer. p. 13. ISBN 9781974130924.
…if two roots are imaginary, the product is positive…
- ^ «Solution for a depressed cubic equation». Math solution. Retrieved 2022-11-23.
- ^ Zucker, I.J. (July 2008). «The cubic equation — a new look at the irreducible case». Mathematical Gazette. 92: 264–268. doi:10.1017/S0025557200183135. S2CID 125986006.
- ^ Shelbey, Samuel, ed. (1975). CRC Standard Mathematical Tables. CRC Press. ISBN 0-87819-622-6.
- ^ These are Formulas (80) and (83) of Weisstein, Eric W. ‘Cubic Formula’. From MathWorld—A Wolfram Web Resource. http://mathworld.wolfram.com/CubicFormula.html, rewritten for having a coherent notation.
- ^ Holmes, G. C., «The use of hyperbolic cosines in solving cubic polynomials», Mathematical Gazette 86. November 2002, 473–477.
- ^ Abramowitz, Milton; Stegun, Irene A., eds. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, Dover (1965), chap. 22 p. 773
- ^ Gleason, Andrew Mattei (March 1988). «Angle trisection, the heptagon, and the triskaidecagon» (PDF). The American Mathematical Monthly. 95 (3): 185–194. doi:10.2307/2323624. JSTOR 2323624. Archived from the original (PDF) on 2015-12-19.
- ^ Nickalls, R. W. D. (November 1993), «A new approach to solving the cubic: Cardan’s solution revealed» (PDF), The Mathematical Gazette, 77 (480): 354–359, doi:10.2307/3619777, ISSN 0025-5572, JSTOR 3619777, S2CID 172730765 See esp. Fig. 2.
- ^ Henriquez, Garcia (June–July 1935), «The graphical interpretation of the complex roots of cubic equations», American Mathematical Monthly, 42 (6): 383–384, doi:10.2307/2301359, JSTOR 2301359
- ^ Barr, C. F. (1918), «Discussions: Relating to the Graph of a Cubic Equation Having Complex Roots», American Mathematical Monthly, 25 (6): 268–269, doi:10.2307/2972885, JSTOR 2972885
- ^ Irwin, Frank; Wright, H. N. (1917), «Some Properties of Polynomial Curves.», Annals of Mathematics, 19 (2): 152–158, doi:10.2307/1967772, JSTOR 1967772
- ^ van der Waerden, Bartel Leenert (1985), «From Viète to Descartes», A History of Algebra: From al-Khwārizmī to Emmy Noether, Springer-Verlag, ISBN 3-540-13610-X
- ^ Lagrange, Joseph-Louis (1869) [1771], «Réflexions sur la résolution algébrique des équations», in Serret, Joseph-Alfred (ed.), Œuvres de Lagrange, vol. III, Gauthier-Villars, pp. 205–421
- ^ Prasolov, Viktor; Solovyev, Yuri (1997), Elliptic functions and elliptic integrals, AMS Bookstore, ISBN 978-0-8218-0587-9, §6.2, p. 134
- ^ Kline, Morris (1990), Mathematical Thought from Ancient to Modern Times, Oxford University Press US, ISBN 978-0-19-506136-9, Algebra in the Eighteenth Century: The Theory of Equations
- ^ a b Daniel Lazard, «Solving quintics in radicals», in Olav Arnfinn Laudal, Ragni Piene, The Legacy of Niels Henrik Abel, pp. 207–225, Berlin, 2004. ISBN 3-540-43826-2
References[edit]
- Guilbeau, Lucye (1930), «The History of the Solution of the Cubic Equation», Mathematics News Letter, 5 (4): 8–12, doi:10.2307/3027812, JSTOR 3027812
Further reading[edit]
- Anglin, W. S.; Lambek, Joachim (1995), «Mathematics in the Renaissance», The Heritage of Thales, Springers, pp. 125–131, ISBN 978-0-387-94544-6 Ch. 24.
- Dence, T. (November 1997), «Cubics, chaos and Newton’s method», Mathematical Gazette, Mathematical Association, 81 (492): 403–408, doi:10.2307/3619617, ISSN 0025-5572, JSTOR 3619617, S2CID 125196796
- Dunnett, R. (November 1994), «Newton–Raphson and the cubic», Mathematical Gazette, Mathematical Association, 78 (483): 347–348, doi:10.2307/3620218, ISSN 0025-5572, JSTOR 3620218, S2CID 125643035
- Jacobson, Nathan (2009), Basic algebra, vol. 1 (2nd ed.), Dover, ISBN 978-0-486-47189-1
- Mitchell, D. W. (November 2007), «Solving cubics by solving triangles», Mathematical Gazette, Mathematical Association, 91: 514–516, doi:10.1017/S0025557200182178, ISSN 0025-5572, S2CID 124710259
- Mitchell, D. W. (November 2009), «Powers of φ as roots of cubics», Mathematical Gazette, Mathematical Association, 93, doi:10.1017/S0025557200185237, ISSN 0025-5572, S2CID 126286653
- Press, W. H.; Teukolsky, S. A.; Vetterling, W. T.; Flannery, B. P. (2007), «Section 5.6 Quadratic and Cubic Equations», Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8
- Rechtschaffen, Edgar (July 2008), «Real roots of cubics: Explicit formula for quasi-solutions», Mathematical Gazette, Mathematical Association, 92: 268–276, doi:10.1017/S0025557200183147, ISSN 0025-5572, S2CID 125870578
- Zucker, I. J. (July 2008), «The cubic equation – a new look at the irreducible case», Mathematical Gazette, Mathematical Association, 92: 264–268, doi:10.1017/S0025557200183135, ISSN 0025-5572, S2CID 125986006
External links[edit]
- «Cardano formula», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- History of quadratic, cubic and quartic equations on MacTutor archive.
- 500 years of NOT teaching THE CUBIC FORMULA. What is it they think you can’t handle? – YouTube video by Mathologer about the history of cubic equations and Cardano’s solution, as well as Ferrari’s solution to quartic equations








































































![{displaystyle {sqrt[{3}]{u_{1}}}+{sqrt[{3}]{u_{2}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8caf13f05988e4c3653018e7e09313e0a663034b)
![{displaystyle C-{frac {p}{3C}}quad {text{with}}quad C={sqrt[{3}]{-{frac {q}{2}}+{sqrt {{frac {q^{2}}{4}}+{frac {p^{3}}{27}}}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c87abe575ce3101b7076ebb7dd0b960d85195d3f)

![{displaystyle C={sqrt[{3}]{frac {Delta _{1}pm {sqrt {Delta _{1}^{2}-4Delta _{0}^{3}}}}{2}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57102b328503b04914d43ce3ab469e53c6fad58d)


![{displaystyle t_{k}=2,{sqrt {-{frac {p}{3}}}},cos left[,{frac {1}{3}}arccos left({frac {3q}{2p}}{sqrt {frac {-3}{p}}},right)-{frac {2pi k}{3}},right]qquad {text{for }}k=0,1,2.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1852f999463435d82a62acdf648b210b1794be56)



![{displaystyle t_{k}=2,{sqrt {-{frac {p}{3}}}},cos left[{frac {1}{3}}arccos left({frac {3q}{2p}}{sqrt {frac {-3}{p}}}right)-{frac {2pi k}{3}}right]qquad {text{for }}k=0,1,2.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a702d0b6878463d3444d0ae34beee3fb9ea2d1c3)
![{displaystyle {begin{aligned}t_{0}&=-2{frac {|q|}{q}}{sqrt {-{frac {p}{3}}}}cosh left[{frac {1}{3}}operatorname {arcosh} left({frac {-3|q|}{2p}}{sqrt {frac {-3}{p}}}right)right]qquad {text{if }}~4p^{3}+27q^{2}>0~{text{ and }}~p<0,\t_{0}&=-2{sqrt {frac {p}{3}}}sinh left[{frac {1}{3}}operatorname {arsinh} left({frac {3q}{2p}}{sqrt {frac {3}{p}}}right)right]qquad {text{if }}~p>0.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4db866023eccccd6a208cdff730a2614478b136)


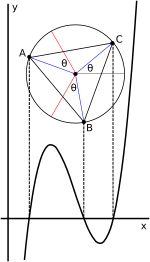








![{displaystyle u={sqrt[{3}]{-{frac {q}{2}}+{sqrt {{frac {q^{2}}{4}}+{frac {p^{3}}{27}}}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d5bf9eaebfd5896d4f8dde09d59ff00381d33a9)
![{displaystyle v={sqrt[{3}]{-{frac {q}{2}}-{sqrt {{frac {q^{2}}{4}}+{frac {p^{3}}{27}}}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a7232f72d8ec7b6cee76973ccfc6189a981b1dd)
![{displaystyle t={sqrt[{3}]{-{q over 2}+{sqrt {{q^{2} over 4}+{p^{3} over 27}}}}}+{sqrt[{3}]{-{q over 2}-{sqrt {{q^{2} over 4}+{p^{3} over 27}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d62f2e04f38bbf3c00fc86f15fe1a717fa25d82)







