Как найти дискриминант в уравнении с параметром

Чтобы решить квадратное уравнение с параметром, нужно понять, при каких значениях параметра существуют корни, и найти их, выразив через параметр. Обычно это делается просто через анализ дискриминанта. (см. пример 1)
Но иногда в задачах с параметром просят найти такие значения параметра, при которых корни принадлежат определенному числовому промежутку. Например:

• Найдите такие значения параметра, чтобы оба корня были меньше некоторого числа (γ): (x_1≤x_2<γ).
• Только один из корней принадлежит какому-то промежутку ((γ;β):)
  2 случая: (γ<x_1<β≤x_2;) или (x_1≤γ<x_2<β.)
• Некоторое число (∝) лежит между корнями: ((x_1<γ<x_2)).
• И т.д. Условия могут быть различными.

Теперь разберемся, как при помощи математики записать те или иные условия. Разберем условие: (x_1≤x_2<γ). Точно такие же рассуждения будут справедливы и для других условий.

1. Очевидно, что (D≥0), для того, чтобы корни существовали (либо один, либо два корня — то и то нас устраивает – именно поэтому знак неравенства больше либо равно).
2. Чтобы некоторое число лежало вне отрезка ((x_1,x_2)), необходимо рассмотреть два случая: ветки параболы направлены вверх ((a>0)); ветки параболы направлены вниз ((a<0)).
   • (a>0). Значит, между корнями функция принимает отрицательные значения, а вне этого отрезка – положительные. Так как наше число (γ) должно по условию лежать вне отрезка ((x_1,x_2)), то (f(γ)>0).
   • (a<0). Значит, между корнями функция принимает положительные значения, а вне этого отрезка – отрицательные. Так как наше число (γ) должно по условию лежать вне отрезка ((x_1,x_2)), то (f(γ)<0).

Используем небольшую хитрость, чтобы описать оба этих условия: (a*f(γ)>0). Этим условием мы накладываем ограничение, что наши корни должны лежать слева или справа от числа (γ).

В итоге получаем:

если (a*f(γ)<0), то (γ∈(x_1,x_2)),

если (a*f(γ)>0), то (γ∉(x_1,x_2)).

Нам осталось наложить условие, чтобы наши корни были слева от числа (γ). Здесь нужно просто сравнить положение вершины нашей параболы (x_0) относительно (γ). Заметим, что вершина лежит между точками (x_1) и (x_2). Если (x_0<γ), то в системе с предыдущими условиями это будет означать, что число (γ) лежит справа от отрезка ((x_1,x_2)) и соответственно удовлетворяет условию задачи (x_1≤x_2<γ).

Таким образом, для того, чтобы решить задачу с условием (x_1≤x_2<γ) необходимо решить следующую систему:

$$begin{cases} D≥0,\ a*f(γ)>0, \x_0<γ.end{cases}$$

То, что дискриминант неотрицательный дает нам существование корней. Второе неравенство указывает, что (γ∉(x_1,x_2)). И последнее в совокупности с первыми двумя, что оба корня лежат слева от (γ).
Аналогичные рассуждения можно провести для любых условий. Настоятельно рекомендую разобраться во всех пунктах и откуда возникает вышеуказанная система неравенств, и вы легко сможете проводить анализ квадратных уравнений с параметром.

Ниже приведена таблица, в которой разобраны все варианты расположения нулей квадратичной функции на числовой прямой и соответствующие им условия. (см. таблицу)

Пример 1

При каких значениях параметра a уравнение
$$a(a+3) x^2+(2a+6)x-3a-9=0$$
имеет более одного корня?

Решение:

1 случай:
Если (a(a+3)=0), то уравнение будет линейным. При (a=0) исходное уравнение превращается в (6x-9=0), корень которого (x=1,5). Таким образом, при (a=0) уравнение имеет один корень.

При (a=-3) получаем (0*x^2+0*x-0=0), корнями этого уравнения являются любые рациональные числа. Уравнение имеет бесконечное количество корней.

2 случай:
Если (a≠0; a≠-3), то получим квадратное уравнение. При положительном дискриминанте уравнение будет иметь более одного корня:
$$D>0$$ $$D/4=(a+3)^2+3a(a+3)^2>0$$ $$(a+3)^2 (3a+1)>0$$ $$a>-frac{1}{3}.$$
С учетом (a≠0;) (a≠-3), получим, что уравнение имеет два корня при (a∈(-frac{1}{3};0)∪(0;+∞)).

Объединив оба случая получим (внимательно прочитайте, что от нас требуется):

Ответ: (a ∈ {-3} ∪(-frac{1}{3};0)∪(0;+∞)).

Пример 2

Найти все значения параметра a, при которых корни уравнения
$$(a+1) x^2-(a^2+2a)x-a-1=0$$
принадлежат отрезку ([-2;2]).

Решение:

1 случай: Если (a=-1), то (0*x^2-x+1-1=0) отсюда (x=0). Это решение принадлежит ([-2;2]).

2 случай: При (a≠-1), получаем квадратное уравнение, с условием, что все корни принадлежат ([-2;2]). Для решения введем функцию (f(x)=(a+1) x^2-(a^2+2a)x-a-1) и запишем систему, которая задает требуемые условия:

$$begin{cases} (a+1)*f(-2) ≥ 0, \(a+1)*f(2) ≥ 0, \D≥0, \-2 < x_0 < 2.end{cases}$$

(x_0=frac{a^2+2a}{2(a+1)}) -вершина параболы.

$$ f(-2)=(a+1)*4-(a^2+2a)*(-2)-a-1=2a^2+7a+3; $$
$$ f(2)=(a+1)*4-(a^2+2a)*(2)-a-1=-2a^2-a+3; $$
$$ D=(a^2+2a)^2+4(a+1)^2=(a^2+2a+2)^2=(1+(a+1)^2 )^2>0.$$

Подставляем полученные выражения в систему:

$$ begin{cases} (a+1)(2a^2+7a+3) ≥ 0, \(a+1)(-2a^2-a+3) ≥ 0,\ -2 < frac{a^2+2a}{2(a+1)} < 2. end{cases} $$
Или
$$ begin{cases} 2(a+1)(a+3)(a+0,5) ≥ 0,\ -2(a+1)(a-1)(a+1,5) ≥ 0,\ frac{(a-1-sqrt{5})(a-1+sqrt{5})}{2(a+1)} < 0,\ frac{(a+3-sqrt{5})(a+3+sqrt{5})}{2(a+1)} > 0.end{cases} $$

Ответ: ([-3;-1,5]∪[-0,5;1]).

Пример 3

Решить уравнение (sqrt{x-5}=x+a), где (a) параметр.

Решение:

После равносильных преобразований получим систему:

$$ begin{cases} x-5=(x+a)^2, \x≥-a; end{cases} $$
$$ begin{cases} x^2+(2a-1)x+(a^2+5)=0, \x≥-a. end{cases} $$

Наша задача свелась к исследованию квадратного многочлена:

$$ f(x)=x^2+(2a-1)x+(a^2+5). $$

Для этого найдем дискриминант, вершину параболы и (f(-a)).
$$ D=(2a-1)^2-4(a^2+5)=-4a-19;$$
$$ {x}_{0}=-frac{2a-1}{2}=frac{1-2a}{2}; $$
$$ f(-a)=a+5.$$

Из второго неравенства системы следует, что нас устраивают случаи, когда ({x}_{1} < -a ≤ {x}_{2}) (нас будет устраивать только один корень ({x}_{2})) и (-a ≤ {x}_{1} ≤ {x}_{2}) (под условие системы будут подходить оба корня), где ({x}_{1},{x}_{2})- нули (f(x)).

Обратим внимание, что коэффициент при (x^2) положителен, т.е. ветки параболы направлены вверх.

Первый случай: ({x}_{1} < -a ≤ {x}_{2}) (см. таблицу)

$$ f(-a)≤0 ⇔ a+5≤0 ⇔ a≤-5;$$

Таким образом, при (a ≤ -5) мы имеем одно решение:

$$ x=frac{1-2a+sqrt{-4a-19}}{2}. $$

Второй случай: (-a ≤ {x}_{1} ≤ {x}_{2}) (см. таблицу)

$$ begin{cases} f(-a)≥0, \D≥0, \{x}_{0}>-a; end{cases} $$
$$ begin{cases} a+5≥0, \-4a-19≥0, \ frac{1-2a}{2}>-a; end{cases} $$
$$ begin{cases} a≥-5, \a≤-frac{19}{4}, \ 1>0. end{cases} $$

Получаем, что при (a∈[-5;-4.75]) уравнение имеет два решения:

$$ {x}_{1,2}=frac{1-2a±sqrt{-4a-19}}{2}. $$

Ответ: при (a≤-5) $$ x=frac{1-2a+sqrt{-4a-19}}{2};$$
при (a∈[-5;-4.75]) $$ {x}_{1,2}=frac{1-2a±sqrt{-4a-19}}{2}; $$
при (a>-4.75) решений нет.

Квадратные уравнения с параметром

Уравнение называется квадратным, если имеет вид (ax^2+bx+c=0,) где (a,b,c) — любые числа ((a≠0)). При этом надо быть внимательным, если (a=0), то уравнение будет линейным, а не квадратным. Поэтому, первым делом при решении квадратного уравнения с параметром, рекомендую смотреть на коэффициент при (x^2) и рассматривать 2 случая: (a=0) (линейное уравнение); (a≠0) (квадратное уравнение). Квадратное уравнение часто решается при помощи дискриминанта или теоремы Виета.

Исследование квадратного многочлена

Чтобы решить квадратное уравнение с параметром, нужно понять, при каких значениях параметра существуют корни, и найти их, выразив через параметр. Обычно это делается просто через анализ дискриминанта. (см. пример 1) Но иногда в задачах с параметром просят найти такие значения параметра, при которых корни принадлежат определенному числовому промежутку. Например:

• Найдите такие значения параметра, чтобы оба корня были меньше некоторого числа (γ): (x_1≤x_2 0)); ветки параболы направлены вниз ((a 0). Значит, между корнями функция принимает отрицательные значения, а вне этого отрезка – положительные. Так как наше число (γ) должно по условию лежать вне отрезка ((x_1,x_2)), то (f(γ)>0).
• (a 0). Этим условием мы накладываем ограничение, что наши корни должны лежать слева или справа от числа (γ).

В итоге получаем:

если (a*f(γ) 0), то (γ∉(x_1,x_2)).

Нам осталось наложить условие, чтобы наши корни были слева от числа (γ). Здесь нужно просто сравнить положение вершины нашей параболы (x_0) относительно (γ). Заметим, что вершина лежит между точками (x_1) и (x_2). Если (x_0 0, \x_0

При каких значениях параметра a уравнение $$a(a+3) x^2+(2a+6)x-3a-9=0$$ имеет более одного корня?

1 случай: Если (a(a+3)=0), то уравнение будет линейным. При (a=0) исходное уравнение превращается в (6x-9=0), корень которого (x=1,5). Таким образом, при (a=0) уравнение имеет один корень.
При (a=-3) получаем (0*x^2+0*x-0=0), корнями этого уравнения являются любые рациональные числа. Уравнение имеет бесконечное количество корней.

2 случай: Если (a≠0; a≠-3), то получим квадратное уравнение. При положительном дискриминанте уравнение будет иметь более одного корня: $$D>0$$ $$D/4=(a+3)^2+3a(a+3)^2>0$$ $$(a+3)^2 (3a+1)>0$$ $$a>-frac<1><3>.$$ С учетом (a≠0;) (a≠-3), получим, что уравнение имеет два корня при (a∈(-frac<1><3>;0)∪(0;+∞)). Объединив оба случая получим (внимательно прочитайте, что от нас требуется):

Найти все значения параметра a, при которых корни уравнения $$(a+1) x^2-(a^2+2a)x-a-1=0$$ принадлежат отрезку ([-2;2]).

1 случай: Если (a=-1), то (0*x^2-x+1-1=0) отсюда (x=0). Это решение принадлежит ([-2;2]).

2 случай: При (a≠-1), получаем квадратное уравнение, с условием, что все корни принадлежат ([-2;2]). Для решения введем функцию (f(x)=(a+1) x^2-(a^2+2a)x-a-1) и запишем систему, которая задает требуемые условия:

Подставляем полученные выражения в систему:

Методика обучения решению квадратных уравнений с параметром

Разделы: Математика

Решение задач с параметром вызывает затруднения у учащихся, так как практических заданий по данной теме в школьных учебниках недостаточно.

Цели разработки темы

• формирование устойчивого интереса к познавательному процессу при изучении математики и оценка возможности овладения предметом с точки зрения дальнейшей перспективы;
• обеспечение прочного и сознательного усвоения учащимися системой математических знаний, умений и навыков;
• формирование качества мышления, характерного для математической деятельности и необходимые человеку для жизни в современном обществе;
• выявление и развитие математических способностей учащихся.
• Задачи разработки темы:
• показать универсальные алгоритмы для решения квадратных уравнений с параметром;
• научить приемам решения различного класса задач с параметром, способствовать овладению технических и интеллектуальных математических умений на уровне свободного их использования;
• использование новых современных педагогических технологий обучения.

В математике параметр – это постоянная величина, выраженная буквой, сохраняющая свое постоянное значение лишь в условиях данной задачи (“параметр” с греческого “parametron” – отмеривающий)..

Если ставится задача для каждого значения параметра а из некоторого числового множества А решить уравнение F(х;а)= 0 относительно х, то это уравнение называют уравнением с переменной х и параметром а, а множество А – областью изменения параметра. Под областью определения уравнения F(х;а)=0 с параметром а понимаются такие системы значений х и а, при которых F(х;а) имеет смысл. Все значения параметра а, при которых F(х;а) не имеет смысла, включать в число значений параметра, при которых уравнение не имеет решений. Под областью изменения параметра (если не сделано специальных оговорок) берется множество всех действительных чисел, а задачу решения уравнения с параметром формулировать следующим образом: решить уравнение F(х;а)=0 (с переменной х и параметром а) – это значит на множестве действительных чисел решить семейство уравнений, получающихся из данного уравнения при всех действительных значениях параметра или установить, что решений нет.

В связи с тем, что выписать каждое уравнение из бесконечного семейства уравнений невозможно, но каждое уравнение семейства должно быть решено, следовательно, необходимо по некоторому целесообразному признаку разбить множество всех значений параметра на подмножества и решить затем заданное уравнение на каждом из этих подмножеств. Для разбиения множества значений параметра на подмножества, удобно пользоваться теми значениями параметра, при которых или при переходе через которые происходят качественные изменения уравнения. Такие значения параметра называются контрольными.

1. КВАДРАТНЫЕ УРАВНЕНИЯ С ПАРАМЕТРОМ

Задачи с параметрами можно разделить на два больших класса:

• задачи, в которых необходимо при всех значениях параметра из некоторого множества решить уравнение;
• задачи, в которых требуется найти все значения параметра, при каждом из которых решение уравнения удовлетворяют некоторым условиям.

В зависимости от типа задачи изменяется и вид ответа. В первом случае в решении и ответе должны быть рассмотрены все возможные значения параметров. Если хотя бы одно значение какого-либо параметра не исследовано, решение задачи не может быть признано полным.

Во втором случае в ответе перечисляются только те значения параметра, при которых выполнены условия задачи, а при решении подобных задач обычно решать заданное уравнение нет необходимости.

Уравнение вида Ах 2 + Вх + С= 0 , где А, В, С — выражения, зависимые от параметра, х – переменная — называется квадратным уравнением с параметром.

Уравнение вида ах 2 +вх+с=0, где , а, в, с – действительные числа, называют квадратным уравнением. D=в 2 -4ас называется дискриминантом квадратного уравнения (“дискриминант” по – латыни “различитель”).

В зависимости от значения дискриминанта возможны три случая:

D > 0. Данное квадратное уравнение имеет два действительных корня

D=0. Данное уравнение имеет корень двойной кратности

D 2 +2кх+с=0 со вторым коэффициентом (в=2к) четным, для нахождения корней удобно пользоваться формулами: , где D₁= =к 2 -ас.

№ 1.1. Определите все значения параметра а при которых уравнение ах 2 +2(а+1)х+а+3=0 имеет два неравных корня.

Если а=0, то имеем 0·х 2 +2(0+1)х+0+3=0, 2х+3=0 — данное уравнение является линейным, х=-1,5 – единственный корень. Итак, а=0 не удовлетворяет условию задачи.

Если а?0, то уравнение имеет два различных корня, когда дискриминант >0.

Найдем=(а+1) 2 -а(а+3)=-а+1,-а+1>0, а 2 -4(а+1)х+4а+1=0 имеет один корень.

Если а=0, то имеем 2·0·х 2 -4(0+1)х+4·0+1=0, -4х+1=0 — данное уравнение является линейным, х=0,25 – единственный корень. Итак, а=0 удовлетворяет условию задачи.

Если а 0, то исходное уравнение является квадратным и имеет единственный корень при =0. Найдем =(2(a+1)) 2 -2a(4а+1) = -4a 2 +6a+4,4a 2 +6a+4=0, а₁=2, а₂=-0,5.

С учетом а=0, запишем ответ: а=-0,5, а=0, а=2.

№ 1.3. При каких значениях параметра а квадратное уравнение (5а-1)х 2 -(5а+2)х+3а-2=0 не имеет корней?

Если 5а-1=0,а=0,2, то имеем (5*0,2-1)х 2 -(5*0,2+2)х+3*0,2-2=0,

-3х-1,4=0 — данное уравнение является линейным, х = — единственный корень.

Итак, а=0,2 не удовлетворяет условию задачи.

Если а 0,2, то квадратное уравнение не имеет корней, если дискриминант квадратного уравнения D 2 -4(5a-1)(3а-2)=-35a 2 +72a-4,-35a 2 +72a-4 2 -72a+4>0, а₁=2, а₂=, (а-2)(а-)>0. С учетом а 0,2 ответ:

№ 1.4. Определите все значения параметра а при которых уравнение (2а-1)х 2 +ах+2а-3=0 имеет не более одного решения.

Если 2а-1=0,а=0,5, то имеем (2·0,5-1)х 2 +0,5·х+2·0,5-3=0, 0,5х-2=0 — данное уравнение является линейным, х=4 — единственный корень.

Итак, а=0,5 удовлетворяет условию задачи.

Если а 0,5, то квадратное уравнение имеет не более одного решения, если дискриминант квадратного уравнения D0.

Найдем D=а 2 -4(2a-1)(2а-3)=-15a 2 +32a-12, -15a 2 +32a-120,

15a 2 -32a+12?0, а₁=, а₂=, (а-)(а-) 0.

С учетом а 0,5, имеем .

С учетом а=0,5, запишем ответ: .

2. НЕПОЛНЫЕ КВАДРАТНЫЕ УРАВНЕНИЯ С ПАРАМЕТРОМ.

Квадратное уравнение ах 2 +вх+с=0, где а 0 называется неполным, если хотя бы один из коэффициентов в или с равен 0.

Общая схема решения неполных квадратных уравнений с параметрами.

ах 2 =0, где а 0, в=0, с=0. Если а 0 ,то уравнение примет вид: х 2 =0, х=0.

Следовательно, уравнение имеет два совпадающих корня, равных нулю.

Если а=0, то х — любое действительное число.

ах 2 +с=0, где а0, в=0, с0. Если а0,то уравнение примет вид: следовательно, уравнение имеет корни, то они равны по абсолютной величине, но противоположны по знаку; 2 +вх=0, где а0, в0, с=0. Если а0,то уравнение примет вид: х(а+в)=0,или Если а=0, то вх=0, х=0.

№ 2.1. При каких значениях параметра а оба корня уравнения 2х 2 +(3а 2 -|а|)х-а 2 -3а=0 равны нулю?

Оба корня квадратного уравнения равны нулю, когда

№ 2.2. При каких значениях параметра а, корни уравнения 2 х 2 -(5а-3)х+1=0 равны по модулю, но противоположны по знаку?

Корни квадратного уравнения равны по модулю, но противоположны по знаку, когда 5а-3=0,а=0,6, но с учетом того, что имеем уравнение 2х 2 +1=0, х 2 =-0,5, которое корней не имеет. Ответ: .

№ 2.3. При каких значениях параметра а один из двух различных корней уравнения 3х 2 +х+2а-3=0 равен нулю?

Параметр должен удовлетворять условию: 2а-3=0, а=1,5. Ответ: а=1,5.

№ 2.4. При каких значениях параметра а корни уравнения 3х 2 +(а 2 -4а)х+а-1=0 равны по модулю, но противоположны по знаку?

Корни квадратного уравнения равны по модулю, но противоположны по знаку, когда:

Ответ: а=0.

№ 2.5. Решить относительно х неполное квадратное уравнение х 2 -2а+1=а.

х 2 =а+2а-1; х 2 =3а-1.

Если 3а-1=0, а= ,то уравнение имеет два совпадающих корня, равных нулю.

Если 3а-1 0. а>, то уравнение имеет два корня .

Ответ: при арешений нет; при а= х=0; при

3. ИССЛЕДОВАНИЕ И РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ С ПАРАМЕТРОМ.

№ 3.1. Исследовать и решить уравнение с параметром х 2 –2(а-1)х+2а+1=0.

Найдем дискриминант: D=(а — 1) 2 -2а – 1= а 2 -2а+1-2а-1= а 2 — 4а.

D > 0, а 2 — 4а > 0, а (а -4) > 0, а 4, то уравнение имеет два действительных корня ;

D =0, а (а-4)=0, а=0, то х=а-1, х=0-1, х=-1, а=4,то х=а-1, х=4-1, х=3;

D 2 +2(а+1)х+а–2= 0.

1) При а-1=0, а=1 имеем линейное уравнение 4х-1=0, х=– единственное решение.

2) При а 1 уравнение является квадратным, найдем дискриминант:

D₁ = (а+1) 2 -(а–1)(2а-2)=а 2 +2а+1-а 2 +2а+а-2=5а-1.

D₁>0. 5а-1>0, а>, а 1, то уравнение имеет два корня .

D₁=0. 5а-1=0, а=, то уравнение имеет два равных корня .

х 2 +2х-8–ах+4а=0; х 2 +(2-а)х+4а-8=0. Уравнение является квадратным.

Найдем дискриминант: D=(2-а) 2 -4(4а-8)=4-4а+а 2 -16а+32= а 2 -20а+36.

D>0. а 2 20а+36>0, (а-18)(а -2)>0, а 18, то уравнение имеет два действительных корня .

D=0. (а-18)(а-2)=0, а=2, то ; а=18, то ;

D 2 равен 1, то уравнение принимает вид х 2 +px+q, где p и q — некоторые числа называется приведенным квадратным уравнением.

Теорема Виета: Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

ах 2 +вх+с=0, где х₁ и х₂ – корни квадратного уравнения, то

Справедливо утверждение, обратное теореме Виета.

Теорема: Если числа p и q таковы, что их сумма равна -p, а произведение равно q. то эти числа являются корнями уравнения х 2 +px+q=0.

№ 4.1. При каком значении параметра а сумма обратных величин действительных корней уравнения 2х 2 -2ах+а 2 -2=0 равна ?

Пусть х₁ и х₂ – корни квадратного уравнения, по условию _.

По теореме Виета: Используя соотношения между корнями и условие задачи, имеем:

Найдем дискриминант квадратного уравнения:

Имеем: Ответ: при

№ 4.2. В уравнении (а 2 -5а+3)х 2 +(3а-1)х+2=0 определите а так, чтобы один из корней был вдвое больше другого.

Пусть х₁ и х₂ – корни квадратного уравнения, по условию х₁ =2 х_2. Заметим, что кратное сравнение выполняется только для положительных чисел.

По теореме Виета и условию задачи имеем систему:

Составим и решим уравнение:

Можно вычислить дискриминант данного уравнения, а затем проверить, удовлетворяет ли данное значение параметра а условию, что дискриминант неотрицателен, а так же, что корни положительны. Однако в данной задаче значительно проще сделать проверку, подставив это значение а в исходное уравнение.

При Корни отрицательны и кратно не сравниваются, поэтому задача решений не имеет. Ответ: решений нет.

№ 4.3. Найти все значения параметра а, при которых квадратное уравнение (а+2)х 2 –ах-а=0 имеет два корня, расположенных на числовой прямой симметрично относительно точки х=1.

При а+2=0, а=-2, то 2х+2=0, х=-1 – единственное решение, следовательно данное значение а не удовлетворяет условию задачи.

При а-2. Пусть х₁ и х₂ – корни квадратного уравнения, по условию х₁ =1-у, х_2.=1+у, где у – некоторое действительное число.

По теореме Виета имеем:

Решим первое уравнение системы: 2(а+2)=а, а=-4.

Найдем дискриминант данного квадратного уравнения:

Данное значение а=-4 удовлетворяет полученным значениям. Ответ: а=-4.

Ответ: при а = — 4.

1. ИСПОЛЬЗУЕМАЯ ЛИТЕРАТУРА.
2. Азаров А.И., Барвенов С.А., Федосенко В.С. Методы решения задач с параметрами. Минск; “Аверсэв”. 2005.
3. Амелькин В. В., Рабцевич В. Л. Задачи с параметрами. Минск; “Асар”. 1996.
4. Данкова И. Н., Бондаренко Т. Е., Емелина Л. Л., Плетнева О. К.Предпрофильная подготовка учащихся 9 классов по математике. Москва; “5 за знания”.2006.
5. Литвиненко В. Н., Мордкович А. Г.. Практикум по элементарной математике. Москва; “Просвещение”.1991.
6. Родионов Е. М. Решение задач с параметрами. Москва; “Русь – 90”. 1995.
7. Студенецкая В. Н., Сагателова Л. С. Математика 8 – 9классы: сборник элективных курсов. Волгоград; “Учитель”. 2006.
8. Шарыгин И. Ф. Решение задач. Москва; “Просвещение”. 1994.
9. Шахмейстер А. Х. Уравнения и неравенства с параметрами. Санкт-Петербург; “Петроглиф”. 2006.

Квадратные уравнения и квадратичные неравенства с параметрами

Дорогой друг! Если ты никогда не решал задач с параметрами – прочитай статьи «Что такое параметр» и «Графический способ решения задач с параметрами». Квадратные уравнения, а тем более неравенства с параметрами только на первый взгляд кажутся простыми. Чтобы уверенно решать их, надо знать определенные приемы. О некоторых мы расскажем.

Разберем сначала подготовительные задачи. А в конце – реальную задачу ЕГЭ.

1. Найдите все значения a, при которых уравнение не имеет действительных корней.

Всегда ли это уравнение является квадратным относительно переменной х? – Нет, не всегда. В случае, когда коэффициент при равен нулю, оно станет линейным.

Рассмотрим два случая – когда это уравнение квадратное и когда оно линейное.

Тогда уравнение примет вид 2 = 0. Такое уравнение не имеет действительных корней, что удовлетворяет условию задачи.

Уравнение будет квадратным. Квадратное уравнение не имеет действительных корней тогда и только тогда, когда его дискриминант отрицательный.

Если и – корни квадратного уравнения
, то по теореме Виета:

Решим первое неравенство системы

Квадратный трехчлен в левой части не имеет корней, так как дискриминант равен -32, то есть отрицателен. Поэтому неравенство будет выполняться для всех действительных значений .

Возведем второе уравнение системы в квадрат:

Из этих двух уравнений выразим сумму квадратов и .

Значит, сумму квадратов корней уравнения можно выразить через параметр

График функции — парабола, ее ветви направлены вверх, минимум будет достигаться в ее вершине. Найдем вершину параболы:

3) Найдите все значения , при каждом из которых все решения уравнения

Как и в первой задаче, уравнение является квадратным, кроме случая, когда . Рассмотрим этот случай отдельно

1) . Получим линейное уравнение

У него единственный корень, причем положительный. Это удовлетворяет условию задачи.

2) При уравнение будет квадратным. Нам надо, чтобы решения существовали, причем были положительными. Раз решения есть, то .

Покажем один из приемов решения квадратичных уравнений и неравенств с параметрами. Он основан на следующих простых утверждениях:

— Оба корня квадратного уравнения и положительны тогда и только тогда, когда их сумма положительна и произведение положительно.

Очевидно, что сумма и произведение двух положительных чисел также положительны. И наоборот – если сумма и произведение двух чисел положительны, то и сами числа положительны.

— Оба корня квадратного уравнения и отрицательны тогда и только тогда, когда их сумма отрицательна, а произведение положительно.

Корни квадратного уравнения и имеют разные знаки тогда и только тогда, когда их произведение отрицательно.

Сумма и произведение корней входят в формулировку теоремы Виета, которой мы и воспользуемся. Получим

Второе и третье неравенства имеют одинаковое решение . Решение первого неравенства:
.

С учетом пункта 1 получим ответ

4. При каких значениях параметра a уравнение

имеет единственное решение?

Уравнение является показательным, причем однородным. Мы умеем решать такие уравнения! Разделим обе части на .

Сделаем замену

Для того, чтобы исходное уравнение имело единственное решение, нужно, чтобы уравнение относительно t имело ровно один положительный корень.

1) В случае уравнение будет линейным

Значит, подходит. В этом случае уравнение имеет единственный положительный корень.

2) Если , уравнение будет квадратным.

Дискриминант является полным квадратом и поэтому всегда неотрицателен. Уравнение имеет либо один, либо два корня. В этом случае несложно найти корни в явном виде.

Один корень получился не зависящим от параметра, причем положительным. Это упрощает задачу.

Для того, чтобы уравнение имело единственный положительный корень, нужно, чтобы либо второй был отрицательным, либо равным нулю, либо чтобы корни совпадали. Рассмотрим все случаи.

Объединив все случаи, получим ответ.

И наконец – реальная задача ЕГЭ.

5. При каких значениях a система имеет единственное решение?

Решением квадратного неравенства может быть:

В каких случаях система двух квадратных неравенств имеет единственное решение:

1) единственная общая точка двух лучей-решений ( или интервалов-решений)

2) одно из неравенств имеет решение – точку, которая является решением второго неравенства

Рассмотрим первый случай.

Если является решением 1 и 2 уравнений, то является решением уравнения (вытекает из второго первое) ⇒ или

Если , при этом система примет вид:

Второй корень первого уравнения:

Второй корень второго первого:

Если , при этом система примет вид:

– бесконечно много решений, не подходит.

Рассмотрим второй случай.

– решением является точка, если – является решением второго неравенства.

– решением является точка, если – не является решением первого неравенства.

МИНИСТЕРСТВО ОБОРОНЫ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ
ГОСУДАРСТВЕННОЕ КАЗЁННОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

«ОРЕНБУРГКОЕ
ПРЕЗИДЕНТСКОЕ КАДЕТСКОЕ УЧИЛИЩЕ»

РЕШЕНИЕ КВАДРАТНЫХ
УРАВНЕНИЙ С ПАРАМЕТРАМИ

(методическое
пособие для воспитанников и преподавателей)

Составила
преподаватель математики

высшей
квалификационной категории

Зевина Елена Петровна

2013г.

УДК 372.

Зевина Е.П.: РЕШЕНИЕ  КВАДРАТНЫХ
УРАВНЕНИЙ С ПАРАМЕТРАМИ.

Методическое
пособие для воспитанников и преподавателей.

–
Оренбург: ФГКОУ  Оренбургское ПКУ, 2013. –32с.

В
пособии представлен опыт практической деятельности преподавателя училища по
методике обучения решению квадратных уравнений с параметрами.

Методическое
пособие содержит задачи с параметрами, при решении которых возникают наибольшие
затруднения во время обучения. Методами решения таких задач уделяется минимум
внимания, и целью данного пособия является помощь учащимся в устранении данного
пробела.

Данное
методическое пособие составлено по итогам многолетней практики работы и
подготовки учащихся к сдаче экзамена по математике в формате ЕГЭ и ГИА.

Рассмотрено
на заседании методического совета ФГКОУ Оренбургское ПКУ.

ФГОУ «Оренбургское
президентское кадетское училище», 2013

Содержание

1.                
Введение. . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4

2.                
§1. Квадратные уравнения  с параметром . .
. . . . . . . . . . . . . . . . . . . . . .  5

1.1           
Понятие уравнения с параметром . . . .. .
. .  . . . . . .
. . . . . . . . . . . . . 5

1.2           
Квадратные уравнения . . . . . . . . . . .
. . . . . . . . . . . . . .  . . . . . . . . . . 5

1.3           
Теорема Виета . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . .. . . . . . . . . . 6

3.                
§2. Примеры
решения квадратных уравнений с параметром . . . . . . . . . 7

4.                
§3.
Задачи для самостоятельной работы по решению квадратных  

               
уравнений с параметром . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . 14

5.                
§4. Решение уравнений
с параметром, приводимых к квадратным. . . .15

6.                
§5. Задачи для
самостоятельной работы по решению уравнений,

          
приводимых к квадратным . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . .17

7.                
§6. Задачи, связанные с расположением
корней квадратного трехчлена.

              
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . 18

8.                
§7. Задачи для
самостоятельного решения, связанные с

          
расположением корней квадратного трехчлена . . . . . . . . . . .  . . . . . . .
25

9.                
Заключение. . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26

10.           
Список использованной литературы . . . . .
. . . . . . . . . . . . . . . . . . . . . . . 27

Введение

У большинства выпускников
и абитуриентов задачи с параметрами вызывают серьезные затруднения (как решать
задачу и как довести решение до правильного ответа). Трудности при решении
таких задач обусловлены во-первых: решением не по шаблону, во- вторых:
рассмотрением различных случаев, в которых методы решения существенно
отличаются друг от друга; в-третьих: хорошими знаниями свойств функций и
правильным выделением тех свойств, которые нужно применить.

Предлагаемое пособие
построено так, чтобы учащиеся самостоятельно могли понять логику решения задач
с параметрами, и научились их решать.

Пособие разбито на
параграфы, в конце которых приведены упражнения для самостоятельного решения.
Разобраны примеры, которые расположены в последовательности «от простого к
сложному», при этом предполагается, что учащийся имеет хорошие знания по
математике и изучает пособие последовательно.

Пособие может быть
использовано как для самостоятельной подготовки к вступительным экзаменам, так
и в качестве пособия на индивидуальных и групповых занятиях.

Функции вида , где   –
квадратный трехчлен, в школьном курсе математики придается большое значение.
Для нее строго доказываются все свойства, нужные в теории и для решения задач. Безукоризненное
знание необходимых свойств квадратного трехчлена требуется от каждого
абитуриента, так как квадратный трехчлен с параметром часто включается в
варианты письменных работ и в тесты для собеседования на вступительных
экзаменах в ВУЗы. Как правило, большая часть абитуриентов с этими задачами не
справляется. Значит, им надо уделять больше внимания на факультативных занятиях
в школе, на страницах печати.

§1.
Квадратные уравнения с параметром

1.1 Понятие уравнения с
параметром

Определение.
Пусть задано уравнение , если ставится задача,
для каждого действительного значения  решить уравнение
относительно , то это уравнение
называют уравнением с переменной  и параметром
.

Решить уравнение с параметром
– это значит, для каждого действительного значения  найти значение , удовлетворяющее данному
уравнению.

Назовем
контрольными значениями параметра (КЗП) те его значения, при
которых обращается в нуль: 1) старший коэффициент в уравнении или неравенстве; 2)
знаменатель дроби; 3) дискриминант квадратного уравнения.

1.2 Квадратные уравнения

Определение. Квадратным
уравнением называют уравнение вида

,

(1)

где  – переменная,  и , ,  – некоторые
действительные числа или выражения, зависящие от параметров.

Левая
часть уравнения является квадратным трехчленом, то есть многочленом второй
степени.

Корни
квадратного уравнения (1) находят по формуле

.

(2)

Выражение  называют дискриминантом
квадратного уравнения (1).

В
случае, когда второй коэффициент квадратного уравнения четное число , корни удобно находить
по формуле

.

(3)

Число корней квадратного уравнения
зависит от дискриминанта:

если
, то уравнение имеет два
различных действительных корня;

если , то уравнение имеет два
равных действительных корня

 

или
один корень, но двойной кратности.

если , то уравнение не
имеет действительных корней.

При
решении неполного квадратного уравнения , где  удобно пользоваться
разложением на множители левой части уравнения:

.

1.3 Теорема Виета

При
решении полных квадратных уравнений применяют теорему Виета: если  и  – корни
квадратного уравнения , где , то справедливы формулы
для суммы и произведения этих корней:

,  .

(4)

Формулы (4) называют формулами
Виета.

Верно и обратное
утверждение: если числа  и  удовлетворяют равенствам
(4), то эти числа являются корнями квадратного уравнения.

Формулы
Виета верны и для приведенного квадратного уравнения . В этом случае они
приобретают вид:

,  .

Квадратный
трехчлен можно разложить на линейные множители:

1)   если
, то ;

2)   если
, то .

§2.
Примеры решения квадратных уравнений с параметром

Пример 1.
Найти все значения параметра а, для которых квадратное уравнение

1)               
имеет два различных корня;

2)               
не имеет корней;

3)               
имеет один корень.

Решение. Так как по
условию старший коэффициент , то уравнение является
квадратным. Найдем его дискриминант: .

Контрольными
значениями параметра будут те значения, при которых дискриминант равен нулю.

КЗП:   или .

Далее определим знак дискриминанта,
а для этого заметим, что он представляет собой квадратичную функцию, графиком
которой является парабола, причем ветви её направлены вверх.

Знак
:                      
1)     +      2)         3)       2)     +    1)

                             
               – 4       
      –            4                   а

Возможны
три случая.

1)
Если , то  и уравнение имеет два различных
действительных корня

.

2)       
Если  или , то  и уравнение имеет один двукратный
корень , причем если , то , а если , то .

3) Если , то  и уравнение не имеет
действительных корней.

Ответ:
при   ;

при
  корней нет;

при
  ;

при
  .

Пример 2. Решить уравнение .

Решение. Поскольку старший
коэффициент данного уравнения зависит от параметр , то это уравнение нельзя
считать квадратным. Поэтому найдем первое контрольное значение параметра, приравняв
старший коэффициент к нулю.

КЗП:
.

1)       
Если , то исходное уравнение
принимает вид:

,

то
есть становится линейным и его корнем является .

2)       
Если , то исходное уравнение
является квадратным, поэтому вычислим его дискриминант :

.

Найдём
другие контрольные значения параметра, из условия, что дискриминант
квадратного уравнения равен нулю.

КЗП: 
 или .

Определим знак
дискриминанта. Поскольку он представляет собой квадратичную функцию, то графиком
его является парабола c ветвями
направленными вниз.

Знак                 а)              б) 
+   в)    б)       а)

 
                               –      1                      6     –      b

Возможны
следующие три подслучая.

а)
Если , то , а значит, уравнение не имеет
корней.

б)
Если  или , то  и найти значение корня
уравнения можно по формуле , то есть

при
 получим ,

при
 получим .

в)
Если , то  и уравнение имеет два различных
корня

.

В
ходе решения данного квадратного уравнения получили три контрольных значения
параметра b, которые наносим на
числовую прямую для удобства записи ответа.

                                   
               1            2             6              b

Ответ:
при   корней нет;

при  ;

при
  ;

при
  ;

при
  .

Пример 3. Найти все значения
параметра, для которых квадратное уравнение  имеет хотя бы один общий
корень с уравнением .

Решение. В первом
уравнении старший коэффициент – это выражение, содержащее параметр с.
Поэтому первым контрольным значением параметра с будет то, при
котором старший коэффициент уравнения равен нулю.

КЗП:
.

Возможны
два случая.

1)       
Если , то получим уравнение , которое не имеет
решений.

2)       
Если , уравнение является
квадратным и найдём его дискриминант:

Дискриминант представляет собой выражение
первой степени. Найдем второе контрольное значение параметра, приравняв  к нулю.

КЗП:
.

Определим
знак .

                     
                                      а)                           б)    
+ 

                              
                              –           –1                            с

Итак,
возможны два подслучая.

а)
Если , то  и уравнение корней не
имеет.

б)
Если , то  уравнение имеет два
различных корня

.

Рассмотрим
второе уравнение . Его корнями являются
числа  и .

По
условию задачи хотя бы один из найденных корней должен быть также корнем уравнения
, то есть при подстановке
найденного корня в это уравнение должно получиться тождество.

Если
, то получаем равенство:

,

,

откуда
. Аналогично найдём значение
с, при котором корнем уравнения  является .

Имеем

,

,

=0,

.

Значит,
при  и  уравнение  имеет, по крайней мере,
один общий корень с уравнением .

Ответ:
  и  .

Пример 4. Дано уравнение . Доказать, что если , ,  – попарно различные
действительные корни этого уравнения, то

.

Решение. По условию , ,  – попарно различные
действительные корни уравнения , поэтому одновременно выполняются
следующие равенства:

0,

0,

0.

Почленно
вычитая из первого равенства сначала второе, а затем третье равенство, получим:

Поскольку по условию корни уравнения , ,  – попарно различные, то  и , следовательно,

 и .

Тогда
и разность этих выражений также равна нулю:

,

.

Так
как , то .

Подставив
 в равенство , найдем, что .

Тогда
из исходного уравнения следует, что . Что требовалось
доказать.

Пример 5. При каких
значениях параметра с уравнение

имеет
более двух корней?

Решение. Квадратное
уравнение имеет более двух корней, если все его коэффициенты равны нулю (см. пример
4), поэтому

Первое
уравнение имеет корни  и ; корнями второго
уравнения являются числа  и , а третьего –  и .

Общим
для всех является корень .

Ответ:
.

Пример 6. Решить
относительно х уравнение .

Решение. Раскрыв скобки,
получим уравнение вида:

.

Приравняв
старший коэффициент к нулю, найдем контрольное значение параметра.

КЗП:

                 
                                 –        2)          0            3)    +  а

                   
                                                      1)

Возможны
три случая:

1)       
Если , то уравнение примет вид
. Это уравнение решений не имеет.

2)       
Если , то разделив обе части
исходного уравнения на а, получим уравнение вида:

.

Преобразуем его,
выделив в левой части уравнения полный квадрат:

,

,

корнями этого
уравнения являются  и .

3)       
Если , то  и уравнение  корней не имеет.

Ответ: при   ,  ,

при
  корней нет.

Пример 7.  При каких
значениях параметра m
корни уравнения

 равны по модулю и
противоположны по знаку?

Решение. 1 способ –
найти все значения параметра т, при которых уравнение имеет два корня, найти
эти корни, а затем определить при каких значениях параметра m
корни уравнения противоположные числа.

2 способ. Сначала найти
при каких значениях параметра т уравнение имеет два корня, затем по
теореме Виета найти их сумму

.

Так
как корни уравнения противоположные числа, то их сумма равна нулю,
следовательно, , откуда .

Ответ:
.

Пример 8. Решите уравнение
 относительно
х.

Решение. Данное
уравнение является неполным квадратным, поэтому приведём его к виду: .

Рассмотрим
следующие случаи в зависимости от знака параметра .

1)       
Если , то , следовательно,
уравнение имеет два корня

 и
.

2)       
Если , то уравнение примет вид
 и имеет один двукратный
корень  .

3)       
Если , то , следовательно, уравнение
 корней не имеет.

Ответ:
при   ,  ,

при
  ;

при
 корней нет.

Пример 9. При каких
значениях параметра а уравнение

имеет
более одного корня?

Решение. Найдем
контрольные значения параметра, приравняв старший коэффициент к нулю.

КЗП:
,   или .

1)       
Если ,
то данное уравнение примет вид

 или , откуда .

2)       
Если , то уравнение
примет вид

 или ,

решением
последнего уравнения является любое действительное число.

3)       
Если  и , то данное уравнение является
квадратным, поэтому найдём дискриминант:

.

По условию данное
уравнение должно иметь более одного корня, поэтому найдём, при каких значениях
параметра а дискриминант , то есть

.

Так как , то , тогда  или .

Ответ: при  и при  уравнение имеет более
одного корня.

§3.
Задачи для самостоятельной работы

по решению квадратных
уравнений с параметром

1.    
Найти все значения параметра а, при
каждом из которых уравнение

 не имеет решений.  .

2.     Найти
все значения параметра а, при каждом из которых уравнение

 имеет два различных
корня.

.

3.     При
каких значениях параметра m
оба корня уравнения

 равны нулю?  .

4.     При
каких значениях параметра а сумма квадратов величин, обратных корням
уравнения , меньше обоих корней
уравнения

?  .

5.    
Найти все значения параметра а, при
которых уравнения

 и

имеют хотя бы один общий корень?  .

6.     Найти
все значения параметра а, при которых один корень квадратного уравнения  в два раза больше
другого.  .

7.    
Для каждого значения параметра a решить
относительно х следующие уравнения:

§4.
Решение уравнений с параметром,
приводимых к квадратным.

Пример 1.  Решите
уравнение  .

Решение. Дробь равна нулю тогда,
когда числитель дроби равен нулю, а знаменатель отличен от нуля. Найдём сначала
допустимые значения для переменной: .

Тогда
, это квадратное уравнение,
так как его старший коэффициент равен 1. Найдём дискриминант:

.

Определим
контрольное значение параметра, приравняв дискриминант к нулю.

КЗП:
.

1)          
Если , то  и уравнение имеет один
двукратный корень , который принадлежит
области допустимых значений.

2)          
Если , то  и уравнение имеет два
корня

  и  .

Выясним,
при каких значениях параметра с эти корни удовлетворяют условию .

Если
, то  при условии, что  или .

Если
, то  при условии, что  или .

Найдём
корни уравнения при значениях параметра  и .

Если
, то корень уравнения
находим по формуле

,

а
если , то по формуле .

Ответ:
при  и   ;

при
 и   ;

при
  ;

при
  ;

при
  .

Пример 2.  Решите
относительно х уравнение  .

Решение. Преобразуем данное уравнение
следующим образом:

;

;

.

Определим
контрольное значение параметра, при котором знаменатель дроби равен нулю.

КЗП:
.

1)       
Если , то уравнение решений не
имеет.

2)       
Если , то  при условии, что  или .

Решим
квадратное уравнение .

Найдем
дискриминант

КЗП:
.

а)
Если , то  и уравнение имеет один
двукратный корень, который находим по формуле . Так как , то  и он удовлетворяет
условию .

б)
Если , то  и уравнение  имеет
два корня

  и  .

Так
как , то определим, при каких
значениях параметра а найденные корни удовлетворяют этому условию.

Если
, то  при условии, что , то есть .

Если
, то  при условии, что  или .

Найдём
корни уравнения при значениях параметра  и .

При
 корнем уравнения будет , а при  по формуле  находим, что .

Ответ:
при ,  и   ;

при
,  и   ;

при
  ;

при
  решений нет.

§5.
Задачи для самостоятельной работы

по решению уравнений,
приводимых к квадратным

1.          
Решить уравнение

(–6,
при     –5, при     2, при;

3,
при ;      или  во всех остальных
случаях)

2.                
При каких значениях параметра а
уравнение

имеет единственное
решение?  (при , , )

3.                
Найдите все значения а, при которых
вершины парабол

 и

лежат по разные
стороны от прямой .

§6. Задачи, связанные с расположением
корней квадратного трехчлена.

При
решении задач с параметрами приходится работать с тремя типами моделей:

1)    вербальная
модель – словесное описание задачи;

2)    геометрическая
модель – график квадратичной функции;

3)    аналитическая
модель – система неравенств, при помощи которой описывается геометрическая
модель.

Важно
уметь устанавливать связь между этими моделями. Это означает, что для любого
свойства, сформулированного на алгебраическом языке, нужно уметь давать
геометрическую интерпретацию и, наоборот, по поведению графика параболы дать
общую оценку коэффициентов квадратного трехчлена и его корней. Например,

если
старший коэффициент квадратного трехчлена меньше нуля, то ветви параболы
направлены вниз;

если
, то трехчлен имеет
различные действительные корни и парабола пересекает ось абсцисс в двух точках;

если
график функции  находится выше оси
абсцисс, то  и .

Последнюю
геометрическую модель можно описать еще тремя способами: неравенство  выполняется
при любом х; неравенство  не
имеет решений; трехчлен  не
имеет действительных корней и его старший коэффициент положителен.

Многие
задачи решают по следующему алгоритмическому предписанию:

1)       
уравнение записывают в виде ;

2)               
находят контрольные значения параметра и для
каждого случая строят параболу (геометрическую модель);

3)               
геометрическую модель описывают системой
неравенств (аналитическая модель);

4)               
решают систему неравенств.

Рассмотрим
несколько примеров теоретического плана, показывающих некоторые общие подходы к
решению задач о расположении корней квадратного трехчлена.

Пусть  – квадратный трёхчлен. Рассмотрим
случай, когда старший коэффициент  .

Обозначим корни
квадратного уравнения  через  и , причём .

Пусть  и В – некоторые
числа на оси Ох.

Задача 1.
При каких условиях оба корня квадратного уравнения, не
обязательно различные, меньше некоторого числа ?

Решение.
Обозначим через  абсциссу вершины
параболы, .

Так
как графиком квадратного трёхчлена является парабола, то построим
геометрическую модель данной задачи.

Оба
корня  и  квадратного уравнения меньше
некоторого числа  тогда
и только тогда, когда выполняются следующие условия:

  или 

2)
Корни  и  квадратного уравнения лежат
по разные стороны от числа  тогда и только тогда,
когда выполняются следующие условия:

  или 

3) Оба корня  и  квадратного уравнения больше
некоторого числа  тогда
и только тогда, когда выполняются следующие условия:

  или 

4) Оба корня  и  квадратного уравнения лежат
между числами  и В тогда и
только тогда, когда выполняются следующие условия:

  или 

5)
Корни  и  квадратного уравнения лежат
по разные стороны отрезка  на оси Ох тогда
и только тогда, когда выполняются следующие условия:

  или 

6) Квадратное уравнение
имеет два различных корня  и  и только один из
них принадлежит интервалу  или, другими словами,
для
того, чтобы парабола пересекала интервал  оси Ох только
в одной точке, необходимо и достаточно, чтобы значения
квадратного трехчлена

 в точках А и В
были разных знаков, то есть искомое условие имеет вид:

.

Очевидно,
что если

то
в рассматриваемом интервале лежит больший корень, а если

то
рассматриваемому интервалу принадлежит меньший корень.

7) Квадратное уравнение
имеет два отрицательных корня при условиях:

  Û 

Квадратное уравнение
имеет два положительных корня при условиях:

  Û 

Из приведенных примеров достаточно
ясно виден общий подход к решению задач рассматриваемого вида. Как правило,
задачи с ограничениями на корни квадратного трехчлена сводятся к системе
рациональных неравенств, которая легко решается методом интервалов. При этом
для определения условий, накладываемых на коэффициенты квадратного трехчлена,
рассматриваются следующие его свойства:

·              
расположение параболы относительно оси Ох;

·              
значения квадратного трехчлена в некоторых
заданных точках;

·              
положение оси симметрии параболы
относительно некоторых заданных точек.

Пример 1.
Найдите все значения параметра а, при которых корни уравнения  действительные,
различные и оба больше а.

Решение. Графическая
интерпретация задачи показана на рисунке. Обозначим через

.

Уравнение
 будет
иметь
два различных действительных корня, которые
одновременно больше а, тогда и только тогда, когда выполняются следующие
условия:

  Û 

Решая
полученную систему методом интервалов, найдем .

Ответ:
.

Пример 2. Найдите все
значения параметра а, при которых корни квадратного уравнения  неположительные.

Решение. Так как уравнение
квадратное, то . Обозначим через .

Рассмотрим
два случая.

1) 
Пусть . Для того чтобы
уравнение

имело
неположительные корни, необходимо и

достаточно
выполнение следующих условий:

  Û 

Применив
к системе метод интервалов, получим .

2)       
Пусть . Тогда положение
параболы определяется условиями:

  Û 

Решением этой системы является пустое
множество.

Ответ:
.

Пример 3. При каких
значениях а уравнение

имеет
корни разных знаков?

Решение. Для того чтобы парабола
– график

функции
,

пересекала
ось Ox,
в точках, между которыми

лежит
начало координат, необходимо и достаточно,

чтобы
квадратный трехчлен  принимал в точке  отрицательное значение,
поэтому искомое условие имеет вид:

 или .

Ответ:
.

Пример 4. При каких значениях
параметра  оба корня уравнения  принадлежат отрезку ?

Решение. Так как оба корня уравнения

 принадлежат отрезку ,

то
положение параболы

определяется
условиями:

  Û 

Данную
систему решаем методом интервалов, получаем .

Ответ:
.

Пример 5. При каких
значениях параметра а больший корень уравнения  принадлежит промежутку ?

Решение. Положение параболы,
являющейся графиком квадратного трехчлена , при котором только лишь
её правая ветвь пересекает промежуток  оси Оx определяется условиями:

  Û 
 

 Û 
  Û    Û 

Ответ:
.

Пример 6. При каких
значениях параметра а все корни уравнения  лежат
вне отрезка ?

Решение. При  данное уравнение имеет
вид  и,
следовательно, корней не имеет.

Если , то квадратный трехчлен

 всегда имеет два корня
разных знаков, так как .

Положение
параболы показано на рисунке.

Необходимые
и достаточные условия имеют

вид:

           

Ответ:
.

Пример 7. Найти все
значения параметра m,
при которых один из корней уравнения  находится между числами
0 и 2, а второй между 3 и 5.

Решение. Найдём дискриминант
квадратного уравнения

.

Так
как , то уравнение имеет два
корня:  и . Очевидно, что , поэтому

            .

Ответ:
 

§7.
Задачи для самостоятельного решения,

связанные с расположением
корней квадратного трехчлена.

1.                
Найдите все значения параметра а,
при каждом из которых все корни уравнений  и  различны и между двумя
корнями одного из них находится ровно один корень другого.  

2.                
Найдите все значения параметра а,
при которых корни уравнения

 неотрицательны.  

3.                
При каких значениях параметра а
существует единственный корень уравнения , удовлетворяющий условию
?

.

4.                
Найдите все значения параметра k,
при которых корни уравнения

 имеет два корня, причем
один из них меньше 1, а другой больше 2. 

5.        
Сколько решений, удовлетворяющих условию , имеет уравнение  в зависимости от значений
параметра а?

Заключение

Параметр – это величина,
значения которой служат для различения элементов некоторого множества между
собой, при этом он требует к себе осторожного и вдумчивого отношения. Ведь,
являясь фиксированным, но неизвестным числом, параметр ограничивает степень свободы
общения с ним. Задачи с параметром – это задачи исследовательского характера,
которые требуют хорошего понимания изучаемого теоретического материала.

Автор надеется, что данное
методическое пособие будет полезно кадетам как в процессе изучения рассмотренных
тем, так и для успешной сдачи экзаменов.

Список использованной литературы:

1.     Математика
для старшеклассников. Методы решения задач с параметрами /А.И. Азаров,С.А.
Барвенков-Мн.:»Аверсэв»,2003-272с.

2.     Большой
энциклопедический словарь. Математика. — М.: Научное издательство «Большая Российская
Энциклопедия», 1998.

3.     Задачи
с параметрами. Горнштейн П.И., Полонский В.Б., Якир М.С.  – М.: Илекса,
Харьков: Гимназия, 2003.

4.      Задачи
с параметрами. Егерман Е – Математика №2, 2003.

5.     Задачи
с параметром, сводящиеся к квадратным уравнениям/ Мещерякова Г.П.. – Математика
в школе №5, 2001.

6.     Математика:
интенсивный курс подготовки к экзамену. Черкасов О.Ю., Якушев А.Г.  – М.:
Рольф, 1997.

7.     .
Задачи с параметром. Линейные уравнения и их системы: 8-9 классы. Шевкин А.В –
М.: ТИД «Русское слово – РС», 2003.

На этой странице вы узнаете

• Игра в прятки: как значение одной переменной может помочь найти другую?
• Парадокс: как стоять на месте и бежать с любой скоростью одновременно? 
• Решаем параметры осторожно: как не совершить ошибку в квадратном уравнении с параметром? 

Мы привыкли, что в уравнении коэффициенты не меняются. Но возможно ли из одного уравнения составить бесконечное множество различных его вариантов? Узнаем об этом в статье. 

Что такое параметр 

Утром на термометре было некоторое количество градусов, которое мы обозначим за х. В обед температура воздуха изменилась в несколько раз. Во сколько раз должна была измениться температура воздуха, чтобы на термометре было 20 градусов? 

Такие задачи достаточно легко решаются. Если бы изначально было пять градусов, то искомое число было бы равно (frac{20}{5} = 4). А если было 10 градусов, то искомое число было бы равно (frac{20}{10} = 2). 

Но не все так просто. Мы не знаем, какой изначально была температура. Также мы не знаем, во сколько раз она изменилась. То есть мы получили уравнение с двумя неизвестными переменными. 

Обозначим вторую переменную a, у нас получится уравнение вида ax=20. Только что введенная нами переменная “a”  называется параметр. 

Параметр — это условная буква, вместо которой можно подставить число. 

То есть параметр — это еще одна переменная, которая может принять несколько значений. 

Как решать уравнения с параметром, если у нас целых две (а то и больше) неизвестных переменных? Нужен иной подход, чем при решении обычного уравнения.

Решить уравнение с параметром — это найти такие числовые значения параметра, при которых условие выполняется. 

Мы ищем не единственное значение параметра, а все возможные его значения для заданного условия.

Линейные уравнения с параметром

Вернемся к нашей погоде. У нас получилось уравнение ax = 20. Как найти, сколько градусов было изначально? Разделить все уравнение на число a. 

(x = frac{20}{a})

Какие значения может принимать параметр? Любые. Например, при a = 1 x = 20.
При a = 2 x = 10.
При a = 40 x = 0,5 

Что, если a=0? Мы получаем уравнение (x = frac{20}{0}), у которого нет решения, поскольку на 0 делить нельзя. 

Если мы не будем преобразовывать изначальное уравнение, то получится 0*x=20, то есть уравнение не будет выполняться: какое бы число мы ни умножили на 0, получится 0. 

Получается, решение есть при любых значениях a, кроме 0. Таким образом, мы и нашли ответ: при a = 0 решений нет, при a (neq) 0 — x = 20a. 

Добавим немного теории. Представим наше уравнение в виде ax = b, где a, b — действительные числа. Рассмотрим несколько случаев. 

1) b (neq) 0. 

Предположим, Пете необходимо в несколько раз увеличить скорость х, пробежать дистанцию и поставить рекорд. Чтобы поставить рекорд, он должен бежать со скоростью 15 км/ч — это и будет коэффициент b. 

Получаем уравнение ax = 15. Как найти начальную скорость Пети? (x = frac{15}{a}). 

Такое уравнение мы уже решали выше. Получаем два случая: 

• Если a = 0 — решений нет. 
• Если a (neq) 0, то изначальная скорость Пети была равна (x = frac{15}{a}). 

2) b = 0. 

Мы получаем уравнение ax = 0. Также разберем два случая значений параметра: 

• a = 0. Мы получаем уравнение 0 * x = 0. Какое значение х нужно подставить, чтобы уравнение выполнялось? 

Какое бы число мы ни умножили на 0, получим 0. Получаем бесконечное множество решений. 

• a (neq) 0. Здесь получается, что равен 0 уже х: (x = frac{0}{a} = 0). 

Подведем итог. Как можно решить уравнение вида ax = b?

• Если a = 0, b = 0 — бесконечное множество решений. 
• Если a = 0, b (neq) 0 — решений нет. 
• Если a (neq) 0, b (neq) 0 — решением будет (x = frac{b}{a}). 

Квадратные уравнения с параметром

Прежде чем приступать к изучению следующего материала, рекомендуем ознакомиться с понятием квадратного уравнения в статье «Линейные, квадратные и кубические уравнения». Также важно ориентироваться в графиках параболы из статьи «Основные элементарные функции». 

Квадратное уравнение имеет вид ax² + bx + c = 0, а графиком функции y = ax² + bx + c будет парабола. 

Как работать с такими уравнениями, если в них присутствует параметр? В первую очередь, важны рассуждения. Любое задание с параметром можно решить, проанализировав функцию.  

Решение квадратного уравнения опирается на понятие дискриминанта. В зависимости от его значений может получиться разное количество корней: 

• При D > 0 уравнение имеет два корня. 
• При D = 0 уравнение имеет один корень. 
• При D < 0 уравнение не имеет корней. 

Как это проверить на графике? Корни уравнения — это точки, в которых парабола пересекает ось абсцисс, то есть ось х. 

Рассмотрим три уравнения. 

1) x² — x — 2 = 0
Решим уравнение с помощью дискриминанта. 
D = 1² — 4 * 1 * (-2) = 1 + 8 = 9
Поскольку дискриминант больше 0, то уравнение имеет два корня. 

(x_1 = frac{1 + 3}{2} = 2)
(x_2 = frac{1 — 3}{2} = -1)

Проверим с помощью графика функции. Построим параболу и заметим, что она действительно дважды пересекает ось абсцисс, а координаты этих точек равны (−1; 0) и (2; 0) . 

2) x² -4x + 4 = 0
Решим уравнение с помощью дискриминанта. 
D = 16 — 4 * 1 * 4 = 16 — 16 = 0
Поскольку дискриминант равен 0, у уравнения всего один корень. 

(x = frac{4}{2} = 2)

Проверим на графике. И действительно, парабола касается оси х только один раз в вершине, координаты которой (2; 0). 

3) x² — 5x + 7 = 0
Решим уравнение с помощью дискриминанта. 
D = 25 — 4 * 1 * 7 = 25 — 28 = -3

Поскольку дискриминант отрицательный, у уравнения нет корней. И это отлично видно, если посмотреть на график функции: парабола лежит выше оси х и никогда ее не пересечет. 

Где можно применить эти знания, решая параметры? 

Пример 1. Найдите все значения параметра a, при которых уравнение x² + (3a + 11)x + 18,25 + a = 0 имеет два различных решения. 

Решение. Перед нами квадратное уравнение с коэффициентами b = 3a + 11, c = a + 18,25. В каких случаях это уравнение будет иметь два различных корня?

Квадратное уравнение имеет два корня, если D > 0. Нужно найти все значения параметра, при которых дискриминант будет положительным. 

1. Для начала найдем сам дискриминант. 

D = (3a + 11)² — 4 * 1 * (a + 18,25) = 9a² + 66a + 121 — 4a — 73 = 9a² + 62a + 48

2. Поскольку дискриминант должен быть больше 0, то получаем неравенство 9a² + 62a + 48 > 0

3. Решим его «Методом интервалов».

9a² + 62a + 48 = 0
D = 3844 — 1728 = 2116
(a_1 = frac{-62 + 46}{18} = -frac{16}{18} = -89)
(a_2 = frac{-62 — 46}{18} = -frac{108}{18} = -6)

4. Дискриминант будет положительным при (a in (-infty; -6) cup (-frac{8}{9}; +infty)). Это и будет ответ. 

Ответ: (a in (-infty; -6) cup (-frac{8}{9}; +infty)).

Важно: в уравнении мы указываем не сами решения уравнения, а значения параметра, при которых уравнение имеет два решения. 

Пример 2. При каких значениях параметра a уравнение (2a + 1)x² — ax + 3a + 1 = 0 имеет два различных решения? 

Решение. Этот пример похож на предыдущий, однако здесь есть одна важная особенность. Что произойдет с уравнением, если 2a+1 = 0? 

Мы получим уравнение 0,5x — 0,5 = 0, то есть линейное уравнение. У уравнения будет всего одно решение, что уже не подходит под условие задачи. 

1. Поскольку по условию должно быть 2 решения, мы получаем, что a (neq) -0,5. 

2. Найдем дискриминант уравнения. Он должен быть строго больше 0, чтобы у уравнения было два решения. 

D = a² — 4 * (2a + 1) * (3a + 1) = a² — 24a² — 20a -4 = -23a² — 20a — 4

3. Составим неравенство и решим его:

-23a² — 20a — 4 > 0
23a² + 20a + 4 < 0
23a² + 20a + 4 = 0
D = 400 — 4 * 23 * 4 = 400 — 368 = 32
(a_1 = frac{-20 + 4 sqrt{2}}{46} = frac{2sqrt{2} — 10}{23})
(a_2 = frac{-20 — 4sqrt{2}}{46} = frac{-2sqrt{2} — 10}{23})

4. Разложим уравнение на множители: 

(23a^2 + 20a + 4 = 23(a — frac{2sqrt{2} — 10}{23})(a — frac{-2sqrt{2} — 10}{23}))

5. Получаем неравенство:

(23(a — frac{2sqrt{2} — 10}{23})(a — frac{-2sqrt{2} — 10}{23} < 0)

6.Тогда  (a in (frac{-2sqrt{2} — 10}{23}; frac{2sqrt{2} — 10}{23})). Вспомним, что a (neq) -0,5, следовательно, мы получаем ответ (a in (frac{-2sqrt{2} — 10}{23}; -0,5) cup (-0,5; frac{2sqrt{2} — 10}{23})).

Ответ: (a in (frac{-2sqrt{2} — 10}{23}; -0,5) cup (-0,5; frac{2sqrt{2} — 10}{23}))

Теорема Виета 

Дискриминант — не единственный способ решить квадратное уравнение. Обратимся к теореме Виета. Если нам дано уравнение ax² + bx + c = 0, то его корни можно найти с помощью следующей системы: 

Теорему Виета удобно использовать, если на корни уравнения наложены дополнительные ограничения. 

Пример 3. При каких значениях параметра a корни уравнения x² — 3ax — a(a — 1) = 0 удовлетворяют условию x₁ = 5x₂. 

Решение. 1. Корни уравнения — это два различных числа. Значит, дискриминант должен быть строго больше 0: 

D = 9a² — 4 * 1 * (-a² + a) = 9a² + 4a² — 4a = 13a² — 4a = a(13a — 4)

Получаем неравенство a(13a — 4) > 0, следовательно, (a in (-infty; 0) cup (frac{4}{13}; +infty)). 

2. По теореме Виета найдем корни уравнения: 

3. По условию x₁ = 5x₂, тогда 5x₂ + x2 = 6x₂ = 3a, откуда получаем:
(x_2 = frac{3a}{6} = frac{a}{2})
(x_1 = 5 * a_2 = frac{5a}{2})

4. Подставим во второе уравнение системы:
(frac{a}{2} * frac{5a}{2} = a — a^2)
(frac{5a^2}{4} = a — a^2 | * 4)
5a² = 4a — 4a²
(9a^2 — 4a = 0 rightarrow a(9a — 4) = 0 rightarrow a = 0, a = frac{4}{9})

5. Мы нашли значения параметра, при которых выполняется условие. Осталось проверить, чтобы при этих значениях у уравнения было два корня. 

a = 0 не подходит, поскольку ограничение (a in (-infty; 0) cup (frac{4}{13}; +infty)) не включает точку 0. 

(a = frac{4}{9}) подходит, поскольку (frac{4}{9} > frac{4}{13}). 

Ответ: (a = frac{4}{9})

Условия на корни квадратного трехчлена 

Однако могут встретиться еще более сложные задания с параметрами. Рассмотрим каждый из этих случаев. 

1. Корни квадратного трехчлена меньше, чем число N. 

Построим параболу. Вспомним, что ветви параболы могут быть направлены или вверх, или вниз. 

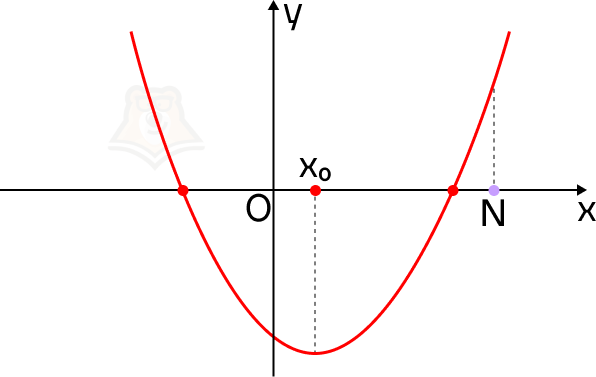
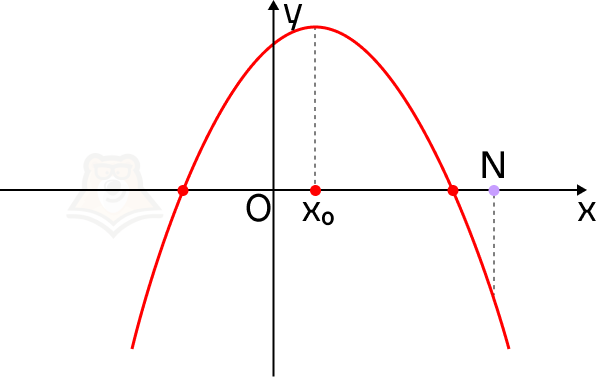
Если ветви параболы направлены вверх. Отметим на оси х точку N так, чтобы она лежала правее обоих корней уравнения. Так мы зададим условие, что корни уравнения меньше, чем число N. 

Представим, что мы идем по холмистой местности, и у нас есть ее карта. Имея перед собой плоскую картинку, мы понимаем, как относительно друг друга располагаются точки в пространстве. Но посмотрев на рельеф сбоку, заметим, что точки имеют разную высоту. 

Пусть в точках, где парабола пересекает ось х, будут привалы на экскурсионном маршруте, а в точке N будет смотровая площадка. 

Что можно сказать про смотровую площадку на этой карте? Она находится выше, чем привалы, и лежит правее, чем самая низкая точка рельефа. 

Рассмотрим эти условия на графике. В точке N значение функции f(x) больше, чем в корнях уравнения. Более того, она лежит правее, чем вершина параболы, то есть ее абсцисса больше абсциссы параболы. 

Почему эти условия так важны? Пусть точка N будет лежать левее вершины параболы. Тогда не выполняется условие, что корни меньше, чем N. 

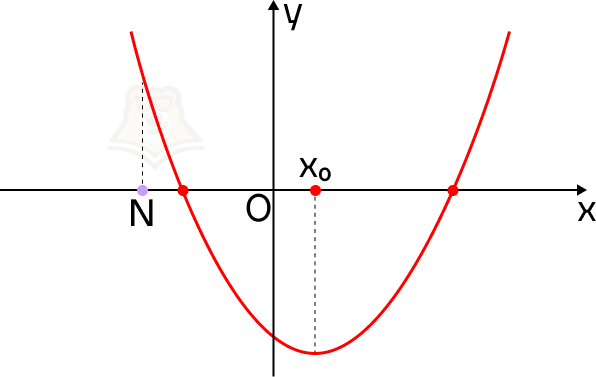
В этом случае на нашем экскурсионном маршруте смотровая площадка будет лежать до привалов. 

А если значение функции в точке N будет меньше, чем в корнях уравнения? Точка N будет лежать между ними. 

В этом случае смотровая площадка окажется между привалами. 

Аналогичным способом можно проследить изменение условий при любом положении точки N на графике. 

Для того чтобы оба корня квадратного трехчлена ax² + bx + c были меньше, чем число N, необходимо и достаточно выполнение следующих условий: 

Что произойдет, если ветви параболы будут направлены вниз? Наш экскурсионный маршрут немного поменяется: появится гора, а не овраг. 

Где теперь располагается смотровая площадка? Она будет ниже, чем привалы, и дальше, чем самая высокая точка горы. 

Мы можем сделать вывод, что точка N на графике будет лежать правее вершины параболы, а значение функции в ней будет меньше, чем значение функции в корнях уравнения. 

Для того чтобы оба корня квадратного трехчлена ax² + bx + c были меньше, чем число N, необходимо и достаточно выполнение следующих условий: 

2. Корни квадратного трехчлена больше, чем число N. 

Рассуждаем так же, как и в предыдущей функции, однако теперь точка N перемещается левее параболы. 

Если ветви параболы направлены вверх, то функция в точке N принимает большее значение, чем в корнях уравнения, а сама точка N будет лежать левее параболы. 

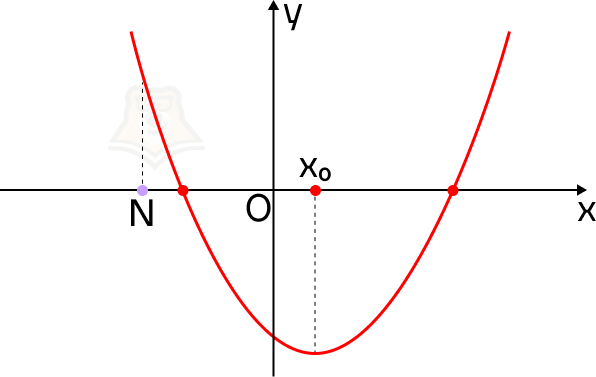
Для того чтобы оба корня квадратного трехчлена ax² + bx + c были больше, чем число N, необходимо и достаточно выполнение следующих условий: 

Теперь направим ветви параболы вниз. Значение функции в точке N будет меньше, чем в корнях уравнения. 

Для того чтобы оба корня квадратного трехчлена ax² + bx + c были больше, чем число N, необходимо и достаточно выполнение следующих условий: 

С помощью анализа расположения точек на графике функций можно задать условия для любой ситуации, даже если точек будет несколько. 

В итоге должна получиться система, с помощью которой можно решить задачу.

Фактчек

• Параметр — это буква a, вместо которой можно подставить число. Решить уравнение с параметром — это найти такие числовые значения параметра, при которых условие выполняется. 
• При решении линейного уравнения ax=b в зависимости от значения коэффициентов может получиться несколько вариантов решений. Если a = 0, b = 0 — бесконечное множество решений. Если a = 0, b (neq) 0 — решений нет. Если a (neq) 0, b (neq) 0 — решением будет (x = frac{b}{a}). 
• При решении квадратного уравнения обязательно проверять коэффициент перед x². Если коэффициент будет равен 0, то уравнение станет линейным.
• При решении квадратного уравнения важно учитывать значение дискриминанта: если он строго больше 0, то корней у уравнения два, если дискриминант равен 0, то у уравнения один корень, если дискриминант меньше 0, то у уравнения нет корней. 
• Решить квадратное уравнение можно и с помощью теоремы Виета. 
• Если в задаче даны дополнительные условия на корни уравнения (например, они должны быть больше или меньше определенного числа), то задать их можно с помощью системы. Неравенства в системе можно составить с помощью анализа примерного графика функций. 

Проверь себя

Задание 1. 
Что такое параметр?

1. Это буква a, вместо которой можно подставить число.
2. Это коэффициент перед x² в квадратном уравнении.
3. Это переменная х.
4. Это значение функции в определенной точке. 

Задание 2. 
Дано уравнение ax = b. Сколько решений оно имеет, если a = 0 и b = 0?

1. Решений нет.
2. Одно решение.
3. Бесконечное множество решений.
4. Невозможно определить количество решений. 

Задание 3. 
При каких значениях дискриминанта уравнение будет иметь корни?

1. D > 0
2. D = 0
3. D < 0
4. D (neq) 0

Задание 4. 
Корни квадратного уравнения меньше числа А. Где будет лежать вершина параболы относительно точки А?

1. Справа.
2. Слева.
3. Совпадать с точкой А.
4. Невозможно определить расположение вершины. 

Задание 5. 
Меньший корень квадратного уравнения больше числа А, но меньше числа В. Ветви параболы направлены вниз. Чему будет равно значение функции в точке В?

1. Значение функции в точке В будет меньше 0.
2. Значение функции в точке В будет равно 0.
3. Значение функции в точке В будет больше 0.
4. Невозможно определить значение функции. 

Ответы: 1. — 1 2. — 3 3. — 4 4. — 2 5. — 3.

Дорогой друг! Если ты никогда не решал задач с параметрами – прочитай статьи «Что такое параметр» и «Графический способ решения задач с параметрами». Квадратные уравнения, а тем более неравенства с параметрами только на первый взгляд кажутся простыми. Чтобы уверенно решать их, надо знать определенные приемы. О некоторых мы расскажем.

И заодно – стоит повторить темы «Квадратные уравнения» и «Квадратичные неравенства».

Разберем сначала подготовительные задачи. А в конце – реальную задачу ЕГЭ.

1. Найдите все значения a, при которых уравнение не имеет действительных корней.

Всегда ли это уравнение является квадратным относительно переменной х? – Нет, не всегда. В случае, когда коэффициент при равен нулю, оно станет линейным.

Рассмотрим два случая – когда это уравнение квадратное и когда оно линейное.

1)

Тогда уравнение примет вид 2 = 0. Такое уравнение не имеет действительных корней, что удовлетворяет условию задачи.

2)

Уравнение будет квадратным. Квадратное уравнение не имеет действительных корней тогда и только тогда, когда его дискриминант отрицательный.

Найдем дискриминант :

< 0.

< 0

< 0

Решив неравенство, получим

С учетом пункта 1, получим ответ: .

2. Найдите все значения a, при каждом из которых сумма квадратов действительных корней уравнения

минимальна.

Мы привыкли находить корни квадратного уравнения по известной формуле, с помощью дискриминанта. Однако для задач с параметрами такой способ подходит не всегда. А вот теорема Виета нам поможет.

В условии сказано: «Сумма квадратов действительных корней…» Это значит, во-первых, что корни есть, а во-вторых, их должно быть два. А это будет в случае, когда дискриминант положителен ( > 0).

Если и – корни квадратного уравнения
, то по теореме Виета:

В нашем случае:

Решим первое неравенство системы

Квадратный трехчлен в левой части не имеет корней, так как дискриминант равен -32, то есть отрицателен. Поэтому неравенство будет выполняться для всех действительных значений .

Возведем второе уравнение системы в квадрат:

Из этих двух уравнений выразим сумму квадратов и .

Значит, сумму квадратов корней уравнения можно выразить через параметр

График функции — парабола, ее ветви направлены вверх, минимум будет достигаться в ее вершине. Найдем вершину параболы:

Ответ: 1

3) Найдите все значения , при каждом из которых все решения уравнения

положительны.

Как и в первой задаче, уравнение является квадратным, кроме случая, когда . Рассмотрим этот случай отдельно

1) . Получим линейное уравнение

У него единственный корень, причем положительный. Это удовлетворяет условию задачи.

2) При уравнение будет квадратным. Нам надо, чтобы решения существовали, причем были положительными. Раз решения есть, то .

Покажем один из приемов решения квадратичных уравнений и неравенств с параметрами. Он основан на следующих простых утверждениях:

— Оба корня квадратного уравнения и положительны тогда и только тогда, когда их сумма положительна и произведение положительно.

Очевидно, что сумма и произведение двух положительных чисел также положительны. И наоборот – если сумма и произведение двух чисел положительны, то и сами числа положительны.

— Оба корня квадратного уравнения и отрицательны тогда и только тогда, когда их сумма отрицательна, а произведение положительно.

Корни квадратного уравнения и имеют разные знаки тогда и только тогда, когда их произведение отрицательно.

Сумма и произведение корней входят в формулировку теоремы Виета, которой мы и воспользуемся. Получим

Второе и третье неравенства имеют одинаковое решение . Решение первого неравенства:
.

Решение системы: .

С учетом пункта 1 получим ответ

Ответ:

4. При каких значениях параметра a уравнение

имеет единственное решение?

Уравнение является показательным, причем однородным. Мы умеем решать такие уравнения! Разделим обе части на .

Получим:

Сделаем замену 

Для того, чтобы исходное уравнение имело единственное решение, нужно, чтобы уравнение относительно t имело ровно один положительный корень.

1) В случае уравнение будет линейным

Значит, подходит. В этом случае уравнение имеет единственный положительный корень.

2) Если , уравнение будет квадратным.

Его дискриминант

Дискриминант является полным квадратом и поэтому всегда неотрицателен. Уравнение имеет либо один, либо два корня. В этом случае несложно найти корни в явном виде.

Один корень получился не зависящим от параметра, причем положительным. Это упрощает задачу.

Для того, чтобы уравнение имело единственный положительный корень, нужно, чтобы либо второй был отрицательным, либо равным нулю, либо чтобы корни совпадали. Рассмотрим все случаи.

а)

Тогда

б)

Объединив все случаи, получим ответ.

Ответ:

И наконец – реальная задача ЕГЭ.

5. При каких значениях a система имеет единственное решение?

Решением квадратного неравенства может быть:

1) отрезок

2) 2 луча

3) точка

4) ∅

В каких случаях система двух квадратных неравенств имеет единственное решение:

1) единственная общая точка двух лучей-решений ( или интервалов-решений)

2) одно из неравенств имеет решение – точку, которая является решением второго неравенства

Рассмотрим первый случай.

Решим систему

Если является решением 1 и 2 уравнений, то является решением уравнения (вытекает из второго первое) ⇒ или

Если , при этом система примет вид:

Второй корень первого уравнения:

Второй корень второго первого:

Единственное решение

Если , при этом система примет вид:

– бесконечно много решений, не подходит.

Рассмотрим второй случай.

– решением является точка, если – является решением второго неравенства.

– решением является точка, если – не является решением первого неравенства.

Ответ: