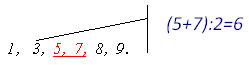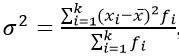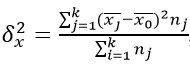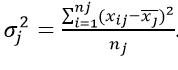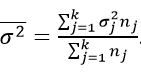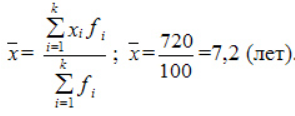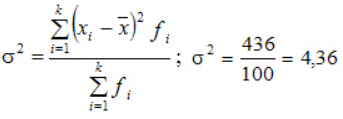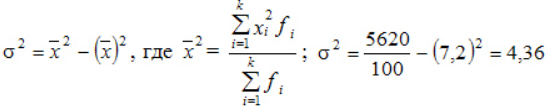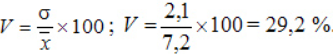Урок по теории вероятностей и статистике в 7 классе
Тема «Отклонения. Дисперсия». 7-й класс
Цель: сформировать у учащихся представление о понятиях “отклонение” и “дисперсия” и навыки их применения в реальных статистических исследованиях
Задачи урока:
- образовательные – показать, что окружающий нас изменчивый мир можно описать математическими понятиями, числовыми показателями;
- развивающие– формировать современное мировоззрение и умение ориентироваться в изменчивом информационном мире;
- воспитательные – учить мыслить категориями, имеющими вероятностный характер, применять вводимые понятия в практической жизни.
Планируемые результаты:
- знать, что такое отклонение от среднего арифметического и дисперсия;
- уметь вычислять отклонения, квадраты отклонений и дисперсию на коротких наборах;
- уметь применять понятия квадратов отклонений и дисперсии при анализе реальных ситуаций;
Оборудование:
- мультимедийный проектор, экран.
Дидактические материалы:
- карточки с таблицами.
Ход урока
I. Организационный момент
Сообщить тему и цели урока. (Слайд 1).
II. Актуализация знаний учащихся
На предыдущих уроках мы рассмотрели так называемые средние характеристики числового ряда, позволяющие оценить его поведение “в среднем”. Повторим их определения и способы нахождения.
Слайд 2 – задание на повторение (комментарии учителя, проверка ответов учеников с помощью слайда).
Задание. Дан числовой набор.
|
Х |
1 |
2 |
3 |
5 |
8 |
100 |
Найти среднее арифметическое и медиану, определить, какая из характеристик лучше характеризует числовой набор и почему?
III. Изучение нового материала, формирование знаний, умений и навыков
Слайд 3 — характеристики числового ряда (комментарии учителя).
Средние характеристики числового ряда (среднее арифметическое, медиана), позволяют оценить поведение ряда “в среднем”. Но это не всегда наиболее полно характеризуют выборку. Чтобы получить полное представление о поведении числового ряда, помимо средних характеристик надо знать характеристики разброса, показывающие, насколько сильно значения ряда отличаются друг от друга, как сильно они разбросаны вокруг средних.
Рассмотрим следующий пример ( раздать карточки с таблицами, которых нужно заполнять по ходу урока)
Слайд 4-5 – задание 1 (комментарий учителя).
Международные спортивные игры «Дети Азии» получили свое начало в 1996 г. по инициативе первого Президента Республики Саха (Якутия) М.Е.Николаева и были посвящены 100-летию олимпийского движения. С тех пор они проводятся совместно с Олимпийским комитетом России, Росспортом, Министерством иностранных дел Министерством образования и науки Российской Федерации. Летом 2012 года будет V международная спортивная игра «Дети Азии».
Для участия в V международных спортивных играх «Дети Азии» нужно выбрать лучших футболистов республики. На одно место футболиста претендуют двое. Для каждого из них установили испытательный срок, в течение которого они должны были участвовать в отборных играх. Результаты спортсменов представлены в таблице
Вопрос: кого из футболистов предпочтительнее взять на спортивные игры?
|
Номер сезона |
||
|
1-й футболист (Х) |
2-й футболист (Y) |
|
|
(кол-во голов) |
(кол-во голов) |
|
|
1 |
18 |
19 |
|
2 |
23 |
16 |
|
3 |
19 |
22 |
|
4 |
17 |
23 |
|
5 |
23 |
20 |
Рассчитаем, сколько голов забил каждый из футболистов за 5 сезонов.
|
Номер сезона |
||
|
1-й футболист (Х) |
2-й футболист (Y) |
|
|
(кол-во голов) |
(кол-во голов) |
|
|
1 |
18 |
19 |
|
2 |
23 |
16 |
|
3 |
19 |
22 |
|
4 |
17 |
23 |
|
5 |
23 |
20 |
|
Итого: |
100 |
100 |
Вывод: количество голов одинаково.
Рассчитаем, сколько голов в сезон забивал в среднем каждый футболист. Для этого найдём среднее арифметическое числовых наборов Х и Y.
|
Номер сезона |
||
|
1-й футболист (Х) |
2-й футболист (Y) |
|
|
(кол-во голов) |
(кол-во голов) |
|
|
1 |
18 |
19 |
|
2 |
23 |
16 |
|
3 |
19 |
22 |
|
4 |
17 |
23 |
|
5 |
23 |
20 |
|
Итого: |
100 |
100 |
|
Среднее арифметическое |
20 |
20 |
Среднее арифметическое у обоих футболистов тоже одинаковое.
На данном примере мы увидели, что с помощью средних характеристик сравнение выполнить не всегда возможно.
Как поступить?
В данном случае критерием сравнения может выступать стабильность игры– у какого футболиста количество забитых им голов в сезон менее отличается друг от друга, тот играет стабильнее.
Если количество забитых в сезон голов сильно разнится, то в какой-то сезон футболист играет не в полную силу, забивает меньше голов, а в какой-то сезон навёрстывает упущенное, а это всегда сказывается на качестве игры.
Стабильность можно оценивать с помощью отклонений элементов числового набора от среднего значения (отклонение – это разность между числом из данного набора и средним арифметическим этого набора)
Слайд 6 – пример вычисления отклонений (комментарии учителя).
Отклонение – разность между средним значением и числом набора
Набор отклонений:
|
X — X |
-2 |
-4 |
0 |
2 |
4 |
Логично предположить, что чем меньше будет разброс (отклонения от среднего значения) – тем стабильнее играет футболист.
Но когда набор чисел велик, рассматривать отклонения практически неудобно, нужно описать разнообразие чисел в наборе одним числом.
Попробуем найти сумму отклонений.
Слайд 6 – пример вычисления суммы отклонений (комментарии учителя, вывод).
-2-4+0+2+4=0
В сумме получилось 0 (т.к. при вычислении “среднего разброса” часть отклонений входит в сумму со знаком “+”, часть со знаком “-” и в сумме всегда получается 0). Следовательно сумма отклонений не может нести информацию о разбросе.
Какой же выход?
Можно суммировать квадраты отклонений (они всегда неотрицательны).
Слайд 7 – пример вычисления квадратов отклонений (комментарии учителя)
Набор квадратов отклонений:
|
(X – X)² |
4 |
16 |
0 |
4 |
16 |
Сумма квадратов отклонений:
4+16+0+4+16 = 40
Чем меньше сумма квадратов отклонений, тем меньше разброс чисел относительно среднего значения, тем более стабилен набор.
Итак, рассчитаем сумму квадратов отклонений для нашего примера.
|
Номер сезона |
||
|
1-й футболист (Х) |
2-й футболист (Y) |
|
|
(кол-во голов) |
(кол-во голов) |
|
|
1 |
18 |
19 |
|
2 |
23 |
16 |
|
3 |
19 |
22 |
|
4 |
17 |
23 |
|
5 |
23 |
20 |
|
Итого: |
100 |
100 |
|
Среднее арифметическое |
20 |
20 |
|
Сумма квадратов отклонений |
32 |
30 |
Вывод: второй футболист играет более стабильно, у него меньше сумма квадратов отклонений. Вероятно, тренер предпочтёт взять на соревнование его.
В данном примере футболисты играли одинаковое количество сезонов. А если они количество сезонов неодинаково?
Тогда стабильность игры каждого можно было бы оценить по величине среднего арифметического квадратов отклонений от среднего значения – дисперсии.
Слайд 8 – пример вычисления дисперсии (комментарии учителя).
Дисперсия — среднее арифметическое квадратов отклонений:
Dx= (4+16+0+4+16)/5 = 40/5 = 8
Дисперсия – характеристика разброса, мера стабильности.
Чем больше дисперсия, тем ниже стабильность
Рассмотрим следующий пример.
Слайд 9 – задание 2 (комментарии учителя).
(Ученикам открыть лист “Задание 2” файла с заданиями).
|
Номер сезона |
||
|
1-й футболист (Х) |
2-й футболист (Y) |
|
|
(кол-во голов) |
(кол-во голов) |
|
|
1 |
17 |
— |
|
2 |
21 |
17 |
|
3 |
20 |
20 |
|
4 |
16 |
18 |
|
5 |
15 |
21 |
|
6 |
19 |
14 |
Аналогично заданию 1 рассчитаем, сколько голов забил каждый футболист и сумму квадратов отклонений.
|
Номер сезона |
||
|
1-й футболист (Х) |
2-й футболист (Y) |
|
|
(кол-во голов) |
(кол-во голов) |
|
|
1 |
17 |
— |
|
2 |
21 |
17 |
|
3 |
20 |
20 |
|
4 |
16 |
18 |
|
5 |
15 |
21 |
|
6 |
19 |
14 |
|
Итого: |
108 |
90 |
|
Среднее арифметическое |
18 |
18 |
|
Сумма квадратов отклонений |
28 |
30 |
Т.к. футболисты играли разное количество сезонов, рассчитаем и сравним дисперсии числовых наборов X и Y.
|
Номер сезона |
||
|
1-й футболист (Х) |
2-й футболист (Y) |
|
|
(кол-во голов) |
(кол-во голов) |
|
|
1 |
17 |
— |
|
2 |
21 |
17 |
|
3 |
20 |
20 |
|
4 |
16 |
18 |
|
6 |
19 |
14 |
|
Итого: |
108 |
90 |
|
Среднее арифметическое |
18 |
18 |
|
Сумма квадратов отклонений |
28 |
30 |
|
Дисперсия |
4,6 |
6 |
Вывод: первый футболист играет стабильнее второго.
3. Самостоятельная практическая работа.
Слайд 10 — задание 3.
С 28 марта по 2 апреля в Южной Якутии пройдёт II Спартакиада зимних видов спорта Республики Саха (Якутия). Примут её опять Алдан и Нерюнгри.
Для участия в II Спартакиаде зимних видов спорта Республики Саха (Якутия)нужно выбрать лучших лыжников района. На одно место претендуют двое. Для каждого из них установили испытательный срок, в течение которого они должны были участвовать в отборных соревнованиях. Результаты спортсменов на 10 км.представлены в таблице
Вопрос: кого из спортсменов предпочтительнее взять на спартакиаду?
|
Номер сезона |
||
|
1-й спортсмен (Х) |
2-й спортсмен(Y) |
|
|
(время в мин.) |
(время в мин.) |
|
|
1 |
26,5 |
26,4 |
|
2 |
26,6 |
26,6 |
|
3 |
27 |
26,5 |
|
4 |
26 |
26,3 |
|
5 |
26,1 |
26,4 |
Подвести итог самостоятельной работы.
4. Итог урока.
Слайд 11 – выводы (комментарии учителя).
Слайд 12 – вопросы (ответы учеников).
Вася Иванов
Мореплаватель — имя существительное, употребляется в мужском роде. К нему может быть несколько синонимов.
1. Моряк. Старый моряк смотрел вдаль, думая о предстоящем опасном путешествии;
2. Аргонавт. На аргонавте были старые потертые штаны, а его рубашка пропиталась запахом моря и соли;
3. Мореход. Опытный мореход знал, что на этом месте погибло уже много кораблей, ведь под водой скрывались острые скалы;
4. Морской волк. Старый морской волк был рад, ведь ему предстояло отчалить в долгое плавание.
Изучая математическую статистику в 7-м классе,
важно наглядно представить учащимися образец
для решения практических задач. Именно для этого
мною был разработан данный справочный материал.
1.Представление данных.
1.1. Таблицы
Смета расходов на покупку спортивного
инвентаря.
| № | Наименование | Ед. измерения | Количество | Цена (едруб) | Стоимость (руб) |
| 1 | Мяч футбольный | Шт. | 30 | 1000 | |
| 2 | Мяч волейбольный | Шт. | 15 | 800 | 12000 |
| 3 | Ракетка | Шт. | 24 | 250 | 6000 |
| 4 | Воланы | коробка | 10 | 300 | 3000 |
| ИТОГО: | 51000 |
Таблицы предназначены для упорядочивания
большого количества данных. Часто в таблицы
заносят результаты вычислений, измерений.
1.2. Диаграммы.
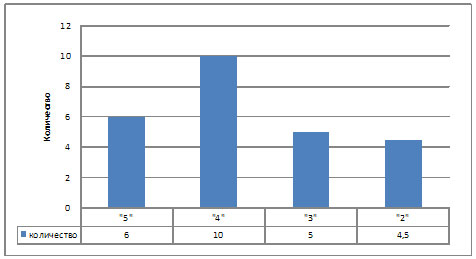
За контрольную работу по математике
школьники получили 6 оценок “отлично”, 10 оценок
“хорошо”, 5 оценок “ удовлетворительно” и 3
оценки “не удовлетворительно”.
Столбиковая диаграмма.
Построим столбиковую диаграмму по
этим данным.
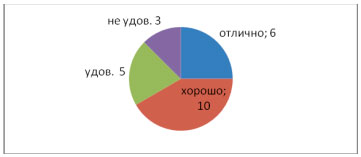
Круговая диаграмма.
Построим круговую диаграмму по этим
данным.
Для построения этой диаграммы мы:
- Разделили 360° на общее число учащихся (24)
- Затем последовательно умножаем 15° на
количество учащихся, получивших ту или иную
оценку. - Затем круг делим на полученные сектора,
подписываем данные.
360°24=15° (такому углу соответствует
оценка одного учащегося)
15°6=90° —
сектор образованный этим углом соответствует
учащимся с оценкой “5”
15°10=150°
— сектор образованный этим углом соответствует
учащимся с оценкой “4”
15°5=75° —
сектор образованный этим углом соответствует
учащимся с оценкой “3”
15°3=45° —
сектор образованный этим углом соответствует
учащимся с оценкой “2”
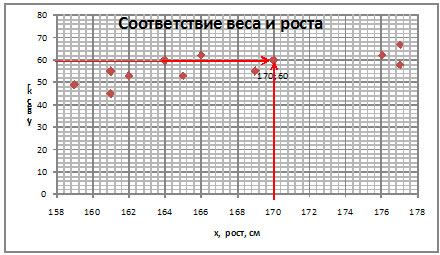
Диаграмма рассеивания.
Для выявления связи между величинами
применяются диаграммы рассеивания.
В таблице приведены данные о весе и
росте 12 девушек.
|
Рост, см |
165 |
177 |
161 |
162 |
170 |
176 |
177 |
164 |
166 |
161 |
169 |
159 |
Х |
|
Вес, кг |
53 |
67 |
45 |
53 |
60 |
62 |
58 |
60 |
62 |
55 |
55 |
49 |
У |
Для построения этой диаграммы нужно в
системе координат поставить точки, абсциссы
которых – рост, а ординаты – вес.
- Описательная статистика
2.1. Среднее значение
Определение: Средним арифметическим
нескольких чисел называется число, равное
отношение суммы этих чисел к их количеству.
Среднее арифметическое набора чисел х1,х2,х3,х4,х5
принято обозначать . Например, среднее арифметическое
пяти чисел запишется так:
Здесь в числителе дроби — сумма данных пяти
чисел, а в знаменателе – их количество – 5.
Найти среднюю оценку учащегося по
математике, если за истекший период он получил: 3,
4, 4, 5, 3, 2, 4, 3.
Запишем дробь и вычислим ее значение:
2.2. Медиана
Определение: Число, разделяющее набор
чисел на две части, равные по численности, так что
с одной стороны от этого числа все значения
больше медианы, а с другой – меньше.
Метод вычисления медианы: Чтобы найти
медиану набора чисел нужно:
- Записать числа в порядке возрастания.
- Если в полученном наборе нечетное количество
членов, то медианой служит число стоящее
посередине. - Если в полученном наборе четное количество
членов, то медианой набора – есть полусумма двух
чисел, расположенных посередине.
Найти медиану набора чисел: 9,3, 1, 5, 7.
Запишем числа в порядке возрастания.
1, 3, 5, 7, 9.
Здесь медиана набора число, стоящее
посередине – 5.
Найти медиану набора чисел: 9,3, 1, 5, 7,8
Запишем числа в порядке возрастания.
Выберем два центральных числа: 5 и 7. Найдем их
полусумму: (5+7):2=6. То есть медиана
данного набора есть число-6.
2.3. Наибольшее и наименьшее значение и размах.
Найти наибольшее, наименьшее значение и
размах для ряда чисел:
12,7,25,3,19,15.
Очевидно, что наибольшим значением данного
ряда является число 25, тогда как наименьшим число
– 3. Найдем размах данного ряда.
Определение: Разность между наибольшим и
наименьшим числом называется размахом набора
чисел.
Размах показывает насколько велико
рассеивание в числовом наборе. Итак, размах
данного набора равен разности 25 и 3, т.е. 22.
2.4. Отклонение.
Определение: Отклонением данного
значения от среднего арифметического значения
данного набора является разность между этим
числом и средним арифметическим. Соответственно
если некоторое значение меньше среднего, то его
отклонение отрицательно, если больше среднего –
его отклонение положительно. Так же необходимо
помнить, что сумма всех отклонений ряда чисел от
среднего арифметического этих чисел равна нулю.
Составить таблицу отклонений от
среднего арифметического для набора чисел:
2,4,5,7,10.
Вычислим среднее арифметическое этих чисел:
Составим таблицу отклонений.
| Число | Отклонение от среднего арифметического |
| 2 | 2-5,6= -3,6 |
| 4 | 4-5,6= -1,6 |
| 5 | 5-5,6= -0,6 |
| 7 | 7-5,6=1,4 |
| 10 | 10-5,6=4,4 |
2.5. Дисперсия.
Определение: Среднее арифметическое
квадратов отклонений от среднего значения
называется дисперсией набора чисел. Дисперсию
обозначают S2.
В таблице представлены средние
месячные температуры, в градусах. Вычислите
дисперсию температуры за приведенный период.
| Месяцы | Январь | Февраль | Март | Апрель | Май |
| Средняя температура | -12 | -7 | 0 | 9 | 16 |
Решение:
- Вычислим среднюю температуру за 5 месецев.
- .Составим таблицу отклонений и их квадратов.
- Найдем среднее арифметическое для квадратов
отклонений от среднего значения
Итак, средняя температура составила 6
градусов.
| Число (температура) | Отклонение от среднего | Квадрат отклонения |
| -12 | -12-6=-18 | (-18)2=324 |
| -7 | -13 | 169 |
| 0 | -6 | 36 |
| 9 | 3 | 9 |
| 16 | 10 | 100 |
( последний столбец таблицы)
Итак, дисперсия средних температур за 5 месяцев
составила 127,6. Ответ: S2=127,6
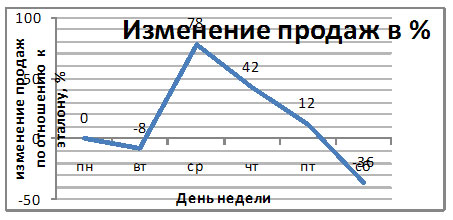
Составление таблицы изменений в процентах.
В таблице представлено количество
продаваемых за неделю шоколадок в школьном
буфете. Составьте таблицу изменения продаж по
отношению к понедельнику в процентах.
|
День недели |
понедельник |
вторник |
среда |
четверг |
пятница |
суббота |
|
Количество |
50 |
46 |
89 |
71 |
44 |
32 |
Число проданных в понедельник шоколадок
составляет 100% — эталон.
Вычислим, сколько составляет 1% эталона.
1% =50:100=0,5.
Вычислим, сколько процентов эталона составляет
количество проданных шоколадок в другие дни
недели.
Вторник – 46. Какой процент составляет 46 от 50.
46:0,5=92
Среда -89. 89 : 0,5= 178
Четверг – 71. 71 :0,5=142
Пятница – 44 44:0,5=88
Суббота -32 32 :0,5 =64
|
День недели |
понедельник |
вторник |
среда |
четверг |
пятница |
суббота |
|
Количество проданных |
50 |
46 |
89 |
71 |
44 |
32 |
|
% от эталона |
100 |
92 |
178 |
142 |
88 |
64 |
|
Изменение продаж в % |
0 |
-8 |
78 |
42 |
-12 |
-36 |
Алгебра 7 класс. Что такое отклонение? например: 2,7,3,5,11,15
Дисперсией числового ряда называется среднее арифметическое квадратов отклонений от среднего арифметического.
Пусть есть некий ряд (значения некоторой случайной величины — скажем, возраст детей в семье): 2,7,3,5,11,15.
1) находим среднее арифметическое: (2+7+3+5+11+15) / 6= 7,17
2) находим среднее арифметическое квадратов отклонений:
(2-7,17)^2+(7-7,17)^2+(3-7,17)^2+(5-7,17)^2+(11-7,17)^2+(15-7,17)^2/6=
Дисперсия характеризует разброс — чем больше дисперсия, тем сильнее «разбросан» (варьируется) признак относительно центрального значения.
Как посчитать среднее значение, квадратическое отклонение и погрешность
wikiHow работает по принципу вики, а это значит, что многие наши статьи написаны несколькими авторами. При создании этой статьи над ее редактированием и улучшением работали, в том числе анонимно, 24 человек(а).
Количество просмотров этой статьи: 62 795.
После сбора данных их нужно проанализировать. Обычно нужно найти среднее значение, квадратичное отклонение и погрешность. Мы расскажем вам, как это сделать.
- Например, 5 школьникам был предложен письменный тест. Их результаты (в баллах по 100 бальной системе): 12, 55, 74, 79 и 90 баллов.
- Среднее значение (μ) = Σ/N, где Σ сумма всех числовых значений, а N количество значений.
- Для вышеуказанного примера это квадратный корень из [((12-62)^2 + (55-62)^2 + (74-62)^2 + (79-62)^2 + (90-62)^2)/(5)] = 27,4. (Обратите внимание, что если это выборочное среднеквадратическое отклонение, то делить нужно на N-1, где N количество значений.)
- Если в нашем примере 5 школьников, а всего в классе 50 школьников, и среднее отклонение, посчитанное для 50 школьников равно 17 (σ = 21), средняя погрешность = 17/кв. корень(5) = 7.6.
Метод вычисления отклонений каждого значения от среднего арифметического
Для вычисления отклонений всех чисел выполним следующие действия:
. Находим среднее арифметическое;
2. Для вычисления отклонение из данного набора чисел вычитаем среднее арифметическое.
Среднее арифметическое нескольких величин — это отношение суммы величин к их количеству.
Среднее арифметическое находится по формуле


Найти отклонений всех чисел от среднего арифметического.
Сумма чисел в массиве (2):
Вычисление отклонения (3):
Блок схема 2 — Вычисление отклонений каждого значения от среднего арифметического
Описание методов создания, уничтожения и синхронизации потоков, примененных в программе
Создание потоков
Для создания многопоточных приложений в C++Builder реализован абстрактный класс TThread.- абстрактный класс, который допускает создание отдельных потоков выполняющихся в приложении.
Создайте потомка класса TThread, чтобы представить выполняемый поток в многопоточном приложении.
Каждый новый экземпляр потомка TThread — новый поток выполнения.
Множество экземпляров, полученные от класса TThread, делает C++Builder многопоточным приложением.
__fastcall TMyThread:: TMyThread (bool CreateSuspended)
// B метод объекта Execute (), вставьте код, который должен выполняться, когда поток выполняется.
void __fastcall TMyThread:: Execute ()
// — — Place thread code here — —
Для получения безопасного доступа куправлению свойствами и методами VCL-объектов в потоке предусмотрен метод Synchronize ()
ResetEvent (FMain->g_BusyEvent [1]); // запрещаем переформирование массива(FMain->g_BusyEvent [0]); // запрещаем переформирование массива
>++;(Terminated) break; // прекратить извне поток
Synchronize (&Mon); // блокирует одновременный доступ к компоненту нескольких потоков
SetEvent (FMain->g_BusyEvent [0]); // разрешаем параллельную обработку(FMain->g_BusyEvent [1]); // разрешаем параллельную обработку
Синхронизация потоков
Синхронизации потоков основывается на использовании событий (event). Объект типа событие может принимать одно из двух состояний: активное или пассивное. Когда событие находится в активном состоянии, его видят многие потоки одновременно. В результате такой объект можно использовать для управления работой сразу многих потоков. В библиотеке VCL события представлены классом TEvent.
Метод CreatEvents (): Создает объект класса TEvent, представляющий объект события.
Метод ResetEvent (): Переводит объект события в пассивное состояние.
Метод SetEvent (): Переводит объект события в активное состояние.
WaitForSingleObject (): Заставляет ждать, пока другой поток или процесс не пошлют сигнал об активизации объекта событие.
Завершение потоков
Потоки могут быть запущены и остановлены сколько угодно раз в процессе их выполнения. Для временной остановки запущенного потока можно обратиться к методу потока suspend. Для продолжения выполнения приостановленного потока вызовите метод потока Resume. Вы можете использовать вложенные вызовы вышеперечисленных методов, т.к. метод Suspend увеличивает внутренний счетчик потока, a Resume уменьшает. Поток не будет выполняться до тех пор, пока счетчик не обратиться в ноль, т.е., если вы вызвали пять раз метод Suspend, а затем четыре раза Resume, вам понадобится еще один (пятый) вызов метода Resume для продолжения выполнения потока.
Выполнение потока автоматически завершается после завершения функции Execute () или закрытии приложения.
Чтобы занятая потоком память освобождалась при завершении потока надо установить FreeOnTerminate=false.
Что такое дисперсия в статистике
Статистика, в частности, оперирует рядами данных, характеризующих какой-либо признак, явление. Интересует их изменение.
Вариация представляет собой отличие величин одинакового показателя у разных предметов. Ее изучение позволит понять причины отклонений от нормы, анализировать их и в какой-то мере прогнозировать. Также станет возможным выявить факторы, влияющие на значения, отсеяв случайные.
Характеристики равномерного распределения представлены на картинке:
При значительном объеме статистики, средняя величина очевидно близка к нормальной. Об этом говорят и законы распределения. Отклонения от нее будут являться объективной характеристикой.
Только вот отрицательные значения этих разбросов будут сбивать с толку при расчетах, погашая положительные. А оставлять лишь модули – для математика не корректно. Напрашивается возвести в четную степень, а именно – во вторую.
Решение оказалось не только удобным. Оно открыло бо́льшие возможности в изучении отклонений. А важны именно они, поскольку сама по себе средняя мало что дает.
В качестве одного из важных показателей вариации, вводится понятие «дисперсия» – усредненный квадрат отклонений численных значений каких-либо событий от средней величины.
Кратко записывается D[X] в русскоязычных источниках и Var[X] (от «variance») в английских. В статистических выкладках используется σ2.
Никакого наглядного смысла величина не несет. Другое дело, среднее квадратическое отклонение – корень квадратный из дисперсии.
Виды дисперсии дискретной случайной величины
Для анализа данных цифр в таком виде недостаточно. Гораздо больше можно выжать из последовательности, если разбить ее на группы по определенному признаку.
Общая дисперсия
Как можно заметить, вычисленная по приведенному выше определению величина характеризует отклонения в целом. Без учета определяющих вариацию факторов. Вернее, с учетом всех, включая совершенно случайные. Поэтому и называется «общей» и рассчитывается по формулам, указанным ниже.
Простая дисперсия, без разделения на группы:
Или в несколько преобразованном виде:
Взвешенная дисперсия, для вариационного ряда:
где xi – значение из ряда;
fi – частота, количество повторений;
k – групп;
n – число вариантов.
Черта сверху указывает на среднюю величину.
Межгрупповая дисперсия
Характеризует систематическое отклонение, возникающее из-за фактора, по которому производилось выделение признаков в группы. Поэтому также называется «факторной».
Как найти данную дисперсию? По формуле:
где k – количество групп;
nj – элементов в группе с индексом j.
Внутригрупповая дисперсия
Возникает по хаотичной причине, не связанной с причиной сделанной выборки. Неучтенный фактор. Еще обозначается как «остаточная».
Например, рассматривается количество выпущенных деталей за месяц каждым фрезеровщиком цеха.
В качестве критерия отбора в группу выбираем возраст оборудования. Он-то и не будет влиять на производительность внутри подборки: там станки у всех практически одинаковые.
Если вычислить среднюю величину от всех групповых,
то получим характеристику случайного разброса. Иными словами, составляющую вариации, зависящую от чего угодно, кроме фактора отбора.
Взаимосвязь
В соответствии с правилом сложения, общая D[X] включает средние выражения остаточной и факторной. И это логично, поскольку учитывает и случайное изменение в группе, и систематическое в факторной.
Свойства дисперсии
Опишем основные:
-
Если последовательность состоит из одинаковых чисел, то D[X] будет нулевой.
-
Уменьшение всех значений на постоянную величину на дисперсию не влияет. Иначе говоря, рассчитать σ2 можно по отклонениям от фиксированного числа.
-
Уменьшение всех цифр в k раз приведет к падению D[X] в k2 раз. Можно, например, иметь в виду значения в метрах, а результат вычислить в футах. Достаточно учесть один раз то, на что следует умножить.
-
Средний квадрат отклонений от постоянной величины X отличается в большую сторону от того же с использованием среднего значения. Разница составит (Xcр – X)2.
Показатели вариаций
Кроме размаха (разницы максимального и минимального значений), среднего линейного и дисперсии, изменения описываются коэффициентом вариации:
Оценить масштаб разброса проще по относительной величине. Тем более, что измеряются в одних единицах.
Пример расчета дисперсии
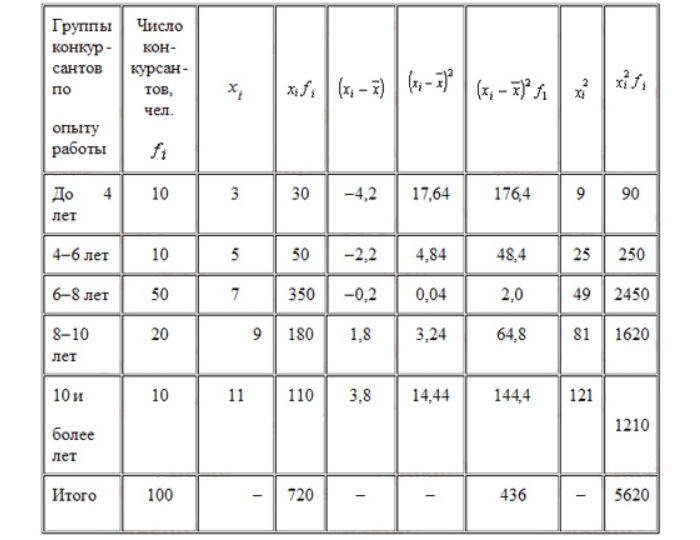
Компания объявила конкурсный отбор для приема сотрудников. В качестве критерия принят стаж работы по специальности. Приведем исходные данные и расчеты.
Усредненный стаж:
Дисперсия:
По альтернативной формуле:
Среднеквадратическое:
Коэффициент вариации:
Заключение
Статистика оперирует значительными объемами данных. Вариация, как одно из основных понятий – не исключение. И дисперсия в качестве основной характеристики.
Для упрощения расчетов существует масса онлайн калькуляторов. Имеется упомянутый инструмент в MS Excel.