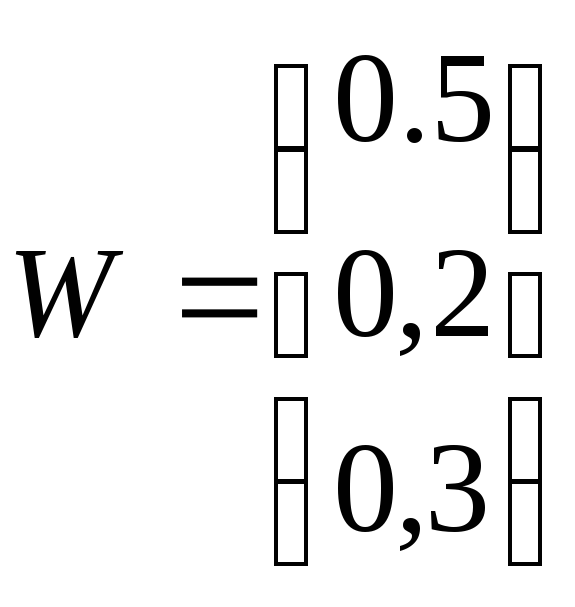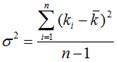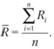Мишель Мэтьюз, MBA, CPCC
6 октября 2021 г.
Основатель RBG Royalty Enterprises Мишель Мэтьюз — сертифицированный профессиональный карьерный коуч и специалист по работе с кредиторской задолженностью, которая помогает людям вырабатывать стратегические подходы на рабочем месте, используя свою фирменную структуру Boss Up & Hustle.
Что такое дисперсия?
Дисперсия — это статистическое измерение, позволяющее увидеть, насколько далеко каждое число в наборе данных от среднего. Дисперсия часто обозначается этим символом: σ². Этот расчет может быть индикатором для аналитиков и трейдеров того, как часто меняется число, также называемое волатильностью, что также может быть сигналом дальнейших изменений и риска, который они представляют для людей, на которых они влияют. Квадратный корень из дисперсии представляет собой стандартное отклонение (σ), которое помогает определить постоянство доходности инвестиций в течение определенного периода времени.
Прочитайте больше: Меры вариации: определения, примеры и карьера
Понимание дисперсии
Чем выше дисперсия числа, тем больше оно отделено от среднего, рассчитанного на основе чисел набора данных. С другой стороны, небольшая дисперсия оказывает противоположное влияние, делая ее ближе к среднему значению, тогда как нулевая дисперсия показывает, что числа имеют одинаковое значение в наборе данных. Дисперсия не может быть отрицательным значением, так как квадрат числа никогда не может стать отрицательным значением.
Говоря об инвестициях, дисперсия является важным показателем. Волатильность — это показатель риска, который позволяет инвесторам оценить риск, связанный с покупкой конкретного актива, а также его потенциальную прибыльность. Инвесторы могут анализировать дисперсию доходности различных активов в портфеле, чтобы определить наилучшее распределение активов. В финансах дисперсия используется для сравнения эффективности элементов портфеля друг с другом и со средним значением.
Прочитайте больше: Как выполнить анализ рисков
Как рассчитать дисперсию
В статистике дисперсия рассчитывается путем взятия различий между каждым числом в наборе данных и средним значением, затем возведения в квадрат различий, чтобы сделать их положительными, и, наконец, деления суммы квадратов на количество значений в наборе данных.
Дисперсия рассчитывается по следующей формуле:
Стоимость акций, которые вы инвестируете на открытом рынке, может меняться ежедневно, но вы все равно можете просматривать финансовые отчеты, чтобы отслеживать эффективность ваших инвестиций за определенный период. Мы начнем с определения дисперсии доходности акций, которую можно использовать для помощи в постановке целей в отношении финансового будущего вашей компании. Вот пример и список шагов для расчета дисперсии:
1. Определите доходность акций за определенный период
Для этого примера мы скажем, что вы отслеживаете свои инвестиции в течение трех лет, и они принесли 13% прибыли в первый год, 24% во второй год и -10% в течение третьего года.
2. Рассчитайте среднее значение доходности
Сложите 13, 24 и -10 вместе, и вы получите в общей сложности 27. Вы делите 27 на 3, так как вы вычисляете сумму по числам в наборе данных, и вы получаете 9% как среднюю доходность акций за три года. срок год.
3. Найдите разницу между каждым доходом и средним значением за каждый год.
Затем вам нужно сравнить доход, который вы получали от акций каждый год, и среднее значение, которое вы рассчитали ранее. Для этого вычтите процент доходности акций от среднего, чтобы найти разницу.
Первый год: 13% — 9% = 4%
Второй год: 24% — 9% = 15%
Третий год: -10% — 9% = -19%
4. Возведите в квадрат разницы (отклонения) и сложите их за каждый год.
4² = 16%
15² = 225%
-19²= 361%
16% + 225% + 361% = 602%
5. Разделите сумму отклонений на количество возвратов в вашем наборе данных, чтобы получить дисперсию.
602% / 3 = 206,67%
Это означает, что доходность акций отличается от среднего значения, что означает, что в вашем портфеле находятся акции с высоким риском.
Важно: Волатильность может быть отмечена как стандартное отклонение, а не как дисперсия, потому что ее часто легче интерпретировать.
Чтобы получить стандартное отклонение, вычислите квадратный корень из дисперсии. Используя данный пример, это будет 14,37% для возврата.
Прочитайте больше: Узнайте о том, как стать финансовым консультантом
Дисперсия населения
Далее мы рассмотрим дисперсию с точки зрения населения.
См. шаги и расчет в примере ниже:
1. Определите население по числам в наборе данных.
Вместо использования процентов числа в наборе данных представляют собой целые числа для каждого человека.
Для этого примера мы скажем, что общее количество каждой совокупности включает 4, 22, 99, 204, 18 и 20.
2. Сложите все числа в наборе данных
4 + 22 + 99 + 204 + 18 + 20 = 367
3. Возведите в квадрат сумму всех чисел
367² = 134 689
4. Разделите сумму на количество чисел, включенных в набор данных.
134 689/6 = 22 448,1667 или 22 448,2
5. Возведите в квадрат числа из исходного набора данных и сложите их.
16 + 484 + 9 801 + 204 + 41 616 + 400 = 52 521
6. Вычтите сумму ваших ответов на пятом шаге из суммы на четвертом шаге.
52 521 — 22 448,2 = 30 072,8
7. Вычтите единицу из количества чисел, включенных в ваш набор данных.
6 — 1 = 5
8. Разделите сумму шестого шага на результат седьмого шага, чтобы получить общую дисперсию населения.
30 072,8 / 5 = 6 014,56
Дисперсия населения составляет 6 014,56 человек.
Доходность и
риск портфеля из Nбумаг.
Пусть
необходимо сформировать портфель,
состоящий из N
акций. Известны ri
доходности,
—дисперсия
(вариации
доходности) и ковариационная матрица.
Эти данные, как было показано выше,
рассчитывается финансовыми аналитиками,
например, по историческим данным. Пусть
доля капитала, которая вложена в i
–тую акцию равна
.
Эти доли обычно называют весами.
Доходность портфеля равна средневзвешенной
доходности активов
(4.19)
Под
риском портфеля, как и отдельного актива,
понимается корень квадратный из дисперсии
(4.20)
ковариационная
матрица активов, входящих в портфель.
Для проведения расчетов удобно ввести
матричную форму записи доходности и
вариации портфеля. Обозначим доходности
активов, как вектор–строку
R
= (r1,
r1,r3,…..rN) (4.21)
Доли активов
(ценных бумаг) в портфеле обозначим как
вектор – столбец
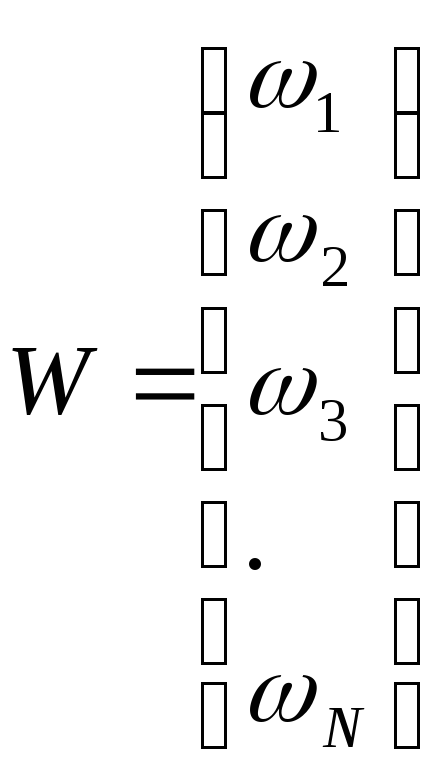
Матрицу
вариаций-ковариаций активов обозначим,
как VCV
VCV=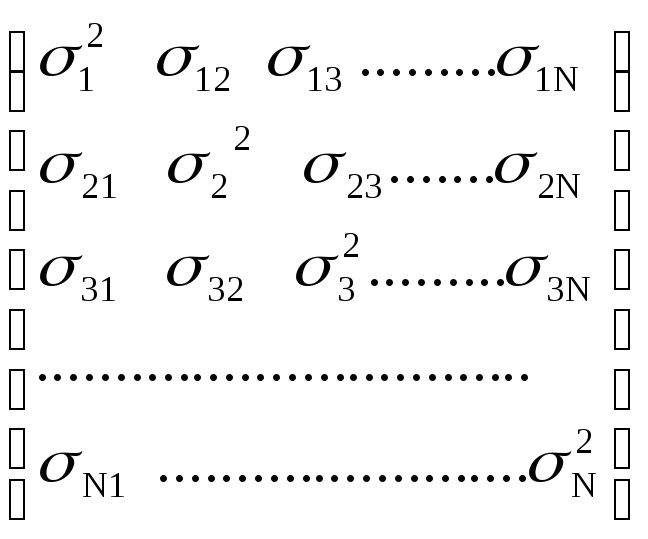
где
Доходность портфеля равна произведению
матрицы доходностей активовна
матрицу долей активов
(4.24)
Дисперсия доходности
портфеля равна произведению трех матриц
(4.25)
Матричная форма
записи доходности и вариации портфеля
из N
акций позволяет использовать для
вычисления характеристик портфеля
методы линейной алгебры. В Excel для этого
существуют встроенные математические
функции, которые существенно облегчает
процедуру расчета.
Пример
3. Рассчитать
доходность и риск портфеля, состоящего
из 3-х акций, доли которых относятся как
5:2:3. Риски, доходности и ковариация акций
приведены ниже в таблицах доходности
и матрицы вариаций ковариаций.
Таблица 4.3.
Доходности и риск акций.
-
акции
Акции
1Акции
2Акции
3r-доходность
0,23
0,14
0,05
риск
(стандартное отклонение)0,96
0,93
0,73
Таблица 4.4. Матрица
вариаций ковариаций.
-
Акции
1Акции
2Акции
3Акции
10,922
0,070
-0,647
Акции
20,070
0,861
-0,399
Акции
3-0,647
-0,399
0,528
Решение. Сформируем
вектора доходности и весов акций,
входящих в портфель.
Вектор строк
доходностей равен R=
(0,23; 0,14; 0,5)
Вектор долей акций
равен
Доходность портфеля
равна
Дисперсия доходности
равна
=
= 0,084
Риск портфеля
равен
=
0,29.
Расчет в Excel
приведен ниже. Риск портфеля меньше,
чем риск входящих в него активов.
Р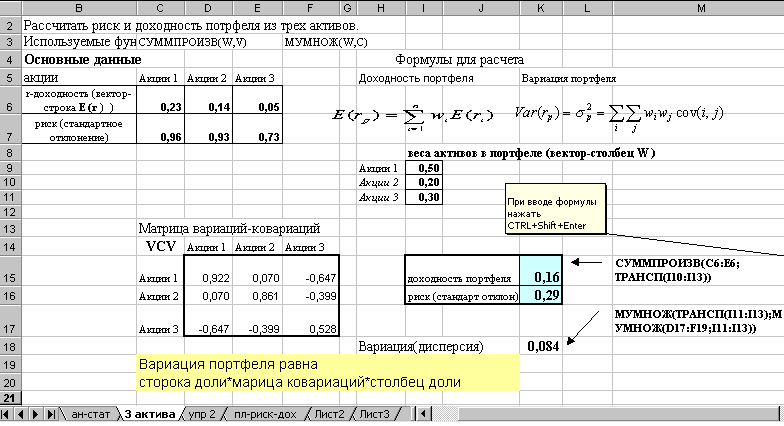
4.2. Пример расчета доходности и риска
портфеля вExcel.
Для расчета
доходности курсор поместить в ячейку
К15, затем вызвать функцию
CУММПРОИЗВ(
) в опцию массив1
записать адреса ячеек, содержащих
доходности акций (С6:E6),
а в опцию массив
2 записать
функцию ТРАНСП(адреса ячеек, содержащих
веса акций в портфеле). Эта формула, как
видно на рис. 4.2 и записана в ячейке K14.
Затем нажать комбинацию клавиш
CTRL+Shift+Enter.
Для расчета
дисперсии в ячейку К18 записать формулу,
МУМНОЖ(ТРАНСП(I11:I13);
МУМНОЖ(D17:F19;
I11:I13)),
нажать комбинацию клавиш CTRL+Shift+Enter.
Диверсификация.
Основной задачей
для инвестора при формировании портфеля
ценных бумаг является создание портфеля
с максимально возможной доходностью и
минимальным риском. Теория портфеля
решает эту задачу. В основном риск и
доходность портфеля зависят от числа
различных акций (диверсификация) в
портфеле, от долей акций в портфеле и
коэффициента корреляции между акциями.
Диверсификация –
это способ уменьшения риска путем
инвестирования в несколько акций. Если
доли акций в портфеле одинаковы, то
такую диверсификацию называют наивной.
Рассмотрим, как
влияет число акций в портфеле на значение
его риска. Вариация портфеля из N
бумаг равна.
(4.26)
Если веса акций в
портфеле равны, то
,
гдеN
– число бумаг в портфеле. После подстановки
i
=1/N
в (4.26) получим
(4.27)
Как видно из формулы
(4.27) риск портфеля состоит риска, вносимого
каждой акцией – специфический риск
и риска, связанного с другими акциями
— неустранимый риск. Поскольку все
вариации и ковариации не могут более
некоторой величины
, (4.28)
то вариация портфеля
не может быть больше, чем
. (4.29)
При увеличении
числа бумаг в портфеле специфический
риск сводится к нулю
.
Это так называемый диверсифицируемый
риск. Остается неустранимый риск или
недиверсифицируемый риск
(4.30)
И
недиферсифицируемый риск невозможно,
его можно только за счет включения в
портфель некоррелируемых акций у которыхcov(i,j)
0. В литературе диверсифицируемый риск
называют специфическим (присущим данному
активу), а недиверсифицирумый риск
называют систематическим (неспецифическим).
Недиверсифицируемый риск связан со
стохастической природой финансового
рынка. В работах по исследованию влияния
числа акций в портфеле на величину риска
портфеля было получено, что для случайным
образом сформированных портфелей с
различными весами и размерами, начиная
с 15-20 акций в портфеле, величина риска
портфеля практически не изменяется.
Таким образом, небольшие портфели,
имеющие небольшие транзакционные
издержки могут иметь тот же риск, что и
наивно сформированные портфели, с
большим количеством бумаг.
Рассмотрим, как
влияют веса акций в портфеле на риск и
доходность портфеля.
Пример .
Для акций трех фирм рассмотренных выше
(таблицы 4.3-4.4) сформируем несколько
портфелей с разными весами. Пусть доли
акций в портфеле меняются, как показано
в таблице.
Таблица 4.5. Доли
акций в портфелях.
-
портфели
1
2
3
4
5
6
7
8
9
10
Акции
10
0,5
0,2
0
0,3
0,5
0,5
0,5
1
0
Акции
20
0
0,3
0,5
0,2
0,5
0,2
0,3
0
1
Акции
31
0,5
0,5
0,5
0,5
0
0,3
0,2
0
0
Рассчитаем
доходность и риск каждого портфеля по
формулам (4.24, 4.25). В теории портфеля
принято изображать множество возможных
портфелей на плоскости «Доходность –
риск» — (,
). Каждый портфель на этой плоскости
изображается точкой.
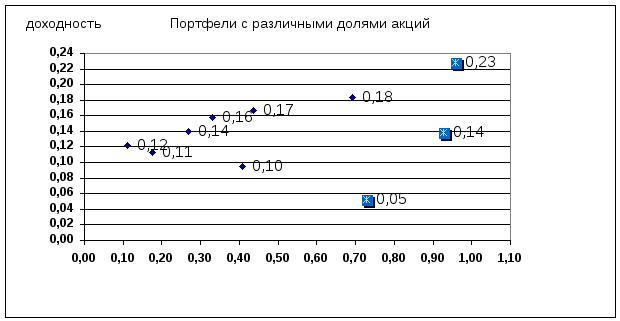
Рис. 4.3. Портфели
с различными долями акций.
На рисунке квадратами
отмечены портфели, состоящие из одной
акции. Как видно из рисунка портфели,
составленные из нескольких акций, имеют
риск, меньший, чем из одной акции. Все
портфели, составленные из трех акций,
расположены левее портфелей состоящих
из одной акции. Они имеют меньший риск.
Можно найти такие доли акций в портфеле,
при которых риск портфеля минимален.
Таким образом, управлять риском портфеля
можно, изменяя веса акций в портфеле и
число акций в портфеле. Вклад в величину
риска портфеля каждой акцией осуществляется
через свою вариацию и ковариацию.
Рассмотрим, как влияет коэффициент
корреляции между акциями на риск и
доходность портфеля.
Пример
5.
Для портфеля из двух акций А и В. Построить
множество возможных портфелей для
различных значений коэффициентов
корреляции и долей акций в портфеле.
Для акции А доходность равна 10%, дисперсия
равна 2%. Для акции В доходности равна
20%, дисперсия равна 8%.
Решение. Построим
множество возможных портфелей для
коэффициентов корреляции равных
{-1;-0,5;0;0,5;1}, задавая различные доли акции
А в портфеле
= (0; 0,1; 0,2; …0,9; 1). Доля акций В равна
.
Доходность и риск портфеля из двух бумаг
легко рассчитать аналитически из формул
(4.19 – 4.20)
Проведя в Excel
расчеты по этим формулам, получим
множество возможных портфелей для
различных значений коэффициентов
корреляций (рис.4.8).
Р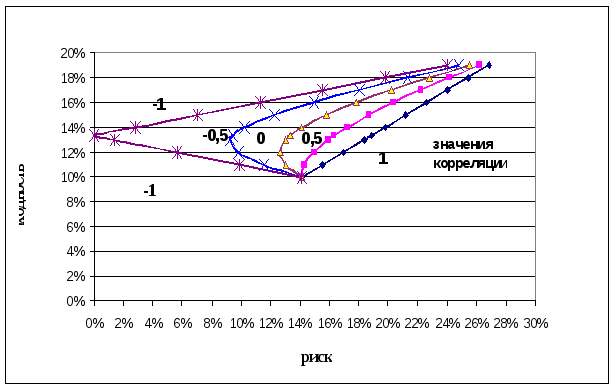
Множество возможных портфелей для
различных значений коэффициентов
корреляций активов, входящих в портфель
и различных долей этих активов.
Как видно из
рисунка корреляция между акциями
оказывает сильное влияние на риск
портфеля. Множество возможных портфелей
при различных коэффициентах корреляций
ограничено. Границей множества являются
портфели с коэффициентом корреляции
.
Эта граница имеет вид «пули». При
некоторых долях акций риск можно
полностью исключить, если бумаги имеют
отрицательную корреляцию. С ростом
корреляции доходностей активов, входящих
в портфель, увеличивается риск портфеля
при равных долях акций в портфеле. При
отрицательной корреляции акций в
портфеле, его риск уменьшается. На
практике активов с отрицательными
корреляциями очень мало.
Пример Тобина
Тобин показал,
что для принятия решений о выборе того
или иного портфеля среднее и дисперсия
не являются достаточными критериями,
если учитывать вероятности реализации
той или иной доходности. Пусть имеется
следующая статистика
|
Портфель |
Доходность |
Вероятность |
Ожидаемaя |
Дисперсия |
коэффициент |
|
1 |
0,24 |
1/3 |
0,12 |
0,098 |
0,82 |
|
0,12 |
1/3 |
||||
|
0,00 |
1/3 |
||||
|
2 |
0,14 |
1/3 |
0,06 |
0,065 |
0,92 |
|
0,06 |
1/3 |
||||
|
-0,02 |
1/3 |
||||
|
3 |
0,1429 |
0,98 |
0,12 |
0,16 |
0,75 |
|
-1,0 |
0,02 |
||||
|
4 |
1,2421 |
0,02 |
0,12 |
0,16 |
0,75 |
|
0,0971 |
0,98 |
Из таблицы следует,
что портфели 3 и 4 имеют одинаковые
соотношения риска и доходности, однако
вероятность получения высокодоходного
исхода для портфеля 3 очень мала.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
What Is Portfolio Variance?
Portfolio variance is a measurement of risk, of how the aggregate actual returns of a set of securities making up a portfolio fluctuate over time. This portfolio variance statistic is calculated using the standard deviations of each security in the portfolio as well as the correlations of each security pair in the portfolio.
Key Takeaways
- Portfolio variance is a measure of a portfolio’s overall risk and is the portfolio’s standard deviation squared.
- Portfolio variance takes into account the weights and variances of each asset in a portfolio as well as their co-variances.
- A lower correlation between securities in a portfolio results in a lower portfolio variance.
- Portfolio variance (and standard deviation) define the risk-axis of the efficient frontier in modern portfolio theory (MPT).
Portfolio Variance
Understanding Portfolio Variance
Portfolio variance looks at the co-variance or correlation co-efficients for the securities in a portfolio. Generally, a lower correlation between securities in a portfolio results in a lower portfolio variance.
Portfolio variance is calculated by multiplying the squared weight of each security by its corresponding variance and adding twice the weighted average weight multiplied by the co-variance of all individual security pairs.
Modern portfolio theory says that portfolio variance can be reduced by choosing asset classes with a low or negative correlation, such as stocks and bonds, where the variance (or standard deviation) of the portfolio is the x-axis of the efficient frontier.
Formula and Calculation of Portfolio Variance
The most important quality of portfolio variance is that its value is a weighted combination of the individual variances of each of the assets adjusted by their co-variances. This means that the overall portfolio variance is lower than a simple weighted average of the individual variances of the stocks in the portfolio.
The formula for portfolio variance in a two-asset portfolio is as follows:
- Portfolio variance = w12σ12 + w22σ22 + 2w1w2Cov1,2
Where:
- w1 = the portfolio weight of the first asset
- w2 = the portfolio weight of the second asset
- σ1 = the standard deviation of the first asset
- σ2 = the standard deviation of the second asset
- Cov1,2 = the co-variance of the two assets, which can thus be expressed as p(1,2)σ1σ2, where p(1,2) is the correlation co-efficient between the two assets
The portfolio variance is equivalent to the portfolio standard deviation squared.
As the number of assets in the portfolio grows, the terms in the formula for variance increase exponentially. For example, a three-asset portfolio has six terms in the variance calculation, while a five-asset portfolio has 15.
Portfolio Variance and Modern Portfolio Theory
Modern portfolio theory (MPT) is a framework for constructing an investment portfolio. MPT takes as its central premise the idea that rational investors want to maximize returns while also minimizing risk, sometimes measured using volatility. Investors seek what is called an efficient frontier, or the lowest level of risk and volatility at which a target return can be achieved.
Risk is lowered in MPT portfolios by investing in non-correlated assets. Assets that might be risky on their own can actually lower the overall risk of a portfolio by introducing an investment that will rise when other investments fall. This reduced correlation can reduce the variance of a theoretical portfolio.
In this sense, an individual investment’s return is less important than its overall contribution to the portfolio, in terms of risk, return, and diversification.
The level of risk in a portfolio is often measured using standard deviation, which is calculated as the square root of the variance. If data points are far away from the mean, then the variance is high, and the overall level of risk in the portfolio is high as well. Standard deviation is a key measure of risk used by portfolio managers, financial advisors, and institutional investors. Asset managers routinely include standard deviation in their performance reports.
Example of Portfolio Variance
For example, assume there is a portfolio that consists of two stocks. Stock A is worth $50,000 and has a standard deviation of 20%. Stock B is worth $100,000 and has a standard deviation of 10%. The correlation between the two stocks is 0.85. Given this, the portfolio weight of Stock A is 33.3% and 66.7% for Stock B. Plugging in this information to the formula, the variance is calculated to be:
- Variance = (33.3%^2 × 20%^2) + (66.7%^2 × 10%^2) + (2 × 33.3% × 20% × 66.7% × 10% × 0.85) = 1.64%
Variance is not a particularly easy statistic to interpret on its own, so most analysts calculate the standard deviation, which is simply the square root of variance. In this example, the square root of 1.64% is 12.81%.
What is portfolio variance?
Portfolio variance measures the risk in a given portfolio, based on the variance of the individual assets that make up the portfolio. The portfolio variance is equal to the portfolio’s standard deviation squared.
How is variance used in constructing a portfolio?
Most portfolio managers seek to minimize risk and maximize value, along the lines of modern portfolio theory (MPT). The greater the variance in the portfolio indicates the greater the variance of the individual assets, and hence the greater the risk. Portfolio managers thus seek to reduce risk by incorporating assets with low correlations, meaning there is little relationship in the movement of the assets in the portfolio.
Where does standard deviation fit in?
Most portfolio analysts focus on the standard deviation of the portfolio as a whole to get the best picture of the range of outcomes in the portfolio. Standard deviation is the square root of the variance and provides a more realistic look at the level of risk of the portfolio. The higher the standard deviation, the more volatile a portfolio is likely to be, and vice versa.
The Bottom Line
Variance is a statistical measure of the volatility or risk of a portfolio and the individual securities in it. Variance itself is not the main number to pay attention to, but rather its standard deviation, which is the square root of a portfolio’s variance. The higher the standard deviation, the more risk the portfolio is carrying, while the opposite is true for a low standard deviation.
Standard deviation is in turn a factor of the variance and correlation of the securities in a portfolio. If the standard deviation is deemed too high or risky, the portfolio manager can adjust their holdings to incorporate lower correlation assets in the portfolio and potentially lower the standard deviation or risk of the portfolio.
Дисперсия (вариация) | Variance
В статистике дисперсия или вариация (англ. Variance) является показателем, который используется для оценки разброса значений случайной величины относительно ее математического ожидания. В портфельной теории дисперсия доходности является мерой риска, связанного с инвестированием в определенный актив или портфель активов.
Если известен полный набор вероятностей исхода события, что крайне редко встречается на практике, для расчета величины дисперсии используется следующая формула:
где ki – доходность ценной бумаги или актива при i-ом варианте исхода событий;

pi – вероятность i-го варианта исхода событий.
В реальной практике инвестирования аналитику обычно доступны исторические данные о доходности ценной бумаги или актива. Если он располагает всем массивом информации, то есть оценивает дисперсию на основании генеральной совокупности данных, необходимо использовать следующую формулу:
где ki – i-ое значение доходности ценной бумаги;

n – количество наблюдений.
Однако чаще оценку риска проводят на основании некоторой выборки из генеральной совокупности данных, поэтому для получения несмещенной оценки дисперсии количество степеней свободы уменьшают на 1. В этом случае формула для ее оценки будет выглядеть следующим образом:
Интерпретации дисперсии
Чем выше значение дисперсии, то есть чем выше разброс доходности актива или портфеля активов относительно его ожидаемой доходности, тем выше будет уровень риска. Напротив, низкие значения этого показателя свидетельствуют о низком уровне риска, связанного с осуществлением инвестиций.
Также следует отметить, что квадратный корень от дисперсии случайной величины является ее среднеквадратическим отклонением.
Пример расчета
Пример 1. Предположим, что финансовому аналитику необходимо произвести оценку риска, связанного с приобретением акций Компании А и Компании Б. Предположим, что аналитику известен полный набор вероятностей событий, который представлен в таблице.
Ожидаемая доходность для акций Компании составит 18,75%, а для акций Компании Б 19,45%.


В свою очередь, дисперсия доходности акций Компании А будет равна 24,288%, а акций Компании Б 217,948%.
σ 2 А = (7-18,75)2*0,05 + (15-18,75)2*0,2 + (18-18,75)2*0,5 + (24-18,75)2*0,2 + (32-18,75)2*0,05 = 24,288%
σ 2 Б = (-24-19,45)2*0,05 + (8-19,45)2*0,2 + (20-19,45)2*0,5 + (31-19,45)2*0,2 + (57-19,45)2*0,05 = 217,948%
Хотя ожидаемая доходность у акций обеих компаний практически одинаковая, риски инвестирования в акции Компании Б будут существенно выше.
Пример 2. Историческая доходность акций за последние пять лет представлена в таблице.
Средняя доходность акции составит 5,784%.

Поскольку анализируется не вся генеральная совокупность данных, а только выборку из нее, оценка дисперсии составит 58,42%.
σ 2 = ((5,78-5,784)2 + (12,33-5,784)2 + (-7,21-5,784)2 + (8,25-5,784)2 + (9,77-5,784)2)/(5-1) = 58,42%
Дисперсия как мера финансового инвестиционного риска. Оценка дисперсии и среднеквадратического отклонения доходности ценных бумаг.
В статистике дисперсия или вариация является показателем, который используется для оценки разброса значений случайной величины относительно ее математического ожидания. В портфельной теории дисперсия доходности является мерой риска, связанного с инвестированием в определенный актив или портфель активов.
Если известен полный набор вероятностей исхода события, что крайне редко встречается на практике, для расчета величины дисперсии используется следующая формула:
где ki – доходность ценной бумаги или актива при i-ом варианте исхода событий;

pi – вероятность i-го варианта исхода событий.
В реальной практике инвестирования аналитику обычно доступны исторические данные о доходности ценной бумаги или актива. Если он располагает всем массивом информации, то есть оценивает дисперсию на основании генеральной совокупности данных, необходимо использовать следующую формулу:
где ki – i-ое значение доходности ценной бумаги;

n – количество наблюдений.
Однако чаще оценку риска проводят на основании некоторой выборки из генеральной совокупности данных, поэтому для получения несмещенной оценки дисперсии количество степеней свободы уменьшают на 1. В этом случае формула для ее оценки будет выглядеть следующим образом:
Чем выше значение дисперсии, то есть чем выше разброс доходности актива или портфеля активов относительно его ожидаемой доходности, тем выше будет уровень риска. Напротив, низкие значения этого показателя свидетельствуют о низком уровне риска, связанного с осуществлением инвестиций.
Также следует отметить, что квадратный корень от дисперсии случайной величины является ее среднеквадратическим отклонением.
Под риском можно понимать вероятность возникновения каких-либо отклонений от ожидаемого события. Основополагающими мерами риска финансового актива являются такие показатели, как стандартное отклонение (σ) и дисперсия (D = σ2) сто доходности. В качестве синонима понятия «стандартное отклонение» используют также термин «волатильность». Стандартное отклонение и дисперсия доходности актива отражают степень возможного разброса его фактической доходности вокруг его средней (наиболее вероятной) доходности. Данные меры риска можно определить на основе прошлых данных статистики доходности актива.
Доходность актива на рассматриваемом интервале определяется следующим образом:
где St-1 – стоимость актива в начале интервала наблюдения; St – стоимость актива в конце интервала наблюдения.
Пусть имеются значения доходности акции за п равных интервалов наблюдения. За первый интервал она составила величину R1, за второй – R2 и т.д., за п-й интервал – Rn
Средняя доходность актива за наблюдаемый период (R) рассчитывается по формуле
Дисперсия доходности актива определяется как мера разброса наблюдаемой доходности (в процентах) от ее математического ожидания (средней величины). Формула генеральной дисперсии имеет вид
В случае если количество наблюдений незначительно (меньше 30), то для получения несмещенной оценки рекомендуется использовать так называемую исправленную дисперсию:
Показателем, характеризующим относительный уровень риска финансового актива, является стандартное отклонение его доходности от ожидаемой (средней за период):
При этом оценка допустимого уровня стандартного отклонения является субъективной и характеризует готовность инвестора принимать риск с учетом возможной доходности финансового актива.
§ 4.2. Диверсификация инвестиций и дисперсия дохода
Определим теперь, что дает диверсификация для уменьшения риска, и выявим условия, когда эта цель достигается. В качестве объекта анализа примем некоторый абстрактный портфель ценных бумаг (далее для краткости — портфель). Такой выбор объясняется методологическими преимуществами — в этом случае проще выявить зависимости между основными переменными. Однако многие из полученных результатов без большой натяжки можно распространить и на производственные инвестиции.
В § 4.1 отмечалось, что в качестве измерителя риска в долгосрочных финансовых операциях широко распространена такая мера, как дисперсия дохода во времени. Диверсификация портфеля при правильном ее применении приводит к уменьшению этой дисперсии при всех прочих равных условиях. Диверсификация базируется на простой гипотезе. Если каждая компонента портфеля (в рассматриваемой задаче — вид ценной бумаги) характеризуется некоторой дисперсией дохода, то доход от портфеля имеет дисперсию, определяемую его составом. Таким образом, изменяя состав портфеля, можно менять суммарную дисперсию дохода, а в некоторых случаях свести ее к минимуму.
Итак, пусть имеется портфель из п видов ценных бумаг. Доход от одной бумаги вида i составляет величину di. Суммарный доход А равен:

Если di представляет собой средний доход от бумаги вида i, то величина А характеризует средний доход от портфеля бумаг в целом.
Для начала положим, что показатели доходов различных видов бумаг являются статистически независимыми величинами (иначе говоря, не коррелируют между собой). Дисперсия дохода портфеля (обозначим ее D) в этом случае находится как

где Di — дисперсия дохода от бумаги вида i.
Для упрощения, которое нисколько не повлияет на результаты дальнейших рассуждений, перейдем от абсолютного измерения количества ценных бумаг к относительному. Пусть теперь ai характеризует долю в портфеле бумаги вида i. Соответственно 0 


Для зависимых в статистическом смысле показателей дохода отдельных бумаг дисперсию суммарного дохода находим следующим образом 19 :

где Di — дисперсия дохода от бумаги вида i;
rij — коэффициент корреляции дохода от бумаг вида i и j;


Коэффициент корреляции двух случайных переменных х и у 20 , как известно, определяется по формуле:

где 
Для расчетов часто применяется следующая рабочая формула:

Поскольку коэффициент корреляции может быть как положительной, так и отрицательной величиной, то при положительной корреляции дисперсия суммарного дохода увеличивается, при отрицательной — сокращается. В самом деле, при заметной отрицательной корреляции положительные отклонения от среднего дохода одних бумаг погашаются отрицательными отклонениями у других. И наоборот, при положительной корреляции отклонения суммируются, что увеличивает общую дисперсию и риск.
Проследим теперь, каково влияние масштаба диверсификации на размер риска. Под масштабом диверсификации будем понимать количество объектов, возможных для инвестирования (количество видов ценных бумаг). Обратимся к условному примеру, который позволяет наиболее отчетливо выделить влияние указанного фактора. Итак, пусть портфель состоит из бумаг различного вида, но имеющих одинаковую дисперсию дохода 

где п — количество видов ценных бумаг.
Воспользуемся приведенной формулой и определим дисперсию дохода для портфеля, состоящего из двух и трех видов бумаг. Так, для двух бумаг имеем

Для трех видов бумаг квадратическое отклонение портфеля составит 0,58
Увеличение масштабов диверсификации оказывает наибольшее влияние на начальных стадиях — при малых значениях n. Например, в рамках рассмотренного примера переход от одного вида бумаг к четырем сокращает квадратическое отклонение на 50%, а от одного к восьми — на 65%.
Полученные выше выводы в отношении тенденции изменения среднего квадратического отклонения в зависимости от числа составляющих при условии, когда дисперсии составляю-
щих одинаковы, справедливы и для более общих случаев. Однако зависимость этого параметра от степени диверсификации проявляется здесь не столь четко.
Посмотрим теперь, как изменяются доход и величина риска при изменении структуры портфеля. Для этого вернемся к формулам (4.2) и (4.3) и запишем их только для двух видов бумаг (X и Y). Такой анализ вряд ли имеет практическое значение. Однако с его помощью наглядно демонстрируются последствия «смешения» ценных бумаг с различными доходностью и дисперсией. Для независимых доходов получим:

и для зависимых доходов

В этом случае среднее значение суммарного дохода определяется как
Положим, что dy > dx и 
Что касается дисперсии, то, как следует из (4.6), положение не столь однозначно и зависит от знака и степени корреляции. В связи с этим подробно рассмотрим три ситуации:
полная положительная корреляция доходов (rxy = +1),
независимость доходов или нулевая корреляция (rху = 0).
В первом случае увеличение дохода за счет включения в портфель бумаги вида Y помимо X сопровождается ростом как дохода, так и дисперсии. Для портфеля, содержащего оба вида бумаг, квадратическое отклонение находится в пределах 
Для частного случая, когда 

При полной отрицательной корреляции доходов динамика квадратического отклонения доходов от портфеля более сложная. По мере движения от точки X к точке Y эта величина сначала сокращается и доходит до нуля в точке B, затем растет (рис. 4.4).
В последней из рассматриваемых ситуаций (rху = 0) квадратическое отклонение при увеличении доли бумаги Y проходит точку минимума, равного 

Совместим теперь все три графика на одном (рис. 4.6). Как видим, все возможные варианты зависимости «доход — среднее квадратическое отклонение» находятся в треугольнике XBY.
Из сказанного непосредственно следует, что эффективность диверсификации (в отношении сокращения риска) наблюдается только при отрицательной или, в крайнем случае, нулевой корреляции.
Портфель должен состоять из двух видов бумаг, параметры которых: dx = 2; 

Доход от портфеля: А = 2ах + 3ау . Таким образом, доход в зависимости от величины долей находится в пределах 2

Дисперсия суммы дохода составит:

Определим доход и дисперсию для портфеля с долями, равными, допустим, 0,3 и 0,7. Получим по формулам (4.5) и (4.6):
Таким образом, при полной положительной корреляции D = 0,854, при полной отрицательной корреляции D = 0,484 . В итоге с вероятностью 95% можно утверждать, что суммарный доход находится в первом случае в пределах
во втором он определяется пределами

При нулевой корреляции доходов пределы составят

Продолжим анализ с двумя бумагами и проследим, как влияет включение в портфель безрисковой (risk free) инвестиции 21 . Для этого заменим в портфеле бумагу Y с параметрами dy, 

Дисперсия и среднее квадратическое отклонение дохода портфеля теперь зависят от удельного веса безрисковой составляющей:

Таким образом, «разбавление» портфеля безрисковой бумагой снижает риск портфеля в целом, а квадратическое отклонение дохода портфеля определяется убывающей линейной функцией доли безрисковой бумаги. Если dx > dy (в противном случае проблема выбора портфеля отпадает — он должен состоять только из безрисковых бумаг), то доход от портфеля по мере увеличения доли безрисковой бумаги уменьшается от dx до dy, а величина квадратического отклонения сокращается от 
Последнее утверждение для портфеля, состоящего из двух видов бумаг, иллюстрируется уравнением (4.10):
В свою очередь, на основе (4.9) находим

В итоге получим интересное соотношение

Дробь в приведенном выражении иногда называют рыночной ценой риска. Если эта величина равна, скажем, 0,5, то при росте квадратического отклонения на 1% доход увеличится на 0,5%.
Источники: http://allfi.biz/financialmanagement/RiskAndReturns/dispersija.php, http://infopedia.su/15x1cfe.html, http://studfiles.net/preview/2214105/page:17/
Практически всегда действует правило: чем выше возможная доходность, тем выше риски.
Но вот в обратную сторону правило работает не всегда, и это обидно: потенциальная доходность по активу так себе, а риск этого актива довольно высокий. Получается, для относительно невысокой доходности приходится рисковать так, будто вкладываешься в высокодоходный актив. В этом случае на помощь инвестору может прийти расчет соотношения «риск-доходность».
В статье я рассмотрю показатели, по которым можно оценить, насколько адекватно у определенного актива соотношение его риска и доходности. Вот какие показатели буду рассматривать:
- Коэффициент вариации — coefficient of variation.
- Коэффициент Шарпа — Sharpe ratio.
- Коэффициент информации — information ratio.
- Коэффициент Сортино — Sortino ratio.
- Коэффициент Трейнора — Treynor ratio.
Но прежде чем разбираться с показателями риска-доходности, нужно разобраться и с основой — с тем, как считаются сами доходность и риск.
Как считается доходность
Доходность — это показатель, характеризующий финансовый результат от инвестирования. Простыми словами, это процент от стоимости актива, который инвестор заработал «сверху». В общем виде доходность от вложения в финансовый актив считается так:
(Pt + 1 − Pt + CF) / Pt,
где Pt + 1 — цена актива сейчас или на момент продажи,
Pt — цена актива на момент покупки,
CF — промежуточный денежный поток, который принес актив за время владения им, — например, выплаченные дивиденды.
Бытовой пример: инвестор купил акцию за 100 $ и продал за 150 $, а за время владения получил 3 $ дивидендов. Доходность по формуле выше будет считаться так:
(150 − 100 + 3) / 100 = 0,53, или 53%
Для упрощения расчетов из формулы иногда убирают CF — промежуточные денежные потоки в виде дивидендов.
В зависимости от того, за какой период мы рассчитываем доходность, она может быть дневной, месячной, квартальной, годовой или общей.
Например, акции Apple 31 декабря 2016 стоили 27,4 $, а 30 сентября 2020 — 115,6 $. Посчитаем общую доходность за этот период:
(115,6 − 27,4) / 27,4 = 3,22, или 322%
Но доходность за все время владения инструментом не так показательна, если мы хотим сравнить активы, которыми владели в течение разных периодов. Например, один актив принес вам 11% за полгода, а второй — 30% за полтора года. Чтобы сравнить эффективность этих инструментов, их доходности нужно привести к общему знаменателю — годовой доходности. Годовая доходность показывает, сколько в среднем приносил актив за год владения им.
Для расчета годовой доходности можно использовать три подхода — в зависимости от того, какими данными владеет инвестор. Если есть сразу все данные, можно использовать любой из способов — результат будет одинаковый.
Если есть информация о доходности за каждый год владения активом, то доходность рассчитывается по следующей формуле:
((1 + r1) × (1 + r2) × (1 + r3) × (1 + rn))1/n − 1,
где rn — доходность за каждый анализируемый период,
n — количество периодов (лет).
Например, инвестор купил акцию компании за 100 $ и владел ею 3 года. За первый год стоимость акции выросла на 20%, во второй год — упала на 10% по отношению к прошлому периоду, а за третий год акции прибавили в цене 30%. Общая годовая доходность за эти три года будет считаться так:
((1 + 20%) × (1 − 10%) × (1 + 30%))1/3 − 1 = 11,98%
Кажется, что формула слишком сложная и что можно было бы просто взять доходность за каждый год, сложить и поделить на три — то есть посчитать среднее арифметическое. Но корректнее считать не среднее арифметическое, а среднее геометрическое — что и делает наша формула. И этому есть причина.
Для примера выше среднее арифметическое составило бы 13,33%:
(20% − 10% + 30%) / 3
Наше значение, полученное через среднее геометрическое, на 1,35 процентного пункта меньше. Геометрический показатель учитывает, что доходность неравномерна и меняется от года к году, — то есть такая доходность уже учитывает в себе некоторую волатильность.
Другими словами, чем выше волатильность актива, тем ниже будет значение среднего геометрического доходности к среднему арифметическому.
Для примера возьмем акции A и B и предположим, что за 4 года после покупки акции показали одинаковую итоговую доходность. Но на протяжении этих четырех лет вели себя по-разному: акции A росли более плавно, а акции B сильнее проседали и сильнее росли, то есть были более волатильными.
Котировки акций A и B за 4 года
| Покупка | Первый год | Второй год | Третий год | Четвертый год | |
|---|---|---|---|---|---|
| Акция A | 100 $ | 140 $ (+40%) | 150 $ (+7%) | 125 $ (−17%) | 180 $ (+44%) |
| Акция B | 100 $ | 70 $ (−30%) | 120 $ (+71%) | 100 $ (−17%) | 180 $ (+80%) |
Четвертый год
180 $ (+44%)
Четвертый год
180 $ (+80%)
Посчитаем данные для обоих активов: среднее арифметическое и среднее геометрическое, то есть годовую доходность.
Актив A:
Среднее арифметическое: (40% + 7% − 17% + 44%) / 4 = 18,5%.
Среднее геометрическое (годовая доходность): (1 + 40%) × (1 + 7%) × (1 − 17%) × (1 + 44%)1/4 = 15,8%.
Актив B:
Среднее арифметическое: (−30% + 71% − 17% + 80%) = 26%.
Среднее геометрическое (годовая доходность): (1 − 30%) × (1 + 71%) × (1 − 17%) × (1 + 80%)1/4 = 15,8%.
Среднее арифметическое актива А больше, чем актива В, — и если бы мы посчитали только среднее арифметическое, то сделали бы ложный вывод, что акции актива B выгоднее. Но ведь мы знаем, что это не так: в результате акции принесли одинаковую прибыль.
Годовая доходность по обеим акциям одинаковая — 15,8%. Но у акций B больше волатильность — и это выражается в разнице между средним арифметическим и средним геометрическим: чем она больше, тем больше волатильность.
В случае с акцией A разница между двумя арифметическим и геометрическим равна 2,8 процентных пункта. А у акции B эта разница составляет 10,4 процентных пункта — при равных доходностях по этой разнице можно сделать вывод, что акции B более волатильны.
Если известна совокупная доходность за весь срок владения, то формула для расчета годовой доходности будет выглядеть так:
(1 + Общая доходность)(365 / Количество дней владения активом) − 1
Например, инвестор купил акцию компании за 100 $, держал ее 714 дней, а на 715-й день продал и получил доходность 74% за весь период владения. Общая годовая доходность за рассматриваемый период будет считаться так:
(1 + 74%)(365 / 715) − 1 = 32,68%
Таким образом, на инвестициях в компанию инвестор заработал 32,68% годовых за рассматриваемый период.
Если известна начальная и конечная стоимость инвестиций, то общую годовую доходность можно вычислить по следующей формуле:
(Конечная стоимость актива / Начальная стоимость актива)(1 / Количество периодов) − 1
Например, инвестор купил 20 акций по 200 $ и решил удерживать их 2 года. За этот период компания каждый год выплачивала 1 $ дивидендов на акцию. На момент продажи цена акции составила 270 $. В этом случае общая годовая доходность будет такой:
((270 × 20 + 2 × 20) / 200 × 20)(1/2) − 1 = 16,62%
Совокупная доходность в данном кейсе составила 36%, а общая годовая доходность — 16,62%.
Как считается риск
Риск — это вероятность частичной или полной потери вложенного капитала. В классической портфельной теории риск вложения определяется как стандартное отклонение его доходности — то есть возможный разброс его фактической доходности вокруг средней доходности.
Предположим, в среднем акция растет на 10% в год, но при этом возможны отклонения на 5% в каждую сторону — то есть она может вырасти как на 15% в год, так и на 5%. Вот эти возможные отклонения нам и нужно рассчитать. Рассчитывается стандартное отклонение по следующей формуле:
где rn — доходность за n-й период, обычно годовая,
r̄ — среднее арифметическое доходности актива за все время владения,
n — количество периодов: если считаем по годовой доходности, то количество лет.
Например, инвестор владел активом 4 года — он знает доходность за каждый год и теперь хочет рассчитать стандартное отклонение доходности этого актива.
Доходность актива
| Период | Доходность |
|---|---|
| Первый год | −11,5% |
| Второй год | 15,9% |
| Третий год | 10% |
| Четвертый год | 7,2% |
Чтобы посчитать стандартное отклонение доходности, в первую очередь посчитаем — среднее арифметическое доходности:
(−11,5% + 15,9% + 10% + 7,2%) / 4 = 5,4%
Теперь можем подставить данные в формулу выше:
Стандартное отклонение составило 11,8%. Если допустить, что доходность акции нормально распределена, то по правилу трех сигм инвестор вправе ожидать, что с вероятностью 68,3% (одно стандартное отклонение — 68,3% вероятности) доходность акции в следующем году будет находиться в диапазоне от −6,4% до 17,2% — то есть от (5,4% − 11,8%) до (5,4% + 11,8%).
Чем сильнее значения фактической доходности отклоняются от ее среднего значения, тем больше стандартное отклонение, а значит, больше риск. Низкое значение стандартного отклонения означает, что годовые доходности лежат вблизи среднего значения и риск от вложения в актив невелик.
Формулу выше используют в случаях, если берутся котировки по акции не за весь период ее существования, а, предположим, за 2—3 года из возможных 10 лет, прошедших с момента первичного размещения акции на фондовом рынке. А если берутся котировки за весь период существования акции, то для расчета стандартного отклонения используется следующая формула — она отличается только знаменателем — берется полное количество периодов:
Анализируем на примере портфеля Баффетта
Итак, в общем виде мы рассмотрели понятия доходности и риска. Теперь я построю диаграмму «риск-доходность», чтобы проанализировать, какие активы показывают оптимальное отношение риска к доходности. Простыми словами, по диаграмме можно понять, какой актив дает максимальную доходность на единицу риска.
Для примера возьмем портфель Уоррена Баффетта: я взял те активы, по которым есть данные котировок за период с 2012 по 2020 год. По отчетным данным на 30 сентября 2020 года в портфель Баффетта входило 49 компаний, но лишь по 6 компаниям, составляющим существенную долю портфеля, были данные за нужный период.
6 крупнейших по весу компаний в портфеле Berkshire Hathaway на 30.09.2020
| Компания | Тикер | Вес актива в портфеле |
|---|---|---|
| Apple | AAPL | 47,78% |
| Bank of America | BAC | 10,63% |
| Coca-Cola | KO | 8,63% |
| American Express | AXP | 6,64% |
| Moody’s | MCO | 3,12% |
| US Bancorp | USB | 2,07% |
Вес актива в портфеле
47,78%
Вес актива в портфеле
10,63%
Вес актива в портфеле
8,63%
Вес актива в портфеле
6,64%
Вес актива в портфеле
3,12%
Вес актива в портфеле
2,07%
В расчетах для повышения точности я опираюсь на ежедневные котировки акций с 2012 по 2020 год — данные и расчеты представлены в гугл-таблице.
Еще для расчетов нам понадобится бенчмарк и безрисковая ставка. Бенчмарк — это портфель, с которым мы будем сравнивать эффективность наших активов. Обычно в качестве бенчмарка берут индекс на широкий рынок США — я взял ETF SPDR S&P 500.
Безрисковая ставка нужна для расчета показателей эффективности инвестиций: в ряде этих показателей она используется как доходность от вложения в безрисковый актив, то есть актив, риск наступления дефолта по которому стремится к нулю. Конечно, абсолютно безрисковых активов не существует, поэтому в качестве безрисковой ставки часто используют процентную ставку по государственным облигациям или определяют ее равной нулю. В качестве безрисковой ставки (RFR, risk-free rate) я взял 10-летние казначейские облигации США — 10-Year Treasury Constant Maturity Rate.
Шаги будут такие:
- Берем дневные доходности активов.
- Рассчитываем по ним среднюю годовую доходность и стандартное отклонение — как делали в разделе с расчетом риска.
- Строим карту «риск-доходность».
Показатели доходности и риска
| Компания | Тикер | Среднегодовая доходность | Стандартное отклонение |
|---|---|---|---|
| Apple | AAPL | 30,2% | 28,6% |
| Bank of America | BAC | 18,4% | 31,1% |
| Coca-Cola | KO | 10,0% | 18,3% |
| American Express | AXP | 15,0% | 29,3% |
| Moody’s | MCO | 27,1% | 27,7% |
| US Bancorp | USB | 10,8% | 26,1% |
| ETF S&P 500 | SPY | 15,5% | 16,8% |
| 10-Y Treasury Bonds | DGS10 | 2,1% | 0,0% |
Среднегодовая доходность
30,2%
Стандартное отклонение
28,6%
Среднегодовая доходность
18,4%
Стандартное отклонение
31,1%
Среднегодовая доходность
10,0%
Стандартное отклонение
18,3%
Среднегодовая доходность
15,0%
Стандартное отклонение
29,3%
Среднегодовая доходность
27,1%
Стандартное отклонение
27,7%
Среднегодовая доходность
10,8%
Стандартное отклонение
26,1%
Среднегодовая доходность
15,5%
Стандартное отклонение
16,8%
Среднегодовая доходность
2,1%
Стандартное отклонение
0,0%
Теперь строим карту по данным из таблицы: данные по среднегодовой доходности откладываем по вертикали, а по стандартному отклонению (риску) — по горизонтали.
Из диаграммы выше можно сделать ряд выводов относительно соотношения доходности и риска активов, определить наиболее предпочтительные и исключить наиболее убыточные из них: например, можно сделать вывод, что акции AAPL дают большую доходность, чем BAC и AXP, но при этом риск инвестирования в AAPL ниже.
Но зачастую неочевидно, какой из активов лучше, — в таком случае на помощь приходят показатели оценки соотношения риска и доходности.
Считаем индикаторы привлекательности активов
Индикаторы привлекательности активов приводят данные из таблицы выше к одному знаменателю: мы можем посчитать конкретные показатели для каждой бумаги и сравнить их. Разберем основные показатели.
Коэффициент вариации показывает величину риска, приходящуюся на единицу доходности. Он рассчитывается по следующей формуле:
CV = σ / r̄,
где σ — стандартное отклонение доходности актива,
r̄ — среднее арифметическое доходности актива.
Коэффициент вариации применяется для сравнения активов с разными доходностями и стандартными отклонениями. Применение показателя позволяет ранжировать активы по степени их рискованности. Чем больше значение показателя, тем выше риск инвестиций.
Коэффициент вариации для рассматриваемых акций
| Тикер | Среднегодовая доходность | Стандартное отклонение | Коэффициент вариации |
|---|---|---|---|
| AAPL | 30,2% | 28,6% | 0,95 |
| MCO | 27,1% | 27,7% | 1,03 |
| SPY | 15,5% | 16,8% | 1,09 |
| BAC | 18,4% | 31,1% | 1,70 |
| KO | 10,0% | 18,3% | 1,82 |
| AXP | 15,0% | 29,3% | 1,95 |
| USB | 10,8% | 26,1% | 2,40 |
Среднегодовая доходность
30,2%
Стандартное отклонение
28,6%
Коэффициент вариации
0,95
Среднегодовая доходность
27,1%
Стандартное отклонение
27,7%
Коэффициент вариации
1,03
Среднегодовая доходность
15,5%
Стандартное отклонение
16,8%
Коэффициент вариации
1,09
Среднегодовая доходность
18,4%
Стандартное отклонение
31,1%
Коэффициент вариации
1,70
Среднегодовая доходность
10,0%
Стандартное отклонение
18,3%
Коэффициент вариации
1,82
Среднегодовая доходность
15,0%
Стандартное отклонение
29,3%
Коэффициент вариации
1,95
Среднегодовая доходность
10,8%
Стандартное отклонение
26,1%
Коэффициент вариации
2,40
Можно сделать вывод относительно того, какой из активов несет больше или меньше риска. Теперь мы видим, что инвестиции в AAPL выгоднее не только инвестиций в BAC и AXP, но и вообще в любой из рассматриваемых активов: на единицу риска тут приходится наибольшая доходность. Самый рискованный актив — USB: на 1% доходности приходится 2,4% стандартного отклонения.
Коэффициент Шарпа показывает, во сколько раз избыточная доходность от инвестирования в портфель по сравнению с безрисковым активом выше уровня риска инвестиций. Избыточная доходность показывает, насколько доходность инвестиционного портфеля выше доходности безрискового актива, в роли которого чаще всего выступают государственные облигации.
Коэффициент Шарпа определяется по следующей формуле:
R̄x − R̄f / σx,
где R̄x — средняя доходность актива (среднемесячная, среднегодовая и так далее),
R̄f — средняя доходность безрискового актива за сопоставимый период,
σx — стандартное отклонение доходности актива за сопоставимый период.
Рассмотрим пример. Предположим, что средняя доходность по акции составляет 30% годовых при 20% стандартного отклонения, а средняя доходность по государственным облигациям США (безрисковый актив) равна 3% годовых. Тогда коэффициент Шарпа для нашей акции будет считаться так:
(30% − 3%) / 20% = 1,35
Это значение показателя говорит о высокой инвестиционной привлекательности нашей акции: доходность по ней выше доходности безрискового актива и превышает уровень риска.
Из формулы видно, что коэффициент Шарпа измеряет вознаграждение в виде средней избыточной доходности на единицу риска. Также следует отметить, что коэффициент был создан для анализа портфелей, а не отдельных инструментов, но все же его следует учитывать при отборе активов в портфель: он позволяет сделать вывод об эффективности вложения.
Критерии эффективности инвестиций на основе коэффициента Шарпа
| Критерий | Вывод по активу |
|---|---|
| Коэффициент Шарпа > 1 | Доходность инвестиций выше доходности безрискового актива и превышает уровень риска |
| 1 > коэффициент Шарпа > 0 | Риск инвестирования выше, чем доходность от инвестирования, — необходимо пересмотреть инвестиционное решение относительно этого актива или группы активов. Инвестирование в актив не приносит достаточной доходности |
| Коэффициент Шарпа < 0 | Доходность от инвестирования ниже доходности безрискового актива. Вероятно, лучше инвестировать в безрисковый актив |
Коэффициент Шарпа > 1
Доходность инвестиций выше доходности безрискового актива и превышает уровень риска
1 > коэффициент Шарпа > 0
Риск инвестирования выше, чем доходность от инвестирования, — необходимо пересмотреть инвестиционное решение относительно этого актива или группы активов. Инвестирование в актив не приносит достаточной доходности
Коэффициент Шарпа < 0
Доходность от инвестирования ниже доходности безрискового актива. Вероятно, лучше инвестировать в безрисковый актив
Рассмотрим результаты расчетов по коэффициенту Шарпа для акций в нашем примере.
Коэффициент Шарпа у акций из портфеля Баффетта
| AAPL | 0,98 |
| MCO | 0,90 |
| SPY | 0,79 |
| BAC | 0,52 |
| AXP | 0,44 |
| KO | 0,43 |
| USB | 0,33 |
Коэффициент информации характеризует соотношение риска-доходности актива или портфеля по сравнению с бенчмарком. Коэффициент расчетами напоминает коэффициент Шарпа, только вместо безрисковой ставки используется определенный эталон — бенчмарк. Бенчмарком могут выступать широкие рыночные индексы — MSCI, S&P 500, отраслевые индексы — DJA, собственноручно разработанные бенчмарки и так далее.
Иными словами, коэффициент информации — это отношение сверхдоходности к стандартному отклонению этой сверхдоходности у актива и бенчмарка. Коэффициент помогает понять, выгодно ли инвестировать в актив или набор активов — или проще и безопасней инвестировать в актив, выбранный бенчмарком. В нашем случае в качестве бенчмарка мы взяли ETF на S&P 500.
Формула выглядит так:
R̄x − R̄m / σx − m,
где R̄x — средняя доходность актива (среднемесячная, среднегодовая и так далее),
R̄m — средняя доходность бенчмарка за сопоставимый период,
σx − m — стандартное отклонение разности доходности актива и бенчмарка за сопоставимый период.
На примере AAPL и S&P 500 все будет выглядеть так:
В числителе: считаем разницу между средней доходностью акции AAPL (30,2% годовых) и средней доходностью индекса S&P 500 (15,5% годовых).
В знаменателе: сначала считаем разницу между дневными доходностями акции AAPL и индекса S&P 500, а потом по полученной совокупности дневных сверхдоходностей определяем стандартное отклонение и приводим дневное значение стандартного отклонения к годовому, перемножив дневное стандартное отклонение на корень из 252. Перемножаем на 252, так как в году 252 торговых дня. В нашей таблице этот расчет произведен на листе «Дневная доходность».
Итого получается:
(30,2% − 15,5%) / 21,28% = 0,69. Значение показателя выше 0,5 говорит о хорошей инвестиционной привлекательности акции.
Следует отметить, что этот коэффициент показывает эффективность активного управления, — при пассивном управлении, если мы просто покупаем индексный фонд и держим его, коэффициент будет равен нулю.
Чем больше значение коэффициента, тем выше избыточная «отдача» от инвестирования в определенный актив или портфель по сравнению с бенчмарком. Значение коэффициента информации в диапазоне от 0,5 до 0,74 считается хорошим, значение от 0,75 до 0,99 считается очень хорошим, а значение свыше 0,99 считается отличным. Ниже представлены результаты расчетов коэффициента информации для рассматриваемых акций.
Коэффициент информации у рассматриваемых акций
| AAPL | 0,69 |
| MCO | 0,63 |
| BAC | 0,13 |
| SPY | 0 |
| AXP | −0,02 |
| KO | −0,36 |
| USB | −0,26 |
Можно заметить, что для SPY (ETF на S&P 500) коэффициент информации равен нулю, так как он отражает движение рынка и не подразумевает сверхдоходности за активное управление. Напротив, хорошее значение коэффициента имеют акции AAPL и MCO, у которых на 1% стандартного отклонения сверхдоходности приходится 0,69 и 0,63% сверхдоходности соответственно. В случае с KO, AXP и USB отрицательные значения коэффициента связаны с отрицательными избыточными доходностями относительно бенчмарка.
Коэффициент Сортино — показатель, напоминающий коэффициент Шарпа, он отличается лишь расчетом риска. В коэффициенте Сортино для расчета риска учитываются только доходности актива ниже определенного уровня — чаще всего этот уровень определяется как доходность безрискового актива за сопоставимый период либо нулевая ставка.
Предполагается, что положительные отклонения доходностей — выше доходности безрискового актива — не несут риск, так как повышают доходность актива, — соответственно, учитывать их при расчете риска не нужно. Таким образом, для расчета стандартного отклонения необходимо выбрать только те дневные доходности, значение которых будет ниже доходности безрискового актива за этот же день. В нашей таблице все посчитано на листе «Кф. Сортино». Вот по какой формуле этот коэффициент рассчитывается:
R̄x − R̄f / σxd,
где R̄x — средняя доходность актива (среднемесячная, среднегодовая и так далее),
R̄f — средняя доходность безрискового актива за сопоставимый период,
σxd — стандартное отклонение доходности актива ниже заданного уровня.
Для примера рассмотрим логику, по которой фильтруются доходности для расчета риска по коэффициенту Сортино.
Месячные доходности акции и безрискового актива
| Период | Доходность акции | Доходность безрискового актива | Отфильтрованная доходность |
|---|---|---|---|
| 1 месяц | 0,16% | 0,18% | 0,16% |
| 2 месяц | −2,54% | 0,18% | −2,54% |
| 3 месяц | 0,29% | 0,18% | 0,00% |
| 4 месяц | 0,00% | 0,18% | 0,00% |
| 5 месяц | 2,24% | 0,18% | 0,00% |
| 6 месяц | −11,80% | 0,18% | −11,80% |
| 7 месяц | 14,10% | 0,18% | 0,00% |
| 8 месяц | 8,36% | 0,18% | 0,00% |
| 9 месяц | −2,14% | 0,18% | −2,14% |
| 10 месяц | 9,67% | 0,18% | 0,00% |
| 11 месяц | 7,00% | 0,18% | 0,00% |
| 12 месяц | 0,90% | 0,18% | 0,00% |
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,16%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
−2,54%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
−11,80%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
−2,14%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
В последней колонке оказались лишь те значения доходности акции, которые были ниже доходности безрискового актива за соответствующий период. Затем с помощью формулы стандартного отклонения рассчитываем риск по отфильтрованной доходности — он составит 3,54%. Среднемесячная доходность по акции — 2,19%, а среднемесячная доходность по безрисковому активу — 0,18%. Таким образом, коэффициент Сортино для акции из примера считается так:
(2,19% − 0,18%) / 3,54% = 0,57. Значение показателя ниже единицы указывает на то, что актив не обеспечивает должного уровня доходности на единицу нисходящего риска.
Чем больше значение коэффициента, тем выше вероятность безубыточности вложения и тем большей инвестиционной привлекательностью обладает рассматриваемый актив. Минимально допустимое значение показателя, определяющее инвестиционную привлекательность актива, — 1. Таким образом, на примере портфеля Баффетта допустимая и большая привлекательность у AAPL, MCO и SPY, а остальные же активы по коэффициенту Сортино непривлекательны, потому что не обеспечивают должного уровня доходности на единицу нисходящего риска.
Коэффициент Сортино у рассматриваемых акций
| AAPL | 1,59 |
| MCO | 1,40 |
| SPY | 1,19 |
| BAC | 0,86 |
| AXP | 0,73 |
| KO | 0,66 |
| USB | 0,53 |
Коэффициент Трейнора — еще один показатель, напоминающий коэффициент Шарпа и отличающийся только расчетом риска. В качестве риска берется коэффициент бета акции — он отражает волатильность актива по отношению к рынку. Коэффициент Трейнора показывает отношение сверхдоходности к рыночному риску.
Для расчета коэффициента бета акции используется следующая формула — рассчитанную бета акции можно найти на Yahoo Finance в разделе Summary на странице акции:
где σxm — ковариация между доходностью актива (портфеля) и доходностью рынка,
σm2 — дисперсия доходности рынка.
Методика расчета коэффициента бета акции раскрыта на листе «Дневная доходность» нашей таблицы, в столбце «Рыночный риск».
Коэффициент бета, находящийся в диапазоне от 0 до 1, свидетельствует о том, что акция движется в целом в одном направлении с рынком: если фондовый индекс растет, то растет и акция. Но значение коэффициента меньше 1 говорит о том, что актив менее чувствителен к движению рынка.
Коэффициент бета, равный 1, говорит о том, что движение актива полностью повторяет движение фондового индекса. Можно заметить, что значение 1 наблюдается у SPY, то есть у рыночного индекса.
Коэффициент бета больше 1 говорит о том, что динамика акции коррелирует с движением индекса, но при этом акция более чувствительно реагирует на любое движение рыночного индекса.
Коэффициент бета у рассматриваемых акций
| BAC | 1,38 |
| MCO | 1,26 |
| AXP | 1,26 |
| AAPL | 1,14 |
| SPY | 1,00 |
| USB | 1,15 |
| KO | 0,69 |
Зная коэффициент бета, доходность актива и доходность безрискового актива, мы можем рассчитать коэффициент Трейнора по следующей формуле:
R̄x − R̄f / βx,
где R̄x — средняя доходность актива (среднемесячная, среднегодовая и так далее),
R̄f — средняя доходность безрискового актива за сопоставимый период,
βx — коэффициент бета актива.
Допустим, необходимо рассчитать коэффициент Трейнора для акции USB — US Bancorp. Переходим на страницу компании на Yahoo Finance и находим Beta — 1,14 на момент написания статьи. Далее для расчета коэффициента Трейнора достаточно найти разницу между среднегодовой доходностью акции — 10,8% и среднегодовой доходностью безрискового актива — 2,1% и поделить полученное значение на бета акции.
Для акции USB:
(10,8% − 2,1%) / 1,14 = 0,076
Значение показателя выше нуля указывает на то, что инвестирование в актив более привлекательно, чем в рыночный индекс. Если коэффициент ниже нуля, то целесообразнее вкладывать в рыночный индекс, так как актив проигрывает рынку по соотношению риска и доходности. Таким образом, все акции портфеля инвестиционно привлекательны по этому показателю.
Коэффициент Трейнора у рассматриваемых акций
| AAPL | 0,24 |
| MCO | 0,20 |
| SPY | 0,13 |
| BAC | 0,12 |
| KO | 0,11 |
| AXP | 0,10 |
| USB | 0,08 |
Выводы
Теперь мы можем собрать сводную таблицу и оценить инвестиционную привлекательность активов на примере акций из портфеля Баффетта.
По данным из таблицы можно сделать вывод, что из рассмотренных активов наиболее привлекательны для инвестора Apple (AAPL), Moody’s (MCO) и SPDR S&P 500 (SPY).
Но важно помнить: кроме расчета индикаторов нужно оценивать перспективы отрасли и самой компании — и только когда картина собрана целиком, можно решать, инвестировать ли в компанию.