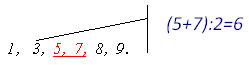Как найти дисперсию температуры в градусах

В некоторых странах температуру измеряют не в градусах Цельсия, а в градусах
Фаренгейта. Для перевода используют следующую формулу:
F C = + 1,8 32 ,
где F — температура в градусах Фаренгейта, C — та же температура,
выраженная в градусах Цельсия.
В картинных галереях важно следить за температурой. Для этого разработан
специальный кондиционер. На испытаниях в результате ряда измерений
получилось, что средняя температура в помещении на протяжении суток равна
20 C° , а дисперсия равна 4.
Чтобы опубликовать эту информацию в иностранном журнале, потребовалось
перевести эти данные в шкалу Фаренгейта.
а) Найдите среднее значение температуры в градусах Фаренгейта.
б) Найдите дисперсию температуры, выраженной в градусах Фаренгейта.

Источник

Изучая математическую статистику в 7-м классе,
важно наглядно представить учащимися образец
для решения практических задач. Именно для этого
мною был разработан данный справочный материал.

1.Представление данных.

1.1. Таблицы

Смета расходов на покупку спортивного
инвентаря.

№ Наименование Ед. измерения Количество Цена (едруб) Стоимость (руб)
1 Мяч футбольный Шт. 30 1000
2 Мяч волейбольный Шт. 15 800 12000
3 Ракетка Шт. 24 250 6000
4 Воланы коробка 10 300 3000
  ИТОГО:       51000

Таблицы предназначены для упорядочивания
большого количества данных. Часто в таблицы
заносят результаты вычислений, измерений.

1.2. Диаграммы.

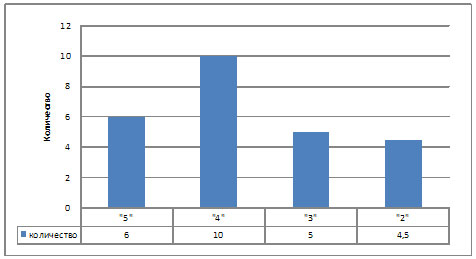
За контрольную работу по математике
школьники получили 6 оценок “отлично”, 10 оценок
“хорошо”, 5 оценок “ удовлетворительно” и 3
оценки “не удовлетворительно”.

Столбиковая диаграмма.

Построим столбиковую диаграмму по
этим данным.

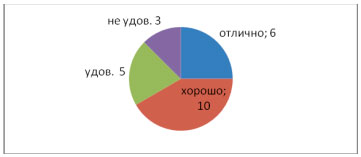
 Круговая диаграмма.

Построим круговую диаграмму по этим
данным.

Для построения этой диаграммы мы:

  1. Разделили 360° на общее число учащихся (24)

    2. 360°24=15° (такому углу соответствует
    оценка одного учащегося)

  2. Затем последовательно умножаем 15° на
    количество учащихся, получивших ту или иную
    оценку.

    3. 15°6=90° —
    сектор образованный этим углом соответствует
    учащимся с оценкой “5”

    15°10=150°
    — сектор образованный этим углом соответствует
    учащимся с оценкой “4”

    15°5=75° —
    сектор образованный этим углом соответствует
    учащимся с оценкой “3”

    15°3=45° —
    сектор образованный этим углом соответствует
    учащимся с оценкой “2”

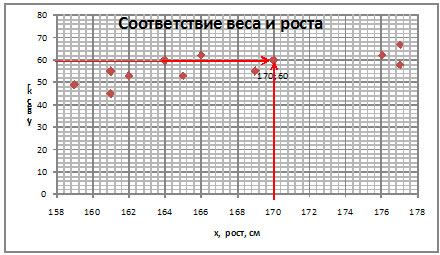
  3. Затем круг делим на полученные сектора,
    подписываем данные.

Диаграмма рассеивания.

Для выявления связи между величинами
применяются диаграммы рассеивания.

В таблице приведены данные о весе и
росте 12 девушек.

Рост, см

165

177

161

162

170

176

177

164

166

161

169

159

Х

Вес, кг

53

67

45

53

60

62

58

60

62

55

55

49

У

Для построения этой диаграммы нужно в
системе координат поставить точки, абсциссы
которых – рост, а ординаты – вес.



  1. Описательная статистика

2.1. Среднее значение

Определение: Средним арифметическим
нескольких чисел называется число, равное
отношение суммы этих чисел к их количеству.

Среднее арифметическое набора чисел х1,х2,х3,х4,х5
принято обозначать . Например, среднее арифметическое
пяти чисел запишется так:

Здесь в числителе дроби — сумма данных пяти
чисел, а в знаменателе – их количество – 5.

Найти среднюю оценку учащегося по
математике, если за истекший период он получил: 3,
4, 4, 5, 3, 2, 4, 3.

Запишем дробь и вычислим ее значение:

2.2. Медиана

Определение: Число, разделяющее набор
чисел на две части, равные по численности, так что
с одной стороны от этого числа все значения
больше медианы, а с другой – меньше.

Метод вычисления медианы: Чтобы найти
медиану набора чисел нужно:

  1. Записать числа в порядке возрастания.
  2. Если в полученном наборе нечетное количество
    членов, то медианой служит число стоящее
    посередине.
  3. Если в полученном наборе четное количество
    членов, то медианой набора – есть полусумма двух
    чисел, расположенных посередине.


Найти медиану набора чисел: 9,3, 1, 5, 7.

Запишем числа в порядке возрастания.

1, 3, 5, 7, 9.

Здесь медиана набора число, стоящее
посередине – 5.

Найти медиану набора чисел: 9,3, 1, 5, 7,8

Запишем числа в порядке возрастания.

Выберем два центральных числа: 5 и 7. Найдем их
полусумму: (5+7):2=6. То есть медиана
данного набора есть число-6.

2.3. Наибольшее и наименьшее значение и размах.

Найти наибольшее, наименьшее значение и
размах для ряда чисел:

12,7,25,3,19,15.

Очевидно, что наибольшим значением данного
ряда является число 25, тогда как наименьшим число
– 3. Найдем размах данного ряда.

Определение: Разность между наибольшим и
наименьшим числом называется размахом набора
чисел.

Размах показывает насколько велико
рассеивание в числовом наборе. Итак, размах
данного набора равен разности 25 и 3, т.е. 22.

2.4. Отклонение.

Определение: Отклонением данного
значения от среднего арифметического значения
данного набора является разность между этим
числом и средним арифметическим. Соответственно
если некоторое значение меньше среднего, то его
отклонение отрицательно, если больше среднего –
его отклонение положительно. Так же необходимо
помнить, что сумма всех отклонений ряда чисел от
среднего арифметического этих чисел равна нулю.

Составить таблицу отклонений от
среднего арифметического для набора чисел:
2,4,5,7,10.

Вычислим среднее арифметическое этих чисел:

Составим таблицу отклонений.

Число Отклонение от среднего
арифметического
2 2-5,6= -3,6
4 4-5,6= -1,6
5 5-5,6= -0,6
7 7-5,6=1,4
10 10-5,6=4,4

2.5. Дисперсия.

Определение: Среднее арифметическое
квадратов отклонений от среднего значения
называется дисперсией набора чисел. Дисперсию
обозначают S2.

В таблице представлены средние
месячные температуры, в градусах. Вычислите
дисперсию температуры за приведенный период.

Месяцы Январь Февраль Март Апрель Май
Средняя температура -12 -7 0 9 16

Решение:

  1. Вычислим среднюю температуру за 5 месецев.

    2. Итак, средняя температура составила 6
    градусов.

  2. .Составим таблицу отклонений и их квадратов.

    3. Число (температура) Отклонение от среднего Квадрат отклонения
    -12 -12-6=-18 (-18)2=324
    -7 -13 169
    0 -6 36
    9 3 9
    16 10 100

  3. Найдем среднее арифметическое для квадратов
    отклонений от среднего значения

( последний столбец таблицы)

Итак, дисперсия средних температур за 5 месяцев
составила 127,6. Ответ: S2=127,6

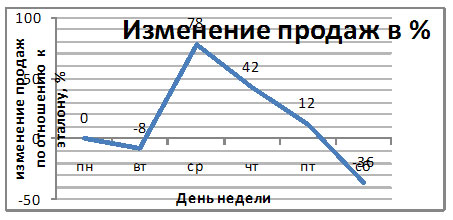
Составление таблицы изменений в процентах.

В таблице представлено количество
продаваемых за неделю шоколадок в школьном
буфете. Составьте таблицу изменения продаж по
отношению к понедельнику в процентах.

День недели

понедельник

вторник

среда

четверг

пятница

суббота

Количество

50

46

89

71

44

32

Число проданных в понедельник шоколадок
составляет 100% — эталон.

Вычислим, сколько составляет 1% эталона.

1% =50:100=0,5.

Вычислим, сколько процентов эталона составляет
количество проданных шоколадок в другие дни
недели.

Вторник – 46. Какой процент составляет 46 от 50.
46:0,5=92

Среда -89. 89 : 0,5= 178

Четверг – 71. 71 :0,5=142

Пятница – 44 44:0,5=88

Суббота -32 32 :0,5 =64

День недели

понедельник

вторник

среда

четверг

пятница

суббота

Количество проданных
шоколадок

50

46

89

71

44

32

% от эталона

100

92

178

142

88

64

Изменение продаж в %

0

-8

78

42

-12

-36

Источник

Станция

Срок

Месяц

I

IV

VII

X

Кемь

1

49,2

21,9

9,5

14,2

7

47,8

22,1

13,3

14,6

13

43,2

17,7

21,6

11,9

19

46,2

16,5

15,1

12,8

Сутки

47,2

17,8

13,3

12,0

Киров

1

73,6

17,3

14,6

16.5

7

76,4

18,3

15,2

17,8

13

68,2

26,2

27,3

17,4

19

68,7

21,3

23,0

16,0

Сутки

61,5

18,7

17,0

18,9

Ростов-на-Дону

1

45,9

15,2

9,1

19,0

7

47,7

13,2

7,4

18,2

13

37,2

27,8

15,4

24,8

19

42,0

21,5

13,1

19,8

Сутки

40,3

14,5

9,2

19,1

Гораздо более устойчивыми оказываются
пространственные корреляционные функции
температуры воздуха. Это хорошо видно,
например, из рис. 4.8, на котором, представлены
корреляционные функции средней
суточной температуры воздуха в
различных районах Евразии. Для Европы
и Забайкалья летом отмечается несколько
более быстрое затухание корреляции с
расстоянием, чем зимой; для Западной
Сибири таких различий не наблюдается.
Различия между корреляционными функциями
сравнительно невелики (например,
коэффициенту корреляции 0,6 соответствуют
расстояния от 500 до 700 км), тем не менее
их, по-видимому, следует считать
существенными. Еще более существенным
оказывается влияние географического
фактора на степень мелкомасштабной
неоднородности поля температуры,
определяющей значения меры случайных
ошибок наблюдений η2. Если
для равнинных территорий Западной
Сибири они имеют порядок 0,01, то для
Забайкалья с его более пересеченным
рельефом мера ошибки η2
достигает значений 0,05—0,07. При временном
осреднении поля степень пространственной
связности его, естественно, возрастает.
Это хорошо видно при сравнении
представленных на рис. 4.9 корреляционных
функций средней суточной, средней
декадной и средней месячной температуры
для июля в центре EЧР.
Значения меры ошибок исходных данных
η2 для средних суточных
температур достигают 0,1, что соответствует
ошибкам за счет совокупного влияния
погрешностей наблюдений и
микрометеорологических процессов около
1ОС. Для средних декадных и средних
месячных температур значения η2
имеют порядок 0,01, что соответствует
средней квадратической погрешности
около 0,2°С, обусловленной главным образом
микроклиматическими различиями в
расположении станций.

Рис.
4.8. Корреляционная функция средней
суточной температуры
воздуха для Европы за январь (1
и
июнь (2) и для Западной Сибири и Забайкалья
за январь
(3, 4)
и
июль (5, 6).

Рис. 4.9. Пространственная корреляция
средней температуры воздуха при
различных периодах осреднения. Центр
EЧР, лето. 1 — сутки; 2
— декада; 3 — месяц.

3. Пространственная корреляция средней
месячной температуры воздуха для
центра EЧР. Имеет место
четко выраженный годовой ход параметров
пространственной структуры,
характеризующийся более быстрым
затуханием корреляции с расстоянием в
летние месяцы по сравнению с зимними.

Полученные корреляционные функции
хорошо аппроксимируются выражением
вида


(4.17)

Параметры
этой аппроксимационной формулы приведены
в
табл. 4.6.

Эти данные получены путем
осреднения корреляции по градациям
расстояния, без учета направления, т.
е. в предположении изотропии поля
температуры. Наряду с этим были выполнены
оценки реальной анизотропии этого поля.
Зависимость
корреляции от направления получена по
данным 172 станций, что позволило исключить
влияние несущественных особенностей
отдельных станций.

Таблица 4.6

Параметры аппроксимационной формулы
(4.17) для корреляционной функции средней
месячной температуры воздуха в центре
Eвропейской части России
(ЕЧР)

Параметр

XII

I

II

IV

VII

X

0,994

0,998

0,996

0,993

0,992

0,995

ρо
тыс. км

1,92

3,20

1,77

1,30

1,49

2,59

α

1,60

1,49

1,54

1,59

1,67

1,49

σ (°С)

3,3

4,7

3,5

2,1

2,0

2,1

η2

0,006

0,002

0,004

0,007

0,008

0,005

Δ(°С)

0,25

0,21

0,22

0,18

0,18

0,15

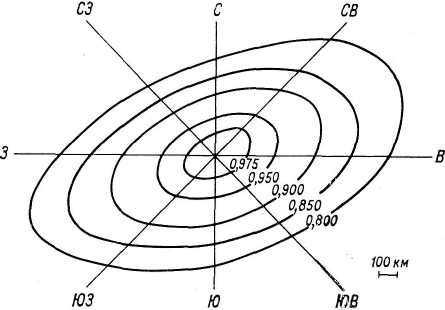
Рис. 4.10. Зависимость корреляции средней
месячной температуры от направления.
Центр ЕЧР, февраль.

Поля изокоррелят для каждого месяца
имеют вид эллипсов, большая ось которых
ориентирована в направлении преобладающего
переноса воздушных масс. В качестве
примера на рис. 4.10 приводится поле
изокоррелят для февраля, для которого
большая ось направлена на восток-северо-восток.
При переходе от зимних месяцев к летним
в соответствии с изменением характера
циркуляции имеет место поворот большой
оси эллипса изокоррелят, которая,
согласно рис. 4.11 а, от почти зонального
направления в декабре переходит к
близкому к меридиональному направлению
в июле.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

2020/06/26 10:12:20

Статистические метрики (выборка, дисперсия)

.

Содержание

    • Выборка
    • Дисперсия
    • Примечания

Выборка

Выборка — это набор данных, которые попали в исследование. Она может быть репрезентативной, не совсем или совсем не. К примеру, мы хотим посчитать среднюю зарплату в городе. Наша выборка по демографическим соотношениям должна совпадать с общегородской статистикой — тогда она будет репрезентативной.

Дисперсия

Дисперсия — это разброс данных в нашем исследовании, этот параметр позволяет понять, что вообще с выборкой делать. Допустим, мы хотим посчитать среднюю температуру по больнице. Дисперсия будет от +34 до +42 градусов по Цельсию, она достаточно низкая, чтобы применить метод среднего арифметического. А вот если добавить в выборку труп комнатной температуры, дисперсия окажется слишком большой, чтобы выборка была репрезентативной[1].

Дисперсия — это мера «разброса» случайной величины от ее самого вероятного значения. У учеников оценка может быть от 2 до 5. Если мы считаем, что наиболее вероятная оценка у школьников 3,5, то мы имеем дисперсию, равную 1,5. Это небольшая дисперсия. Она позволяет нам говорить о том, что среднее арифметическое класса достаточно показательно, если мы хотим сравнить, какой класс знает математику лучше. При помощи такой аргументации гораздо проще объяснить маме тройку, чем доказывать, что у всех вообще два. Согласитесь, «Мама, я сделал вывод, что моя тройка с плюсом выше среднего арифметического в классе, что говорит о том, что я заслуживаю поощрения, а не наказания» звучит гораздо убедительнее, чем «Мама! Да у всех вообще двойки!».

В случае со средней температурой по больнице всё становится интереснее. Дисперсия температуры у живого человека не такая уж большая — от примерно +34 до +42 °С при максимально ожидаемой +36,6 °С. Это позволяет нам говорить, что среднее арифметическое достаточно показательно для оценки ситуации. Можно сказать, что в среднем пациенты в инфекционном отделении теплее пациентов в травматологическом. Однако всё меняется, если добавить труп с комнатной температурой. Это увеличивает дисперсию и приводит к тому, что среднее становится совершенно нерепрезентативным.

Точно так же можно посмотреть на статистику среднего возраста рождения первого/второго/третьего ребенка у женщины. Почему все учитывают именно женщин, а не мужчин? С агрегацией данных по мужчинам возникает много проблем: разная дисперсия по сравнению с женщинами (у женщин период, когда они могут иметь детей, гораздо короче, чем у мужчин), принципиально разное количество детей, которые могут появиться в течение жизни, сложности с достоверным установлением отцовства.

Примечания

  1. ↑ «Я на обед ем капусту, мой сосед ест котлеты, а в среднем мы с ним едим голубцы». Как понимать статистику

Источник

В некоторых странах температуру измеряют не в градусах Цельсия, а в градусах

Фаренгейта. Для перевода используют следующую формулу:

F C = + 1,8 32 ,

где F — температура в градусах Фаренгейта, C — та же температура,

выраженная в градусах Цельсия.

В картинных галереях важно следить за температурой. Для этого разработан

специальный кондиционер. На испытаниях в результате ряда измерений

получилось, что средняя температура в помещении на протяжении суток равна

20 C° , а дисперсия равна 4.

Чтобы опубликовать эту информацию в иностранном журнале, потребовалось

перевести эти данные в шкалу Фаренгейта.

а) Найдите среднее значение температуры в градусах Фаренгейта.

б) Найдите дисперсию температуры, выраженной в градусах Фаренгейта.

Источник

Понравилась статья? Поделить с друзьями:
  • Профессиональный профиль сотрудника как составить
  • Как найти длину проекции прямой на плоскость
  • Как исправить огурцы если банка вздулась
  • Как найти обьем части конуса
  • Как найти длину биссектрисы правильного треугольника