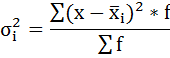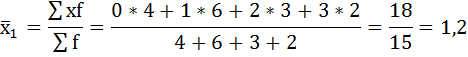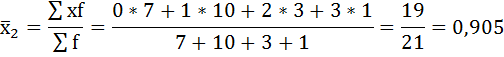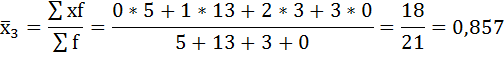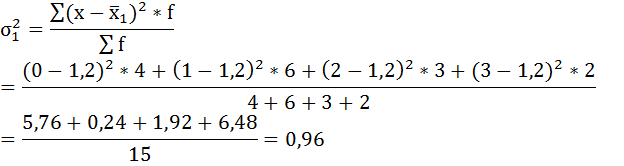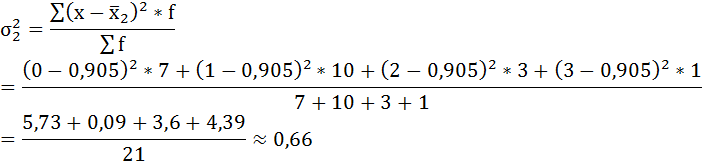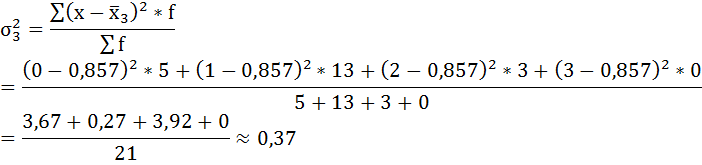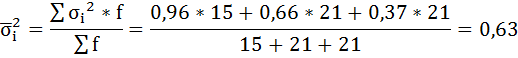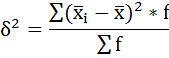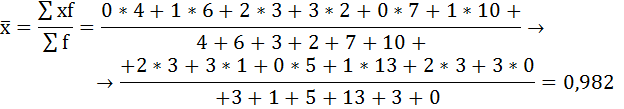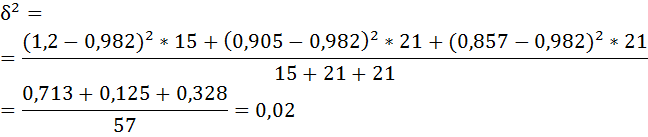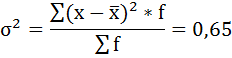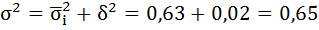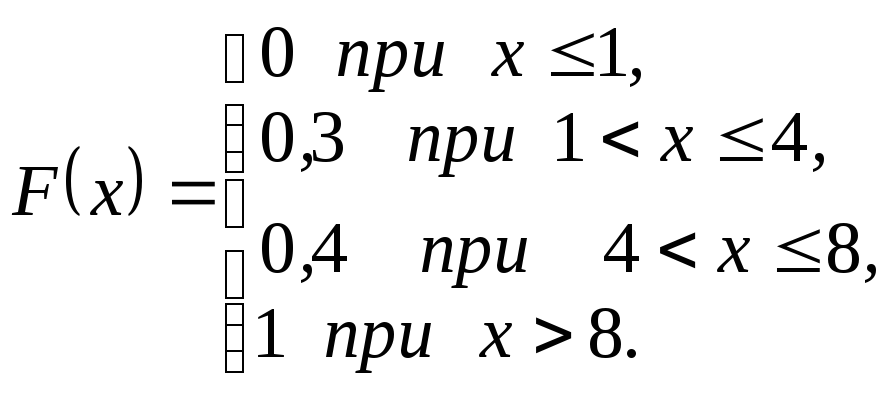Как найти дисперсию?
Лучшее спасибо — порекомендовать эту страницу
Дисперсия — это мера разброса значений случайной величины $X$ относительно ее математического ожидания $M(X)$ (см. как найти математическое ожидание случайной величины). Дисперсия показывает, насколько в среднем значения сосредоточены, сгруппированы около $M(X)$: если дисперсия маленькая — значения сравнительно близки друг к другу, если большая — далеки друг от друга (см. примеры нахождения дисперсии ниже).
Если случайная величина описывает физические объекты с некоторой размерностью (метры, секунды, килограммы и т.п.), то дисперсия будет выражаться в квадратных единицах (метры в квадрате, секунды в квадрате и т.п.). Ясно, что это не совсем удобно для анализа, поэтому часто вычисляют также корень из дисперсии — среднеквадратическое отклонение $sigma(X)=sqrt{D(X)}$, которое имеет ту же размерность, что и исходная величина и также описывает разброс.
Еще одно формальное определение дисперсии звучит так: «Дисперсия — это второй центральный момент случайной величины» (напомним, что первый начальный момент — это как раз математическое ожидание).
Нужна помощь? Решаем теорию вероятностей на отлично
Формула дисперсии случайной величины
Дисперсия случайной величины Х вычисляется по следующей формуле:
$$
D(X)=M(X-M(X))^2,
$$
которую также часто записывают в более удобном для расчетов виде:
$$
D(X)=M(X^2)-(M(X))^2.
$$
Эта универсальная формула для дисперсии может быть расписана более подробно для двух случаев.
Если мы имеем дело с дискретной случайной величиной (которая задана перечнем значений $x_i$ и соответствующих вероятностей $p_i$), то формула принимает вид:
$$
D(X)=sum_{i=1}^{n}{x_i^2 cdot p_i}-left(sum_{i=1}^{n}{x_i cdot p_i} right)^2.
$$
Если же речь идет о непрерывной случайной величине (заданной плотностью вероятностей $f(x)$ в общем случае), формула дисперсии Х выглядит следующим образом:
$$
D(X)=int_{-infty}^{+infty} f(x) cdot x^2 dx — left( int_{-infty}^{+infty} f(x) cdot x dx right)^2.
$$
Пример нахождения дисперсии
Рассмотрим простые примеры, показывающие как найти дисперсию по формулам, введеным выше.
Пример 1. Вычислить и сравнить дисперсию двух законов распределения:
$$
x_i quad 1 quad 2 \
p_i quad 0.5 quad 0.5
$$
и
$$
y_i quad -10 quad 10 \
p_i quad 0.5 quad 0.5
$$
Для убедительности и наглядности расчетов мы взяли простые распределения с двумя значениями и одинаковыми вероятностями. Но в первом случае значения случайной величины расположены рядом (1 и 2), а во втором — дальше друг от друга (-10 и 10). А теперь посмотрим, насколько различаются дисперсии:
$$
D(X)=sum_{i=1}^{n}{x_i^2 cdot p_i}-left(sum_{i=1}^{n}{x_i cdot p_i} right)^2 =\
= 1^2cdot 0.5 + 2^2 cdot 0.5 — (1cdot 0.5 + 2cdot 0.5)^2=2.5-1.5^2=0.25.
$$
$$
D(Y)=sum_{i=1}^{n}{y_i^2 cdot p_i}-left(sum_{i=1}^{n}{y_i cdot p_i} right)^2 =\
= (-10)^2cdot 0.5 + 10^2 cdot 0.5 — (-10cdot 0.5 + 10cdot 0.5)^2=100-0^2=100.
$$
Итак, значения случайных величин различались на 1 и 20 единиц, тогда как дисперсия показывает меру разброса в 0.25 и 100. Если перейти к среднеквадратическому отклонению, получим $sigma(X)=0.5$, $sigma(Y)=10$, то есть вполне ожидаемые величины: в первом случае значения отстоят в обе стороны на 0.5 от среднего 1.5, а во втором — на 10 единиц от среднего 0.
Ясно, что для более сложных распределений, где число значений больше и вероятности не одинаковы, картина будет более сложной, прямой зависимости от значений уже не будет (но будет как раз оценка разброса).
Пример 2. Найти дисперсию случайной величины Х, заданной дискретным рядом распределения:
$$
x_i quad -1 quad 2 quad 5 quad 10 quad 20 \
p_i quad 0.1 quad 0.2 quad 0.3 quad 0.3 quad 0.1
$$
Снова используем формулу для дисперсии дискретной случайной величины:
$$
D(X)=M(X^2)-(M(X))^2.
$$
В случае, когда значений много, удобно разбить вычисления по шагам. Сначала найдем математическое ожидание:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i} =-1cdot 0.1 + 2 cdot 0.2 +5cdot 0.3 +10cdot 0.3+20cdot 0.1=6.8.
$$
Потом математическое ожидание квадрата случайной величины:
$$
M(X^2)=sum_{i=1}^{n}{x_i^2 cdot p_i}
= (-1)^2cdot 0.1 + 2^2 cdot 0.2 +5^2cdot 0.3 +10^2cdot 0.3+20^2cdot 0.1=78.4.
$$
А потом подставим все в формулу для дисперсии:
$$
D(X)=M(X^2)-(M(X))^2=78.4-6.8^2=32.16.
$$
Дисперсия равна 32.16 квадратных единиц.
Пример 3. Найти дисперсию по заданному непрерывному закону распределения случайной величины Х, заданному плотностью $f(x)=x/18$ при $x in(0,6)$ и $f(x)=0$ в остальных точках.
Используем для расчета формулу дисперсии непрерывной случайной величины:
$$
D(X)=int_{-infty}^{+infty} f(x) cdot x^2 dx — left( int_{-infty}^{+infty} f(x) cdot x dx right)^2.
$$
Вычислим сначала математическое ожидание:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx = int_{0}^{6} frac{x}{18} cdot x dx = int_{0}^{6} frac{x^2}{18} dx =
left.frac{x^3}{54} right|_0^6=frac{6^3}{54} = 4.
$$
Теперь вычислим
$$
M(X^2)=int_{-infty}^{+infty} f(x) cdot x^2 dx = int_{0}^{6} frac{x}{18} cdot x^2 dx = int_{0}^{6} frac{x^3}{18} dx = left.frac{x^4}{72} right|_0^6=frac{6^4}{72} = 18.
$$
Подставляем:
$$
D(X)=M(X^2)-(M(X))^2=18-4^2=2.
$$
Дисперсия равна 2.
Другие задачи с решениями по ТВ
Подробно решим ваши задачи на вычисление дисперсии
Вычисление дисперсии онлайн
Как найти дисперсию онлайн для дискретной случайной величины? Используйте калькулятор ниже.
- Введите число значений случайной величины К.
- Появится форма ввода для значений $x_i$ и соответствующих вероятностей $p_i$ (десятичные дроби вводятся с разделителем точкой, например: -10.3 или 0.5). Введите нужные значения (проверьте, что сумма вероятностей равна 1, то есть закон распределения корректный).
- Нажмите на кнопку «Вычислить».
- Калькулятор покажет вычисленное математическое ожидание $M(X)$ и затем искомое значение дисперсии $D(X)$.
Видео. Полезные ссылки
Видеоролики: что такое дисперсия и как найти дисперсию
Если вам нужно более подробное объяснение того, что такое дисперсия, как она вычисляется и какими свойствами обладает, рекомендую два видео (для дискретной и непрерывной случайной величины соответственно).
Полезная страница? Сохрани или расскажи друзьям
Полезные ссылки
Не забывайте сначала прочитать том, как найти математическое ожидание. А тут можно вычислить также СКО: Калькулятор математического ожидания, дисперсии и среднего квадратического отклонения.
Что еще может пригодиться? Например, для изучения основ теории вероятностей — онлайн учебник по ТВ. Для закрепления материала — еще примеры решений задач по теории вероятностей.
А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике или заказать в МатБюро:
Дисперсия и ее свойства.
Среднее квадратическое отклонение
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Краткая теория
Дисперсия и формула для ее вычисления
На практике часто требуется оценить рассеяние возможных значений случайной величины вокруг ее среднего значения. Например, в артиллерии важно знать, насколько кучно лягут снаряды вблизи цели, которая должна быть поражена.
На первый взгляд может показаться, что для оценки рассеяния проще всего вычислить все возможные значения отклонения случайной величины и затем найти их среднее значение. Однако такой путь ничего не даст, так как среднее значение отклонения, т. е. M[X-M(X)], для любой случайной величины равно нулю. Это свойство объясняется тем, что одни возможные отклонения положительны, а другие — отрицательны; в результате их взаимного погашения среднее значение отклонения равно нулю. Эти соображения говорят о целесообразности заменить возможные отклонения их абсолютными значениями или их квадратами. Так и поступают на деле. Правда, в случае, когда возможные отклонения заменяют их абсолютными значениями, приходится оперировать с абсолютными величинами, что приводит иногда к серьезным затруднениям. Поэтому чаще всего идут по другому пути, то есть вычисляют среднее значение квадрата отклонения, которое и называют дисперсией.
Дисперсией называется
математическое ожидание квадрата отклонения случайной величины
от
:
Для того чтобы найти дисперсию, достаточно вычислить сумму произведений возможных значений квадрата отклонения на их вероятности.
Для вычисления дисперсии
на практике удобно пользоваться следующей формулой:
Свойства дисперсии
Свойство 1.
Дисперсия равна разности между
математическим ожиданием квадрата случайной величины
и
квадратом ее математического ожидания.
Свойство 2.
Дисперсия константы
равна нулю:
Свойство 3.
Постоянный множитель
выносится из-под знака дисперсии в квадрате:
Свойство 4.
Дисперсия суммы
случайных величин:
где
–
ковариация случайных величин
и
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Следствия из свойств дисперсии.
В частности, если
и
независимы, то
Прибавление константы
в
случайной величине не меняет ее дисперсии:
Дисперсия разности равна сумме дисперсий:
Среднеквадратическое отклонение
Для оценки рассеяния возможных значений случайной величины вокруг ее среднего значения кроме дисперсии служат и некоторые другие характеристики. К их числу относится среднее квадратическое отклонение.
Стандартное (среднее
квадратичное) отклонение случайной величины
определяется
как корень из дисперсии и обозначается
Легко показать, что дисперсия имеет размерность, равную квадрату размерности случайной величины. Так как среднее квадратическое отклонение равно квадратному корню из дисперсии, то ее размерность совпадает с размерностью X. Поэтому в тех случаях, когда желательно, чтобы оценка рассеяния имела размерность случайной величины, вычисляют среднее квадратическое отклонение, а не дисперсию. Например, если X выражается в линейных метрах, то среднее квадратичное отклонение X будет выражаться также в линейных метрах, a дисперсия X — в квадратных метрах.
Смежные темы решебника:
- Математическое ожидание и его свойства
- Дискретная случайная величина
- Непрерывная случайная величина
Примеры решения задач
Пример 1
В коробке 20 конфет, из которых 4 с
вареньем. Х – число конфет с вареньем среди двух случайно выбранных. Найти
дисперсию случайной величины Х.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Случайная
величина
– число конфет с вареньем, может принимать
значения 0,1,2
Найдем
соответствующие вероятности:
Проверка:
Получаем
следующий закон распределения СВ
:
Математическое
ожидание:
Дисперсию
можно вычислить по формуле:
Искомая
дисперсия:
Пример 2
Даны
законы распределения независимых случайных величин X и Y:
и
Найти
закон распределения суммы (X+Y). Проверить равенство D(X+Y)=D(X)+D(Y).
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Распределение суммы
:
Окончательно получаем:
|
|
2 | 3 | 4 | Итого |
|
|
0.2 | 0.5 | 0.3 | 1 |
Вычислим математические ожидания:
Вычислим
дисперсии:
Проверим
равенство
:
Равенство
выполняется.
Пример 3
Вероятность
изготовления бракованной детали на первом станке составляет 3%, на втором
станке 5%. На первом станке было изготовлено 20 деталей, на втором 40 деталей.
Найти математическое ожидание и дисперсию числа бракованных деталей.
Решение
Математическое
ожидание биномиального распределения:
Дисперсия:
Математическое
ожидание величины
– числа бракованных деталей на 1-м станке:
Дисперсия:
Математическое
ожидание величины
– числа бракованных деталей на 2-м станке:
Дисперсия:
Математическое
ожидание числа бракованных деталей:
Дисперсия
числа бракованных деталей:
Ответ:
;
.
Пример 4
Случайные
величины X,Y распределены по закону
Пуассона. Найдите M{(X+Y)2}, если M(X)=40 и
M(Y)=70, а коэффициент корреляции X и Yравен 0,8.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Поскольку
случайные величины
и
распределены по закону Пуассона и известны их
математические ожидания, соответствующие дисперсии равны:
Пользуясь
свойствами математического ожидания и дисперсии:
Подставляя
числовые значения, получаем:
Ответ:
.
Задачи контрольных и самостоятельных работ
Задача 1
Независимые случайные величины X и Y
заданы следующими законами:
| x | 2.3 | 2.5 | 2.7 | 2.9 |
| p | 0.4 | 0.3 | 0.2 | 0.1 |
Укажите
законы распределения случайной величины X+Y, X-Y и найдите их
математическое ожидание и дисперсию.
Задача 2
Найти
дисперсию, математическое ожидания, среднекваратическое отклонение ДСВ X,
заданной законом распределения.
| x | -5 | 2 | 3 | 4 |
| p | 0,4 | 0,3 | 0,1 | 0,2 |
Написать F(x) и построить ее график.
Задача 3
Случайная
величина X имеет плотность вероятности
Требуется
найти дисперсию Dx.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 4
Вероятность
того, что прибор исправен, равна 0,8. X – число исправных приборов
из двух выбранных. Найти дисперсию случайной величины X.
Задача 5
Случайные
величины X и Y независимы. Найти
дисперсию случайной величины Z=2X+3Y, если известно, что D(X)=4, D(Y)=5.
Задача 6
Найти
дисперсию дискретной случайной величины X – числа отказов элемента
некоторого устройства в десяти независимых опытах, если вероятность отказа
элемента в каждом опыте равна 0,9.
Задача 7
Дискретная
случайная величина X имеет только два возможных значения: x1 и x2, причем x2>x1. Вероятность того, что X
примет значение x1, равна 0,6. Найти закон распределения величины X, если
математическое ожидание и дисперсия известны: M(X)=1,4; D(X)=0,24.
Задача 8
Закон
распределения случайной величины ξ имеет вид:
| ξ | -1 | 2 | 3 | 5 |
| P | 1/4 | 1/2 | 1/8 | 1/8 |
Найти функцию распределения случайной величины ξ,
вычислить ее математическое ожидание, дисперсию и среднее квадратическое
отклонение. Вычислить вероятность P{5⁄2<ξ<5}.
Задача 9
Дискретная
случайная величины X принимает лишь два значения. Большее из значений 3
она принимает с вероятностью 0,4. Кроме того, известна дисперсия случайной
величины D(X)=6. Найти математическое
ожидание случайной величины.
Задача 10
Найти
дисперсию по заданному непрерывному закону распределения случайной величины X,
заданному плотностью вероятности
при
и
в остальных точках.
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Имеются данные о распределении семей сотрудников финансовой корпорации по количеству детей:
| Число детей | Число семей сотрудников по подразделениям | ||
|---|---|---|---|
| первое | второе | третье | |
| 0 | 4 | 7 | 5 |
| 1 | 6 | 10 | 13 |
| 2 | 3 | 3 | 3 |
| 3 | 2 | 1 | — |
Вычислить:
а) внутригрупповые дисперсии;
б) среднюю из внутригрупповых дисперсий;
в) межгрупповую дисперсию;
г) общую дисперсию;
Проверьте правильность произведения расчётов с помощью правила сложения дисперсий.
Решение:
Совокупность семей сотрудников финансовой корпорации разбита на три группы по количеству детей.
а) Групповая дисперсия равна среднему квадрату отклонений отдельных значений признака внутри группы от средней арифметической этой группы. Внутригрупповые дисперсии вычисляются по формуле:
Нахождению внутригрупповой дисперсии предшествует расчёт средней арифметической по каждой группе.
Рассчитаем внутригрупповые дисперсии:
б) Средняя из внутригрупповых дисперсий – это средняя арифметическая взвешенная из дисперсий групповых:
в) Межгрупповая дисперсия равна среднему квадрату отклонений групповых средних от общей средней:
Для её расчета необходимо вычислить общую среднюю:
Определим межгрупповую дисперсию:
Вычислим общую дисперсию обычным способом:
Проверим полученный результат, исчислив общую дисперсию по правилу сложения дисперсий: общая дисперсия равна сумме средней из внутригрупповых дисперсий и межгрупповой дисперсии:
Вычисление дисперсии
Теорема.
Дисперсия
равна разности между математическим
ожиданием квадрата случайной величины
и квадратом ее математического ожидания.
Доказательство.
С учетом того, что математическое
ожидание
и квадрат математического ожидания
– величины постоянные, можно записать:
Применим
эту формулу для рассмотренного
выше примера:
-
0
1
2
0
1
4
0,0625
0,375
0,5625
Свойства дисперсии
-
Дисперсия
постоянной величины равна нулю.
2.
Постоянный множитель можно выносить
за знак дисперсии, возводя его в квадрат.
3.
Дисперсия суммы двух независимых
случайных величин равна сумме дисперсий
этих величин.
4.
Дисперсия разности двух независимых
случайных величин равна сумме дисперсий
этих величин.
Справедливость
этого равенства вытекает из свойства
2.
Теорема.
Дисперсия
числа появления события
в
независимых испытаний, в каждом из
которых вероятность
появления события постоянна, равна
произведению числа испытаний на
вероятности появления и не появления
события в каждом испытании.
Среднее квадратическое отклонение
Определение.
Средним
квадратическим отклонением
случайной
величины Х называется квадратный корень
из дисперсии.
Теорема.
Среднее
квадратичное отклонение суммы конечного
числа взаимно независимых случайных
величин равно квадратному корню из
суммы квадратов средних квадратических
отклонений этих величин.
Пример
18. Завод
выпускает 96% изделий первого сорта и 4%
изделий второго сорта. Наугад выбирают
1000 изделий. Пусть
– число изделий первого сорта в данной
выборке. Найти закон распределения,
математическое ожидание и дисперсию
случайной величины.
Выбор
каждого из 1000 изделий можно считать
независимым испытанием, в котором
вероятность появления изделия первого
сорта одинакова и равна р
= 0,96.
Таким
образом, закон распределения может
считаться биноминальным.
Пример
19. Найти
дисперсию дискретной случайной величины
– числа появлений события
в двух независимых испытаниях, если
вероятности появления этого события в
каждом испытании равны и известно, что.
Так
как случайная величина
распределена по биноминальному закону,
то
Функция распределения
Во
всех рассмотренных выше случаях случайная
величина определялась путем задания
значений самой величины и вероятностей
этих значений.
Однако,
такой метод применим далеко не всегда.
Например, в случае непрерывной случайной
величины, ее значения могут заполнять
некоторый произвольный интервал.
Очевидно, что в этом случае задать все
значения случайной величины просто
нереально.
Даже
в случае, когда это сделать можно,
зачастую задача решается чрезвычайно
сложно. Рассмотренный только что пример
даже при относительно простом условии
(приборов только четыре) приводит к
достаточно неудобным вычислениям, а
если в задаче будет несколько сотен
приборов?
Поэтому
встает задача по возможности отказаться
от индивидуального подхода к каждой
задаче и найти по возможности наиболее
общий способ задания любых типов
случайных величин.
Пусть
х
– действительное число. Вероятность
события, состоящего в том, что
примет значение, меньшеех,
то есть
,
обозначим через.
Определение.
Функцией
распределения
называют функцию
,
определяющую вероятность того, что
случайная величинав результате испытания примет значение,
меньшеех.
Функцию
распределения также называют интегральной
функцией.
Функция
распределения существует как для
непрерывных, так и для дискретных
случайных величин. Она полностью
характеризует случайную величину и
является одной из форм закона распределения.
Для
дискретной случайной величины функция
распределения имеет вид:
Знак
неравенства под знаком суммы показывает,
что суммирование распространяется на
те возможные значения случайной величины,
которые меньше аргумента х.
Функция
распределения дискретной случайной
величины
разрывна и возрастает скачками при
переходе через каждое значениехi.
Пример
20. Задана
интегральная функция распределения:
П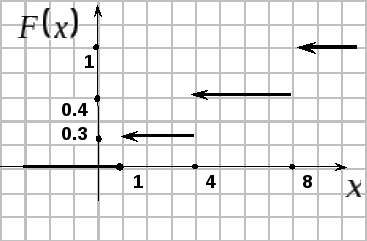
ее график.
|
|
1 |
4 |
8 |
|
|
0,3 |
0,1 |
0,6 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Загрузить PDF
Загрузить PDF
Дисперсия случайной величины является мерой разброса значений этой величины. Малая дисперсия означает, что значения сгруппированы близко друг к другу. Большая дисперсия свидетельствует о сильном разбросе значений. Понятие дисперсии случайной величины применяется в статистике. Например, если сравнить дисперсию значений двух величин (таких как результаты наблюдений за пациентами мужского и женского пола), можно проверить значимость некоторой переменной.[1]
Также дисперсия используется при построении статистических моделей, так как малая дисперсия может быть признаком того, что вы чрезмерно подгоняете значения.[2]
-
1
Запишите значения выборки. В большинстве случаев статистикам доступны только выборки определенных генеральных совокупностей. Например, как правило, статистики не анализируют расходы на содержание совокупности всех автомобилей в России – они анализируют случайную выборку из нескольких тысяч автомобилей. Такая выборка поможет определить средние расходы на автомобиль, но, скорее всего, полученное значение будет далеко от реального.
- Например, проанализируем количество булочек, проданных в кафе за 6 дней, взятых в случайном порядке. Выборка имеет следующий вид: 17, 15, 23, 7, 9, 13. Это выборка, а не совокупность, потому что у нас нет данных о проданных булочках за каждый день работы кафе.
- Если вам дана совокупность, а не выборка значений, перейдите к следующему разделу.
-
2
Запишите формулу для вычисления дисперсии выборки. Дисперсия является мерой разброса значений некоторой величины. Чем ближе значение дисперсии к нулю, тем ближе значения сгруппированы друг к другу. Работая с выборкой значений, используйте следующую формулу для вычисления дисперсии:[3]
-
3
Вычислите среднее значение выборки. Оно обозначается как x̅.[4]
Среднее значение выборки вычисляется как обычное среднее арифметическое: сложите все значения в выборке, а затем полученный результат разделите на количество значений в выборке.- В нашем примере сложите значения в выборке: 15 + 17 + 23 + 7 + 9 + 13 = 84
Теперь результат разделите на количество значений в выборке (в нашем примере их 6): 84 ÷ 6 = 14.
Выборочное среднее x̅ = 14. - Выборочное среднее – это центральное значение, вокруг которого распределены значения в выборке. Если значения в выборке группируются вокруг выборочного среднего, то дисперсия мала; в противном случае дисперсия велика.
- В нашем примере сложите значения в выборке: 15 + 17 + 23 + 7 + 9 + 13 = 84
-
4
Вычтите выборочное среднее из каждого значения в выборке. Теперь вычислите разность
— x̅, где
– каждое значение в выборке. Каждый полученный результат свидетельствует о мере отклонения конкретного значения от выборочного среднего, то есть как далеко это значение находится от среднего значения выборки.[5]
-
5
Возведите в квадрат каждый полученный результат. Как отмечалось выше, сумма разностей
— x̅ должна быть равна нулю. Это означает, что средняя дисперсия всегда равна нулю, что не дает никакого представления о разбросе значений некоторой величины. Для решения этой проблемы возведите в квадрат каждую разность
— x̅. Это приведет к тому, что вы получите только положительные числа, которые при сложении никогда не дадут 0.[6]
-
6
-
7
Полученный результат разделите на n — 1, где n – количество значений в выборке. Некоторое время назад для вычисления дисперсии выборки статистики делили результат просто на n; в этом случае вы получите среднее значение квадрата дисперсии, которое идеально подходит для описания дисперсии данной выборки. Но помните, что любая выборка – это лишь небольшая часть генеральной совокупности значений. Если взять другую выборку и выполнить такие же вычисления, вы получите другой результат. Как выяснилось, деление на n — 1 (а не просто на n) дает более точную оценку дисперсии генеральной совокупности, в чем вы и заинтересованы. Деление на n – 1 стало общепринятым, поэтому оно включено в формулу для вычисления дисперсии выборки.[7]
- В нашем примере выборка включает 6 значений, то есть n = 6.
Дисперсия выборки =33,2
- В нашем примере выборка включает 6 значений, то есть n = 6.
-
8
Отличие дисперсии от стандартного отклонения. Заметьте, что в формуле присутствует показатель степени, поэтому дисперсия измеряется в квадратных единицах измерения анализируемой величины. Иногда такой величиной довольно сложно оперировать; в таких случаях пользуются стандартным отклонением, которое равно квадратному корню из дисперсии. Именно поэтому дисперсия выборки обозначается как
, а стандартное отклонение выборки – как
.
- В нашем примере стандартное отклонение выборки: s = √33,2 = 5,76.
Реклама
-
1
Проанализируйте некоторую совокупность значений. Совокупность включает в себя все значения рассматриваемой величины. Например, если вы изучаете возраст жителей Ленинградской области, то совокупность включает возраст всех жителей этой области. В случае работы с совокупностью рекомендуется создать таблицу и внести в нее значения совокупности. Рассмотрим следующий пример:
-
2
Запишите формулу для вычисления дисперсии генеральной совокупности. Так как в совокупность входят все значения некоторой величины, то приведенная ниже формула позволяет получить точное значение дисперсии совокупности. Для того чтобы отличить дисперсию совокупности от дисперсии выборки (значение которой является лишь оценочным), статистики используют различные переменные: [8]
-
3
Вычислите среднее значение совокупности. При работе с генеральной совокупностью ее среднее значение обозначается как μ (мю). Среднее значение совокупности вычисляется как обычное среднее арифметическое: сложите все значения в генеральной совокупности, а затем полученный результат разделите на количество значений в генеральной совокупности.
- Имейте в виду, что средние величины не всегда вычисляются как среднее арифметическое.
- В нашем примере среднее значение совокупности: μ =
= 10,5
-
4
Вычтите среднее значение совокупности из каждого значения в генеральной совокупности. Чем ближе значение разности к нулю, тем ближе конкретное значение к среднему значению совокупности. Найдите разность между каждым значением в совокупности и ее средним значением, и вы получите первое представление о распределении значений.
- В нашем примере:
— μ = 5 — 10,5 = -5,5
— μ = 5 — 10,5 = -5,5
— μ = 8 — 10,5 = -2,5
— μ = 12 — 10,5 = 1,5
— μ = 15 — 10,5 = 4,5
— μ = 18 — 10,5 = 7,5
- В нашем примере:
-
5
Возведите в квадрат каждый полученный результат. Значения разностей будут как положительными, так и отрицательными; если нанести эти значения на числовую прямую, то они будут лежать справа и слева от среднего значения совокупности. Это не годится для вычисления дисперсии, так как положительные и отрицательные числа компенсируют друг друга. Поэтому возведите в квадрат каждую разность, чтобы получить исключительно положительные числа.
- В нашем примере:
(— μ)
для каждого значения совокупности (от i = 1 до i = 6):
(-5,5)= 30,25
(-5,5)= 30,25
(-2,5)= 6,25
(1,5)= 2,25
(4,5)= 20,25
(7,5)= 56,25
- В нашем примере:
-
6
Найдите среднее значение полученных результатов. Вы нашли, как далеко каждое значение совокупности расположено от ее среднего значения. Найдите среднее значение суммы квадратов разностей, поделив ее на количество значений в генеральной совокупности.
- В нашем примере:
Дисперсия совокупности =24,25
- В нашем примере:
-
7
Соотнесите это решение с формулой. Если вы не поняли, как приведенное выше решение соотносится с формулой, ниже представлено объяснение решения:
Реклама
Советы
- Дисперсию довольно сложно интерпретировать, поэтому в большинстве случаев она вычисляется как промежуточная величина, которая необходима для нахождения стандартного отклонения.
- При вычислении дисперсии выборки деление на n-1, а не просто на n, называется коррекцией Бесселя. Дисперсия выборки представляет собой только оценочное значение дисперсии генеральной совокупности, при этом выборочное среднее смещено, чтобы соответствовать этому оценочному значению. Коррекция Бесселя устраняет такое смещение.[9]
Это связано с тем, что при анализе n – 1 значения использование n-го значения уже ограничено, так как только определенные значения приводят к выборочному среднему (x̅), которое используется в формуле для вычисления дисперсии.[10]
Реклама
Об этой статье
Эту страницу просматривали 122 522 раза.