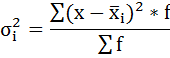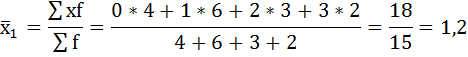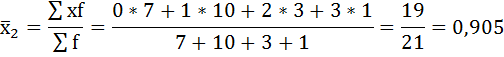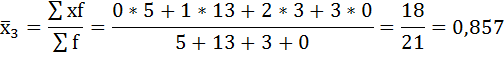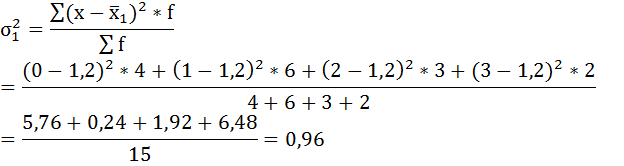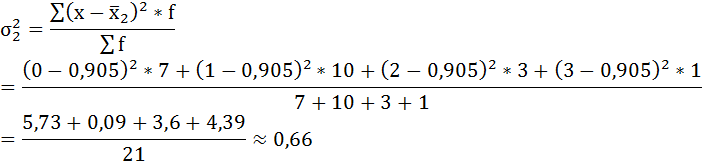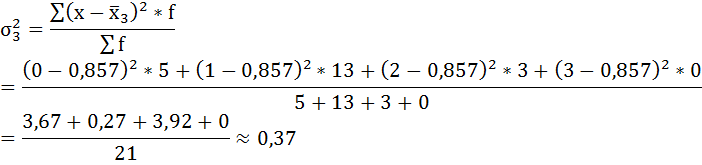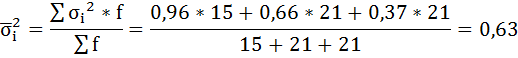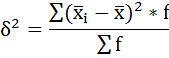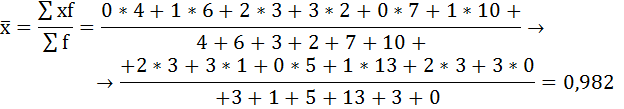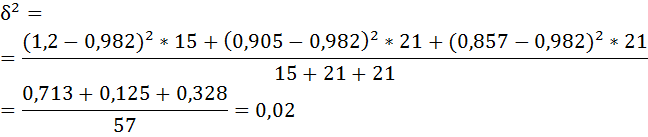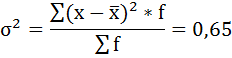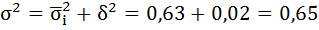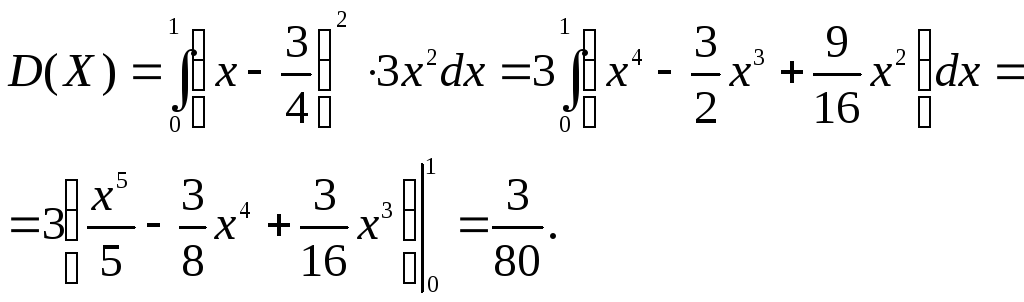Имеются данные о распределении семей сотрудников финансовой корпорации по количеству детей:
| Число детей | Число семей сотрудников по подразделениям | ||
|---|---|---|---|
| первое | второе | третье | |
| 0 | 4 | 7 | 5 |
| 1 | 6 | 10 | 13 |
| 2 | 3 | 3 | 3 |
| 3 | 2 | 1 | — |
Вычислить:
а) внутригрупповые дисперсии;
б) среднюю из внутригрупповых дисперсий;
в) межгрупповую дисперсию;
г) общую дисперсию;
Проверьте правильность произведения расчётов с помощью правила сложения дисперсий.
Решение:
Совокупность семей сотрудников финансовой корпорации разбита на три группы по количеству детей.
а) Групповая дисперсия равна среднему квадрату отклонений отдельных значений признака внутри группы от средней арифметической этой группы. Внутригрупповые дисперсии вычисляются по формуле:
Нахождению внутригрупповой дисперсии предшествует расчёт средней арифметической по каждой группе.
Рассчитаем внутригрупповые дисперсии:
б) Средняя из внутригрупповых дисперсий – это средняя арифметическая взвешенная из дисперсий групповых:
в) Межгрупповая дисперсия равна среднему квадрату отклонений групповых средних от общей средней:
Для её расчета необходимо вычислить общую среднюю:
Определим межгрупповую дисперсию:
Вычислим общую дисперсию обычным способом:
Проверим полученный результат, исчислив общую дисперсию по правилу сложения дисперсий: общая дисперсия равна сумме средней из внутригрупповых дисперсий и межгрупповой дисперсии:
Как найти дисперсию?
Спасибо за ваши закладки и рекомендации
Дисперсия — это мера разброса значений случайной величины $X$ относительно ее математического ожидания $M(X)$ (см. как найти математическое ожидание случайной величины). Дисперсия показывает, насколько в среднем значения сосредоточены, сгруппированы около $M(X)$: если дисперсия маленькая — значения сравнительно близки друг к другу, если большая — далеки друг от друга (см. примеры нахождения дисперсии ниже).
Если случайная величина описывает физические объекты с некоторой размерностью (метры, секунды, килограммы и т.п.), то дисперсия будет выражаться в квадратных единицах (метры в квадрате, секунды в квадрате и т.п.). Ясно, что это не совсем удобно для анализа, поэтому часто вычисляют также корень из дисперсии — среднеквадратическое отклонение $sigma(X)=sqrt{D(X)}$, которое имеет ту же размерность, что и исходная величина и также описывает разброс.
Еще одно формальное определение дисперсии звучит так: «Дисперсия — это второй центральный момент случайной величины» (напомним, что первый начальный момент — это как раз математическое ожидание).
Нужна помощь? Решаем теорию вероятностей на отлично
Формула дисперсии случайной величины
Дисперсия случайной величины Х вычисляется по следующей формуле:
$$
D(X)=M(X-M(X))^2,
$$
которую также часто записывают в более удобном для расчетов виде:
$$
D(X)=M(X^2)-(M(X))^2.
$$
Эта универсальная формула для дисперсии может быть расписана более подробно для двух случаев.
Если мы имеем дело с дискретной случайной величиной (которая задана перечнем значений $x_i$ и соответствующих вероятностей $p_i$), то формула принимает вид:
$$
D(X)=sum_{i=1}^{n}{x_i^2 cdot p_i}-left(sum_{i=1}^{n}{x_i cdot p_i} right)^2.
$$
Если же речь идет о непрерывной случайной величине (заданной плотностью вероятностей $f(x)$ в общем случае), формула дисперсии Х выглядит следующим образом:
$$
D(X)=int_{-infty}^{+infty} f(x) cdot x^2 dx — left( int_{-infty}^{+infty} f(x) cdot x dx right)^2.
$$
Пример нахождения дисперсии
Рассмотрим простые примеры, показывающие как найти дисперсию по формулам, введеным выше.
Пример 1. Вычислить и сравнить дисперсию двух законов распределения:
$$
x_i quad 1 quad 2 \
p_i quad 0.5 quad 0.5
$$
и
$$
y_i quad -10 quad 10 \
p_i quad 0.5 quad 0.5
$$
Для убедительности и наглядности расчетов мы взяли простые распределения с двумя значениями и одинаковыми вероятностями. Но в первом случае значения случайной величины расположены рядом (1 и 2), а во втором — дальше друг от друга (-10 и 10). А теперь посмотрим, насколько различаются дисперсии:
$$
D(X)=sum_{i=1}^{n}{x_i^2 cdot p_i}-left(sum_{i=1}^{n}{x_i cdot p_i} right)^2 =\
= 1^2cdot 0.5 + 2^2 cdot 0.5 — (1cdot 0.5 + 2cdot 0.5)^2=2.5-1.5^2=0.25.
$$
$$
D(Y)=sum_{i=1}^{n}{y_i^2 cdot p_i}-left(sum_{i=1}^{n}{y_i cdot p_i} right)^2 =\
= (-10)^2cdot 0.5 + 10^2 cdot 0.5 — (-10cdot 0.5 + 10cdot 0.5)^2=100-0^2=100.
$$
Итак, значения случайных величин различались на 1 и 20 единиц, тогда как дисперсия показывает меру разброса в 0.25 и 100. Если перейти к среднеквадратическому отклонению, получим $sigma(X)=0.5$, $sigma(Y)=10$, то есть вполне ожидаемые величины: в первом случае значения отстоят в обе стороны на 0.5 от среднего 1.5, а во втором — на 10 единиц от среднего 0.
Ясно, что для более сложных распределений, где число значений больше и вероятности не одинаковы, картина будет более сложной, прямой зависимости от значений уже не будет (но будет как раз оценка разброса).
Пример 2. Найти дисперсию случайной величины Х, заданной дискретным рядом распределения:
$$
x_i quad -1 quad 2 quad 5 quad 10 quad 20 \
p_i quad 0.1 quad 0.2 quad 0.3 quad 0.3 quad 0.1
$$
Снова используем формулу для дисперсии дискретной случайной величины:
$$
D(X)=M(X^2)-(M(X))^2.
$$
В случае, когда значений много, удобно разбить вычисления по шагам. Сначала найдем математическое ожидание:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i} =-1cdot 0.1 + 2 cdot 0.2 +5cdot 0.3 +10cdot 0.3+20cdot 0.1=6.8.
$$
Потом математическое ожидание квадрата случайной величины:
$$
M(X^2)=sum_{i=1}^{n}{x_i^2 cdot p_i}
= (-1)^2cdot 0.1 + 2^2 cdot 0.2 +5^2cdot 0.3 +10^2cdot 0.3+20^2cdot 0.1=78.4.
$$
А потом подставим все в формулу для дисперсии:
$$
D(X)=M(X^2)-(M(X))^2=78.4-6.8^2=32.16.
$$
Дисперсия равна 32.16 квадратных единиц.
Пример 3. Найти дисперсию по заданному непрерывному закону распределения случайной величины Х, заданному плотностью $f(x)=x/18$ при $x in(0,6)$ и $f(x)=0$ в остальных точках.
Используем для расчета формулу дисперсии непрерывной случайной величины:
$$
D(X)=int_{-infty}^{+infty} f(x) cdot x^2 dx — left( int_{-infty}^{+infty} f(x) cdot x dx right)^2.
$$
Вычислим сначала математическое ожидание:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx = int_{0}^{6} frac{x}{18} cdot x dx = int_{0}^{6} frac{x^2}{18} dx =
left.frac{x^3}{54} right|_0^6=frac{6^3}{54} = 4.
$$
Теперь вычислим
$$
M(X^2)=int_{-infty}^{+infty} f(x) cdot x^2 dx = int_{0}^{6} frac{x}{18} cdot x^2 dx = int_{0}^{6} frac{x^3}{18} dx = left.frac{x^4}{72} right|_0^6=frac{6^4}{72} = 18.
$$
Подставляем:
$$
D(X)=M(X^2)-(M(X))^2=18-4^2=2.
$$
Дисперсия равна 2.
Другие задачи с решениями по ТВ
Подробно решим ваши задачи на вычисление дисперсии
Вычисление дисперсии онлайн
Как найти дисперсию онлайн для дискретной случайной величины? Используйте калькулятор ниже.
- Введите число значений случайной величины К.
- Появится форма ввода для значений $x_i$ и соответствующих вероятностей $p_i$ (десятичные дроби вводятся с разделителем точкой, например: -10.3 или 0.5). Введите нужные значения (проверьте, что сумма вероятностей равна 1, то есть закон распределения корректный).
- Нажмите на кнопку «Вычислить».
- Калькулятор покажет вычисленное математическое ожидание $M(X)$ и затем искомое значение дисперсии $D(X)$.
Видео. Полезные ссылки
Видеоролики: что такое дисперсия и как найти дисперсию
Если вам нужно более подробное объяснение того, что такое дисперсия, как она вычисляется и какими свойствами обладает, рекомендую два видео (для дискретной и непрерывной случайной величины соответственно).
Спасибо за ваши закладки и рекомендации
Полезные ссылки
Не забывайте сначала прочитать том, как найти математическое ожидание. А тут можно вычислить также СКО: Калькулятор математического ожидания, дисперсии и среднего квадратического отклонения.
Что еще может пригодиться? Например, для изучения основ теории вероятностей — онлайн учебник по ТВ. Для закрепления материала — еще примеры решений задач по теории вероятностей.
А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике или заказать в МатБюро:
Дисперсия и ее свойства.
Среднее квадратическое отклонение
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Краткая теория
Дисперсия и формула для ее вычисления
На практике часто требуется оценить рассеяние возможных значений случайной величины вокруг ее среднего значения. Например, в артиллерии важно знать, насколько кучно лягут снаряды вблизи цели, которая должна быть поражена.
На первый взгляд может показаться, что для оценки рассеяния проще всего вычислить все возможные значения отклонения случайной величины и затем найти их среднее значение. Однако такой путь ничего не даст, так как среднее значение отклонения, т. е. M[X-M(X)], для любой случайной величины равно нулю. Это свойство объясняется тем, что одни возможные отклонения положительны, а другие — отрицательны; в результате их взаимного погашения среднее значение отклонения равно нулю. Эти соображения говорят о целесообразности заменить возможные отклонения их абсолютными значениями или их квадратами. Так и поступают на деле. Правда, в случае, когда возможные отклонения заменяют их абсолютными значениями, приходится оперировать с абсолютными величинами, что приводит иногда к серьезным затруднениям. Поэтому чаще всего идут по другому пути, то есть вычисляют среднее значение квадрата отклонения, которое и называют дисперсией.
Дисперсией называется
математическое ожидание квадрата отклонения случайной величины
от
:
Для того чтобы найти дисперсию, достаточно вычислить сумму произведений возможных значений квадрата отклонения на их вероятности.
Для вычисления дисперсии
на практике удобно пользоваться следующей формулой:
Свойства дисперсии
Свойство 1.
Дисперсия равна разности между
математическим ожиданием квадрата случайной величины
и
квадратом ее математического ожидания.
Свойство 2.
Дисперсия константы
равна нулю:
Свойство 3.
Постоянный множитель
выносится из-под знака дисперсии в квадрате:
Свойство 4.
Дисперсия суммы
случайных величин:
где
–
ковариация случайных величин
и
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Следствия из свойств дисперсии.
В частности, если
и
независимы, то
Прибавление константы
в
случайной величине не меняет ее дисперсии:
Дисперсия разности равна сумме дисперсий:
Среднеквадратическое отклонение
Для оценки рассеяния возможных значений случайной величины вокруг ее среднего значения кроме дисперсии служат и некоторые другие характеристики. К их числу относится среднее квадратическое отклонение.
Стандартное (среднее
квадратичное) отклонение случайной величины
определяется
как корень из дисперсии и обозначается
Легко показать, что дисперсия имеет размерность, равную квадрату размерности случайной величины. Так как среднее квадратическое отклонение равно квадратному корню из дисперсии, то ее размерность совпадает с размерностью X. Поэтому в тех случаях, когда желательно, чтобы оценка рассеяния имела размерность случайной величины, вычисляют среднее квадратическое отклонение, а не дисперсию. Например, если X выражается в линейных метрах, то среднее квадратичное отклонение X будет выражаться также в линейных метрах, a дисперсия X — в квадратных метрах.
Смежные темы решебника:
- Математическое ожидание и его свойства
- Дискретная случайная величина
- Непрерывная случайная величина
Примеры решения задач
Пример 1
В коробке 20 конфет, из которых 4 с
вареньем. Х – число конфет с вареньем среди двух случайно выбранных. Найти
дисперсию случайной величины Х.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Случайная
величина
– число конфет с вареньем, может принимать
значения 0,1,2
Найдем
соответствующие вероятности:
Проверка:
Получаем
следующий закон распределения СВ
:
Математическое
ожидание:
Дисперсию
можно вычислить по формуле:
Искомая
дисперсия:
Пример 2
Даны
законы распределения независимых случайных величин X и Y:
и
Найти
закон распределения суммы (X+Y). Проверить равенство D(X+Y)=D(X)+D(Y).
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Распределение суммы
:
Окончательно получаем:
|
|
2 | 3 | 4 | Итого |
|
|
0.2 | 0.5 | 0.3 | 1 |
Вычислим математические ожидания:
Вычислим
дисперсии:
Проверим
равенство
:
Равенство
выполняется.
Пример 3
Вероятность
изготовления бракованной детали на первом станке составляет 3%, на втором
станке 5%. На первом станке было изготовлено 20 деталей, на втором 40 деталей.
Найти математическое ожидание и дисперсию числа бракованных деталей.
Решение
Математическое
ожидание биномиального распределения:
Дисперсия:
Математическое
ожидание величины
– числа бракованных деталей на 1-м станке:
Дисперсия:
Математическое
ожидание величины
– числа бракованных деталей на 2-м станке:
Дисперсия:
Математическое
ожидание числа бракованных деталей:
Дисперсия
числа бракованных деталей:
Ответ:
;
.
Пример 4
Случайные
величины X,Y распределены по закону
Пуассона. Найдите M{(X+Y)2}, если M(X)=40 и
M(Y)=70, а коэффициент корреляции X и Yравен 0,8.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Поскольку
случайные величины
и
распределены по закону Пуассона и известны их
математические ожидания, соответствующие дисперсии равны:
Пользуясь
свойствами математического ожидания и дисперсии:
Подставляя
числовые значения, получаем:
Ответ:
.
Задачи контрольных и самостоятельных работ
Задача 1
Независимые случайные величины X и Y
заданы следующими законами:
| x | 2.3 | 2.5 | 2.7 | 2.9 |
| p | 0.4 | 0.3 | 0.2 | 0.1 |
Укажите
законы распределения случайной величины X+Y, X-Y и найдите их
математическое ожидание и дисперсию.
Задача 2
Найти
дисперсию, математическое ожидания, среднекваратическое отклонение ДСВ X,
заданной законом распределения.
| x | -5 | 2 | 3 | 4 |
| p | 0,4 | 0,3 | 0,1 | 0,2 |
Написать F(x) и построить ее график.
Задача 3
Случайная
величина X имеет плотность вероятности
Требуется
найти дисперсию Dx.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 4
Вероятность
того, что прибор исправен, равна 0,8. X – число исправных приборов
из двух выбранных. Найти дисперсию случайной величины X.
Задача 5
Случайные
величины X и Y независимы. Найти
дисперсию случайной величины Z=2X+3Y, если известно, что D(X)=4, D(Y)=5.
Задача 6
Найти
дисперсию дискретной случайной величины X – числа отказов элемента
некоторого устройства в десяти независимых опытах, если вероятность отказа
элемента в каждом опыте равна 0,9.
Задача 7
Дискретная
случайная величина X имеет только два возможных значения: x1 и x2, причем x2>x1. Вероятность того, что X
примет значение x1, равна 0,6. Найти закон распределения величины X, если
математическое ожидание и дисперсия известны: M(X)=1,4; D(X)=0,24.
Задача 8
Закон
распределения случайной величины ξ имеет вид:
| ξ | -1 | 2 | 3 | 5 |
| P | 1/4 | 1/2 | 1/8 | 1/8 |
Найти функцию распределения случайной величины ξ,
вычислить ее математическое ожидание, дисперсию и среднее квадратическое
отклонение. Вычислить вероятность P{5⁄2<ξ<5}.
Задача 9
Дискретная
случайная величины X принимает лишь два значения. Большее из значений 3
она принимает с вероятностью 0,4. Кроме того, известна дисперсия случайной
величины D(X)=6. Найти математическое
ожидание случайной величины.
Задача 10
Найти
дисперсию по заданному непрерывному закону распределения случайной величины X,
заданному плотностью вероятности
при
и
в остальных точках.
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Примеры решения задач
Задача
1. Вероятность
всхожести семян пшеницы равна 0,9. Какова
вероятность того, что из четырех посеянных
семян взойдут не менее трех?
Решение. Пусть
событие А
– из 4 семян взойдут не менее 3 семян;
событие В
– из 4 семян взойдут 3 семени; событие С
– из 4 семян взойдут 4 семени. По теореме
сложения вероятностей
.
Вероятности
и
определим по формуле Бернулли, применяемой
в следующем случае. Пусть проводится
серия п
независимых испытаний, при каждом из
которых вероятность наступления события
постоянна и равна р,
а вероятность ненаступления этого
события равна .
Тогда вероятность того, что событие А
в п
испытаниях появится ровно
раз, вычисляется по формуле Бернулли
,
где
– число сочетаний из п
элементов по .
Тогда
Искомая вероятность
.
Задача
2. Вероятность
всхожести семян пшеницы равна 0,9. Найти
вероятность того, что из 400 посеянных
семян взойдут 350 семян.
Решение. Вычислить
искомую вероятность
по формуле Бернулли затруднительно
из-за громоздкости вычислений. Поэтому
применим приближенную формулу, выражающую
локальную теорему Лапласа:
,
где
и .
Из условия задачи
.
Тогда
.
Из таблицы 1
приложений находим .
Искомая вероятность равна
.
Задача
3. Среди семян
пшеницы 0,02% сорняков. Какова вероятность
того, что при случайном отборе 10000 семян
будет обнаружено 6 семян сорняков?
Решение. Применение
локальной теоремы Лапласа из-за малой
вероятности
приводит к значительному отклонению
вероятности от точного значения .
Поэтому при малых значениях р
для вычисления
применяют асимптотическую формулу
Пуассона
,
где .
Эта формула
используется при ,
причем чем меньше р
и больше п,
тем результат точнее.
По условию задачи
;
.
Тогда
и
.
Задача
4. Процент
всхожести семян пшеницы равен 90%. Найти
вероятность того, что из 500 посеянных
семян взойдут от 400 до 440 семян.
Решение. Если
вероятность наступления события А
в каждом из п
испытаний постоянна и равна р,
то вероятность
того, что событие А
в таких испытаниях наступит не менее
раз и не более
раз определяется по интегральной теореме
Лапласа следующей формулой:

где
,
.
Функция
называется функцией Лапласа. В приложениях
(табл. 2) даны значения этой функции для
.
При
функция .
При отрицательных значениях х
в силу нечетности функции Лапласа .
Используя функцию Лапласа, имеем:
.
По условию задачи
.
По приведенным выше формулам находим
и :
.
Тогда
Задача 5. Задан
закон распределения дискретной случайной
величины Х:
|
Х |
40 |
42 |
41 |
44 |
||
|
р |
0,1 |
0,3 |
0,2 |
0,4 |
-
Найти: 1) математическое ожидание ; 2) дисперсию ; 3) среднее квадратическое отклонение .
Решение.
1) Если закон распределения дискретной
случайной величины задан таблицей
|
Х |
|
х2 |
х3 |
х4 |
||
|
р |
р1 |
р2 |
р3 |
р4, |
-
Где в первой строке даны значения случайной величины х, а во второй – вероятности этих значений, то математическое ожидание вычисляется по формуле
.
Тогда .
2) Дисперсия
дискретной
случайной величины Х
называется математическое ожидание
квадрата отклонения случайной величины
от ее математического ожидания, т.е.
.
Эта величина
характеризует среднее ожидаемое значение
квадрата отклонения Х
от .
Из последней формулы имеем
Дисперсию
можно найти другим способом, исходя из
следующего ее свойства: дисперсия
равна разности между математическим
ожиданием квадрата случайной величины
Х
и квадратом ее математического ожидания
,
то есть
.
Для вычисления
составим следующий закон распределения
величины :
|
Х2 |
402 |
422 |
412 |
442 |
||
|
р |
0,1 |
0,3 |
0,2 |
0,4 |
Тогда
3) Для характеристики
рассеяния возможных значений случайной
величины вокруг ее среднего значения
вводится среднее квадратическое
отклонение
случайной величины Х,
равное квадратному корню из дисперсии
,
то есть
.
Из этой формулы
имеем:
Задача
6. Непрерывная
случайная величина Х
задана интегральной функцией распределения
Найти: 1)
дифференциальную функцию распределения
;
2) математическое ожидание ;
3) дисперсию .
Решение. 1)
Дифференциальной функцией распределения
непрерывной случайной величины Х
называется производная от интегральной
функции распределения ,
то есть
.
Искомая
дифференциальная функция имеет следующий
вид:
2) Если непрерывная
случайная величина Х
задана функцией ,
то ее математическое ожидание определяется
формулой
Так как функция
при
и при
равна нулю, то из последней формулы
имеем
.
3) Дисперсию
определим по формуле
Тогда
Задача
7. Длина
детали представляет собой нормально
распределенную случайную величину с
математическим ожиданием 40 мм и средним
квадратическим отклонением 3 мм. Найти:
1) вероятность того, что длина произвольно
взятой детали будет больше 34 мм и меньше
43 мм; 2) вероятность того, что длина детали
отклонится от ее математического
ожидания не более чем на 1,5 мм.
Решение. 1) Пусть
Х
– длина детали. Если случайная величина
Х
задана дифференциальной функцией ,
то вероятность того, что Х
примет значения, принадлежащие отрезку
,
определяется по формуле
.
Вероятность
выполнения строгих неравенств
определяется той же формулой. Если
случайная величина Х
распределена по нормальному закону, то
, (1)
где
– функция Лапласа, .
В задаче .
Тогда
2) По условию задачи
,
где .
Подставив в (1) ,
имеем
то есть
. (2)
Из формулы (2) имеем:
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
- Примеры с решением
Разность 
Дисперсией, или рассеянием, случайной величины X называется математическое ожидание квадрата ее отклонения:
Из определения и свойств математического ожидания следует, чтс дисперсия любой случайной величины неотрицательна, т.е.
Для вычисления дисперсии применяется формула
По этой ссылке вы найдёте полный курс лекций по теории вероятности:
Дисперсия случайной величины обладает следующими свойствами:
1. Дисперсия постоянной величины равна нулю:
2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
4. Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий:
5. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий:
Возможно вам будут полезны данные страницы:
Замечание.
Свойство 3 распространяется на п независимых случайных величин:
Дисперсия дискретной случайной величины с законом распределения
определяется формулой
или формулой
где
— другое обозначение для математического ожидания. Этим обозначением будем пользоваться и в дальнейшем, в зависимости от обстоятельств.
Если дискретная случайная величина принимает бесконечную по-следовательность-значений с законом распределения
то ее дисперсия определяется формулой
при условии, что этот ряд сходится.
Дисперсия непрерывной случайной величины X, все значения которой принадлежат отрезку 

где р(х) — плотность распределения вероятностей этой величины, 
Дисперсию можно вычислять по формуле

Дисперсия непрерывной случайной величины X, все значения которой принадлежат отрезку 

если этот несобственный интеграл сходится.абсолютно.
Средним квадратическим отклонением, или стандартным отклонением, случайной величины X называется корень квадратный из ее дисперсии:
Это определение имеет смысл, поскольку выполнено условие (2.5.3).
Пример с решением
Пример 1.
Доказать формулы (2.5.1) и (2.5.4).
Решение:
Так как математическое ожидание М(Х) — постоянная величина, математическое ожидание постоянной равно этой постоянной, математическое ожидание разности случайных величин равно разности их математических ожиданий, то
равенство (2.5.1) доказано.
Учитывая свойства математического ожидания, получаем

равенство (2.5.4) доказано.
Пример 2.
Доказать равенства (2.5.5) — (2.5.8).
Решение:
Принимая во внимание определение дисперсии и тот факт, что математическое ожидание постоянной равно этой постоянной, получаем
Из определения дисперсии и свойств математического ожидания следует, что
Для доказательства формулы (2.5.8) воспользуемся формулой (2.5.4):
Равенство (2.5.8) следует из формул (2.5.6) и (2.5.7):
Пример 3.
Дискретная случайная величина X имеет закон распределения

Решение:
По формуле (2.4.3) находим
Запишем закон распределения квадрата отклонения этой величины, т.е. величины

В соответствии с формулой (2.5.16) находим среднее квадратическое отклонение
Замечание. Дисперсию можно вычислить и по формуле (2.5.4). Найдем для этого математическое ожидание квадрата случайной величины X, предварительно записав закон распределения случайной величины X2;

В соответствии с формулой (2.5.4) находим
Пример 4.
Закон распределения дискретной случайной величины X задан таблицей

Решение:
Сначала найдем математическое ожидание случайной величины^:
Запишем закон распределения случайной величины

Квадрат случайной величины X, т.е. X2 — это новая случайная величина, которая с теми же вероятностями, что и случайная величина X, принимает значения, равные квадратам ее значений.
Квадраты значений случайной величины X равны: 





По формуле (2.4.3) находим
Следовательно, по формуле (2.5.4) имеем
Пример 5.
Симметричная монета подбрасывается 4 раза. Случайная величина X- «число выпадений герба при этих подбрасываниях». Найти числовые характеристики случайной величины
Решение:
Данная дискретная случайная величина X может принимать пять значений: 
Закон распределения случайной величины X можно задать таблицей Находим математическое ожидание
Закон распределения случайной величины 



Пример 6.
Найти дисперсию дискретной случайной величины X -числа очков, выпадающих при подбрасывании игрального кубика.
Решение:
Запишем сначала закон распределения этой случайной величины в виде таблицы


Дисперсию вычислим по формуле (2.5.4):
Пример 7.
Даны все возможные значения дискретной случайной величины


Решение:
Запишем законы распределения дискретных случайных величин X и X2.



Поскольку 
откуда 
Итак, закон распределения случайной величины X определяется таблицей
Пример 8.
Дискретная случайная величина X может принимать только два значения 




Решение:
Поскольку 



Решая систему уравнений
и учитывая условие 

Пример 9.
Найти числовые характеристики 
Решение:
Сначала находим М(Х) по формуле (2.4.7):

В соответствии с формулой (2.5.13) найдем D(X) :
По формуле (2.5.16) находим
Пример 10.
Найти числовые характеристики 
Решение:
С помощью формулы (2.4.7) находим математическое ожидание:
По формулам (2.5.13) и (2.5.16) соответственно получаем

Пример 11.
Случайная величина X задана функцией распределения
Найти числовые характеристики случайной величины
Решение:
Сначала найдем плотность распределения р(х) с помощью формулы (2.3.5). Так как 

По формуле (2.4.7) вычисляем математическое ожидание:
В соответствии с формулами (2.5.13) и (2.5.16) находим дисперсию и среднее квадратическое отклонение:

Пример 12.
Независимые случайные величины 
при 
Решение:
С учетом формулы (2.4.13) и условия (I) находим

т.е. математическое ожидание среднего арифметического п независимых одинаково распределенных случайных величин равно математическому ожиданию каждой из этих величин.
Учитывая формулы (2.5.6), (2.5.9) и условие (I), получаем
т.е. дисперсия среднего арифметического п независимых одинаково распределенных случайных величин в л раз меньше дисперсии каждой из этих величин.
Учитывая определение и условие (I), находим
Таким образом, среднее квадратическое отклонение среднего арифметического n независимых одинаково распределенных случайных величин в 
Лекции:
- Математическое ожидание: пример решения
- Законы распределения случайных величин
- Моменты случайной величины
- Моменты высших порядков
- Метод моментов
- Непрерывные случайные величины примеры с решением
- Числовые характеристики непрерывной случайной величины
- Функция случайной величины
- Математическая дисперсия случайной величины
- Дисперсия суммы случайных величин