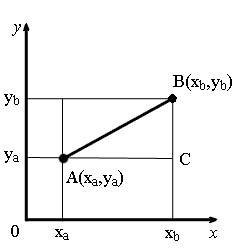Как найти дистанцию между двумя точками - Исправление недочетов и поиск решений вместе с Examum.ru

Вывод формулы для вычисления расстояния между двумя точками на плоскости

Из точек A и B опустим перпендикуляры на оси координат.

Рассмотрим прямоугольный треугольник ∆ABC. Катеты этого треугольника равны:

AC = x_b — x_a;

BC = y_b — y_a.

Воспользовавшись теоремой Пифагора, вычислим длину отрезка AB:

AB = √AC² + BC².

Подставив в это выражение длины отрезков AC и BC, выраженные через координаты точек A и B, получим формулу для вычисления расстояния между точками на плоскости.

Формула для вычисления расстояния между двумя точками в пространстве выводится аналогично.

Источник

Загрузить PDF

Представьте расстояние между двумя точками в виде отрезка прямой линии, соединяющего эти точки. Длину этого отрезка можно найти по формуле: √ $(x2-x1)^{2}+(y2-y1)^{2}$ .

Шаги

1
Определите координаты двух точек, расстояние между которыми вы хотите вычислить. Обозначим их Точка 1 (x1,y1) и Точка 2 (x2,y2). Неважно, как именно вы обозначите точки, главное, не перепутать их координаты при расчетах.^[1]
- x1 − это горизонтальная координата (вдоль оси x) Точки 1, а x2 − горизонтальная координата Точки 2. Соответственно, y1 − вертикальная координата (вдоль оси y) Точки 1, и y2 − вертикальная координата Точки 2.
- Возьмем, например, точки (3,2) и (7,8). Если мы примем, что (3,2) − это (x1,y1), тогда (7,8) − это (x2,y2).
2

Ознакомьтесь с формулой для вычисления расстояния. Эта формула позволяет найти длину прямого отрезка, соединяющего две точки, Точку 1 и Точку 2. Длина этого отрезка равна квадратному корню от суммы квадратов расстояний между точками по горизонтали и вертикали. Проще говоря, это квадратный корень из $(x2-x1)^{2}+(y2-y1)^{2}$ .^[2]
3
Найдите, чему равны расстояния между точками по горизонтали и вертикали. Расстояние по вертикали найдем в виде разности y2 — y1. Соответственно, расстояние по горизонтали составит x2 — x1. Не волнуйтесь, если в результате вычитания вы получите отрицательное значение. Следующим шагом будет возведение найденных расстояний в квадрат, что в любом случае даст положительное целое число.^[3]
- Найдите расстояние вдоль оси y. Для нашего примера с точками (3,2) и (7,8), где координаты (3,2) соответствуют Точке 1, а координаты (7,8) − Точке 2, находим: (y2 — y1) = 8 — 2 = 6. Это значит, что расстояние между нашими точками по оси y равно шести единицам длины.
- Найдите расстояние вдоль оси x. Для нашего примера с точками (3,2) и (7,8) получаем: (x2 — x1) = 7 — 3 = 4. Это значит, что по оси x наши точки разделяет расстояние, равное четырем единицам длины.
4

Возведите оба значения в квадрат. Необходимо по отдельности возвести в квадрат расстояние вдоль оси x, равное (x2 — x1), и расстояние вдоль оси y, составляющее (y2 — y1):
5

Сложите полученные значения. В результате вы найдете квадрат диагонали, то есть расстояния между двумя точками. В нашем примере для точек с координатами (3,2) и (7,8) находим: (7 — 3) в квадрате равно 36, и (8 — 2) в квадрате равно 16. Складывая, получаем 36 + 16 = 52.
6
Извлеките квадратный корень из найденной величины. Это последний шаг. Расстояние между двумя точками равно квадратному корню от суммы квадратов расстояний вдоль оси x и вдоль оси y.^[4]
- Для нашего примера находим: расстояние между точками (3,2) и (7,8) равно корню квадратному из 52, то есть примерно 7,21 единицы длины.
Реклама

Советы

Не страшно, если в результате вычитания y2 — y1 или x2 — x1 у вас получилось отрицательное значение. Поскольку затем разность возводится в квадрат, расстояние все равно будет равно положительному числу.

Об этой статье

Эту страницу просматривали 89 414 раз.

Была ли эта статья полезной?

Источник

The length of the line segment connecting two points is defined as the distance between them. The length of the line segment connecting the specified coordinates can be used to compute the distance between two points in coordinate geometry. Let’s look at the formula for calculating the distance between two points in a two-dimensional or three-dimensional plane.

What is the Distance Between Two Points?

The distance of the line segment connecting any two points is the distance between them. There is only one line that connects two points. As a result, the distance between two points may be computed by determining the length of the line segment that connects the two spots. For example, if A and B are two points and A B = 20 cm, it implies the distance between A and B is 20 cm.

The length of the line segment connecting two points is the distance between them (but this CANNOT be the length of the curve joining them). It is important to note that the distance between two places is always positive.

Distance Between Two Points Formula

The distance formula is used to determine the distance between two points using the provided coordinates. We use the 2D distance formula or the Euclidean distance formula to calculate the distance between any two points in the 2-D plane.

Formula for Distance Between Two Points

The formula for the distance, d, between two points whose coordinates are (x₁, y₁) and (x_2,y₂) is

$d = sqrt{[(x_2 - x_1 )^2 +(y_2 - y_1)^2]}$

This is called the Distance Formula.

To find the distance between two points given in 3-D plane, we can apply the 3D distance formula, given as,

$d = sqrt{[(x_2 - x_1 )^2 +(y_2 - y_1)^2 + (z_2 - z_1 )^2]}$

Derivation of Formula for Distance Between Two Points

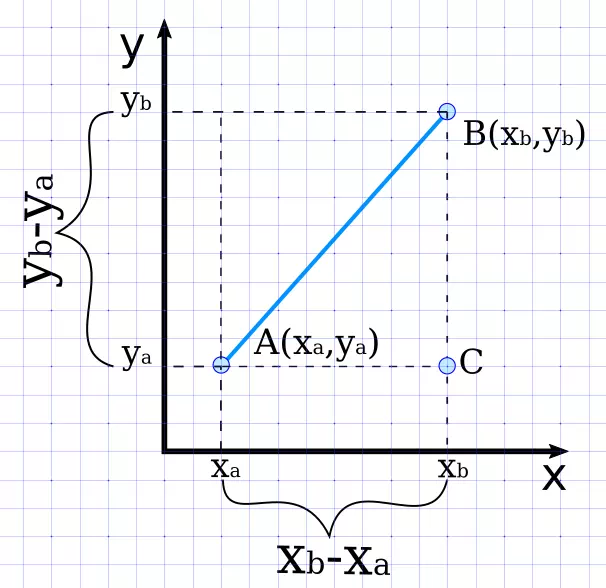
To obtain the formula for calculating the distance between two points on a two-dimensional plane, assume there are two points with the coordinates, A (x₁,y₁) and B (x₂,y₂). Following that, we will suppose that the line segment connecting A and B is AB = d. We will now plot the specified points on the coordinate plane and connect them with a line.

Next, we will construct a right-angled triangle using AB as the hypotenuse.

Using Pythagoras Theorem,

AB²= AC²+ BC²

d² = (x₂−x₁)² + (y₂−y₁)²

Here, the vertical distance between the given points is | y₂ – y₁|

The horizontal distance between the given points is | x₂ – x₁ |

$d = sqrt{[(x_2 - x_1)^2 + (y_2 - y_1)^2] }$ (Taking square root on both sides)

Thus, the distance formula to find the distance between two points is proved.

Using similar steps and concept, we can also derive the formula to find the distance between two points given in the 3D plane.

Steps to find the distance between two points

The following steps may be used to determine the distance between two places using the provided coordinates:

Make a note of the coordinates of the two given points on the coordinate plane as follows: A(x₁,y₁) and B(x₂,y₂).
We may use the distance formula to calculate the distance between two places, $d = sqrt{[(x_2 - x_1)^2 + (y_2 - y_1)^2]}.$
Express the given answer in units.

Note: We can apply the 3D distance formula in case the two points are given in 3D plane,

Sample Problems

Problem 1: Find the distance between the two points with the coordinates given as, A(1,5) and B (2,7).

Solution:

Let (x₁, y₁) be (2,7) and (x₂, y₂) be (1,5).

The distance d between the points : $d = sqrt{[(x_2 - x_1)^2 + (y_2 - y_1)^2]}$

$implies sqrt{[(2-1)^2 + (7-5)^2]}$

$implies sqrt{[1^2 + 2^2]}$

The distance between the two points is √5 units.

Problem 2: Find the distance between the two points with the coordinates given as, P (2,-6,2) and Q(7, 3, 1).

Solution:

Let (x₁, y₁, z₁) be P (2,-6,2) and (x₂, y₂, z₂) be Q (7,3,1).

The distance d between the points P and Q : $d = sqrt{[(x_2 - x_1)^2 + (y_2 - y_1)^2+(z_2-z_1)^2]}$

$implies sqrt{(7-2)^2+(3-(-6))^2+(1-2)^2)}$

$implies sqrt{ 5^2+9^2+(-1)^2}$

Problem 3: Prove that the vertices of a right-angled triangle are the points (3, 4), (7, 4), and (3, 8).

Solution:

Let us say the given points be:

P = (3, 4)

Q = (7, 4)

R = (3,

Now, we will find each vertices of the right-angle triangle by distance formula.

$AB=sqrt{(7-3)^2+(4-4)^2}=sqrt{4^2}=4units$

$BC=sqrt{(3-7)^2+(8-4)^2}=sqrt{(-4)^2+4^2}=4sqrt{2}units$

$AC=sqrt{(3-3)^2+(8-4)^2}=sqrt{4^2}=4units$

As we know the length of the sided of the right-angled triangle, by Pythagoras Theorem;

AB²+ AC²= BC²

4²+4²=(4√2)²

16+16 = 32⟹32 = 32

This proves that ABC is a right-angle triangle.

Distance Between Two Points in Complex Plane

The distance between two points in a complex plane or two complex numbers z₁=a+ib and z₂=c+id in the complex ⟹1−2k=9+4k plane is the distance between points (a, b) and (c, d), given as,

$| z_2 - z_1 |= sqrt{[(a − c)^2 + (b − d)^2]}$

Problem 4: Find the distance between the two complex numbers z₁= 2−5i and z₂= 7+7i

Solution:

Here, we have two complex numbers z₁= 2-5i and z₂= 7+7i.

The distance between these complex numbers is equidistance to the two points in the plane, with coordinates, (2,-5) and (7,7).

Thus, distance between the two points is

$implies sqrt{(7-2)^2+(7-(-5))^2}$

$implies sqrt{5^2+12^2}implies sqrt{25+144}$

Hence, the distance between two complex numbers z_1=2-5i and z_2=7+7i is 13 units.

Problem 5: A complex number ω is 6 units apart from z₁= -3 – i and 6 units apart from z₂= 3 + 5i. Check whether the triangle formed by ω, z₁, z₂ is right – angled or not.

Solution:

There are 3 complex numbers ω, z₁, z₂.

As we know the distance between ω and z₁ is 6 units and distance between ω and z₂ is 6 units.

Given, ω, z₁= 6 units

ω, z₂= 6 units

Now, we will find the distance between z₁and z₂ by using distance formula.

$z_1z_2=sqrt{(3-(-3)+(5-(-1))}$

$implies sqrt{6^2+6^2}$

By Pythagoras Theorem, we have;

(z₁z₂)²=(ωz₁)²+(ωz₂)²

$implies (6sqrt{2})^2=6^2+6^2$

Hence, we conclude that the given triangle is right-angle triangle.

Problem 6: Find a point on the x-axis that is equidistant from the points (1, -2) and (-2, -3).

Solution:

We know that any point on the x-axis has an y-coordinate of 0. As a result, we consider the point equidistant from the provided points to be (k,0). i.e., Distance between ( k,0) and (1, -2) = Distance between (k, 0) and (-2, -3).

$implies sqrt{[(1-k)^2 + (-2-0)^2]} = sqrt{[(-2-k)^2 + (-3-0)^2]}$

implies -4k-2k= 9-1

$implies k=frac{-4}{3}$

Therefore, the required point is (k, 0) = $(frac{-4}{3}, 0).$

Источник

На этой странице находится все необходимое, чтобы найти расстояние между двумя точками. Просто введите координаты точек и получите ответ и подробное решение с помощью наших онлайн-калькуляторов. Кроме того на сайте можно найти координаты середины отрезка.

Расстояние между двумя точками — это длина отрезка, соединяющего эти точки.

Формула расстояния между двумя точками на плоскости:

d=sqrt{{(x_b — x_a)}^2 + {(y_b — y_a)^2}}

x_a и y_a — координаты первой точки A,

x_b и y_b — координаты второй точки B

Нахождение расстояния между двумя точками на плоскости сводится к решению треугольника, а точнее — нахождению его гипотенузы. Для этого используется теорема Пифагора. Посмотрите на рисунок.

Соединив отрезком точки A и B, а также опустив перпендикуляры на оси мы получим треугольник ABC. В этом треугольнике стороны AC и BC являются катетами прямоугольного треугольника, а AB — его гипотенузой. Длины катетов AC и BC найти довольно просто:

AC = x_b — x_a

BC = y_b — y_a

Осталось применить теорему Пифагора и получить сторону AB, которая является гипотенузой прямоугольного треугольника и расстоянием между точками A и B:

AB=sqrt{{AC}^2 + {BC^2}}

Подставив вместо отрезков AC и BC их длины, получим итоговую формулу расстояния между двумя точками:

AB=sqrt{{(x_b — x_a)}^2 + {(y_b — y_a)^2}} или d=sqrt{{(x_b — x_a)}^2 + {(y_b — y_a)^2}}

Формула расстояния между двумя точками в пространстве:

{d=sqrt{{(x_b — x_a)}^2 + {(y_b — y_a)^2} + {(z_b — z_a)^2}}}

x_a, y_a и z_a — координаты первой точки A,

x_b, y_b и z_b — координаты второй точки B

Примеры задач на вычисление середины отрезка

Задача 1

Найдите расстояние между точками А и В, если А(2; 7), В(-2; 7).

Решение

Подставим координаты точек в формулу расстояния между двумя точками на плоскости и вычислим результат:

d=sqrt{{(x_b — x_a)}^2 + {(y_b — y_a)^2}} = sqrt{{(-2 — 2)}^2 + {(7 — 7)^2}} = sqrt{{-4}^2 + {0^2}} = sqrt{16 + 0} = sqrt{16} = 4

Мы получили расстояние между точками и оно равно 4.

Ответ: 4.

Проверим результат с помощью калькулятора .

Источник

Решение задач по математике у учащихся часто сопровождается многими трудностями. Помочь учащемуся справиться с этими трудности, а так же научить применять имеющиеся у него теоретические знания при решении конкретных задач по всем разделам курса предмета «Математика» – основное назначение нашего сайта.

Приступая к решению задач по теме «Расстояние между двумя точками на плоскости», учащиеся должны уметь строить точку на плоскости по ее координатам, а так же находить координаты заданной точки.

Вычисление расстояния между взятыми на плоскости двумя точками А(х_А; у_А) и В(х_В; у_В), выполняется по формуле d = √((х_А – х_В)² + (у_А – у_В)²), где d – длина отрезка, который соединяет эти точки на плоскости.

Если один из концов отрезка совпадает с началом координат, а другой имеет координаты М(х_М; у_М), то формула для вычисления d примет вид ОМ = √(х_М² + у_М²).

1. Вычисление расстояния между двумя точками по данным координатам этих точек

Пример 1.

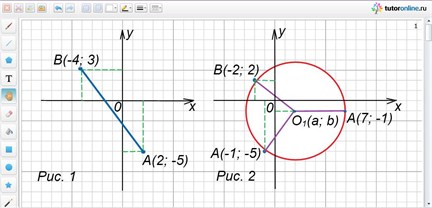
Найти длину отрезка, который соединяет на координатной плоскости точки А(2; -5) и В(-4; 3) (рис. 1).

Решение.

В условии задачи дано: х_А = 2; х_В = -4; у_А = -5 и у_В = 3. Найти d.

Применив формулу d = √((х_А – х_В)² + (у_А – у_В)²), получим:

d = АВ = √((2 – (-4))² + (-5 – 3)²) = 10.

2. Вычисление координат точки, которая равноудалена от трех заданных точек

Пример 2.

Найти координаты точки О₁, которая равноудалена от трех точек А(7; -1) и В(-2; 2) и С(-1; -5).

Решение.

Из формулировки условия задачи следует, что О₁А = О₁В = О₁С. Пусть искомая точка О₁ имеет координаты (а; b). По формуле d = √((х_А – х_В)² + (у_А – у_В)²) найдем:

О₁А = √((а – 7)² + (b + 1)²);

О₁В = √((а + 2)² + (b – 2)²);

О₁С = √((а + 1)² + (b + 5)²).

Составим систему из двух уравнений:

{√((а – 7)² + (b + 1)²) = √((а + 2)² + (b – 2)²),
{√((а – 7)² + (b + 1)²) = √((а + 1)² + (b + 5)²).

После возведения в квадрат левой и правой частей уравнений запишем:

{(а – 7)² + (b + 1)² = (а + 2)² + (b – 2)²,
{(а – 7)² + (b + 1)² = (а + 1)² + (b + 5)².

Упростив, запишем

{-3а + b + 7 = 0,
{-2а – b + 3 = 0.

Решив систему, получим: а = 2; b = -1.

Точка О₁(2; -1) равноудалена от трех заданных в условии точек, которые не лежат на одной прямой. Эта точка – есть центр окружности, проходящей через три заданные точки (рис. 2).

3. Вычисление абсциссы (ординаты) точки, которая лежит на оси абсцисс (ординат) и находится на заданном расстоянии от данной точки

Пример 3.

Расстояние от точки В(-5; 6) до точки А, лежащей на оси Ох равно 10. Найти точку А.

Решение.

Из формулировки условия задачи следует, что ордината точки А равна нулю и АВ = 10.

Обозначив абсциссу точки А через а, запишем А(а; 0).

По формуле d = √((х_А – х_В)² + (у_А – у_В)²) находим:

АВ = √((а + 5)² + (0 – 6)²) = √((а + 5)² + 36).

Получаем уравнение √((а + 5)² + 36) = 10. Упростив его, имеем

а² + 10а – 39 = 0.

Корни этого уравнения а₁ = -13; а₂ = 3.

Получаем две точки А₁(-13; 0) и А₂(3; 0).

Проверка:

А₁В = √((-13 + 5)² + (0 – 6)²) = 10.

А₂В = √((3 + 5)² + (0 – 6)²) = 10.

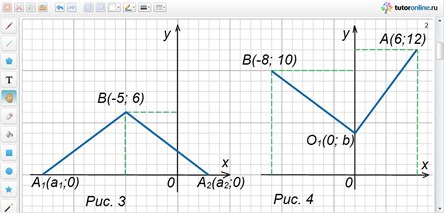
Обе полученные точки подходят по условию задачи (рис. 3).

4. Вычисление абсциссы (ординаты) точки, которая лежит на оси абсцисс (ординат) и находится на одинаковом расстоянии от двух заданных точек

Пример 4.

Найти на оси Оу точку, которая находится на одинаковом расстоянии от точек А(6; 12) и В(-8; 10).

Решение.

Пусть координаты нужной по условию задачи точки, лежащей на оси Оу, будут О₁(0; b) (у точки, лежащей на оси Оу, абсцисса равна нулю). Из условия следует, что О₁А = О₁В.

По формуле d = √((х_А – х_В)² + (у_А – у_В)²) находим:

О₁А = √((0 – 6)² + (b – 12)²) = √(36 + (b – 12)²);

О₁В = √((а + ² + (b – 10)²) = √(64 + (b – 10)²).

Имеем уравнение √(36 + (b – 12)²) = √(64 + (b – 10)²) или 36 + (b – 12)² = 64 + (b – 10)².

После упрощения получим: b – 4 = 0, b = 4.

Необходимая по условию задачи точка О₁(0; 4) (рис. 4).

5. Вычисление координат точки, которая находится на одинаковом расстоянии от осей координат и некоторой заданной точки

Пример 5.

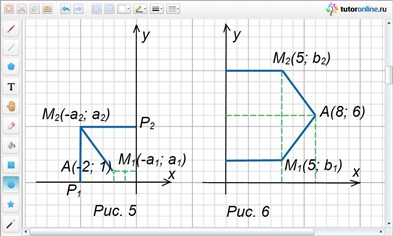
Найти точку М, расположенную на координатной плоскости на одинаковом расстоянии от осей координат и от точки А(-2; 1).

Решение.

Необходимая точка М, как и точка А(-2; 1), располагается во втором координатном углу, так как она равноудалена от точек А, Р₁ и Р₂ (рис. 5). Расстояния точки М от осей координат одинаковые, следовательно, ее координатами будут (-a; a), где а > 0.

Из условия задачи следует, что МА = МР₁ = МР₂, МР₁ = а; МР₂ = |-a|,

т.е. |-a| = а.

По формуле d = √((х_А – х_В)² + (у_А – у_В)²) находим:

МА = √((-а + 2)² + (а – 1)²).

Составим уравнение:

√((-а + 2)² + (а – 1)²) = а.

После возведения в квадрат и упрощения имеем: а² – 6а + 5 = 0. Решим уравнение, найдем а₁ = 1; а₂ = 5.

Получаем две точки М₁(-1; 1) и М₂(-5; 5), удовлетворяющие условию задачи.

6. Вычисление координат точки, которая находится на одинаковом заданном расстоянии от оси абсцисс (ординат) и от данной точки

Пример 6.

Найти точку М такую, что расстояние ее от оси ординат и от точки А(8; 6) будет равно 5.

Решение.

Из условия задачи следует, что МА = 5 и абсцисса точки М равна 5. Пусть ордината точки М равна b, тогда М(5; b) (рис. 6).

По формуле d = √((х_А – х_В)² + (у_А – у_В)²) имеем:

МА = √((5 – ² + (b – 6)²).

Составим уравнение:

√((5 – ² + (b – 6)²) = 5. Упростив его, получим: b² – 12b + 20 = 0. Корни этого уравнения b₁ = 2; b₂ = 10. Следовательно, есть две точки, удовлетворяющие условию задачи: М₁(5; 2) и М₂(5; 10).

Известно, что многие учащиеся при самостоятельном решении задач нуждаются в постоянных консультациях по приемам и методам их решения. Зачастую, найти путь к решению задачи без помощи преподавателя учащемуся не под силу. Необходимые консультации по решению задач учащийся и может получить на нашем сайте.

Остались вопросы? Не знаете, как найти расстояние между двумя точками на плоскости?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

Зарегистрироваться

Источник