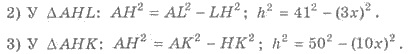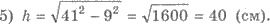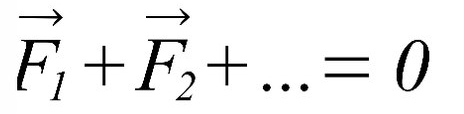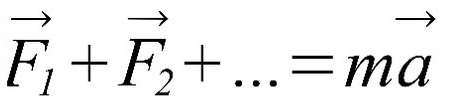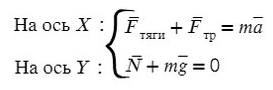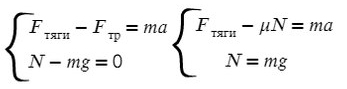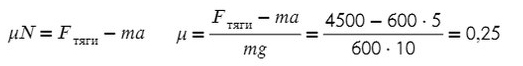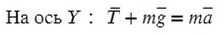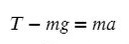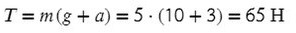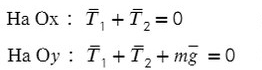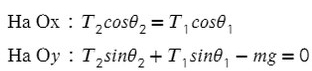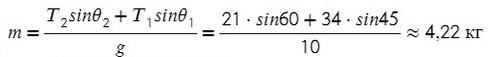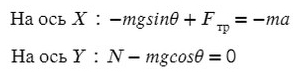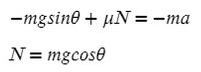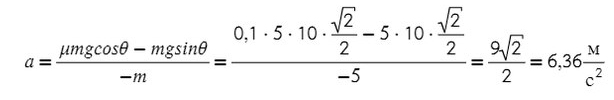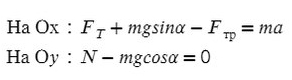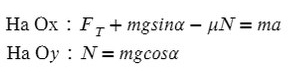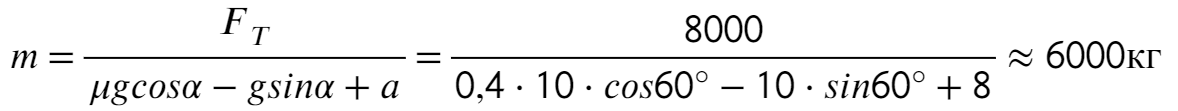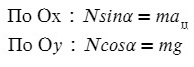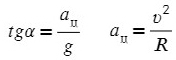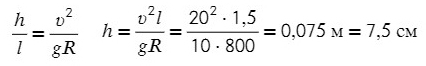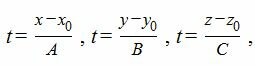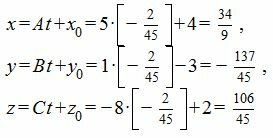Как найти длинны проекций наклонных

Перпендикуляр и наклонная к прямой

Если через какую-нибудь точку, взятую вне прямой, провести прямую, перпендикулярную к ней, то отрезок от данной точки до прямой для краткости называют одним словом перпендикуляр.

Отрезок СО — перпендикуляр к прямой АВ. Точка О называется основанием перпендикуляра СО (рис).

Если прямая, проведённая через данную точку, пересекает другую прямую, но не перпендикулярна к ней, то отрезок её от данной точки до точки пересечения с другой прямой называют наклонной к этой прямой.

Отрезок ВС — наклонная к прямой АО. Точка С называется основанием наклонной (рис.).

Если из концов какого-нибудь отрезка опустим перпендикуляры на произвольную прямую, то отрезок прямой, заключённый между основаниями перпендикуляров, называется проекцией отрезка на эту прямую.

Отрезок А&#146В&#146 — проекция отрезка АВ на ЕС. Отрезок ОМ&#146 — также называется проекцией отрезка ОМ на ЕС.

Проекцией отрезка КР, перпендикулярного к ЕС, будет точка К&#146 (рис.).

2. Свойства перпендикуляра и наклонных.

Теорема 1. Перпендикуляр, проведённый из какой-нибудь точки к прямой, меньше всякой наклонной, проведённой из той же точки к этой прямой.

Отрезок АС (рис.) является перпендикуляром к прямой ОВ, а АМ — одна из наклонных, проведённых из точки А к прямой ОВ. Требуется доказать, что АМ > АС.

В ΔМАС отрезок АМ является гипотенузой, а гипотенуза больше каждого из катетов этого треугольника. Следовательно, АМ > АС. Так как наклонная АМ взята нами произвольно, то можно утверждать, что всякая наклонная к прямой больше перпендикуляра к этой прямой (а перпендикуляр короче всякой наклонной), если они проведены к ней из одной и той же точки.

Верно и обратное утверждение, а именно: если отрезок АС (рис.) меньше всякого другого отрезка, соединяющего точку АС любой точкой прямой ОВ, то он является перпендикуляром к ОВ. В самом деле, отрезок АС не может быть наклонной к ОВ, так как тогда он не был бы самым коротким из отрезков, соединяющих точку А с точками прямой ОВ. Значит, он может быть только перпендикуляром к ОВ.

Длина перпендикуляра, опущенного из данной точки на прямую, принимается за расстояние от данной точки до этой прямой.

Теорема 2. Если две наклонные, проведённые к прямой из одной и той же точки, равны, то равны и их проекции .

Пусть ВА и ВС — наклонные, проведённые из точки В к прямой АС (рис.), причём АВ = ВС. Нужно доказать, что равны и их проекции.

Для доказательства опустим из точки В перпендикуляр ВО на АС. Тогда АО и ОС будут проекции наклонных АВ и ВС на прямую АС. Треугольник АВС равнобедренный по условию теоремы. ВО — высота этого треугольника. Но высота в равнобедренном треугольнике, проведённая к основанию, является в то же время и медианой этого треугольника.

Теорема 3 (обратная). Если две наклонные, проведённые к прямой из одной и той же точки, имеют равные проекции, то они равны между собой.

Пусть АС и СВ — наклонные к прямой АВ (рис.). СО ⊥ АВ и АО = ОВ.

Требуется доказать, что АС = ВС.

В прямоугольных треугольниках АОС и ВОС катеты АО и ОВ равны. СО — общий катет этих треугольников. Следовательно, ΔAOС = ΔВОС. Из равенcтва треугольников вытекает, что АС = ВС.

Теорема 4. Если из одной и той же точки проведены к прямой две наклонные, то та из них больше, которая имеет большую проекцию на эту прямую.

Пусть АВ и ВС — наклонные к прямой АО; ВО ⊥ АО и АО>СО. Требуется доказать, что АВ > ВС.

1) Наклонные расположены по одну сторону перпендикуляра.

Угол АСЕ внешний по отношению к прямоугольному треугольнику СОВ (рис.), а поэтому ∠АСВ > ∠СОВ, т. е. он тупой. Отсюда следует, что АВ > СВ.

2) Наклонные расположены по обе стороны перпендикуляра. Для доказательства отложим на АО от точки О отрезок ОК = ОС и соединим точку К с точкой В (рис.). Тогда по теореме 3 имеем: ВК = ВС, но АВ > ВК, следовательно, АВ > ВС, т. е. теорема справедлива и в этом случае.

Теорема 5 (обратная). Если из одной и той же точки проведены к прямой две наклонные, то большая наклонная имеет и большую проекцию на эту прямую.

Пусть КС и ВС — наклонные к прямой КВ (рис.), СО ⊥ КВ и КС > ВС. Требуется доказать, что КО > ОВ.

Между отрезками КО и ОВ может быть только одно из трёх соотношений:

КО не может быть меньше ОВ, так как тогда по теореме 4 наклонная КС была бы меньше наклонной ВС, а это противоречит условию теоремы.

Точно так же КО не может равняться ОВ, так как в этом случае по теореме 3 КС = ВС, что также противоречит условию теоремы.

Следовательно, остаётся верным только последнее соотношение, а именно, что КО > ОВ.

Как найти проекцию наклонной

Раздел ІІ. СТЕРЕОМЕТРИЯ

§8. ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ. ПРОЕКЦИЯ НАКЛОННОЙ НА ПЛОСКОСТЬ.

2. Свойства перпендикуляра и наклонной.

Рассмотрим свойства перпендикуляра и наклонной.

1) Перпендикуляр, опущенный из данной точки к плоскости, меньше любой наклонной, проведенной из этой же точки к плоскости.

На рисунке 411: АН АК.

2) Если две наклонные, проведенные из данной точки к плоскости, равны, то равны их проекции.

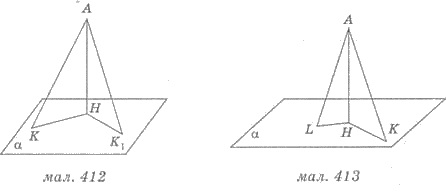
На рисунке 412 из точки А к плоскости а проведены две наклонные АК и А K 1 и перпендикуляр АН и АК = АК 1 . Тогда по свойству: НК = НК1.

3) Если две наклонные, проведенные из данной точки к данной плоскости, имеют равные проекции, то они равны между собой.

На рисунке 412 из точки А к плоскости а проведены две наклонные АК и А K 1 и перпендикуляр АН, причем КН = К 1 Н. Тогда по свойству: АК = АК 1 .

4) Если из данной точки проведены к плоскости две наклонные, то большая наклонная имеет большую проекцию.

На рисунке 413 из точки А к плоскости а проведены две наклонные АК и А L и перпендикуляр АН, A К > AL . Тогда по свойству: H К > HL .

5) Если из данной точки проведены к плоскости две наклонные, то большей из них является та, которая имеет большую проекцию на данную плоскость.

На рисунке 413 из точки А к плоскости а проведены две наклонные АК и А L и перпендикуляр АН, НК > Н L . Тогда по свойству: АК > А L .

Пример 1. Из точки к плоскости проведены две наклонные, длины которых 41 см и 50 см. Найти проекции наклонных, если они относятся, как 3 : 10, и расстояние от точки до плоскости.

Решения. 1) А L = 41 см; АК = 50 см (рис. 413). По свойством имеем Н L НК. Обозначим Н L = 3 х см, НК = 10 х см, АН = h см. АН — расстояние от точки А до плоскости α .

4) Приравнивая, получаем 41 2 — 9х 2 = 50 2 — 100 х 2 ; х 2 = 9; х = 3 (учитывая х > 0). Итак, Н L = 3 ∙ 3 = 9 (см), НК = 10 ∙ 3 = 30 (см).

Пример 2. С данной точки к плоскости проведены две наклонные, каждая по см. Угол между наклонными равен 60°, а угол между их проекциями — прямой. Найти расстояние от точки до плоскости.

1) АС = ВС = см — наклонные, ВАС = 60°; ВНС = 90° (рис. 414). Необходимо найти АН.

2) В рівнобедреному треугольнике АВС: 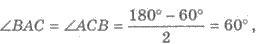поэтому ∆ АВС — равносторонний; ВС = см.

3) Так как АВ = АС, то НВ = НС ; обозначим НВ = НС = х см. Тогда в ∆ ВНС :

Как найти проекцию наклонной

Задачи по динамике.

I и II закон Ньютона.

Ввод и направление осей.

Проецирование сил на оси.

Решение систем уравнений.

Самые типовые задачи по динамике

Начнем с I и II законов Ньютона.

Откроем учебник физики и прочтем. I закон Ньютона: существуют такие инерциальные системы отсчета в которых. Закроем такой учебник, я тоже не понимаю. Ладно шучу, понимаю, но объясню проще.

I закон Ньютона: если тело стоит на месте либо движется равномерно (без ускорения), сумма действующих на него сил равна нулю.

Вывод: Если тело движется с постоянной скоростью или стоит на месте векторная сумма сил будет ноль.

II закон Ньютона: если тело движется равноускоренно или равнозамедленно (с ускорением), сумма сил, действующих на него, равна произведению массы на ускорение.

Вывод: Если тело двигается с изменяющейся скоростью, то векторная сумма сил, которые как-то влияют на это тело ( сила тяги, сила трения, сила сопротивления воздуха), равна массе этого тело умножить на ускорение.

При этом одно и то же тело чаще всего движется по-разному (равномерно или с ускорением) в разных осях. Рассмотрим именно такой пример.

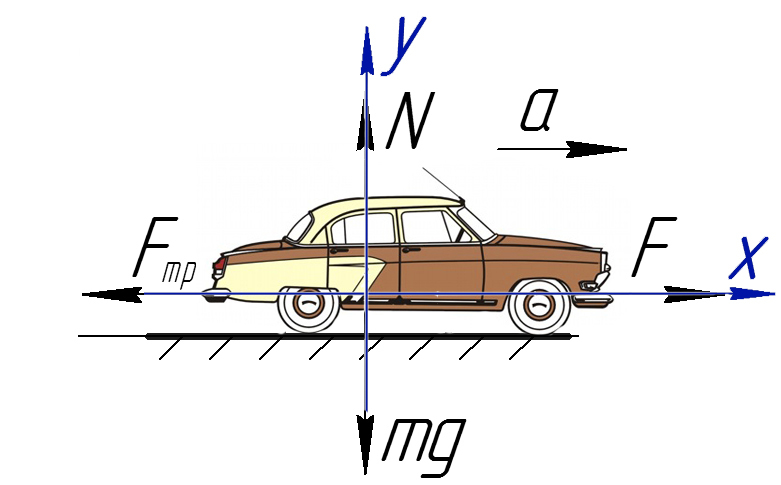
Задача 1. Определите коэффициент трения шин автомобиля массой 600 кг, если сила тяги двигателя 4500 Н вызывает ускорение 5 м/с².

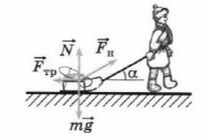
Обязательно в таких задачах делать рисунок, и показывать силы, которые дествуют на машину:

На Ось Х: движение с ускорением

На Ось Y: нет движения (здесь координата, как была ноль так и останется, машина не поднимает в горы или спускается вниз)

Те силы, направление которых совпадает с направлением осей, будут с плюсом, в противоположном случае — с минусом.

По оси X: сила тяги направлена вправо, так же как и ось X, ускорение так же направлено вправо.

Fтр = μN, где N — сила реакции опоры. На оси Y: N = mg, тогда в данной задаче Fтр = μmg.

Коэффициент трения — безразмерная величина. Следовательно, единиц измерения нет.

Задача 2. Груз массой 5кг, привязанный к невесомой нерастяжимой нити, поднимают вверх с ускорением 3м/с². Определите силу натяжения нити.

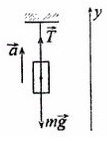
Сделаем рисунок, покажем силы, которые дествуют на груз

T — сила натяжения нити

На ось X: нет сил

Разберемся с направлением сил на ось Y:

Выразим T (силу натяжения) и подставим числительные значения:

Самое главное не запутаться с направлением сил (по оси или против), все остальное сделает калькулятор или всеми любимый столбик.

Далеко не всегда все силы, действующие на тело, направлены вдоль осей.

Простой пример: мальчик тянет санки

Если мы так же построим оси X и Y, то сила натяжения (тяги) не будет лежать ни на одной из осей.

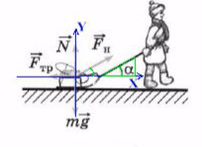
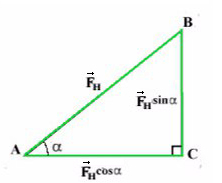
Чтобы спроецировать силу тяги на оси, вспомним прямоугольный треугольник.

Отношение противолежащего катета к гипотенузе — это синус.

Отношение прилежащего катета к гипотенузе — это косинус.

Сила тяги на ось Y — отрезок (вектор) BC.

Сила тяги на ось X — отрезок (вектор) AC.

Если это непонятно, посмотрите задачу №4.

Чем длинее будет верека и, соответсвенно, меньше угол α, тем проще будет тянуть санки. Идеальный вариант, когда веревка параллельна земле , ведь сила, которая действуют на ось X— это Fнcosα. При каком угле косинус максимален? Чем больше будет этот катет, тем сильнее горизонтальная сила.

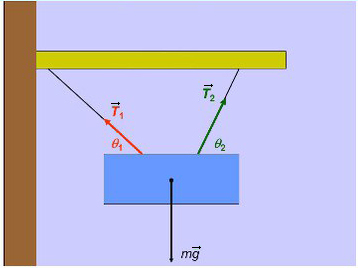
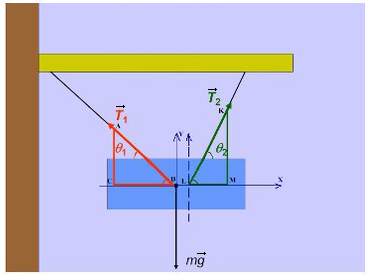
Задача 3. Брусок подвешен на двух нитях. Сила натяжения первой составляет 34 Н, второй — 21Н, θ1 = 45°, θ2 = 60°. Найдите массу бруска.

Введем оси и спроецируем силы:

Получаем два прямоугольных треугольника. Гипотенузы AB и KL — силы натяжения. LM и BC — проекции на ось X, AC и KM — на ось Y.

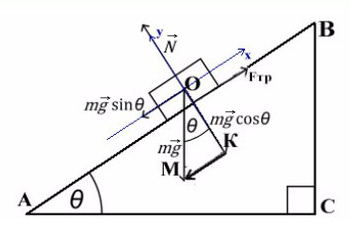
Задача 4. Брусок массой 5 кг (масса в этой задаче не нужна, но, чтобы в уравнениях все было известно, возьмем конкретное значение) соскальзывает с плоскости, которая наклонена под углом 45°, с коэффициентом трения μ = 0,1. Найдите ускорение движения бруска?

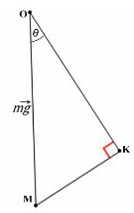
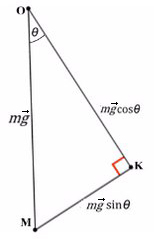
Когда же есть наклонная плоскость, оси (X и Y) лучше всего направить по направлению движения тела. Некоторые силы в данном случае ( здесь это mg) не будут лежать ни на одной из осей. Эту силу нужно спроецировать, чтобы она имела такое же направление, как и взятые оси.
Всегда ΔABC подобен ΔKOM в таких задачах (по прямому углу и углу наклона плоскости).

Рассмотрим поподробнее ΔKOM:

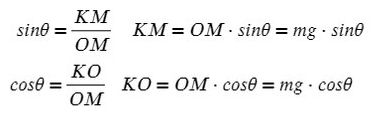
Получим, что KO лежит на оси Y, и проекция mg на ось Y будет с косинусом. А вектор MK коллинеарен (параллелен) оси X, проекция mg на ось X будет с синусом, и вектор МК направлен против оси X (то есть будет с минусом).

Не забываем, что, если направления оси и силы не совпадают, ее нужно взять с минусом!

Из оси Y выражаем N и подставляем в уравнение оси X, находим ускорение:

Как видно, массу в числителе можно вынести за скобки и сократить со знаменаталем. Тогда знать ее не обязательно, получить ответ реально и без нее.
Да-да, в идеальных условиях (когда нет силы сопротивления воздуха и т.п.), что перо, что гиря скатятся (упадут) за одно и тоже время.

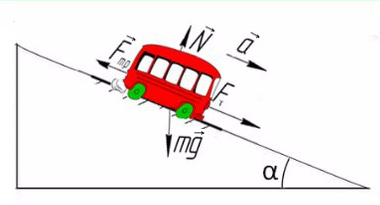
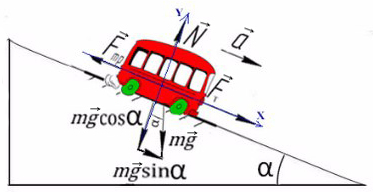
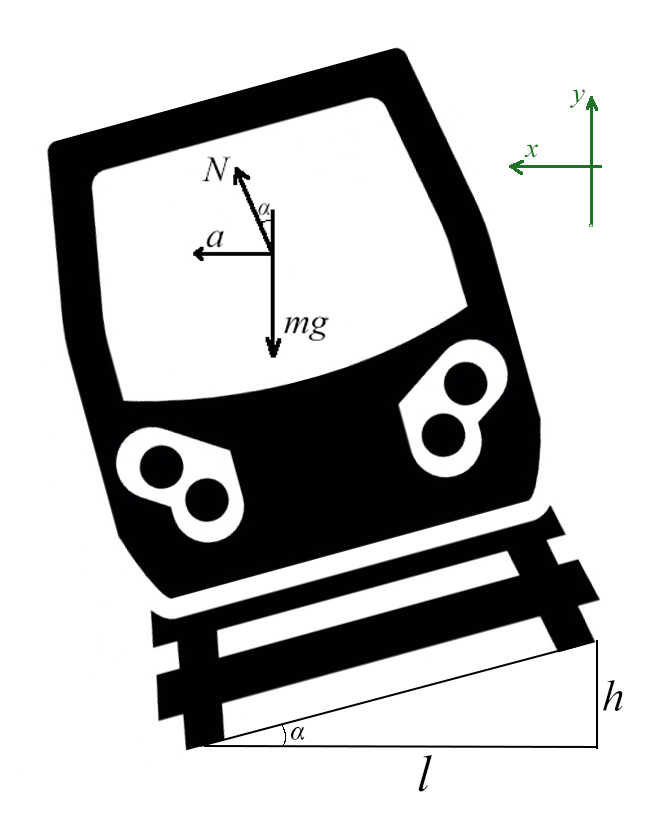
Задача 5. Автобус съезжает с горки под уклоном 60° с ускорением 8 м/с² и с силой тяги 8 кН. Коэффициент трения шин об асфальт равен 0,4. Найдите массу автобуса.

Сделаем рисунок с силами:

Введем оси X и Y. Спроецируем mg на оси:

Запишем второй закон Ньютона на X и Y:

Задача 6. Поезд движется по закруглению радиуса 800 м со скоростью 72 км/ч. Определить, на сколько внешний рельс должен быть выше внутреннего. Расстояние между рельсами 1,5 м.

Самое сложное — понять, какие силы куда действуют, и как угол влияет на них.

Вспомни, когда едешь по кругу на машине или в автобусе, куда тебя выталкивает? Для этого и нужен наклон, чтобы поезд не упал набок!

Угол α задает отношение разницы высоты рельсов к расстоянию между ними (если бы рельсы находились горизонтально)

Запишем какие силы действуют на оси:

Ускорение в данной задачи центростремительное!

Поделим одно уравнение на другое:

Тангенс — это отношение противолежащего катета к прилежащему:

Как мы выяснили, решение подобных задач сводится к расстановке направлений сил, проецированию их на оси и к решению систем уравнений, почти сущий пустяк.

В качестве закрепления материала решите несколько похожих задач с подсказками и ответами.

Источник

На чтение 8 мин Просмотров 3.7к. Опубликовано 04.07.2019

Содержание

  1. Теоретические материалы
  2. Предупреждение
  3. Проекция точки на плоскость − теория, примеры и решения
  4. Проекция прямой на плоскость
  5. Угол между прямой и плоскостью
  6. Теорема о трех перпендикулярах

Теоретические материалы

Глава 9. Прямые и плоскости в пространстве

9.5. Наклонные и их проекции на плоскость. Угол наклонной с плоскостью

Прямая, пересекающая плоскость, но не перпендикулярная к ней, называется наклонной к этой плоскости.

Точка пересечения перпендикуляра (наклонной) с плоскостью называется основанием перпендикуляра (наклонной).

Отрезок, соединяющий основания наклонной и перпендикуляра, проведенных к плоскости из одной и той же точки вне ее, называется проекцией наклонной на эту плоскость.

Если из одной и той же точки, взятой вне плоскости, проведены к этой плоскости перпендикуляр и наклонные, то:
1) две наклонные, имеющие равные проекции, равны;
2) из двух наклонных та больше, проекция которой больше;
3) (обратная) равные наклонные имеют равные проекции;
4) (обратная) большей наклонной соответствует большая проекция.

Повернув прямоугольные треугольники вокруг общего их катета (перпендикуляра к плоскости) до совмещения их плоскостей, получим все наклонные (гипотенузы) и их проекции (другие катеты) в одной плоскости, где эти теоремы верны.

Перпендикуляр к плоскости меньше всякой наклонной, проведенной к той же плоскости из той же точки вне ее (катет меньше гипотенузы).

Расстоянием точки от плоскости называется длина перпендикуляра, опущенного из этой точки на данную плоскость.

Углом между наклонной и плоскостью называется острый угол между наклонной и ее проекцией на эту плоскость.

Угол между наклонной и ее проекцией на плоскость является наименьшим из всех углов, образуемых данной наклонной с прямыми, лежащими в данной плоскости.

С помощю этого онлайн калькулятора можно найти проекцию точки на заданную плоскость. Дается подробное решение с пояснениями. Для построения проекции точки на данную плоскость введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку «Решить».

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Проекция точки на плоскость − теория, примеры и решения

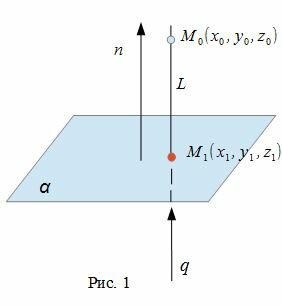
Для нахождения проекции точки M на плоскость α, необходимо:

  • построить прямую L, проходящую через точку M и ортогональной плоскости α.
  • найти пересечение данной плоскости α с прямой L(Рис.1).

Общее уравнение плоскости имеет вид:

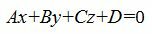(1)

где n(A,B,C)− называется нормальным вектором плоскости.

Уравнение прямой, проходящей через точку M(x, y, z) и имеющий направляющий вектор q(l, m, n) имеет следующий вид:

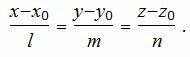(2)

Для того, чтобы прямая (2) была ортогональна плоскости (1), направляющий вектор q(l, m, n) прямой (2) должен быть коллинеарным нормальному вектору n(A,B,C) плоскости (1)(Рис. 1). Следовательно, в качестве направляющего вектора прямой (2) можно взять нормальный вектор плоскости (1) .

Таким образом, уравнение прямой, проходящей через точку M(x, y, z) и ортогональной плоскости (1) имеет следующий вид:

(3)

Для нахождения точку пересечения прямой L с плоскостью α, проще всего рассматривать параметрическое уравнение прямой. Составим ее

Выразим переменные x, y, z через рараметр t.

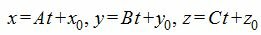(4)

Подставим значения x,y,z из выражения (4) в (1) и решим относительно t.

A(At+x)+B(Bt+y)+C(At+z)+D=0,

A 2 t+Ax+B 2 t+By+C 2 t+Cz+D=0,

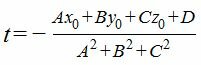(5)

Подставляя значение параметра t в выражения (4), находим проекцию M1 точки M на плоскость (1).

Пример 1. Найти проекцию M1 точки M(4, -3, 2) на плоскость

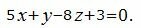(6)

Нормальный вектор плоскости имеет вид:

Подставляя координаты точки M и нормального вектора плоскости в (5), получим:

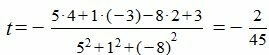(7)

Из выражений (7) находим:

Проекцией точки M(4, -3, 2) на плоскость (6) является точка:

Проекция прямой на плоскость

Определение 1. Ортогональной проекцией точки на плоскость называют основание перпендикуляра, опущенного из этой точки на плоскость.

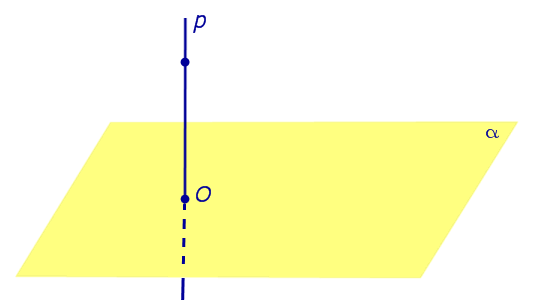
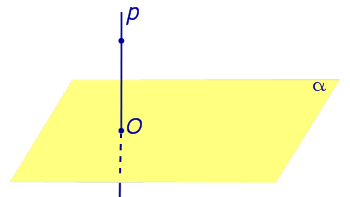
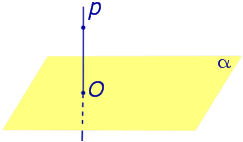
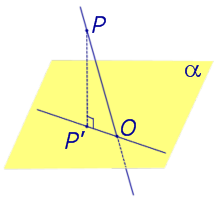
Рассмотрим рисунок 1, на котором изображены прямая p, перпендикулярная к плоскости α и пересекающая плоскость α в точке O.

Точка O является ортогональной проекцией на плоскость α каждой точки прямой p.

Замечание 1. Рассматриваемый в данном разделе случай ортогонального проектирования точки на плоскость α представляет собой частный случай более общего понятия проектирования точки на плоскость параллельно некоторой прямой, необязательно перпендикулярной к плоскости. Такое проектирование используется в нашем справочнике при определении понятия «призма».

Замечание 2. Если это не приводит к разночтениям, для упрощения формулировок термин «ортогональная проекция на плоскость» часто сокращают до термина «проекция на плоскость».

Определение 2. Проекцией фигуры a на плоскость α называют фигуру a’, образованную проекциями всех точек фигуры a на плоскость α.

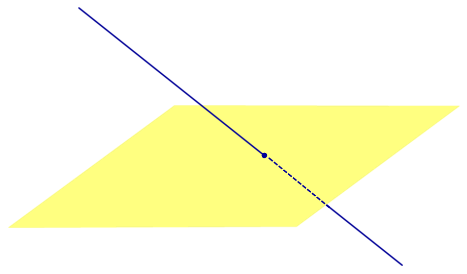
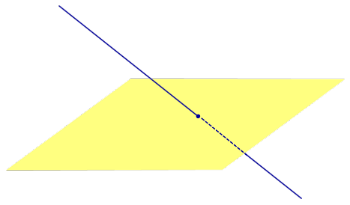
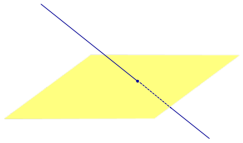
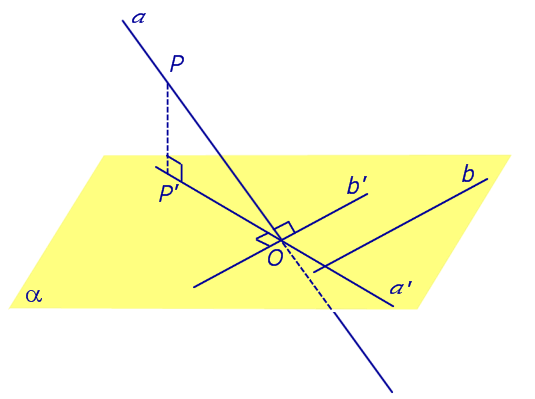
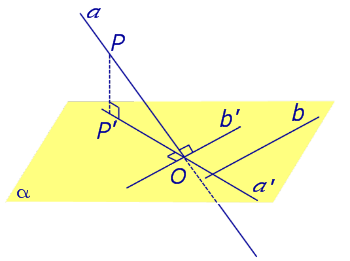
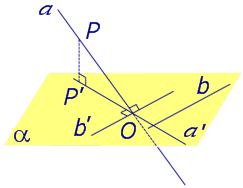
Определение 3. Прямую, пересекающую плоскость и не являющуюся перпендикуляром к плоскости, называют наклонной к этой плоскости (рис. 2).

Все возможные случаи, возникающие при ортогональном проектировании прямой на плоскость представлены в следующей таблице

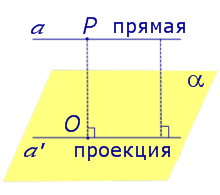
Если прямая PO пересекает плоскость α в точке O и является наклонной к плоскости α, а точка P’ является проекцией произвольной точки P этой прямой на плоскость α, то прямая P’O, лежащая в плоскости α, является проекцией прямой PO на плоскость α.

На рисунке прямая PO, где P – любая точка прямой a, является перпендикуляром к плоскости α.

Если прямая a параллельна плоскости α , то проекцией прямой a является прямая a’, лежащая в плоскости α, параллельная прямой a и проходящая через основание O перпендикуляра PO.

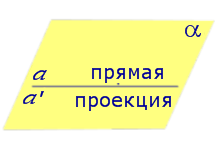
Если прямая a лежит в плоскости, то ее проекция a’, совпадает с прямой a .

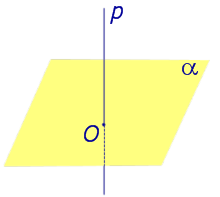
Если прямая перпендикулярна плоскости α и пересекает плоскость α в точке O , то точка O и является проекцией этой прямой на плоскость α.

Если прямая PO пересекает плоскость α в точке O и является наклонной к плоскости α, а точка P’ является проекцией произвольной точки P этой прямой на плоскость α, то прямая P’O, лежащая в плоскости α, является проекцией прямой PO на плоскость α.

На рисунке прямая PO, где P – любая точка прямой a, является перпендикуляром к плоскости α.

Если прямая a параллельна плоскости α , то проекцией прямой a является прямая a’, лежащая в плоскости α, параллельная прямой a и проходящая через основание O перпендикуляра PO.

Если прямая a лежит в плоскости, то ее проекция a’, совпадает с прямой a .

Если прямая перпендикулярна плоскости α и пересекает плоскость α в точке O , то точка O и является проекцией этой прямой на плоскость α.

Угол между прямой и плоскостью

Все возможные случаи, возникающие при определении понятия угла между прямой и плоскостью, представлены в следующей таблице.

Фигура Рисунок Свойство проекции
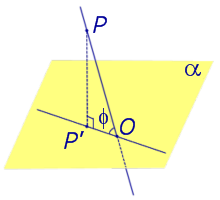
Наклонная к плоскости α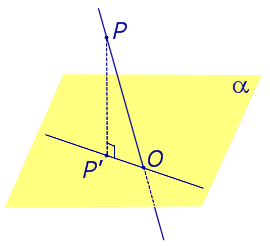
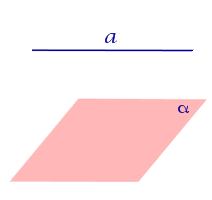
Прямая, параллельная плоскости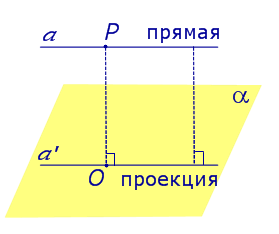
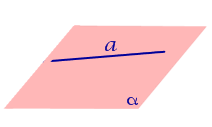
Прямая, лежащая на плоскости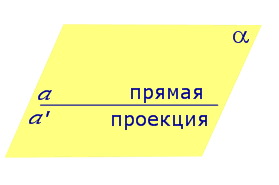
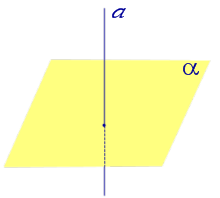
Прямая, перпендикулярная к плоскости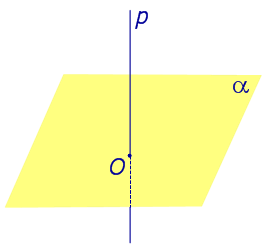

Углом между наклонной к плоскости (прямая PO ) и плоскостью называют угол между этой наклонной и ее проекцией на плоскость (прямая P’O. )

На рисунке это угол φ

Если прямая параллельна плоскости, то угол между прямой и плоскостью считается равным нулю.

Если прямая лежит в плоскости, то угол между прямой и плоскостью считается равным нулю.

Если прямая перпендикулярна плоскости, то угол между прямой и плоскостью считается равным 90° ( радиан).

Углом между наклонной к плоскости (прямая PO ) и плоскостью называют угол между этой наклонной и ее проекцией на плоскость (прямая P’O )

На рисунке это угол φ

Если прямая параллельна плоскости, то угол между прямой и плоскостью считается равным нулю.

Если прямая лежит в плоскости, то угол между прямой и плоскостью считается равным нулю.

Если прямая перпендикулярна плоскости, то угол между прямой и плоскостью считается равным 90° ( радиан).

Теорема о трех перпендикулярах

Теорема о трех перпендикулярах. Если наклонная a к плоскости α перпендикулярна к прямой b, лежащей на плоскости α, то и проекция наклонной a’ на плоскость α перпендикулярна к прямой b.

Доказательство. Рассмотрим следующий рисунок 3.

На рисунке 3 буквой O обозначена точка пересечения наклонной a с плоскостью α. Точка P – произвольная точка на прямой a, а точка P’ – это проекция точки P на плоскость α. Проведем через точку O прямую b’, параллельную прямой параллельную прямой b. Если прямая b проходит через точку O, то прямая b’, совпадет с прямой b.

Поскольку PP’ – перпендикуляр к плоскости α, то прямая PP’ перпендикулярна к прямой b’. Прямая a перпендикулярна к прямой b’ по условию. Таким образом, прямая b’ перпендикулярна к двум пересекающимся прямым PO и PP’, лежащим в плоскости POP’. В силу признака перпендикулярности прямой и плоскости получаем, что прямая b’ перпендикулярна к плоскости POP’, откуда вытекает, что прямая b’ перпендикулярна и к прямой a’, лежащей на плоскости POP’.

Теорема, обратная теореме о трех перпендикулярах. Если проекция a’ наклонной a к плоскости α перпендикулярна к прямой b, лежащей на плоскости α, то и сама наклонная a перпендикулярна к прямой b.

Доказательство. Как и для доказательства прямой теоремы о трех перпендикулярах, воспользуемся рисунком 3.

Прямая a’ перпендикулярна к прямой b по условию обратной теоремы. Прямая PP’ перпендикулярна к прямой b’, поскольку PP’ – перпендикуляр к плоскости α. Таким образом, прямая b’, перпендикулярна к двум пересекающимся прямым P’O и PP’, лежащим в плоскости POP’. В силу признака перпендикулярности прямой и плоскости прямая b’ перпендикулярна к плоскости POP’. Тогда, в частности, прямая b’ перпендикулярна к прямой a, лежащей на плоскости POP’.

Фигура Рисунок Определение
Наклонная к плоскости α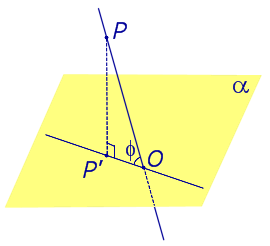
Прямая, параллельная плоскости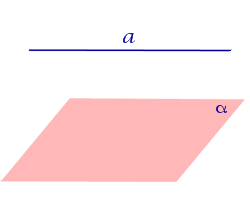
Прямая, лежащая на плоскости
Прямая, перпендикулярная к плоскости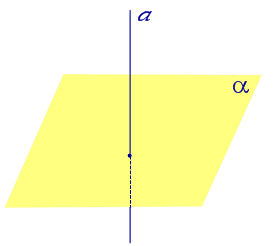
Источник

Государственное
бюджетное образовательное учреждение

профессиональная
образовательная организация

«Магнитогорский
технологический колледж имени В.П.Омельченко»

 

Методическая разработка

урока по математике

Тема: «Наклонная и ее проекция»

Разработчик: преподаватель   Шаранова Т.Б.

Магнитогорск

2017г

Введение.

Методическая
разработка урока усвоения новых знаний по математике   по теме «Наклонная и ее проекция» предназначена для текущего урока  по
разделу: « Геометрия»  

Методическая идея проведения урока усвоения новых знаний с использованием интерактивных технологий , воплощенная в
данной разработке и реализованная преподавателем, способствует воспитанию чувств коллективизма,;
развитию сотрудничества педагога и учащихся; развитию познавательного интереса
к математике, навыков  вычислительной культуры
при решении задач, внимательности,  аккуратности и трудолюбия;
реализации внутрипредметных и межпредметных связей, формирует у учащихся
целостную научную картину мира.

 

Методическая разработка включает в себя:

·       
Технологическую карту урока
усвоения новых знаний;

·       
Описание хода урока;

·       
Отражение собственного опыта проведения урока.

 

Проведение урока
усвоения новых знаний по данному
разделу подразумевает не только взаимосвязь знаний по разным темам на одном
занятии, но и интегрирование педагогических технологий, методов и форм обучения
в пределах занятия.

Данная
методическая разработка может быть рекомендована к использованию в средних
профессиональных учебных заведениях.

План урока

теоретического обучения

1. Тема урока: «Наклонная и ее проекция».

2. Тип урока: урока усвоения новых знаний

3. Форма проведения урока: Комбинированный.

 

 

Параметры качества обучения

4. Цели урока

Воспитательная:  Воспитание положительной мотивации и
интереса к изучению математики, ориентации на успех, корпоративной культуры,
коммуникативных навыков. умения
рационально использовать рабочее время, организованности, дисциплинированности, навыков  вычислительной культуры при решении задач,
внимательности,  аккуратности и трудолюбия.

Развивающая: Развитие профессионально-значимых
психофизиологических свойств личности: мыслительных опера­ций (анализ, синтез,  обобщение);
произвольного внимания; смысловой памяти; интеллектуальных
чувств любознательности, стремления к новому, прогрессивному,
удовлетворения от правильно выполненного задания.

Обучающая: сформировать  знания о понятиях перпендикуляра и наклонной, умения
решать  простейшие стереометрические задачи на вычисление расстояния от точки
до плоскости, длин наклонной и её проекции.

Знать:

•                  
определения и теоремы о
перпендикулярности в пространстве;

•                  
определения понятий
«перпендикуляр», «наклонная»;

Уметь:

•                  
распознавать на чертежах и
моделях пространственные формы; соотносить трехмерные объекты с их описаниями,
изображениями;

 5. Методическая характеристика урока

Метод

Методический
прием

Средства
обучения

Методы стимулирования и
мотивации интереса к учению.

Создание  
ситуаций   познавательной новизны.

Поощрение в
учении.

Постановка проблемы

Примеры использования стереометрический понятий
применения в жизни, в профессиональной деятельности.

Психологическое
поглаживание.

Словесный.

Проблемная беседа.

1)                 
Вопросник;

2)                 
Атанасян,
Л. С.  и др.  «Геометрия,  10-11: Учеб. для общеобразоват. учреждений / Л.С.
Атанасян, В. Ф. Бутузов, С.Б. Кадомцев и др. – 11-е изд. —  М.: Просвещение,
2002. – 206с.

Наглядно-демонстрационный.

— Использование ИКТ.

— Использование доски, цветных мелков

-Презентация.

-Доска, цветные мелки,

-примеры на доске.

Практический.

Решение задач.

-Алгоритмическая запись на доске и в тетрадях решения типовых задач;

-Разбор разных
способов решения задач на наклонную и ее проекцию;

-Оформление конспекта.

 — Атанасян, Л. С.  и др.  «Геометрия,  10-11», стр.
40 – 42, 44-46, §2, п. 19-20

— Доска, мел, тетради, ручки

Методы контроля.

— Входной контроль.

— Текущий контроль.

— Самоконтроль.

— Взаимоконтроль.

Вопросник.

Задания
на доске

Раздаточный материал: дидактические карточки по
вариантам

Критерий оценок.

6. Ход урока

№ и название этапа

Дидактические задачи этапа

Деятельность преподавателя

ЦОР

Рефлексивная деятельность учащихся

1

2

3

4

5

I. Организационный
этап.

Подготовка учащихся к работе на уроке.

Предъявление единых педагогических требований:

—         
приветствие;

—         
выявление отсутствующих на уроке;

—         
проверка внешнего вида (соответствие требованиям
внутреннего распорядка лицея).

Отвечают на приветствие. Староста
докладывает о явке учащихся на занятие. Приводят в соответствие с
требованиями внешний вид, рабочее место.

Психологическая установка на восприятие
материала урока.

Организация внимания и готовности учащихся к
уроку (устранение отвлекающих факторов: посторонний шум, лишние предметы на
рабочем месте).

Готовятся к восприятию урока.

II. Вводный
этап урока.

Подготовка к основному этапу урока.

Проверка домашнего
задания.

Установление правильности и полноты
выполнения домашнего задания.

Организация контроля знаний и умений учащихся
и коррекция

Самоосмысление учебного материала.

Мотивация.

Обеспечение возникновения у учащихся мотива
– внутреннего побудителя деятельности, придающего ей личностный смысл и
соответствующего требованиям учения и будущей профессии.

-Знаете ли вы как называется процесс получения неразъёмных
соединений посредством установления межатомных связей между свариваемыми
частями при их местном или общем нагреве, пластическом деформировании или
совместном действии того и другого?

—
Правильно, сва́рка 

— А
как называется неразъёмное соединение, выполненное с помощью сварки?

— сварным
соединением;

— А
какими основными умениями должен обладать сварщик?

—производить сварку конструкций во всех пространственных
положениях сварного шва и уметь читать рабочие чертежи и схемы;

Рассмотрим
сварку закладных деталей.

   Закладные детали – это специальные металлические элементы, которые
состоят из полосовой, круглой, уголковой стали.

 Бывают
открытые закладные конструкции и закрытые, закладные детали с перпендикулярными,
параллельным, наклонным или же смешанным размещением анкерных стержней (последние
могут быть с резьбой).

 Т.о., простейшие приемы сварки вполне доступы,
нужно иметь богатую фантазию и хорошо владеть сварочными аппаратами. От того
как вы привариваете детали, можно получить нужную конструкцию.

Скажите, как с точки зрения геометрии можно  расположить
деталь относительно плоскости (поверхности)?

(Предполагаемый ответ: параллельно, перпендикулярно
и под углом).

Совершенно верно, причем в геометрии для
каждого такого положения детали– «прямо» и « под углом» есть свое название:
перпендикуляр и наклонная, а для их стыковки на плоскости  —  «проекция
наклонной». Сегодня на уроке мы  и познакомимся с этими геометрическими понятиями.

Осмысливают значимость материала данного
урока в формировании профессионального опыта.

Сообщение темы

Тема сегодняшнего урока: «Наклонная и ее проекция».

Запишите тему в тетради.

Слушают название темы. Записывают в тетрадь.

Постановка цели.

Обеспечение самоосмысления через постановку
цели.

Перед вами стоит следующая цель:

Знать:

•определения и теоремы о перпендикулярности в пространстве;

•определения понятий «перпендикуляр», «наклонная»;

уметь:

•распознавать на чертежах и моделях пространственные формы; соотносить
трехмерные объекты с их описаниями, изображениями;

•описывать взаимное расположение прямых и плоскостей в пространстве;

анализировать в простейших случаях взаимное
расположение объектов в пространстве.

Учащиеся осмысливают и записывают цель в терминалах
«иметь представление», «знать», «уметь».

Входной контроль.

Актуализация опорных знаний.

Реализация связей:

—    межпредметных (производственное обучение – спецпредметы – общеобразовательные
предметы);

—    внутрепредметных (материал предыдущих и данного уроков).

Входной контроль.

Входной тест  проводить в виде фронтального
опроса все задачи решаются устно (См. приложение
№1).

Вопросы базовых дисциплин или предыдущих уроков:

1) Сформулируйте теорему Пифагора.

2)      
Продолжить фразу: «Прямая d
перпендикулярна плоскости β, если …»

Ответ: 1)
называют определение перпендикулярности прямой и плоскости;

 2)называют  признак
перпендикулярности прямой и плоскости

Отвечают на вопросы. Сравнивают свои ответы
с эталонами (прилагаются).  Определяют Ку – коэф. усвоения Ку
= РпрР, где Р – общее число существенных операций (ответов),
Рпр. – число правильно выполненных существенных операций (ответов).

Коррекция опорных
знаний.

Выявление пробелов и внесение исправлений,
поправок в опорных знаниях учащихся.

Разбор вопросов, вызвавших затруднения. Доведение
до Ку=0,7 опорных знаний.

Определяют и восполняют пробелы в знаниях.

Организация взаимопомощи

Сильные помогают более слабым.

II. Формирование

 ориен-тировчной
основы учебной деятельности. Получение новой информации.

Обеспечение восприятия и осмысления способов
действий.

Разберём  возможное применение понятия перпендикулярности
прямой. Изобразите рисунок у себя в тетради.

Возьмём на данной прямой некоторую точку А.

Назовите понятие, которое определяет прямая
по отношению точки А и плоскости.

С помощью перпендикулярной прямой можно
определить расстояние от точки А до данной плоскости.

Отрезок АО называют расстоянием от точки А
до данной плоскости, под которым понимают длину перпендикуляра опущенного на
данную плоскость из данной точки.

Осмысливают .

Записывают в тетради.

АО – перпендикуляр.

Можно вместе с учащимися сформулировать определение
данного понятия и затем записать в тетради.

С помощью преподавателя формулируют
определение перпендикуляра

Через точку А можно провести различные прямые,
назовите прямую проходящую под прямым углом.

Назовите прямые, проходящие через точку А 
под углом к плоскости меньше  900.

Прямая проходящая под прямым углом к
плоскости является перпендикулярной прямой к плоскости.

Такие прямые можно назвать наклонные.

Сформулируем определение наклонной прямой, и
записывают его в тетради.

С помощью преподавателя формулируют
определение наклонной.

Проведя различные прямые, мы получили
множество точек в пересечении этих прямых и плоскости.

Назовём их: О – основание перпендикуляра.

С — основание наклонной.

Записывают новые понятия.

Мы назвали два отрезка: АО-перпендикуляр, АС
– наклонная. Остался ещё один отрезок СО, соединяющий основания
перпендикуляра и наклонной. Этот отрезок называют проекцией наклонной.
Запишите это определение (можно пояснить, что СО состоит из совокупности точек,
являющихся проекциями точек прямой АС).

Записывают новые понятия.

Первичное закрепление
базисного уровня

Обеспечение репродуктивного воспроизведения
материала на основе алгоритма действий.

Итак, перечислите понятия, с которыми мы познакомились.

АО – перпендикуляр,

АС – наклонная,

СО – проекция наклонной.

Проверка
понимания алгоритма

действий.

Определение
возможности допуска студентов к самостоятельной работе.

Рассмотрим задачи на закрепление данных понятий.
 (см. Приложение №
2)

Задача 1. Из
точки А на плоскость опущен перпендикуляр длиной 4
см и проведена наклонная длиной 5 см. найдите длину проекции наклонной.

Отвечают на вопросы. Воспроизведение знаний
ориентировочной основы действий.

С помощью преподавателя решают данную задачу
(метод решения: Th Пифагора).

Организация самоконтроля.

Сравнение своих ответов с эталонами

Ответ: 3
см

Закрепление базисного уровня.

Обеспечение репродуктивного воспроизведения
материала.

Задача 2. Из
точки к плоскости проведены перпендикуляр и наклонная. Длина наклонной равна 8
см., а угол между ею  и перпендикуляром равен 600. Найти длины
перпендикуляра и проекции наклонной.

Метод решения:

1 способ: можно воспользоваться соотношениями Sin, Cos, Tg.

2 способ: угол между наклонной и её проекцией равен 300. Следовательно,
перпендикуляр равен 4см. Длину проекции можно найти с помощью Th Пифагора.

Организация самоконтроля.

Сравнение своих ответов с эталонами

Ответ: 4
см, 4√3 см.

Проверка понимания алгоритма действий.

Определение возможности допуска учащихся к
итоговому тесту.

Задача 3. Из
точки А к плоскости проведены две наклонные равные 10
см и 12 см. разность проекций этих наклонных равна 9
см. найдите проекции наклонных.

С помощью
преподавателя решают данную задачу (Метод решения: рассматривается два прямоугольных
треугольника, для которых по теореме Пифагора записываются формулы для вычисления
длины перпендикуляра. Из этих формул приравниваются правые части, не содержащие
отрезок-перпендикуляр и решается квадратное уравнение).

Организация самоконтроля.

Сравнение своих ответов с эталонами

Ответ: 6см и 15
см.

Коррекция знаний ориентировочной основы действий

Выявление пробелов и исправление ошибок в
понимании ориентировочной основы действий.

Организация взаимопомощи.

Определяют и восполняют пробелы в знаниях.
Задают вопросы.

Сильные помогают более слабым.

III.
Основной этап работы.

Самостоятельная работа студентов по применению
полученных знаний.

Обеспечение самореализации через
саморегуляцию и

 самоосмысление. Обеспечение усвоения новых
знаний и способов действий на уровне применения в знакомой и измененной
ситуации.

Предлагается выполнить итоговый контроль  по
индивидуальным карточкам

 (см. Приложение № 3)

Самостоятельное
выполнение заданий с применением знаний в знакомой и измененной ситуациях.

IV. Заключительный этап урока

Анализ и оценка успешности достижения цели
урока.
  1. Подвести итоги за урок

Анализ работы каждого
учащегося.

  1. Сообщить оценку качества работы каждого
    учащегося.
  2. Отметить, кто достиг отличного качества работы.
  3. Разобрать наиболее характерные недочёты  в
    работе учащихся и рекомендации по их устранению.

Слайд текст с целями проведённого мероприятия.

Самоанализ выполненной работы.

Самокоррекция.

Самооценка.

Развитие творческих способностей.

Саморегуляция.

Мотивация.

Формирование у учащихся ориентации на успех.

Поощрение учащихся в процессе достижения ими
поставленной цели (в т.ч. слабых).

Самоактуализация

Саморегуляция через достижения цели

Домашнее задание.

Обеспечение понимания цели домашнего
задания. Обеспечение понимания содержания и способов выполнения домашнего
задания.

1) Выучить определения перпендикуляра, наклонной
и проекции наклонной, признак перпендикулярности прямой и плоскости

2) Домашнее задание. Атанасян, Л. С.  и др. 
«Геометрия,  10-11», с 40-42, №139.

Самоосмысливают способов выполнения
домашнего задания.

Постановка новой цели к следующему уроку.

Создание мотивации через анализ результатов 
достигнутого, развивает аналитико – синтетическую деятельность учащихся.

— Тема следующего урока:

«Плоскости
в пространстве.».

 На
следующем уроке мы рассмотрим:

Двугранный
угол

Перпендикулярные
плоскости.

 Параллельные плоскости.

Самоосмысление информации о задачах на ближайший
урок.

Приложение № 1.

1)     
Решить квадратное
уравнение: х2 + 3х – 4 = 0

2)     
Вычислить длину гипотенузы
прямоугольного треугольника, если длины его катетов равны 2см и 3
см.

3)     
Длина одного из катетов
прямоугольного треугольника равен 4см, острый угол 300. Вычислите длины
гипотенузы и второго катета.

(Можно предложить учащимся
данные задания в 2 вариантах)

Приложение №2


Тема: «Перпендикуляр и наклонная»

               

 АС – перпендикуляр –
отрезок, соединяющий данную точку с точкой плоскости и лежащий  на прямой,
перпендикулярной плоскости.

АВ – наклонная –
любой отрезок, соединяющий
данную точку с точкой плоскости и не являющийся перпендикуляром.

ВС – проекция
наклонной  —  отрезок,
соединяющий основания перпендикуляра и наклонной, проведенных из одной и той
же точки.

Точка С —
основание перпендикуляра — конец
перпендикуляра, лежащий в плоскости.

Точка В — основание
наклонной  — конец
наклонной, лежащий в плоскости.

Примеры решения задач

Задача 1. Из точки на плоскость проведены перпендикуляр
и наклонная длиной 10 см. Найдите длину перпендикуляра, если длина проекции наклонной
равна 6см.

Задача
2. Из точки  к плоскости
проведены две наклонные, длины проекций которой  которых равны 9см и 5см.
Найдите длины наклонных, если разность их длин равна 2
см.

Дано:

АС – перпендикуляр,

АВ – наклонная,

ВС – проекция наклонной,

ВС = 6см.

АВ = 10см,

Найти: АС.

Дано:

АС – перпендикуляр,

АВ и АД – наклонные,

ВС и СД – проекции наклонных
АВ и АД,

ВС = 10см,

СД = 6см,

АВ – АД = 2см → АВ
=  АД + 2 (см).

Найти: АД,  АВ

Решение:

Рассмотрим 
Δ АВС – прямоугольный (АС – перпендикуляр). 

По теореме Пифагора:  АС2
= АВ2 — ВС2 ,

АС2 = 102
— 62 = 100 — 36 = 64,

АС = 8см.

Ответ: 8см.

Решение: 

Рассмотрим
Δ АСВ и  Δ АСД – прямоугольные  (АС – перпендикуляр).   

АС
– общая сторона.

По теореме Пифагора:

Из Δ АСВ: АС2 =
АВ2 — ВС2,

Из Δ АСД: АС2 =
АД2 — СД2,

Т.к. левые части
уравнений равны, то должны равняться и правые части, поэтому справедливо
следующее равенство:

АВ2 — ВС2
= АД2 — СД2. 

Пусть АД = х см,  
тогда  АВ = х + 2 (см).

Получаем  (х+2)2
— 102 = 62 -х2;

х2 + 2х + 4  —  100 = 36 -х2;

х2 + 2х + х2 = 36  + 96; 

2х = 132; 

                  
х = 66 см – длина наклонной АД.

АВ = 66 + 2 = 68
см.                                                    Ответ: 66
см, 68 см.
Источник

Как найти стороны прямоугольного треугольника

Онлайн калькулятор

Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):

  • для гипотенузы (с):
    • длины катетов a и b
    • длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
    • длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
  • для катета:
    • длину гипотенузы (с) и длину одного из катетов
    • длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
    • длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
    • длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
    • длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)

Введите их в соответствующие поля и получите результат.

Найти гипотенузу (c)

Найти гипотенузу по двум катетам

Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?

Формула

следовательно: c = √ a² + b²

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:

c = √ 3² + 4² = √ 9 + 16 = √ 25 = 5 см

Найти гипотенузу по катету и прилежащему к нему острому углу

Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?

Формула
Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:

c = 2 / cos(60) = 2 / 0.5 = 4 см

Найти гипотенузу по катету и противолежащему к нему острому углу

Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?

Формула
Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:

c = 2 / sin(30) = 2 / 0.5 = 4 см

Найти гипотенузу по двум углам

Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.

Найти катет

Найти катет по гипотенузе и катету

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?

Формула
Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:

a = √ 5² — 4² = √ 25 — 16 = √ 9 = 3 см

Найти катет по гипотенузе и прилежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?

Формула
Пример

Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:

b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см

Найти катет по гипотенузе и противолежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?

Формула
Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:

a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см

Найти катет по второму катету и прилежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?

Формула
Пример

Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:

b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см

Найти катет по второму катету и противолежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?

Формула
Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:

Наклонная к прямой

Что такое наклонная к прямой? Сколько наклонных можно провести из одной точки к данной прямой? Как найти расстояние между основаниями наклонных?

Наклонной, проведенной из точки A к прямой a, называется отличный от перпендикуляра отрезок, соединяющий точку A с некоторой точкой на прямой a.

Рисунок наклонной, проведенной из данной точки к данной прямой, начинают с изображения перпендикуляра (даже если в условии задачи о перпендикуляре не упоминается).

Чтобы нарисовать наклонную, нужно соединить точку, из которой проводится наклонная, с любой точкой на данной прямой.

На рисунке 1 AB — перпендикуляр, проведенный из точки A к прямой a, AC — наклонная.

Точка B — основание перпендикуляра, точка C — основание наклонной AC.

Отрезок BC, соединяющий основание перпендикуляра с основанием наклонной, — проекция наклонной AC на прямую a.

Из точки к прямой можно провести бесконечно много наклонных.

Две наклонные проведенные из данной точки к данной прямой, могут быть расположены как по одну сторону от перпендикуляра, так и по разные стороны от него.

На рисунке 2 наклонные AC и AD расположены по одну сторону от перпендикуляра AB.

BC — проекция наклонной AC на прямую a,

BD — проекция наклонной AD на прямую a.

CD — расстояние между основаниями наклонных

Если наклонные расположены по одну сторону от перпендикуляра, чтобы найти расстояние между основаниями наклонных, надо найти разность между длинами их проекций.

На рисунке 3 наклонные AC и AD расположены по разные стороны от перпендикуляра AB.

BC — проекция наклонной AC на прямую a,

BD — проекция наклонной AD на прямую a.

CD — расстояние между основаниями наклонных

Если наклонные расположены по разные стороны от перпендикуляра, расстояние между основаниями наклонных равно сумме длин проекций этих наклонных.

В следующий раз рассмотрим свойства наклонных.

2 Comments

Если наклонные расположены по разные стороны от перпендикуляра, расстояние между основаниями наклонных равно сумме длин проекций этих наклонных.

Все формулы для треугольника

1. Как найти неизвестную сторону треугольника

Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.

a , b , c — стороны произвольного треугольника

α , β , γ — противоположные углы

Формула длины через две стороны и угол (по теореме косинусов), ( a ):

* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение

Формула длины через сторону и два угла (по теореме синусов), ( a):

2. Как узнать сторону прямоугольного треугольника

Есть следующие формулы для определения катета или гипотенузы

a , b — катеты

c — гипотенуза

α , β — острые углы

Формулы для катета, ( a ):

Формулы для катета, ( b ):

Формулы для гипотенузы, ( c ):

Формулы сторон по теореме Пифагора, ( a , b ):

3. Формулы сторон равнобедренного треугольника

Вычислить длину неизвестной стороны через любые стороны и углы

b — сторона (основание)

a — равные стороны

α — углы при основании

β — угол образованный равными сторонами

Формулы длины стороны (основания), (b ):

Формулы длины равных сторон , (a):

4. Найти длину высоты треугольника

Высота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).

Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.

H — высота треугольника

a — сторона, основание

b, c — стороны

β , γ — углы при основании

p — полупериметр, p=(a+b+c)/2

R — радиус описанной окружности

S — площадь треугольника

Формула длины высоты через стороны, ( H ):

Формула длины высоты через сторону и угол, ( H ):

Формула длины высоты через сторону и площадь, ( H ):

Формула длины высоты через стороны и радиус, ( H ):

источники:

Наклонная к прямой

http://www-formula.ru/2011-10-09-11-08-41

Источник

§ 10.Перпендикуляр и наклонная к плоскости.

Теорема о трёх перпендикулярах

Отрезок прямой, перпендикулярной данной плоскости, один конец которого принадлежит этой плоскости, а другой — данная точка, называется перпендикуляром, проведённым из данной точки на данную плоскость. Конец этого отрезка, принадлежащий плоскости, называется основанием перпендикуляра. Длина перпендикуляра, опущенного из данной точки на данную плоскость, называется расстоянием от этой точки до данной плоскости.

На рисунке 64 отрезок CD — перпендикуляр, проведённый из точки C на плоскость α, точка D — основание этого перпендикуляра; длина отрезка CD — расстояние от точки C до плоскости α. Это расстояние обозначают: | C, α | = | CD | или ρ(C; α). (Можно сказать, что через точку C проведён перпендикуляр CD к плоскости α или из точки C опущен перпендикуляр CD на плоскость α, или из точки D восставлен перпендикуляр DC к плоскости α.)

Рис. 64

Наклонной, проведённой из данной точки к данной плоскости, называется всякий отрезок, который соединяет данную точку с точкой на плоскости и не является перпендикуляром к этой плоскости. Конец этого отрезка, принадлежащий плоскости, называется основанием наклонной. Отрезок, соединяющий основания перпендикуляра и наклонной, проведённых к плоскости из одной точки, называется ортогональной проекцией наклонной на эту плоскость.

На рисунке 64 отрезок PO — перпендикуляр, проведённый из точки P на плоскость α; отрезок PH — наклонная, проведённая из точки P к плоскости α; отрезок OH — проекция этой наклонной на плоскость α; в плоскости α проведены прямые a и b через основание H наклонной PH.

Докажите самостоятельно следующие утверждения:

 если из одной точки, не принадлежащей плоскости, проведены к этой плоскости перпендикуляр и наклонная, то длина наклонной больше длины перпендикуляра;

 длина проекции наклонной меньше длины самой наклонной;

 длины наклонных, проведённых из одной точки, не принадлежащей плоскости, равны тогда и только тогда, когда равны длины их проекций;

 если из одной точки, не принадлежащей плоскости, проведены две наклонные к этой плоскости, то бó́льшей наклонной соответствует бó́льшая проекция. (Сформулируйте обратное утверждение.)

Обратите внимание! Данные утверждения аналогичны соответствующим утверждениям в планиметрии относительно перпендикуляра, наклонной и её проекции на прямую.

Наклонной к плоскости называют также любую прямую, пересекающую плоскость и не перпендикулярную к ней. В таком случае ортогональной проекцией наклонной является прямая. (Подробнее с параллельным проектированием вы познакомитесь в § 12.)

Докажите самостоятельно, что если AM — наклонная к плоскости α, то основания перпендикуляров, проведённых к плоскости α через все точки наклонной AM, принадлежат одной прямой. Эту прямую называют ортогональной проекцией наклонной AM на плоскость α. Доказанное утверждение подсказывает способ построения ортогональной проекции наклонной на данную плоскость.

Теорема 16 (теорема о трёх перпендикулярах). Если прямая, лежащая на плоскости, перпендикулярна проекции наклонной на эту плоскость, то данная прямая перпендикулярна и самой наклонной.

Дано: AC — наклонная к плоскости α, m — прямая, лежащая в плоскости α, перпендикулярная проекции наклонной AC (рис. 65, а).

Доказать: m ⊥ AC.

Доказательство. Проведём AB ⊥ α (рис. 65, б). Тогда BC — ортогональная проекция наклонной AC на плоскость α. Рассмотрим прямую m и плоскость ABC. Имеем: m ⊥ BC (по условию) и m ⊥ AB (так как AB ⊥ α), т. е. прямая m перпендикулярна двум пересекающимся прямым плоскости ABC. Тогда по признаку перпендикулярности прямой и плоскости прямая m перпендикулярна самой плоскости ABC, а следовательно, и прямой AC, лежащей в этой плоскости. Теорема доказана. ▼

Справедлива и обратная теорема.

Теорема 17. Если на плоскости проведена прямая перпендикулярно наклонной, то эта прямая перпендикулярна проекции наклонной.

Дано: AC — наклонная к плоскости α, m — прямая плоскости α, перпендикулярная AC (рис. 65).

Доказать: m ⊥ BC (проекция наклонной AC).

Рис. 65

Доказательство. Проведём AB ⊥ α. Тогда BC — ортогональная проекция наклонной AC на плоскость α. Рассмотрим прямую m и плоскость ABC. Имеем: m ⊥ AB (так как AB — перпендикуляр к плоскости α) и m ⊥ AC (по условию). Таким образом, прямая m перпендикулярна двум пересекающимся прямым плоскости ABC. Тогда по признаку перпендикулярности прямой и плоскости прямая m перпендикулярна самой плоскости ABC, а следовательно, и прямой BC, лежащей в этой плоскости. Теорема доказана. ▼

Векторное доказательство теорем 16 и 17 проведено в пункте 23.3.

Обе эти теоремы можно объединить одним предложением:

наклонная к плоскости тогда и только тогда перпендикулярна прямой, лежащей в этой плоскости, когда проекция наклонной перпендикулярна данной прямой.

Или, иначе говоря:

для того чтобы проекция наклонной к плоскости была перпендикулярна прямой, лежащей в этой плоскости, необходимо и достаточно, чтобы сама наклонная была перпендикулярна данной прямой.

Придумайте ещё несколько аналогичных формулировок теоремы о трёх перпендикулярах и заодно подумайте: что это за «три перпендикуляра».

Заметим, что теорема о трёх перпендикулярах позволяет построить проекцию наклонной c к плоскости α, не опуская на эту плоскость перпендикуляра, если в плоскости α дана прямая b, перпендикулярная наклонной c. В таком случае достаточно через основание наклонной провести в плоскости α прямую a, перпендикулярную прямой b. Прямая a является искомой проекцией наклонной c на плоскость α. Этот приём часто используется при решении задач.

Рис. 66

 ЗадаЧа 3.050. К плоскости прямоугольного треугольника ABC (∠ C = 90°) проведён перпендикуляр BP. На наклонных PA и PC отмечены соответственно такие точки E и K, что отрезок EK параллелен AC (рис. 66). Верно ли, что треугольник BKE — прямоугольный?

Решение. Имеем BP ⊥ (ABC) ⇒ BP ⊥ AC. Кроме того, AC ⊥ BC (∠ ACB = 90°). Следовательно, по признаку перпендикулярности прямой и плоскости AC ⊥ (BCP). Тогда AC ⊥ BK. А так как KE ‖ AC и AC ⊥ BK, то KE ⊥ BK. Это означает, что ∠ BKE = 90°, т. е. ⧌ BKE — прямоугольный.

Рис. 67

ЗадаЧа 3.069. Через вершину прямого угла равнобедренного прямоугольного треугольника ABC проведена прямая CM, перпендикулярная его плоскости. Найти расстояние от точки M до прямой AB, если AC = 4 см, CM =  см.

Решение. Пусть точка K — середина гипотенузы AB треугольника ABC (рис. 67). Так как AC = CB, то CK ⊥ AB, и по теореме о трёх перпендикулярах отрезок MK перпендикулярен AB. Это означает, что длина отрезка MK — искомое расстояние от точки M до прямой AB.

Далее, так как MC ⊥ (ABC), то MC ⊥ CK (по определению прямой, перпендикулярной плоскости). Поэтому ⧌ MCK — прямоугольный, значит, MK2 = MC2 + CK2.

Так как ⧌ ABC — равнобедренный прямоугольный (∠ C = 90°) и CK — его медиана, то ⧌ CBK — равнобедренный прямоугольный (∠ K = 90°). Тогда CK2 =  BC2 = 8. Учитывая, что MK2 = MC2 + CK2, получаем MK = 6 (см).

Источник

Понравилась статья? Поделить с друзьями:
  • Как составить исковое заявление апк
  • Как найти корни уравнения на заданном промежутке
  • Шишки у детей как исправить
  • Неправильный запуск аквариума как исправить
  • Как можно исправить недержание мочи у женщин