Почему никто в мире не может точно измерить береговую линию
В Интернете можно найти множество самых противоречивых данных о длинах береговых линий разных стран. Можно подумать, что это всемирный заговор — однако на самом деле виновата лишь наша математика.

Измерить точную длину береговой линии — задача не из простых. Даже крупные исследовательские центры США Исследовательский институт Конгресса, ЦРУ и NOAA публикуют совершенно разные цифры. Но как такое возможно? Все дело в так называемом парадоксе береговой линии.
РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ
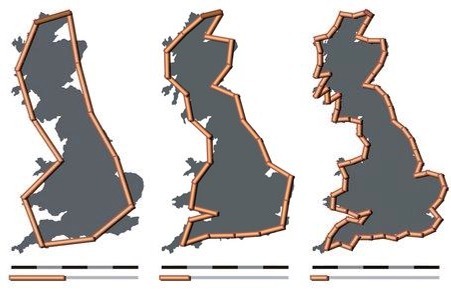
Как поясняет канал RealLifeLore, этот парадокс досаждал исследователям и особенно картографам с момента его открытия математиком Льюисом Фрай Ричардсоном в 1951 году. Объяснение этого феномена на удивление простое: в отличие от геометрических фигур, которые рисует человек, береговая линия полна укромных уголков и неровностей. Она никогда не станет прямой, сколько не приближай масштаб. Именно поэтому длина береговой линии полностью зависит от того, какую единицу измерения вы используете при ее изучении. К примеру, если для измерения береговой линии Великобритании взять шаг в 100 км, то ее длина будет равна 2800 км. Но если взять шаг в 50 км (то есть в два раза точнее учитывать все неровности линии), то длина внезапно вырастет до 3400 км!
Математики сравнивают береговые линии с фракталами: чем точнее измерения, тем сложнее оказывается структура. Кстати, именно знаменитый исследователь фракталов Бенуа Мандельброт расширил и дополнил работу Ричардсона над означенным парадоксом. Таким образом, если попытаться измерить береговую линию с шагом в один атом, длина ее, вероятно, приблизится к бесконечности — и это есть не учитывать то, что во время приливов и отливов структура береговой линии может кардинальным образом изменяться…
РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ
Конечно, для практических нужд ученых это не сулит ничего хорошего. Это также объясняет некоторые странные измерения береговых линий, которые можно найти в Интернете. Например, ЦРУ называет Норвегию обладательницей второй самой длинной береговой линии в мире после Канады. Это абсурд — длина береговой линии Канады составляет 202 080 км, а Норвегии — всего 25 148 км. Но если вы посмотрите на побережье Норвегии, похожее на изрезанную ножницами бумагу, то все становится на свои места.
Время прочтения: 6 минут
Введение
Картография – наука, в которой ответ на вопрос, какой длины тот или иной объект, может иметь множество самых разных значений, несмотря на простоту задания. Казалось бы, даже ребенок может взять линейку и измерить линию на карте, но все не так просто. На протяжении веков картографию окружает множество проблем, которые мешают идеально точно измерять размеры объектов, выявляемых с каждым годом все больше. Об одной из причин таких неточностей, называемой “парадокс береговой линии” пойдет речь в этой статье.
Эффект Ричардсона
Прародителем парадокса береговой линии считается, замеченный в 1951 году эффект Ричардсона.
Английский ученый с широким кругом интересов от математики до психологии, доктор Льюис Фрай Ричардсон был еще известен как убежденный пацифист. Некоторые из его работ были посвящены использованию математики для объяснения причин военных конфликтов с целью их предотвращения. В одной из своих статей доктор Ричардсон выдвинул теорию о том, что склонность войны между двумя нациями как-то связана с длиной и формой общей государственной границы между ними.
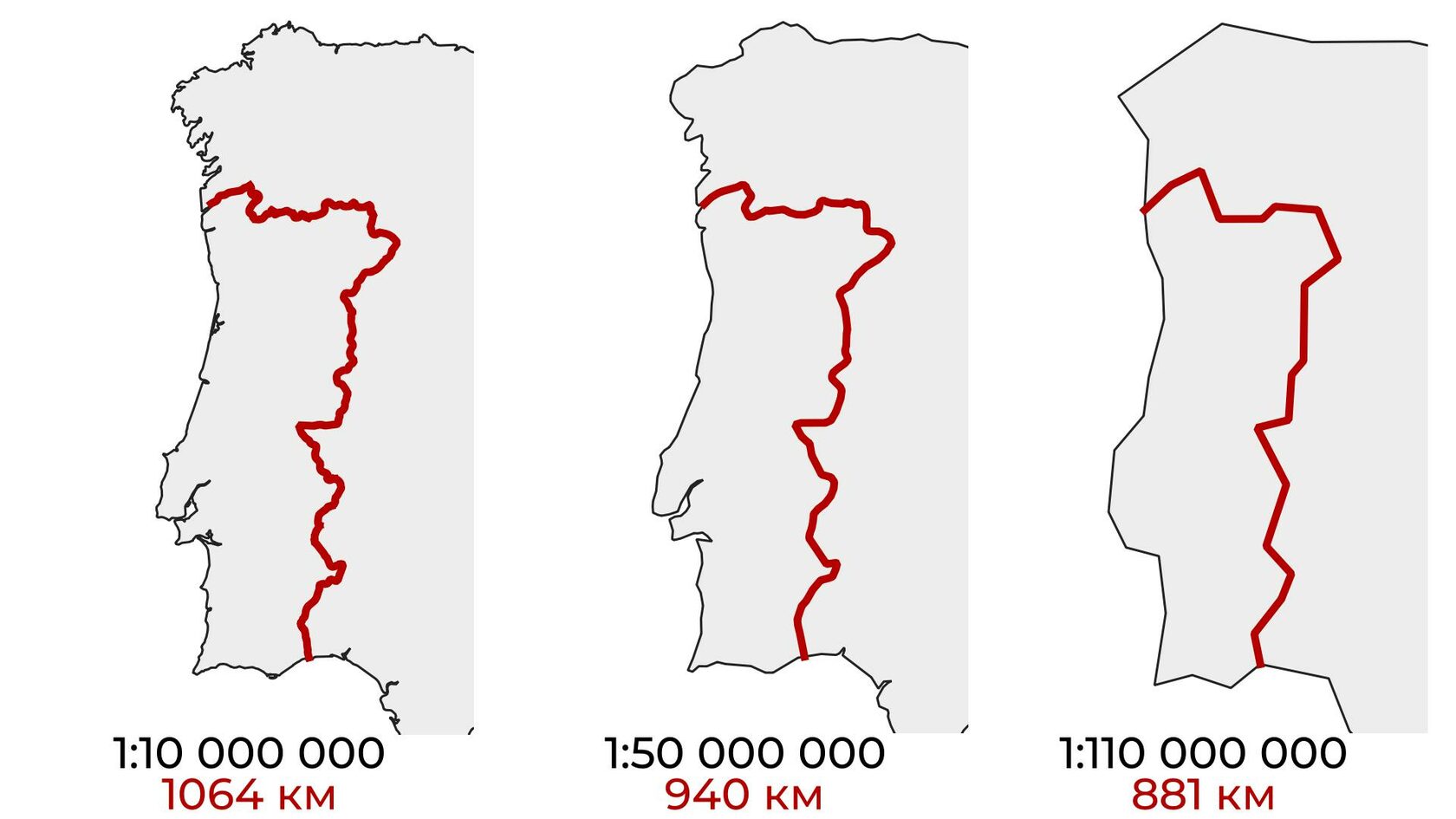
Для проверки своей теории английский математик собирал множество различных данных, формируя свою относительно репрезентативную статистическую выборку, пока не наткнулся на занимательный факт. Протяженность границ в разных источниках между Испанией и Португалией варьировалась от 987 до 1214 километров, а между Бельгией и Нидерландами – от 380 до 449 километров.
Причина такого различия в измерениях кроется в генерализации карт. Карта – образно-знаковая модель земной поверхности и объектов на ней. Точность и детальность отображения объекта зависит от масштаба карты и степени обобщения элементов. В докомпьютерные времена карты рисовались на бумаге для того, чтобы люди работали с ними на бумаге, используя такие инструменты, как циркули, кульвиметры, логарифмические линейки и прочие измерительные приборы.
Измерения на картах зависят от нижнего предела длины географически значимых объектов (его обозначают еще как G), обычно это расстояние, которое на карте определенного масштаба докомпьютерной эпохи имело длину 1 мм, так как 1 мм – приблизительно наименьший отрезок, который на бумажной карте можно, во-первых, точно нарисовать, а во вторых, точно измерить. С развитием компьютерных технологий такой нижний предел длины географически значимых объектов встречается все реже, так как скорость обработки информации и требуемая точность ее воспроизведения стали приоритетнее возможностей работы с бумагой.
Изучая информацию о длине границ Испании и Португалии, доктор Ричардсон выяснил, что протяженность границ в разных источниках измерялась на картах разного масштаба. Чем больше расстояние 1 мм на карте в реальности, тем большее количество деталей упускается из виду: объекты обобщаются и выпрямляются, игнорируя изгибы.
Исследуя данный эффект, доктор Ричардсон заметил, что чем меньше длина отрезка на карте в действительности, тем больше становится длина объекта, состоящего из множества таких объектов. Английский математик предполагал, что в какой-то момент длина объекта перестанет расти и придет к истинному значению, подобно тому, как периметр многоугольника, вписанного в окружность, тем ближе к длине окружности, тем больше у него сторон. Собственно это и есть основное отличие эффекта Ричардсона от парадокса береговой линии – эффект Ричардсона предполагает, что даже береговая линия Великобритании с множеством мысов и заливов – это кривая, которую рано или поздно можно спрямить.
Парадокс береговой линии
В своем исследовании доктор Ричардсон задумался о том, что береговая полоса – еще более искривленная линия, чем государственные границы, но все же точность ее измерения его не сильно интересовала. Для него береговая линия была лишь отметкой, от которой отсчитываются границы, отделяющие территориальные воды одного государства от территориальных вод другого или международных вод.
Спустя более десяти лет после открытия эффекта Ричардсона другой ученый, Бенуа Мандельброт, более плотно занялся вопросом точности измерения длин кривых линий, что вскоре привело к созданию фрактальной геометрии, да и в принципе к возникновению слова «фрактал» в научном поле.
Во фрактальной геометрии как раз и кроется определение парадокса береговой линии. Статью Мандельброта “Какова протяженность побережья Британии? Статистическая самоподобие и дробная размерность” считают истоком фрактальной геометрии за 10 лет до того, как Бенуа Мандельброт самолично введет понятие фрактал.
фрактал – множество, обладающее свойством самоподобия (объект, в точности или приближенно совпадающий с частью себя самого, то есть целое имеет ту же форму, что и одна или более частей)
Мандельброт описывает формы морского побережья как сложные кривые, каждую часть которых можно назвать уменьшенным изображением целого. Это свойство он тогда назвал “статическим самоподобием”. Более того, в своей работе он вообще предполагает, что понятие “длина” для них не имеет смысла, так как географические кривые из-за различных масштабов представления на разных картах с разными целями находятся в суперпозиции, то есть одновременно могут иметь широкий разброс характерных размеров. Например, измеряя побережье Великобритании условными линейками 50 и 100 км, мы получим протяженность побережья соответственно около 3500 и 2800 км.
Самоподобие береговой линии выражено чередованием заливов и мысов. Чем точнее мы описываем побережье, тем больше заливов и мысов мы можем выделить, и, более того, сами заливы и мысы содержат внутри себя другие заливы и мысы. Таким образом мы можем бесконечно точно описывать береговую линию чего угодно. Чем точнее мы будем ее описывать, тем больше будет ее протяженность, и когда в конце концов минимальное расстояние нашей условной линейки будет стремиться к нулю, общая длина измеряемой береговой линии будет стремиться к бесконечности.
Парадокс береговой линии – это теоретическая модель, которая говорит нам о невозможности и даже бессмысленности в выполнении задачи по точному измерению береговой линии, так как она представлена виде бесконечного количества самоподобных форм. Государственные же границы далеко не всегда обладают такими свойствами, ведь они проходят не только по границам рек и морей, а частенько просто проведены прямыми линиями вдоль меридианов и параллелей.
Практические выводы
Парадокс береговой линии – теоретическая концепция, и за истину все же принимать ее не стоит, если говорить с практической точки зрения. В реальности нет никакой необходимости измерять береговую полосу до песчинки или до атома, к тому же с каждым приливом и отливом, с каждым ударом морской волны о песчаный пляж береговая линия подвергается эрозии, и задача по идеально точному ее измерению представляет собой сизифов труд.
Но что же тогда дает на практике нам парадокс береговой линии? Еще один занимательный факт? Повод придумать шутку, про невозможность строительства стены от мигрантов вдоль границы США проходящей по реке Рио-Гранде, так как стоимость строительства будет стоить бесконечно много денег?
На мой взгляд, парадокс береговой линии – это лишний повод держать в голове тот факт, что в работах на стыке географии и математики нужно искать баланс между точностью и целесообразностью. В попытках идеально точно изобразить объект можно обнаружить, что либо на карте не видны все эти усилия, либо ни одна ЭВМ в мире не способна прогрузить ваше творение быстрее среднестатистического тиктока, что для пользователей веб-карт имеет существенное значение.
Работа “Какова протяженность побережья Британии? Статистическая самоподобие и дробная размерность” была не первой статьей Бенуа Мандельброта, связанной с фракталами. В одной из своих аннотаций ученый пишет, что до этой работы его предыдущие выступления на тему “фрактальной размерности” встречали слышимое неодобрение, а его работы считались бесполезными для науки. Находка в виде эффекта Ричардсона стала настоящим “Троянским конем” в мире сложной математики через легко объяснимые явления, которые можно встретить, сравнив между собой две карты разных масштабов.
Та самая шутка (источник – SMBC)
Источники:
- http://li.mit.edu/Stuff/CNSE/Paper/Mandelbrot67Science.pdf – How long is the coast of Britain? Statistical self-similarity and fractional dimension
- https://users.math.yale.edu/~bbm3/web_pdfs/howLongIsTheCoastOfBritain.pdf – How long is the coast of Britain? Statistical self-similarity and fractional dimension (с аннотациями автора)
- https://www.futilitycloset.com/2013/12/02/the-richardson-effect/– про Эффект Ричардсона
Длина береговой линии
Измерима ли она?
Вправе ли мы приводить в учебниках длину
береговой линии и не оконфузимся ли,
спрашивая эту цифру с учеников?
К.С. ЛАЗАРЕВИЧ
На уроках географии мы
оперируем множеством статистических
показателей. Большинство из них на вид очень
просты и четки: столько-то миллионов человек,
столько-то миллионов тонн угля, столько-то
километров. Но это если не вдумываться. А стоит
только копнуть любую цифру поглубже — и она
перестает быть четкой. Иногда же — рассыпается в
прах. Вот примеры.
Открываем недавно изданный и только что
поступивший в продажу Атлас мира (М.: ФГУП
Производственное картосоставительское
объединение «Картография», 2003.). В таблице
«Государства и территории мира» находим:
«Столица Франции — Париж (2 125,2 тыс. жителей). Если
ученик приведет на экзамене такую цифру, будет ли
экзаменатор удовлетворен? Ведь Париж — один из
крупнейших центров Европы и никак не меньше
Петербурга. Но в приведенной цифре нет ошибки:
это Париж в административных границах города
Парижа. А в границах реально сложившегося
городского сгустка — это десятимиллионник.
Очень многое зависит от того, как считать.
Сказанное не значит, что мы можем принять от
ученика в качестве ответа любую цифру в
диапазоне от 2,2 до 10; приводя то или иное число,
учащийся должен понимать, что за ним стоит, что и
как измерено.
Миллион тонн высококалорийного угля и угля
бурого — разные миллионы.
Но вот, казалось бы, километры. Километр — он и в
Африке километр. И что уж измеренное в километрах
можно подвергнуть сомнению? Но, оказывается, и
приводя длины в километрах, автор учебника
должен сначала подумать. Учитель же, пользуясь
учебником, также должен подвергнуть цифру
критическому анализу, прежде чем транслировать
ее ученикам и требовать ее запоминания. Читаем
учебник для 10-го класса: «Канада выходит к трем
океанам, и общая протяженность ее береговой
линии (около 250 тыс. км) не имеет себе равных в
мире». Как была измерена береговая линия, что
мерили, как мерили, чем мерили? Как вообще можно
измерить береговую линию?
Неправильные кривые по карте можно измерять
при помощи курвиметра — колесико этого прибора
катят по кривой, тщательно выписывая каждую
извилину. Однако извилистость береговой линии
часто бывает столь велика, что курвиметром по ней
не пройти. Приходится вышагивать по кривой
циркулем-измерителем. Наиболее удобная длина
шага — 2 мм. В разных масштабах этот шаг
соответствует, конечно, разным расстояниям,
точной длины такое измерение никогда не даст, так
как каждый шаг спрямляет кривую на небольшом
отрезке, но относительная погрешность более или
менее сохраняется.
Давайте, ради примера, попробуем измерить длину
береговой линии Чукотского а.о. Возьмем карту из
Школьного атласа по географии России (масштаб 1 :
22 000 000) и двухмиллиметровым шагом циркуля (44 км)
прошагаем все чукотское побережье. Результат
будет 4300 км (98 шагов циркуля). Произведем то же
измерение по карте масштаба
1 : 7 500 000. Здесь мы уже насчитаем 345
двухмиллиметровых (15 км) шажков, то есть
5 200 км. Логично предположить, что если в
измерениях будет использована карта еще
большего масштаба, измеренная береговая линия
станет еще протяженнее.
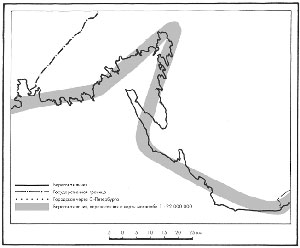
Поставим еще один эксперимент. Длина береговой
линии Ленинградской обл. по карте
1 : 22 000 000 — 300 км, по карте 1 : 2 500 000 — 555 км, а по
топографической карте
1 : 500 000 — 670 км. При этом длина береговой линии
одного только Выборгского залива (где берега
особо изрезаны заливчиками и бухточками),
измеренная по топографической карте, составляет
338 км, тогда как по школьному атласу — 65 км
(разница более чем в
5 раз!).
Таким образом, наблюдается закономерное
увеличение длины измеренной береговой линии с
укрупнением масштаба. Причина не только в том,
что двухмиллиметровый шаг циркуля соответствует
всё меньшей величине на местности, но главным
образом в том, что сама линия, даже если ее очень
точно измерить и перевести в соответствии с
масштабом в километры, действительно становится
длиннее (рис. 1). На карте России у берега
Ленинградской обл. угадываются лишь Выборгский
залив, Невская губа и небольшие изгибы южного
берега Финского залива. На карте масштаба
1 : 2 500 000 очертания Выборгского залива
уже довольно сложные, а на юге ясно видны
Копорская и Лужская губы. На полумиллионной
карте в пределах Выборгского залива множество
других мелких заливов, некоторые из которых
имеют собственные имена (зал. Балтиец, бухта
Ключевская), и лишь южный берег Финского залива
выглядит мало изменившимся по сравнению с
предыдущим масштабом, там изрезанность берега
гораздо меньше.
|
|
|
Рис. 1 Береговая линия Выборгского заливаСнята с карты масштаба |
Как же установить точную длину
береговой линии?
Этой целью задался английский метеоролог
Ричардсон, выбрав в качестве полигона свой
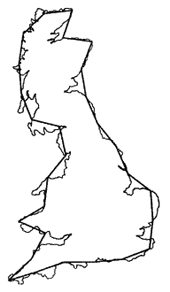
родной остров — Великобританию. Он и пришел к
выводу об увеличении длины береговой линии с
увеличением масштаба карты, по которой эту длину
измеряют (рис. 2). Есть ли предел такого
увеличения? Едва ли. Длину береговой линии
увеличивает каждая небольшая песчаная коса,
вдающаяся в море, каждая ложбинка, создающая
крохотный залив, каждый камешек, который
обтекает вода. Даже на самой крупномасштабной
карте их не видно, между тем в действительности
все эти неровности береговой линии существуют.
|
|
|
Рис. 2 Береговая линия Великобритании
|
Приводят много примеров того, как
использование математических методов позволяет
сделать географические исследования более
убедительными, более достоверными. Здесь же
произошло обратное: географическое исследование
— изучение длины береговой линии —
способствовало возникновению нового
математического понятия. Английское название
этого понятия — fractal, по-русски же оно еще
окончательно не устоялось и встречается в трех
вариантах: фрактал (родительный и
творительный падежи будут фрактала, фракталом),
фракталь в мужском роде (фракталя, фракталем)
и фракталь в женском роде (фрактали, фракталью);
за последнее время, кажется, склоняются к фракталу.
Фрактал — это линия, каждый фрагмент которой
бесконечно усложняется, длина каждого фрагмента
и всей линии постоянно увеличивается. В качестве
примера можно привести фигуру, обычно называемую
снежинкой Коха, хотя название это неверно:
построила эту снежинку в начале ХХ в. Хельга фон
Кох, и склонять ее фамилию не следует.
Возьмем равносторонний треугольник. Разделим
каждую его сторону на три равные части и на
среднем отрезке каждой стороны построим
равносторонний треугольник. Получится
правильная шестиконечная звезда, фигура с шестью
выпуклыми углами и шестью входящими. Разделим
каждую ее сторону (а этих сторон 12) на три равные
части и на среднем отрезке каждой стороны снова
построим равносторонний треугольник. Получится
фигура уже с 48 сторонами, с 18 выпуклыми и 30
входящими углами. Повторяя эту операцию
бесконечное число раз (сделать это можно,
конечно, лишь мысленно), мы получим фигуру,
площадь которой постоянно увеличивается, но все
медленнее, постепенно приближаясь к некоторому
пределу (рис. 3). Периметр же этой фигуры
увеличивается беспредельно, так как каждый раз,
когда мы строим на стороне фигуры новый
равносторонний треугольничек, сколь бы мал он ни
был, три равных отрезка этой стороны заменяются
на четыре таких же и потому длина каждой стороны
(и следовательно всего периметра) увеличивается
в 4/3 раза, а любое число больше единицы в степени,
равной бесконечности (а построение мы делаем
бесконечное число раз), стремится к
бесконечности.
|
|
|
Рис. 3 Снежинка Кох —разные стадии построения |
Граница снежинки будет представлять
собой что-то вроде широкой, мохнатой линии,
заполняющей собою всю приграничную область этой
фигуры. Понятия «широкая линия», «толстая
поверхность», казалось бы, абсурдные с точки
зрения классической математики (линия там не
имеет ширины, а поверхность — толщины), с
развитием теории фракталов приобрели права
гражданства. Считается, что линия одномерна, она
имеет только длину, положение точки на ней
определяется одной координатой; поверхность
двумерна, она имеет площадь, положение точки на
ней определяется двумя координатами; тело
трехмерно, оно имеет объем, нужны уже три
координаты. А теория фракталов вводит понятие
дробной размерности: линия не стала двумерной, но
уже перестала быть одномерной.
Неподготовленному человеку это довольно трудно
понять (нельзя же чихнуть полтора раза), но если
мы вспомним, как ведет себя береговая линия — не
только на карте, но и в природе, как она меняется,
если смотреть на нее, присев на корточки, потом
выпрямившись во весь рост, потом поднявшись на
гору, потом взлетев на самолете или космическом
корабле, мы не столько поймем, сколько
почувствуем, какую сложную систему представляет
собой эта линия; для нее определенно мало одной
характеристики — длины.
И теория фракталов, родившаяся из географических
исследований, уже сама приходит на помощь
географии. Еще не разработан, но определенно
имеет перспективы метод изучения рельефа как
фрактала. Рассматривая рельеф в общем виде, рисуя
его на мелкомасштабной карте, мы видим горные
хребты, плато, глубокие долины. В среднем
масштабе вырисовываются уже холмы, небольшие
долины, овраги. Еще крупнее — и видны кочки,
ветровая рябь на песке. Но и это не предел: есть
отдельные камешки, песчинки. В практическом
отношении все это важно потому, что нужно
научиться правильно отбирать объекты для
изображения на картах разных масштабов; одна из
главных ошибок составителей карт —
несоответствие содержания карты ее масштабу,
карта или недогружена, или перегружена.
А что же все-таки делать с длиной береговой линии?
Отказаться ее измерять, потому что она
неизмерима?
Нет, это не выход. Просто, приводя длину
береговой линии, следует всегда указывать, по
картам какого масштаба она измерялась, каким
способом. И обязательно оговаривать при
этом, учитывалась береговая линия островов
или нет. Без указания масштаба карт и того,
учтены острова или нет, всякие данные о длине
береговой линии теряют смысл. К сожалению, даже в
источниках, претендующих на сугубую солидность,
можно встретить страшные нелепости. Например,
известный сайт ЦРУ «The World Factbook». Здесь для каждой
страны и океана приведены данные по береговой
линии, но способ измерения не указан. В
результате береговая линия Канады оказывается
больше 200 тыс. км, Северного Ледовитого
океана — 45,4 тыс. км, Атлантического —
111,9 тыс. км (данные приведены — не подумайте
плохого! — с точностью до километра). Канаду
считали с учетом островов, это несомненно; как
считали океаны, неизвестно, но береговая линия
двух из трех океанов, омывающих Канаду, в сумме
меньше береговой линии одной только Канады. Для
Норвегии приведена цифра 21 925 км и дано
примечание: «Материк 3419 км, большие острова
2413 км, длинные фьорды, многочисленные
маленькие острова и мелкие изгибы [в буквальном
переводе зазубрины] береговой линии
16 093 км». В сумме получается как раз
указанная общая длина береговой линии. Но вот
почему берега фьордов — не часть береговой линии
материка, почему длина зазубрин приплюсована к
длине береговой линии материка, какие острова
считать большими — обо всем этом приходится
только догадываться. Совершенно бесспорные
данные в этой таблице приведены только для
Андорры, Австрии, Ботсваны, Венгрии, Свазиленда и
подобных им стран, выхода к морю не имеющих, —
написано: «0 км».
Вот казалось бы, что сложного измерить береговую линию. Ну да, она сложная, искривленная. Но это же не бактерия какая нибудь миниатюрная. Прошелся да измерил все вдоль границы. Однако, как вы поняли, тут совсем не все так просто.
Незадолго до 1951 года Льюис Фрай Ричардсон в ходе исследования предполагаемого влияния длины государственных границ на вероятность начала военных конфликтов заметил следующее: Португалия заявила, что её сухопутная граница с Испанией равна 987 км, а Испания определила её равной 1 214 км.
Этот факт послужил отправной точкой для изучения проблемы береговой линии и к необычному выводу: длина береговой линии оказывается недостижимым понятием, скользящим между пальцами тех, кто пытается его понять.
Основным методом оценки длины границы или береговой линии было наложение N равных отрезков длиной l на карту или аэрофотоснимок с помощью циркуля. Каждый конец отрезка должен принадлежать измеряемой границе. Исследуя расхождения в оценке границ, Ричардсон обнаружил то, что сейчас называется эффектом Ричардсона: масштаб измерений обратно пропорционален общей длине всех отрезков. То есть чем короче используемая линейка, тем длиннее измеряемая граница. Таким образом, испанские и португальские географы попросту руководствовались измерениями разных масштабов.
Наиболее поразительным для Ричардсона оказалось то, что когда величина линейки стремится к нулю, длина побережья стремится к бесконечности. Изначально Ричардсон полагал, опираясь на Евклидову геометрию, что эта длина достигнет фиксированной величины, как это происходит в случае с правильными геометрическими фигурами. Например, периметр правильного многоугольника, вписанного в окружность, приближается к длине самой окружности с увеличением числа сторон (и уменьшением длины каждой стороны). В теории геометрических измерений такая гладкая кривая, как окружность, которая может быть приближённо представлена в виде небольших отрезков с заданным пределом, называется спрямляемой кривой.
Спустя более десяти лет после завершения Ричардсоном своей работы Мандельброт разработал новую ветвь математики — фрактальную геометрию — для описания таких неспрямляемых комплексов, существующих в природе, как бесконечная береговая линия
Ключевым свойством фракталов является самоподобие, заключающееся в проявлении одной и той же общей фигуры на любом масштабе. Береговая линия воспринимается как чередование заливов и мысов. Гипотетически, если данная береговая линия имеет свойство самоподобия, то независимо от того, насколько сильно масштабируется та или иная часть, всё равно проявляется аналогичная картина меньших заливов и мысов, наложенная на бо́льшие заливы и мысы, вплоть до песчинок. На таких масштабах береговая линия оказывается мгновенно изменяющейся, потенциально бесконечной нитью со стохастическим расположением заливов и мысов. В таких условиях (в отличие от гладких кривых) Мандельброт утверждает: «Длина береговой линии оказывается недостижимым понятием, скользящим между пальцами тех, кто пытается его понять»
В реальности на береговых линиях отсутствуют детали меньше 1 см[источник не указан 918 дней]. Это связано с эрозией и другими морскими явлениями. В большинстве мест минимальный размер гораздо больше. Поэтому модель бесконечного фрактала не подходит для береговых линий.
Из практических соображений выбирают минимальный размер деталей равным порядку единиц измерения. Так, если береговая линия измеряется в километрах, то небольшие изменения линий, гораздо меньшие одного километра, просто не принимаются во внимание. Для измерения береговой линии в сантиметрах должны быть рассмотрены все небольшие вариации размером около одного сантиметра. Однако на масштабах порядка сантиметров должны быть сделаны различные произвольные нефрактальные допущения, например, там, где устье присоединяется к морю, или в тех местах, где должны быть проведены измерения на широких ваттах. Кроме того, использование различных методов измерения для разных единиц измерения не позволяет сделать преобразование этих единиц с помощью простого умножения.
Для определения государственных территориальных вод строят так называемые прямые исходные линии, соединяющие официально установленные точки побережья. Длину такой официальной береговой линии тоже не составляет труда измерить.
Предельные случаи парадокса береговой линии включают побережья с большим числом фьордов: это побережья Норвегии, Чили, северо-западное побережье Северной Америки и другие. От южной оконечности острова Ванкувер в северном направлении до южной оконечности Юго-Восточной Аляски изгибы побережья канадской провинции Британская Колумбия составляют более 10 % длины канадской береговой линии (с учётом всех островов Канадского Арктического архипелага) — 25 725 км из 243 042 км на линейном расстоянии, равном всего 965 км
[источники]источники
https://ru.wikipedia.org/wiki/%D0%9F%D0%B0%D1%80%D0%B0%D0%B4%D0%BE%D0%BA%D1%81_%D0%B1%D0%B5%D1%80%D0%B5%D0%B3%D0%BE%D0%B2%D0%BE%D0%B9_%D0%BB%D0%B8%D0%BD%D0%B8%D0%B8
http://en.wikipedia.org/wiki/Coastline_paradox