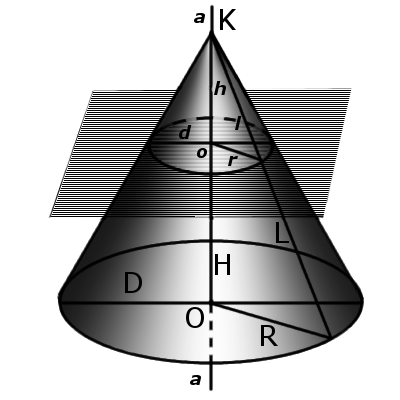
Элементы конуса
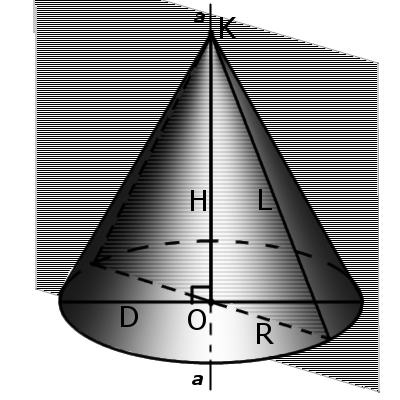
Определение. Вершина конуса — это точка (K), из которой исходят лучи.
Определение. Основание конуса — это плоскость, образованная в результате пересечения плоской поверхности и всех лучей, исходящих из вершины конуса. У конуса могут быть такие основы, как круг, эллипс, гипербола и парабола.
Определение. Образующей конуса (L) называется любой отрезок, который соединяет вершину конуса с границей основания конуса. Образующая есть отрезок луча, выходящего из вершины конуса.
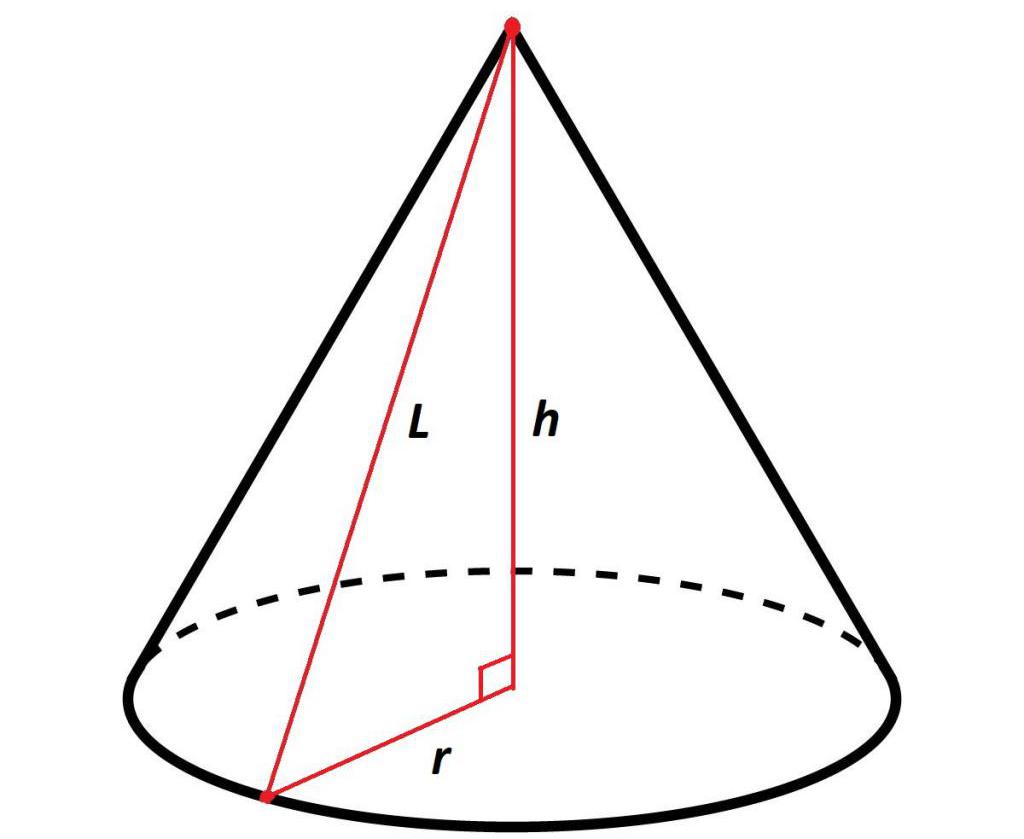
Формула. Длина образующей (L) прямого кругового конуса через радиус R и высоту H (через теорему Пифагора):
L2 = R2 + H2
Определение. Направляющая конуса — это кривая, которая описывает контур основания конуса.
Определение. Боковая поверхность конуса — это совокупность всех образующих конуса. То есть, поверхность, которая образуется движением образующей по направляющей конуса.
Определение. Поверхность конуса состоит из боковой поверхности и основания конуса.
Определение. Высота конуса (H) — это отрезок, который выходит из вершины конуса и перпендикулярный к его основанию.
Определение. Ось конуса (a) — это прямая, проходящая через вершину конуса и центр основания конуса.
Определение. Конусность (С) конуса — это отношение диаметра основания конуса к его высоте. В случае усеченного конуса — это отношение разности диаметров поперечных сечений D и d усеченного конуса к расстоянию между ними:
где C — конусность, D — диаметр основания, d — диаметр меньшего основания и h — расстояние между основаниями.
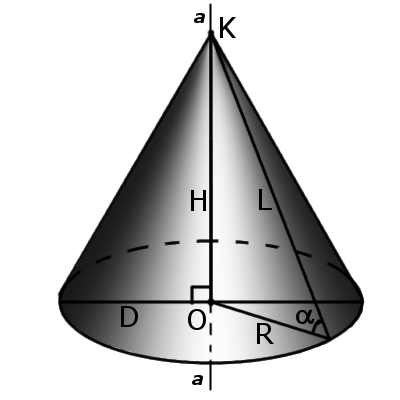
Конусность характеризует остроту конуса, то есть, угол наклона образующей к основанию конуса. Чем больше конусность, тем острее угол наклона. угол конуса α будет:
где R — радиус основы, а H — высота конуса.
Определение. Осевое сечение конуса — это сечение конуса плоскостью, проходящей через ось конуса. Такое сечение образует равнобедренный треугольник, у которого стороны образованы образующими, а основание треугольника — это диаметр основания конуса.
Определение. Касательная плоскость к конусу — это плоскость, проходящая через образующую конуса и перпендикулярна к осевому сечению конуса.
Определение. Конус, что опирается на круг, эллипс, гиперболу или параболу называется соответственно круговым, эллиптическим, гиперболическим или параболическим конусом (последние два имеют бесконечный объем).
Определение. Прямой конус — это конус у которого ось перпендикулярна основе. У такого конуса ось совпадает с высотой, а все образующие равны между собой.
Формула. Объём кругового конуса:
где R — радиус основы, а H — высота конуса.
Формула. Площадь боковой поверхности (Sb) прямого конуса через радиус R и длину образующей L:
Sb = πRL
Формула. Общая площадь поверхности (Sp) прямого кругового конуса через радиус R и длину образующей L:
Sp = πRL + πR2
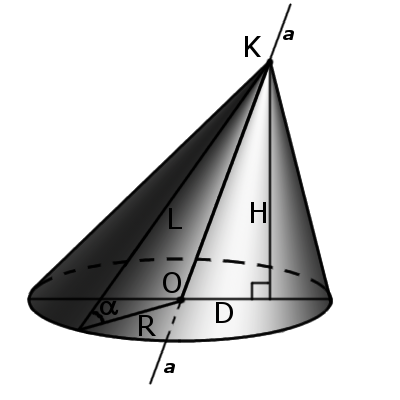
Определение. Косой (наклонный) конус — это конус у которого ось не перпендикулярна основе. У такого конуса ось не совпадает с высотой.
Формула. Объём любого конуса:
где S — площадь основы, а H — высота конуса.
Определение. Усеченный конус — это часть конуса, которая находится между основанием конуса и плоскостью сечения, параллельная основе.
Формула. Объём усеченного конуса:
где S1 и S2 — площади меньшей и большей основы соответственно, а H и h — расстояние от вершины конуса до центра нижней и верхней основы соответственно.
Уравнение конуса
1. Уравнение прямого кругового конуса в декартовой системе координат с координатами (x, y, z):
| x2 | + | y2 | — | z2 | = 0 |
| a2 | a2 | c2 |
2. Уравнение прямого эллиптического конуса в декартовой системе координат с координатами (x, y, z):
| x2 | + | y2 | = | z2 |
| a2 | b2 | c2 |
Основные свойства кругового конуса
1. Все образующие прямого кругового конуса равны между собой.
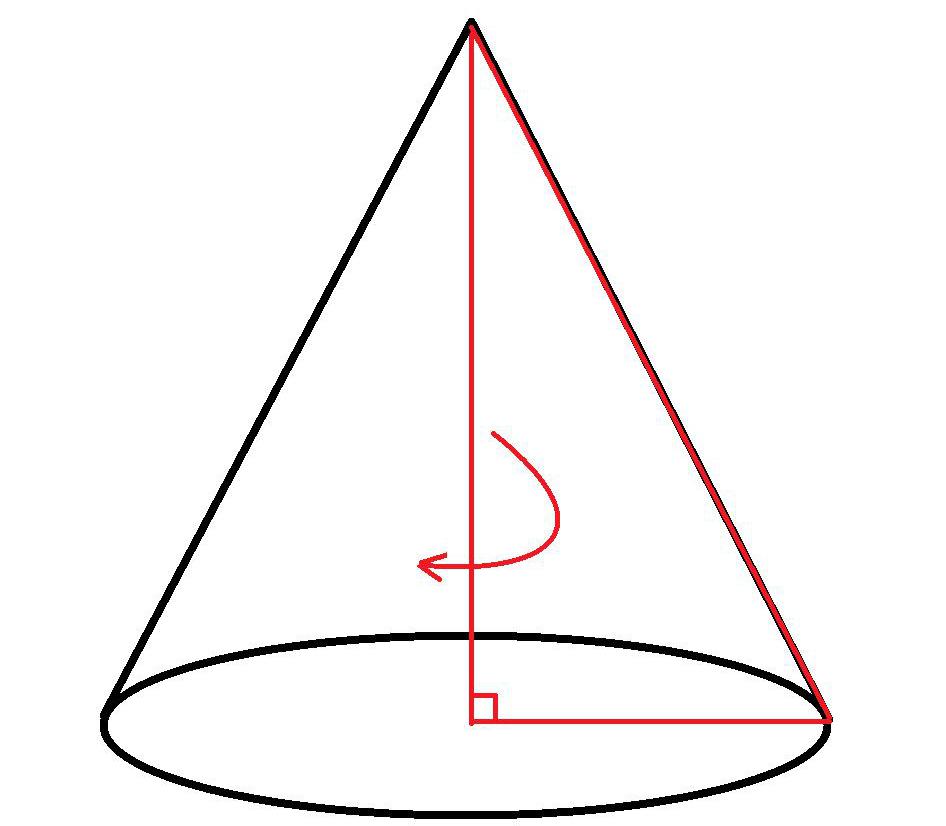
2. При вращении прямоугольного треугольника вокруг своего катета на 360 ° образуется прямой круговой конус.
3. При вращении равнобедренного треугольника вокруг своей оси на 180 ° образуется прямой круговой конус.
4. В месте пересечения конуса плоскостью, параллельной основанию конуса, образуется круг. (см. Срезанный конус)
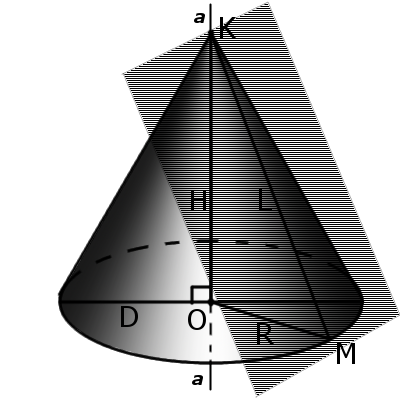
5. Если при пересечении плоскость не параллельна основе конуса и не пересекается с основанием, то в месте пересечения образуется эллипс (рис. 3).
6. Если плоскость сечения проходит через основание, то в месте пересечения образуется парабола (рис. 4).
7. Если плоскость сечения проходит через вершину, то в месте пересечения образуется равнобедренный треугольник (см. Осевое сечение).
8. Центр тяжести любого конуса находится на одной четвертой высоты от центра основы.
Конус — тело вращения, которое получается в результате вращения прямоугольного треугольника вокруг его катета.
Треугольник (POA) вращается вокруг стороны (PO).
(PO) — ось конуса и высота конуса.
(P) — вершина конуса.
(PA) — образующая конуса.
Круг с центром (O) — основание конуса.
(AO) — радиус основания конуса.
Осевое сечение конуса — это сечение конуса плоскостью, которая проходит через ось (PO) конуса.
Осевое сечение конуса — это равнобедренный треугольник.
(APB) — осевое сечение конуса.
— углы между образующими и основанием конуса.
Для конуса построим развёртку боковой поверхности. Это круговой сектор.

Сектор имеет длину дуги, равную длине окружности в основании конуса
2πR
, угол развёртки боковой поверхности
α
.
В конусе нельзя обозначить угол развёртки.
На развёртке конуса нельзя обозначить высоту и радиус конуса.
Образующая конуса (l) является радиусом сектора.
Таким образом, боковая поверхность конуса является частью полного круга с радиусом (l):
Длина дуги также является частью длины полной окружности с радиусом (l), но в то же время длина дуги — это длина окружности основания конуса с радиусом (R).
Сравним выражения длины дуги и выразим
α
через (R):
2πl⋅α360°=2πR;α=2πR⋅360°2πl=R⋅360°l.
Получаем ещё одну формулу боковой поверхности конуса; не используется угол развёртки боковой поверхности:
.
Если провести сечение конуса плоскостью, перпендикулярной оси конуса, то эта плоскость разбивает конус на две части, одна из которых — конус, а другую часть называют усечённым конусом.
Также усечённый конус можно рассматривать как тело вращения, которое образовалось в результате вращения прямоугольной трапеции вокруг боковой стороны (которая перпендикулярна к основанию трапеции) или в результате вращения равнобедренной трапеции вокруг высоты, проведённой через серединные точки оснований трапеции.
— ось конуса и высота конуса.
Круги с центрами (O) и
O1
— основания усечённого конуса.
(AO) и
A1O1
— радиусы оснований конуса.
Осевое сечение конуса — это сечение конуса плоскостью, которая проходит через ось
OO1
конуса.
Осевое сечение конуса — это равнобедренная трапеция.
— осевое сечение конуса.
Боковая поверхность определяется как разность боковой поверхности данного конуса и отсечённого конуса:
Sбок.=πR⋅PA−πr⋅PA1=πR⋅PA1+AA1−πr⋅PA1==πR⋅PA1+πR⋅AA1−πr⋅PA1==πR⋅l+πR−πr⋅PA1.
Так как
ΔPAO∼ΔPA1O1
, то стороны их пропорциональны:
PAPA1=Rr;l+PA1PA1=Rr;r⋅l+PA1=R⋅PA1;rl=R⋅PA1−r⋅PA1;PA1⋅R−r=rl;PA1=rlR−r.
Таким образом получаем формулу боковой поверхности усечённого конуса, которая содержит радиусы оснований и образующую усечённого конуса:
Sбок.=πRl+π⋅PA1⋅R−r=πRl+π⋅rlR−r⋅R−r;Sбок.=πRl+πrl=πl⋅R+r.
Геометрия является разделом математики, изучающим структуры в пространстве и отношение между ними. В свою очередь она также состоит из разделов, и одним из них является стереометрия. Она предусматривает изучение свойств объемных фигур, находящихся в пространстве: куба, пирамиды, шара, конуса, цилиндра и др.
Конус – это тело в евклидовом пространстве, которое ограничивает коническая поверхность и плоскость, на которой лежат концы ее образующих. Его образование происходит в процессе вращения прямоугольного треугольника вокруг любого из его катетов, поэтому он относится к телам вращения.
Составляющие конуса
Различают следующие виды конусов: косой (или наклонный) и прямой. Косым называется тот, ось которого пересекается с центром его основания не под прямым углом. По этой причине высота в таком конусе не совпадает с осью, так как она является отрезком, который опущен из вершины тела на плоскость его основания под углом 90°.
Тот конус, ось которого расположена перпендикулярно к его основанию, называется прямым. Ось и высота в таком геометрическом теле совпадают по причине того, что вершина в нем расположена над центром диаметра основания.
Конус состоит из следующих элементов:
- Круга, являющегося его основанием.
- Боковой поверхности.
- Точки, не лежащей в плоскости основания, называющейся вершиной конуса.
- Отрезков, которые соединяют точки круга основания геометрического тела и его вершину.
Все эти отрезки являются образующими конуса. Они наклонные к основанию геометрического тела, и в случае прямого конуса их проекции равны, так как вершина равноотдалена от точек круга основания. Таким образом, можно сделать вывод, что в правильном (прямом) конусе образующие равны, то есть имеют одинаковую длину и образуют одинаковые углы с осью (или высотой) и основанием.
Так как в косом (или наклонном) теле вращения вершина смещена по отношению к центру плоскости основания, образующие в таком теле имеют разную длину и проекцию, поскольку каждая из них находится на разном расстоянии от двух любых точек круга основания. Кроме того, углы между ними и высотой конуса также будут отличаться.
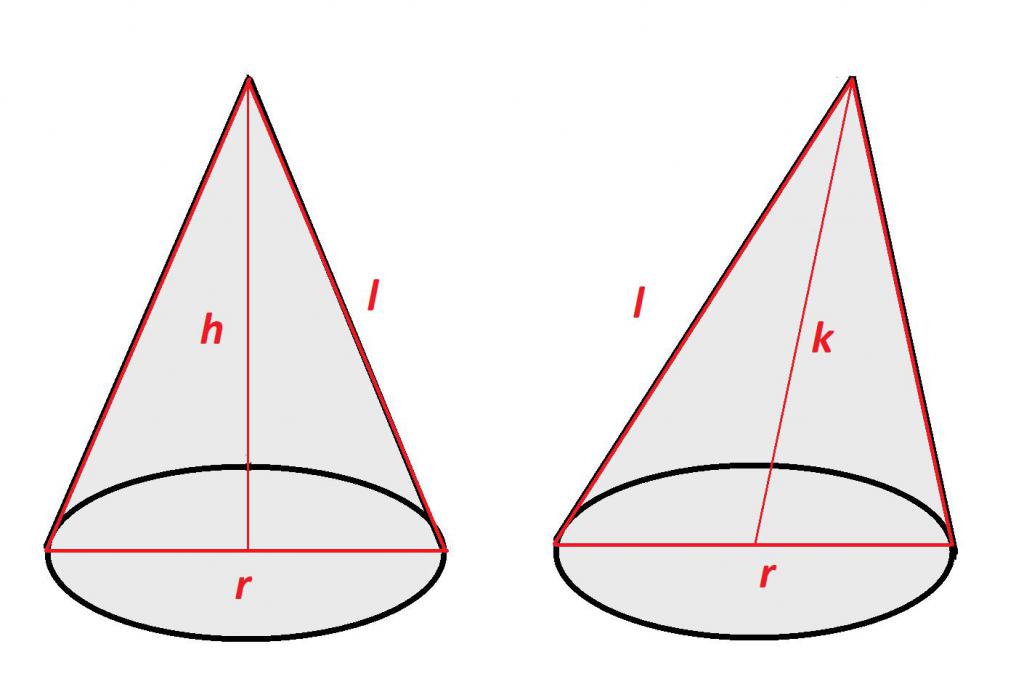
Длина образующих в прямом конусе
Как написано ранее, высота в прямом геометрическом теле вращения перпендикулярна плоскости основания. Таким образом, образующая, высота и радиус основания создают в конусе прямоугольный треугольник.
То есть, зная радиус основания и высоту, при помощи формулы из теоремы Пифагора, можно вычислить длину образующей, которая будет равна сумме квадратов радиуса основания и высоты:
l2 = r2+ h2 или l = √r2 + h2
где l – образующая;
r – радиус;
h – высота.
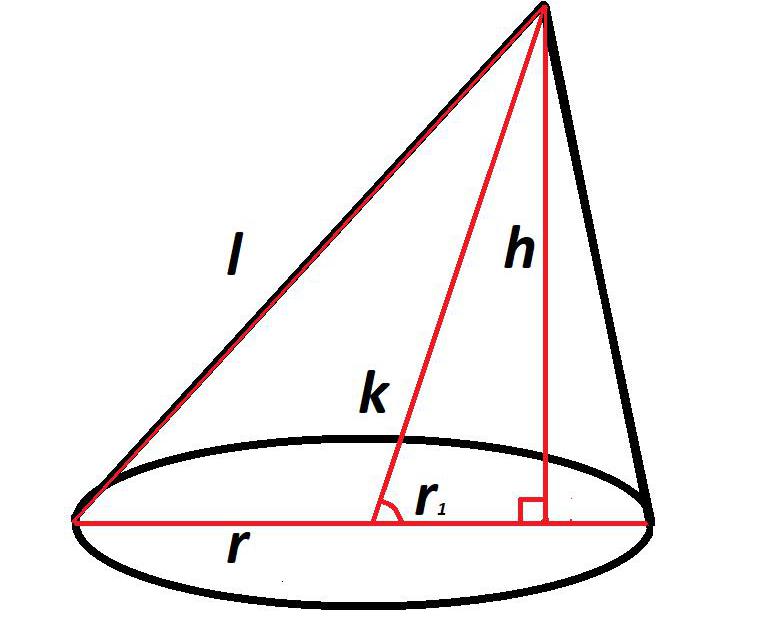
Образующая в наклонном конусе
Исходя из того, что в косом, или наклонном конусе образующие имеют не одинаковую длину, рассчитать их без дополнительных построений и вычислений не получится.
Прежде всего необходимо знать высоту, длину оси и радиус основания.
Имея эти данные, можно рассчитать часть радиуса, лежащую между осью и высотой, по формуле из теоремы Пифагора:
r1= √k2 — h2
где r1 – это часть радиуса между осью и высотой;
k – длина оси;
h – высота.
В результате сложения радиуса (r) и его части, лежащей между осью и высотой (r1), можно узнать полную сторону прямоугольного треугольника, сформированного образующей конуса, его высотой и частью диаметра:
R = r + r1
где R – катет треугольника, образованного высотой, образующей и частью диаметра основания;
r – радиус основания;
r1 – часть радиуса между осью и высотой.
Пользуясь все той же формулой из теоремы Пифагора, можно найти длину образующей конуса:
l = √h2+ R2
или, не производя отдельно расчет R, объединить две формулы в одну:
l = √h2 + (r + r1)2.
Несмотря на то, прямой или косой конус и какие вводные данные, все способы нахождения длины образующей всегда сводятся к одному итогу — использованию теоремы Пифагора.
Сечение конуса
Осевым сечением конуса называется плоскость, проходящая по его оси либо высоте. В прямом конусе такое сечение представляет собой равнобедренный треугольник, в котором высотой треугольника является высота тела, его сторонами выступают образующие, а основание – это диаметр основания. В равностороннем геометрическом теле осевое сечение является равносторонним треугольником, так как в этом конусе диаметр основания и образующие равны.
Плоскость осевого сечения в прямом конусе является плоскостью его симметрии. Причиной этому служит то, что его вершина находится над центром его основания, то есть плоскость осевого сечения делит конус на две одинаковые части.
Так как в наклонном объемном теле высота и ось не совпадают, плоскость осевого сечения может не включать в себя высоту. Если осевых сечений в таком конусе можно построить множество, так как для этого необходимо соблюдать лишь одно условие — оно должно проходить только через ось, то осевое сечение плоскости, которому будет принадлежать высота этого конуса, можно провести лишь одно, потому что количество условий увеличивается, а, как известно, две прямые (вместе) могут принадлежать только одной плоскости.
Площадь сечения
Упомянутое ранее осевое сечение конуса представляет собой треугольник. Исходя из этого, его площадь можно рассчитать по формуле площади треугольника:
S = 1/2 * d * h или S = 1/2 * 2r * h
где S – это площадь сечения;
d – диаметр основания;
r – радиус;
h – высота.
В косом, или наклонном конусе сечение по оси также является треугольником, поэтому в нем площадь сечения рассчитывается аналогично.
Объем
Поскольку конус является объемной фигурой в трехмерном пространстве, то можно вычислить его объем. Объемом конуса называется число, которое характеризует это тело в единице измерения объема, то есть в м3. Расчет не зависит от того, прямой он или косой (наклонный), так как формулы для двух этих видов тел не отличаются.
Как указано ранее, образование прямого конуса происходит вследствие вращения прямоугольного треугольника по одному из его катетов. Наклонный же, или косой конус образуется иначе, поскольку его высота смещена в сторону от центра плоскости основания тела. Тем не менее такие отличия в строении не влияют на методику расчета его объема.
Расчет объема
Формула объема любого конуса выглядит следующим образом:
V = 1/3 * π * h * r2
где V – это объем конуса;
h – высота;
r – радиус;
π — константа, равная 3,14.
Для того чтобы рассчитать обьем конуса, необходимо иметь данные о высоте и радиусе основания тела.
Для расчета высоты тела необходимо знать радиус основания и длину его образующей. Поскольку радиус, высота и образующая объединяются в прямоугольный треугольник, то высоту можно рассчитать по формуле из теоремы Пифагора (a2+ b2= c2 или в нашем случае h2+ r2= l2, где l – образующая). Высота при этом будет рассчитываться путем извлечения квадратного корня из разности квадратов гипотенузы и другого катета:
a = √c2— b2
То есть высота конуса будет равна величине, полученной после извлечения квадратного корня из разности квадрата длины образующей и квадрата радиуса основания:
h = √l2 — r2
Рассчитав таким методом высоту и зная радиус его основания, можно вычислить объем конуса. Образующая при этом играет важную роль, так как служит вспомогательным элементом в расчетах.
Аналогичным образом, если известна высота тела и длина его образующей, можно узнать радиус его основания, извлекая квадратный корень из разности квадрата образующей и квадрата высоты:
r = √l2 — h2
После чего по той же формуле, что указана выше, рассчитать объем конуса.
Объем наклонного конуса
Так как формула объема конуса одинакова для всех видов тела вращения, отличие в его расчете составляет поиск высоты.
Для того чтобы узнать высоту наклонного конуса, вводные данные должны включать длину образующей, радиус основания и расстояние между центром основания и местом пересечения высоты тела с плоскостью его основания. Зная это, можно с легкостью рассчитать ту часть диаметра основания, которая будет являться основанием прямоугольного треугольника (образованного высотой, образующей и плоскостью основания). После чего, снова используя теорему Пифагора, произвести расчет высоты конуса, а впоследствии и его объема.
Напомним,
что конус – это тело, полученное при вращении прямоугольного
треугольника вокруг прямой, проходящей через один из его катетов.
Назовём
элементы конуса.
Осью
конуса называется прямая вращения.
Основание конуса
– круг радиуса ,
который равен катету треугольника вращения.
Радиус
конуса –
это радиус его основания.
Вершина
конуса – неподвижная вершина треугольника вращения.
Образующая
конуса –
отрезок, соединяющий вершину конуса с любой точкой окружности основания. Все
образующие конуса равны между собой.
Высота конуса
–
перпендикуляр, опущенный из вершины конуса на плоскость его основания. Высота
конуса совпадает с неподвижным катетом треугольника вращения.
В
конусе радиус основания ,
высота и
образующая связаны
следующим соотношением:
.
Сечение
конуса плоскостью, проходящей через его вершину, представляет собой
равнобедренный треугольник, у которого боковые стороны являются образующими
конуса.
Осевым
сечением конуса называется сечение конуса плоскостью,
проходящей через его ось.
Осевое
сечение конуса – равнобедренный треугольник, боковые стороны
которого – образующие, а основание – диаметр основания конуса.
Боковую
поверхность конуса, как и боковую поверхность цилиндра,
можно развернуть на плоскость, разрезав её по одной из образующих. Развёрткой
боковой поверхности конуса является круговой сектор.
Обратите
внимание, радиус сектора равен образующей конуса,
а длина дуги сектора равна длине окружности основания конуса.
Площадь
боковой поверхности конуса можно вычислить по следующим
формулам:
,
,
,
где
–
длина окружности основания, –
радиус основания, –
образующая.
Площадь
полной поверхности конуса равна сумме площади боковой поверхности конуса и
площади его основания.
Тогда
площадь полной поверхности конуса можно вычислить по формуле^
,
где
–
радиус основания конуса, –
его образующая.
Объём конуса
равен одной третьей произведения площади основания на высоту.
Тогда
его можно вычислить по формуле:
,
где
–
радиус основания конуса, –
его высота.
Плоскость,
параллельная плоскости основания конуса, пересекает конус по кругу, а боковую
поверхность – по окружности с центром на оси конуса. Эта плоскость разбивает
конус на две части. Одна из частей (верхняя) представляет собой конус, а вторая
(нижняя) называется усечённым конусом.
Усечённым
конусом называется часть конуса, ограниченная его основанием
и сечением, параллельным плоскости основания. Усечённый конус имеет ось,
высоту ,
радиусы оснований и
,
образующую .
Осевое сечение усечённого конуса – равнобедренная трапеция.
Площадь
боковой поверхности усечённого конуса и объём усечённого конуса равен разности
площадей боковых поверхностей и объёмов полного конуса и отсечённого.
,
Площадь
боковой поверхности усечённого конуса можно найти по следующим
формулам:
,
Объём
усечённого конуса можно вычислить по следующим формулам:
,
где
и
–
площади оснований, –
высота усечённого конуса;
или
,
где
–
высота усечённого конуса, и
–
радиусы верхнего и нижнего оснований.
Основные
моменты мы с вами повторили, а теперь давайте перейдём к практической части
занятия.
Задача
первая. Радиус основания конуса равен см,
высота конуса равна см.
Найдите площадь боковой поверхности и объём конуса.
Решение.
Задача
вторая. В конус вписана правильная треугольная пирамида с
площадью основания см2
и углом наклона бокового ребра к основанию, равным .
Найдите объём и площадь полной поверхности конуса.
Решение.
Задача
третья. В равносторонний конус с радиусом основания, равным см,
вписан прямоугольный параллелепипед в основании которого лежит квадрат, с
высотой см
так, что одно его основание принадлежит основанию конуса, а вершины другого
основания принадлежат боковой поверхности конуса. Найдите объём
параллелепипеда. В ответе запишите значение .
Решение.
Задача
четвёртая. Длины радиусов оснований и образующей усечённого
конуса равны соответственно см,
см
и см.
Вычислите его высоту.
Решение.
§ 18. Конус
18.1.Определение конуса и его элементов
Определение. Тело, которое образуется при вращении прямоугольного треугольника вокруг прямой, содержащей его катет, называется прямым круговым конусом (рис. 165, 166).
Отрезок оси вращения, заключённый внутри конуса, называется осью конуса.
Круг, образованный при вращении второго катета, называется основанием конуса. Длина этого катета называется радиусом основания конуса или, короче, радиусом конуса. Вершина острого угла вращающегося треугольника, лежащая на оси вращения, называется вершиной конуса. На рисунках 165, б и 166 вершиной конуса является точка Р.
Высотой конуса называется отрезок, проведённый из вершины конуса перпендикулярно его основанию. Длину этого перпендикуляра также называют высотой конуса. Высота конуса имеет своим основанием центр круга — основания конуса — и совпадает с осью конуса.
Отрезки, соединяющие вершину конуса с точками окружности его основания, называются образующими конуса. Все образующие конуса равны между собой (почему?).
Как и в случае с цилиндром, можно рассматривать конус в более широком, чем у нас, понимании, когда в основании конуса может быть, например, эллипс (эллиптический конус), парабола (параболический конус). Мы будем изучать только определённый выше прямой круговой конус (конус вращения), поэтому слова «прямой круговой» мы будем опускать.
Рис. 165
Рис. 166
Рис. 167
Поверхность, полученная при вращении гипотенузы, называется боковой поверхностью конуса, а её площадь — площадью боковой поверхности конуса и обозначается Sбок. Боковая поверхность конуса является объединением всех его образующих.
Объединение боковой поверхности конуса и его основания называется полной поверхностью конуса, а её площадь называется площадью полной поверхности конуса или, короче, площадью поверхности конуса и обозначается Sкон. Из этого определения следует, что
Sкон = Sбок + Sосн.
Если вокруг данной прямой — оси — вращать пересекающую её прямую, то при этом вращении образуется поверхность, которую называют круговой конической поверхностью или конической поверхностью вращения. Уравнение 


18.2. Сечения конуса
Определение. Сечение конуса плоскостью, проходящей через его ось, называется осевым сечением конуса.
Рис. 168
Рис. 169
Рис. 170
Так как все образующие конуса равны, то его осевым сечением является равнобедренный треугольник, боковыми сторонами которого являются образующие конуса, а основанием — диаметр конуса. При этом все осевые сечения конуса — равные равнобедренные треугольники. На рисунке 168 осевым сечением конуса является треугольник ABP (АР = ВР). Угол АPВ называют углом при вершине осевого сечения конуса.
Конус, в осевом сечении которого правильный треугольник, называется равносторонним конусом.
Если секущая плоскость проходит через вершину конуса, пересекает конус, но не проходит через его ось, то в сечении конуса также получается равнобедренный треугольник (см. рис. 168: △ DCP).
Так как конус — тело вращения, то любое сечение конуса плоскостью, перпендикулярной его оси (т. е. параллельной основанию конуса), есть круг, а сечение боковой поверхности конуса такой плоскостью — окружность этого круга; центром круга (окружности) является точка пересечения оси конуса и секущей плоскости (рис. 169).
Если секущая плоскость не параллельна плоскости основания конуса и не пересекает основание, то сечением боковой поверхности конуса такой плоскостью является эллипс (рис. 170). Поэтому эллипс называют коническим сечением.
Рис. 171

О конических сечениях можно прочитать в очерках «Элементарная геометрия», «Проективная геометрия» в конце этой книги.
ЗАДАЧА (3.047). Высота конуса равна радиусу R его основания. Через вершину конуса проведена плоскость, отсекающая от окружности основания дугу: а) в 60°; б) в 90°. Найти площадь сечения.
Решение. Рассмотрим случай а). Пусть плоскость α пересекает поверхность конуса с вершиной Р по образующим РА и РВ (рис. 172); △ АВР — искомое сечение. Найдём площадь этого сечения.
Хорда АВ окружности основания стягивает дугу в 60°, значит, △ AOB — правильный и АВ = R.
Рис. 172
Если точка С — середина стороны АB, то отрезок PC — высота треугольника АВР. Поэтому S△ ABP = 



Тогда S△ ABP = 

Ответ: а) 
18.3. Касательная плоскость к конусу
Определение. Касательной плоскостью к конусу называется плоскость, проходящая через образующую конуса перпендикулярно осевому сечению, проведённому через эту образующую.
Рис. 173
Говорят, что плоскость α касается конуса по образующей РА (рис. 173): каждая точка образующей РА является точкой касания плоскости α и данного конуса.
Через любую точку боковой поверхности конуса проходит только одна его образующая. Через эту образующую можно провести только одно осевое сечение и только одну плоскость, перпендикулярную плоскости этого осевого сечения. Следовательно, через каждую точку боковой поверхности конуса можно провести лишь одну плоскость, касательную к данному конусу в этой точке.
18.4. Изображение конуса
Рис. 174
Для изображения конуса достаточно построить: 1) эллипс, изображающий окружность основания конуса (рис. 174); 2) центр О этого эллипса; 3) отрезок ОР, изображающий высоту конуса; 4) касательные прямые РА и PB из точки Р к эллипсу (их проводят с помощью линейки на глаз).
Для достижения наглядности изображения невидимые линии изображают штрихами.
Необходимо заметить, что отрезок АВ, соединяющий точки касания образующих и окружности основания конуса, ни в коем случае не является диаметром основания конуса, т. е. этот отрезок не содержит центра О эллипса. Следовательно, △ АBP — не осевое сечение конуса. Осевым сечением конуса является △ ACP, где отрезок AC проходит через точку О, но образующая PC не является касательной к окружности основания.
18.5. Развёртка и площадь поверхности конуса
Пусть l — длина образующей, R — радиус основания конуса с вершиной Р.
Рис. 175
Рис. 176
Поверхность конуса состоит из боковой поверхности конуса и его основания. Если эту поверхность разрезать по одной из образующих, например по образующей PA (рис. 175), и по окружности основания, затем боковую поверхность конуса развернуть на плоскости (рис. 176, a), то получим развёртку поверхности конуса (рис. 176, б), состоящую из: а) кругового сектора, радиус которого равен образующей l конуса, а длина дуги сектора равна длине окружности основания конуса; б) круга, радиус которого равен радиусу R основания конуса. Угол сектора развёртки боковой поверхности конуса называют углом развёртки конуса; его численная величина равна отношению длины окружности основания конуса к его образующей (радиусу сектора развёртки):
α = 
За площадь боковой поверхности конуса принимается площадь её развёртки. Выразим площадь боковой поверхности конуса через длину l его образующей и радиус R основания.
Площадь боковой поверхности — площадь кругового сектора радиуса длины l — вычисляется по формуле
Sбок = 
где α — величина угла (в радианах) сектора — развёртки. Учитывая, что α = 
Sбок = πRl.(2)
Таким образом, доказана следующая теорема.
Теорема 27. Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую. ▼
Площадь полной поверхности конуса равна сумме площадей его боковой поверхности и основания, т. е.
Sкон = πRl + πR2.(3)
Следствие. Пусть конус образован вращением прямоугольного треугольника ABC вокруг катета АС (рис. 177). Тогда Sбок = π•BC•АВ. Если D — середина отрезка АВ, то AB = 2AD, поэтому
Sбок = 2 π ВС•AD.(4)
Рис. 177
Проведём DE ⟂ АB (E ∈ l = AС). Из подобия прямоугольных треугольников ADE и ACB (у них общий угол А) имеем


Тогда соотношение (4) принимает вид
Sбок = (2π•DE)•AC,(6)
т. е. площадь боковой поверхности конуса равна произведению высоты конуса на длину окружности, радиус которой равен длине серединного перпендикуляра, проведённого из точки на оси конуса к его образующей.
Это следствие будет использовано в п. 19.7.
18.6. Свойства параллельных сечений конуса
Теоремa 28. Если конус пересечён плоскостью, параллельной основанию, то: 1) все образующие и высота конуса делятся этой плоскостью на пропорциональные части; 2) в сечении получается круг; 3) площади сечения и основания относятся, как квадраты их расстояний от вершины.
Рис. 178
Доказательство. 1) Пусть конус с вершиной Р и основанием F пересечён плоскостью α, параллельной плоскости β основания конуса и расположенной между Р и β (рис. 178).
Проведём высоту РО конуса, где точка О — центр круга F. Так как РО ⟂ β, α || β, то α ⟂ РО. Значит, в сечении конуса плоскостью α получается круг с центром в точке O1 = α ∩ РО. Обозначим этот круг F1.
Рассмотрим гомотетию 
Так как при гомотетии её центр является неподвижной точкой, прямая, проходящая через центр гомотетии, отображается на себя, а пересечение двух фигур — на пересечение их образов, то гомотетия 



где k — коэффициент гомотетии 
А поскольку гомотетия является подобием, то круг F1, являющийся параллельным сечением конуса, подобен его основанию.
Вследствие того что отношение площадей гомотетичных фигур равно квадрату коэффициента гомотетии и k = PO1 : РО, где РO1 и PO — расстояния соответственно параллельного сечения и основания пирамиды от её вершины, то
Sсечен : Sоснов = k2 = 
Теорема доказана. ▼
18.7.Вписанные в конус и описанные около конуса пирамиды
Определение. Пирамида называется вписанной в конус, если у них вершина общая, а основание пирамиды вписано в основание конуса. В этом случае конус называется описанным около пирамиды.
Для построения изображения правильной пирамиды, вписанной в конус:
—строят изображение основания пирамиды — правильного многоугольника, вписанного в основание конуса;
—соединяют отрезками прямых вершину конуса с вершинами построенного многоугольника;
—выделяют видимые и невидимые (штрихами) линии изображаемых фигур.
На рисунках 179—182 изображена вписанная в конус пирамида, в основаниях которой лежит:
—прямоугольный треугольник (см. рис. 179);
—правильный треугольник (см. рис. 180);
—квадрат (см. рис. 181);
—правильный шестиугольник (см. рис. 182).
Рис. 179
Рис. 180
Рис. 181
Рис. 182
Определение. Пирамида называется описанной около конуса, если у них вершина общая, а основание пирамиды описано около основания конуса. В этом случае конус называют вписанным в пирамиду (рис. 183).
Рис. 183
Рис. 184
ЗАДАЧА (3.080). В равносторонний конус вписана правильная пирамида. Найти отношение площадей боковых поверхностей пирамиды и конуса, если пирамида: а) треугольная; б) четырёхугольная; в) шестиугольная.
Решение. Рассмотрим случай а). Пусть R — радиус основания равностороннего конуса, РАВС — правильная пирамида, вписанная в этот конус (рис. 184); △ DPE — осевое сечение конуса, CF — медиана △ АBС. Тогда в △ АВС (правильный): АВ = R



PF = 

Так как CF — медиана △ АВС, то PF — высота равнобедренного треугольника АВР. Поэтому
S△ ABP = 




Обозначим: S1 — площадь боковой поверхности пирамиды, S2 — площадь боковой поверхности конуса. Тогда
S1 = 3S△ ABP = 
S
2 = πR•PA = πR•2R = 2πR2.
Следовательно,
S1 : S2 = 

Ответ: а) 


18.8. Усечённый конус
Рис. 185
Пусть дан конус с вершиной Р. Проведём плоскость α, параллельную плоскости основания конуса и пересекающую этот конус (рис. 185). Эта плоскость пересекает данный конус по кругу и разбивает его на два тела: одно из них является конусом, а другое (расположенное между плоскостью основания данного конуса и секущей плоскостью) называют усечённым конусом. Таким образом, усечённый конус представляет собой часть полного конуса, заключённую между его основанием и параллельной ему плоскостью. Основание данного конуса и круг, полученный в сечении этого конуса плоскостью α, называются соответственно нижним и верхним основаниями усечённого конуса. Высотой усечённого конуса называется перпендикуляр, проведённый из какой-либо точки одного основания к плоскости другого. Длину этого перпендикуляра также называют высотой усечённого конуса. (Часто за высоту усечённого конуса принимают отрезок, соединяющий центры его оснований.)
Рис. 186
Рис. 187
Часть боковой поверхности данного конуса, ограничивающая усечённый конус, называется боковой поверхностью усечённого конуса, а отрезки образующих конуса, заключённые между основаниями усечённого конуса, называются образующими усечённого конуса. Так как все образующие данного конуса равны и равны все образующие отсечённого конуса, то равны все образующие усечённого конуса.
Построение изображения усечённого конуса следует начинать с изображения того конуса, из которого получился усечённый конус (рис. 186).
На рисунке 187 показана развёртка усечённого конуса.
Из теоремы 28 следует, что основания усечённого конуса — подобные круги.
Определения усечённой пирамиды, вписанной в усечённый конус и описанной около него, аналогичны определениям пирамиды, вписанной в конус и описанной около него.
Заметим, что построение изображений усечённой пирамиды, вписанной в усечённый конус и описанной около него, следует начинать с изображений того конуса или той пирамиды, из которых получены соответственно усечённые конус и пирамида.
Полной поверхностью усечённого конуса называется объединение боковой поверхности этого конуса и двух его оснований. Иногда полную поверхность усечённого конуса называют его поверхностью, а её площадь — площадью поверхности усечённого конуса. Эта площадь равна сумме площадей боковой поверхности и оснований усечённого конуса.
Усечённый конус может быть образован также вращением прямоугольной трапеции вокруг боковой стороны трапеции, перпендикулярной её основанию.
Рис. 188
На рисунке 188 изображён усечённый конус, образованный вращением прямоугольной трапеции ABCD вокруг стороны CD. При этом боковая поверхность усечённого конуса образована вращением боковой стороны АВ, а основания его — вращением оснований AD и ВС трапеции.
18.9. Поверхность усечённого конуса
Выразим площадь Sбок боковой поверхности усечённого конуса через длину l его образующей и радиусы R и r оснований (R > r).
Рис. 189
Пусть точка Р — вершина конуса, из которого получен усечённый конус; точки О, O1 — центры оснований усечённого конуса; AA1 = l — одна из образующих усечённого конуса (рис. 189).
Используя формулу (2) п. 18.5, получаем
Sбок = πR•PA – πr•РA1 =
= πR(РA1 + А1A) – πr•PA1 =
= πR•A1A + π(R – r)•PA1.
Учитывая, что A1A = l, имеем
Sбок = πRl + π(R – r)PA1.(7)
Выразим PA1 через l, R и r. Так как O1A1 || OA и OO1 — высота усечённого конуса, то прямоугольные треугольники POA и PO1A1 подобны. Поэтому АО : А1O1 = PA : PA1 или
R : r = (PA1 + A1A) : PA1, откуда
R•PA1 = r(PA1 + l) ⇒ (R – r)PA1 = rl ⇒ PA1 = 
Подставив это значение РА1 в (7), получаем
Sбок = π(R + r)l.(8)
Таким образом, доказана следующая теорема.
Теорема 29. Площадь боковой поверхности усечённого конуса равна произведению полусуммы длин окружностей оснований на образующую. ▼
Площадь полной поверхности усечённого конуса находится по формуле:
Sполн = π•(R + r)•l + π•R2 + π•r2.
Следствие. Пусть усечённый конус образован вращением прямоугольной трапеции ABCD вокруг её высоты AD (рис. 190). Тогда Sбок = π (АВ + DC)•ВС. Если KЕ — средняя линия трапеции, то АВ + DC = 2KE, поэтому
Sбок = 2π•KE•BC.(9)
Рис. 190
Проведём EF ⟂ ВС. Из подобия прямоугольных треугольников ВСН и EFK имеем
BC : EF = BH : KE ⇒ ⇒ KE•BC = EF•BH.(10)
Тогда равенство (9) принимает вид
Sбок = (2π•EF)•ВH,(11)
т. е. боковая поверхность усечённого конуса равна произведению его высоты на длину окружности, радиус которой равен серединному перпендикуляру, проведённому из точки оси конуса к его образующей.
18.10. Объёмы конуса и усечённого конуса
Найдём объём конуса, высота которого равна h и радиус основания — R. Для этого расположим этот конус и правильную четырёхугольную пирамиду, высота которой равна h и сторона основания — R, так, чтобы их основания находились на одной и той же плоскости α, а вершины — также в одной и той же плоскости β, параллельной плоскости α и удалённой от неё на расстояние h (рис. 191).
Рис. 191
Каждая плоскость, параллельная данным плоскостям и пересекающая конус, пересекает также пирамиду; причём площади сечений, образованных при пересечении обоих тел, относятся к площадям оснований этих тел, как квадраты их расстояний от вершин. А так как секущие плоскости для пирамиды и для конуса равноудалены от их вершин, то 




Vкон : Vпир = π : 1 или Vкон : 
Vкон = 
Рис. 192
Самостоятельно рассмотрите усечённые конус и пирамиду, расположенные в соответствии с условиями принципа Кавальери. Тогда вы получите формулу вычисления объёма усечённого конуса:
Vус. кон = 
Эту же формулу вы можете вывести, если используете идею подобия так же, как это сделано в случае с выводом формулы площади боковой поверхности усечённого конуса.
Используя принцип Кавальери, докажите, что объём каждого из тел, на которые конус разбивается его сечением плоскостью, проходящей через вершину (рис. 192), может быть вычислен по формуле V =