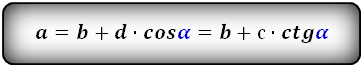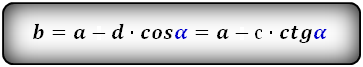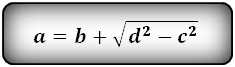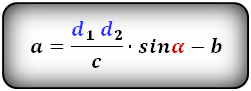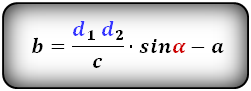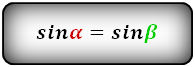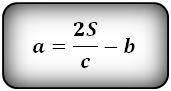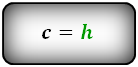1. Формула длины оснований прямоугольной трапеции через среднюю линию
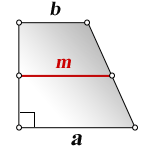
a — нижнее основание
b — верхнее основание
m — средняя линия
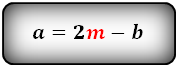
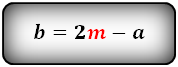
Формулы длины оснований :
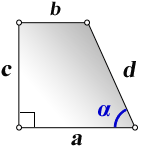
2. Формулы длины оснований через боковые стороны и угол при нижнем основании
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
α — угол при нижнем основании
Формулы длины оснований :
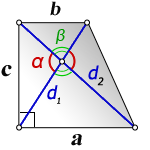
3. Формулы длины оснований трапеции через диагонали и угол между ними
a — нижнее основание
b — верхнее основание
c — боковая сторона под прямым углом к основаниям
d1 , d2 — диагонали трапеции
α , β — углы между диагоналями
Формулы длины оснований :
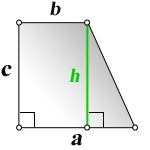
4. Формулы длины оснований трапеции через площадь
a — нижнее основание
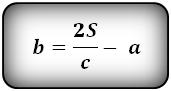
b — верхнее основание
c — боковая сторона под прямым углом к основаниям
h — высота трапеции
Формулы длины оснований :
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
- Подробности
-
Опубликовано: 15 октября 2013
-
Обновлено: 13 августа 2021
Как найти основания прямоугольной трапеции
Математическая фигура с четырьмя углами называется трапецией, если пара противоположных ее сторон параллельна, а другая пара — нет. Параллельные стороны называют основаниями трапеции, две другие — боковыми. В прямоугольной трапеции один из углов при боковой стороне — прямой.
Инструкция
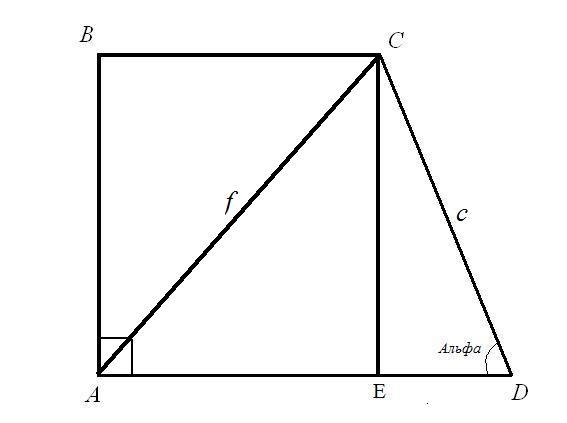
Задача 1.Найдите основания BC и AD прямоугольной трапеции, если известна длина диагонали AC = f; длина боковой стороны CD = c и угол при ней ADC = α.Решение:Рассмотрите прямоугольный треугольник CED. Известны гипотенуза c и угол между гипотенузой и катетом EDC. Найдите длины сторон CE и ED: по формуле угла CE = CD*sin(ADC); ED = CD*cos(ADC). Итак: CE = c*sinα; ED=c*cosα.
Рассмотрите прямоугольный треугольник ACE. Гипотенуза AC и катет CE вам известны, найдите сторону AE по правилу прямоугольного треугольника: сумма квадратов катетов равна квадрату гипотенузы. Итак: AE(2) = AC(2) — CE(2) = f(2) — c*sinα. Вычислите квадратный корень из правой части равенства. Вы нашли верхнее основание прямоугольной трапеции.
Длина основания AD является суммой длин двух отрезков AE и ED. AE = квадратный корень(f(2) — c*sinα); ED = c*cosα).Итак: AD = квадратный корень(f(2) — c*sinα) + c*cosα.Вы нашли нижнее основание прямоугольной трапеции.
Задача 2.Найдите основания BC и AD прямоугольной трапеции, если известна длина диагонали BD = f; длина боковой стороны CD = c и угол при ней ADC = α.Решение:Рассмотрите прямоугольный треугольник CED. Найдите длины сторон CE и ED: CE = CD*sin(ADC) = c*sinα; ED = CD*cos(ADC) = c*cosα.
Рассмотрите прямоугольник ABCE. По свойству прямоугольника AB = CE = c*sinα.Рассмотрите прямоугольный треугольник ABD. По свойству прямоугольного треугольника квадрат гипотенузы равен сумме квадратов катетов. Поэтому AD(2) = BD(2) — AB(2) = f(2) — c*sinα.Вы нашли нижнее основание прямоугольной трапеции AD = квадратный корень(f(2) — c*sinα).
По правилу прямоугольника BC = AE = AD — ED = квадратный корень(f(2) — c*sinα) — с*cosα.Вы нашли верхнее основание прямоугольной трапеции.
Я начал бы свои рассуждения с того, что есть теорема про сумму внутренних углов выпуклого многоугольника, которая равна 180 ̊ * (n — 2), где n — число сторон этого многоугольника. В нашей задаче сумма всех внутренних углов стало быть равна 360 ̊. Стало быть угол при вершине D будет равен 360 — 90 — 90 — 45 = 135 ̊.
Тепрь если из точки D опустить перпендикуляр на основание трапеции AB, то угол при вершине D разделится на две составляющих 45 ̊ и 90 ̊ (как известно — основания у трапеции параллельны по определению). При этом длина перпендикуляра DD’ равна длине стороны трапеции CB (противоположные стороны прямоугольника равны между собой).
Треугольник ADD’ будет прямоугольным и равносторонним, поскольку равны углы, лежащие у его основания (основанием мы считаем самую длинную его сторону).
Отсюда следует, что длина основания трапеции DC = AB — AD’ = AB — CB = 31 — 19 = 12.
Вот и вся недолга
Вася Иванов
Мореплаватель — имя существительное, употребляется в мужском роде. К нему может быть несколько синонимов.
1. Моряк. Старый моряк смотрел вдаль, думая о предстоящем опасном путешествии;
2. Аргонавт. На аргонавте были старые потертые штаны, а его рубашка пропиталась запахом моря и соли;
3. Мореход. Опытный мореход знал, что на этом месте погибло уже много кораблей, ведь под водой скрывались острые скалы;
4. Морской волк. Старый морской волк был рад, ведь ему предстояло отчалить в долгое плавание.
Найди длину большего основания ML прямоугольной трапеции MNKL , где ∠M=90°. Сторона MN=12 м, диагональ MK=13 м, SΔMKL=120 м^2.