Домашняя лабораторная работа
« Измерение размеров бруска (спичечного коробка)»
Цель: Измерить длину, ширину и высоту бруска, указав погрешность измерений.
Оборудование: линейка измерительная, деревянный брусок или спичечный коробок.
Порядок выполнения работы:
-
Вычислите цену деления шкалы линейки.
-
Укажите предел измерения этой шкалы.
-
Вычислите погрешность измерений.
-
Измерьте линейкой длину, ширину и высоту бруска.
-
Результаты всех измерений запишите в тетрадь.
-
Сделайте вывод об итогах работы.
Домашняя лабораторная работа
« Измерение размеров бруска (спичечного коробка)»
Цель: Измерить длину, ширину и высоту бруска, указав погрешность измерений.
Оборудование: линейка измерительная, деревянный брусок или спичечный коробок.
Порядок выполнения работы:
-
Вычислите цену деления шкалы линейки.
-
Укажите предел измерения этой шкалы.
-
Вычислите погрешность измерений.
-
Измерьте линейкой длину, ширину и высоту бруска.
-
Результаты всех измерений запишите в тетрадь.
-
Сделайте вывод об итогах работы.
Домашняя лабораторная работа
« Измерение размеров бруска (спичечного коробка)»
Цель: Измерить длину, ширину и высоту бруска, указав погрешность измерений.
Оборудование: линейка измерительная, деревянный брусок или спичечный коробок.
Порядок выполнения работы:
-
Вычислите цену деления шкалы линейки.
-
Укажите предел измерения этой шкалы.
-
Вычислите погрешность измерений.
-
Измерьте линейкой длину, ширину и высоту бруска.
-
Результаты всех измерений запишите в тетрадь.
-
Сделайте вывод об итогах работы.
Домашняя лабораторная работа
« Измерение размеров бруска (спичечного коробка)»
Цель: Измерить длину, ширину и высоту бруска, указав погрешность измерений.
Оборудование: линейка измерительная, деревянный брусок или спичечный коробок.
Порядок выполнения работы:
-
Вычислите цену деления шкалы линейки.
-
Укажите предел измерения этой шкалы.
-
Вычислите погрешность измерений.
-
Измерьте линейкой длину, ширину и высоту бруска.
-
Результаты всех измерений запишите в тетрадь.
-
Сделайте вывод об итогах работы.
Домашняя лабораторная работа
« Измерение размеров бруска (спичечного коробка)»
Цель: Измерить длину, ширину и высоту бруска, указав погрешность измерений.
Оборудование: линейка измерительная, деревянный брусок или спичечный коробок.
Порядок выполнения работы:
-
Вычислите цену деления шкалы линейки.
-
Укажите предел измерения этой шкалы.
-
Вычислите погрешность измерений.
-
Измерьте линейкой длину, ширину и высоту бруска.
-
Результаты всех измерений запишите в тетрадь.
-
Сделайте вывод об итогах работы.
Домашняя лабораторная работа
« Измерение размеров бруска (спичечного коробка)»
Цель: Измерить длину, ширину и высоту бруска, указав погрешность измерений.
Оборудование: линейка измерительная, деревянный брусок или спичечный коробок.
Порядок выполнения работы:
-
Вычислите цену деления шкалы линейки.
-
Укажите предел измерения этой шкалы.
-
Вычислите погрешность измерений.
-
Измерьте линейкой длину, ширину и высоту бруска.
-
Результаты всех измерений запишите в тетрадь.
-
Сделайте вывод об итогах работы.
Изготовление модели нониуса и измерение
линейных размеров и объёмов тел
О.Г.ЦАРЬКОВА olga@kapella.gpi.ru,
ФМШ № 2007, г. Москва
Изготовление модели нониуса и
измерение линейных размеров и объёмов тел
Физический практикум. 11-й класс
Цель работы. Изучение работы
нониуса и его изготовление. Измерения размеров
бруска с помощью нониуса и определение
абсолютной и относительных погрешностей
измерений.
Оборудование: брусок в форме
параллелепипеда; тело цилиндрической формы; лист
плотной бумаги; ножницы; масштабная линейка.
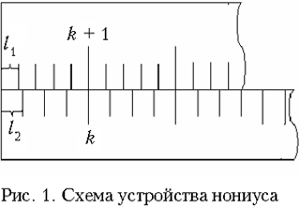
Принцип действия нониуса.
Представим себе две линейки, сложенные вместе,
рис. 1.
Пусть цена деления верхней линейки
равна l1, а нижней – l2.
Линейки образуют нониус, если существует такое
целое число k, при котором
kl2
=(k+1)l1
(1)
На рис.1 k = 4. Величина
(2)
называется точностью нониуса. В
частности, при l1 = 1 мм, k = 10
точность нониуса = 0,1 мм. Как видно из рис. 1, при совпадении
нулевых делений нижней и верхней шкал совпадают
ещё k-е деление нижней и (k+1)-е деление
верхней шкал, а также 2k-е деление нижней и 2(k
+ 1)-е деление верхней шкал и т.д.
Начнём постепенно сдвигать верхнюю
линейку вправо. Сначала совпадут первые деления
линеек – при сдвиге l2 – l1,
равном точности нониуса . При двойном сдвиге совпадут вторые
деления линеек и т.д. Если совпали m-е
деления, то можно, очевидно, утверждать, что их
нулевые деления сдвинуты на m.
Высказанные утверждения справедливы,
если сдвиг верхней линейки относительно нижней
не превышает одного деления нижней линейки. При
сдвиге ровно на одно деление (или на несколько
делений) нулевое деление верхней шкалы совпадает
уже с первым (или n-м) делением нижней
линейки. При дальнейшем сдвиге с делением нижней
линейки совпадает 1-е деление верхней и т.д. В
технических нониусах (например, в
штангенциркуле) нижнюю линейку делают короткой,
так что совпадать с верхними может лишь одно из
делений этой линейки.
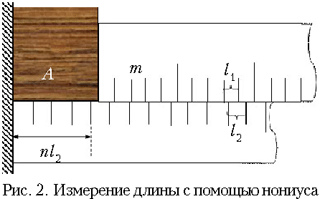
Применим нониус для измерения длины
тела А. Как видно из рис. 2,
L=nl2+m
(3)
Здесь n – целое число делений
нижней шкалы вдоль измеряемого тела, а m –
номер деления верхней линейки (начиная с
нулевого), совпадающего с одним из делений нижней
шкалы. В качестве m берут номер деления,
ближайшего к одному из делений нижней шкалы.
Аналогичным образом можно строить не только
линейные, но и угловые нониусы. Нониусами
снабжаются штангенциркули, теодолиты и многие
другие приборы.
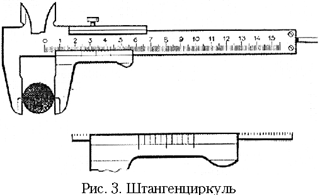
Устройство штангенциркуля.
Измерять размеры малых деталей с точностью до
десятых долей миллиметра можно штангенциркулем
(рис. 3).
Основная часть штангенциркуля –
линейка с сантиметровыми и миллиметровыми
делениями. На ней закреплён зажим, позволяющий
измерять внешние и внутренние размеры тел. По
линейке скользит рамка, по внутреннему краю
которой нанесена шкала – нониус. Десять делений
этой шкалы равны 9 мм, таким образом, одно деление
составляет 0,9 мм. У некоторых штангенциркулей на
рамке имеются 20 делений, соответствующих 19
мм шкалы линейки.
Для определения размера детали её
зажимают и находят число целых миллиметров по
делению на шкале линейки, ближайшему к 0-му штриху
нониуса. Затем смотрят, какой из штрихов шкалы
нониуса совпадает со штрихом шкалы на линейке, и
получают число десятых долей миллиметра. Размер
детали получают сложением числа целых
миллиметров, отсчитанных по линейке, и десятых
долей миллиметра, определённых по шкале нониуса.
Погрешности измерений,
выполненных с помощью нониуса
Граница абсолютной погрешности
прямого измерения x складывается из приборной
погрешностипр
и погрешности отсчёта от:
x=
пр+
от
(4)
Обе составляющие погрешности прямого
измерения следует учитывать лишь в том случае,
если они близки друг к другу. Любым из этих
слагаемых можно пренебречь, если оно не
превосходит 1/3–1/4 от другого. В этом состоит так
называемое правило «ничтожных погрешностей».
В данной работе нониус
изготавливается с использованием масштабной
линейки, поэтому приборная погрешность такого
нониуса (аккуратно сделанного!) будет такая же,
как и у линейки:пр
= ±1 мм на 30 см длины линейки. То есть на каждый
сантиметр изготовленного нониуса «приходится»
примерно пр
= ±0,03 мм.
Погрешность отсчёта от зависит от цены деления
измерительного прибора. Для нониуса она
считается по формуле (2).
Знание границ абсолютной погрешности
не всегда даёт полное представление о точности
выполненных измерений. Показателем качества
измерений служит величина, называемая максимальной
относительной погрешностью (границей относительной
погрешности). Это отношение максимальной
абсолютной погрешности к значению измеряемой
величин xизм:
(5)
Часто эту величину выражают в
процентах:
(6)
Погрешности косвенных измерений.
Измерения называются косвенными, если результат
определяется на основе расчётов. Так
определяется объём тела, если уже измерены и
известны его линейные размеры. Понятно, что,
поскольку измерения длины x, ширины y и
высоты z выполнены с определённой
погрешностью, то и объём можно определить только
с какой-то погрешностью. Максимальная
относительная погрешность определения объёма
тела V1 в форме параллелепипеда равна
(7)
Абсолютная погрешность:
(8)
После того как вычислена абсолютная
погрешность, её значение обычно округляется до
одной значащей цифры. После этого и результат
измерений записывается с числом десятичных
знаков, не большим, чем их имеется в абсолютной
погрешности. Например, запись = (0,56032 ± 0,028) м/с не совсем
удачна. Желательно записать: = 0,03
м/с и = (0,56 ± 0,03)
м/с.
Поскольку формула для расчёта объёма
тела цилиндрической формы имеет вид:
(9)
где h – высота цилиндра, R –
радиус основания, D – диаметр, – константа. Максимальная
относительная погрешность равна
(10)
а абсолютная погрешность
(11)
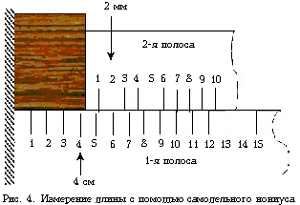
Порядок работы
1. Вырежьте из плотной бумаги полосу
длиной 20 см и шириной 3 см. Нанесите по краю полосы
деления через 1 см.
2. Отрежьте вторую полосу такой же
ширины длиной немного больше 9 см. По краю этой
полосы, строго от края, нанесите 10 делений через
0,9 см.
3. Рассчитайте точность нониуса по
формуле (2).
4. Приложите первую полосу к грани
бруска так, чтобы «0» совпал с одним краем. Ко
второму краю грани приставьте вторую полосу (рис.
4).
5. Определите длину бруска по формуле
(3).
6. Поворачивая брусок на столе, таким же
способом измерьте его ширину и высоту.
7. Рассчитайте границы абсолютной (4) и
относительной погрешностей прямых измерений (5)
линейных размеров бруска, выполненных с помощью
изготовленного нониуса.
8. Рассчитайте объём бруска в форме
параллелепипеда, а также границы абсолютной, по
формуле (8), и относительной, по формуле (7),
погрешностей косвенных измерений его объёма.
9. Аналогичным образом измерьте высоту
и диаметр цилиндра. Повторите п. 7 для цилиндра.
10. Повторите п. 8 для цилиндра,
использовав формулы (9)–(11).
11. Все измеренные и рассчитанные
значения занесите в таблицу:
12. Сформулируйте вывод.
Контрольные вопросы
1. Какой должна быть шкала нониуса на
модели для измерения длины с точностью до 0,5 мм?
2. Можно ли изготовить нониус для
измерений, абсолютная погрешность которых
меньше 0,01? Почему?
Литература
Кабардин О.Ф., Орлов В.А., Пономарёва
А.В. Факультативный курс физики. 8 класс: Учеб.
пособие для учащихся. – М.: Просвещение, 1985.
Руководство к лабораторным занятиям
по физике: Под ред. Л.Л.Гольдина. – М.: Наука, 1973.
Физика: Учеб. пособие для 10 кл. шк. и классов с
угл. изуч. физики: Под ред. А.А.Пинского. – М.:
Просвещение, 1993.
ЭЗ-02. Измерение размеров бруска
|
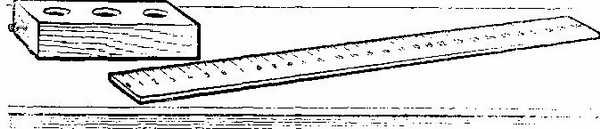
Приборы и материалы (рис. 2): линейка измерительная, брусок деревянный.
Методические рекомендации
Цель задания — дать понятие об измерении физической величины, научить практически вычислять цену деления шкалы прибора, ознакомить учащихся с правилами записи результатов измерения. Все это учитель должен предварительно объяснить учащимся, а потом предложить им выполнить задания. |
Категория: 1. Введение | Добавил: Alex (12.03.2012) |
| Просмотров: 3647 | Теги: эксперимент, экспериментальные задания, длина, 7 класс | Рейтинг: 0.0/0 |
Задания
Версия для печати и копирования в MS Word
Длину бруска измеряют с помощью линейки (см. рис.). Запишите результат измерения, учитывая, что погрешность измерения равна цене деления шкалы линейки.
1) (4,5 ± 0,5) см
2) (5,5 ± 0,5) см
3) (4,50 ± 0,25) см
4) (5,50 ± 0,25) см
Спрятать решение
Решение.
Заметим, что линейка приложена отметкой «1» к левому краю бруска, длина бруска равна 5, 5 — 1 = 4,5 см. Цена деления шкалы линейки равна 0,5 см. По условию погрешность измерения равна цене деления. Следовательно, измеренное значение длины бруска можно записать как (4,5 ± 0,5) см.
Ответ: 1.
Погрешности измерений, представление результатов эксперимента
- Шкала измерительного прибора
- Цена деления
- Виды измерений
- Погрешность измерений, абсолютная и относительная погрешность
- Абсолютная погрешность серии измерений
- Представление результатов эксперимента
- Задачи
п.1. Шкала измерительного прибора
Шкала – это показывающая часть измерительного прибора, состоящая из упорядоченного ряда отметок со связанной с ними нумерацией. Шкала может располагаться по окружности, дуге или прямой линии.
Примеры шкал различных приборов:
п.2. Цена деления
Цена деления измерительного прибора равна числу единиц измеряемой величины между двумя ближайшими делениями шкалы. Как правило, цена деления указана на маркировке прибора.
Алгоритм определения цены деления
Шаг 1. Найти два ближайшие пронумерованные крупные деления шкалы. Пусть первое значение равно a, второе равно b, b > a.
Шаг 2. Посчитать количество мелких делений шкалы между ними. Пусть это количество равно n.
Шаг 3. Разделить разницу значений крупных делений шкалы на количество отрезков, которые образуются мелкими делениями: $$ triangle=frac{b-a}{n+1} $$ Найденное значение (triangle) и есть цена деления данного прибора.
Пример определения цены деления:
 |
Определим цену деления основной шкалы секундомера. Два ближайших пронумерованных деления на основной шкале:a = 5 c b = 10 cМежду ними находится 4 средних деления, а между каждыми средними делениями еще 4 мелких. Итого: 4+4·5=24 деления. Цена деления: begin{gather*} triangle=frac{b-a}{n+1}\ triangle=frac{10-5}{24+1}=frac15=0,2 c end{gather*} |
п.3. Виды измерений
Вид измерений
Определение
Пример
Прямое измерение
Физическую величину измеряют с помощью прибора
Измерение длины бруска линейкой
Косвенное измерение
Физическую величину рассчитывают по формуле, куда подставляют значения величин, полученных с помощью прямых измерений
Определение площади столешницы при измеренной длине и ширине
п.4. Погрешность измерений, абсолютная и относительная погрешность
Погрешность измерений – это отклонение измеренного значения величины от её истинного значения.
Составляющие погрешности измерений
Причины
Инструментальная погрешность
Определяется погрешностью инструментов и приборов, используемых для измерений (принципом действия, точностью шкалы и т.п.)
Погрешность метода
Определяется несовершенством методов и допущениями в методике.
Погрешность теории (модели)
Определяется теоретическими упрощениями, степенью соответствия теоретической модели и реальности.
Погрешность оператора
Определяется субъективным фактором, ошибками экспериментатора.
Инструментальная погрешность измерений принимается равной половине цены деления прибора: $$ d=frac{triangle}{2} $$
Если величина (a_0) — это истинное значение, а (triangle a) — погрешность измерения, результат измерений физической величины записывают в виде (a=a_0pmtriangle a).
Абсолютная погрешность измерения – это модуль разности между измеренным и истинным значением измеряемой величины: $$ triangle a=|a-a_0| $$
Отношение абсолютной погрешности измерения к истинному значению, выраженное в процентах, называют относительной погрешностью измерения: $$ delta=frac{triangle a}{a_0}cdot 100text{%} $$
Относительная погрешность является мерой точности измерения: чем меньше относительная погрешность, тем измерение точнее. По абсолютной погрешности о точности измерения судить нельзя.
На практике абсолютную и относительную погрешности округляют до двух значащих цифр с избытком, т.е. всегда в сторону увеличения.
Значащие цифры – это все верные цифры числа, кроме нулей слева. Результаты измерений записывают только значащими цифрами.
Примеры значащих цифр:
0,403 – три значащих цифры, величина определена с точностью до тысячных.
40,3 – три значащих цифры, величина определена с точностью до десятых.
40,300 – пять значащих цифр, величина определена с точностью до тысячных.
В простейших измерениях инструментальная погрешность прибора является основной.
В таких случаях физическую величину измеряют один раз, полученное значение берут в качестве истинного, а абсолютную погрешность считают равной инструментальной погрешности прибора.
Примеры измерений с абсолютной погрешностью равной инструментальной:
- определение длины с помощью линейки или мерной ленты;
- определение объема с помощью мензурки.
Пример получения результатов прямых измерений с помощью линейки:
 |
Измерим длину бруска линейкой, у которой пронумерованы сантиметры и есть только одно деление между пронумерованными делениями. Цена деления такой линейки: begin{gather*} triangle=frac{b-a}{n+1}= frac{1 text{см}}{1+1}=0,5 text{см} end{gather*} Инструментальная погрешность: begin{gather*} d=frac{triangle}{2}=frac{0,5}{2}=0,25 text{см} end{gather*} Истинное значение: (L_0=4 text{см}) Результат измерений: $$ L=L_0pm d=(4,00pm 0,25) text{см} $$ Относительная погрешность: $$ delta=frac{0,25}{4,00}cdot 100text{%}=6,25text{%}approx 6,3text{%} $$ |
 |
Теперь возьмем линейку с n=9 мелкими делениями между пронумерованными делениями. Цена деления такой линейки: begin{gather*} triangle=frac{b-a}{n+1}= frac{1 text{см}}{9+1}=0,1 text{см} end{gather*} Инструментальная погрешность: begin{gather*} d=frac{triangle}{2}=frac{0,1}{2}=0,05 text{см} end{gather*} Истинное значение: (L_0=4,15 text{см}) Результат измерений: $$ L=L_0pm d=(4,15pm 0,05) text{см} $$ Относительная погрешность: $$ delta=frac{0,05}{4,15}cdot 100text{%}approx 1,2text{%} $$ |
Второе измерение точнее, т.к. его относительная погрешность меньше.
п.5. Абсолютная погрешность серии измерений
Измерение длины с помощью линейки (или объема с помощью мензурки) являются теми редкими случаями, когда для определения истинного значения достаточно одного измерения, а абсолютная погрешность сразу берется равной инструментальной погрешности, т.е. половине цены деления линейки (или мензурки).
Гораздо чаще погрешность метода или погрешность оператора оказываются заметно больше инструментальной погрешности. В таких случаях значение измеренной физической величины каждый раз немного меняется, и для оценки истинного значения и абсолютной погрешности нужна серия измерений и вычисление средних значений.
Алгоритм определения истинного значения и абсолютной погрешности в серии измерений
Шаг 1. Проводим серию из (N) измерений, в каждом из которых получаем значение величины (x_1,x_2,…,x_N)
Шаг 2. Истинное значение величины принимаем равным среднему арифметическому всех измерений: $$ x_0=x_{cp}=frac{x_1+x_2+…+x_N}{N} $$ Шаг 3. Находим абсолютные отклонения от истинного значения для каждого измерения: $$ triangle_1=|x_0-x_1|, triangle_2=|x_0-x_2|, …, triangle_N=|x_0-x_N| $$ Шаг 4. Находим среднее арифметическое всех абсолютных отклонений: $$ triangle_{cp}=frac{triangle_1+triangle_2+…+triangle_N}{N} $$ Шаг 5. Сравниваем полученную величину (triangle_{cp}) c инструментальной погрешностью прибора d (половина цены деления). Большую из этих двух величин принимаем за абсолютную погрешность: $$ triangle x=maxleft{triangle_{cp}; dright} $$ Шаг 6. Записываем результат серии измерений: (x=x_0pmtriangle x).
Пример расчета истинного значения и погрешности для серии прямых измерений:
Пусть при измерении массы шарика с помощью рычажных весов мы получили в трех опытах следующие значения: 99,8 г; 101,2 г; 100,3 г.
Инструментальная погрешность весов d = 0,05 г.
Найдем истинное значение массы и абсолютную погрешность.
Составим расчетную таблицу:
| № опыта | 1 | 2 | 3 | Сумма |
| Масса, г | 99,8 | 101,2 | 100,3 | 301,3 |
| Абсолютное отклонение, г | 0,6 | 0,8 | 0,1 | 1,5 |
Сначала находим среднее значение всех измерений: begin{gather*} m_0=frac{99,8+101,2+100,3}{3}=frac{301,3}{3}approx 100,4 text{г} end{gather*} Это среднее значение принимаем за истинное значение массы.
Затем считаем абсолютное отклонение каждого опыта как модуль разности (m_0) и измерения. begin{gather*} triangle_1=|100,4-99,8|=0,6\ triangle_2=|100,4-101,2|=0,8\ triangle_3=|100,4-100,3|=0,1 end{gather*} Находим среднее абсолютное отклонение: begin{gather*} triangle_{cp}=frac{0,6+0,8+0,1}{3}=frac{1,5}{3}=0,5 text{(г)} end{gather*} Мы видим, что полученное значение (triangle_{cp}) больше инструментальной погрешности d.
Поэтому абсолютная погрешность измерения массы: begin{gather*} triangle m=maxleft{triangle_{cp}; dright}=maxleft{0,5; 0,05right} text{(г)} end{gather*} Записываем результат: begin{gather*} m=m_0pmtriangle m\ m=(100,4pm 0,5) text{(г)} end{gather*} Относительная погрешность (с двумя значащими цифрами): begin{gather*} delta_m=frac{0,5}{100,4}cdot 100text{%}approx 0,050text{%} end{gather*}
п.6. Представление результатов эксперимента
Результат измерения представляется в виде $$ a=a_0pmtriangle a $$ где (a_0) – истинное значение, (triangle a) – абсолютная погрешность измерения.
Как найти результат прямого измерения, мы рассмотрели выше.
Результат косвенного измерения зависит от действий, которые производятся при подстановке в формулу величин, полученных с помощью прямых измерений.
Погрешность суммы и разности
Если (a=a_0+triangle a) и (b=b_0+triangle b) – результаты двух прямых измерений, то
- абсолютная погрешность их суммы равна сумме абсолютных погрешностей
$$ triangle (a+b)=triangle a+triangle b $$
- абсолютная погрешность их разности также равна сумме абсолютных погрешностей
$$ triangle (a-b)=triangle a+triangle b $$
Погрешность произведения и частного
Если (a=a_0+triangle a) и (b=b_0+triangle b) – результаты двух прямых измерений, с относительными погрешностями (delta_a=frac{triangle a}{a_0}cdot 100text{%}) и (delta_b=frac{triangle b}{b_0}cdot 100text{%}) соответственно, то:
- относительная погрешность их произведения равна сумме относительных погрешностей
$$ delta_{acdot b}=delta_a+delta_b $$
- относительная погрешность их частного также равна сумме относительных погрешностей
$$ delta_{a/b}=delta_a+delta_b $$
Погрешность степени
Если (a=a_0+triangle a) результат прямого измерения, с относительной погрешностью (delta_a=frac{triangle a}{a_0}cdot 100text{%}), то:
- относительная погрешность квадрата (a^2) равна удвоенной относительной погрешности
$$ delta_{a^2}=2delta_a $$
- относительная погрешность куба (a^3) равна утроенной относительной погрешности
$$ delta_{a^3}=3delta_a $$
- относительная погрешность произвольной натуральной степени (a^n) равна
$$ delta_{a^n}=ndelta_a $$
Вывод этих формул достаточно сложен, но если интересно, его можно найти в Главе 7 справочника по алгебре для 8 класса.
п.7. Задачи
Задача 1. Определите цену деления и объем налитой жидкости для каждой из мензурок. В каком случае измерение наиболее точно; наименее точно?
Составим таблицу для расчета цены деления:
| № мензурки | a, мл | b, мл | n | (triangle=frac{b-a}{n+1}), мл |
| 1 | 20 | 40 | 4 | (frac{40-20}{4+1}=4) |
| 2 | 100 | 200 | 4 | (frac{200-100}{4+1}=20) |
| 3 | 15 | 30 | 4 | (frac{30-15}{4+1}=3) |
| 4 | 200 | 400 | 4 | (frac{400-200}{4+1}=40) |
Инструментальная точность мензурки равна половине цены деления.
Принимаем инструментальную точность за абсолютную погрешность и измеренное значение объема за истинное.
Составим таблицу для расчета относительной погрешности (оставляем две значащих цифры и округляем с избытком):
| № мензурки | Объем (V_0), мл | Абсолютная погрешность (triangle V=frac{triangle}{2}), мл |
Относительная погрешность (delta_V=frac{triangle V}{V_0}cdot 100text{%}) |
| 1 | 68 | 2 | 3,0% |
| 2 | 280 | 10 | 3,6% |
| 3 | 27 | 1,5 | 5,6% |
| 4 | 480 | 20 | 4,2% |
Наиболее точное измерение в 1-й мензурке, наименее точное – в 3-й мензурке.
Ответ:
Цена деления 4; 20; 3; 40 мл
Объем 68; 280; 27; 480 мл
Самое точное – 1-я мензурка; самое неточное – 3-я мензурка
Задача 2. В двух научных работах указаны два значения измерений одной и той же величины: $$ x_1=(4,0pm 0,1) text{м}, x_2=(4,0pm 0,03) text{м} $$ Какое из этих измерений точней и почему?
Мерой точности является относительная погрешность измерений. Получаем: begin{gather*} delta_1=frac{0,1}{4,0}cdot 100text{%}=2,5text{%}\ delta_2=frac{0,03}{4,0}cdot 100text{%}=0,75text{%} end{gather*} Относительная погрешность второго измерения меньше. Значит, второе измерение точней.
Ответ: (delta_2lt delta_1), второе измерение точней.
Задача 3. Две машины движутся навстречу друг другу со скоростями 54 км/ч и 72 км/ч.
Цена деления спидометра первой машины 10 км/ч, второй машины – 1 км/ч.
Найдите скорость их сближения, абсолютную и относительную погрешность этой величины.
Абсолютная погрешность скорости каждой машины равна инструментальной, т.е. половине деления спидометра: $$ triangle v_1=frac{10}{2}=5 (text{км/ч}), triangle v_2=frac{1}{2}=0,5 (text{км/ч}) $$ Показания каждого из спидометров: $$ v_1=(54pm 5) text{км/ч}, v_2=(72pm 0,5) text{км/ч} $$ Скорость сближения равна сумме скоростей: $$ v_0=v_{10}+v_{20}, v_0=54+72=125 text{км/ч} $$ Для суммы абсолютная погрешность равна сумме абсолютных погрешностей слагаемых. $$ triangle v=triangle v_1+triangle v_2, triangle v=5+0,5=5,5 text{км/ч} $$ Скорость сближения с учетом погрешности равна: $$ v=(126,0pm 5,5) text{км/ч} $$ Относительная погрешность: $$ delta_v=frac{5,5}{126,0}cdot 100text{%}approx 4,4text{%} $$ Ответ: (v=(126,0pm 5,5) text{км/ч}, delta_vapprox 4,4text{%})
Задача 4. Измеренная длина столешницы равна 90,2 см, ширина 60,1 см. Измерения проводились с помощью линейки с ценой деления 0,1 см. Найдите площадь столешницы, абсолютную и относительную погрешность этой величины.
Инструментальная погрешность линейки (d=frac{0,1}{2}=0,05 text{см})
Результаты прямых измерений длины и ширины: $$ a=(90,20pm 0,05) text{см}, b=(60,10pm 0,05) text{см} $$ Относительные погрешности (не забываем про правила округления): begin{gather*} delta_1=frac{0,05}{90,20}cdot 100text{%}approx 0,0554text{%}approx uparrow 0,056text{%}\ delta_2=frac{0,05}{60,10}cdot 100text{%}approx 0,0832text{%}approx uparrow 0,084text{%} end{gather*} Площадь столешницы: $$ S=ab, S=90,2cdot 60,1 = 5421,01 text{см}^2 $$ Для произведения относительная погрешность равна сумме относительных погрешностей слагаемых: $$ delta_S=delta_a+delta_b=0,056text{%}+0,084text{%}=0,140text{%}=0,14text{%} $$ Абсолютная погрешность: begin{gather*} triangle S=Scdot delta_S=5421,01cdot 0,0014=7,59approx 7,6 text{см}^2\ S=(5421,0pm 7,6) text{см}^2 end{gather*} Ответ: (S=(5421,0pm 7,6) text{см}^2, delta_Sapprox 0,14text{%})


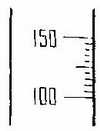 Полезно рекомендовать учащимся кратко описать порядок действий при вычислении цены деления шкалы, сделав соответствующий рисунок (рис. 55), например, так:
Полезно рекомендовать учащимся кратко описать порядок действий при вычислении цены деления шкалы, сделав соответствующий рисунок (рис. 55), например, так: