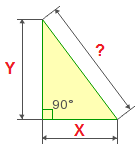
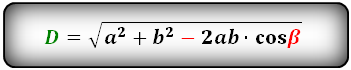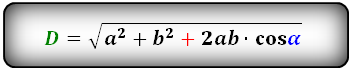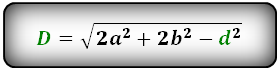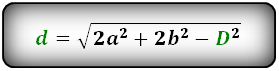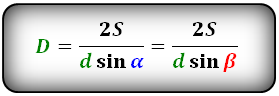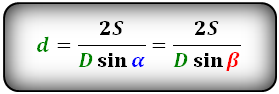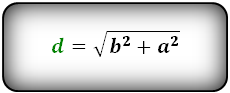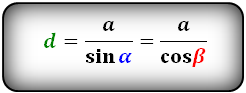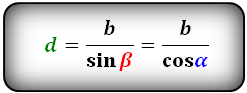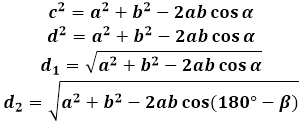Расчет диагонали для угла 90 градусов
Расчет диагоналей для разметки фундамента
Укажите необходимые размеры в миллиметрах
X — длина фундамента
Y — ширина фундамента
Возможности программы.
Расчет диагонали для разметки фундамента или стен.
Используется для установления точного угла в 90 градусов.
Место приема благодарностей…
Укажите размеры:
Диагональ =
Решение:
Ссылка на страницу с результатом:
# Теория
Прямоугольник — это четырёхугольник у которого все углы прямые (по 90 градусов).
Диагональ прямоугольника — это прямая линия соединяющая противоположные углы. Диагонали прямоугольника обладают следующими свойствами:
- Диагонали прямоугольника равны.
- Диагональ делит прямоугольник на два равных прямоугольных треугольника и является их гипотенузой.
Формула диагонали прямоугольника
Так как диагональ делит прямоугольник на два одинаковых труегольника и является их гипотенузой, то длина и ширина прямоугольника будут катетами образованного треугольника. Поэтому для расчёта диагонали мы применяем теорему Пифагора:
Квадрат гипотенузы равен сумме квадратов катетов: c² = a² + b²
Отсюда, формула для расчётадиагонали прямоугольника выглядит следующим образом:
a
b
d
d = sqrt{a^2 + b^2}
- d — диагональ прямоугольника
- a — длина прямоугольника
- b — ширина прямоугольника
Похожие калькуляторы:
Войдите чтобы писать комментарии
Свойства параллелограмма:
1. Противоположные стороны равны и параллельны
2. Противоположные углы равны
3. Точка пересечения диагоналей, делит их пополам
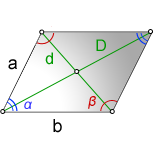
1. Длина диагонали параллелограмма через стороны, известную диагональ и угол.
a, b — стороны параллелограмма
D — большая диагональ
d — меньшая диагональ
α, β — углы параллелограмма
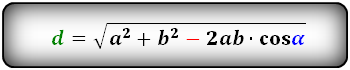
Формулы диагонали через стороны и углы параллелограмма (по теореме косинусов), (D, d):
Формулы диагонали через стороны и известную диагональ (по формуле- сумма квадратов диагоналей), (D, d):
2. Длина диагонали параллелограмма через площадь, известную диагональ и угол.
D — большая диагональ
d — меньшая диагональ
α, β — углы между диагоналями
S — площадь параллелограмма
Формулы диагонали через площадь, известную диагональ и угол между диагоналями, (D, d):
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
- Подробности
-
Опубликовано: 03 ноября 2011
-
Обновлено: 13 августа 2021
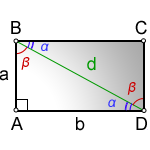
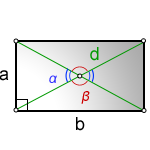
Диагонали прямоугольника равны между собой. Диагональ делит прямоугольник на два равных прямоугольных треугольника ABC и ACD. Диагональ равна диаметру описанной окружности.
1. Формулы длины диагонали в прямоугольнике.
d — диагональ прямоугольника
a, b — стороны
α, β — углы полученные от деления, диагональю, прямого угла
Формула диагонали через стороны, (d):
Формулы диагонали через сторону и угол, (d):
Формулы величины углов через диагональ и стороны, (α, β):
2. Формулы углов между диагоналями в прямоугольнике.
d — диагонали прямоугольника
a, b — стороны
α, β — углы между диагоналями
Формулы углов между диагоналями через стороны и диагональ, (α, β ):
- Подробности
-
Опубликовано: 27 октября 2011
-
Обновлено: 13 августа 2021
Параллелограмм — это четырехугольник, у которого по определению противоположные стороны параллельны и равны. Как следствие, противоположные углы параллелограмма также будут между собой равны, а так как сумма всех углов в четырехугольнике равна 360 градусам, то можно сделать вывод, что сумма двух последовательных углов будет равна 180 градусам. Данное свойство будет играть существенную роль для нахождения диагоналей параллелограмма, с учетом того, что они разной длины.
Так как каждая диагональ параллелограмма делит его на два равновеликих треугольника, именно их свойства и будут использованы для выведения формулы диагонали параллелограмма.
В любом треугольнике угол и сторона, лежащие напротив, пропорциональны друг другу. Для параллелограмма это будет значить, что более длинная диагональ будет лежать напротив тупого угла, а более короткая диагональ — напротив острого.С учетом того, что стороны треугольников, полученных в результате проведения диагоналей, одинаковы — это стороны параллелограмма, значение градусной меры угла между данными сторонами определяет чему будет равна длина диагонали,вычисленной по формуле. Другими словами, если в формулудиагонали подставить значение острого угла параллелограмма, то калькулятор вычислит длину короткой диагонали, а если подставить значение тупого угла — то длинной.
Для того чтобы перейти от одного угла к другому, используется разность 180 градусов и заданного угла, таким образом калькулятор одновременно может вычислить обе диагонали.
α=180°-β
Чтобы вывести формулу диагонали параллелограмма, используется теорема косинусов в треугольнике, который диагональ образует со сторонами. В любом из подобных треугольников, диагональ является стороной, противолежащей углу параллелограмма и, соответственно, ее квадрат равен сумме квадратов двух других сторон треугольника (сторон параллелограмма, в данном случае) за вычетом удвоенного произведения тех же сторон на косинус приведенного угла. Чтобы найти длину диагонали параллелограмма, калькулятор вычисляет квадратный корень из данного выражения.