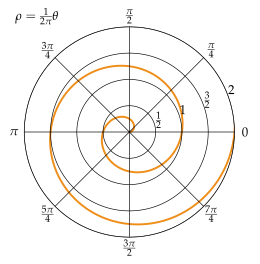
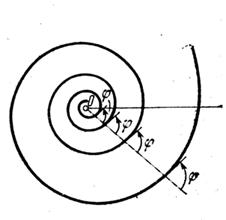
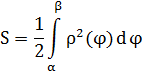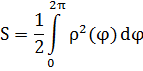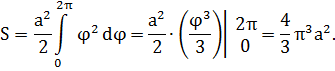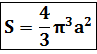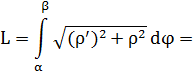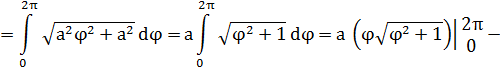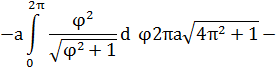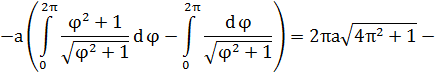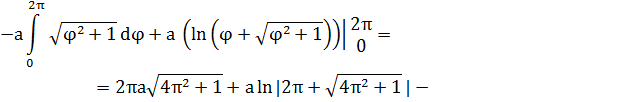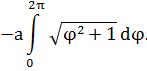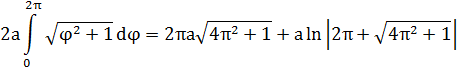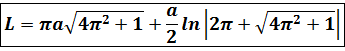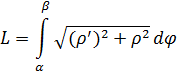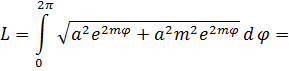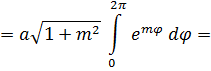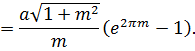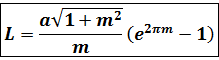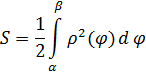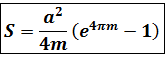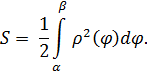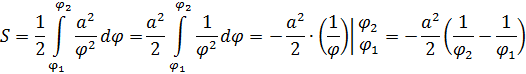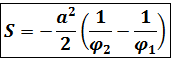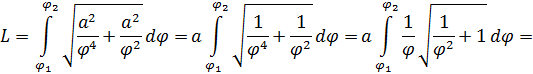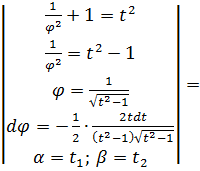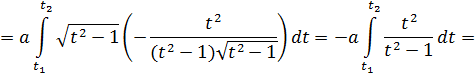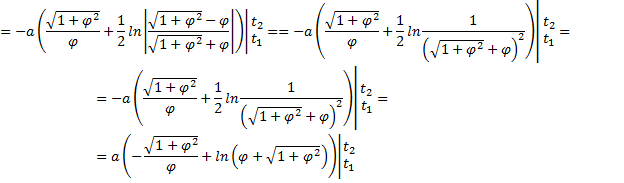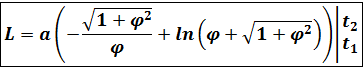Решение. Концам первого витка соответствуют значения 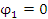
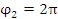
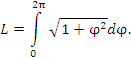
Интегрируем по частям, положив 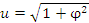
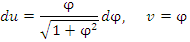
и
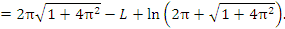
Таким образом,
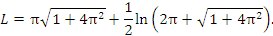
Сообщения без ответов | Активные темы
| Автор | Сообщение | ||
|---|---|---|---|
|
Заголовок сообщения: Найти длину дуги архимедовой спирали
|
|||
|
Пожалуйста, помогите разобраться, как вычисляется длина дуги архимедовой спирали!
|
||
| Вернуться к началу |
|
||
|
Kirrrrrrr |
Заголовок сообщения: Re: Найти длину дуги архимедовой спирали
|
|
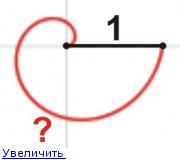
С величиной [math]a[/math] ясно, пусть это константа, но от этого не легче. Допустим, беру [math]a=1[/math]. Луч сделал первый оборот на 360 градусов, и точка [math]a[/math] сдвинулась по нему на 1, то бишь расстояние между соседними точками пересечения спирали с осью абсцисс равно 1.
|
|
| Вернуться к началу |
|
|
Shaman |
Заголовок сообщения: Re: Найти длину дуги архимедовой спирали
|
|
Если полагать шаг спирали равным a, то уравнение выглядит так: Например, для a=1: Вики: http://ru.wikipedia.org/wiki/%D0%90%D1% … 0%BB%D1%8C
|
|
| Вернуться к началу |
|
|
Kirrrrrrr |
Заголовок сообщения: Re: Найти длину дуги архимедовой спирали
|
|
Prokop, я имею в виду, что мы это расстояние (между соседними точками пересечения спирали с осью абсцисс), допустим, обозначаем за 1 см. Сколько см тогда будет длина первого витка спирали?
|
|
| Вернуться к началу |
|
|
Kirrrrrrr |
Заголовок сообщения: Re: Найти длину дуги архимедовой спирали
|
|
Shaman, формула, которую я привел, указана и в Википедии и в этих источниках: Формула там упоминается [math]l = frac{a}{2}left[ {phi sqrt {1 + phi ^2 } + ln left( {phi + sqrt {1 + phi ^2 } } right)} right][/math]. Еще раз уточнил: [math]phi[/math] — число витков спирали в радианах, [math]a[/math] — расстояние между соседними точками пересечения спирали с осью абсцисс, так называемый шаг спирали. Shaman, будьте добры, объясните, почему вы взяли множитель формулы не [math]frac{a}{2}[/math], а [math]frac{a}{{4pi }}[/math]. И если ваша формула правильная, то почему везде указывают хотя и похожую, но другую?
|
|
| Вернуться к началу |
|
|
Shaman |
Заголовок сообщения: Re: Найти длину дуги архимедовой спирали
|
|
Заглядываю в Вики, там под a понимается именно шаг спирали, а в формуле L= используется k/2, а не a/2, а чуть выше объяснено что такое k Kirrrrrrr, забейте, a — это просто буква и обозначить ей можно что угодно.
|
|
| Вернуться к началу |
|
|
Kirrrrrrr |
Заголовок сообщения: Re: Найти длину дуги архимедовой спирали
|
|
Ну наконец-то)) Невнимательность не дружит с точными науками! Просто еще и источники слегка внесли путаницу, обозначение в формуле то [math]a[/math], то [math]k[/math]. А я плоховато разобрался в теме, и был уверен, что эта величина обозначает именно шаг спирали как таковой. Очень благодарен за помощь!!! А то неприятное ощущение было: формула же есть, но посчитать не могу, это по готовой-то формуле.
|
|
| Вернуться к началу |
|
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Найти длину дуги
в форуме Интегральное исчисление |
351w |
7 |
817 |
28 мар 2021, 21:18 |
|
Найти длину дуги
в форуме Интегральное исчисление |
351w |
7 |
274 |
30 мар 2021, 09:28 |
|
Найти длину дуги
в форуме Интегральное исчисление |
Shapeshifter |
7 |
491 |
26 май 2015, 18:59 |
|
Найти длину дуги L
в форуме Интегральное исчисление |
kolpachek |
2 |
276 |
09 дек 2018, 15:19 |
|
Найти длину дуги
в форуме Интегральное исчисление |
madam9707 |
5 |
569 |
07 июн 2014, 18:53 |
|
Найти длину дуги кривой
в форуме Интегральное исчисление |
sergeydubr |
1 |
671 |
01 фев 2016, 09:22 |
|
Найти длину дуги кривой
в форуме Интегральное исчисление |
elinka1995 |
1 |
701 |
17 июн 2014, 23:01 |
|
Найти длину проекции дуги
в форуме Аналитическая геометрия и Векторная алгебра |
AlexKey |
7 |
913 |
15 фев 2017, 20:05 |
|
Найти длину дуги кривой
в форуме Интегральное исчисление |
Salibekova |
1 |
439 |
30 апр 2015, 15:57 |
|
Найти длину дуги кривой
в форуме Интегральное исчисление |
elinka1995 |
1 |
634 |
17 июн 2014, 23:03 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 13 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
From Wikipedia, the free encyclopedia
Three 360° loops of one arm of an Archimedean spiral
The Archimedean spiral (also known as the arithmetic spiral) is a spiral named after the 3rd-century BC Greek mathematician Archimedes. It is the locus corresponding to the locations over time of a point moving away from a fixed point with a constant speed along a line that rotates with constant angular velocity. Equivalently, in polar coordinates (r, θ) it can be described by the equation
with real numbers a and b. Changing the parameter a moves the centerpoint of the spiral outward from the origin (positive a toward θ = 0 and negative a toward θ = π) essentially through a rotation of the spiral, while b controls the distance between loops.
From the above equation, it can thus be stated: position of particle from point of start is proportional to angle θ as time elapses.
Archimedes described such a spiral in his book On Spirals. Conon of Samos was a friend of his and Pappus states that this spiral was discovered by Conon.[1]
Derivation of general equation of spiral[edit]
A physical approach is used below to understand the notion of Archimedean spirals.
Suppose a point object moves in the Cartesian system with a constant velocity v directed parallel to the x-axis, with respect to the xy-plane. Let at time t = 0, the object was at an arbitrary point (c, 0, 0). If the xy plane rotates with a constant angular velocity ω about the z-axis, then the velocity of the point with respect to z-axis may be written as:
The xy plane rotates to an angle ωt (anticlockwise) about the origin in time t. (c, 0) is the position of the object at t = 0. P is the position of the object at time t, at a distance of R = vt + c.
Here vt + c is the modulus of the position vector of the particle at any time t, vx is the velocity component along the x-axis and vy is the component along the y-axis. The figure shown alongside explains this.
The above equations can be integrated by applying integration by parts, leading to the following parametric equations:
Squaring the two equations and then adding (and some small alterations) results in the Cartesian equation
(using the fact that ωt = θ and θ = arctan y/x) or
Its polar form is
Arc length and curvature [edit]
Osculating circles of the Archimedean spiral, tangent to the spiral and having the same curvature at the tangent point. The spiral itself is not drawn, but can be seen as the points where the circles are especially close to each other.
Given the parametrization in cartesian coordinates
the arc length from 

or, equivalently:
The total length from 

The curvature is given by
Characteristics[edit]
Archimedean spiral represented on a polar graph
The Archimedean spiral has the property that any ray from the origin intersects successive turnings of the spiral in points with a constant separation distance (equal to 2πb if θ is measured in radians), hence the name «arithmetic spiral». In contrast to this, in a logarithmic spiral these distances, as well as the distances of the intersection points measured from the origin, form a geometric progression.
The Archimedean spiral has two arms, one for θ > 0 and one for θ < 0. The two arms are smoothly connected at the origin. Only one arm is shown on the accompanying graph. Taking the mirror image of this arm across the y-axis will yield the other arm.
For large θ a point moves with well-approximated uniform acceleration along the Archimedean spiral while the spiral corresponds to the locations over time of a point moving away from a fixed point with a constant speed along a line which rotates with constant angular velocity[2] (see contribution from Mikhail Gaichenkov).
As the Archimedean spiral grows, its evolute asymptotically approaches a circle with radius |v|/ω.
General Archimedean spiral[edit]
Sometimes the term Archimedean spiral is used for the more general group of spirals
The normal Archimedean spiral occurs when c = 1. Other spirals falling into this group include the hyperbolic spiral (c = −1), Fermat’s spiral (c = 2), and the lituus (c = −2).
Applications[edit]
One method of squaring the circle, due to Archimedes, makes use of an Archimedean spiral. Archimedes also showed how the spiral can be used to trisect an angle. Both approaches relax the traditional limitations on the use of straightedge and compass in ancient Greek geometric proofs.[3]
Mechanism of a scroll compressor
The Archimedean spiral has a variety of real-world applications. Scroll compressors, used for compressing gases, have rotors that can be made from two interleaved Archimedean spirals, involutes of a circle of the same size that almost resemble Archimedean spirals,[4] or hybrid curves.
Archimedean spirals can be found in spiral antenna, which can be operated over a wide range of frequencies.
The coils of watch balance springs and the grooves of very early gramophone records form Archimedean spirals, making the grooves evenly spaced (although variable track spacing was later introduced to maximize the amount of music that could be cut onto a record).[5]
Asking for a patient to draw an Archimedean spiral is a way of quantifying human tremor; this information helps in diagnosing neurological diseases.
Archimedean spirals are also used in digital light processing (DLP) projection systems to minimize the «rainbow effect», making it look as if multiple colors are displayed at the same time, when in reality red, green, and blue are being cycled extremely quickly.[6] Additionally, Archimedean spirals are used in food microbiology to quantify bacterial concentration through a spiral platter.[7]
They are also used to model the pattern that occurs in a roll of paper or tape of constant thickness wrapped around a cylinder.[8][9]
Many dynamic spirals (such as the Parker spiral of the solar wind, or the pattern made by a Catherine’s wheel) are Archimedean. For instance, the star LL Pegasi shows an approximate Archimedean spiral in the dust clouds surrounding it, thought to be ejected matter from the star that has been shepherded into a spiral by another companion star as part of a double star system.[10]
See also[edit]
- Archimedes’ screw – Water pumping mechanism
- Euler spiral – Curve whose curvature changes linearly
- Fermat’s spiral – Spiral that surrounds equal area per turn
- Golden spiral – Self-similar curve related to golden ratio
- Hyperbolic spiral – Spiral asymptotic to a line
- List of spirals
- Logarithmic spiral – Self-similar growth curve
- Spiral of Theodorus – Polygonal curve made from right triangles
- Triple spiral symbol – Various symbols with three-fold rotational symmetry
References[edit]
- ^ Bulmer-Thomas, Ivor. «Conon of Samos». Dictionary of Scientific Biography. Vol. 3. p. 391.
- ^ Sloane, N. J. A. (ed.). «Sequence A091154». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Boyer, Carl B. (1968). A History of Mathematics. Princeton, New Jersey: Princeton University Press. pp. 140–142. ISBN 0-691-02391-3.
- ^ Sakata, Hirotsugu; Okuda, Masayuki. «Fluid compressing device having coaxial spiral members». Retrieved 2006-11-25.
- ^ Penndorf, Ron. «Early Development of the LP». Archived from the original on 5 November 2005. Retrieved 2005-11-25.. See the passage on Variable Groove.
- ^ Ballou, Glen (2008), Handbook for Sound Engineers, CRC Press, p. 1586, ISBN 9780240809694
- ^ Gilchrist, J. E.; Campbell, J. E.; Donnelly, C. B.; Peeler, J. T.; Delaney, J. M. (1973). «Spiral Plate Method for Bacterial Determination». Applied Microbiology. 25 (2): 244–52. doi:10.1128/AEM.25.2.244-252.1973. PMC 380780. PMID 4632851.
- ^ Peressini, Tony (3 February 2009). «Joan’s Paper Roll Problem» (PDF). Archived from the original (PDF) on 3 November 2013. Retrieved 2014-10-06.
- ^ Walser, H.; Hilton, P.; Pedersen, J. (2000). Symmetry. Mathematical Association of America. p. 27. ISBN 9780883855324. Retrieved 2014-10-06.
- ^ Kim, Hyosun; Trejo, Alfonso; Liu, Sheng-Yuan; Sahai, Raghvendra; Taam, Ronald E.; Morris, Mark R.; Hirano, Naomi; Hsieh, I-Ta (March 2017). «The large-scale nebular pattern of a superwind binary in an eccentric orbit». Nature Astronomy. 1 (3): 0060. arXiv:1704.00449. Bibcode:2017NatAs…1E..60K. doi:10.1038/s41550-017-0060. S2CID 119433782.
External links[edit]
- Jonathan Matt making the Archimedean spiral interesting — Video : The surprising beauty of Mathematics — TedX Talks, Green Farms
- Weisstein, Eric W. «Archimedes’ Spiral». MathWorld.
- archimedean spiral at PlanetMath.
- Page with Java application to interactively explore the Archimedean spiral and its related curves
- Online exploration using JSXGraph (JavaScript)
- Archimedean spiral at «mathcurve»
Спираль Архимеда. Логарифмическая, гиперболическая спираль
1. Спираль Архимеда
.1 Исторические
сведения
Архимед (287 г. до н. э. —
212г. до н. э.) — древнегреческий математик, физик и инженер из Сиракуз (остров
Сицилия). Он сделал множество открытий в геометрии. Заложил основы механики,
гидростатики, автор ряда важных изобретений.
Архимедова спираль была открыта
Архимедом. Это произошло в III веке до н.э., когда он экспериментировал с
компасом. Он тянул стрелку компаса с постоянной скоростью, вращая сам компас по
часовой стрелке. Получившаяся кривая была спиралью, которая сдвигались на ту же
величину, на которую поворачивался компас, и между витками спирали сохранялось
одно и то же расстояние.
Архимедову спираль использовали
в древности, как наилучший способ определения площади круга. С ее помощью был
улучшен древний греческий метод нахождения площади круга через измерение длины
окружности. Спираль дала возможность более точного измерения длины окружности,
а следовательно, и площади круга.
В III веке да нашей эры Архимед
на основе своей спирали изобрёл винт, который успешно применяли для передачи
воды в оросительные каналы из водоёмов, расположенных ниже. Позже на основе
винта Архимеда создали шнек («улитку»). Его очень известная разновидность —
винтовой ротор в мясорубке. Шнек используют в механизмах для перемешивания
материалов различной консистенции.
1.2
Определение
спирали Архимеда
Кривую можно рассматривать как
траекторию точки, равномерно движущейся по лучу, исходящему из полюса, в то
время как этот луч равномерно вращается вокруг полюса.
Представим себе циферблат часов
с длинной стрелкой. Стрелка движется по окружности циферблата. А по стрелке в
это время перемещается с постоянной скоростью маленький жучок. Траектория
движения жучка представляет собой спираль Архимеда.
1.3
Построение
спирали Архимеда
Чтобы понять, как получается
спираль Архимеда, отметим на чертеже точку, которая является центром спирали
Архимеда.
Построим из центра спирали
окружность, радиус которой равен шагу спирали. Шаг спирали Архимеда равен
расстоянию, которое проходит точка по поверхности круга за один его полный
оборот.
Разделим окружность на
несколько равных частей с помощью прямых линий. На первой линии откладываем
одно деление, на второй-два деления, на третьей-три деления и т. д. Затем
чертим соответствующее число дуг из центра окружности, проходящих через первое
деление,2-ое и т. д.
Расстояния витков правой
спирали, считая по лучу, равны ,а расстояния
соседних витков, равны.
Уравнение Архимедовой спирали
имеет вид:
,
где —
радиус-вектор,— угол вращения,
—
шаг спирали.
Полярный угол мы
отсчитываем от полярной оси, считая его положительным против часовой стрелки.
При вращении луча против
часовой стрелки получается правая спираль (синяя линия) при вращении — по
часовой стрелке — левая спираль (красная линия).
Полярный радиус-вектор мы
будем брать как положительным, так и отрицательным; в первом случае его
откладывают в направлении, определяемом углом ,
а во втором в противоположном направлении.
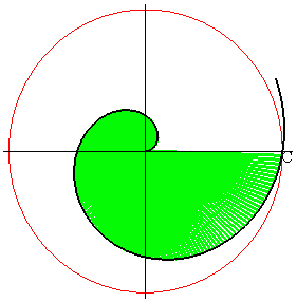
I.Вычислим
площадь, описываемую полярным радиусом спирали при одном его обороте, если
началу движения соответствует ,
.
Итак,
Если мы найдем площадь круга
радиуса ,то
получим
.
То есть, мы получили, что
площадь фигуры, ограниченной полярной осью и первым витком спирали, равна площади
круга с радиусом, равным наибольшему из полярных радиусов витка.
II.Найдем
длину первого витка спирали Архимеда.
2.
Логарифмическая спираль
.1
Исторические
сведения
Логарифмическая спираль была
впервые описана Декартом (1638 г., опубликовано в 1657 г). Декарт искал кривую,
обладающую свойством, подобным свойству окружности, так чтобы касательная в
каждой точке образовывала с радиус-вектором в каждой точке один и тот же угол.
Отсюда и название равноугольная. Он показал, что это условие равносильно тому,
что полярные углы для точек кривой пропорциональны логарифмам радиус-векторов.
Отсюда и второе название: логарифмическая спираль. Независимо от Декарта она
была открыта Э. Торричелли в 1644 г. Свойства логарифмической спирали
исследовал Я. Бернулли (1692 г.). Её название предложено П. Вариньоном (1704
г.).
2.2 Определение
логарифмической спирали
Логарифмическая
спираль —
кривая,
которая пересекает все лучи, выходящие из одной точки О, под одним и тем же
углом.
Уравнение кривой в полярных
координатах:
,
где 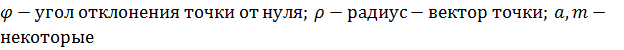
Расстояние между витками растет
с увеличением угла.
.3
Построение
логарифмической спирали
гиперболический
спираль архимед логарифмический
Логарифмическую спираль можно
построить с помощью так называемого «золотого прямоугольника», т.е. такого, у
которого отношение сторон равно золотому сечению:
,
Если от золотого прямоугольника
отрезать квадрат со стороной, равной меньшей стороне прямоугольника, то снова
получим золотой прямоугольник, но меньших размеров. Если продолжить этот
процесс далее, а затем соединить плавной кривой вершины квадратов, то получим
логарифмическую спираль. Точки, делящие стороны прямоугольников в среднем и
крайнем отношении, лежат на логарифмической спирали, закручивающейся внутрь.
. Найдем длину дуги
логарифмической спирали
0≤
≤
2,
используя формулу:
Итак,
II.
Вычислим площадь фигуры, ограниченной первым витком логарифмической спирали,
используя формулу:
Итак,
.4
Основные
свойства логарифмической спирали
1.Угол,
составляемый касательной в произвольной точке логарифмической спирали с
радиус-вектором точки касания, постоянный и зависит лишь от параметра .
2.Параметр m определяет,
насколько плотно и в каком направлении закручивается спираль. В предельном
случае, когда =0 спираль
вырождается в окружность
<#»816334.files/image048.gif»>. Наоборот,
когда стремится к
бесконечности
<#»816334.files/image049.gif»> спираль стремится к
прямой линии. Угол, дополняющий до 90°, называется наклоном спирали.
3.Размер витков логарифмической
спирали постепенно увеличивается, но их форма остаётся неизменной.
4. Если угол возрастает
или убывает в арифметической прогрессии, то возрастает (убывает) в
геометрической.
5.Поворачивая полярную ось
вокруг полюса, можно добиться полного уничтожения параметра a и привести
уравнение к виду r=, где
— новый
параметр.
6. Радиус кривизны в каждой
точке спирали пропорционален длине дуги спирали от ее начала до этой точки.
2.5 Логарифмическая
спираль в природе
Логарифмическая спираль —
единственный тип спирали, не меняющей своей формы при увеличении размеров. Это
свойство объясняет, почему логарифмическая спираль так часто встречается в
природе.
Царство животных предоставляет нам
примеры спиралей раковин, улиток и моллюсков.
Все эти формы указывают на природное
явление: процесс накручивания связан с процессом роста. В самом деле, раковина
улитки — это не больше, не меньше, чем конус, накрученный на себя. Если мы
внимательно посмотрим на рост раковин и рогов, то заметим еще одно любопытное
свойство: рост происходит только на одном конце. И это свойство сохраняет форму
полностью уникальную среди кривых в математике, форму логарифмической, или
равноугольной спирали.
Галактики, штормы и ураганы дают
впечатляющие примеры логарифмических спиралей.
И наконец, в любом месте, где есть
природное явление, в котором сочетаются расширение или сжатие с вращением
появляется логарифмическая спираль.
В растительном мире примеры еще
более бросаются в глаза, потому что у растения может быть бесконечное число
спиралей, а не только одна спираль у каждого.
Расположение семечек в любом
подсолнечнике, чешуек в любом ананасе и другие разнообразные виды растений,
простые ромашки… дают нам настоящий парад переплетающихся спиралей.
Паук плетет паутину спиралеобразно.
.6 Логарифмическая
спираль в технике
Применения логарифмической спирали в
технике основаны на свойстве этой кривой пересекать все свои радиус-векторы под
одним и тем же углом.
Так, вращающиеся ножи в различных
режущих машинах имеют профиль, очерченный по дуге спирали, благодаря чему угол
резания (угол между лезвием ножа и направлением его скорости вращения) остается
постоянным вдоль всей кромки подвижного ножа, что обеспечивает меньший его
износ.
3. Гиперболическая
спираль
.1 Определение
гиперболической спирали
Гиперболическая спираль — плоская
трансцендентная кривая
<#»816334.files/image054.gif»>
Кривая состоит из двух ветвей,
симметричных относительно прямой (см. рис.). Начало координат
является асимптотической точкой. Асимптота — прямая, параллельная полярной оси
и отстоящая от нее на расстоянии .
Гиперболическая спираль получается
при движении точки по вращающейся прямой таким образом, что ее расстояние от
центра вращения всегда будет обратно пропорционально углу поворота прямой,
измеренному от начального положения.
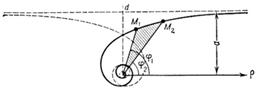
I.Найдем
площадь сектора :
Итак,
II.Вычислим
длину дуги гиперболической спирали, используя формулу:
=
Итак, длина дуги между точками
M1(,
)
и M2(,
)
имеет вид:
Список
литературы
1. Большой энциклопедический словарь
«Математика»,
Гл. редактор Ю.В. Прохоров, Научное изд-во
«Большая Российская Энциклопедия», М.: 1998
2. <http://mathemlib.ru>
. <http://www.phisiki.com/>
. Маркушевич
А.И., Замечательные кривые, М., 1978 г.
. <http://hijos.ru/>
. Википедия
. Фихтенгольц
Г.М., Курс дифференциального и интегрального исчисления; том I,II- М.: Наука,
1969
. Математическая
энциклопедия. Главный редактор И.М. Виноградов, т.3 — М.: «Советская
энциклопедия», 1982
. Графики
функций. Справочник. Вирченко Н.А., Ляшко И.И., Швецов К.И.,1979 г.
Данный калькулятор позволяет рассчитать неизвестные параметры спирали по известным параметрам.

Есть пять параметров спирали: внешний диаметр — D, внутренний диаметр — d, толщина (шаг спирали) — t, длина спирали — L, число витков — n. Есть уравнения, устанавливающие связь между этими параметрами (формулы приведены под калькулятором). По этим уравнениям, зная какие-либо три параметра, можно вычислить два оставшихся неизвестных параметра.
Где мы встречаемся со спиралью? Чаще всего при покупке каких-либо материалов в рулонах, будь то рулоны обоев или рулоны туалетной бумаги. Используя калькулятор ниже, можно рассчитать, например, количество погонных метров в рулоне т.е. длину спирали, зная или измерив толщину материала или посчитав количество витков, и измерив внутренний и внешний диаметры рулона. Калькулятор также может решать и обратные задачи , например, по длине спирали и её диаметрам найти толщину и количество витков спирали. Теория и формулы, как обычно, приведены под калькулятором.
При вводе известных параметров проверяйте правильно ли указана размерность для введенных значений. 20 метров это не тоже самое что 20 миллиметров…
Расчет спирали
Точность вычисления
Знаков после запятой: 4
Архимедова спираль
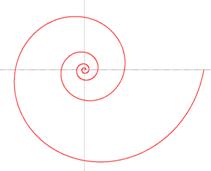
Под Архимедовой спиралью понимают плоскую кривую (спираль), которая отображает траекторию точки М, равномерно движущейся вдоль луча ОА, в то время как сам луч равномерно вращается вокруг точки О.

Если обозначить расстояние от О до М как ρ, а угол поворота луча как φ, то в полярных координатах зависимость расстояния вдоль луча от угла поворота луча можно записать как
,
где k это параметр спирали, соответствующий величине смещения точки вдоль луча при повороте на один радиан. Повороту на 2π будет соответствовать смещение на 2πk.
Так как 2π это полный оборот, число a, также называемое шагом спирали, будет соответствовать расстоянию между двумя соседними витками спирали и начальное уравнение можно переписать в виде.
Так как шаг спирали постоянный, то чем дальше от центра, тем больше витки спирали по форме напоминают окружность. К слову, если движение точки описывается другим уравнением, то это какая-то другая спираль.
Для того, чтобы вывести формулу вычисления длины спирали, рассмотрим бесконечно малое приращение длины.
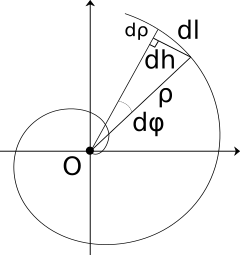
Бесконечно малый отрезок дуги dl можно представить как гипотенузу прямоугольного треугольника с катетами dρ и dh. По теореме Пифагора гипотенуза равна
Бесконечно малый отрезок dh можно заменить на бесконечно малую часть дуги окружности с радиусом ρ, длина которой ρdφ.
Из уравнения спирали заменяем ρ на kφ, и dρ на kdφ
Таким образом мы получили зависимость dl от dφ. Чтобы найти длину L достаточно взять интеграл от начального угла поворота луча до конечного угла поворота луча.
Интеграл я выводить не буду, его уже вывели до меня. Конечный результат
В случае если спираль выходит из точки О, то есть начальный угол поворота луча равен 0, формула упрощается
Если мы говорим о рулоне, то там скорее всего начальный угол все же не равен нулю, то есть есть ненулевой внутренний диаметр (например, там есть втулка). Как же перейти от углов к диаметрам, и найти число витков спирали?
Число витков спирали связано с углами следующим очевидным соотношением:
Диаметры можно связать с углом непосредственно по уравнению спирали (если вспомнить что диаметр это два радиуса)
Эти соотношения и используются для нахождения неизвестных параметров спирали по известным. Осталось только заметить, что уравнение длины является трансцендентным, и решение обратной задачи — по известной длине найти что-то неизвестное, невозможно найти аналитически. Для получения решения приходится прибегать к численным методам, в частности, в калькуляторе выше используется метод секущих.

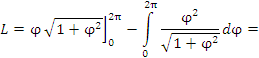
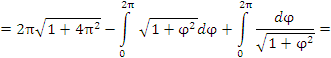
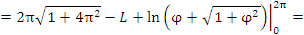
















![{displaystyle {frac {b}{2}}left[theta ,{sqrt {1+theta ^{2}}}+ln left(theta +{sqrt {1+theta ^{2}}}right)right]_{theta _{1}}^{theta _{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8ba4747b8530f217bf568171fb75502e3db3c14)
![{displaystyle {frac {b}{2}}left[theta ,{sqrt {1+theta ^{2}}}+operatorname {arsinh} theta right]_{theta _{1}}^{theta _{2}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7407551b0b01564d1712f0c8c499eca9f6422ae0)
![{displaystyle {frac {b}{2}}left[theta ,{sqrt {1+theta ^{2}}}+ln left(theta +{sqrt {1+theta ^{2}}}right)right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fad4b1b8b488492829597996d5357f1e5399d1a)