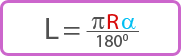Arc length is defined as the distance between the two points placed on the circumference of the circle and measured along the circumference. Arc length is the curved distance along the circumference of the circle. Length of the arc between two points is always greater than the chord between those two points.
What is Arc Length?
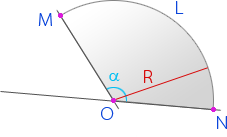
The arc length is defined as the circular distance between two points along the circumference of the circle. The length of the arc is directly dependent on the radius and central angle of the circle. The central angle is the angle subtended by the endpoints of the arc to the center of the circle. It is denoted by θ. It is measured both in degrees and radians. The figure given below shows the arc AB when the radius is r and the central angle is θ.
Arc Length Formula
Length of the arc is calculated using different formulas, the formula used is based on the central angle of the arc. Central angle is measured in degrees or radians, and accordingly, the length of an arc of the circle is calculated. For a circle, the formula for arc length formula is θ times the radius of the circle.
| Arc Length Formula (θ in degrees) | s = 2×π×r ×(θ/360°) |
| Arc Length Formula (θ in radians) | s = θ × r |
| Arc Length Formula (Integral Form) | s = ∫√(1 + (dy/dx)2dx |
There are different cases that are used accordingly to find the required Arc Length
Case 1: When Radius and Angle are given
Formula to calculate the length of an arc is given by:
L = 2πr × (θ / 360)… (1)
where
r is the radius of the circle
θ is the angle in degrees
L is the Arc lengthArc length when the angle is represented in radians
1 radian = π/180°
Substituting the value of radian in equation (1)
L = 2πr × (θ × / 360)
L = r θ…(2)
where,
r is the radius of the circle
θ is the angle in radians.
Case 2: When Area and Central Angle of the Arc are given
Formula to calculate the length of an arc is given by:
L = 2πr × (θ / 360)
where,
r is the radius of the circle
θ is the angle in degreesWe need to find the radius of the circle from the given area. After finding the radius, we will substitute the value of radius in the formula.
Area of the circle = πr2
Example: If area of the circle is 314 m2 and centeral angle of the arc is π radian find the length of the arc.
Sloution:
πr2 = 314 m2
r2 = 314/π (π = 3.14)
r2 = 314/3.14
r2 = 100
r = √100 = 10 m
Length of the arc with angle π radians will be:
L = r θ
L = 10 × π
L = 10 × 3.1415
L = 31.415 m
The value of r can be used in the same formula, as discussed above.
Case 3: Arc length In Integral Form
Arc length in integral form is given by:
L = ∫√(1 + (dy/dx)2)dx
where,
Y is the f(x) function
limit of integral is [a, b]
How to Find Arc Length?
Use the steps given below to find the Arc length of the given arc.
Step 1: Mark the central angle and length of the radius of the given arc.
Step 2: Use the formula as given above according to the value of the angle in degrees or radians accordingly.
Step 3: Simplify the above equation to get the required answer.
Also, Check
- Equation of a Circle
- Degrees To Radians
- Radians to Degrees
Solved Examples on Arc Length
Example 1: Find the length of the arc with a radius of 2m and angle π/2 radians.
Solution:
The formula to calculate the length of the arc is given by:
L = r θ
Where,
L is the length of the arc
Given: r = 2m and θ = π/2 radians
Length of arc = 2 × π/2
Length of arc = π
(π = 3.1415)
Length of arc = 3.1415 m
Thus, the length of the arc is 3.1415 m.
Example 2: Find the length of the arc of function f(x) = 8 between x =2 and x = 4.
Solution:
The formula to calculate the arc length for the function is given by:
L = ∫√(1 + (dy/dx)2)dx
The limit of integral is [a, b]
Substituting the values a = 2, b = 4, and y = 6 or dy/dx = 0 in the above formula,
L = ∫√(1 + (0)2)dx
L = ∫√1 dx
L = ∫1 dx
L = x
(Integral of 1 is x)
The limit of integral is [2, 4]
L = (4 – 2)
L = 2
Thus, the length of the arc of function f(x) = 8 between x = 2 and x = 4 is 2.
Example 3: Find the length of the arc with a radius of 5cm and an angle of 60°.
Solution:
The formula to calculate the length of the arc is given by:
L = 2πr × (θ / 360)
Where,
L is the length of the arc
Given: r = 5cm and θ = 60°
Length of arc = 2πr × (60 / 360)
Length of arc = 2πr × 1/6
Length of arc = 2 × 3.1415 × 5/6
(π = 3.1415)
Length of arc = 5.235cm
Thus, the length of the arc is 5.235cm
Example 4: Find the length of the arc with a radius of 0.5m and an angle of π/4 radians.
Solution:
The formula to calculate the length of the arc is given by:
L = r θ
Where,
L is the length of the arc
Given: r = 0.5m and θ = π/4 radians
Length of arc = 0.5 × π/4
Length of arc = 0.392 m
(π = 3.1415)
Thus, the length of the arc is 0.392 m
Example 5: Find the length of the arc with a radius of 10cm and an angle of 135°.
Solution:
The formula to calculate the length of the arc is given by:
L = 2πr × (θ / 360)
Where,
L is the length of the arc
Given: r = 10cm and θ = 135°
Length of arc = 2πr × (135/360)
Length of arc = (2 × 3.1415 × 10 × 135)/360°
(π = 3.1415)
Length of arc = 23.56cm
Thus, the length of the arc is 23.56cm.
Example 6: Find the length of the arc with a radius of 20mm and angle π/6 radians.
Solution:
The formula to calculate the length of the arc is given by:
L = r θ
Where,
L is the length of the arc
Given: r = 20mm and θ = π/6 radians
Length of arc = 20 × π/6
Length of arc = 10.47 mm
(π = 3.1415)
Thus, the length of the arc is 10.47 mm
Example 7: Find the length of the arc with a radius of 2 cm and an angle of 90°.
Solution:
The formula to calculate the length of the arc is given by:
L = 2πr × (θ / 360)
Where,
L is the length of the arc
Given: r = 2cm and θ = 90°
Length of arc = 2πr × (90 / 360)
Length of arc = 2πr × 1/4
Length of arc = 2 ×3.1415 × 2 × 1/4
(π = 3.1415)
Length of arc = 3.1415 cm
Thus, the length of the arc is 3.1415 cm.
FAQs on Arc Length
Question 1: What is the Arc Length of a Circle?
Answer:
Arc length of a circle is the length made by the arc which is measured along its circimference.
Question 2: Length of the arc is measured in which unit?
Answer:
Length of arc is of a circle is either measured in m or in cm.
Question 3: Does arc length is measured in radians?
Answer:
Angles are measured in radians and arc length is a measurement of distance, thus it cannot be measured in radians.
Question 4: How do you find the circumference if the arc length (l) and central angle (θ) are given?
Answer:
When arc length (l) and central angle (θ) is given then the circumference by the formula
Arc Length (L) / Circumference = θ/360º
Last Updated :
20 Jan, 2023
Like Article
Save Article

{L = dfrac{pi R alpha}{180degree}}
Длина дуги окружности — важный параметр, который используется в геометрии и математике для решения различных задач. На этой странице приведены две формулы для расчета длины дуги окружности — через радиус и угол между радиусами и по формуле Гюйгенса. Также вы можете рассчитать длину дуги окружности с помощью калькулятора, которые используют эти формулы.
Дуга — одно из двух подмножеств окружности, на которые её разбивают любые две различные принадлежащие ей точки. Любые две точки окружности разбивают её на две части, при этом каждая из частей является дугой.
Содержание:
- калькулятор длины дуги окружности
- формула длины дуги окружности через радиус и угол
- формула длины дуги окружности по формуле Гюйгенса
- примеры задач
Если обобщить, то дуга окружности — это часть окружности, ограниченная двумя ее точками. Ниже приведены несколько примеров дуг окружностей:
-
Полная окружность — это дуга, которая охватывает всю окружность. Угол, определяющий полную окружность, равен 360° или 2π радиан. Длина дуги полной окружности равна общей длине окружности, которая может быть вычислена по формуле L = 2πr, где r — радиус окружности.
-
Полуокружность — это дуга, которая охватывает половину окружности. Угол, определяющий полуокружность, равен 180° или π радиан. Длина дуги полуокружности равна половине общей длины окружности и может быть вычислена по формуле L = πr.
-
Сектор окружности — это область, ограниченная дугой окружности и двумя ее радиусами.
Это только несколько примеров дуг окружности. Дуги могут быть разных размеров и форм, в зависимости от угла, определяющего их, и расположения на окружности.
Формула длины дуги окружности через радиус и угол
{L = dfrac{pi R alpha}{180degree}}
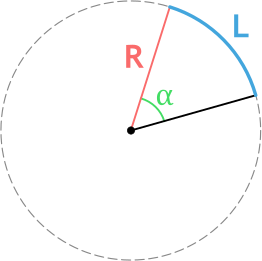
R — радиус окружности
α — центральный угол (угол между радиусами) в градусах
{L = R alpha}
R — радиус окружности
α — центральный угол (угол между радиусами) в радианах
Формула длины дуги окружности по формуле Гюйгенса
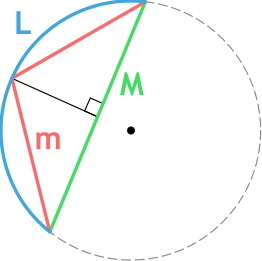
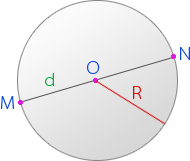
{L approxeq 2m + dfrac{2m-M}{3}}
m — длина хорды m
M — длина хорды M
Обратите внимание, что в данной формуле используется не привычный знак равно «=», а знак «равно или почти равно», который записывается так — «approxeq». Это связано с тем, что формула Гюйгенса дает погрешность при вычислении. Хоть величина погрешности невелика, знать об этом надо.
Относительная погрешность формулы Гюйгенса составляет порядка 0,5% когда угол дуги равен 60°. Если же угловая мера дуги уменьшается, то уменьшается и погрешность. Например, для дуги в 45° относительная погрешность будет равна примерно 0,02%.
Примеры задач на нахождение длины дуги
Задача 1
Найдите длину дуги окружности радиуса 6см, если ее градусная мера равна 30.
Решение
Для решения этой задачи нам подойдет первая формула. Подставим в нее значение радиуса и угла и произведем вычисления:
L = dfrac{pi R alpha}{180degree} = dfrac{pi cdot 6 cdot 30degree}{180degree} = dfrac{pi cdot 180degree}{180degree} = pi : см approx 3.14 : см.
Ответ: {pi : см approx 3.14 : см.}
Введем известные значения в калькулятор для проверки полученного ответа.
Задача 2
Найдите длину дуги окружности радиуса 3см, если ее градусная мера равна 150 градусов.
Решение
Задача аналогична предыдущей. Также воспользуемся первой формулой.
L = dfrac{pi R alpha}{180degree} = dfrac{pi cdot 3 cdot 150degree}{180degree} = dfrac{pi cdot 3 cdot 5}{6} = dfrac{pi cdot 5}{2} = dfrac{5}{2} pi : см = 2.5 pi : см approx 7.85398 : см.
Ответ: {2.5 pi : см approx 7.85398 : см.}
В проверке ответа нам снова поможет калькулятор .
Длина дуги окружности имеет множество применений в математике и ее приложениях. Например, она используется для вычисления длины дуги графика функции, заданной в полярных координатах. Также длина дуги окружности используется при вычислении пути, пройденного телом при движении по окружности, а также для вычисления объема тела, полученного путем вращения дуги окружности вокруг ее диаметра.
В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить длину дуги сектора круга, а также разберем примеры решения задач для демонстрации их применения на практике.
- Определение дуги сектора круга
-
Формулы для нахождения длины дуги сектора
- Через центральный угол в градусах и радиус
- Через угол сектора в радианах и радиус
- Примеры задач
Определение дуги сектора круга
Дуга – это участок между двумя точками на окружности.
Дуга сектора круга – это участок между двумя точками на окружности, которые получены в результате пересечения этой окружности двумя радиусами, образовавшими сектор круга.
На рисунке ниже: AB – это дуга зеленого сектора круга с радиусом R (или r).
- OA = OB = R (r);
- α – угол сектора или центральный угол.
Формулы для нахождения длины дуги сектора
Через центральный угол в градусах и радиус
Длина (L) дуги сектора равняется числу π, умноженному на радиус круга (r), умноженному на центральный угол в градусах (α°), деленному на 180°.
Примечание: в расчетах используется число π, приблизительно равное 3,14.
Через угол сектора в радианах и радиус
Длина (L) дуги сектора равна произведению радиуса (r) и центрального угла, выраженного в радианах (aрад).
Примеры задач
Задание 1
Дан круг с радиусом 15 см. Найдите длину дуги сектора, угол которого равен 30°.
Решение
Воспользуемся формулой расчета, в которой используется центральный угол в градусах:
Задание 2
Длина дуги сектора равняется 24 см. Найдите, чему равен его угол (в радианах и градусах), если радиус круга составляет 12 см.
Решение
Для начала вычислим угол в радианах:
1 радиан ≈ 57,2958°
Следовательно, центральный угол приблизительно равняется 114,59° (2 рад ⋅ 57,2958°).
Перейти к содержанию
Длина дуги окружности
На чтение 1 мин
Дуга – это часть окружности, отсекаемая хордой.
R – радиус окружности
α – центральный угол дуги
O – центр окружности
Длина дуги (L) определяется по формуле:
Вам также может понравиться
Окружность – геометрическое место точек, равноудаленных
0124
Окружность – геометрическое место точек, равноудаленных
0123
Эллипс – это множество точек плоскости, для которых
03.2к.
Многоугольник – это геометрическая фигура, которая
0141
Шестиугольник – это многоугольник, который имеет шесть углов.
0442
Пятиугольник – это многоугольник, который имеет пять углов.
0349
Трапеция – это четырехугольник, у которого параллельна
088
Квадрат – это параллелограмм, у которого все углы и
090
Площадь круга и его частей. Длина окружности и ее дуг
Основные определения и свойства
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности
Часть окружности, расположенная между двумя точками окружности
Конечная часть плоскости, ограниченная окружностью
Часть круга, ограниченная двумя радиусами
Часть круга, ограниченная хордой
Выпуклый многоугольник, у которого все стороны равны и все углы равны
Около любого правильного многоугольника можно описать окружность
| Фигура | Рисунок | Определения и свойства |
| Окружность |  |
|
| Дуга |  |
|
| Круг |  |
|
| Сектор |  |
|
| Сегмент |  |
|
| Правильный многоугольник |  |
|
 |
| Окружность |
 |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности
Дуга
Часть окружности, расположенная между двумя точками окружности
Круг
Конечная часть плоскости, ограниченная окружностью
Сектор
Часть круга, ограниченная двумя радиусами
Сегмент
Часть круга, ограниченная хордой
Правильный многоугольник
Выпуклый многоугольник, у которого все стороны равны и все углы равны
Около любого правильного многоугольника можно описать окружность
Определение 1 . Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Определение 2 . Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Замечание 1 . Доказательство того, что пределы площадей и периметров правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится.
Определение 3 . Числом π (пи) называют число, равное площади круга радиуса 1.
Замечание 2 . Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью:
Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами.
Формулы для площади круга и его частей

где R – радиус круга, D – диаметр круга

если величина угла α выражена в радианах

если величина угла α выражена в градусах

если величина угла α выражена в радианах

если величина угла α выражена в градусах
| Числовая характеристика | Рисунок | Формула |
| Площадь круга |  |
|
| Площадь сектора |  |
|
| Площадь сегмента |  |
| Площадь круга |
 |

где R – радиус круга, D – диаметр круга
Площадь сектора

если величина угла α выражена в радианах

если величина угла α выражена в градусах
Площадь сегмента

если величина угла α выражена в радианах

если величина угла α выражена в градусах
Формулы для длины окружности и её дуг
где R – радиус круга, D – диаметр круга
если величина угла α выражена в радианах

если величина угла α выражена в градусах
| Длина окружности |
 |
где R – радиус круга, D – диаметр круга
Длина дуги
если величина угла α выражена в радианах

если величина угла α выражена в градусах
Площадь круга
Рассмотрим две окружности с общим центром ( концентрические окружности ) и радиусами радиусами 1 и R , в каждую из которых вписан правильный n – угольник (рис. 1).
Обозначим через O общий центр этих окружностей. Пусть внутренняя окружность имеет радиус 1 .
Поскольку при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса 1 , стремится к π , то при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса R , стремится к числу πR 2 .
Таким образом, площадь круга радиуса R , обозначаемая S , равна
Длина окружности
то, обозначая длину окружности радиуса R буквой C , мы, в соответствии с определением 2, при увеличении n получаем равенство:
откуда вытекает формула для длины окружности радиуса R :
Следствие . Длина окружности радиуса 1 равна 2π.
Длина дуги
Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла.
В случае, когда величина α выражена в градусах, справедлива пропорция
из которой вытекает равенство:
В случае, когда величина α выражена в радианах, справедлива пропорция
из которой вытекает равенство:
Площадь сектора
Рассмотрим круговой сектор, изображённый на рисунке 4, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего центрального угла.
В случае, когда величина α выражена в градусах, справедлива пропорция
из которой вытекает равенство:
В случае, когда величина α выражена в радианах, справедлива пропорция
из которой вытекает равенство:
Площадь сегмента
Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла.
Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах, получаем
В случае, когда величина α выражена в в радианах, получаем
Сегмент круга
Вычисляет площадь, длину дуги, длину хорды, высоту и периметр сегмента круга. Описывается несколько вариантов расчета по параметрам сегмента — по углу, по хорде, по радиусу, по высоте и длине дуги.

Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).
На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота
Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:
Формулы вычисления параметров сегмента
Площадь сегмента:
[1]
Длина дуги:
Длина дуги
На этой странице приведены две формулы для расчета длины дуги окружности — через радиус и угол между ними и по формуле Гюйгенса. Также вы можете рассчитать длину дуги окружности с помощью калькуляторов, которые используют эти формулы.
Дуга — одно из двух подмножеств окружности, на которые её разбивают любые две различные принадлежащие ей точки. Любые две точки окружности разбивают её на две части, при этом каждая из частей является дугой.
http://planetcalc.ru/1421/
http://mnogoformul.ru/dlina-dugi