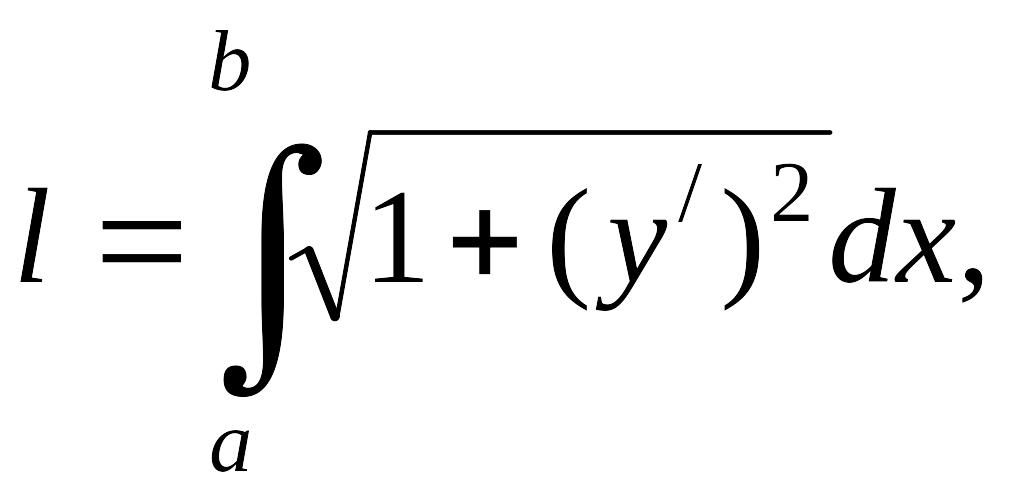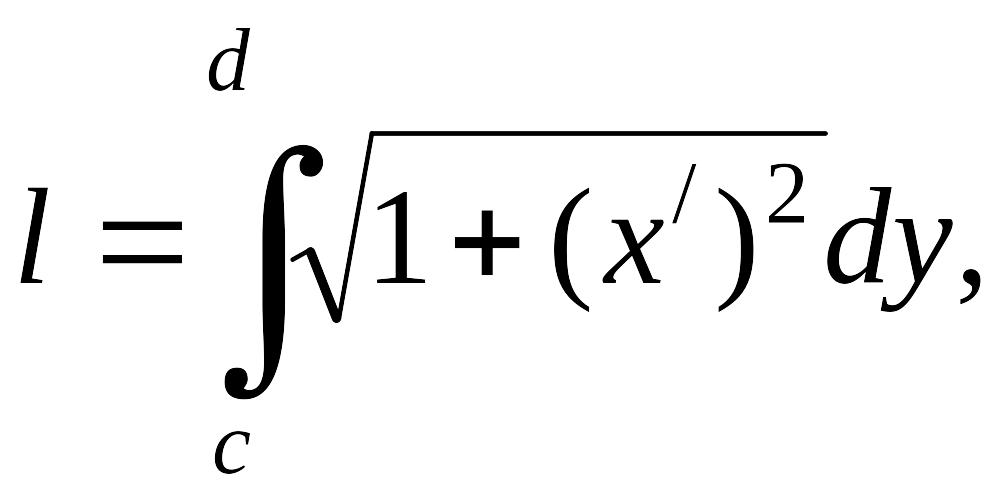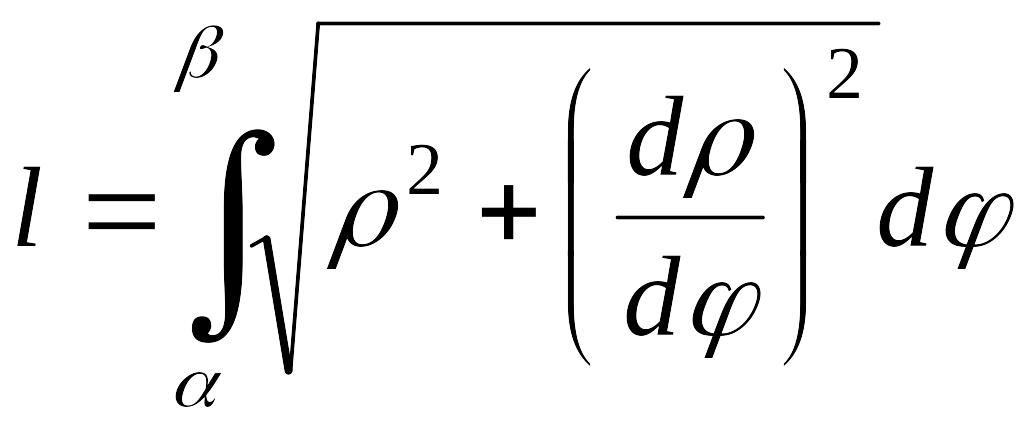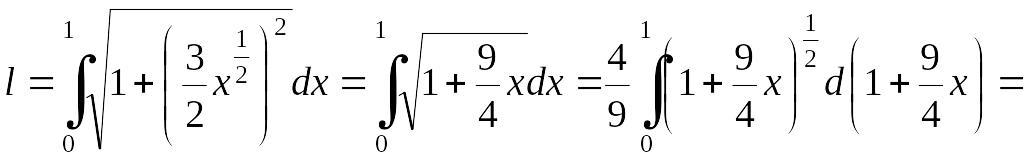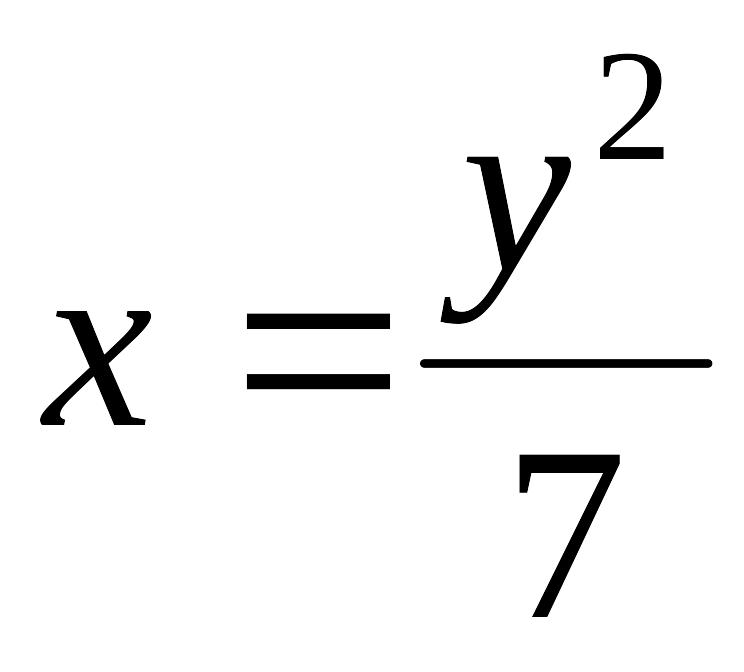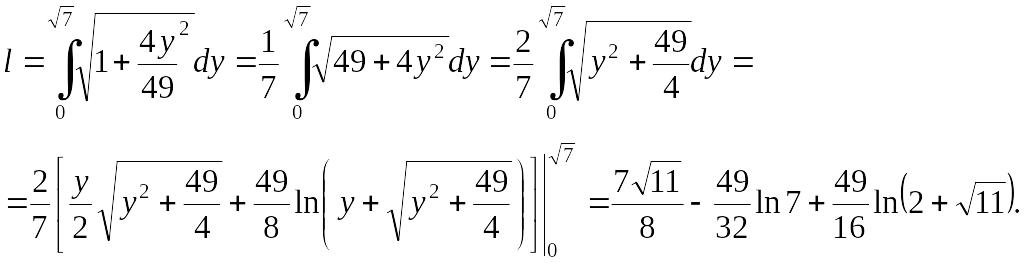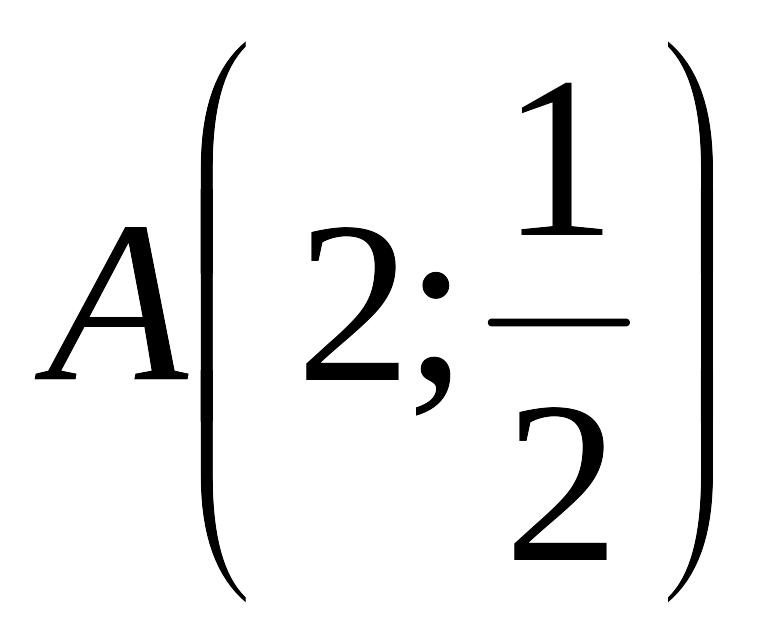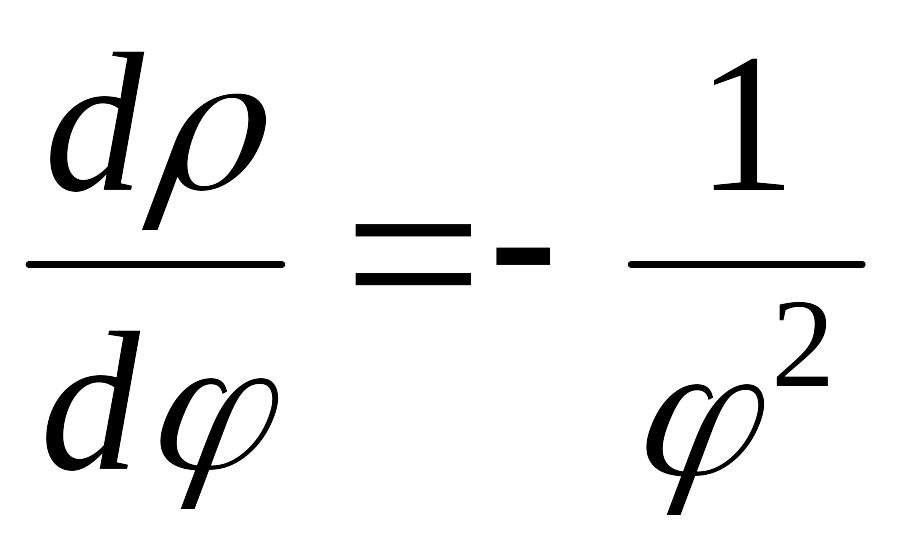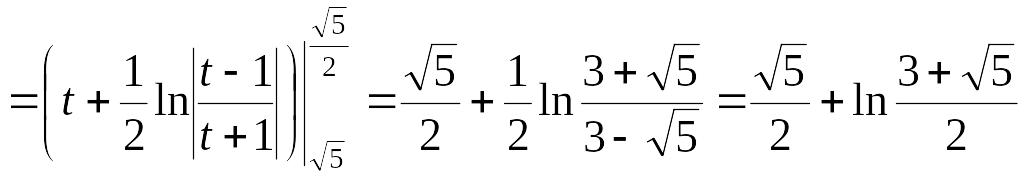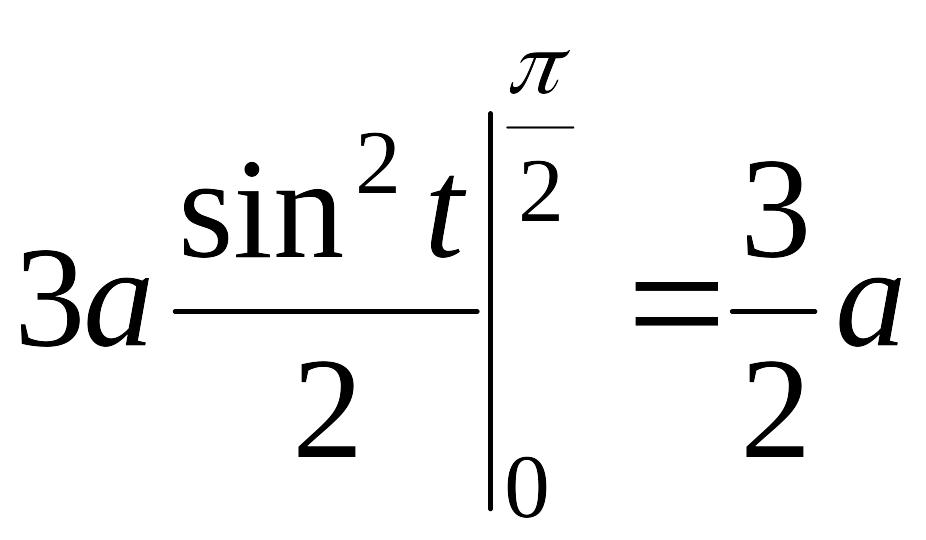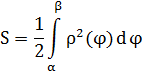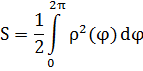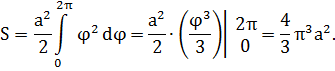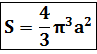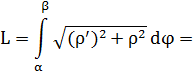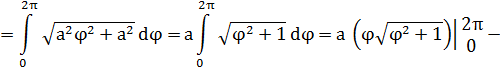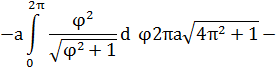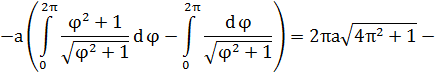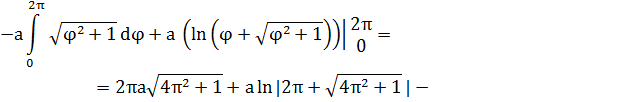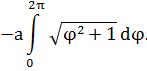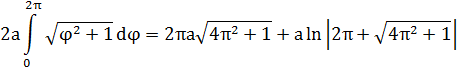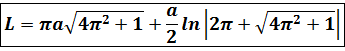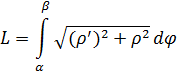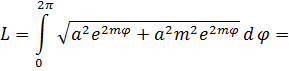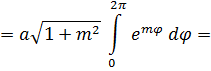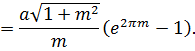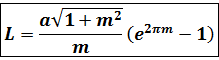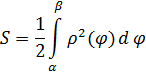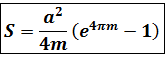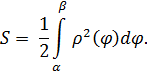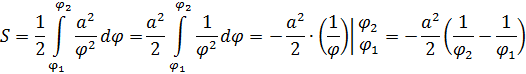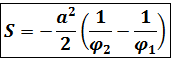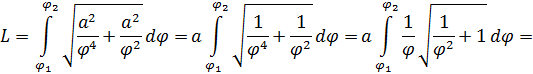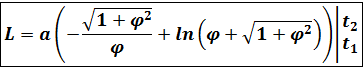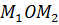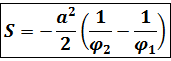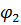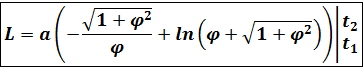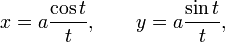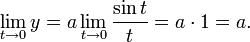From Wikipedia, the free encyclopedia
Hyperbolic spiral: branch for φ > 0
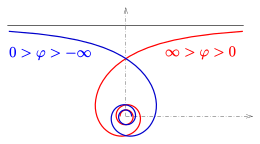
Hyperbolic spiral: both branches
A hyperbolic spiral is a plane curve, which can be described in polar coordinates by the equation
of a hyperbola. Because it can be generated by a circle inversion of an Archimedean spiral, it is called Reciprocal spiral, too.[1][2]
Pierre Varignon first studied the curve in 1704.[2] Later Johann Bernoulli and Roger Cotes worked on the curve as well.
The hyperbolic spiral has a pitch angle that increases with distance from its center, unlike the logarithmic spiral (in which the angle is constant) or Archimedean spiral (in which it decreases with distance). For this reason, it has been used to model the shapes of spiral galaxies, which in some cases similarly have a similarly increasing pitch angle. However, this model does not provide a good fit to the shapes of all spiral galaxies.[3][4]
In cartesian coordinates[edit]
the hyperbolic spiral with the polar equation
can be represented in Cartesian coordinates (x = r cos φ, y = r sin φ) by
The hyperbola has in the rφ-plane the coordinate axes as asymptotes. The hyperbolic spiral (in the xy-plane) approaches for φ → ±∞ the origin as asymptotic point. For φ → ±0 the curve has an asymptotic line (see next section).
From the polar equation and φ = a/r, r = √x2 + y2 one gets a representation by an equation:
Geometric properties[edit]
Asymptote[edit]
Because
the curve has an asymptote with equation y = a.
Polar slope[edit]
Definition of sector (light blue) and polar slope angle α
From vector calculus in polar coordinates one gets the formula tan α = r′/r for the polar slope and its angle α between the tangent of a curve and the tangent of the corresponding polar circle.
For the hyperbolic spiral r = a/φ the polar slope is
Curvature[edit]
The curvature of a curve with polar equation r = r(φ) is
From the equation r = a/φ and the derivatives r′ = −a/φ2 and r″ = 2a/φ3 one gets the curvature of a hyperbolic spiral:
Arc length[edit]
The length of the arc of a hyperbolic spiral between (r(φ1), φ1) and (r(φ2), φ2) can be calculated by the integral:
Sector area[edit]
The area of a sector (see diagram above) of a hyperbolic spiral with equation r = a/φ is:
Inversion[edit]
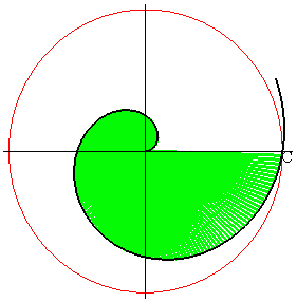
Hyperbolic spiral (blue) as image of an Archimedean spiral (green) with a circle inversion
The inversion at the unit circle has in polar coordinates the simple description: (r, φ) ↦ (1/r, φ).
The image of an Archimedean spiral r = φ/a with a circle inversion is the hyperbolic spiral with equation r = a/φ. At φ = a the two curves intersect at a fixed point on the unit circle.
The osculating circle of the Archimedean spiral r = φ/a at the origin has radius ρ0 = 1/2a (see Archimedean spiral) and center (0, ρ0). The image of this circle is the line y = a (see circle inversion). Hence the preimage of the asymptote of the hyperbolic spiral with the inversion of the Archimedean spiral is the osculating circle of the Archimedean spiral at the origin.
- Example: The diagram shows an example with a = π.
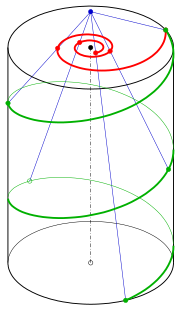
Central projection of a helix[edit]
Hyperbolic spiral as central projection of a helix
Consider the central projection from point C0 = (0, 0, d) onto the image plane z = 0. This will map a point (x, y, z) to the point d/d − z(x, y).
The image under this projection of the helix with parametric representation
is the curve
with the polar equation
which describes a hyperbolic spiral.
For parameter t0 = d/c the hyperbolic spiral has a pole and the helix intersects the plane z = d at a point V0. One can check by calculation that the image of the helix as it approaches V0 is the asymptote of the hyperbolic spiral.
References[edit]
- ^ Bowser, Edward Albert (1880), An Elementary Treatise on Analytic Geometry: Embracing Plane Geometry and an Introduction to Geometry of Three Dimensions (4th ed.), D. Van Nostrand, p. 232
- ^ a b Lawrence, J. Dennis (2013), A Catalog of Special Plane Curves, Dover Books on Mathematics, Courier Dover Publications, p. 186, ISBN 9780486167664.
- ^ R. C., Jr. Kennicutt (December 1981), «The shapes of spiral arms along the Hubble sequence», The Astronomical Journal, American Astronomical Society, 86: 1847, Bibcode:1981AJ…..86.1847K, doi:10.1086/113064
- ^ Savchenko, S. S.; Reshetnikov, V. P. (September 2013), «Pitch angle variations in spiral galaxies», Monthly Notices of the Royal Astronomical Society, 436 (2): 1074–1083, doi:10.1093/mnras/stt1627
- Hans-Jochen Bartsch, Michael Sachs: Taschenbuch mathematischer Formeln für Ingenieure und Naturwissenschaftler, Carl Hanser Verlag, 2018, ISBN 3446457070, 9783446457072, S. 410.
- Kinko Tsuji, Stefan C. Müller: Spirals and Vortices: In Culture, Nature, and Science, Springer, 2019, ISBN 3030057984, 9783030057985, S. 96.
- Pierre Varignon: Nouvelle formation de Spirales – exemple II, Mémoires de l’Académie des sciences de l’Institut de France, 1704, pp. 94–103.
- Friedrich Grelle: Analytische Geometrie der Ebene, Verlag F. Brecke, 1861 hyperbolische Spirale, S. 215.
- Jakob Philipp Kulik: Lehrbuch der höhern Analysis, Band 2, In Commiss. bei Kronberger u. Rziwnatz, 1844, Spirallinien, S. 222.
External links[edit]
- Weisstein, Eric W. «Hyperbolic Spiral». MathWorld.
- Online exploration using JSXGraph (JavaScript)
- 2dcurves «hyperbolic spiral» page
Если кривая задана
уравнением вида у
= f(x),
то длина дуги вычисляется по формуле
EMBED Equation.3
(2.2.1)
где а
и b
– абсциссы
начала и конца дуги.
Если кривая задана
уравнением вида EMBED Equation.3
,
то длина дуги вычисляется по формуле
EMBED Equation.3
(2.2.2)
где с
и d
– ординаты начала и конца дуги.
Если кривая задана
уравнением в полярных координатах
EMBED Equation.3
,
то, принимая за параметр угол EMBED
Equation.3
и учитывая, что EMBED Equation.3
получаем формулу (2.2.3) для вычисления
длины дуги:
EMBED Equation.3
.
(2.2.3)
Если кривая задана
параметрическими уравнениями EMBED
Equation.3
то длина ее дуги вычисляется по формуле
(2.2.4):
EMBED Equation.3
(2.2.4)
где EMBED Equation.3
и EMBED Equation.3
— значения параметра, соответствующие
концам дуги.
Пример 2.2.1.
Найти длину дуги полукубической
параболы у
= x3/2 от
ее вершины до точки В(1,
1).
Решение.
Для того, чтобы длину дуги вычислить по
формуле (2.2.1) найдем производную функции
у = x3/2.
Она равна EMBED Equation.3
.
Тогда по формуле (2.2.1) имеем
EMBED Equation.3
EMBED Equation.3

EMBED Equation.3
(ед.)
Пример 2.2.2.
Вычислить
длину дуги параболы EMBED Equation.3
от вершины до точки А(1;
EMBED Equation.3
).
Решение. Из
данного уравнения параболы выразим
переменную х:
EMBED Equation.3
,
найдем производную
EMBED Equation.3
.
По условию переменная EMBED Equation.3
изменяется от 0 до EMBED Equation.3
,
следовательно, по формуле (2.2.2) найдем:
EMBED Equation.3
При вычислении
данного определенного интеграла
воспользовались ранее известным
результатом: EMBED Equation.3
.
Пример 2.2.3.
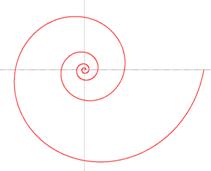
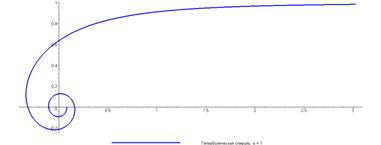
Найти длину дуги гиперболической спирали
EMBED Equation.3
между точками EMBED Equation.3
и EMBED Equation.3
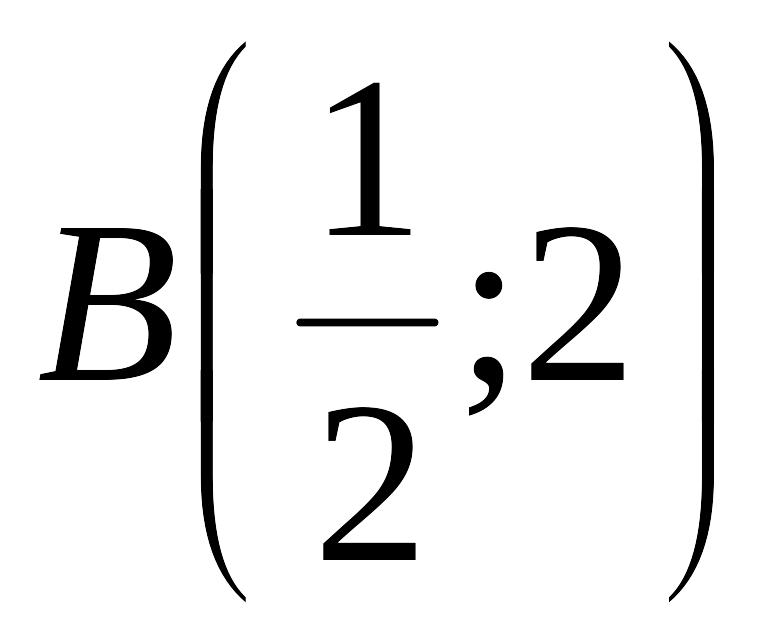
Решение.
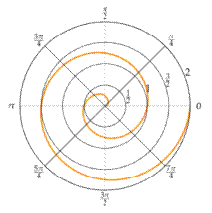
Гиперболическая спираль, заданная
уравнением EMBED Equation.3
,
изображена на рис.2.2.1.
SHAPE * MERGEFORMAT

Рисунок
2.2.1 — Гиперболическая спираль
Разрешим данное
уравнение EMBED Equation.3
относительно EMBED Equation.3
:
EMBED Equation.3
При EMBED Equation.3
радиус-вектор спирали неограниченно
уменьшается и витки спирали неограниченно
приближаются к полюсу. Требуется найти
длину дуги АВ
спирали,
соответствующей значениям полярного
угла от EMBED Equation.3
до EMBED Equation.3
.
Из уравнения
спирали найдем EMBED Equation.3
,
затем для нахождения искомой длины
воспользуемся формулой (2.2.3):
EMBED Equation.3
=
EMBED Equation.3
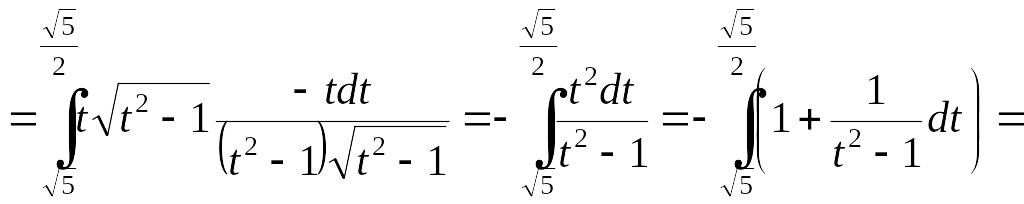
EMBED Equation.3
(ед.).
Пример 2.2.4.
Вычислить длину астроиды EMBED Equation.3
Решение.
Из рис. 2.2.2, на котором изображена
астроида, видно, что кривая симметрична
относительно осей координат, поэтому
можно вычислить ее четвертую часть,
расположенную в первом квадранте.
SHAPE * MERGEFORMAT

Рис. 2.2.2 — Астроида
EMBED Equation.3
Найдем производные:
EMBED Equation.3
Параметр EMBED Equation.3
изменяется от EMBED Equation.3
до EMBED Equation.3
.
Следовательно, по формуле (2.2.4.) получим:
EMBED Equation.3

= EMBED Equation.3
.
Таким образом,
искомая длина дуги равна EMBED Equation.3
(ед.)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
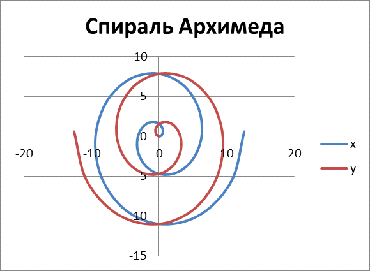
Спираль Архимеда. Логарифмическая, гиперболическая спираль
1. Спираль Архимеда
.1 Исторические
сведения
Архимед (287 г. до н. э. —
212г. до н. э.) — древнегреческий математик, физик и инженер из Сиракуз (остров
Сицилия). Он сделал множество открытий в геометрии. Заложил основы механики,
гидростатики, автор ряда важных изобретений.
Архимедова спираль была открыта
Архимедом. Это произошло в III веке до н.э., когда он экспериментировал с
компасом. Он тянул стрелку компаса с постоянной скоростью, вращая сам компас по
часовой стрелке. Получившаяся кривая была спиралью, которая сдвигались на ту же
величину, на которую поворачивался компас, и между витками спирали сохранялось
одно и то же расстояние.
Архимедову спираль использовали
в древности, как наилучший способ определения площади круга. С ее помощью был
улучшен древний греческий метод нахождения площади круга через измерение длины
окружности. Спираль дала возможность более точного измерения длины окружности,
а следовательно, и площади круга.
В III веке да нашей эры Архимед
на основе своей спирали изобрёл винт, который успешно применяли для передачи
воды в оросительные каналы из водоёмов, расположенных ниже. Позже на основе
винта Архимеда создали шнек («улитку»). Его очень известная разновидность —
винтовой ротор в мясорубке. Шнек используют в механизмах для перемешивания
материалов различной консистенции.
1.2
Определение
спирали Архимеда
Кривую можно рассматривать как
траекторию точки, равномерно движущейся по лучу, исходящему из полюса, в то
время как этот луч равномерно вращается вокруг полюса.
Представим себе циферблат часов
с длинной стрелкой. Стрелка движется по окружности циферблата. А по стрелке в
это время перемещается с постоянной скоростью маленький жучок. Траектория
движения жучка представляет собой спираль Архимеда.
1.3
Построение
спирали Архимеда
Чтобы понять, как получается
спираль Архимеда, отметим на чертеже точку, которая является центром спирали
Архимеда.
Построим из центра спирали
окружность, радиус которой равен шагу спирали. Шаг спирали Архимеда равен
расстоянию, которое проходит точка по поверхности круга за один его полный
оборот.
Разделим окружность на
несколько равных частей с помощью прямых линий. На первой линии откладываем
одно деление, на второй-два деления, на третьей-три деления и т. д. Затем
чертим соответствующее число дуг из центра окружности, проходящих через первое
деление,2-ое и т. д.
Расстояния витков правой
спирали, считая по лучу, равны ,а расстояния
соседних витков, равны.
Уравнение Архимедовой спирали
имеет вид:
,
где —
радиус-вектор,— угол вращения,
—
шаг спирали.
Полярный угол мы
отсчитываем от полярной оси, считая его положительным против часовой стрелки.
При вращении луча против
часовой стрелки получается правая спираль (синяя линия) при вращении — по
часовой стрелке — левая спираль (красная линия).
Полярный радиус-вектор мы
будем брать как положительным, так и отрицательным; в первом случае его
откладывают в направлении, определяемом углом ,
а во втором в противоположном направлении.
I.Вычислим
площадь, описываемую полярным радиусом спирали при одном его обороте, если
началу движения соответствует ,
.
Итак,
Если мы найдем площадь круга
радиуса ,то
получим
.
То есть, мы получили, что
площадь фигуры, ограниченной полярной осью и первым витком спирали, равна площади
круга с радиусом, равным наибольшему из полярных радиусов витка.
II.Найдем
длину первого витка спирали Архимеда.
2.
Логарифмическая спираль
.1
Исторические
сведения
Логарифмическая спираль была
впервые описана Декартом (1638 г., опубликовано в 1657 г). Декарт искал кривую,
обладающую свойством, подобным свойству окружности, так чтобы касательная в
каждой точке образовывала с радиус-вектором в каждой точке один и тот же угол.
Отсюда и название равноугольная. Он показал, что это условие равносильно тому,
что полярные углы для точек кривой пропорциональны логарифмам радиус-векторов.
Отсюда и второе название: логарифмическая спираль. Независимо от Декарта она
была открыта Э. Торричелли в 1644 г. Свойства логарифмической спирали
исследовал Я. Бернулли (1692 г.). Её название предложено П. Вариньоном (1704
г.).
2.2 Определение
логарифмической спирали
Логарифмическая
спираль —
кривая,
которая пересекает все лучи, выходящие из одной точки О, под одним и тем же
углом.
Уравнение кривой в полярных
координатах:
,
где 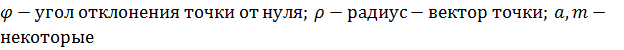
Расстояние между витками растет
с увеличением угла.
.3
Построение
логарифмической спирали
гиперболический
спираль архимед логарифмический
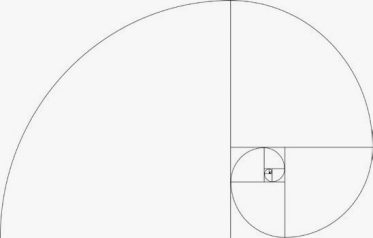
Логарифмическую спираль можно
построить с помощью так называемого «золотого прямоугольника», т.е. такого, у
которого отношение сторон равно золотому сечению:
,
Если от золотого прямоугольника
отрезать квадрат со стороной, равной меньшей стороне прямоугольника, то снова
получим золотой прямоугольник, но меньших размеров. Если продолжить этот
процесс далее, а затем соединить плавной кривой вершины квадратов, то получим
логарифмическую спираль. Точки, делящие стороны прямоугольников в среднем и
крайнем отношении, лежат на логарифмической спирали, закручивающейся внутрь.
. Найдем длину дуги
логарифмической спирали
0≤
≤
2,
используя формулу:
Итак,
II.
Вычислим площадь фигуры, ограниченной первым витком логарифмической спирали,
используя формулу:
Итак,
.4
Основные
свойства логарифмической спирали
1.Угол,
составляемый касательной в произвольной точке логарифмической спирали с
радиус-вектором точки касания, постоянный и зависит лишь от параметра .
2.Параметр m определяет,
насколько плотно и в каком направлении закручивается спираль. В предельном
случае, когда =0 спираль
вырождается в окружность
<#»816334.files/image048.gif»>. Наоборот,
когда стремится к
бесконечности
<#»816334.files/image049.gif»> спираль стремится к
прямой линии. Угол, дополняющий до 90°, называется наклоном спирали.
3.Размер витков логарифмической
спирали постепенно увеличивается, но их форма остаётся неизменной.
4. Если угол возрастает
или убывает в арифметической прогрессии, то возрастает (убывает) в
геометрической.
5.Поворачивая полярную ось
вокруг полюса, можно добиться полного уничтожения параметра a и привести
уравнение к виду r=, где
— новый
параметр.
6. Радиус кривизны в каждой
точке спирали пропорционален длине дуги спирали от ее начала до этой точки.
2.5 Логарифмическая
спираль в природе
Логарифмическая спираль —
единственный тип спирали, не меняющей своей формы при увеличении размеров. Это
свойство объясняет, почему логарифмическая спираль так часто встречается в
природе.
Царство животных предоставляет нам
примеры спиралей раковин, улиток и моллюсков.
Все эти формы указывают на природное
явление: процесс накручивания связан с процессом роста. В самом деле, раковина
улитки — это не больше, не меньше, чем конус, накрученный на себя. Если мы
внимательно посмотрим на рост раковин и рогов, то заметим еще одно любопытное
свойство: рост происходит только на одном конце. И это свойство сохраняет форму
полностью уникальную среди кривых в математике, форму логарифмической, или
равноугольной спирали.
Галактики, штормы и ураганы дают
впечатляющие примеры логарифмических спиралей.
И наконец, в любом месте, где есть
природное явление, в котором сочетаются расширение или сжатие с вращением
появляется логарифмическая спираль.
В растительном мире примеры еще
более бросаются в глаза, потому что у растения может быть бесконечное число
спиралей, а не только одна спираль у каждого.
Расположение семечек в любом
подсолнечнике, чешуек в любом ананасе и другие разнообразные виды растений,
простые ромашки… дают нам настоящий парад переплетающихся спиралей.
Паук плетет паутину спиралеобразно.
.6 Логарифмическая
спираль в технике
Применения логарифмической спирали в
технике основаны на свойстве этой кривой пересекать все свои радиус-векторы под
одним и тем же углом.
Так, вращающиеся ножи в различных
режущих машинах имеют профиль, очерченный по дуге спирали, благодаря чему угол
резания (угол между лезвием ножа и направлением его скорости вращения) остается
постоянным вдоль всей кромки подвижного ножа, что обеспечивает меньший его
износ.
3. Гиперболическая
спираль
.1 Определение
гиперболической спирали
Гиперболическая спираль — плоская
трансцендентная кривая
<#»816334.files/image054.gif»>
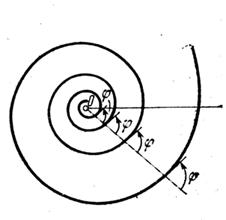
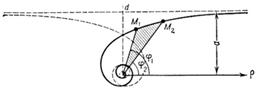
Кривая состоит из двух ветвей,
симметричных относительно прямой (см. рис.). Начало координат
является асимптотической точкой. Асимптота — прямая, параллельная полярной оси
и отстоящая от нее на расстоянии .
Гиперболическая спираль получается
при движении точки по вращающейся прямой таким образом, что ее расстояние от
центра вращения всегда будет обратно пропорционально углу поворота прямой,
измеренному от начального положения.
I.Найдем
площадь сектора :
Итак,
II.Вычислим
длину дуги гиперболической спирали, используя формулу:
=
Итак, длина дуги между точками
M1(,
)
и M2(,
)
имеет вид:
Список
литературы
1. Большой энциклопедический словарь
«Математика»,
Гл. редактор Ю.В. Прохоров, Научное изд-во
«Большая Российская Энциклопедия», М.: 1998
2. <http://mathemlib.ru>
. <http://www.phisiki.com/>
. Маркушевич
А.И., Замечательные кривые, М., 1978 г.
. <http://hijos.ru/>
. Википедия
. Фихтенгольц
Г.М., Курс дифференциального и интегрального исчисления; том I,II- М.: Наука,
1969
. Математическая
энциклопедия. Главный редактор И.М. Виноградов, т.3 — М.: «Советская
энциклопедия», 1982
. Графики
функций. Справочник. Вирченко Н.А., Ляшко И.И., Швецов К.И.,1979 г.
Даже ответ точный знаете
[math]begin{aligned}L&=intlimits_{alpha}^{beta}!sqrt{r^2+r’^2},dvarphi= intlimits_{3/4}^{4/3}!sqrt{{left(frac{1}{varphi}right)!}^2+{left(frac{1}{varphi}right)!}’^2},dvarphi= intlimits_{3/4}^{4/3}!sqrt{frac{1}{varphi^2}+frac{1}{varphi^4}},dvarphi= intlimits_{3/4}^{4/3}frac{sqrt{varphi^2+1}}{varphi^2},dvarphi=\ &= intlimits_{3/4}^{4/3}frac{varphi^2+1}{varphi^2sqrt{varphi^2+1}},dvarphi= intlimits_{3/4}^{4/3}frac{dvarphi}{sqrt{varphi^2+1}}+ intlimits_{3/4}^{4/3}frac{dvarphi}{varphi^2sqrt{varphi^2+1}}= left.{ln!left(varphi+ sqrt{varphi^2+1}right)}!right|_{3/4}^{4/3}+ intlimits_{3/4}^{4/3}frac{varphi^{-3},dvarphi}{sqrt{1+varphi^{-2}}}=\ &= ln!left(frac{4}{3}+ sqrt{frac{16}{9}+1}right)- ln!left(frac{3}{4}+sqrt{frac{9}{16}+1}right)- frac{1}{2}intlimits_{3/4}^{4/3}(1+varphi^{-2})^{-1/2},d(1+varphi^{-2})=\ &= ln!left(frac{4}{3}+frac{5}{3}right)- ln!left(frac{3}{4}+frac{5}{4}right)- left.{sqrt{1+varphi^{-2}}} right|_{3/4}^{4/3}= ln3-ln2-left(sqrt{1+frac{9}{16}}-sqrt{1+frac{16}{9}}right) =\ &= ln frac{3}{2}-left(sqrt{frac{25}{16}}-sqrt{frac{25}{9}}right)= lnfrac{3}{2} — left(frac{5}{4}-frac{5}{3}right) = lnfrac{3}{2} + frac{5}{12} approx 0.82212end{aligned[/math]
К ответу допишите (лин. ед.).
Гиперболическая спираль. Гиперболическая спираль в жизни
Гиперболическая спираль
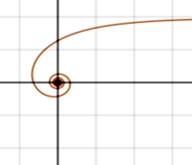
Гиперболическая спираль — плоская трансцендентная кривая. Уравнение гиперболической спирали в полярной системе координат является обратным для уравнения Архимедовой спирали и записывается так:
ρ φ = a
Кривая состоит из двух ветвей, симметричных относительно прямой. Начало координат является асимптотической точкой. Асимптота — прямая, параллельная полярной оси и отстоящая от нее на расстоянии.
Гиперболическая спираль получается при движении точки по вращающейся прямой таким образом, что ее расстояние от центра вращения всегда будет обратно пропорционально углу поворота прямой, измеренному от начального положения.
Найдем площадь сектора:
Итак,
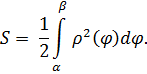
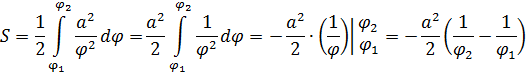
Вычислим длину дуги гиперболической спирали, используя формулу:
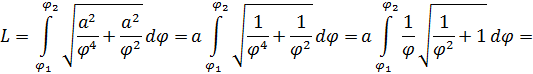
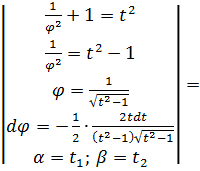
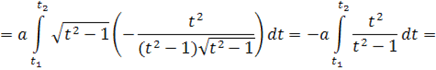
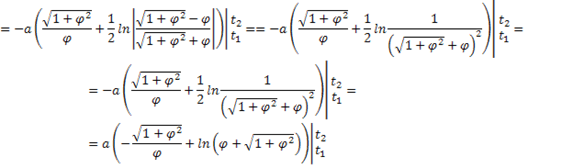
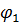
Итак, длина дуги между точками M1(, ) и M2(, ) имеет вид:
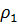
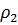
Уравнение гиперболической спирали в декартовых координатах:
Параметрическая запись уравнения:
Спираль имеет асимптоту y = a: при t стремящемся к нулю ордината стремится к a, а абсцисса уходит в бесконечность:
Гиперболическая спираль в жизни

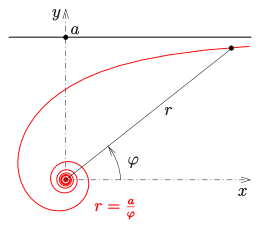









![{displaystyle {begin{aligned}L&=int _{varphi _{1}}^{varphi _{2}}{sqrt {left(r^{prime }(varphi )right)^{2}+r^{2}(varphi )}},dvarphi =cdots \&=aint _{varphi _{1}}^{varphi _{2}}{frac {sqrt {1+varphi ^{2}}}{varphi ^{2}}},dvarphi \&=aleft[-{frac {sqrt {1+varphi ^{2}}}{varphi }}+ln left(varphi +{sqrt {1+varphi ^{2}}}right)right]_{varphi _{1}}^{varphi _{2}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/21a80ceb06fb95bfde4e98c04ebc702924d2f00c)