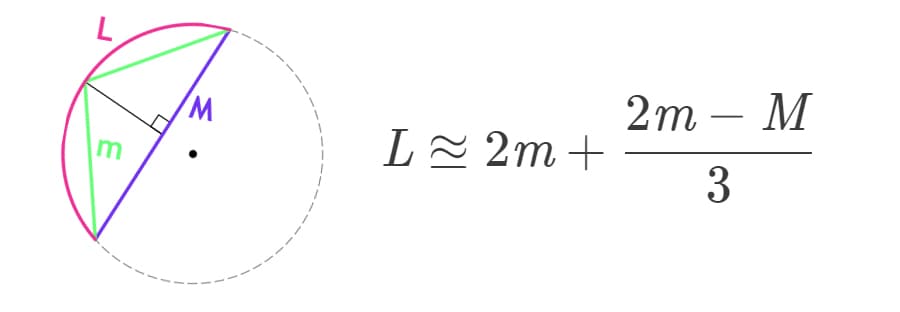Как найти длину дуги на поверхности - Исправление недочетов и поиск решений вместе с Examum.ru

Содержание

Длина дуги, угол между линиями, площадь области на поверхности

Краткие теоретические сведения

Зная первую квадратичную форму поверхности, мы можем решить три задачи:

1. Найти длину дуги на поверхности:
begin{equation*}
s=intlimits_{t_1}^{t_2}|vec{r’}(t)dt|=intlimits_{P_1}^{P_2}|dvec{r}(u,v)|=intlimits_{P_1}^{P_2}sqrt{I_1}.
end{equation*}
begin{equation*}
s=intlimits_{t_1}^{t_2}sqrt{Eleft(frac{du}{dt}right)^2+2Ffrac{du}{dt}frac{dv}{dt}+Gleft(frac{dv}{dt}right)^2}dt.
end{equation*}

2. Найти угол между двумя линиями на поверхности в точке их пересечения:

Если две линии, лежащие на поверхности с первой квадратичной формой $I_1=E,du^2+2F,du,dv+G,dv^2$, пересекаются в некоторой точке $P$ поверхности и имеют в этой точке направления $(du:dv)$ и $(delta u:delta v)$, то косинус угла между ними определяется по формуле:
begin{gather*}
mbox{cos},varphi = displaystylefrac{I_1(d,delta)}{sqrt{I_1(d)}cdotsqrt{I_1(delta)}} \
mbox{cos},varphi = displaystylefrac{E,du,delta u+F,(du,delta v+delta u,dv)+G,dv,delta v}{sqrt{E,du^2+2F,du,dv+G,dv^2}cdotsqrt{E,delta u^2+2F,delta u,delta v+G,delta v^2}}.
end{gather*}
Говорим, что кривая на поверхности $vec{r}=vec{r}(u,v)$ в точке $(u,v)$ имеет направление $(du:dv)$, если вектор $dvec{r}=vec{r}_udu+vec{r}_vdv$ является касательным вектором кривой в этой точке.

3. Найти площадь области $Omega$ на поверхности:
begin{equation*}
S = iintlimits_{D}sqrt{EG-F^2}du,dv,
end{equation*}
где $D$ — прообраз $Omega$ на плоскости $(u,v)$.

Решение задач

Задача 1 (почти Феденко 684)

Найти длину дуги кривой, заданной уравнениями $v=3u$ на поверхности с первой квадратичной формой
begin{equation*}
I_1=du^2+frac19,mbox{sh}^2u,dv^2
end{equation*}
между точками $M_1(u_1,v_1)$ и $M_2(u_2,v_2)$.

Решение задачи 1

begin{equation*}
E=1, ,, F=0,,, G=frac19,mbox{sh}^2u.
end{equation*}
begin{equation*}
v=3u ,, Rightarrow ,,dv=3du.
end{equation*}
begin{equation*}
I_1=du^2+frac19,mbox{sh}^2ucdot9,du^2=(1+mbox{sh}^2u)du^2=mbox{ch}^2u,du^2.
end{equation*}
begin{equation*}
s=left|intlimits_{u_1}^{u_2} mbox{ch},u,duright| = |mbox{sh},u_2-mbox{sh},u_1|.
end{equation*}

Задача 2 (почти Феденко 682)

Под каким углом пересекаются линии
$$ u+v=a, ,, u-v=a,$$
лежащие на поверхности:
begin{equation*}
x=u,mbox{cos}v, ,, y=u,mbox{sin},v, ,, z=au.
end{equation*}

Решение задачи 2

Первая квадратичная форма данной поверхности:
begin{equation*}
I_1=(1+a^2),du^2+u^2,dv^2.
end{equation*}

Данные линии пересекаются в точке:
begin{equation*}
left{
begin{aligned}
u+v&=a,\
u-v&=a.
end{aligned}
right. quad Rightarrow quad P(u=a,v=0).
end{equation*}

Направления данных линий:
begin{equation*}
du+dv=0, ,, delta u-delta v=0,, Rightarrow
end{equation*}
begin{equation*}
du = -dv, ,, delta u = delta v.
end{equation*}

Подставляем всё в формулу:
begin{gather*}
mbox{cos},varphi = displaystylefrac{(1+a^2),du,delta u + u^2,dv,delta v}{sqrt{(1+a^2),du^2+u^2,dv^2}cdotsqrt{(1+a^2),delta u^2+u^2,delta v^2}} = \
= left( dv = -du, ,, delta v = delta u right) = \
= displaystylefrac{(1+a^2- u^2),du,delta u}{sqrt{(1+a^2+u^2)^2,du,delta u}}= frac{1+a^2-u^2}{1+a^2+u^2}=\
= left(P(u=a,v=0)right) = \
= frac{1}{1+2a^2}.
end{gather*}

Задача 3

Дана поверхность:
$$z=axy.$$
Найти углы между координатными линиями.

Решение задачи 3

Координатные линии на данной поверхности задаются уравнениями: $x=x_0$, $y=y_0$.
Запишем коэффициенты первой квадратичной формы:
begin{align*}
&E=1+(z_x)^2=1+a^2y^2,\
&F=z_xz_y=a^2xy, \
&G=1+(z_y)^2=1+a^2x^2.
end{align*}

Направления координатных линий:
begin{align*}
&x=x_0 ,, Rightarrow dx=0,\
&y=y_0 ,, Rightarrow delta y=0.
end{align*}

Угол между линиями $x=x_0$, $y=y_0$ в точке $(x_0,y_0)$:
begin{align*}
&mbox{cos}, varphi = displaystylefrac{E,dx,delta x + F(dxdelta y+delta xdy)+Gdydelta y}{sqrt{Edx^2+2Fdxdy+Gdy^2}cdotsqrt{Edelta x^2+2Fdelta xdelta y+Gdelta y^2}}=\
&= displaystylefrac{Fdelta xdy}{sqrt{Gdy^2}cdotsqrt{Edelta x^2}}=displaystylefrac{(a^2x_0y_0)delta xdy}{sqrt{(1+a^2x_0^2)dy^2}cdotsqrt{(1+a^2y_0^2)delta x^2}}=\
& = displaystylefrac{a^2x_0y_0}{sqrt{(1+a^2x_0^2) }cdotsqrt{(1+a^2y_0^2) }}.
end{align*}

Задача 4 (Дополнение к Задаче 3)

Как мы вывели в примере выше, угол между координатными линиями равен

begin{equation*}
mbox{cos}, varphi = displaystylefrac{F}{sqrt{EG}}.
end{equation*}

Из формулы следует, что координатная сеть поверхности ортогональна (координатные линии пересекаются под прямым углом), тогда и только тогда, когда $F$=0.

Задача 5 (Феденко 683)

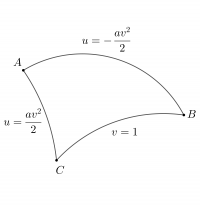
Найти периметр и внутренние углы криволинейного треугольника
$$ u=pm av^2/2,,, v=1,$$
расположенного на поверхности
$$I_1=du^2+(u^2+a^2)dv^2.$$

Вершины треугольника:
begin{align*}
&A(u=0,, v=0),\
&B(u=-frac{a}{2},, v=1), \
&C(u=frac{a}{2},, v=1).
end{align*}

Зная координаты вершин и уравнения сторон, найдем длины дуг, составляющих стороны треугольника $ABC$, и углы между линиями в точках их пересечения, то есть в вершинах треугольника:
begin{align*}
&s_1 = |BC| = a,\
&s_2 = |AC| = frac76 a,\
&s_3 = |BC| = frac76 a,\
&P_{triangle ABC}=s_1+s_2+s_3=frac{10}{3}a.
end{align*}
begin{align*}
&mbox{cos},A = 1, ,, mbox{cos},B=mbox{cos},C=frac23.
end{align*}

Источник

После исправления кривая дает отрезок прямой, длина которого равна длине дуги кривой.

Длина дуги расстояние между двумя точками на участке изгиб.

Определение длины сегмента неправильной дуги также называется исправление кривой. Появление исчисление бесконечно малых привели к общей формуле, которая обеспечивает закрытые решения в некоторых случаях.

Основной подход

Аппроксимация несколькими линейными отрезками

А изгиб в самолет можно аппроксимировать, подключив конечный количество точки на кривой с помощью отрезки линии создать многоугольный путь. Поскольку вычислить длина каждого линейного сегмента (используя теорема Пифагора в евклидовом пространстве, например), общая длина приближения может быть найдена как подведение итогов длины каждого линейного сегмента; это приближение известно как (совокупно) хордовый расстояние.^[1]

Если кривая еще не является многоугольной траекторией, использование все большего числа сегментов меньшей длины приведет к лучшему приближению. Длины последовательных приближений не будут уменьшаться и могут увеличиваться бесконечно, но для гладких кривых они будут стремиться к конечному пределу по мере того, как длины сегментов становятся произвольно маленький.

Для некоторых кривых есть наименьшее число это верхняя граница длины любого полигонального приближения. Эти кривые называются исправимый и число определяется как длина дуги.

Определение гладкой кривой

Позволять ${ displaystyle f двоеточие [a, b] to mathbb {R} ^ {n}}$ быть непрерывно дифференцируемый функция. Длина кривой, определяемая можно определить как предел суммы длин отрезков для регулярного разбиения поскольку количество сегментов приближается к бесконечности. Это означает

${ displaystyle L (f) = lim _ {N to infty} sum _ {i = 1} ^ {N} { bigg |} f (t_ {i}) - f (t_ {i-1 }) { bigg |}}$

куда ${ displaystyle t_ {i} = a + i (b-a) / N = a + i Delta t}$ за Это определение эквивалентно стандартному определению длины дуги как интеграла:

${ displaystyle lim _ {N to infty} sum _ {i = 1} ^ {N} { bigg |} f (t_ {i}) - f (t_ {i-1}) { bigg |} = lim _ {N to infty} sum _ {i = 1} ^ {N} left | { frac {f (t_ {i}) - f (t_ {i-1})} { Delta t}} right | Delta t = int _ {a} ^ {b} { Big |} f '(t) { Big |} dt.}$

Последнее равенство выше верно по следующим причинам: (i) посредством теорема о среднем значении, ${ displaystyle { frac {f (t_ {i}) - f (t_ {i-1})} { Delta t}} = f '(t_ {i-1} + theta _ {i} (t_ {i} -t_ {i-1})),}$ куда ${ Displaystyle 0 < theta _ {я} <1}$ ^{[сомнительный – обсуждать]}. (ii) функция непрерывно, таким образом, он равномерно непрерывен, поэтому существует положительная действительная функция положительного реального epsilon такой, что подразумевает ${ displaystyle left | { Big |} f '(t_ {i-1} + theta _ {i} (t_ {i} -t_ {i-1})) { Big |} - { Big |} f '(t_ {i}) { Big |} right | < epsilon.}$ Это означает

${ displaystyle sum _ {i = 1} ^ {N} left | { frac {f (t_ {i}) - f (t_ {i-1})} { Delta t}} right | Дельта t- sum _ {i = 1} ^ {N} { Big |} f '(t_ {i}) { Big |} Delta t}$

имеет абсолютное значение меньше, чем за Это означает, что в пределе левый член выше равен правому члену, который является просто Интеграл Римана из на Это определение длины дуги показывает, что длина кривой ${ displaystyle f: [a, b] rightarrow mathbb {R} ^ {n}}$ непрерывно дифференцируемый на всегда конечно. Другими словами, кривая всегда исправима.

Определение длины дуги гладкой кривой как интеграла от нормы производной эквивалентно определению

${ Displaystyle L (е) = sup sum _ {я = 1} ^ {N} { bigg |} f (t_ {i}) - f (t_ {i-1}) { bigg |}}$

где супремум взяты на все возможные перегородки ${ displaystyle a = t_ {0} <t_ {1} < dots <t_ {N-1} <t_ {N} = b}$ из ^[2] Это определение также верно, если просто непрерывный, не дифференцируемый.

Кривую можно параметризовать бесконечно многими способами. Позволять быть любым непрерывно дифференцируемым биекция. потом ${ displaystyle g = f circ varphi ^ {- 1}: [c, d] to mathbb {R} ^ {n}}$ — еще одна непрерывно дифференцируемая параметризация кривой, первоначально заданной формулой Длина дуги кривой одинакова независимо от параметризации, используемой для определения кривой:

${ displaystyle { begin {align} L (f) & = int _ {a} ^ {b} { Big |} f '(t) { Big |} dt = int _ {a} ^ {b} { Big |} g '( varphi (t)) varphi' (t) { Big |} dt & = int _ {a} ^ {b} { Big |} g '( varphi (t)) { Big |} varphi' (t) dt quad { textrm {поскольку}} varphi { textrm {must}} { textrm {be}} { textrm {неубывающая}} & = int _ {c} ^ {d} { Big |} g '(u) { Big |} du quad { textrm {using}} { textrm {интеграция}} { textrm {by}} { textrm {substitution}} & = L (g). end {выравнивается}}}$

Определение длины дуги путем интегрирования

Четверть круга

Если плоская кривая в $mathbb {R} ^ {2}$ определяется уравнением куда является непрерывно дифференцируемый, то это просто частный случай параметрического уравнения, где х = т и Тогда длина дуги определяется как:

${ displaystyle s = int _ {a} ^ {b} { sqrt {1+ left ({ frac {dy} {dx}} right) ^ {2}}} dx.}$

Кривые с закрытые решения для длины дуги включают цепная связь, круг, циклоида, логарифмическая спираль, парабола, полукубическая парабола и прямая линия. Отсутствие решения замкнутой формы для длины дуги эллиптический и гиперболический дуга привела к развитию эллиптические интегралы.

Численное интегрирование

В большинстве случаев, включая даже простые кривые, нет замкнутых решений для длины дуги и численное интегрирование необходимо. Численное интегрирование интеграла длины дуги обычно очень эффективно. Например, рассмотрим задачу определения длины четверти единичной окружности путем численного интегрирования интеграла длины дуги. Верхняя половина единичного круга может быть параметризована как ${ displaystyle y = { sqrt {1-x ^ {2}}}.}$ Интервал соответствует четверти круга. С ${ displaystyle dy / dx = -x / { sqrt {1-x ^ {2}}}}$ и ${ displaystyle 1+ (dy / dx) ^ {2} = 1 / (1-x ^ {2}),}$ длина четверти единичного круга равна

${ displaystyle int _ {- { sqrt {2}} / 2} ^ {{ sqrt {2}} / 2} { frac {1} { sqrt {1-x ^ {2}}}} , dx.}$

15 очков Гаусс – Кронрод оценка правила для этого интеграла 1.570796326808177 отличается от истинной длины

${ displaystyle { Big [} arcsin x { Big]} _ {- { sqrt {2}} / 2} ^ {{ sqrt {2}} / 2} = { frac { pi} { 2}}}$

к 1.3×10⁻¹¹ и 16-точечный Квадратура Гаусса оценка правила 1.570796326794727 отличается от истинной длины только на 1.7×10⁻¹³. Это означает, что этот интеграл можно оценить почти до точность станка всего 16 оценок интегранта.

Кривая на поверхности

Позволять отображение поверхности и пусть — кривая на этой поверхности. Подынтегральное выражение интеграла длины дуги равно Оценка производной требует Правило цепи для векторных полей:

${ Displaystyle D ( mathbf {x} circ mathbf {C}) = ( mathbf {x} _ {u} mathbf {x} _ {v}) { binom {u '} {v' }} = mathbf {x} _ {u} u '+ mathbf {x} _ {v} v'.}$

Квадрат нормы этого вектора равен ${ displaystyle ( mathbf {x} _ {u} u '+ mathbf {x} _ {v} v') cdot ( mathbf {x} _ {u} u '+ mathbf {x} _ { v} v ') = g_ {11} (u') ^ {2} + 2g_ {12} u'v '+ g_ {22} (v') ^ {2}}$ (куда ${ displaystyle g_ {ij}}$ это первая фундаментальная форма коэффициент), поэтому подынтегральное выражение интеграла длины дуги можно записать как ${ displaystyle { sqrt {g_ {ab} (u ^ {a}) '(u ^ {b})'}}}$ (куда ${ displaystyle u ^ {1} = u}$ и ${ displaystyle u ^ {2} = v}$ ).

Другие системы координат

Позволять быть кривой, выраженной в полярных координатах. Отображение, которое преобразует полярные координаты в прямоугольные координаты:

{ displaystyle mathbf {x} (r, theta) = (r cos theta, r sin theta).}

Подынтегральное выражение интеграла длины дуги равно Цепное правило для векторных полей показывает, что ${ displaystyle D ( mathbf {x} circ mathbf {C}) = mathbf {x} _ {r} r '+ mathbf {x} _ { theta} theta'.}$ Таким образом, квадрат подынтегральной функции интеграла длины дуги равен

${ displaystyle ( mathbf {x_ {r}} cdot mathbf {x_ {r}}) (r ') ^ {2} +2 ( mathbf {x} _ {r} cdot mathbf {x} _ { theta}) r ' theta' + ( mathbf {x} _ { theta} cdot mathbf {x} _ { theta}) ( theta ') ^ {2} = (r') ^ {2} + r ^ {2} ( theta ') ^ {2}.}$

Таким образом, для кривой, выраженной в полярных координатах, длина дуги равна

${ displaystyle int _ {t_ {1}} ^ {t_ {2}} { sqrt { left ({ frac {dr} {dt}} right) ^ {2} + r ^ {2} left ({ frac {d theta} {dt}} right) ^ {2}}} dt = int _ { theta (t_ {1})} ^ { theta (t_ {2})} { sqrt { left ({ frac {dr} {d theta}} right) ^ {2} + r ^ {2}}} d theta.}$

Теперь позвольте — кривая в сферических координатах, где theta полярный угол, отсчитываемый от положительного ось и phi азимутальный угол. Отображение, которое преобразует сферические координаты в прямоугольные координаты:

{ displaystyle mathbf {x} (r, theta, phi) = (r sin theta cos phi, r sin theta sin phi, r cos theta).}

Повторное использование цепного правила показывает, что ${ displaystyle D ( mathbf {x} circ mathbf {C}) = mathbf {x} _ {r} r '+ mathbf {x} _ { theta} theta' + mathbf {x} _ { phi} phi '.}$ Все точечные продукты ${ displaystyle mathbf {x} _ {i} cdot mathbf {x} _ {j}}$ куда и различны равны нулю, поэтому квадрат нормы этого вектора равен

${ displaystyle ( mathbf {x} _ {r} cdot mathbf {x} _ {r}) (r '^ {2}) + ( mathbf {x} _ { theta} cdot mathbf { x} _ { theta}) ( theta ') ^ {2} + ( mathbf {x} _ { phi} cdot mathbf {x} _ { phi}) ( phi') ^ {2 } = (r ') ^ {2} + r ^ {2} ( theta') ^ {2} + r ^ {2} sin ^ {2} theta ( phi ') ^ {2}.}.}$

Таким образом, для кривой, выраженной в сферических координатах, длина дуги равна

${ displaystyle int _ {t_ {1}} ^ {t_ {2}} { sqrt { left ({ frac {dr} {dt}} right) ^ {2} + r ^ {2} left ({ frac {d theta} {dt}} right) ^ {2} + r ^ {2} sin ^ {2} theta left ({ frac {d phi} {dt}} right) ^ {2}}} dt.}$

Очень похожий расчет показывает, что длина дуги кривой, выраженная в цилиндрических координатах, равна

${ displaystyle int _ {t_ {1}} ^ {t_ {2}} { sqrt { left ({ frac {dr} {dt}} right) ^ {2} + r ^ {2} left ({ frac {d theta} {dt}} right) ^ {2} + left ({ frac {dz} {dt}} right) ^ {2}}} dt.}$

Простые случаи

Дуги окружностей

Длины дуги обозначены s, поскольку латинское слово для обозначения длины (или размера) — пространство.

В следующих строках представляет радиус из круг, это его диаметр, это его длина окружности, — длина дуги окружности, а theta — угол, под которым дуга образует центр круга. Расстояния и выражены в тех же единицах.

Дуги больших кругов на Земле

Две единицы длины, морская миля и метр (или километр), изначально были определены так, что длины дуг большие круги на поверхности Земли было бы просто численно связано с углами, которые они составляют в ее центре. Простое уравнение применяется в следующих случаях:

Длины единиц расстояния были выбраны так, чтобы окружность Земли была равна 40000 километров, или 21600 морские мили. Это количество соответствующих угловых единиц за один полный оборот.

Эти определения метра и морской мили были заменены более точными, но исходные определения все еще достаточно точны для концептуальных целей и некоторых расчетов. Например, они подразумевают, что один километр равен 0,54 морской мили. Согласно официальным современным определениям, одна морская миля составляет ровно 1,852 километра,^[3] что означает, что 1 км — это примерно 0.53995680 морские мили.^[4] Это современное соотношение отличается от рассчитанного по исходным определениям менее чем на одну десятую часть.

Длина дуги параболы

Исторические методы

Античность

Для большей части история математики, даже величайшие мыслители считали невозможным вычислить длину неправильной дуги. Несмотря на то что Архимед первым изобрел способ найти область под кривой с помощью его «метод истощения «, мало кто верил, что кривые могут иметь определенную длину, как и прямые линии. Первые шаги в этой области были нарушены, как это часто случалось в исчисление, к приближение. Люди начали писать полигоны внутри кривых и вычислите длину сторон для некоторого точного измерения длины. Используя больше сегментов и уменьшив длину каждого сегмента, они смогли получить все более и более точное приближение. В частности, вписав в круг многоугольник с множеством сторон, они смогли найти приблизительные значения π.^[5]^[6]

17-го века

В 17 веке метод истощения привел к исправлению геометрическими методами нескольких трансцендентные кривые: the логарифмическая спираль к Евангелиста Торричелли в 1645 г. (по некоторым источникам Джон Уоллис в 1650-х гг.) циклоида к Кристофер Рен в 1658 г., а цепная связь к Готфрид Лейбниц в 1691 г.

В 1659 году Уоллис приписал Уильям Нил открытие первого исправления нетривиального алгебраическая кривая, то полукубическая парабола.^[7] Сопутствующие рисунки приведены на странице 145. На странице 91 Уильям Нил упоминается как Гулиельмус Нелиус.

Интегральная форма

До полного формального развития исчисления основа современной интегральной формы для длины дуги была независимо открыта Хендрик ван Хурает и Пьер де Ферма.

В 1659 году ван Хойрает опубликовал конструкцию, показывающую, что задача определения длины дуги может быть преобразована в задачу определения площади под кривой (то есть интеграла). В качестве примера своего метода он определил длину дуги полукубической параболы, что потребовало нахождения площади под парабола.^[8] В 1660 году Ферма опубликовал более общую теорию, содержащую тот же результат в своей работе. De linearum curvarum cum lineis rectis comparatione геометрическая диссертация (Геометрическая диссертация о кривых линиях в сравнении с прямыми).^[9]

Метод Ферма определения длины дуги

Основываясь на своей предыдущей работе с касательными, Ферма использовал кривую

$у = х ^ {3/2} ,$

чей касательная в Икс = а имел склон из

$textstyle {3 over 2} а ^ {1/2}$

так что касательная линия будет иметь уравнение

$у = textstyle {3 более 2} {а ^ {1/2}} (х - а) + е (а).$

Далее он увеличил а на небольшую сумму а + ε, делая сегмент AC относительно хорошее приближение длины кривой от А к D. Чтобы найти длину сегмента AC, он использовал теорема Пифагора:

$begin {align} AC ^ 2 & {} = AB ^ 2 + BC ^ 2 & {} = textstyle varepsilon ^ 2 + {9 over 4} а varepsilon ^ 2 & {} = textstyle varepsilon ^ 2 влево (1 + {9 более 4} а вправо) end {align}$

что, когда решено, дает

AC = textstyle varepsilon sqrt {1 + {9 over 4} a }.

Чтобы приблизиться к длине, Ферма суммировал бы последовательность коротких отрезков.

Кривые бесконечной длины

Кривая Коха.

График Иксгрех (1 /Икс).

Как упоминалось выше, некоторые кривые нельзя исправить. То есть отсутствует верхняя граница длин полигональных аппроксимаций; длина может быть сделана произвольно большой. Неформально говорят, что такие кривые имеют бесконечную длину. Существуют непрерывные кривые, на которых каждая дуга (кроме одноточечной) имеет бесконечную длину. Примером такой кривой является Кривая Коха. Другой пример кривой бесконечной длины — график функции, определяемой ж(Икс) = Икс грех (1 /Икс) для любого открытого множества с 0 в качестве одного из его разделителей и ж(0) = 0. Иногда Хаусдорфово измерение и Мера Хаусдорфа используются для количественной оценки размера таких кривых.

Обобщение на (псевдо) римановы многообразия

Позволять быть (Псевдо) Риманово многообразие, кривая в и (псевдо) метрический тензор.

Длина определяется как

$ell ( gamma) = int_ {0} ^ {1} sqrt { pm g ( gamma '(t), gamma' (t))} , dt,$

куда ${ Displaystyle гамма '(т) в Т _ { гамма (т)} М}$ является касательным вектором в Знак квадратного корня выбирается один раз для данной кривой, чтобы гарантировать, что квадратный корень является действительным числом. Положительный знак выбран для пространственноподобных кривых; в псевдоримановом многообразии отрицательный знак может быть выбран для времениподобных кривых. Таким образом, длина кривой — неотрицательное действительное число. Обычно не рассматриваются кривые, которые частично пространственноподобны, а частично времениподобны.

В теория относительности, длина дуги времениподобных кривых (мировые линии ) это подходящее время вдоль мировой линии, а длина дуги пространственноподобной кривой правильное расстояние по кривой.

Смотрите также

Дуга (геометрия)
Длина окружности
Формула Крофтона
Эллиптический интеграл
Геодезические
Внутреннее уравнение
Интегральные приближения
Линейный интеграл
Дуга меридиана
Многопараметрическое исчисление
Извилистость

Источники

Фаруки, Рида Т. (1999). «Кривые от движения, движение от кривых». В Laurent, P.-J .; Sablonniere, P .; Шумакер, Л. Л. (ред.). Кривая и дизайн поверхностей: Сен-Мало 1999. Vanderbilt Univ. Нажмите. С. 63–90. ISBN 978-0-8265-1356-4.

внешняя ссылка

«Спрямляемая кривая», Энциклопедия математики, EMS Press, 2001 [1994]
История кривизны
Вайсштейн, Эрик В. «Длина дуги». MathWorld.
Длина дуги к Эд Пегг младший, Демонстрационный проект Wolfram, 2007.
^[постоянная мертвая ссылка ] Учебное пособие по исчислению — Длина дуги (исправление)
Индекс известных кривых Архив истории математики MacTutor
Приблизительная длина дуги Чад Пирсон, Джош Фриц и Анджела Шарп, Демонстрационный проект Wolfram.
Эксперимент по длине кривой Иллюстрирует численное решение нахождения длины кривой.

Источник

Оглавление:

📝 Как это работает?
🤔 Частые вопросы и ответы
📋 Похожие материалы
📢 Поделиться и комментировать

Что такое длина дуги?

Дуга — это часть окружности, ограниченная двумя точками на окружности.

Для вычисления длины дуги необходимо знать радиус окружности и центральный угол, охватывающий эту дугу.

Наш онлайн калькулятор длины дуги может вычислить длину дуги через угол в градусах и радианах.

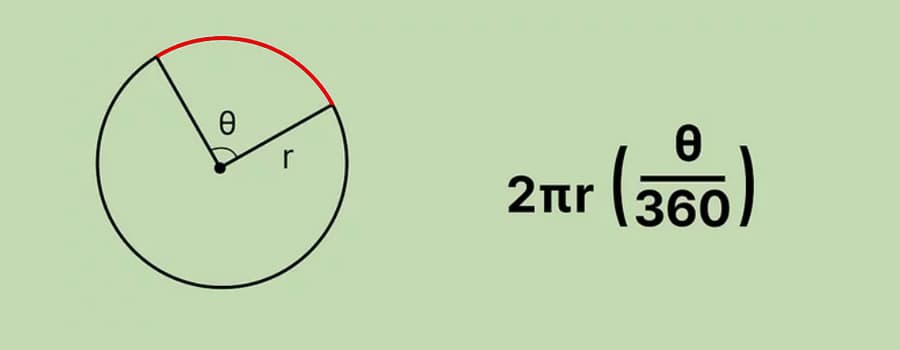
Для вычисления длины дуги через центральный угол в градусах формула выглядит следующим образом:

L = r * θ * π / 180

где L — длина дуги, r — радиус окружности, θ — центральный угол в градусах, π — число Пи (3.14159…).

Для вычисления длины дуги через центральный угол в радианах формула выглядит следующим образом:

L = r * θ

где L — длина дуги, r — радиус окружности, θ — центральный угол в радианах.

Таким образом, чтобы использовать наш калькулятор для вычисления длины дуги через центральный угол в градусах, необходимо ввести радиус и угол в градусах, а для вычисления длины дуги через центральный угол в радианах — радиус и угол в радианах.

🔣 Формула Гюйгенса

Длину дуги можно найти, используя более редкую формула, в которой известны две хорды, как показано на рисунке выше. Это формула называется формулой Гюйгенса.

В формуле Гюйгенса используется знак «равно или почти равно» (≊), потому что вычисления с помощью этой формулы могут содержать погрешности. Эти погрешности обычно малы, но они существуют, и их нужно учитывать. Относительная погрешность формулы Гюйгенса составляет около 0,5% при угле дуги в 60°. Однако, при уменьшении угла дуги, погрешность также уменьшается. Например, при дуге в 45° относительная погрешность составит около 0,02%.

🌈 Пример использования калькулятора в повседневной жизни

Калькулятор для вычисления длины дуги может быть использован и в повседневной жизни в различных ситуациях:

Пример 1. При выборе размера ободной обрезиненной ленты для замены на велосипеде. Чтобы выбрать правильный размер ленты, необходимо знать длину окружности колеса. Калькулятор для вычисления длины дуги поможет быстро и точно вычислить длину окружности колеса по его радиусу.

Пример 2. При планировании работы садовой или дачной зоны. Например, при расчете длины ленточного газона или длины обочин для дорожек. Калькулятор для вычисления длины дуги поможет быстро и точно вычислить необходимую длину материала.

Пример 3. При выборе длины троса для подвешивания карниза или штор в доме. Чтобы подобрать правильную длину троса, необходимо знать длину окна и расстояние от карниза до пола. Калькулятор для вычисления длины дуги поможет быстро и точно вычислить длину троса, необходимую для подвешивания карниза.

Помимо этого, калькулятор для вычисления длины дуги может быть использован для быстрого и удобного решения задач, связанных с геометрией, физикой и техническими науками. Например:

Геометрия: в геометрии часто требуется вычислять длину дуги окружности для построения различных фигур и геометрических конструкций.
Физика: в физике, например, длина дуги может быть использована для вычисления длины траектории движения тела по окружности.
Технические науки: в инженерии и других технических науках, вычисление длины дуги может быть использовано для определения размеров и формы кривых поверхностей и для расчета траекторий движения механизмов и устройств.

Таким образом, калькулятор для вычисления длины дуги может быть полезным инструментом как в повседневной жизни, так и при решении задач, связанных с техническими науками.

🌀 Основные виды дуг

Дуги окружности — это дуги, которые образуются на окружности. Они имеют равные начальный и конечный углы и могут быть выражены через радиус окружности и центральный угол, который они охватывают.
Произвольные дуги — это дуги, которые не являются частью окружности и могут быть описаны любой кривой. Они могут быть параметризованы, то есть выражены через параметр, который изменяется от начального до конечного значения. (Примеры произвольных дуг включают дуги эллипсов, парабол, гипербол и других кривых, которые можно параметризовать).

Круговые дуги — это дуги, которые образуются на круге. Они имеют равные начальный и конечный углы, как дуги окружности, но могут быть на любом расстоянии от центра круга.
Сегменты — это дуги, которые являются частью окружности или круга и имеют начальный и конечный углы, которые не равны 360 градусам.

В зависимости от конкретного контекста могут быть и другие типы дуг, но основные типы — это дуги окружности и произвольные дуги.

В чем разница между градусом от радианом?

Градусы и радианы — это единицы измерения угла. Они могут использоваться для измерения углов различных фигур, таких как треугольники, прямоугольники, круги и другие.

Градус — это одна из самых распространенных единиц измерения угла. Он определяется как 1/360 часть полного угла, который составляет один оборот. Таким образом, полный угол равен 360 градусам.

Радиан — это другая единица измерения угла, которая используется в математике и физике. Радиан определяется как длина дуги, равной радиусу окружности, разделенная на радиус этой окружности. Таким образом, полный угол равен 2π радианам.

Отличие между градусами и радианами заключается в том, как они измеряют углы. Градусы измеряют углы в сотнях долей полного угла, а радианы измеряют углы в длинах дуг окружности.

В математике и физике часто используются радианы, так как они позволяют производить более точные вычисления.

❓ Вопросы и ответы

Некоторые из популярных вопросов и ответы на них по калькулятору длины дуги.

Что такое длина дуги?

Длина дуги — это длина части кривой линии, которая соединяет две заданные точки на кривой.

В каких областях применяется вычисление длины дуги?

Вычисление длины дуги находит применение в различных областях, таких как физика, инженерия, компьютерная графика, дизайн и другие. Например, при моделировании траекторий движения тел, в оптике для расчета оптических путей лучей, при создании графических объектов и многих других задачах.

Как перевести угол из градусов в радианы?

Для перевода угла из градусов в радианы используется следующая формула: θ (в радианах) = θ (в градусах) * π / 180, где π — число Пи (3.14159…).

Какой формат ввода углов используется в калькуляторе длины дуги?

Калькулятор длины дуги использует радианы и градусы для ввода углов.

Какой диапазон углов может быть введен в калькулятор длины дуги?

Углы могут быть введены в диапазоне от 0 до 2π (двух пи), что соответствует полной окружности.

Рассчитать длину дуги, радиус

Порой нужно быстро рассчитать длину дуги, радиус фермы для навеса, для этого на скорую руку был сделан этот простенький калькулятор.
Если известны высота дуги и длина хорды, то это не составит большого труда.

Длина хорды в мм (A)
Высота дуги в мм (B)
Рассчитать

Источник

Содержание

Длина дуги, угол между линиями, площадь области на поверхности

Краткие теоретические сведения

Решение задач

Задача 1 (почти Феденко 684)

Решение задачи 1

Задача 2 (почти Феденко 682)

Решение задачи 2

Задача 3

Решение задачи 3

Задача 4 (Дополнение к Задаче 3)

Задача 5 (Феденко 683)

Основной подход

Определение гладкой кривой

Определение длины дуги путем интегрирования

Численное интегрирование

Кривая на поверхности

Другие системы координат

Простые случаи

Дуги окружностей

Дуги больших кругов на Земле

Длина дуги параболы

Исторические методы

Античность

17-го века

Интегральная форма

Кривые бесконечной длины

Обобщение на (псевдо) римановы многообразия

Смотрите также

Рекомендации

Источники

внешняя ссылка

Что такое длина дуги?

🔣 Формула Гюйгенса

🌈 Пример использования калькулятора в повседневной жизни

🌀 Основные виды дуг

В чем разница между градусом от радианом?

❓ Вопросы и ответы

Что такое длина дуги?

В каких областях применяется вычисление длины дуги?

Как перевести угол из градусов в радианы?

Какой формат ввода углов используется в калькуляторе длины дуги?

Какой диапазон углов может быть введен в калькулятор длины дуги?

Похожие калькуляторы

Есть что добавить?

Рассчитать длину дуги, радиус