Нахождение длины дуги сектора круга
В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить длину дуги сектора круга, а также разберем примеры решения задач для демонстрации их применения на практике.
Определение дуги сектора круга
Дуга – это участок между двумя точками на окружности.
Дуга сектора круга – это участок между двумя точками на окружности, которые получены в результате пересечения этой окружности двумя радиусами, образовавшими сектор круга.
На рисунке ниже: AB – это дуга зеленого сектора круга с радиусом R (или r).
- OA = OB = R (r);
- α – угол сектора или центральный угол.
Формулы для нахождения длины дуги сектора
Через центральный угол в градусах и радиус
Длина (L) дуги сектора равняется числу π , умноженному на радиус круга (r), умноженному на центральный угол в градусах ( α°), деленному на 180°.
Примечание: в расчетах используется число π , приблизительно равное 3,14.
Через угол сектора в радианах и радиус
Длина (L) дуги сектора равна произведению радиуса (r) и центрального угла, выраженного в радианах (aрад).
Примеры задач
Задание 1
Дан круг с радиусом 15 см. Найдите длину дуги сектора, угол которого равен 30°.
Решение
Воспользуемся формулой расчета, в которой используется центральный угол в градусах:
Задание 2
Длина дуги сектора равняется 24 см. Найдите, чему равен его угол (в радианах и градусах), если радиус круга составляет 12 см.
Решение
Для начала вычислим угол в радианах:
1 радиан ≈ 57,2958°
Следовательно, центральный угол приблизительно равняется 114,59 ° (2 рад ⋅ 57,2958°).
Please wait.
We are checking your browser. mathvox.ru
Why do I have to complete a CAPTCHA?
Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.
What can I do to prevent this in the future?
If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.
If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.
Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.
Cloudflare Ray ID: 6cdb5ee05ab316e8 • Your IP : 85.95.179.65 • Performance & security by Cloudflare
Длина дуги окружности через радианы
Во первых, под числом «π» Администрация Сайта понимает величину близкую к:
3.14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679… (100 знаков после запятой)
ФОРМУЛЫ ПЕРЕВОДА
- Перевод радиан в градусы
- Зная, что углу 2•π соответствует угол 360 градусов:
- Ad = Ar • 180 / π
- Где Ad — угол в градусах, Ar — угол в радианах.
- Зная, что углу 2•π соответствует угол 360 градусов:
- Перевод градусов в радианы
- Зная, что углу 360 градусов соответствует угол 2 • π:
- Ar = Ad • π / 180
- Где Ad — угол в градусах, Ar — угол в радианах.
- Зная, что углу 360 градусов соответствует угол 2 • π:
ФОРМУЛЫ РАСЧЕТА ДЛИНЫ
- Длина окружности
- L = 2 • π • R
- Где L — длина окружности, R — радиус окружности.
- L = π • D
- Где L — длина окружности, D — диаметр окружности.
- L = 2 • π • R
- Длина дуги окружности
- L = A • R
- Где L — длина дуги окружности, R — радиус окружности,
- A — центральный угол, выраженный в радианах.
- Так, для окружности, A = 2•π (360 градусов), получим L = 2 • π • R
- L = A • R
ФОРМУЛЫ РАСЧЕТА ПЛОЩАДИ
- Площадь треугольника.
- Формула Герона площади треугольника.
- S = (p • (p-a) • (p-b) • (p-c)) 1/2 .
- Где S — площадь треугольника, a, b, c — длины сторон,
- p=(a+b+c)/2 — полупериметр.
- Площадь круга
- S = π • R 2
- Где S — площадь круга, R — радиус круга.
- S = π • R 2
- Площадь сектора
- S = (Ld • R)/2 = (A • R 2 )/2
- Где S — площадь сектора, R — радиус круга, Ld — длина дуги.
- S = (Ld • R)/2 = (A • R 2 )/2
- Площадь поверхности шара (сферы)
- S = 4 • π • R 2
- Где S — площадь поверхности шара, R — радиус шара.
- S = 4 • π • R 2
- Площадь боковой поверхности цилиндра
- S = 2 • π •R • H
- Где S — площадь боковой поверхности цилиндра, R — радиус основания цилиндра, H — высота цилиндра.
- S = 2 • π •R • H
- Площадь полной поверхности цилиндра
- S = 2 • π • R • H + 2 • π • R 2
- Где S — площадь боковой поверхности цилиндра, R — радиус основания цилиндра, H — высота цилиндра.
- S = 2 • π • R • H + 2 • π • R 2
- Площадь боковой поверхности конуса
- S = π • R • L
- Где S — площадь боковой поверхности конуса, R — радиус основания конуса, L — длина образующей конуса.
- S = π • R • L
- Площадь полной поверхности конуса
- S = π • R • L + π • R 2
- Где S — площадь полной поверхности конуса, R — радиус основания конуса, L — длина образующей конуса.
- S = π • R • L + π • R 2
ФОРМУЛЫ РАСЧЕТА ОБЪЕМА
- Объем шара
- V = 4 / 3 • π • R 3
- Где V — объем шара, R — радиус шара.
- V = 4 / 3 • π • R 3
- Объем цилиндра (прямого, круглого)
- V = π • R 2 ·H
- Где V — объем цилиндра, R — радиус основания цилиндра, H — высота цилиндра.
- Объем конуса (прямого, круглого)
- V = π • R • L = π • R • H/cos (A/2) = π • R • R/sin (A/2)
- Где V — объем конуса, R — радиус основания конуса, L — длина образующей конуса, A — угол при вершине конуса.
- V = π • R • L = π • R • H/cos (A/2) = π • R • R/sin (A/2)
http://mathvox.ru/geometria/okrujnosti-i-ih-svoistva/glava-3-duga-dlina-dugi-radiannaya-mera-ugla/formula-dlini-dugi-okrujnosti/
http://dpva.ru/Guide/GuideMathematics/PerimSqVolGradRad/RadianLengthSquireVolume/RadianLengthSquireVolumePrint/
Длина дуги
- Главная
- /
- Математика
- /
- Геометрия
- /
- Длина дуги
Чтобы найти длину дуги окружности воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Чему равна длина дуги, если:
радиус r =
угол α =
Ответ: L =
0
Округление числа π: Округление ответа:
Просто введите радиус и угол α, и получите ответ.
Теория
Чему равна длина дуги окружности L если её радиус r, а угол между двумя прямыми, проведёнными от центра окружности к конечным точкам дуги — центральный угол α?
Формула
Если угол в градусах:
L = π ⋅ r ⋅ α ⁄ 180
Если угол в радианах:
L = r ⋅ α
Пример
Для примера посчитаем чему равна длина дуги окружности с радиусом r = 2 см и центральным углом α = 45° :
L = 3.14 ⋅ 2 ⋅ 45/180 = 6.28 ⋅ 0.25 = 1.57 см
См. также
Arc length is defined as the distance between the two points placed on the circumference of the circle and measured along the circumference. Arc length is the curved distance along the circumference of the circle. Length of the arc between two points is always greater than the chord between those two points.
What is Arc Length?
The arc length is defined as the circular distance between two points along the circumference of the circle. The length of the arc is directly dependent on the radius and central angle of the circle. The central angle is the angle subtended by the endpoints of the arc to the center of the circle. It is denoted by θ. It is measured both in degrees and radians. The figure given below shows the arc AB when the radius is r and the central angle is θ.
Arc Length Formula
Length of the arc is calculated using different formulas, the formula used is based on the central angle of the arc. Central angle is measured in degrees or radians, and accordingly, the length of an arc of the circle is calculated. For a circle, the formula for arc length formula is θ times the radius of the circle.
| Arc Length Formula (θ in degrees) | s = 2×π×r ×(θ/360°) |
| Arc Length Formula (θ in radians) | s = θ × r |
| Arc Length Formula (Integral Form) | s = ∫√(1 + (dy/dx)2dx |
There are different cases that are used accordingly to find the required Arc Length
Case 1: When Radius and Angle are given
Formula to calculate the length of an arc is given by:
L = 2πr × (θ / 360)… (1)
where
r is the radius of the circle
θ is the angle in degrees
L is the Arc lengthArc length when the angle is represented in radians
1 radian = π/180°
Substituting the value of radian in equation (1)
L = 2πr × (θ × / 360)
L = r θ…(2)
where,
r is the radius of the circle
θ is the angle in radians.
Case 2: When Area and Central Angle of the Arc are given
Formula to calculate the length of an arc is given by:
L = 2πr × (θ / 360)
where,
r is the radius of the circle
θ is the angle in degreesWe need to find the radius of the circle from the given area. After finding the radius, we will substitute the value of radius in the formula.
Area of the circle = πr2
Example: If area of the circle is 314 m2 and centeral angle of the arc is π radian find the length of the arc.
Sloution:
πr2 = 314 m2
r2 = 314/π (π = 3.14)
r2 = 314/3.14
r2 = 100
r = √100 = 10 m
Length of the arc with angle π radians will be:
L = r θ
L = 10 × π
L = 10 × 3.1415
L = 31.415 m
The value of r can be used in the same formula, as discussed above.
Case 3: Arc length In Integral Form
Arc length in integral form is given by:
L = ∫√(1 + (dy/dx)2)dx
where,
Y is the f(x) function
limit of integral is [a, b]
How to Find Arc Length?
Use the steps given below to find the Arc length of the given arc.
Step 1: Mark the central angle and length of the radius of the given arc.
Step 2: Use the formula as given above according to the value of the angle in degrees or radians accordingly.
Step 3: Simplify the above equation to get the required answer.
Also, Check
- Equation of a Circle
- Degrees To Radians
- Radians to Degrees
Solved Examples on Arc Length
Example 1: Find the length of the arc with a radius of 2m and angle π/2 radians.
Solution:
The formula to calculate the length of the arc is given by:
L = r θ
Where,
L is the length of the arc
Given: r = 2m and θ = π/2 radians
Length of arc = 2 × π/2
Length of arc = π
(π = 3.1415)
Length of arc = 3.1415 m
Thus, the length of the arc is 3.1415 m.
Example 2: Find the length of the arc of function f(x) = 8 between x =2 and x = 4.
Solution:
The formula to calculate the arc length for the function is given by:
L = ∫√(1 + (dy/dx)2)dx
The limit of integral is [a, b]
Substituting the values a = 2, b = 4, and y = 6 or dy/dx = 0 in the above formula,
L = ∫√(1 + (0)2)dx
L = ∫√1 dx
L = ∫1 dx
L = x
(Integral of 1 is x)
The limit of integral is [2, 4]
L = (4 – 2)
L = 2
Thus, the length of the arc of function f(x) = 8 between x = 2 and x = 4 is 2.
Example 3: Find the length of the arc with a radius of 5cm and an angle of 60°.
Solution:
The formula to calculate the length of the arc is given by:
L = 2πr × (θ / 360)
Where,
L is the length of the arc
Given: r = 5cm and θ = 60°
Length of arc = 2πr × (60 / 360)
Length of arc = 2πr × 1/6
Length of arc = 2 × 3.1415 × 5/6
(π = 3.1415)
Length of arc = 5.235cm
Thus, the length of the arc is 5.235cm
Example 4: Find the length of the arc with a radius of 0.5m and an angle of π/4 radians.
Solution:
The formula to calculate the length of the arc is given by:
L = r θ
Where,
L is the length of the arc
Given: r = 0.5m and θ = π/4 radians
Length of arc = 0.5 × π/4
Length of arc = 0.392 m
(π = 3.1415)
Thus, the length of the arc is 0.392 m
Example 5: Find the length of the arc with a radius of 10cm and an angle of 135°.
Solution:
The formula to calculate the length of the arc is given by:
L = 2πr × (θ / 360)
Where,
L is the length of the arc
Given: r = 10cm and θ = 135°
Length of arc = 2πr × (135/360)
Length of arc = (2 × 3.1415 × 10 × 135)/360°
(π = 3.1415)
Length of arc = 23.56cm
Thus, the length of the arc is 23.56cm.
Example 6: Find the length of the arc with a radius of 20mm and angle π/6 radians.
Solution:
The formula to calculate the length of the arc is given by:
L = r θ
Where,
L is the length of the arc
Given: r = 20mm and θ = π/6 radians
Length of arc = 20 × π/6
Length of arc = 10.47 mm
(π = 3.1415)
Thus, the length of the arc is 10.47 mm
Example 7: Find the length of the arc with a radius of 2 cm and an angle of 90°.
Solution:
The formula to calculate the length of the arc is given by:
L = 2πr × (θ / 360)
Where,
L is the length of the arc
Given: r = 2cm and θ = 90°
Length of arc = 2πr × (90 / 360)
Length of arc = 2πr × 1/4
Length of arc = 2 ×3.1415 × 2 × 1/4
(π = 3.1415)
Length of arc = 3.1415 cm
Thus, the length of the arc is 3.1415 cm.
FAQs on Arc Length
Question 1: What is the Arc Length of a Circle?
Answer:
Arc length of a circle is the length made by the arc which is measured along its circimference.
Question 2: Length of the arc is measured in which unit?
Answer:
Length of arc is of a circle is either measured in m or in cm.
Question 3: Does arc length is measured in radians?
Answer:
Angles are measured in radians and arc length is a measurement of distance, thus it cannot be measured in radians.
Question 4: How do you find the circumference if the arc length (l) and central angle (θ) are given?
Answer:
When arc length (l) and central angle (θ) is given then the circumference by the formula
Arc Length (L) / Circumference = θ/360º
Last Updated :
20 Jan, 2023
Like Article
Save Article
Дуга окружности — это фрагмент окружности. Если на окружности отметить две точки A И B, то она разобьётся на 2 части, называемые дугами окружности.
Для того, чтобы найти длину дуги окружности, необходимо использовать значение центрального угла, измеряемого в радианах или градусах.
Существует 2 формулы длины дуги окружности:
1) Если дан центральный угол в радианах: l = R*α, где R — радиус, α — величина угла AOB в радианах.
2) Если дан центральный угол в градусах: l = R*π*C/180, где R — радиус, C — величина угла AOB в градусах.
Пример
Дано:
1) радиус окружности R = 6 дм.
2) центральный угол AOB = 45°.
Найти:
Длину дуги AB.
Решение:
l = 6*3,14*1/4 дм. = 4,71 дм.
Найдем длину дуги окружности радиуса R, отвечающей центральному углу в n° (рис.1).
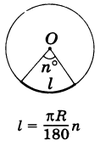
Рис.1
Развернутому углу соответствует длина полуокружности $pi R$. Следовательно, углу в 1° соответствует дуга длины $frac{pi R}{180}$ , а углу в n° соответствует дуга длины
$$ l = frac{pi R}{180}n ,,, (8) $$
Например, длина дуги окружности радиуса 12 м, отвечающей центральному углу в 30°, есть
$$ l = frac{12pi}{180} bullet = 2pi approx 6 text{(м)} $$
Пример 1. По данной хорде к найти длину ее дуги, если она соответствует центральному углу в 60° (рис.2).
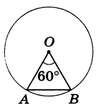
Рис.2
Решение. Так как АО = ВО = R(R — радиус окружности) и ∠ АОВ = 60°, то треугольник АОВ равносторонний: R = АВ = к. Теперь согласно формуле (8)
имеем:
$$ l = frac{pi R}{180} bullet 60 = frac{pi k}{3} $$
Радианной мерой угла называется отношение длины соответствующей дуги к радиусу окружности. Из формулы для длины дуги окружности следует, что
$$ frac{l}{R} = frac{pi}{180}n $$
, т.е. радианная мера угла получается из градусной умножением на $frac{pi}{180}$. В частности, радианная мера угла 180° равна $pi$, радианная мера прямого угла равна $frac{pi}{2}$.
Единицей радианной меры углов является радиан. Угол в один радиан — это центральный угол, у которого длина дуги равна радиусу (рис.3).
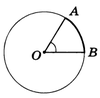
Рис.3
Градусная мера угла в один радиан равна $frac{180^{circ}}{pi} = 57°$ .
Пример 2. Найти радианные меры углов параллелограмма ABCD, если ∠ A = 36°.
Решение. Радианная мера угла А равна $36° bullet frac{pi}{180°} = frac{pi}{5}$ ,а радианная мера угла В равна к $pi — frac{pi}{5} = frac{4pi}{5}$ , так как в параллелограмме сумма углов, прилежащих к одной стороне, равна 180° (теорема 1). Наконец, радианные меры углов C и D соответственно равны $frac{pi}{5}$ и $frac{4pi}{5}$ (в параллелограмме противоположные углы равны).









