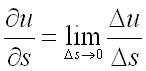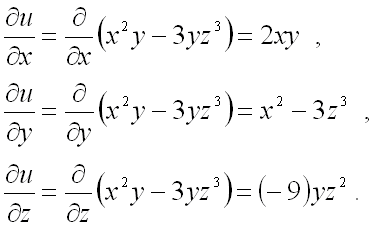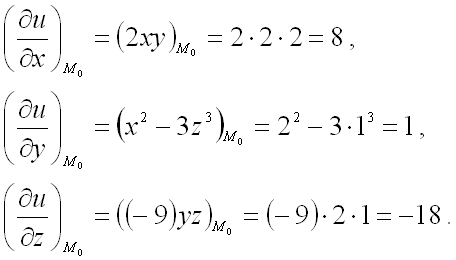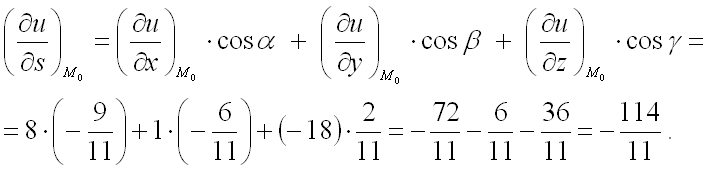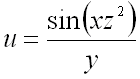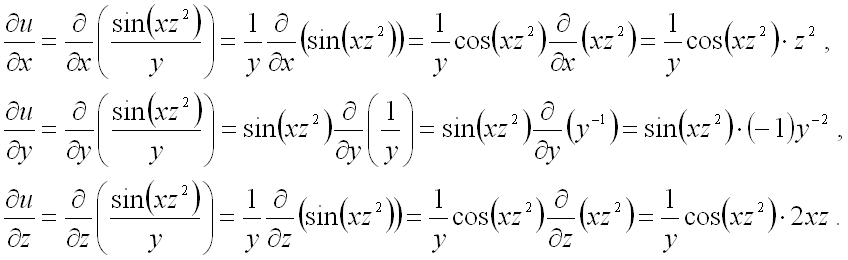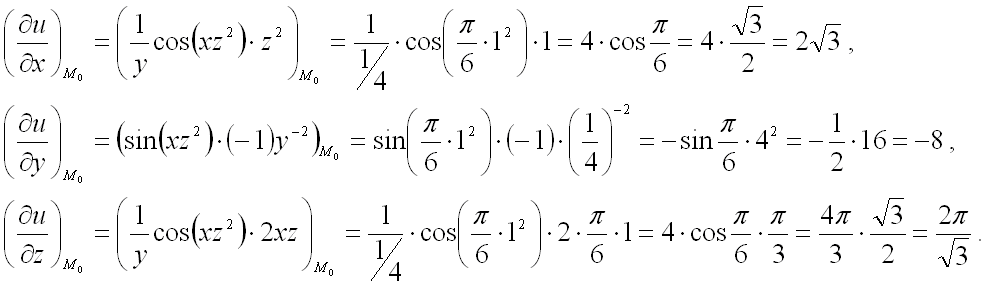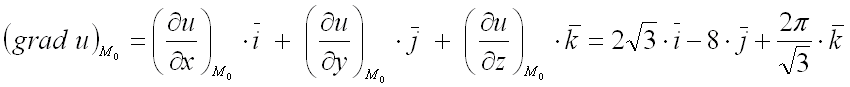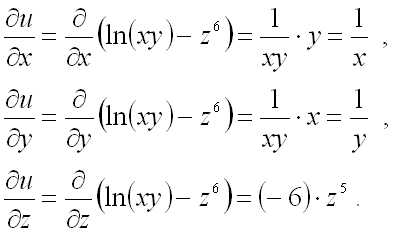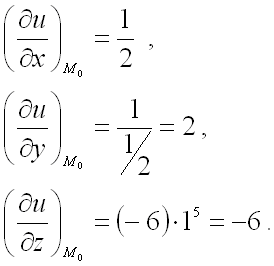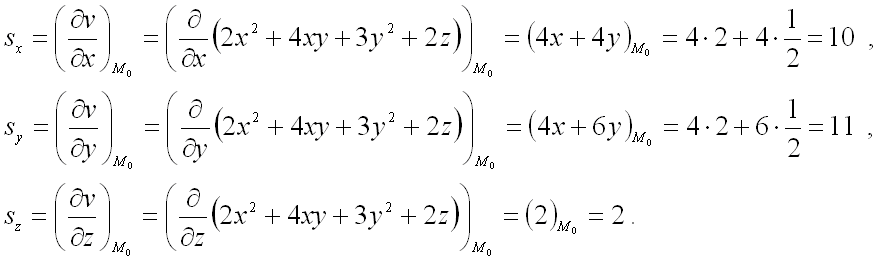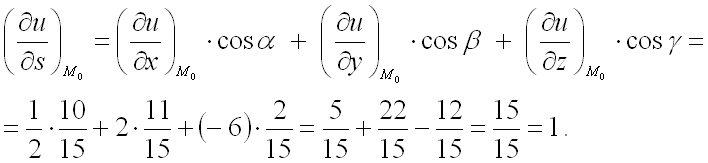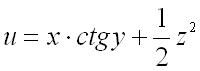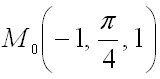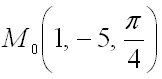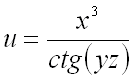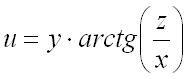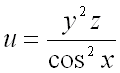Градиент функции онлайн
Градиент функции — это вектор координатами которого являются частные производные этой функции по всем её переменным.
Градиент обозначается символом набла . Выражение градиента некоторой функции записывается следующим образом:
где , , — частные производные функции по переменным , , соответственно.
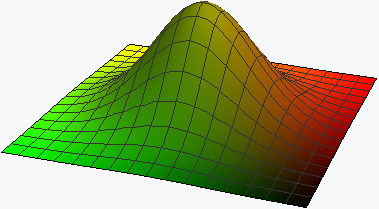
Вектор градиента указывает направление наискорейшего роста функции. Рассмотрим график функции .
Эта функция достигает своего единственного максимума в точке . График градиентного поля данной функции имеет вид:
Из данного градика видно, что в каждой точке вектор градиента направлен в сторону наискорейшего роста функции, т.е. в точку . При этом модуль вектора отражает скорость роста (крутизну подъёма) функции в этом направлении.
Задача вычисления градиента функции очень часто возникает при поиске эстремумов функции с использованием различных численных методов.
Наш онлайн калькулятор позволяет вычислить градиент практически любой функции как общем виде, так и в конкретной точке с описанием подробного хода решения на русском языке.
Производная по направлению, градиент функции: объяснение, примеры
Понятие производной по направлению
Понятие производной по направлению рассматривается для функций двух и трёх переменных. Чтобы понять смысл производной по направлению, нужно сравнить производные по определению
Рассматривая функцию одной переменной, мы выяснили, что на оси Oy отображается приращение функции f(x) , соответствующее приращению аргумента x . Если мы имеем дело с функцией трёх переменных, то приращения аргументов x , y , z отображаются на осях Оx , Оy , Оz . Сам собой напрашивается вопрос: а где можно отобразить приращение уже не аргументов, а функции трёх переменных?
И вот ответ на этот вопрос: приращение функции трёх переменных отображается на некоторой прямой, направление которой определяется вектором, произвольно заданным в задаче.
Если рассматривается функция двух или трёх переменных, то два или три измерения задают аргументы, а упомянутая прямая, на которой отображается приращение функции, — это ещё одно измерение и для его акцентирования назовём это измерение не третьим или четвёртым, а нулевым, следуя программистской традиции (в программировании отсчёт чаще начинается не с единицы, а с нуля).
Для того, чтобы перейти к строгому математическому определению производной по направлению, нужно рассмотреть:
1) функцию u = f(M) , определённую в окрестности точки M с координатами x , y , z ;
Через точку M проводим прямую, одно из двух возможных направлений которых совпадает с направлением вектора l . На получившейся прямой отметим точку M 1 , координаты которой образуют суммы координат точки M и приращений соответствующих аргументов функции трёх переменных:
Величину отрезка MM 1 можно обозначить .
Функция u = f(M) при этом получит приращение
.
Определение производной по направлению. Предел отношения при , если он существует, называется производной функции u = f(M) по направлению вектора l и обозначается , то есть
.
Формула, которой нужно пользоваться для нахождения производной по направлению, следующая:
.
Смысл этой формулы: производная по направлению является линейной комбинацией частных производных, причём направляющие косинусы показывают вклад в производную по направлению соответствующей частной производной.
Примеры нахождения производной по направлению
Пример 1. Найти производную функции в точке M 0 (1; 2; 3) по направлению вектора .
Найдём направляющие косинусы, пользуясь определением скалярного произведения векторов:
Теперь можем найти производную по направлению данной функции по её формуле:
А сейчас — домашнее задание. В нём дана функция не трёх, а лишь двух переменных, но несколько иначе задан направляющий вектор. Так что придётся вновь повторить векторную алгебру.
Пример 2. Найти производную функции в точке M 0 (1; 2) по направлению вектора , где M 1 — точка с координатами (3; 0) .
Вектор, задающий направление производной, может быть дан и в такой форме, как в следующем примере — в виде разложения по ортам координатных осей, но эта хорошо знакомая тема из самого начала векторной алгебры.
Пример 3. Найти производную функции в точке M 0 (1; 1; 1) по направлению вектора .
Решение. Найдём направляющие косинусы вектора
Найдём частные производные функции в точке M 0 :
Следовательно, можем найти производную по направлению данной функции по её формуле:
.
Градиент функции
Градиент функции нескольких переменных в точке M 0 характеризует направление максимального роста этой функции в точке M 0 и величину этого максимального роста.
Как найти градиент?
Нужно определить вектор, проекциями которого на оси координат являются значения частных производных , , этой функции в соответствующей точке:
.
То есть, должно получиться представление вектора по ортам координатных осей, в котором на каждый орт умножается соответствующая его оси частная производная.
Для градиента функции двух переменных формула короче:
.
Пример 4. Найти градиент функции в точке M 0 (2; 4;) .
Решение. Найдём частные производные функции в точке M 0 :
Следовательно, можем записать искомый градиент данной функции:
.
http://function-x.ru/derivative_directional.html
Производная
по направлению. Градиент
Пусть в некоторой области
задана функция
и точка .
Проведем из точки
вектор ,
направляющие косинусы которого .
На векторе ,
на расстоянии
от его начала рассмотрим точку ,
т.е. 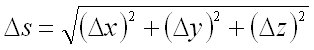
Будем предполагать, что функция
и ее частные производные первого порядка непрерывны в области .
Предел отношения
при называется
производной от функции
в точке по
направлению вектора
и обозначается ,
т.е.
.
Для нахождения производной от функции
в заданной точке по
направлению вектора
используют формулу: 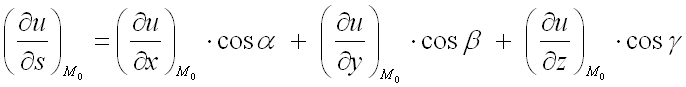
где
– направляющие косинусы вектора ,
которые вычисляются по формулам:
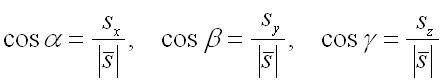
Пусть в каждой точке некоторой
области
задана функция .
Вектор, проекциями которого на оси координат являются значения частных производных
этой функции в соответствующей точке, называется градиентом функции
и обозначается
или
(читается «набла у»): 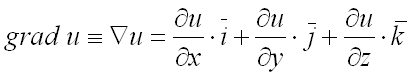
При этом говорят, что в области
определено векторное поле градиентов.
Для нахождения градиента функции
в заданной точке
используют формулу:
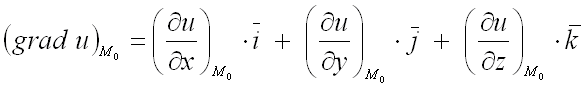
Свойства
градиента
1. Производная
в данной точке по направлению вектора
имеет наибольшее значение, если направление вектора
совпадает с направлением градиента. Это наибольшее значение производной равно
.
2. Производная
по направлению вектора, перпендикулярного к вектору ,
равна нулю.
Примеры
решения задач
Пример 1.
Найти производную от функции
в точке
по направлению вектора .
Решение.
Для решения задачи воспользуемся
формулой для нахождения производной от функции
в заданной точке
по направлению вектора :
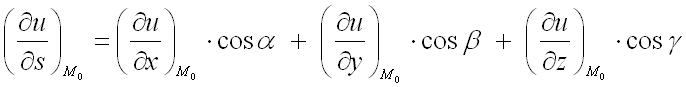
где
– направляющие косинусы вектора ,
которые вычисляются по формулам:
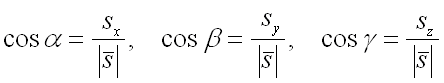
По условию задачи вектор
имеет координаты .
Тогда его длина равна:
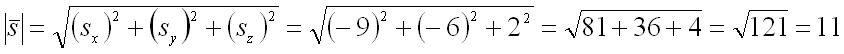
Следовательно, для направляющих косинусов вектора получим следующие значения:
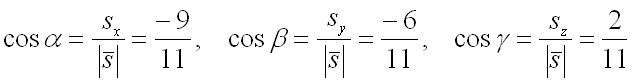
Далее для решения задачи необходимо найти все частные производные первого порядка
от функции :
Вычислим значения этих частных производных первого порядка в точке :
В заключении подставим полученные значения для направляющих косинусов вектора
и значения частных производных первого порядка от функции в
точке
в формулу для нахождения производной по направлению в заданной точке:
Ответ: производная от функции
в точке
по направлению вектора
равна 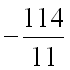
Пример 2.
Найти градиент функции
в точке 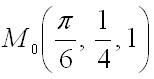
Решение.
Поскольку градиентом функции
называется вектор, проекциями которого на оси координат являются значения частных
производных этой функции в соответствующей точке, то для решения задачи сначала
найдем все частные производные первого порядка от заданной функции:
Далее вычислим значения этих частных производных первого порядка в точке 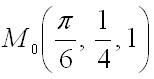
Подставим полученные значения в формулу градиента функции
в заданной точке :
.
Ответ: градиент функции
в точке
равен 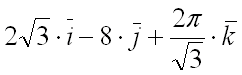
Пример 3.
Найти производную функции
в точке
по направлению градиента функции
в той же точке.
Решение.
Для нахождения производной
от функции
в заданной точке
по направлению вектора
используют формулу:
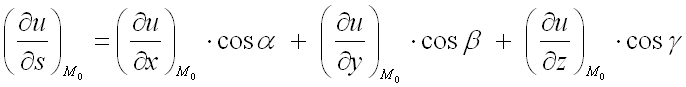
где
– направляющие косинусы вектора ,
которые вычисляются по формулам:
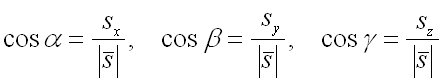
В данном случае вектор совпадает
с градиентом функции
в точке 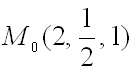
.
Следовательно, для решения задачи необходимо найти значения всех частных производных
первого порядка от функции
в точке ,
а также координаты и длину градиента функции
в той же точке.
Вычислим значения частных производных первого порядка от функции
в точке :
Для нахождения координат вектора ,
равного градиенту функции
в заданной точке ,
вычислим значения частных производных первого порядка от функции
в этой точке:
Длина вектора равна: 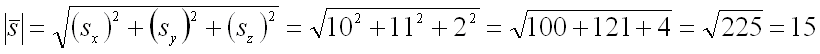
Найдем направляющие косинусы вектор по формулам:
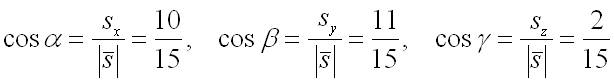
Подставим полученные значения в формулу для нахождения производной от функции
в заданной точке
по направлению вектора :
Ответ: производная функции
в точке 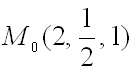
направлению градиента функции
в той же точке равна 1.
Задания
для самостоятельной работы
1.
Найти производную функции
в точке
по направлению вектора .
Ответ: .
2. Найти производную функции
в точке
по направлению вектора .
Ответ: .
3. Найти производную функции
в точке
по направлению вектора .
Ответ: .
4. Найти градиент функции
в точке 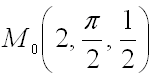
Ответ: .
5. Найти градиент функции
в точке .
Ответ: 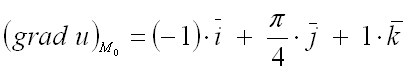
6. Найти градиент функции
в точке 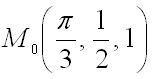
Ответ:
.
Градиент функции
Как найти?
Постановка задачи
Найти градиент функции $ f(x,y,z) $ в точке $ M(x_0,y_0,z_0) $
План решения
Градиент функции $ f(x,y,z) $ — это вектор, каждая координата которого является частной производной первого порядка этой функции:
$$ grad f = frac{partial f}{partial x} overline {i} + frac{partial f}{partial y} overline{j} + frac{partial f}{partial z} overline {k} $$
- Берём частные производные первого порядка от функции $ f(x,y,z) $:
$$ frac{partial f}{partial x}, frac{partial f}{partial y}, frac{partial f}{partial z} $$ - Вычисляем полученные производные в точке $ M(x_0,y_0,z_0) $:
$$ frac{partial f}{partial x} bigg |_{M(x_0,y_0,z_0)}, frac{partial f}{partial y} bigg |_{M(x_0,y_0,z_0)}, frac{partial f}{partial z} bigg |_{M(x_0,y_0,z_0)} $$ - Подставляем, полученные данные в формулу градиента функции:
$$ grad f bigg |_M = frac{partial f}{partial x} bigg |_M overline{i} + frac{partial f}{partial y} bigg |_M overline{j} + frac{partial f}{partial z} bigg |_M overline{k} $$
Примеры решений
| Пример 1 |
| Найти градиент функции $ u = x + ln (z^2+y^2) $ в точке $ M(2,1,1) $ |
| Решение |
|
Находим частные производные первого порядка функции трёх переменных: Вычисляем значение производных в точке $ M(2,1,1) $: $$ frac{partial f}{partial x} bigg |_{M(2,1,1)} = 1 $$ $$ frac{partial f}{partial y} bigg |_{M(2,1,1)} = frac{2 cdot 1}{1^2+1^2} = frac{2}{2}=1 $$ $$ frac{partial f}{partial z} bigg |_{M(2,1,1)} = frac{2cdot 1}{1^2 + 1^2} = frac{2}{2}=1 $$ Подставляем в формулу градиента функции полученные данные: $$ grad f = 1 cdot overline{i} + 1 cdot overline{j} + 1 cdot overline{k} = overline{i}+overline{j}+overline{k} $$ Запишем ответ в координатной форме: $$ grad f = overline{i}+overline{j}+overline{k} = (1,1,1) $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ grad f = (1,1,1) $$ |
| Пример 2 |
| Найти градиент функции $ u = sin(x+2y)+2sqrt{xyz} $ в точке $ M bigg (frac{pi}{2},frac{3pi}{2},3 bigg ) $ |
| Решение |
|
Находим частные производные: $$ frac{partial f}{partial x} = cos(x+2y) + frac{yz}{sqrt{xyz}} $$ $$ frac{partial f}{partial y} = 2cos(x+2y) + frac{xz}{sqrt{xyz}} $$ $$ frac{partial f}{partial z} = frac{xy}{sqrt{xyz}} $$ Вычисляем значения производных в точке $ M bigg (frac{pi}{2},frac{3pi}{2},3 bigg ) $: $$ frac{partial f}{partial x} bigg |_{M(frac{pi}{2},frac{3pi}{2},3)} = cos(frac{pi}{2}+3pi)+ frac{frac{9pi}{2}}{sqrt{frac{9pi^2}{4}}} = cos frac{7pi}{2} + sqrt{9} = 3 $$ $$ frac{partial f}{partial y} bigg |_{M(frac{pi}{2},frac{3pi}{2},3)} = 2 cos(frac{pi}{2}+3pi) + frac{frac{3pi}{2}}{sqrt{frac{9pi^2}{4}}} = 2 cos frac{7pi}{2} + 1 = 2 cdot 0 + 1 = 1 $$ $$ frac{partial f}{partial y} bigg |_{M(frac{pi}{2},frac{3pi}{2},3)} = frac{frac{3pi^2}{4}}{sqrt{frac{9pi^2}{4}}} = sqrt{frac{pi^2}{4}} = frac{pi}{2} $$ Подставляем вычисленные недостающие данные в формулу и получаем: $$ grad f = 3 cdot overline{i}+ 1 cdot overline{j} + frac{pi}{2} cdot overline{k} = 3overline{i}+overline{j}+frac{pi}{2} overline{k} $$ Записываем ответ в координатной форме: $$ grad f = (3,1,frac{pi}{2}) $$ |
| Ответ |
| $$ grad f = (3,1,frac{pi}{2}) $$ |
Содержание:
- Скалярное поле
- Векторный анализ
По этой ссылке вы найдёте полный курс лекций по математике:
Если в каждой точке пространства или части пространства определено значение некоторой величины, то говорят, что задано поле данной величины. Поле называется скалярным, если рассматриваемая величина скалярна, т.е. вполне характеризуется своим числовым значением. Например, поле температур.
Скалярное поле
Скалярное поле задается скалярной функцией точки и = /(М). Если в пространстве введена декартова система координат, то и есть функция трех переменных х, yt z — координат точки М: Определение. Поверхностью уровня скалярного поля называется множество точек, в которых функция f(M) принимает одно и то же значение. Уравнение поверхности уровня Пример 1. Найти поверхности уровня скалярного поля ВЕКТОРНЫЙ АНАЛИЗ Скалярное поле Поверхности и линии уровня Производная по направлению.
Производная Градиент скалярного поля Основные свойства градиента Инвариантное определение градиента Правила вычисления градиента -4 Согласно определению уравнением поверхности уровня будет . Это уравнение сферы (с Ф 0) с центром в начале координат. Скалярное поле называется плоским, если во всех плоскостях, параллельных некоторой плоскости, поле одно и то же.
Если указанную плоскость принять за плоскость хОу, то функция поля не будет зависеть от координаты z, т. е. будет функцией только аргументов х и у, Плоское поле можно характеризовать помощьюлиний уровня — множестваточек плоскости, в которых функция /(ж, у) имеетодно и тоже значение. Уравнение линии уровня — Пример 2.
Найти линии уровня скалярного поля Линии уровня задаются уравнениями При с = 0 получаем пару прямых получаем семейство гипербол (рис. 1). 1.1. Производная по направлению Пусть имеется скалярное поле, определяемое скалярной функцией и = /(Af). Возьмем точку Afo и выберем направление, определяемое вектором I. Возьмем другую точку М так, чтобы вектор М0М был параллелен вектору 1 (рис. 2). Обозначим длину вектора МоМ через А/, а приращение функции /(Af) — /(Afo), соответствующее перемещению Д1, через Ди.
Отношение определяет среднюю скорость изменения скалярного поля на единицу длины поданному направлению Пусть теперь стремится к нулю так, чтобы вектор М0М все время оставался параллельным вектору I. Определение. Если при Д/ О существует конечный предел отношения (5), то его называют производной функции в данной точке Afo поданному направлению I и обозначают символом зг!^ . Так что, по определению, Это определение не связано с выбором системы координат, т. е. носит**вариантный характер.
Найдем выражение для производной по направлению в декартовой системе координат. Пусть функция / дифференцируема в точке . Рассмотрим значение /(Af) в точке . Тогда полное приращение функции можно записать в следующем виде: где а символы означают, что частные производные вычислены в точке Afo. Отсюда Здесь величины jfi, , ^ суть направляющие косинусы вектора . Так как векторы МоМ и I сонаправлены , то их направляющие косинусы одинаковы:
Так как M Afo, осгавая сь все время на прямой, параллельной вектору 1, то углы постоянные потому Окончательно из равенств (7) и (8) получаем Эамуан ис 1. Частные производные , являются производными функции и по направлениям координатныхосей ссчлвешне нно- Пример 3. Найти производную функции по направлению к точке Вектор имеет длину .
Его направляющие косинусы: По формуле (9) будем иметь Тот факт, что , означает, что скалярное поле в точке в данном направлении возраста- Для плоского поля производная по направлению I в точке вычисляется по формуле где а — угол, образованный вектором I с осью Ох. Зммчмм 2. Формула (9) для вычисления производной по направлению I в данной точке Afo остается в силе и тогда, когда точка М стремится к точке Мо по кривой, для которой вектор I является касательным в точке ПрИШр 4.
Вычислить производную скалярного поля в точке Afo(l, 1). принадлежащей параболе по направлению этой кривой (в направлении возрастания абсциссы). Направлением ] параболы в точке считается направление касательной к параболе в этой точке (рис.3). Пусть касательная к параболе в точке Afo образует с осью Ох угол о.
Тогда откуда направляющие косинусы касательной Вычислим значения и в точке . Имеем Теперь по формуле (10) получаем.
Найти производную скалярного поля в точке по направлению окружности Векторное уравнение окружности имеет вид . Находим единичный вектор т касательной к окружности Точке соответствует значение параметра Значение г в точке Afo будет равно Отсюда получаем направляющие косинусы касательной к окружности в точке Вычислим значения частных производных данного скалярного поля в точке Значит, искомая производная .
Возможно вам будут полезны данные страницы:
Градиент скалярного поля Пусть скалярное поле определяется скалярной функцией которая предполагается дифференцируемой. Определение. Градиентом скалярного поля » в данной точке М называется вектор, обозначаемый символом grad и и определяемый равенством Ясно, что этот вектор зависиткак от функции /, так и отточки М, в которой вычисляется ее производная.
Пусгь 1 — единичный вектор в направлении Тогда формулу дл я производной по направлению можно записать в следующем виде: . тем самым производная от функ ии и по направлению 1 равна скалярному произведению градиента функ ии и(М) на орт 1° направления I. 2.1. Основные свойства градиента Теорема 1.
Градиент скалярного поля перпендикулярен к поверхности уровня (или к линии уровня, если поле плоское). (2) Проведем через произвольную точку М поверхность уровня и = const и выберем на этой поверхности гладкую кривую L, проходящую через точку М (рис. 4). Пусть I — векгор, касательный к кривой L в точке М. Так как на поверхности уровня и(М) = и(М|) для любой точки Мj е L, то С другой стороны, = (gradu, 1°). Поэтому .
Это означает, что векторы grad и и 1° ортогональны, Итак, векгор grad и ортогонален к любой касательной к поверхности уровня в точке М. Тем самым он ортогонален к самой поверхности уровня в точке М. Теорема 2. Градиент направлен в сторону возрастания функции поля. Ранее мы доказали, что градиент скалярного поля направлен по нормали к поверхности уровня, которая может быть ориентирована либо в сторону возрастания функции и(М), либо в сторону ее убывания.
Векторный анализ
Обозначим через п нормальк поверхности уровня, ориентированную в сторону возрастания функции ti(M), и найдем производную функции и в направлении этой нормали (рис. 5). Имеем Так как по условию рис.5 и поэтому ВЕКТОРНЫЙ АНАЛИЗ Скалярное поле Поверхности и линии уровня Производная по направлению Производная Градиент скалярного поля Основные свойства градиента Инвариантное определение градиента Правила вычисления градиента Отсюда следует, что grad и направлен в ту же сторону, что и выбранная нами нормаль п, т. е. в сторону возрастания функции и(М).
Теорема 3. Длина градиента равна наибольшей производной по направлению в данной точке поля, (здесь шах $ берется по всевозможным направлениям в данной точке М паю). Имеем где — угол между векторами 1 и grad п. Так как наибольшее значени Пример 1. Найти направление наибольшего иэмонония скалярного поля в точке а также величину этого наибольшего изменения в указанной точке. Направление наибольшего изменения скалярного поля указывается вектором .
Имеем так что Этот вектор определяет направление наибольшего возрастания поля в точко . Величина наибольшого изменения поля в этой точке равна 2.2. Инвариантное определение градиента Величины, характеризующие свойства изучаемого объекта и не зависящие от выбора системы координат, называются инвариантами данного объекта.
Например, длина кривой — инвариант этой кривой, а угол касательной к кривой с осью Ох — не инвариант. Основываясь на доказанных выше трех свойствах градиента скалярного поля, можно дать следующее инвариантное определение градиента. Определение. Градиент скалярного поля есть вектор, направленный по нормали к поверхности уровня в сторону возрастания функции поля и имеющий длину, равную наибольшей производной по направлению (в данной точке).
нормали, направленный в сторону возрастания поля. Тогда Пример 2. Найти градиент расстояния — некоторая фиксированная точка, a M(x,y,z) — текущая. 4 Имеем где — единичный вектор направления . Правила вычисления градиента где с — постоянное число. Приведенные формулы получаются непосредственно из определения градиента и свойств производных.
По правилу дифференцирования произведения Доказательство аналогично доказательству свойства Пусть F(и) — дифференцируемая скалярная функция. Тогда 4 По определению фадиента имеем Применим ко всем слагаемым правой части правило дифференцирования сложной функции. Получим В частности, Формула (6) следует из формулы Пример 3. Майти производную по направлению радиус-воктора г от функции По формуле (3) а по формуле В результате получим, что Пример 4.
Пусть дано плоское скалярное поле — расстояния от некоторой точки плоскости до двух фиксированных точек этой плоскости. Рассмотрим произвольный эллипс с фокусами Fj и F] и докажем, что всякий луч свота, вышедший из одного фокуса эллипса, после отражения от эллипса попадает в другой его фокус. Линии уровня функции (7) суть ВЕКТОРНЫЙ АНАЛИЗ Скалярное поле Поверхности и линии уровня Производная по направлению.
Производная Градиент скалярного поля Основные свойства градиента Инвариантное определение градиента Правила вычисления градиента Уравнения (8) описывают семейство эллипсов с фокусами в точках F) и Fj. Согласно результату примера 2 имеем Тем самым градиент заданного поля равен вектору PQ диагонали ромба, построенного на ортах г? и радиус-векторов. проведенных к точке Р(х, у) из фокусов F| и Fj, и значит, лежит на биссектрисе угла можду этими радиус-векторами (рис. 6).
По тооромо 1 градиент PQ перпендикулярен к эллипсу (8) в точке. Следова- Рис.6 тельно. нормаль к эллипсу (8) в любой ого точке делит пополам угол между радиус-векторами, проведенными в эту точку. Отсюда и из того, что угол падения равон углу отражения, получаем: луч света, вышедший из одного фокуса эллипса, отразившись от него, непременно попадает в другой фокус этого эллипса.
Лекции:
- Система тригонометрических уравнений
- Формула дисперсии
- Криволинейный интеграл 2 рода
- Замечательные пределы, содержащие тригонометрические функции
- Уравнение в полных дифференциалах
- Частные производные первого порядка
- Найти сходимость ряда
- Площади фигур
- Производные высших порядков. Формула Тейлора
- Статистические показатели